Теоретические основы химической технологии, 2023, T. 57, № 1, стр. 3-15

Математическое моделирование процессов разделения методами жидкость-жидкостной хроматографии

А. Е. Костанян^a, *, А. А. Вошкин^a

^a Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия

Поступила в редакцию 23.09.2022
После доработки 25.10.2022
Принята к публикации 25.10.2022

EDN: BOSZPG
DOI: 10.31857/S0040357123010098

Аннотация

Для практической реализации новых высокоэффективных методов жидкость-жидкостной хроматографии необходимо предварительное математическое моделирование применительно к условиям разрабатываемого процесса разделения, включая его аппаратурное оформление. Настоящая работа посвящена теоретическому анализу двух подходов к математическому описанию процессов жидкость-жидкостной хроматографии: 1) на основе решения уравнений материального баланса модели каскада равновесных ступеней; 2) использование распределения Гаусса для описания выходных профилей концентраций компонентов разделяемой смеси. Показано, что при числе равновесных ступеней (эффективности хроматографической установки) N ≥ 50, для математического моделирования процессов разделения можно использовать более простые зависимости, полученные на основе распределения Гаусса. Для условий, когда эффективность хроматографической установки N < 50, получены зависимости на основе модели равновесных ступеней для математического моделирования процессов разделения различными методами жидкость-жидкостной хроматографии.

Ключевые слова: математическое моделирование экстракционных процессов разделения, жидкостная экстракция, методы жидкость-жидкостной хроматографии

ВВЕДЕНИЕ

Жидкостная хроматография без твердого носителя, известная в научной литературе как жидкостная хроматография со свободной неподвижной фазой (ЖХСНФ) [1, 2], противоточная (countercurrent) и центробежная (centrifugal) хроматография [3–27], применяется главным образом для разделения фармацевтических соединений, полученных из растительного сырья, в аналитических и препаративных целях [3, 7, 9, 20–24]. Известны также исследования, направленные на применение методов жидкость-жидкостной хроматографии для разделения неорганических соединений в промышленном масштабе, в частности в гидрометаллургии, с использованием экстракционных аппаратов – каскада смесительно-отстойных экстракторов [4, 5, 12].

Подвижность обеих фаз в процессах жидкость-жидкостной хроматографии позволяет создавать различные методы (схемы и режимы) для решения конкретных задач разделения. Для реализации этих методов на практике необходимо математическое моделирование применительно к условиям разрабатываемого процесса разделения, включая его аппаратурное оформление. Математическое моделирование процессов хроматографии обычно базируется на двух типах гидродинамических моделей: дискретной – ячеечной (каскад ступеней идеального перемешивания) и непрерывной – диффузионной. При относительно не большой интенсивности продольного перемешивания в аппарате моделирование на основе дискретной и непрерывной моделей дает практически идентичные результаты. При этом математический аппарат ячеечной модели существенно проще, поэтому она чаще всего и применяется в виде каскад из N равновесных ступеней. Приводимый ниже анализ хроматографических процессов разделения также базируется на этой модели. В зависимости от эффективности хроматографической установки, измеряемой количеством теоретических (равновесных) ступеней (числом теоретических тарелок) N, возможны два подхода к выводу теоретических зависимостей, необходимых для математического моделирования процессов разделения [17]: 1 – решение уравнений математической модели; 2 – использование распределения Гаусса для описания выходных профилей концентраций компонентов разделяемой смеси.

Решение уравнений материального баланса модели каскада равновесных ступеней для условий обычной элюентной хроматографии имеет вид [17, 27]:

(1)

$X\left( t \right) = \frac{x}{{\bar {x}}} = \frac{{{{N}^{N}}{{a}^{N}}}}{{\left( {N - 1} \right)!}}{{t}^{{N - 1}}}\exp ( - aNt),~$

где $a = \frac{1}{{1 - S + S{{K}_{D}}}}$ – безразмерный параметр; $X = {x \mathord{\left/ {\vphantom {x {\bar {x}}}} \right. \kern-0em} {\bar {x}}}$ – безразмерная концентрация компонента с коэффициентом распределения K_D (K_D = = y/x = const: x – концентрация в подвижной фазе, y – концентрация в неподвижной фазе); $\bar {x} = {Q \mathord{\left/ {\vphantom {Q {{{V}_{c}}}}} \right. \kern-0em} {{{V}_{c}}}}$ – средняя концентрация компонента в хроматографическом устройстве после ввода пробы; Q – количество компонента K_D в пробе; V_c – объем хроматографического устройства; $t = \frac{{\tau F}}{{{{V}_{c}}}}$ – безразмерное время; F – объемная скорость подвижной фазы; S – доля объема, занимаемая неподвижной фазой в хроматографическом устройстве; τ – время.

Второй подход проще. Он позволяет получать более простые и удобные для расчетов зависимости в том числе и для сложных методов хроматографии. Распределение Гаусса описывается двумя безразмерными параметрами: первым начальным (t_R) и вторым центральным (σ²) моментами:

(2)

$X\left( t \right) = \frac{x}{{\bar {x}}} = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left[ { - \frac{{{{{({{t}_{R}} - t)}}^{2}}}}{{2{{\sigma }^{2}}}}} \right].$

Зависимости для моментов функции распределения (хроматографического пика) можно вывести путем преобразования дифференциальных уравнений модели каскада равновесных ячеек в систему алгебраических уравнений, содержащих моменты вместо концентраций [17]. Таким путем можно получить следующие зависимости для условий обычной элюентной хроматографии:

(3)

${{t}_{R}} = \frac{1}{a},~$

(4)

${{\sigma }^{2}} = \frac{1}{{N{{a}^{2}}}}.$

Уравнения (1) и (2) описывают распределение времени пребывания в хроматографическом устройстве компонента с коэффициентом распределения K_D т.е. пик (хроматограмму) одного вещества. Для описания нормированной хроматограммы многокомпонентной смеси можно использовать зависимость:

(5)

${{X}_{c}}\left( t \right) = \mathop \sum \limits_1^m {{q}_{i}}{{X}_{i}}\left( t \right),$

где X_nс(t) – нормированная суммарная концентрация всех (m) компонентов смеси; X_i(t) – концентрации отдельных компонентов, рассчитываются по уравнению (1) или (2); q_i – доли отдельных компонентов в пробе.

Отметим, что для нормирования концентраций X_i(t) в уравнениях (1), (2) и (5) используется величина средней концентрации одного компонента, а для нормирования суммарной концентрации X_c(t) в уравнении (5) используется величина общей средней концентрации всех компонентов в колонке после ввода пробы.

Целью настоящей работы было сравнение двух вышеуказанных подходов к математическому описанию процессов разделения методами жидкостно-жидкостной хроматографии и определение уравнений, применимых для моделирования процессов хроматографического разделения в различных условиях их реализации.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ЖИДКОСТЬ-ЖИДКОСТНОЙ ХРОМАТОГРАФИИ

Как отмечалось выше, жидкостно-жидкостная хроматография располагает различными методами, которые позволяют значительно повысить эффективность процесса разделения. Здесь мы рассмотрим теоретические зависимости, применимые для моделирования процессов обычной элюентной, рециркуляционной и рециркуляционно-противоточной хроматографии.

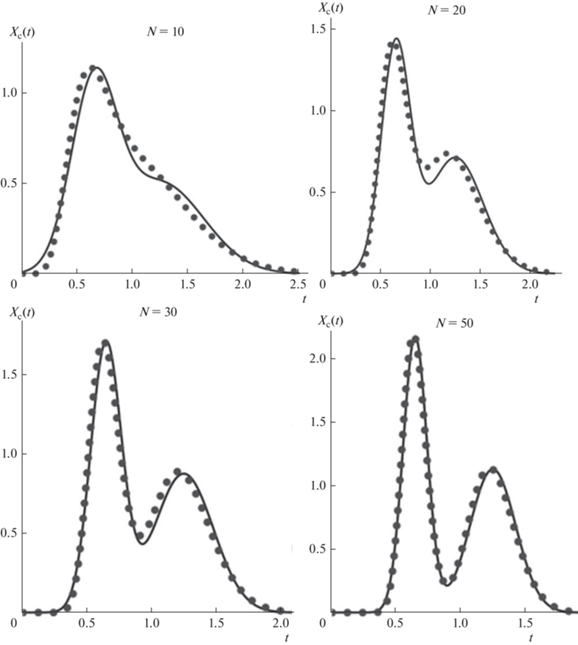
Процессы разделения методом элюентной жидкостно-жидкостной хроматографии. На рис. 1 для условий однократного ввода пробы сопоставлены хроматографические пики компонентов бинарной смеси (K_D1= 0.3, K_D2= 1.5), рассчитанные по уравнениям (1) и (2), при проведении процесса разделения в колонках различной эффективности. На рис. 2 приведены хроматограммы, рассчитанные по уравнениям (1), (2) и (5) для тех же условий процесса разделения при одинаковом содержании компонентов в пробе (q₁ = q₁). Как видно, при эффективности колонки 10, 20 и 30 теоретических ступеней имеется заметное расхождение между результатами расчета по точной (1) и приближенной (2) зависимостям. Однако уже при N = 50, расчет по обеим зависимостям приводит к практически одинаковым результатам.

Рис. 1.

Хроматографические пики компонентов бинарной смеси (K_D1 = 0.3, K_D2 = 1.5), рассчитанные по уравнениям (1) – сплошные линии и (2) – точки, при проведении процесса разделения в колонках различной эффективности при S = 0.5.

Рис. 2.

Хроматограммы бинарной смеси (K_D1 = 0.3, K_D2 = 1.5), рассчитанные по уравнениям (1) – сплошные линии, (2) – точки (2) и (5) при одинаковом содержании компонентов в пробе (q₁ = q₁) и S = 0.5.

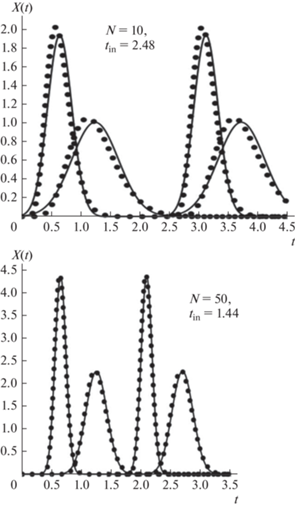
Для моделирования непрерывных процессов хроматографического разделения (при многократном вводе пробы) необходимо иметь теоретическое описание пиков компонентов после двух последовательных вводов пробы. Для описания пиков первой пробы можно использовать уравнения (1) или (2), а для пиков второй пробы уравнения (6) или (7):

(6)

$X\left( t \right) = \frac{x}{{\bar {x}}} = \frac{{{{N}^{N}}{{a}^{N}}}}{{\left( {N - 1} \right)!}}{{\left( {t - {{t}_{{in}}}} \right)}^{{N - 1}}}\exp [ - aN\left( {t - {{t}_{{in}}}} \right)],$

(7)

$X\left( t \right) = \frac{x}{{\bar {x}}} = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left[ { - \frac{{{{{({{t}_{R}} + {{t}_{{in}}} - t)}}^{2}}}}{{2{{\sigma }^{2}}}}} \right],$

где t_in – интервал между вводом в хроматографическое устройство первой и второй пробы. Минимальный интервал, обеспечивающий разделение соседних хроматограмм определяется уравнением [28]:

(8)

${{t}_{{inm}}} = 3\left( {{{\sigma }_{l}} + {{\sigma }_{h}}} \right) - \frac{1}{{{{a}_{l}}}} + \frac{1}{{{{a}_{h}}}},$

где с нижним индексом h обозначены параметры для компонента пробы с максимальным коэффициентом распределения, а с нижним индексом l – параметры для компонента пробы с минимальным коэффициентом распределения.

Для рассмотренной выше бинарной смеси уравнение (8) с учетом формулы (4) можно преобразовать к виду:

(9)

${{t}_{{inm}}} = \frac{3}{{\sqrt N }}~\left( {\frac{1}{{{{a}_{1}}}} + \frac{1}{{{{a}_{2}}}}} \right) + \frac{1}{{{{a}_{2}}}} - \frac{1}{{{{a}_{1}}}}.$

На рис. 3 показаны хроматограммы после двух вводов пробы указанной бинарной смеси, рассчитанные с помощью уравнений (1), (2), (6), (7) и (9). Приведенные на рис. 3 результаты свидетельствуют о применимости уравнений (8), (9) для определения оптимального интервала между вводами проб в непрерывных процессах разделения как при точных, так и при приближенных методах математического моделирования.

Рис. 3.

Хроматограммы бинарной смеси (K_D1 = 0.3, K_D2 = 1.5) после двух вводов пробы, рассчитанные с помощью уравнений (1) и (6) – сплошные линии, (2) и (7) – точки и уравнения (9).

Процессы разделения методом рециркуляционной жидкостно-жидкостной хроматографии. В процессах рециркуляционной хроматографии после ввода пробы выходящая из колонки подвижная фаза снова подается на ее вход, и проба многократно проходит через колонку, циркулируя в замкнутом контуре. После достижения требуемой степени разделения компонентов контур размыкается, и фракции разделенных компонентов выводятся из колонки с потоком подвижной фазы. Возможны две схемы организации процессов рециркуляционной хроматографии: с короткой линией рецикла, когда можно пренебречь влиянием системы рецикла; с длинной линией рецикла, когда необходимо учитывать влияние системы рецикла на процесс разделения. Когда в качестве промышленной хроматографической установки используется каскад смесительно-отстойных экстракторов, в случае первой схемы все ступени каскада соединены одинаково, образуя замкнутый контур, а в случае второй схемы первая и последняя ступени соединены специальным длинным трубопроводом рециркуляции [4].

Для первой схемы рециркуляционной жидкостно-жидкостной хроматографии аналог уравнения (1) имеет вид [29]:

(10)

$X\left( t \right) = \frac{x}{{\bar {x}}} = \frac{{{{{(Na)}}^{{nN}}}}}{{\left( {nN - 1} \right)!}}{{t}^{{nN - 1}}}\exp ( - aNt).$

В приближенной зависимости (2) формулы для моментов функции распределения (3) и (4) приобретают вид:

(11)

${{t}_{R}} = \frac{n}{a},~$

(12)

${{\sigma }^{2}} = \frac{n}{{N{{a}^{2}}}}.$

В уравнениях (10)–(12) n – количество циклов рециркуляции компонента пробы в контуре (номер цикла).

Уравнение (10) и уравнение (2) с параметрами, определяемыми по формулам (11) и (12), описывают пик компонента пробы после n циклов его циркуляции через колонку без учета истории процесса, т.е. влияния предыдущих циклов. С увеличением числа проходов пробы через хроматографическое устройство улучшается разделение компонентов, но одновременно происходит сближение и наложение хроматограмм соседних циклов, когда вышедшие из колонки компоненты с низкими коэффициентами распределения текущего цикла нагоняют, задержавшиеся в колонке, компоненты с высокими коэффициентами распределения предыдущего цикла. Эти противоположно направленные процессы учитываются в следующих зависимостях:

(13)

${{X}_{n}}\left( t \right) = \frac{{{{x}_{n}}\left( t \right)}}{{\bar {x}}} = \exp ( - aNt)\mathop \sum \limits_{i = 1}^n \frac{{{{{(Na)}}^{{iN}}}}}{{\left( {iN - 1} \right)!}}{{t}^{{iN - 1}}},$

(14)

${{X}_{n}}\left( t \right) = \frac{{{{x}_{n}}\left( t \right)}}{{\bar {x}}} = \frac{1}{{\sqrt {2\pi } }}\mathop \sum \limits_{i = 1}^n \frac{1}{{\sigma \left( i \right)}}\exp \left[ { - \frac{{{{{({{t}_{R}}\left( i \right) - t)}}^{2}}}}{{2{{\sigma }^{2}}\left( i \right)}}} \right],$

(15)

${{t}_{R}}\left( i \right) = \frac{i}{a},$

(16)

${{\sigma }^{2}} = \frac{i}{{N{{a}^{2}}}}.$

Точное (13) и приближенное (14) решения уравнений ячеечной модели описывают изменение во времени концентрации компонентов пробы на выходе из хроматографического устройства в течении всего процесса их циркуляции в замкнутом контуре от первого до последнего цикла n.

При количестве теоретических ступеней N > > 30–50 и/или числе циклов n > 2–3 могут возникнуть проблемы при использовании уравнения (13), связанные с вычислением факториалов. Чтобы обойти эти ограничения, используя формулу Стирлинга уравнение (13) можно преобразовать к виду:

(17)

$\begin{gathered} {{X}_{n}}\left( t \right) = \frac{x}{{\bar {x}}} = \\ = \frac{1}{t}\mathop \sum \limits_{i = 1}^n \sqrt {\frac{{iN - 1}}{{2\pi }}} {{\left( {\frac{{Nat}}{{iN - 1}}} \right)}^{{iN}}}\exp (iN - 1 - aNt)\,. \\ \end{gathered} $

В соответствие с физической природой процесса с течением времени (с увеличением количества циклов) вещество, введенное в замкнутый контур, равномерно распределится по всему контуру в обеих фазах в соответствие с его коэффициентом распределения. Эта закономерность иллюстрируется примерами, приведенными на рис. 4 и рис. 5, где показаны процессы распределения компонентов с коэффициентами распределения K_D = 0.8 и K_D = 5 в подвижной фазе при циркуляции пробы в замкнутом контуре, рассчитанные по зависимостям (14)–(17). Сопоставление концентрационных профилей, рассчитанных по уравнениям (14)–(16) и (17), подтверждает вывод о применимости зависимостей, полученных на основе распределения Гаусса, при N ≥ 50.

Рис. 4.

Профили концентрации компонента с коэффициентами распределения K_D = 0.8 в подвижной фазе на выходе из хроматографического устройства с короткой линией рецикла при циркуляции пробы в замкнутом контуре, рассчитанные по зависимостям (17) – сплошные линии и (14)–(16) – точки; S = 0.5.

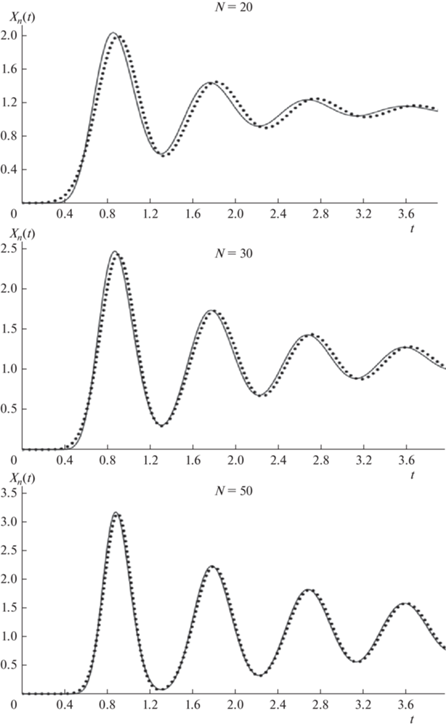
Рис. 5.

Профили концентрации компонента K_D = 5 в подвижной фазе на выходе из хроматографического устройства с короткой линией рецикла, рассчитанные по зависимостям (17) – сплошные линии и (14)–(16) – точки; S = 0.5.

Схема процесса с длинной линией рецикла. Если система рецикла выполнена в виде длинного трубопровода малого диаметра, соединяющего входной и выходной патрубки хроматографического устройства, то для упрощения математической модели можно допустить, что циркулирующий поток в трубопроводе рецикла движется в режиме идеального вытеснения. Для этих условий можно получить следующие зависимости, аналогичные уравнениям (10)–(17):

(18)

$\begin{gathered} X\left( t \right) = \frac{x}{{\bar {x}}} = \frac{{{{{(Na)}}^{{nN}}}}}{{\left( {nN - 1} \right)!}} \times \\ \times \,\,{{(t - \left( {n - 1} \right)b)}^{{nN - 1}}}\exp \left[ { - aN\left( {t - \left( {n - 1} \right)b} \right)} \right],~ \\ \end{gathered} $

(19)

${{t}_{R}} = \frac{n}{a} + b\left( {n - 1} \right),~$

(20)

$\sigma = \sqrt {\frac{n}{{N{{a}^{2}}}}} ,$

(21)

${{t}_{R}}\left( i \right) = \frac{i}{a} + b\left( {i - 1} \right),~$

(22)

$\sigma \left( i \right) = \sqrt {\frac{i}{{N{{a}^{2}}}}} ,$

(23)

$\begin{gathered} {{X}_{n}}\left( t \right) = \frac{x}{{\bar {x}}} = \mathop \sum \limits_1^{nN} \frac{{{{{(Na)}}^{{iN}}}}}{{\left( {iN - 1} \right)!}}{{(t - \left( {i - 1} \right)b)}^{{iN - 1}}} \times \\ \times \,\,\exp \left[ { - aN\left( {t - \left( {i - 1} \right)b} \right)} \right], \\ \end{gathered} $

(24)

$\begin{gathered} {{X}_{n}}\left( t \right) = \mathop \sum \limits_{i = 1}^n \sqrt {\frac{{iN - 1}}{{2\pi }}} {{\left( {\frac{{Na\left[ {t - \left( {i - 1} \right)b} \right]}}{{iN - 1}}} \right)}^{{iN}}} \times \\ \times \,\,\frac{{\exp \{ iN - 1 - Na\left[ {t - \left( {i - 1} \right)b} \right]~\} }}{{t - \left( {i - 1} \right)b}}, \\ \end{gathered} $

Уравнение (14) остается в силе с параметрами, определяемыми по формулам (21) и (22).

На рис. 6 показано изменение во времени концентрации компонента K_D = 1.5 на выходе из хроматографического устройства с длинным трубопроводом рецикла (b = 0.5) в течении трех циклов циркуляции (n = 3) в замкнутом контуре при различной эффективности хроматографического устройства (N = 10 и N = 50). Рис. 6 подтверждает сделанный выше вывод о применимости приближенного подхода (на основе распределения Гаусса) для моделирования процессов при N ≥ 50 и необходимости использования точных зависимостей при N < 50.

Рис. 6.

Профили концентрации компонента K_D = 1.5 на выходе из хроматографического устройства с длинным трубопроводом рецикла (b = 0.5) в течении трех циклов циркуляции (n = 3) в замкнутом контуре, рассчитанные по зависимостям (24) – сплошные линии и (14), (21) и (22) – точки; S = 0.5.

Процессы разделения методом рециркуляционно-противоточной жидкостно-жидкостной хроматографии. Рециркуляционный и метод благодаря многократной циркуляция пробы через хроматографическое устройство позволяют многократно повысить эффективность установок жидкость-жидкостной хроматографии. Путем комбинации этого метода с противоточным методом можно создать еще более эффективные рециркуляционно-противоточные процессы разделения. В общем случае процесс разделения проводится в противоточно-циклическом режиме, включающем периоды рециркуляции обеих фаз. Фракции разделенных компонентов выводятся из аппарата с фазами после периодов их рециркуляции. Возможны различные варианты реализации рассматриваемого метода жидкостно-жидкостной хроматографии для создания эффективных процессов применительно к различным задачам разделения. В работах [16, 17] разработана основанная на распределении Гаусса теория двухстадийного процесса, на первой стадии которого проводится разделение компонентов с низкими коэффициентами распределения в замкнутом контуре при циркуляции фазы “х”, а на второй стадии контур размыкается, и через удерживаемую в установке фазу “х” в обратном направлении прокачивается фаза “у”. На второй стадии с фазой “у” из установки выводятся разделенные фракции компонентов с высокими коэффициентами распределения. Для математического описания второй стадии такого процесса необходимо знать распределение концентраций компонентов в аппарате (устройстве) в конце первой стадии. На основе модели равновесных ступеней искомые зависимости можно получить в следующем виде:

Для схемы первой стадии с короткой линией рецикла. Точные зависимости:

(25)

$X\left( {t,k} \right) = \frac{{{{{(Na)}}^{{\left( {n - 1} \right)N + k}}}}}{{\left[ {\left( {n - 1} \right)N + k - 1} \right]!}}{{t}^{{\left( {n - 1} \right)N + k - 1}}}\exp ( - aNt),$

(26)

$\begin{gathered} {{X}_{n}}\left( {t,k} \right) = \\ = \mathop \sum \limits_{i = 1}^n \frac{{{{{(Na)}}^{{\left( {i - 1} \right)N + k}}}}}{{\left[ {\left( {i - 1} \right)N + k - 1} \right]!}}{{t}^{{\left( {i - 1} \right)N + k - 1}}}\exp ( - aNt). \\ \end{gathered} $

Приближенные зависимости на основе распределения Гаусса:

(27)

$\begin{gathered} X\left( {t,k} \right) = \frac{{Na}}{{\sqrt {2\pi \left[ {N\left( {n - 1} \right) + k} \right]} }} \times \\ \times \,\,\exp \left[ { - \frac{{{{{[N\left( {n - 1} \right) + k - aNt]}}^{2}}}}{{2\left[ {N\left( {n - 1} \right) + k} \right]}}} \right],~ \\ \end{gathered} $

(28)

$\begin{gathered} {{X}_{n}}\left( {t,k} \right) = \mathop \sum \limits_{i = 1}^n \frac{{Na}}{{\sqrt {2\pi \left[ {N\left( {i - 1} \right) + k} \right]} }} \times \\ \times \,\,\exp \left[ { - \frac{{{{{\left[ {N\left( {i - 1} \right) + k - aNt} \right]}}^{2}}}}{{2\left[ {N\left( {i - 1} \right) + k} \right]}}} \right]. \\ \end{gathered} $

Для схемы первой стадии с длинной линией рецикла. Точные зависимости:

(29)

$\begin{gathered} X\left( {t,k} \right) = \frac{{{{{(Na)}}^{{\left( {n - 1} \right)N + k}}}}}{{\left[ {\left( {n - 1} \right)N + k - 1} \right]!}} \times \\ \times \,\,{{\left[ {t - \left( {n - 1} \right)b} \right]}^{{\left( {n - 1} \right)N + k - 1}}}~\exp \left\{ { - aN[t - \left( {n - 1} \right)b} \right\}, \\ \end{gathered} $

(30)

$\begin{gathered} {{X}_{n}}\left( {t,k} \right) = \mathop \sum \limits_{i = 1}^n \frac{{{{{(Na)}}^{{\left( {i - 1} \right)N + k}}}}}{{\left[ {\left( {i - 1} \right)N + k - 1} \right]!}} \times \\ \times \,\,{{\left[ {t - \left( {i - 1} \right)b} \right]}^{{\left( {i - 1} \right)N + k - 1}}}~\exp \left\{ { - aN[t - \left( {i - 1} \right)b} \right\}. \\ \end{gathered} $

Приближенные зависимости:

(31)

$\begin{gathered} X\left( {t,k} \right) = \frac{{Na}}{{\sqrt {2\pi \left[ {N\left( {n - 1} \right) + k} \right]} }} \times \\ \times \,\,\exp \left[ { - \frac{{{{{[N\left( {n - 1} \right)\left( {1 + ab} \right) + k - aNt]}}^{2}}}}{{2\left[ {N\left( {n - 1} \right) + k} \right]}}} \right], \\ \end{gathered} $

(32)

$\begin{gathered} {{X}_{n}}\left( {t,k} \right) = \mathop \sum \limits_{i = 1}^n \frac{{Na}}{{\sqrt {2\pi \left[ {N\left( {i - 1} \right) + k} \right]} }} \times \\ \times \,\,\exp \left[ { - \frac{{{{{[N\left( {i - 1} \right)\left( {1 + ab} \right) + k - aNt)}}^{2}}}}{{2\left[ {N\left( {i - 1} \right) + k} \right]}}} \right].~ \\ \end{gathered} $

Точные (29), (30), (25), (26) и приближенные (27), (28), (31), (32) зависимости описывают изменение во времени концентрации компонентов пробы в ячейке k в течении процесса их циркуляции в замкнутом контуре. При заданном времени они описывают распределение концентраций компонентов в аппарате на первой стадии процесса разделения.

Следует отметить, что в уравнениях (1) и (2) статьи [17] допущена опечатка: в уравнении (1) пропущен член ${{t}^{{\left( {n - 1} \right)N + k - 1}}}$, а в уравнении (2) – член ${{t}^{{\left( {i - 1} \right)N + k - 1}}}$.

При значении k = N вышеприведенные уравнения описывают изменение во времени концентрации компонентов в фазе “х” на выходе из хроматографического устройства при циркуляции пробы в замкнутом контуре на первой стадии процесса разделения. Выходные профили концентраций в фазе “у” на второй стадии процесса можно описать уравнениями [16]:

(33)

$\begin{gathered} Y\left( t \right) = Y\left( {1,t} \right) = \\ = {{K}_{D}}{{e}^{{ - {{K}_{D}}aNt}}}\mathop \sum \limits_{k = 1}^N \frac{{{{{({{K}_{D}}aNt)}}^{{k - 1}}}}}{{\left( {k - 1} \right)!}}{{X}_{n}}\left( {k,{{t}_{x}}} \right), \\ \end{gathered} $

(34)

$\begin{gathered} Y\left( t \right) = {{K}_{D}}{{e}^{{ - {{K}_{D}}aNt}}}\mathop \sum \limits_{k = 1}^{50} \frac{{{{{({{K}_{D}}aNt)}}^{{k - 1}}}}}{{\left( {k - 1} \right)!}}{{X}_{n}}\left( k \right) + \\ + \,\,{{K}_{D}}\mathop \sum \limits_{k = 51}^N \frac{{{{{({{K}_{D}}aNt)}}^{{k - 1}}}}}{{\left( {k - 1} \right)}}\frac{{{{e}^{{k - 1 - {{K}_{D}}aNt}}}}}{{\sqrt {2\pi \left( {k - 1} \right)} }}{{X}_{n}}\left( k \right), \\ \end{gathered} $

где t – безразмерное время, определяемое как $t = {{\tau {{F}_{y}}} \mathord{\left/ {\vphantom {{\tau {{F}_{y}}} {{{V}_{c}}}}} \right. \kern-0em} {{{V}_{c}}}}$; время начала движения потока F_y фазы “у”,$\tau $ = 0; $Y = {y \mathord{\left/ {\vphantom {y {\bar {x}}}} \right. \kern-0em} {\bar {x}}}$ – нормированная концентрация компонента в y-фазе. Нумерация ячеек, как и во всех предыдущих уравнениях начинается со стороны подачи в устройство фазы “х”.

При N < 100 расчет следует вести по уравнению (33), при N > 100 – по уравнению (34). Член ${{X}_{n}}\left( k \right)~$ в уравнениях (33) и (35) описывает распределение концентрации в цепочке из N равновесных ячеек после завершения первой стадии разделения при t = t_x. Выражение для него можно получить, подставив в уравнения (26), (28), (30), (32) значение времени t = t_x. Так для хроматографического устройства с длинным трубопроводом рецикла из уравнений (30) и (32) получаем:

(35)

$\begin{gathered} {{X}_{n}}\left( k \right) = \mathop \sum \limits_{i = 1}^n \frac{{{{{(Na)}}^{{\left( {i - 1} \right)N + k}}}}}{{\left[ {\left( {i - 1} \right)N + k - 1} \right]!}} \times \\ \times \,\,{{\left[ {{{t}_{х}} - \left( {i - 1} \right)b} \right]}^{{\left( {i - 1} \right)N + k - 1}}}~\exp \left\{ { - aN[{{t}_{х}} - \left( {i - 1} \right)b} \right\}, \\ \end{gathered} $

(36)

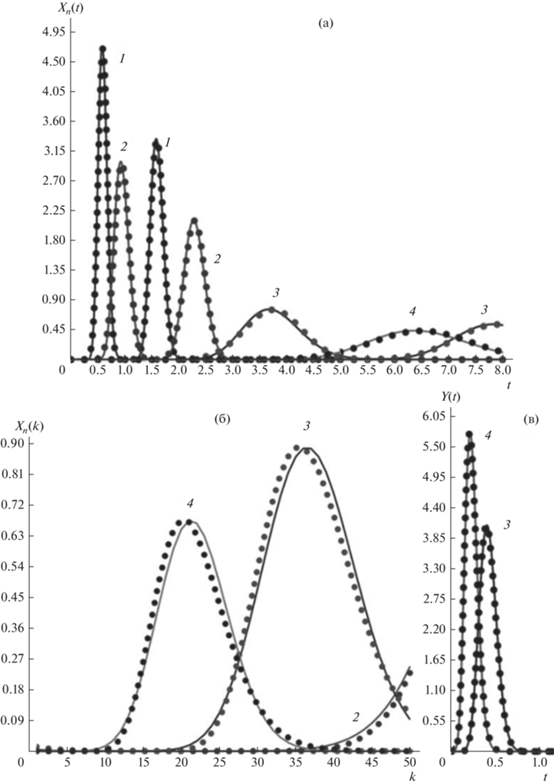
$\begin{gathered} {{X}_{n}}\left( k \right) = \mathop \sum \limits_{i = 1}^n \frac{{Na}}{{\sqrt {2\pi \left[ {N\left( {i - 1} \right) + k} \right]} }} \times \\ \times \,\,\exp \left[ { - \frac{{{{{[N\left( {i - 1} \right)\left( {1 + ab} \right) + k - aN{{t}_{х}})}}^{2}}}}{{2\left[ {N\left( {i - 1} \right) + k} \right]}}} \right],~ \\ \end{gathered} $

где k = 1, 2, 3, …, N.

На рис. 7 и рис. 8 сопоставлены выходные профили концентраций компонентов в фазе “х” (в ячейке N) на первой стадии процесса при циркуляции пробы, содержащей компоненты K_D1 = 0.2, K_D2 = 0.9, K_D3 = 6.5, K_D4 = 12, в течении двух циклов (n = 2), а также распределение концентраций в каскаде ячеек (N = 30 и N = 50) после завершения первой стадии при t = t_x и выходные профили концентраций в фазе “у” (в ячейке 1) на второй стадии, рассчитанные по точным (30), (33), (35) и приближенным (32), (33), (36) зависимостям. Как видно, несмотря на заметное расхождение концентрационных профилей в каскаде ячеек (в хроматографическом устройстве), рассчитанных по точной и приближенной зависимостям, выходные профили концентраций компонентов в обеих фазах идентичны при использовании точных и приближенных зависимостей, когда N = 50.

Рис. 7.

a – Выходные профили концентраций компонентов в фазе “х” (в ячейке N) на первой стадии процесса при циркуляции пробы, содержащей компоненты K_D1 = 0.2, K_D2 = 0.9, K_D3 = 6.5, K_D4 = 12, в течении двух циклов (n = 2); б – распределение концентраций в каскаде ячеек после завершения первой стадии при t = t_x; в – выходные профили концентраций в фазе “у” (в ячейке 1) на второй стадии, рассчитанные по точным (30), (33), (35) и приближенным (32), (33), (36) зависимостям. Параметры процесса: N = 30; S = 0.5; b = 0.6, t_x = 3.

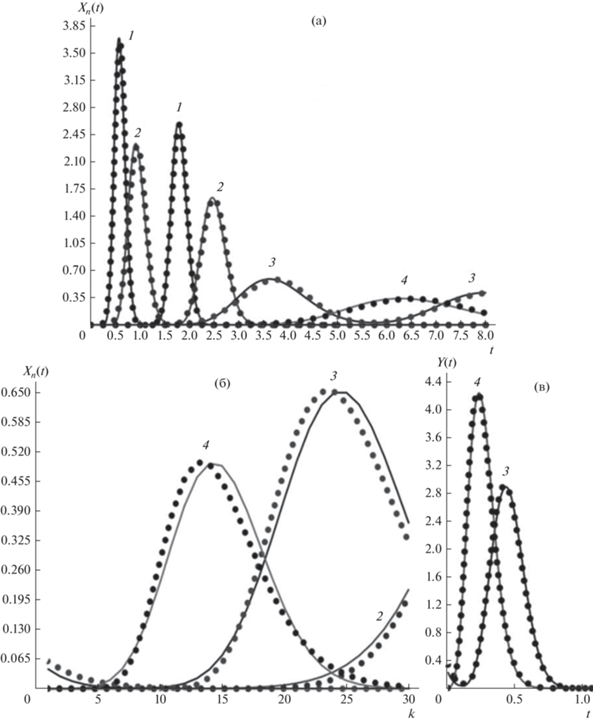
Рис. 8.

a – Выходные профили концентраций компонентов в фазе “х” на первой стадии процесса при циркуляции пробы K_D1 = 0.2, K_D2 = 0.9, K_D3 = 6.5, K_D4 = 12, в течении двух циклов (n = 2); б – распределение концентраций в каскаде ячеек после завершения первой стадии; в – выходные профили концентраций в фазе “у” на второй стадии, рассчитанные по точным (30), (33), (35) и приближенным (32), (33), (36) зависимостям. Параметры процесса: N = 50; S = = 0.5; b = 0.4, t_x = 2.7.

ЗАКЛЮЧЕНИЕ

Проведен теоретический анализ двух методов математического моделирования процессов жидкость-жидкостной хроматографии – на основе решения уравнений материального баланса модели теоретических (равновесных) ступеней и использование распределения Гаусса для описания выходных профилей концентраций компонентов разделяемой смеси. Установлено, что при эффективности хроматографической установки, измеряемой числом теоретических ступеней N ≥ 50, для математического моделирования процессов разделения методами жидкость-жидкостной хроматографии можно использовать более простые зависимости, полученные на основе распределения Гаусса.

Для условий, когда эффективности хроматографической установки N <5 0, получены точные зависимости на основе модели теоретических ступеней для математического моделирования процессов разделения различными методами жидкость-жидкостной хроматографии.

Работа выполнена при финансовой поддержке Минобрнауки России в рамках государственного задания ИОНХ РАН.

ОБОЗНАЧЕНИЯ

x	концентрация в подвижной фазе, мол. д.
y	концентрация в неподвижной фазе, мол. д.
K_D	коэффициент распределения
$\bar {x}$	средняя концентрация компонента в хроматографическом устройстве после ввода пробы, мол. д.
Q	количество компонента K_D в пробе
V_c	объем хроматографического устройства, мл
τ	время, с
S	доля объема, занимаемая неподвижной фазой в хроматографическом устройстве
F	объемная скорость подвижной фазы, мл/с
q	доля отдельного компонента в пробе
X	безразмерная концентрация компонента

ИНДЕКСЫ

i	отдельный компонент пробы
h	параметры для компонента пробы с максимальным коэффициентом распределения
l	параметры для компонента пробы с минимальным коэффициентом распределения

Список литературы

Федотов П. С., Марютина Т.А., Пичугин А.А., Спиваков Б.Я. Влияние кинетических свойств экстракционных систем на разделение некоторых элементов методом жидкостной хроматографии со свободной неподвижной фазой // Журн. неорг. химии. 1993. Т. 38. № 11. С. 1878.
Марютина Т.А., Федотов П.С., Спиваков Б.Я. Использование метода жидкостной хроматографии со свободной неподвижной фазой для концентрирования и разделения неорганических веществ. Двухфазные жидкостные системы // Журн. аналит. химии. 1997. Т. 52. № 12. С. 1263.
Berthod A., Maryutina T., Spivakov B., Shpigun O., Sutherland I.A. Countercurrent chromatography in analytical chemistry (IUPAC technical report) // PureAppl. Chem. 2009. V. 81. P. 355.
Костанян А.Е., Милевский Н.А., Вошкин А.А. Анализ процессов экстракционно-хроматографического разделения в каскаде смесительно-отстойных экстракторов // Теорет. основы хим. технологии. 2021. Т. 55. № 5. С. 559.
Костанян А.Е., Иванов В.К., Вошкин А.А. Теоретический анализ периодических процессов экстракционно-хроматографического разделения в замкнутом каскаде аппаратов // ДАН. Химия, науки о материалах. 2021. Т. 499. № 1. С. 53.
Kostanyan A.E., Voshkin A.A. Closed-loop recycling dual-mode counter-current chromatography with specified sample loading durations: Modeling of preparative and industrial-scale separations // Molecules. 2021. V. 26. Article 6561.
Guilois-Dubois S., Guyot S., Poupard P. Preparative isolation of apple flavan-3-ols monomers and oligomers using pH-zone-refining centrifugal partition chromatography combined with reversed-phase liquid chromatography // J. Chromatogr. A. 2021. V. 1653. Article 462382.
Li H., Zhang F., Jin Q., Zhu T. Preparative separation and purification of Cyclosporin D from fungus Hypoxylon Spp. by improved closed-loop recycling counter-current chromatography // J. Chromatogr. A. 2021. V. 1649. Article 462221.
He J.M., Huang J., Wu W.L., Mu Q. Unlimited recycling counter-current chromatography for the preparative separation of natural products: naph- thaquinones as examples // J. Chromatogr. A. 2020. V. 1626. Article 461368.
Kostanyan A., Martynova M. Modeling of two semi-continuous methods in liquid–liquid chromatography: Comparing conventional and closed-loop recycling modes // J. Chromatogr. A. 2020. V. 1614. Article 460735.
Kostanyan A.E., Belova V.V. Theoretical study of industrial scale closed-loop recycling counter-current chromatography separations // J. Chromatogr. A. 2020. V. 1633. Article 461630.
Kostanyan A.E., Galieva Z.N., Semenov A.A., Aldushkin A.V. Chromatographic behavior of six lanthanides on a centrifugal mixer-settler extractor cascade. // J. Chromatogr. A. 2020. V. 1634. Article 461686.
Kostanyan A.A., Voshkin A.A., Belova V.V. Analytical, Preparative, and Industrial-Scale Separation of Substances by Methods of Countercurrent Liquid-Liquid Chromatography // Molecules. 2020. V. 25. Article 6020.
Jerz G., Winterhalter P. The 10th International Conference on Countercurrent Chromatography held at Technische Universität Braunschweig, Braunschweig, Germany, August 1–3, 2018 // J. Chromatogr. A. 2020. V. 1617. Article 460698.
Morley R., Minceva M. Operating mode and parameter selection in liquid–liquid chromatography // J. Chromatogr. A. 2020. V. 1617. Article 460479.
Kostanya, A.E., Belova V.V. Closed-loop recycling dual-mode counter-current chromatography. A theoretical study // J. Chromatogr. A. 2019. V. 1588. P. 174.
Kostanyan A.E., Galieva Z.N. Modeling of closed-loop recycling dual-mode counter-current chromatography based on non-ideal recycling model // J. Chromatogr. A. 2019. V. 1603. P. 240.
Roehrer S., Minceva M. Evaluation of interapparatus separation method transferability in countercurrent chromatography and centrifugal partition chromatography // Separations. 2019. V. 6. P. 36.
Peng A., Hewitson P., Sutherland I., Chen L., Ignatova S. How changes in column geometry and packing ratio can increase sample load and throughput by a factor of fifty in counter-current chromatography // J. Chromatogr. A. 2018. V. 1580. P.120.
Friesen J.B., McAlpine J.B., Chen S.-N., Pauli G.F. The 9th International Countercurrent Chromatography Conference held at Dominican University, Chicago, USA, August 1–3, 2016 // J. Chromatogr. A. 2017. V. 1520. P. 1.
Ito Y. Golden rules and pitfalls in selecting optimum conditions for high-speed counter-current chromatography // J. Chromatogr. A. 2005. V. 1065. P. 145.
Conway W.D. Counter-current chromatography: Simple process and confusing terminology // J. Chromatogr. A. 2011. V. 1218. P. 6015.
Friesen J.B., McAlpine J.B., Chen S.-N., Pauli G.F. The 9th International Countercurrent Chromatography Conference held at Dominican University, Chicago, USA, August 1–3, 2016. // J. Chromatogr. A 2017. V. 1520. P. 1.
Ignatova S., Sutherland I. The 8th International Conference on Counter-current Chromatography held at Brunel University, London, UK, July 23–25, 2014 // J. Chromatography A. 2015. V. 1425. P. 1.
Kostanyan A.E., Voshkin A.A. Analysis of cyclic liquid chromatography // Theor. Found. Chem. Eng. 2011. V. 45. № 1. P. 68.
Kostanyan A.E., Voshkin A.A. Support-free pulsed liquid-liquid chromatography // J. Chromatogr. A. 2009. V. 1216. P. 7761.
Kostanyan A.E., Voshkin A.A., Kodin N.V. Controlled-cycle pulsed liquid–liquid chromatography. A modified version of Craig’s counter-current distribution // J. Chromatogr. A. 2011. V. 1218. P. 6135.
Kostanyan A.E. A simple and highly efficient counter-current chromatography method for the isolation of concentrated fractions of compounds based on the sequential sample loading technique: Comparative theoretical study of conventional multiple and intermittent sample loading counter-current chromatography separations // J. Chromatogr. A. 2021. V. 1647. Article 462163.
Kostanyan A.E. Simple equations to simulate closed-loop recycling liquid–liquid chromatography: ideal and non-ideal recycling models // J. Chromatogr. A. 2015. V. 1423. P. 71.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал