1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 57, № 1, 2023

Теоретические основы химической технологии, 2023, T. 57, № 1, стр. 16-21

Алгоритм обработки данных по теплофизическим свойствам фосфоритов методом решения обратной коэффициентной задачи теплопроводности

Академик РАН В. П. Мешалкин a, В. И. Бобков b, *, М. И. Дли b, В. А. Орехов b, Т. Б. Чистякова c

a Российский химико-технологический университет имени Д.И. Менделеева, Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия

b Национальный исследовательский университет “МЭИ”
г. Смоленск, Россия

c Санкт-Петербургский государственный технологический институт (технический университет)
Санкт-Петербург, Россия

* E-mail: vovabobkoff@mail.ru

Поступила в редакцию 07.11.2022
После доработки 17.11.2022
Принята к публикации 17.11.2022

Полный текст (PDF)

Аннотация

В данной работе предлагается алгоритм обработки экспериментальных данных по определению теплофизических свойств фосфоритов – теплоемкости и теплопроводности, использующий метод решения обратной коэффициентной задачи теплопроводности, которая сводится к программируемому нагреву, осложненному протеканием термически активируемых эндотермических реакций диссоциации карбонатов и управлению внутренним тепловым состоянием системы с распределенными параметрами. Рассматривается задача математического и компьютерного моделирования системы по обработке экспериментальных данных и обобщения основных зависимостей теплофизических свойств в диапазоне температур функционирования теплотехнологического оборудования термической обработки рудного сырья и практического химического состава фосфоритов методом решения обратной коэффициентной задачи теплопроводности. Параметрами управления являются теплопроводность и теплоемкость – коэффициенты в уравнении теплопроводности для пластины. Критерием оптимальности – принимается наименьшее отклонение полученного в вычислительном эксперименте по модели температурного распределения по толщине пластины от заданного. При решении задачи оптимизации используется метод скользящего допуска с оптимизацией способом деформируемого многогранника. В статье приводятся результаты, полученные в вычислительных экспериментах с использованием фосфатных сырьевых материалов. Представленные численные результаты хорошо согласуются с результатами натурных экспериментов, что подтверждает адекватность разработанной нами математической и компьютерной моделей, а также предлагаемого алгоритма решения обратной коэффициентной задачи теплопроводности.

ВВЕДЕНИЕ

Теплофизические свойства (ТФС) фосфоритов, фосфоросодержащего сырья, полупродуктов, изучены далеко недостаточно [1, 2]. Существенные различия в минералогическом и химическом составе фосфоросодержащих руд требуют проведения огромного количества натурных экспериментов, для нахождения основных закономерностей при описании теплофизических свойств при нагреве [3, 4]. Комплексность исследования ТФС увеличивается из-за физико-химических превращений, которые происходят при воздействии на сырье высоких температур в химико-энерготехнологических процессах сушки, обжига, спекания [5, 6]. Решение этих задач требует комплексного подхода к экспериментам по измерению свойств, учитывающего влияние всех факторов на ТФС, а также принятие во внимание композитной структуры фосфоритов [7, 8]. Имеющиеся экспериментальные данные по кинетике декарбонизации фосфоритов получены без учета структурных особенностей данного типа веществ [9]. Данные по ТФС фосфоритов получены лишь для многослойных засыпок без учета процессов диссоциации карбонатов, что имеет место в процессах обжига [10, 11]. Существующие методы измерения не учитывают особенностей, характерных для такого типа материалов, как фосфориты. Кинетика разложения карбонатов изучалась в режимах, близких к практическим скоростям нагрева для обжиговых машин, т.е. вдали от равновесия [12]. Для изучения кинетики использовалась автоматизированная термовесовая установка [13]. Подробное описание методики эксперимента и анализ результатов приведен в [14]. В этой работе определялась температура отнесения при обработке эксперимента по измерению кинетических параметров в условиях неизотермичности образца, приведены результаты замеров убыли веса фосфоритов при скоростях нагрева, совпадающих со скоростями нагрева кусков на обжиговых машинах. Использована методика измерения ТФС с учетом химического реагирования отдельных составляющих материала в виде минеральных вкраплений в основную массу минерала [15]. Ограничения, которые необходимо принимать во внимание, сводятся к использованию образцов по размерам больше определенного минимального размера, позволяющего включить влияние реагирующих образований в образце и учесть структуру материала, использованию лишь нестационарных методов нагрева пробы для фиксации дериватограммы, а также комплексности подхода для одновременного измерения кинетических и теплофизических характеристик [16].

Методика эксперимента по определению ТФС в режиме монотонного нагрева базируется на сравнительном методе, использующим систему образцов материалов, из которых один имеет известные теплофизические свойства [17]. Теоретической основой сравнительных методов комплексного определения ТФС в первом приближении являются решения уравнений теплопроводности для системы тел простейшей геометрической формы [18]. Нами использовалась симметричная система пластин. В эксперименте измерялись температуры на поверхности системы образцов, перепады температур в измеряемом образце, располагающимся снаружи и в эталонном образце, который находился внутри. Из решения уравнения теплопроводности для многослойной пластины с симметричным нагревом и пренебрежении краевыми эффектами получаются зависимости для расчета теплопроводности [19]. Причем эти соотношения справедливы лишь для небольших разностей температуры в образцах. Поскольку малые перепады температур при скоростях нагрева, характерных для реальных условий, возможно реализовать лишь для тонких образцов, что исключает учет структуры реагирующих вкраплений, требуется подход, позволяющий преодолеть эти противоречия [19]. Поэтому решением проблемы представляется использование идентификации коэффициентов уравнения теплопроводности на основе решения обратной задачи теплопроводности. В качестве эталона использовался плавленный кварц, теплофизические свойства которого с достаточной степенью точности известны в широком диапазоне температур [20]. Достаточно достоверные данные по ТФС фосфатного сырья в диапазоне температур, имеющим практическое значение, получены с применением методов монотонного нагрева и метода решения инверсной задачи теплопроводности, основанного на совместном решении уравнений теплопереноса и кинетики химических превращений с учетом наиболее существенных сопутствующих им явлений [21].

Обработка результатов эксперимента проводилась на основе решения обратной коэффициентной задачи теплопроводности [22]. Результаты исследований ТФС широкого спектра фосфоритов позволили создать базу данных по свойствам в широком диапазоне температур и объемных долей компонентов. Для выявления основных закономерностей, которым подчиняется поведение фосфатного сырья необходимо иметь достаточный объем информации для диапазона изменения температуры, химического и минералогического состава по теплопроводности, теплоемкости, термическому расширению, электропроводности, химической кинетике [23]. Поскольку результаты экспериментальных исследований ТФС фосфоритов и кинетики декарбонизации составили основу других исследований, здесь рассматриваются лишь задачи математического и компьютерного моделирования при обработке эксперимента и обобщения основных зависимостей ТФС для практического диапазона температур и химического состава [24].

Рассматривается обратная задача теплопроводности для плоской пластины, когда по известному измеренному температурному полю определяются коэффициенты уравнения ${{\rho }}{{C}_{p}}$, ${{\lambda }}$.

С учетом основных требований и допущений математическая формулировка задачи в одномерной постановке для плоского образца имеет вид:

(1)
$\left\{ \begin{gathered} \rho {{C}_{p}}\frac{{\partial T}}{{\partial \tau }} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right) - C_{1}^{0}Q_{1}^{{}}\frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }} - C_{2}^{0}Q_{2}^{{}}\frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }}; \hfill \\ \frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }} = {{k}_{{01}}}\exp \left( { - \frac{{{{E}_{1}}}}{{RT}}} \right){{f}_{1}}\left( {{{\alpha }_{1}}} \right); \hfill \\ \frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }} = {{k}_{{02}}}\exp \left( { - \frac{{{{E}_{2}}}}{{RT}}} \right){{f}_{2}}\left( {{{\alpha }_{2}}} \right). \hfill \\ \end{gathered} \right.$

Здесь: α – реакционная переменная, представляющая собой отношение $\alpha = 1 - {{G\left( \tau \right)} \mathord{\left/ {\vphantom {{G\left( \tau \right)} {{{G}_{0}}}}} \right. \kern-0em} {{{G}_{0}}}}$, где G0 – количество карбонатного вещества, вступающего в реакцию, G(τ) – количество не прореагировавшего вещества за время τ, α1 – степень превращения MgCO3, α2 – степень превращения СаСО3, ${{\rho }}{{C}_{p}}$, ${{\lambda }}$ – теплофизические характеристики удельные теплоемкость и теплопроводность, зависящие от температуры и степеней превращения эндотермических реакций диссоциации карбонатов: MgCO3 → MgO + CO2 – Q1 и СаСО3 → CaO + CO2 – Q2, где Q1 = 1.21 × × 105 Дж/моль – тепловой эффект реакции разложения MgCO3, Q2 = 1.78 × 105 Дж/моль – тепловой эффект реакции разложения CaCO3. $C_{1}^{0}$, $C_{2}^{0}$ – теплоемкости веществ прореагировавших карбонатов, E1, E2 – энергии активации диссоциации карбонатов, k01, k02 – предэкспоненциальные множители, x – координата по толщине пластины с полутолщиной X, $x \in \left[ { - X;\;X} \right]$; R – универсальная газовая постоянная, T – температура, $\rho $ – плотность.

Влияние на макрокинетику термического разложения карбонатов, учитывалась с помощью распространенной зависимости: $f\left( \alpha \right) = {{\left( {1 - \alpha } \right)}^{n}}$, где n – число, определяемое экспериментально для конкретного фосфатного сырья.

Система уравнений решалась численно при наличии следующих краевых условий:

– начальные условия:

(2)
$T\left( {x,0} \right) = {{T}_{0}};\,\,\,\,{{\alpha }_{1}}\left( {x,0} \right) = 0;\,\,\,\,{{\alpha }_{2}}\left( {x,0} \right) = 0,$
– граничные условиями первого рода:
(3)
$T\left( {X,\tau } \right) = {{T}_{1}}\left( \tau \right);\,\,\,\,T\left( { - X,\tau } \right) = {{T}_{2}}\left( \tau \right),$
где: T1, T2 – температуры на поверхностях неограниченной пластины, ${{T}_{0}}$ – начальная температура пластины. Решение приведенной системы уравнений осуществлялось методом прогонки по неявной конечно-разностной схеме, с помощью разработанной авторами в Си++ компьютерной модели.

В качестве критерия оптимальности принято наименьшее отклонение рассчитанной температуры $T\left( {х,\tau } \right)$ от заданной $T{\text{*}}\left( {х,\tau } \right)$. Задача в такой постановке эквивалентна обратной коэффициентной задаче, для отыскания теплофизических характеристик материалов $\rho {{C}_{p}}$, ${{\lambda }}$. Вообще говоря, обратные задачи являются некорректно поставленными, поэтому необходимо применение регуляризующих алгоритмов. В данной компьютерной модели использован принцип естественной регуляризации, основанный на демпфирующих свойствах итерационных вычислительных алгоритмов.

Инверсная задача теплопроводности ставит целью определить $\rho {{C}_{p}}$ и ${{\lambda }}$ из условия минимума отклонения значений температуры полученной в натурном эксперименте $T{\text{*}}\left( {х,\tau } \right)$ и рассчитанных $T\left( {х,\tau } \right)$ для всего временного диапазона и толщины пластины. Однако дискретизируя временной интервал, можно минимизировать отклонения температур на каждом временном слое ${{{{\tau }}}_{j}}$ и относить полученные результаты по теплофизическим характеристикам к средней температуре в образце в данный момент времени.

В качестве критерия принимается минимум функционала $\Phi \left( {\rho {{C}_{p}};\lambda } \right)$, а на каждом временном слое ${{\Phi }_{j}}\left( {\rho {{C}_{p}};\lambda } \right)$

${{\Phi }_{j}}\left( {\rho {{C}_{p}};\lambda } \right) = \sqrt {\sum\limits_i {{{{\left[ {T\left( {{{х}_{i}},{{\tau }_{j}}} \right) - T{\text{*}}\left( {{{х}_{i}},{{\tau }_{j}}} \right)} \right]}}^{2}}} } \to \min .$

Минимизация ${{\Phi }_{j}}\left( {\rho {{C}_{p}};\lambda } \right)$ осуществлялась методом деформируемого многогранника, точнее его модификацией для задач с ограничениями методом скользящего допуска, несколько более сложным по сравнению с прямым поиском, но оказавшимся весьма эффективным и легко осуществляемым на ЭВМ. Алгоритм скользящего допуска позволяет улучшить определение значений целевой функции как за счет информации, получаемой в допустимых точках пространства решений, так и за счет информации, которую удается получить при прохождении через некоторые точки, лежащие вне допустимой области, но являющимися близкими к допустимым.

При практической реализации на ЭВМ большинства методов нелинейного программирования значительная доля машинного времени тратится на то, чтобы обеспечить строгое выполнение требований допустимости [25].

Алгоритм скользящего допуска с оптимизацией по методу деформируемого многогранника реализован при решении обратной задачи теплопроводности. Причем, в силу условий конкретного термохимического процесса, на ${{\rho }}{{C}_{p}}$, ${{\lambda }}$ и α были наложены следующие ограничения: 0 < ${{\lambda }}$ < 5; 0 < $\rho {{C}_{p}}$< 5 × 10–6; 0 < α < 1. Для увеличения скорости процедуры минимизации невязки на каждом последующем временном шаге, в качестве начальной точки поиска принималась точка минимума, найденная на предыдущем временном слое.

Алгоритм решения инверсной задачи теплопроводности приведен ниже.

1. Исходные данные: температурное поле $T{\text{*}}\left( {{{х}_{i}},{{\tau }_{j}}} \right)$ по результатам эксперимента, значения теплового потока на границе на рассматриваемом временном интервале, толщина измерительного участка в исследуемом образце, координаты заделки термопар и их количество, значения кинетических констант для реакций декарбонизации, время эксперимента.

2. Задание начальной точки $\left( {\rho C_{p}^{0};{{\lambda }^{0}}} \right)$ для задачи минимизации функционала ${{\Phi }_{j}}\left( {\rho {{C}_{p}};\lambda } \right)$, т.е. исходных значений теплоемкости ${{\rho }}C_{p}^{0}$ и теплопроводности. ${{{{\lambda }}}^{0}}$.

3. Цикл по времени ${{{{\tau }}}_{j}}$.

4. Обращение к программе минимизации методом скользящего допуска из начальной точки.

5. Начало работы подпрограммы минимизации.

6. Обращение к подпрограмме решения уравнения теплопроводности с химической реакцией методом конечных разностей и получение температурного поля для данного временного интервала $T\left( {х,{{\tau }_{j}}} \right)$.

7. Расчет значения функционала для данного временного интервала ${{\Phi }_{j}}\left( {\rho {{C}_{p}};\lambda } \right)$.

8. Окончание работы подпрограммы минимизации при выполнении необходимого критерия.

9. Восстановление новой начальной точки значениями $\left( {\rho C_{p}^{0};{{\lambda }^{0}}} \right)$ в точке минимума функционала.

10. Вывод значений коэффициентов и средней по толщине пластины температуры.

11. Конец цикла по времени.

12. Завершение работы программы.

Решение задачи программно реализовано на языке C++.

Для проверки работоспособности алгоритма оптимизации проводились многочисленные численные эксперименты.

Решением прямой задачи, где ${{\rho }}{{C}_{p}}$ и ${{\lambda }}$ взяты из натурных экспериментов по исследованию ТФС фосфоритов и являются функциями температуры, получено распределение температуры $T{\text{*}}\left( {{{х}_{i}},{{\tau }_{j}}} \right)$.

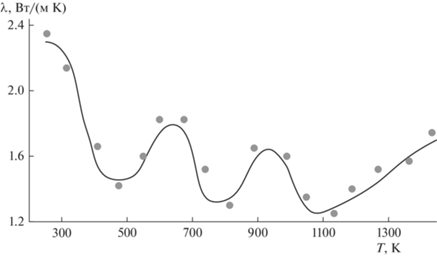
Значения теплофизических характеристик, полученных в вычислительном эксперименте методом решения обратной задачи теплопроводности по разработанной программе, представлены на рис. 1 и 2 и совпадают с экспериментальными данными для конкретного фосфоритного материала.

Рис. 1.

Зависимость теплоемкости от температуры.

Рис. 2.

Зависимость теплопроводности от температуры.

Анализ полученных результатов свидетельствует о том, что исходная теплопроводность и характер ее изменения в процессе нагрева значительно отличаются для различных руд и пород. Термически активируемые процессы существенно влияют на температурную зависимость ТФС. Исследования фосфатного сырья показывают, что измельчение и последующая грануляция материала приводят к значительным изменениям, как абсолютных значений теплопроводности, так и ее температурной зависимости. Так, теплопроводность окомкованного фосфатного сырья в пять раз ниже, чем у аналогичного по составу кускового материала при той же температуре.

Результаты исследований позволяют сделать следующие основные выводы:

– значения коэффициентов исходной теплопроводности фосфоросодержащих руд и пород существенно отличаются (объясняется их различным химическим составом и особенностями композиционной структуры);

– при нагреве под действием ряда физико-химических и структурных превращений теплопроводность материалов претерпевает значительные изменения;

– твердофазные взаимодействия между различными материалами с образованием изоморфных и аморфных фаз и связанные с этими процессами структурные превращения способствуют повышению теплопроводности.

ТФС фосфоритов необходимы для моделирования и количественных расчетов электротермических аппаратов, а также при разработке новых технологических систем термической обработки фосфатного сырья.

ИСТОЧНИКИ ФИНАНСИРОВАНИЯ

Раздел статьи посвященный разработке методики проведения экспериментов по определению теплофизических свойств фосфоритов в режиме монотонного нагрева выполнен при финансовой поддержке РНФ в рамках научного проекта № 21-79-30029.

Раздел по обработке результатов экспериментов и разработке алгоритма решения инверсной задачи теплопроводности выполнен при финансовой поддержке РНФ в рамках научного проекта № 22-11-00335.

ОБОЗНАЧЕНИЯ

α степень реагирования реакции декарбонизации
λ коэффициент теплопроводности, Вт/м К
ρ плотность, кг/м3
τ время, с
Т температура, К
x координата
$C$ теплоемкость, Дж/(кг K)
G количество прореагировавшего вещества, моль
E энергия активации, Дж/моль
k0 предэкспоненциальный множитель, с–1
ИНДЕКСЫ
i номер компонента в смеси

Список литературы

  1. Meshalkin V.P., Dovì V.G., Bobkov V.I., Burukhina T.F., Khodchenko S.M. State of the art and research development prospects of energy and resource-efficient environmentally safe chemical process systems engineering // Mendeleev Communications. 2021. 31(5). P. 593–604.

  2. Цирлин А.М., Гагарина Л.Г., Балунов А.И. Синтез теплообменных систем, интегрированных с технологическим процессом // Теоретические основы химической технологии. 2021. Т. 55. № 3. С. 347–358.

  3. Егоров А.Ф., Савицкая Т.В., Михайлова П.Г. Современное состояние в области анализа, синтеза и оптимального функционирования многоассортиментных цифровых химических производств: аналитический обзор // Теоретические основы химической технологии. 2021. Т. 55. № 2. С. 154–187.

  4. Мешалкин В.П., Дли М.И., Пучков А.Ю., Бобков В.И., Казак А.С. Программное обеспечение эффективных химических технологий переработки отходов апатит-нефелиновых руд // Докл. РАН. Химия, науки о материалах. 2021. Т. 496. № 1. С. 48–54.

  5. Леонтьев Л.И., Григорович К.В., Костина М.В. Фундаментальные исследования как основа создания новых материалов и технологий в области металлургии. Часть 1 // Известия высших учебных заведений. Черная металлургия. 2018. Т. 61. № 1. С. 11–22.

  6. Борисов В.В., Курилин С.П., Луферов В.С. Нечеткие реляционные когнитивные темпоральные модели для анализа и прогнозирования состояния сложных технических систем // Прикладная информатика. 2022. Т. 17. № 1(97). С. 27–38.

  7. Bobkov V.I., Fedulov A.S., Dli M.I., Meshalkin V.P., Morgunova E.V. Scientific basis of effective energy resource use and environmentally safe processing of phosphorus-containing manufacturing waste of ore-dressing barrows and processing enterprises // Clean Technologies and Environmental Policy. 2018. T. 20. № 10. C. 2209–2221.

  8. Курилин С.П., Соколов А.М., Прокимнов Н.Н. Компьютерная программа для эксплуатационной диагностики электромеханических систем на основе топологического подхода // Прикладная информатика. 2021. Т. 16. № 4(94). С. 62–73.

  9. Meshalkin V., Bobkov V., Dli M., Dovì V. Optimization of energy and resource efficiency in a multistage drying process of phosphate pellets // Energies. 2019. T. 12. № 17. C. 3376.

  10. Мешалкин В.П., Панченко С.В., Бобков В.И., Дли М.И. Анализ теплофизических и химико-технологических свойств отходов горно-обогатительных комбинатов // Теоретические основы химической технологии. 2020. Т. 54. № 1. С. 30–37.

  11. Гуськов А.В., Гагарин П.Г., Гуськов В.Н., Тюрин А.В., Гавричев К.С. Теплоемкость и термодинамические функции твердого раствора LU2O3–2HFO2 // Докл. РАН. Химия, науки о материалах. 2021. Т. 500. № 1. С. 84–88.

  12. Гагарин П.Г., Гуськов А.В., Гуськов В.Н., Хорошилов А.В., Гавричев К.С., Иванов В.К. Теплоемкость и термическое расширение М-ортотанталата тербия // Доклады Российской академии наук. Химия, науки о материалах. 2021. Т. 499. № 1. С. 63–65.

  13. Elgharbi S., Horchani-Naifer K., Férid M. Investigation of the structural and mineralogical changes of Tunisian phosphorite during calcinations // J. Thermal Analysis and Calorimetry. 2015. V. 119. № 1. P. 265–271.

  14. Пучков А.Ю., Лобанева Е.И., Култыгин О.П. Алгоритм прогнозирования параметров системы переработки отходов апатит-нефелиновых руд // Прикладная информатика. 2022. Т. 17. № 1(97). С. 55–68.

  15. Буткарев А.А., Вербыло С.Н., Бессмертный Е.А., Буткарева Е.А. Совершенствование и практическое использование методологии ВНИИМТ для оптимизации теплотехнических схем обжиговых конвейерных машин с рабочими площадями 278, 306 и 552 м2 // Сталь. 2020. № 5. С. 7–13.

  16. Wang, S., Guo, Y., Zheng, F., Chen, F., Yang, L. Improvement of roasting and metallurgical properties of fluorine-bearing iron concentrate pellets // Powder Technology. 2020. 376. P. 126–135.

  17. Nayak D., Ray N., Dash N., Pati S., De P.S. Induration aspects of low-grade ilmenite pellets: Optimization of oxidation parameters and characterization for direct reduction application // Powder Technology. 2021. 380. P. 408–420.

  18. Belyakov N.V., Nikolina N.V. Plant protection technologies: From advanced to innovative // J. Physics: Conference Series. 2021. 1942(1). 012072.

  19. Kurilin S., Fedulov Y., Sokolov A. Scientific Substantiation of Topological Diagnostics Methods of Electrical Equipment, 2021 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), 2021. P. 288–293. https://doi.org/10.1109/ICIEAM51226.2021.9446356.

  20. Тураев Д.Ю., Почиталкина И.А. Теоретические и практические основы селективного извлечения фосфат-ионов из фосфатных руд с высоким содержанием примесей железа рециркуляционным методом // Теоретические основы химической технологии. 2022. Т. 56. № 2. С. 252–264.

  21. Кольцов Н.И. Линейные концентрационные и температурные законы сохранения в открытом безградиентном химическом реакторе // Теоретические основы химической технологии. 2021. Т. 55. № 2. С. 210–215.

  22. Ming Yan, Xinnan Song, Jin Tian, Xuebin Lv, Ze Zhang, Xiaoyan Yu, Shuting Zhang. Construction of a New Type of Coal Moisture Control Device Based on the Characteristic of Indirect Drying Process of Coking Coal // Energies 2020. 13(16). 4162. https://doi.org/10.3390/en13164162

  23. Tomtas P., Skwiot A., Sobiecka E., Obraniak A., Ławińska K., Olejnik T.P. Bench Tests and CFD Simulations of Liquid–Gas Phase Separation Modeling with Simultaneous Liquid Transport and Mechanical Foam Destruction // Energies 2021. 14(6). 1740. https://doi.org/10.3390/en14061740

  24. Shekhovtsov V.V., Vlasov V.A., Skripnikova N.K., Semenovykh M.A. Structure Formation of Concrete Systems Modified By Nonstandard Particles // Russian Physics J. 2021. 63(9). P. 1590–1595.

  25. Zhu X., Ji Y. A digital twin–driven method for online quality control in process industry // International J. Advanced Manufacturing Technology. 2022. 119(5–6). P. 3045–3064

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал