1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 57, № 1, 2023

Теоретические основы химической технологии, 2023, T. 57, № 1, стр. 117-124

Использование холодного прессования в переработке композиционного материала на основе фторполимера

А. М. Столин a, *, Л. С. Стельмах a, Э. В. Стельмах a

a Федеральное государственное бюджетное учреждение науки Институт структурной макрокинетики и проблем материаловедения им. А.Г. Мержанова Российской академии наук
142432 г. Черноголовка, ул. Академика Осипьяна, 8, Россия

* E-mail: amstolin@ism.ac.ru

Поступила в редакцию 22.09.2022
После доработки 13.10.2022
Принята к публикации 25.10.2022

Полный текст (PDF)

Аннотация

В настоящей работе проведен теоретический анализ процесса одностороннего холодного прессования в условиях внешнего трения порошковых композиционных полимерных материалов на основе фторопласта с малыми добавками, такими, как диоксид кремния SiO2, каолинит Al4[Si4O10](OH)8, углеродные нанотрубки, углеволокно (менее 5%). Получены аналитические решения в виде формул, позволяющие проанализировать влияние на процесс уплотнения материалов приложенного давления, коэффициента внешнего трения, геометрических размеров прессовок, свойства материала и его пористость. На основе упрощенной системы исходных уравнений с использованием лагранжевых переменных и усреднения по радиусу проведены численные расчеты развития разноплотности по объему материала в зависимости от времени, обусловленные различной скоростью уплотнения нижних и верхних слоев. Установлены новые наглядные представления о кинетике уплотнения порошковых материалов на основе фторопласта, выявлены качественные особенности различных стадий развития разноплотности, Найдены ответы на практически важные вопросы, связанные с экспериментальным определением времени процесса прессования для получений качественной заготовки.

Ключевые слова: фторполимер, холодное прессование, разноплотность, лагранжевы координаты, трение

ВВЕДЕНИЕ

Наиболее распространенным процессом компактирования порошковых материалов для получения заготовок и изделий является прямое одностороннее прессование в закрытых пресс-формах. Реализация этих методов не требует сложного оборудования и позволяет относительно легко создавать условия для массового производства заготовок и изделий различного функционального назначения из порошков различных составов. Прямое прессование в холодном состоянии порошковых материалов широко применяется в технологиях порошковой металлургии и высокотемпературного самораспространяющегося синтеза (СВС) для производства заготовок и изделий сложной формы [1]. Режим прессования должен обеспечить оптимальное значение плотности, которое обуславливает уровень прочностных свойств заготовки для последующего спекания.

Развитие методов прессования на раннем этапе (середина прошлого века) сопровождалось появлением большого количества теоретических исследований, в которых предлагались различные интерполяционные формулы, которые представляли собой аппроксимацию экспериментально полученных зависимостей между давлением и плотностью прессовок. Широкое распространение получили уравнения прессования логарифмического, степенного и экспоненциального вида. Наиболее применимыми считаются уравнения Бережного [2], Покровского [3], Бальшина [4] и др. Однако при этом возникают методические трудности, связанные с тем, что процесс уплотнения является существенно нестационарным и степень уплотнения непрерывно меняется со временем. Поэтому плотность, соответствующая заданному давлению, зависит и от длительности процесса прессования. По этой причине эмпирические уравнения сами по себе не могли заменить разработку теоретической базы процессов получения заготовок и изделий методами прессования.

Важное направление теоретических исследований было развито Я.И. Френкелем, который выдвинул идею о подобии механизмов деформаций твердого тела и жидкости [5]. Согласно Я.И. Френкелю, деформация твердого тела отличается от деформации жидкостей только в количественном отношении и ответственным за уплотнение пористого тела предполагается физический процесс вязкого течения массы в пустоту. При этом вязкости твердых тел он придавал смысл сдвиговой вязкости жидкости.

Развитием этого направления исследований стали работы Маккензи [6] и Скорохода [7], в которых применены идеи механики континуума к сжимаемым средам. В рамках континуального подхода пористое тело представляет собой хаотическую смесь практически несжимаемых твердых частиц и абсолютной пустоты. При этом предполагается, что уплотнение такого тела происходит за счет исчезновения пустот в результате проникновения в них несжимаемого материала. Реологические свойства такой среды, т.е. ее способность к деформированию и течению, определяется свойствами твердой фазы, наличием и степенью пористости [8, 9].

В центре внимания исследователей оказались вопросы распределения напряжений, плотности и скоростей внутри объема порошкового или гранулированного материала при различных приемах прессования [10–12]. Искомые распределения анализировались на основе качественного исследования уравнений равновесия, либо численных расчетов по полной постановке задачи. Полученные решения в виде формул позволяют проанализировать влияние на процесс уплотнения порошковых материалов приложенного давления, коэффициента внешнего трения, геометрических размеров таблетки, свойств твердой фазы материала и пористости. Однако, при изучении этих вопросов в большинстве работ используется предположение об отсутствии в реальных объектах распределения плотности, отсутствие бокового течения, постоянство коэффициента бокового давления, независимость всех переменных от поперечной координаты и т.д.

Отметим, что на практике, как правило, используется только средняя интегральная по объему плотность пористого тела. Однако неравномерность распределения плотности в материале может достигать существенных значений [13–16]. В работах [15, 16] показано, что из-за внешнего трения даже при самых благоприятных условиях одностороннее прессование практически непригодно для получения прессовок с отношением высоты к диаметру более 2.5. Чем больше внешнее трение, тем больше неоородность распределения давления, плотности и прочности [17–19]. Уменьшить влияние сил трения в порошке можно применением смазок и пластификаторов. Применение пластификаторов значительно улучшает равномерность плотности изделия и увеличивает срок службы пресс-форм, однако является источником загрязнения материала или остаточной пористости при спекании, усложняет технологию производства [9, 10].

В литературе уделяется большое внимание теоретическому анализу процесса прессования полимерных порошковых материалов в условиях влияния ряда других факторов, влияющих на прессуемость порошковых заготовок: неизотермичность [18–21], неоднородность распределения плотности и напряжения по объему прессовки [22], различные режимы уплотнения (волновой режим, при котором волна уплотнения перемещается по образцу, или регулярный однородный режим [21]). Эти важные вопросы исследовались в современной теории прессования порошковых материалов на основе общих законов механики и физики [23–30].

Данная работа посвящена теоретическому исследованию кинетики уплотнения композиционных полимерных материалов на основе фторопласта с малыми добавками (менее 5%), такими как диоксид кремния SiO2, каолинит Al4[Si4O10](OH)8, углеродные нанотрубки, углеволокно в условиях одноосного прессования. Отсутствие системных исследований в этой области не позволяют использовать широкие возможности твердофазной технологии. При изучении в этих условиях процесса прессования порошковых материалов на основе фторопласта рассматриваются следующие вопросы:

– изучение распределения разноплотности в зависимости от времени в процессе холодного прессования при наличии внешнего трения;

– в какой степени на конечное состояние заготовки оказывают влияние различные параметры: величина бокового внешнего трения, сжимающее внешнее давление, отношение начальной высоты к диаметру заготовки;

– каковы наиболее рациональные (с точки зрения достижения однородности) приемы одностороннего прессования заготовок различных размеров.

Расчеты выполнялись на основе усреднения исходных двумерных уравнений и использования лагранжевой системы координат, позволяющие сократить объем вычислений ценой некоторых потерь в точности и сохраняющей качественные особенности изучаемого процесса.

ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ ДОПУЩЕНИЯ

Теоретический анализ распределения плотности, скорости и напряжений основывается на известной постановке задач прессования [11], полученной из представлений о порошковой заготовке как о вязком сплошном материале, состоящем из хаотической смеси несжимаемой фазы и пустоты.

Математическая формулировка задачи в цилиндрической системе координат включает в себя уравнения неразрывности, движения и реологические соотношения, которые совместно с начальными и граничными условиями образуют замкнутую систему, в принципе позволяющую определить все искомые зависимости. Введем понятие средней по радиусу функции:

$\overline {f\left( r \right)} = \frac{2}{{r_{0}^{2}}}\mathop \smallint \limits_0^{{{r}_{0}}} rf\left( r \right)dr.$

Постановка задачи в усредненном виде цилиндрической системе координат (индекс усреднения опускаем, вместо Vz пишем V), содержит уравнения неразрывности (1), уравнение равновесия (2), реологические соотношения (3–4):

(1)
$\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho V} \right)}}{{\partial z}} = 0,$
(2)
$\frac{{\partial {{\sigma }_{{zz}}}}}{{\partial z}} + \frac{2}{{{{r}_{0}}}}{{\tau }_{{{\text{fr}}}}} = 0,$
(3)
${{\sigma }_{{zz}}} = \left( {\frac{4}{3}\mu + \xi } \right)\frac{{\partial V}}{{\partial z}},$
(4)
${{\sigma }_{{rr}}} = {{\sigma }_{{\theta \theta }}} = \left( { - \frac{2}{3}\mu + \xi } \right)\frac{{\partial V}}{{\partial z}},$
где ρ1 − плотность несжимаемой основы материала, ρ – относительная плотность материала (плотность деленная на ρ1 ); μ, ξ – сдвиговая и объемная вязкости материала; V – скорость течения материала; σzz, σrr, σθθ – осевые, радиальные и тангенциальные напряжения; r0 – радиус заготовки (внутренний радиус пресс-формы); τfr – напряжение трения на боковой границе.

Здесь вместо уравнений движения используется уравнения равновесия, что было достаточно подробно обосновано ранее [21–25]. В качестве реологических соотношений выбрана модель вязкого сжимаемого тела согласно обобщенному закону Ньютона, который обычно используется при высокотемпературном прессовании. В силу цилиндрической симметрии зависимость всех переменных от угла поворота отсутствует и уравнение по угловой координате выполняется тождественно.

Граничные условия:

(5)
${{\left. {{{\tau }_{{rz}}}} \right|}_{{r = {{r}_{0}}}}} = {{\tau }_{{{\text{fr}}}}},\,\,\,\,{{\left. {{{\sigma }_{{zz}}}} \right|}_{{z = H\left( t \right)}}} = - P\left( t \right),\,\,\,\,{{\left. {{{V}_{z}}} \right|}_{{z = 0}}} = 0.$

Первое соотношение в (5) определяет условие проскальзывания материала относительно боковой стенки цилиндра. Согласно принятому допущению, сила трения рассматривается как эффективная характеристика взаимодействия материала со стенкой и принимается постоянной величиной, доступной для экспериментального определения. На верхней границе принимается условие, соответствующее заданию усилия на плунжере пресса (второе соотношение в (5)) На нижней границе прессуемого образца (z = 0) примем условие прилипания (третье соотношение в (5)).

Интегрируя уравнение (2), от z до H0 и учитывая граничное условие (5), получаем:

(6)
${{\sigma }_{{zz}}} = - P(t) + \frac{2}{{{{r}_{0}}{{\tau }_{{{\text{fr}}}}}}}({{H}_{0}} - z).$

Примем, что сдвиговая μ и объемная ξ вязкости зависят от плотности согласно эмпирическим соотношениям [6]:

(7)
$\mu \left( \rho \right) = {{\mu }_{1}}{{\rho }^{m}},\,\,\,\,\xi \left( \rho \right) = \frac{4}{3}{{\mu }_{1}}\frac{{{{\rho }^{{m + 1}}}}}{{1 - \rho }}.$

Для решения уравнений (1)–(4) необходимо задание начального распределения плотности по координате:

(8)
${{\left. \rho \right|}_{{t = 0}}} = {{\rho }_{0}}\left( {r,z} \right).$

Особенностью задачи является наличие верхней подвижной границы Z = H(t), соответствующей плунжеру пресса. Уравнение движения верхней границы образца:

(9)
$\frac{{dH(t)}}{{dt}} = {{V}_{n}}(t).$

Основная задача теоретического рассмотрения в рамках реодинамических моделей является анализ кинетики уплотнения материала в процессе его прессования в зависимости от давления. Задача решалась в лагранжево-массовой системе координат (q, t) где координата q имеет смысл относительной массы материала в объеме от 0 до z: $q = \int\limits_0^z {\rho (z,t)dz} $.

Эта система координат используется для уменьшения количества подвижных границ – верхняя граница образца в системе (t, q) останавливается, что упрощает численную реализацию модели.

Постановка задачи в лагранжевых координатах:

(10)
$\frac{{\partial \rho }}{{\partial t}} + {{\rho }^{2}}\frac{{\partial \left( V \right)}}{{\partial q}} = 0,$
(11)
${{\sigma }_{{zz}}} = - P(t) + \frac{2}{{{{r}_{0}}{{\rho }_{0}}}}{{\tau }_{{{\text{fr}}}}}\left( {{{q}_{0}} - q} \right),$
(12)
${{\sigma }_{{zz}}} = \left( {\frac{4}{3}\mu + \xi } \right)\rho \frac{{\partial V}}{{\partial q}},$
(13)
${{\sigma }_{{rr}}} = {{\sigma }_{{\theta \theta }}} = \left( { - \frac{2}{3}\mu + \xi } \right)\rho \frac{{\partial V}}{{\partial q}}.$

Из (12) выражаем $\left( {{{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial q}}} \right. \kern-0em} {\partial q}}} \right)$ и подставляем вместо σzz его выражение из (11), получаем:

(14)
$\frac{{\partial V}}{{\partial q}} = - \frac{1}{{\left( {\frac{4}{3}\mu + \xi } \right)\rho }}\left( { - P(t) + \frac{2}{{{{r}_{0}}{{\rho }_{0}}}}{{\tau }_{{{\text{fr}}}}}\left( {{{q}_{0}} - q} \right)} \right).$

Подставляя (14) в (10), получаем:

(15)
$\frac{{\partial \rho }}{{\partial t}} = \frac{\rho }{{\left( {\frac{4}{3}\mu + \xi } \right)}}\left( { - P(t) + \frac{2}{{{{r}_{0}}{{\rho }_{0}}}}{{\tau }_{{fr}}}\left( {{{q}_{0}} - q} \right)} \right).$

Рассмотрим простейшие случаи: m = 1, P(t) = = P = const, $\tau _{{{\text{fr}}}}^{1}$ = τfr/P. Характерное время уплотнения ${{t}_{*}}$ = 4μ/3P. Интегрируя (15) от ρ0 до ρ, получаем распределение пористости Π(t, q) = (1 – ρ) по массовой координате в зависимости от времени:

$\Pi (t,q) = {{\Pi }_{0}}\exp \left( { - \frac{t}{{{{t}_{*}}}}} \right)\left( {1 - \frac{{2{{\tau }_{{{\text{fr}}}}}}}{{{{r}_{0}}{{\rho }_{0}}}}({{q}_{0}} - q)} \right),$
и зависимость скорости:

$\begin{gathered} V(t,q) = - \frac{t}{{{{t}_{*}}}}\int\limits_0^q {\frac{{\Pi (t,q)\left( {1 - \frac{{2{{\tau }_{{{\text{fr}}}}}}}{{{{r}_{0}}{{\rho }_{0}}}}({{q}_{0}} - q)} \right)}}{{{{{(1 - \Pi (t,q))}}^{2}}}}} dq = \\ = - \frac{t}{{{{t}_{*}}}}\int\limits_0^q {\frac{{{{\Pi }_{0}}\exp \left( { - \frac{t}{{{{t}_{*}}}}} \right){{{\left( {1 - \frac{{2{{\tau }_{{{\text{fr}}}}}}}{{{{r}_{0}}{{\rho }_{0}}}}({{q}_{0}} - q)} \right)}}^{2}}}}{{\left( {1 - {{\Pi }_{0}}\exp \left( { - \frac{t}{{{{t}_{*}}}}} \right)\left( {1 - \frac{{2{{\tau }_{{{\text{fr}}}}}}}{{{{r}_{0}}{{\rho }_{0}}}}({{q}_{0}} - q)} \right)} \right)}}} dq. \\ \end{gathered} $

Задача считалась численно. В результате численного решения находятся неизвестные относительная плотность (ρ), скорость (V), и напряжения (${{\sigma }_{{zz}}},{{\sigma }_{{rr}}},{{\sigma }_{{\theta \theta }}}$), которые являются функциями не только координаты времени (t), но и массовой координаты (q).

В расчетах использовались следующие данные для состава фторполимеров и технологические параметры, в следующих пределах: давление на плунжере пресса Р = 108–109 Па, плотность несжимаемой основы материала ρ1 = 2.25 × 103 кг/м3, вязкость несжимаемой основы μ1 = 108–1010 Па с, начальная высота заготовки Н0 = 25 × 10–3–70 × 10–3 м, диаметр заготовки D0 = 12 × 10–3–50 × 10–3 м.

РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ИССЛЕДОВАНИЙ

Главный вопрос, на который авторы решили дать ответ, связан с экспериментальным определением времени процесса прессования для получений качественной заготовки. Зачастую это время прессования относят к условию, когда высота заготовки под действием внешнего сжимающего давления с большой степенью точности остается постоянной. Такой подход к определению времени эксперимента не обеспечивает получение заготовок, имеющих однородное распределение плотности по объему материала. Время наблюдения за экспериментом должно соответствовать времени самого процесса.

Основное внимание проведенных в данной работе численных исследований заключается в получении наглядных представлений о кинетике процесса прессования при наличии внешнего трения на боковой стенке прессформы. В связи с этой целью был проведен взаимосвязанный расчет разноплотности Δ (Δ = ρ(H(t)) – ρ(0)), в образце и скорости плунжера пресса в зависимости от времени для различных параметров: начальной плотности, силы трения, усилия и т.д. Счет этих характеристик ведется до тех пор, пока не выполняется одно из двух условий:

– изменение от времени относительной скорости плунжера меньше заданной малой величины;

– изменение от времени относительной разноплотности становится меньше заданной другой малой величины.

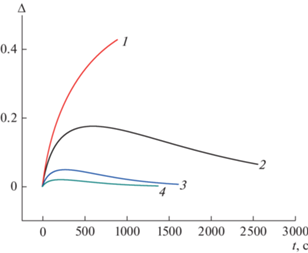
Результаты расчетов разноплотности (Δ = = ρ(H(t)) – ρ(0)) в образце в зависимости от времени представлены на рис. 1.

Рис. 1.

Зависимость разноплотности (Δ) от времени (t) для различных значений давления Р: 1 – P = = 50 МПа, 2 – P = 100 МПа, 3 – P = 200 МПа, 4 – 250 МПа. τfr = 0.05P, Н0 = 5 × 10–2 м, d0 = 2.5 × 10–3 м.

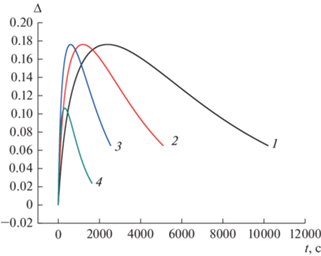
Прежде всего, следует отметить немонотонный характер этих зависимостей (наличие максимума), что является следствием важной особенности кинетики уплотнения: потери усилия прессования на преодоление силы пристенного внешнего трения (см., например, [8]). На первом этапе, соответствующему временному интервалу от начала прессования до времени достижения максимума разноплотности, при больших значениях силы внешнего трения скорость уплотнения нижних слоев меньше скорости уплотнения слоев, примыкающих к подвижному поршню, и нижняя часть заготовки оказывается не охваченной заметным уплотнением (рис. 2, кривые 3–5).

Рис. 2.

Распределение плотности (ρ) по координате (q) в различные моменты времени: 1 – 1646 с (конец прессования), 2 – 500 с, 3 – 250 с, 4 – 100 с, 5 – 2 с. P = = 250 МПа, τfr = 0.05P, Н0 = 5 × 10–2 м, d0 = 2.5 × 10–3 м.

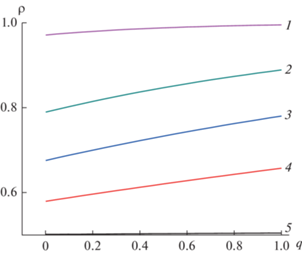
В то же время верхняя часть заготовки уплотняется гораздо быстрее и достигает плотности компактного материала. Это обуславливает возрастание разноплотности во времени до своего максимального значения. С практической точки зрения наличие максимума зависимости разноплотности от времени позволяет определить временной интервал первой активной стадии процесса прессования от начала уплотнения до достижения максимума плотности верхних слоев. Вторая ветвь кинетической кривой разноплотности соответствует дальнейшему уплотнению нижних слоев. Однако на этой стадии происходит заметное уменьшение скорости перемещения плунжера.

Однако процесс уплотнения нижних слоев можно продолжаться и при неподвижном плунжере. Эта стадию процесса прессования можно назвать выдержкой порошкового материала под давлением. За время окончания эксперимента можно принять время, когда разноплотность с условной точностью, например, 1%, достигает минимального значения. По существу, с определенной точностью это значение времени соответствует примерно одинаковому распределению плотности по объему заготовки. Оно соответствует окончанию выдержки под давлением, равного времени процесса прессования. Все сказанное находится в полном согласии с зависимостью скорости плунжера от времени, которая асимптотически стремится к нулю (рис. 3).

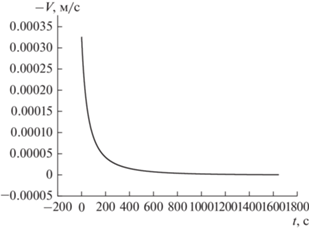
Рис. 3.

Зависимость абсолютного значения скорости плунжера пресса (V) от времени (t). P = 250 МПа , τfr = = 0.05P, Н0 = 5 × 10–2 м, d0 = 2.5 × 10–3 м.

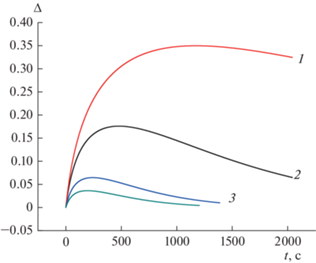
На рис. 4 приведена зависимость разноплотности от времени для различных коэффициентов трения τfr: τfr = 0.02Р–0.06Р. Из рисунка видно, что при малых значениях коэффициента трения зависимость разноплотности от времени сохраняет немонотонный характер, однако сама величина разноплотности меняется незначительно. При увеличении коэффициента трения максимальные значения разноплотности соответственно увеличиваются и для их уменьшения требуются большие времена выдержки под давлением.

Рис. 4.

Зависимость разноплотности (Δ) от времени для различных коэффициентов трения τfr: 1 – τfr = = 0.06Р, 2 – τfr = 0.05Р, 3 – τfr = 0.03Р, 4 – τfr = 0.02Р. Р = 250 МПа, Н0 = 5 × 10–2 м, d0 = 2.5 × 10–3 м.

На рис. 5 представлены зависимость разноплотности (Δ) в образце от времени для различных начальных отношений высоты (H) к диаметру (D) заготовки.

Рис. 5.

Зависимость разноплотности (Δ) от времени (t) для различных отношений высоты к диаметру (H/D): 1 – H/D = 3, 2 – H/D = 2, 3 – H/D = 1, 4 – H/D = = 0.5. P = 250 МПа , τfr = 0.05P.

Заметим, что если плотность не зависит от координаты, то относительная скорость изменения плотности совпадает с относительной скоростью изменения высоты заготовки:

$\frac{1}{\rho }\frac{{d\rho }}{{dt}} = - \frac{1}{H}\frac{{dH}}{{dt}}.$

В общем случае относительная скорость изменения плотности не совпадает со скоростью изменения высоты заготовки. Из рис. 5 (аналогично рис. 1) видно, что кривые для разных Н/D имеют экстремальный характер: сначала разноплотность увеличивается, а затем, после перехода через максимум, падает. В соответствующие моменты времени наименьшее значение разноплотность имеет для образца с отношением H/D = 1 и H/D = 0.5 (кривые 3, 4). При увеличении этого отношения (кривые 1, 2) разноплотность увеличивается. Причиной возникновения перепада плотности прессовок по высоте являются потери усилия прессования на преодоление пристенного трения.

ЗАКЛЮЧЕНИЕ

Проведенный теоретический анализ распределения разноплотности по объему материала во времени в закрытой прессформе позволил выявить основные закономерности процесса одностороннего прессования порошковых композиционных полимерных материалов на основе фторопласта при наличии внешнего бокового трения. Полученные аналитические решения в виде формул позволили проанализировать влияние на процесс уплотнения материалов приложенного давления, коэффициента внешнего трения, геометрических размеров прессовок, свойств материала и его пористости.

Выявлены качественные особенности стадийного развития разноплотности, обусловленные различной скоростью уплотнения нижних и верхних слоев по объему материала. Сформулированы условия выбора времени прессования, обеспечивающие получения качественных заготовок из композиционных полимерных материалов на основе фторопласта.

Результаты проведенных теоретических исследований использовались при отработке оптимальных технологических режимов получения заготовок фторполимера на основе фторопласта с малыми добавками, такими, как диоксид кремния SiO2, каолинит Al4[Si4O10](OH)8, углеродные нанотрубки, углеволокно (менее 5%).

Исследование выполнено за счет гранта Российского научного фонда № 22-13-20056, https://rscf.ru/project/22-13-20056.

ОБОЗНАЧЕНИЯ

D диаметр, м
Δ разноплотность
H высота заготовки, м
H0 начальная высота заготовки, м
P давление, Па
σ напряжение, Па
μ сдвиговая вязкость, Па с
μ1 вязкость несжимаемой основы, Па с
Π  относительная пористость
r радиус, м
ρ относительная плотность
ρ1 плотность несжимаемой основы материала, кг/м3
t время, с
τfr напряжение трения, Па
V скорость, м/с
Z вертикальная координата, м
ξ объемная вязкости материала, Па с

ИНДЕКСЫ

0 начальное значение при t = 0
1 относится к несжимаемой основе
* характерное время
fr трение (friction)

Список литературы

  1. Stolin A.M., Bazhin P.M. Manufacture of Multipurpose Composite and Ceramic Materials in the Combustion Regime and High-temperature Deformation (SHS Extrusion) // Theor. Found. Chem. Eng. 2014. V. 48. № 6. P. 751. [Столин А.М., Бажин П.М. Получение изделий многофункционального назначения из композитных и керамических материалов в режиме горения и высокотемпературного деформирования (СВС-экструзия) // Теорет. основы хим. технологии. 2014. Т. 48. № 6. С. 603]

  2. Бережной А.С. О зависимости между давлением прессования и пористостью необожженных огнеупорных изделий // Огнеупоры. 1947. № 3. С. 124–130.

  3. Покровский Г.И. Исследования по физике грунтов / Изд. Института ВОДГЕО, Гл. ред. строительной литературы. М.–Л.: 1937.

  4. Bal’shin M.Y. Novel principles of calculation and analysis of powder compression // Sov. Powder Metall. Met. Ceram. 1965. V. 4. № 12. P. 975.

  5. Френкель Я.И. Вязкое течение в кристаллических телах. М.: Физматгиз, 1958. Т. 2.

  6. Mackenzie J.K., Shuttworth P.A. Phenomenological theory sintering. Proc. Phys.Soc. B. 1949. 62. № 12. P. 833.

  7. Скороход В.В. Реологические основы спекания. Киев: Наукова думка, 1972.

  8. Штерн М.Б., Сердюк Г.Г., Максименко Л.А., Трухан Ю.В., Шуляков Ю.М. Феноменологические теории прессования порошков. Киев: Наукова думка, 1982.

  9. Бальшин М.Б. Порошковое металловедение. М.: Металлургиздат, 1943.

  10. Жданович Г.М. Теория прессования металлических порошков. М.: Металлургия, 1969.

  11. Скотников М.В, Чулков В.Н., Прилепкин В.Н. Джангирян В.Г. Распределение напряжений и скоростей при уплотнении вязких тел в замкнутых объемах // Порошковая металлургия. 1984. № 6. С. 21.

  12. Горохов В.М., Дорошкевич Е.А., Звонарев В.Н., Рябов И.Н. Напряженно-деформированное состояние пористой заготовки при горячем прессовании и свободной осадке с учетом внешнего трения. Математическое моделирование процессов // Порошковая металлургия. 1987. № 1. С. 34.

  13. Parshin D.A., Stel’makh L.S., Stolin A.M. Mathematical Modeling of Solid-Phase Plunger Extrusion with Two-Stage Compression of Composite Materials // Theor. Found. Chem. Eng. 2015. V. 49. № 3. P. 344. [Паршин Д.А., Стельмах Л.С., Столин А.М. Математическое моделирование твердофазной плунжерной экструзии с двухступенчатым обжатием композитных материалов // Теорет. основы хим. технологии. 2015. Т. 49. № 3. С. 361.]

  14. Бучацкий Л.М., Столин А.М., Худяев С.И. Распределение плотности в пористом теле при горячем одностороннем прессовании // Порошковая металлургия. 1987. № 12. С. 9.

  15. Столин А.М., Стельмах Л.С., Стельмах Э.В. Высокотемпературное прессование порошкового материала в условиях внешнего трения // Композиты и наноструктуры. 2017. Т. 3,4. № 35–36. С. 156–161.

  16. Столин А.М., Стельмах Л.С., Паршин Д.А., Стельмах Э.В. Высокотемпературное прессование порошкового материала в условиях внешнего трения // НАУКА СОВРЕМЕННОСТИ. Сборник материалов международной научной конференции. Москва, 2015. С. 154.

  17. Stolin A.M., Stel’makh L.S., Karpov S.V., Alymov M.I. External friction in SHS compaction // Dokl. Chem. 2019. V. 487. № 2. P. 235.

  18. Korachkin D., Gethin D., Lewis R., Tweed J. Friction measurement and lubrication in unloading and ejection stages in powder pressing cycle. // Powder Metall. 2008. V. 51. № 1. P. 14.

  19. Canta T., Frunza D. Friction-assisted pressing of PM components // J. Mater. Process. Technol. 2003. V. 143, 144. № 1. P. 645.

  20. Sinka I., Cunningham J., Zavaliangos A. The effect of wall friction in the compaction of pharmaceutical tablets with curved faces: a validation study of the Drucker–Prager Cap model // Powder Technol. 2003. V. 133. № 1, 3. P. 33.

  21. Stolin A.M., Stelmakh L.S. Features of compaction kinetics for powder materials under nonisothermal conditions. Part 1. Compaction kinetics in regular and fiber regimes // Powder Metall. Met. Ceram. 2001. V. 40. № 11, 12. P. 556.

  22. Stolin A.M., Stel′makh L.S., Karpov S.V. High-temperature indirect compaction of powder materials with active action of an external friction force // J. Eng. Phys. Thermophys. 2020. V. 93. № 2. P. 317.

  23. Luo J., Stevens R., Ren Y. Constrained sintering of a sphere with radial density gradient: Viscous model // Metall. Mater. Trans. B. 1998. V. 29. № 3. P. 673.

  24. Karpov S.V., Stelmakh L.S., Alymov M., Stolin A.M. Wave mode of compaction of powder materials by unilateral pressing under dry friction // Dokl. Chem. 2020. V. 491. № 1. P. 54.

  25. Stolin A.M., Stel’makh L.S. Mathematical Modeling of SHS-compaction/ Extrusion: An Autoreview // J. SHS. 2008. V. 13. № 1. P. 53.

  26. Рыбин Ю.И., Цеменко В.Н., Александров А.Э. Математическая модель уплотнения порошковых металлических материалов // Металлообработка. 2004. № 6. P. 45.

  27. Berezin I.M., Nesterenko A.V., Zalazinskii A.G. Identification of the modified Drucker–Prager yield condition and modelling of compaction of the plasticized titanium feedstock // Russian J. Non-Ferrous metals. 2017. V. 58. № 3. P. 297.

  28. Cedergren J., Sørensen N.J., Melin S. Numerical investigation of powder compaction of gear wheels // Int. J. Solids Struct. 2003. V. 40. № 19. P. 4989.

  29. Столин А.М., Стельмах Л.С., Карпов С.В., Алымов М.И. Внешнее трение в процессе СВС-компактирования // ДАН, Химическая технология. 2019. Т. 487. № 6. С. 636.

  30. Карпов С.В, Стельмах Л.С., Столин А.М. Математическое моделирование одностороннего прессования порошковых материалов в условиях сухого трения // Известия вузов. Порошковая металлургия и функциональные покрытия. 2020. № 4. С. 22–32.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал