1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 57, № 1, 2023

Теоретические основы химической технологии, 2023, T. 57, № 1, стр. 125-135

Экстрактивная ректификация смеси тетрагидрофуран–ацетонитрил–хлороформ

В. И. Жучков a, Д. А. Рыжкин a, В. М. Раева a, *

a МИРЭА – Российский технологический университет, Институт тонких химических технологий им. М.В. Ломоносова
Москва, Россия

* E-mail: raevalentina1@gmail.com

Поступила в редакцию 10.10.2022
После доработки 25.10.2022
Принята к публикации 25.10.2022

Полный текст (PDF)

Аннотация

Экспериментально изучено парожидкостное равновесие системы тетрагидрофуран–ацетонитрил, смеси тетрагидрофуран–ацетонитрил–хлороформ эквимолярного состава, исследовано влияние разных количеств диметилсульфоксида на относительные летучести компонентов при 101.32 кПа. Проведены расчеты схем экстрактивной ректификации смеси тетрагидрофуран–ацетонитрил–хлороформ с диметилсульфоксидом.

Ключевые слова: трехкомпонентная смесь, азеотроп, структура диаграммы парожидкостного равновесия, экстрактивный агент, экстрактивная ректификация, принципиальная схема разделения

ВВЕДЕНИЕ

Для разделения многокомпонентных азеотропных смесей используются специальные ректификационные методы [1–3]. Экстрактивная ректификация (ЭР) является одним из таких методов в крупнотоннажных технологиях разделения органических продуктов [4–6]. Для процесса ЭР требуется предварительно выбрать экстрактивный агент (ЭА), оказывающий избирательное влияние на парожидкостное равновесие в производной системе “разделяемые компоненты + ЭА”.

Большинство исследований, направленных на разработку методик выбора и сравнения селективных ЭА, относится к бинарным азеотропным системам [7–10]. Независимо от способа отбора высоко кипящих растворителей для тестирования в качестве ЭА, итоговый выбор варианта разделения проводится по результатам сравнения эффективности ЭР [11]. На этапе предпроектной разработки можно оценивать энергозатраты на ректификационное разделение, которые непосредственно зависят от селективности экстрактивных агентов S (1):

(1)
$S = \frac{{\alpha _{{ij}}^{{{\text{ЭА}}}}}}{{{{\alpha }_{{ij}}}}},$
(2)
${{\alpha }_{{ij}}} = \frac{{{{y}_{i}}:{{x}_{i}}}}{{{{y}_{j}}:{{x}_{j}}}}.$

Селективность ЭА позволяет сравнивать относительную летучесть разделяемых веществ i, j в базовой смеси (αij) и в производной системе ($\alpha _{{ij}}^{{{\text{ЭА}}}}$). Чем выше селективность агента, тем меньшее его количество требуется [7, 10, 12–14]. Оценить влияние потенциального ЭА на относительные летучести компонентов, образующих азеотропы, можно по экспериментальным данным парожидкостного равновесия (ПЖР) в изобарических условиях [15, 16]. Тестируемые высоко кипящие растворители должны удовлетворять стандартным требованиям, предъявляемым к экстрактивным агентам [17–19].

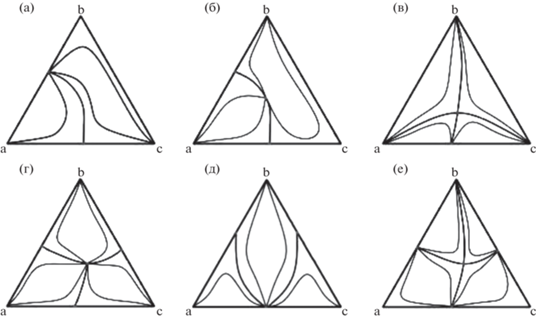
При разработке вариантов ЭР трехкомпонентных систем, содержащих несколько азеотропов, характер влияния ЭА на αij (2) определяет структуру схемы разделения в целом [20–22]. Структуры диаграмм ПЖР конкретных трехкомпонентных систем, разделение которых экстрактивной ректификацией обсуждается в литературе, показаны на рис. 1. Обозначения диаграмм приведены согласно [23].

Рис. 1.

Структуры диаграмм равновесия жидкость – пар трехкомпонентных систем: а – 2.0–2b, б – 2.1–2b, в – 1.1–2, г – 3.1–2, д – 3.0–2, е – 3.1–4. Обозначения структур диаграмм ПЖР даны согласно [23].

При ЭР систем 2.0–2b целесообразно выделять компонент, входящий в состав обоих бинарных азеотропов (рис. 1а). Такой вариант предложен для ЭР смесей ацетонитрил (a) – метанол (b) – вода (c) с глицерином [24, 25], тетрагидрофуран (a) – метанол (b) – вода (c) c этиленгликолем или глицерином [24, 26] и толуол (a) – метанол (b) – вода (c) с диэтиленгликолем [27]. В дистиллатном потоке колонны ЭР выделяют компонент a. Принципиальные схемы разделения приведены на рис. 2а, 2б. Структуры схем различаются очередностью выделения компонентов из зеотропных смесей b–c–ЭА.

Рис. 2.

Принципиальные технологические схемы экстрактивной ректификации трехкомпонентных азеотропных смесей (пояснения в тексте).

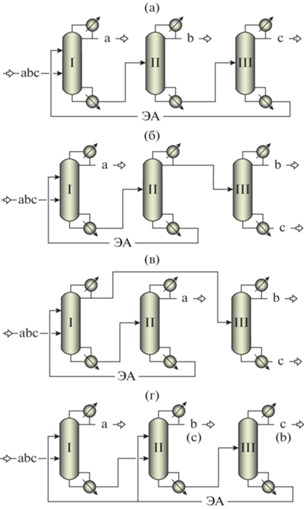
Если азеотропобразующим компонентом в системах 2.0–2b является вода, то она может концентрироваться в кубовом потоке колонны ЭР I. Тогда в колонне II проводится регенерация ЭА и выделение воды (рис. 2в). Такой вариант ЭР обсуждается для смесей вода (a) – ТГФ (b) – этилацетат (c) с ДМСО [28] и вода (a) – этанол (b) – трет.-бутиловый спирт (c) с этиленгликолем. В присутствии указанных агентов увеличивается летучесть органических веществ относительно воды [29].

Схему, представленную на рис. 2в, можно использовать и для разделения смесей 2.1–2b (рис. 1б). Ведение ЭА в этом случае должно увеличивать летучесть компонента а. Если зеотропные смеси b–с характеризуются относительной летучестью, близкой к 1, то разделение в схеме такой структуры не проводят.

Для ЭР смеси вода (а) – уксусная кислота (b) – муравьиная кислота (с) (рис. 1в) с сульфоланом предложена схема, представленная на рис. 2г [30]. Введение сульфолана также во вторую колонну обеспечивает выделение муравьиной кислоты более высокой чистоты. Обычно такой вариант ЭР используют для разделения систем, содержащих три бинарных азеотропа одного типа (min T) (рис. 1г, 1д).

В литературе обсуждаются различные аспекты функционирования схемы, приведенной на рис. 2г. Она предложена для разделения смесей 3.1–2 (рис. 1г): этилацетат (a) – этанол (b) – вода (c) с этиленгликолем [13], ДМСО [31], этилацетат (a) – изопропиловый спирт (b) – вода (c) с бинарным агентом ДМСО – этиленгликоль [32], бензол (a) – 1-пропанол (b) – вода (c) с глицерином [33] и бензол (a) – изопропиловый спирт (b) – вода (c) с этиленгликолем [34]. Схема той же структуры предложена для ЭР смесей 3.0–2 (рис. 1д): метанол (a) – ацетонитрил (b) – бензол (c) с хлорбензолом [35] и ТГФ (a) – этанол (b) – вода (c) с ДМСО, ЭГ или бинарным агентом ДМСО – этиленгликоль [36, 37].

В качестве ЭА для разделения трехкомпонентных водных смесей органических растворителей обычно рекомендуются диолы, глицерин и ДМСО. Выбор агентов определяется известным характером селективного влияния ЭА на бинарные азеотропные составляющие. Только в отдельных случаях сравнивают селективное действие нескольких промышленных высоко кипящих растворителей [31, 36, 37]. Оценка влияния ЭА на ПЖР проводится, в основном, по результатам вычислительных экспериментов. Систематические экспериментальные исследования влияния тестируемых растворителей на ПЖР ($\alpha _{{ij}}^{{{\text{ЭА}}}}$) проводили только для систем ацетат–спирт–вода [38, 39].

При выборе селективных агентов для ЭР систем, содержащих азеотропы разного типа (minT и maxT), сложно подобрать единственный агент, селективный в отношении бинарных азеотропных пар с противоположным отклонением от идеального поведения [21, 40]. Для разделения требуется использовать экстрактивные агенты с различным селективным действием. Выбор ЭА проведен для систем 3.1–4 (рис. 1е): ацетон (a) – хлороформ (b) – метанол (b) [20], метанол (a) – хлороформ (b) – ТГФ (c) [21]. Схемы разделения включают четыре ректификационные колонны. Такие структуры схем здесь не обсуждаются.

В настоящей работе рассматривается ЭР смеси тетрагидрофуран (ТГФ)–ацетонитрил (АЦН)–хлороформ (ХЛФ). Система содержит бинарные азеотропы ТГФ–ХЛФ (max T), ТГФ–АЦН (min T) и зеотропную составляющую АЦН–ХЛФ [41–45]. Данные о тройном азеотропе в системе отсутствуют [45–47]. На этапе формирования множества потенциальных агентов для ЭР смеси ТГФ–АЦН–ХЛФ применили методику, базирующуюся на анализе расчетных данных ПЖР смесей, образованных разделяемыми веществами и тестируемыми агентами [21, 38]. Из высоко кипящих растворителей, традиционно использующихся для ЭР в промышленности, предложен ДМСО, селективный в отношении обеих азеотропных пар ТГФ–ХЛФ (max T) и ТГФ–АЦН (min T).

Выбор селективных ЭА по результатам экспериментальных измерений ПЖР является предпочтительным, т.к. исключает получение некорректных результатов при моделировании фазовых равновесий в многокомпонентных системах со сложным фазовым поведением [48]. Поэтому результаты прогноза селективного действия тестируемых агентов целесообразно подтверждать результатами натурного эксперимента по измерению фазовых равновесий или экстрактивной ректификации.

Целью работы является экспериментальное изучение влияния ДМСО на ПЖР системы ТГФ–АЦН–ХЛФ эквимолярного состава при атмосферном давлении и разработка принципиальной схемы ЭР.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Характеристики реактивов приведены в табл. 1. Дополнительную очистку веществ не проводили.

Таблица 1.  

Характеристика реактивов

Реактив CAS No. Поставщик Содержание вещества*
Тетрагидрофуран 110-91-8 ЛенРеактив ≥0.99
Ацетонитрил 75-05-8 Sigma Aldrich ≥0.995
Хлороформ 67-66-3 Honeywell ≥0.99
Диметилсульфоксид 67-68-5 Sigma Aldrich ≥0.995

* мас. %

Чистота веществ подтверждена методом газожидкостной хроматографии с использованием хроматографа Кристалл-5000 (ХРОМАТЕК, Россия). Условия анализа: температура термостата колонок – 55–160°С, температура испарителя – 190°С, температура детектора (катарометр) – 160°С. Газ-носитель – гелий, расход 0.6 мл/мин. Разделение веществ проводили в капиллярной колонке Z-FFAP (длина 50 м, внутренний диаметр 0.32 мм), толщина нанесенной фазы 0.5 μм. Объем вводимой пробы 0.5 мкл.

Для взвешивания использовали аналитические весы OHAUS Adventurer AX324 (OHAUS, США) с погрешностью измерения ±0.0001 г. Жидкие смеси готовили смешением рассчитанных объемов жидкостей. Точность составов приготовленных смесей не превышала 0.01 мас. %.

Измерения ПЖР проводили в дифференцированном эбуллиометре по стандартной методике [49–51]. Схема прибора для измерения ПЖР приведена на рис. 3.

Рис. 3.

Схема дифференцированного эбуллиометра: 1 – кипятильник с электрообогревателем, 2 – трубка Коттреля, 3 – гильза термометра, 4 – обратный конденсатор, 5 – счетчик капель, 6 – сборник пробы парового конденсата, 7–8 – вентили для отбора проб парового конденсата и жидкости.

Объем прибора 120 мл. Давление поддерживали с точностью 1 мм рт. ст. с помощью системы маностатирования. Температуру определяли электронным термометром ЛТ-300, погрешность измерения ±0.01 град. Отбор проб для анализа состава паровой фазы проводили после достижения равновесия (постоянство температуры в приборе в течение 60 мин). Объем отбираемой для анализа пробы ~1 мкл.

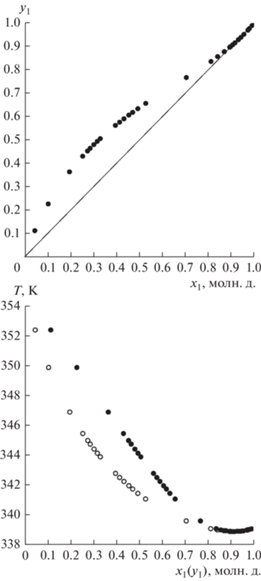
Экспериментальные данные ПЖР системы ТГФ (1)–АЦН (2) приведены в табл. 2.

Таблица 2.  

Экспериментальные данные равновесия жидкость–пар системы ТГФ (1)–АЦН (2) при 101.32 кПа

n x1, мол. д. y1, мол. д. T , K n x1, мол. д. y1, мол. д. T , K
1 0.0448 0.1152 352.29 17 0.7049 0.7613 339.49
2 0.1033 0.2011 349.74 18 0.8118 0.8340 338.94
3 0.1959 0.3657 346.78 19 0.8408 0.8552 338.93
4 0.2529 0.4504 345.27 20 0.8693 0.8778 339.02
5 0.2740 0.4783 344.86 21 0.8700 0.8773 339.04
6 0.2852 0.4793 344.63 22 0.8932 0.8968 338.73
7 0.3018 0.4954 344.35 23 0.8968 0.8980 338.8
8 0.3162 0.4881 344.1 24 0.9066 0.9036 338.71
9 0.3295 0.5006 343.94 25 0.9164 0.9167 338.69
10 0.3958 0.5793 342.88 26 0.9311 0.9248 338.78
11 0.4138 0.5817 342.58 27 0.9422 0.9403 338.69
12 0.4326 0.6018 342.3 28 0.9424 0.9414 338.75
13 0.4540 0.6117 342.03 29 0.9548 0.9530 338.72
14 0.4706 0.6286 341.73 30 0.9725 0.9698 338.74
15 0.4935 0.6330 341.32 31 0.9791 0.9751 338.79
16 0.5275 0.6522 340.93 32 0.9906 0.9895 338.83

Затем были измерены ПЖР смесей ТГФ (1)–АЦН (2)–ХЛФ (3) и ТГФ (1)–АЦН (2)–ХЛФ (3)–ДМСО (4) с разным содержанием агента при 101.32 кПа. К смеси ТГФ–АЦН–ХЛФ (F) эквимолярного состава добавляли разное количество ДМСО (F4). В табл. 3 составы паровой (у) и жидкой (х) фаз приведены в мол. д., температура – в град. К. По результатам анализа ДМСО в паровой фазе отсутствует.

Таблица 3.  

Экспериментальные данные ПЖР смесей ТГФ (1)–АЦН (2)–ХЛФ (3)–ДМСО (4) при 101.32 кПа

F4 : F, моль/моль 0/1 0.5/1 1/1 2/1
Т 342.68 355.56 364.91 375.63
х1 0.3334 0.2221 0.1651 0.1111
х2 0.3333 0.2221 0.1651 0.1111
х3 0.3333 0.2220 0.1650 0.1111
х4 – 0.3338 0.5048 0.6667
у1 0.3213 0.2611 0.2463 0.2588
у2 0.3541 0.3211 0.2956 0.2878
у3 0.3246 0.4178 0.4581 0.4533

ОСНОВНАЯ ЧАСТЬ

Моделирование фазовых равновесий. Проверка термодинамической согласованности данных ПЖР системы ТГФ–АЦН при 101.32 кПа проведена с использованием теста Herington [52]. Согласно тесту Herington, экспериментальные данные должны удовлетворять критерию: |D – J| < 10, где

$D = 100\left| {\frac{{A - B}}{{A + B}}} \right| = 9.3863,$
$J = 150\left| {\frac{{{{T}_{{{\text{max}}}}} - {{T}_{{{\text{min}}}}}}}{{{{T}_{{{\text{max}}}}}}}} \right| = 2.9142.$

Здесь А, В – площади фигур на рис. 4, Tmax, Tmin – максимальная и минимальная температуры в системе. Для массива экспериментальных данных, представленных в табл. 2: А = 0.1669, B = = 0.1833, |D – J| = 6.471. Измеренные экспериментальные данные ПЖР системы ТГФ–АЦН при 101.32 кПа являются термодинамически согласованными.

Рис. 4.

Графическое представление результатов тесту Herington. для ПЖР системы ТГФ (1)–АЦН (2) при 101.32 кПа: а – экспериментальные данные, б – расчетные данные; γ1, γ2 – коэффициенты активности компонентов.

Массив данных ПЖР системы ТГФ–АЦН (табл. 2) описан моделью локальных составов NRTL [53]. Коэффициенты активности компонентов (γ) в модели NRTL рассчитываются следующим образом:

(3)
$\begin{gathered} \ln {{\gamma }_{i}} = \frac{{\sum\limits_j^n {{{x}_{j}}{{\tau }_{{ji}}}{{G}_{{ji}}}} }}{{\sum\limits_k^n {{{x}_{k}}{{G}_{{ji}}}} }} + \\ + \,\,\sum\limits_j^n {\frac{{{{x}_{j}}{{G}_{{ij}}}}}{{\sum\limits_k^n {{{x}_{k}}{{G}_{{kj}}}} }}} \left( {{{\tau }_{{ij}}} - \,\,~\frac{{\sum\limits_i^n {{{x}_{m}}{{\tau }_{{mj}}}{{G}_{{mj}}}} }}{{\sum\limits_k^n {{{x}_{k}}{{G}_{{kj}}}} }}} \right), \\ \end{gathered} $
где x – состав жидкой фазы, τ − параметры бинарного взаимодействия компонентов (i, j, k). Параметры имеют вид:
(4)
${{\tau }_{{ij}}} = {{a}_{{ij}}} + \frac{{{{b}_{{ij}}}}}{T},$
(5)
$\left. {{{G}_{{ij}}} = \exp ( - {{c}_{{ij}}}{{\tau }_{{ij}}}} \right),$
где ${{c}_{{ij}}} = {{c}_{{ji}}}$. Для системы ТГФ–АЦН: aij = 8.2676, aji = –2.875, bij = –417.82, bji = –928.99, cij = 0.02202.

Средние абсолютные отклонения AAD (6), средние относительные отклонения (7) и среднеквадратичное отклонение (RMD) (8) рассчитывали для экспериментальных (exp) и расчетных (calc) значений температуры Т и состава паровой фазы для системы ТГФ–АЦН. Значения (6)–(8) и максимальные абсолютные отклонения Тmax, ymax приведены в табл. 4. Описание массива экспериментальных данных ПЖР является удовлетворительным, т.к. ошибки не превышают 3%.

(6)
$ADD = \frac{1}{n}\mathop \sum \limits_i^n \left| {{{A}_{i}}^{{{\text{exp}}}} - {{A}_{i}}^{{{\text{calс}}}}} \right|,$
(7)
$AARD = \frac{1}{n}\mathop \sum \limits_i^n \left| {\frac{{{{A}_{i}}^{{{\text{exp}}}} - {{A}_{i}}^{{{\text{calс}}}}}}{{{{A}_{i}}^{{{\text{exp}}}}}}} \right|,$
(8)
$RMSD = \sqrt {\frac{{\sum\limits_i^n {{{{({{A}_{i}}^{{{\text{exp}}}} - {{A}_{i}}^{{{\text{calс}}}})}}^{2}}} }}{n}} .$
Таблица 4.  

Ошибки описания равновесия жидкость–пар системы ТГФ–АЦН при 101.32 кПа

Модель Температура Состав паровой фазы
AARD, % ADD, K ADDmax, K RMSD AARD, % ADD, мол. д. ADDmax, мол. д. RMSD
NRTL 0.03 0.12 0.22 0.13 2.26 0.01 0.03 0.0095

Диаграммы фазового равновесия системы ТГФ–АЦН представлены на рис. 5.

Рис. 5.

Диаграммы ПЖР системы ТГФ (1)–АЦН (2) при 101.32 кПа.

Для моделирования фазовых равновесий тройной и четырехкомпонентной систем использовали параметры уравнения NRTL из базы данных программного комплекса Aspen Plus V.10.0. Расчетные азеотропные данные приведены в табл. 5. Структура диаграммы ПЖР (2.1–3b) показана на рис. 6.

Таблица 5.  

Расчетные азеотропные данные системы ТГФ (1)–АЦН (2)–ХЛФ (3) при 101.32 кПа.

ТГФ, мол. д. АЦН, мол. д. ХЛФ, мол. д. Ткип, K
0.9093 0.0907   338.88
0.3510 0.3089 0.3401 344.82
0.5489   0.4511 346.68
Рис. 6.

Структура диаграммы ПЖР системы ТГФ (1)–АЦН (2)–ХЛФ (3) при 101.32 кПа.

Расчетные данные ПЖР для смесей ТГФ–АЦН–ХЛФ и ТГФ–АЦН–ХЛФ–ДМСО приведены в табл. 6. Состав тройного азеотропа близок к эквимолярному. Азеотропные данные системы ТГФ–АЦН согласуются с данными [45].

Таблица 6.  

Расчетные данные ПЖР смесей ТГФ (1)–АЦН (2)–ХЛФ (3)–ДМСО (4) при 101.32 кПа

F4 : F, моль /моль 0/1 0.5/1 1/1 2/1
Т 344.82 358.20 367.59 379.48
х1 0.3334 0.2227 0.1658 0.1111
х2 0.3333 0.2226 0.1657 0.1111
х3 0.3333 0.2226 0.1657 0.1111
х4 – 0.3321 0.5028 0.6667
у1 0.3351 0.5575 0.5913 0.5735
у2 0.3265 0.1978 0.1758 0.1929
у3 0.3384 0.2381 0.2136 0.1891
у4 – 0.007 0.0193 0.0445

По экспериментальным и расчетным данным ПЖР были определены относительные летучести веществ (2) в смесях ТГФ–АЦН–ХЛФ и ТГФ–АЦН–ХЛФ–ДМСО (табл. 7). Согласно экспериментальным и расчетным данным, в присутствии ДМСО увеличивается летучесть ТГФ относительно АЦН (α12) и ХЛФ (α13). При использовании ДМСО возможно выделение ТГФ в дистиллатном потоке колонны ЭР.

Таблица 7.  

Относительная летучесть компонентов в смесях ТГФ (1)–АЦН (2)–ХЛФ (3)–ДМСО (4) при 101.32 кПа

F4 : F, моль/моль 0/1 0.5/1 1/1 2/1 0/1 0.5/1 1/1 2/1
α Эксперимент Расчет NRTL
α12 0.92 1.30 1.55 1.58 1.03 2.82 3.36 2.97
α13 1.01 1.60 1.86 1.75 0.99 2.34 2.77 3.03
α23 1.10 1.23 1.20 1.11 0.96 0.83 0.82 1.02

Разделение смеси ТГФ–АЦН–ХЛФ с ДМСО следует проводить в схемах, представленных на рис. 7. После выделения ТГФ в колонне I возможен разный порядок выделения компонентов из зеотропной смеси АЦН–ХЛФ–ДМСО.

Рис. 7.

Принципиальные схемы экстрактивной ректификации смеси ТГФ–АЦН–ХЛФ с ДМСО: I, II, III – ректификационные колонны, F – разделяемая смесь.

Расчеты схем ЭР проведены по стандартной методике на платформе Aspen Plus V.10.0. Рассмотрено разделение F = 100 кмоль/ч смеси ТГФ–АЦН–ХЛФ эквимолярного состава, что соответствует 7751 кг/ч, состав 31.02, 51.33, 17.65 мас. %. С использованием модуля Sensitivity Analysis выбраны режимы работы ректификационных колонн, обеспечивающие разделение с наименьшими энергозатратами (нагрузки кипятильников колонн Q). В расчетах варьировали число теоретических тарелок (N), уровни ввода жидких потоков (NF, NF4), флегмовое число R и для колонны ЭР – также количество вводимого ДМСО (F4). Разделяемую смесь вводили при температуре кипения, ДМСО – при 313 К, давление колонны ЭР атмосферное. Для колонны II в обеих схемах выбрано давление 30 кПа для предотвращения разложения ДМСО.

В расчетах достигали чистоты с содержанием основного вещества: ТГФ – не менее 99.5 мас. % (ТУ 2631-125-44493179-08), АЦН – не менее 99.8 мас. % (ТУ 2636-092-44493179-04), ХЛФ – не менее 99.5 мас. % (ТУ 2631-014-44493179-98).

Статические параметры колонн и результаты разделения приведены в табл. 8.

Таблица 8.  

Статические параметры ректификационных колонн и результаты разделения

Колонна I II III II III
Схема а, рис. 7 б, рис. 7
Давление, кПа 101.32 30 30 30 101.32
N; NF4/NF 36; 6/12 46; –/20 12;–/5 13;–/5 48; –/25
R 2.1 11.6 0.9 0.8 6.7
Дистиллатный поток Т, К 339.13 302.22 316.42 307.15 334.25
Состав, мас. % х1 99.98 0.01 – 0.01 –
х2 – 3.22 78.06 25.59 0.02
х3 0.02 96.77 21.94 74.4 99.98
х4 – – – – –
Кубовый поток Т, К 406.55 381.32 421.75 421.75 354.78
Состав, мас. % х1 – – – – 0.03
х2 5.68 6.13 – – 99.84
х3 16.51 1.73 0.01 0.01 0.13
х4 77.81 92.14 99.99 99.99 –
Q, МВт 1.93 3.04 1.15 1.03 2.16

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Расчет по модели NRTL обеспечивает удовлетворительное описание данных ПЖР тройной смеси (табл. 3, 6). Состав тройного азеотропа при 101.32 кПа близок к эквимолярному. Сравнение данных табл. 7 показывает, что значения αij (2) для эквимолярной смеси ТГФ–АЦН–ХЛФ, определенные по экспериментальным и расчетным данным, практически совпадают. Это дополнительно подтверждает адекватность математической модели для расчетов ПЖР тройной системы.

Для смесей, содержащих ДМСО, зафиксированы различия экспериментальных и расчетных значений относительной летучести $\alpha _{{ij}}^{{{\text{ЭА}}}}$ (табл. 7). Однако характер селективного влияния ДМСО на ПЖР веществ одинаковый.

Расчеты ректификационного разделения подтвердили возможность выделения в дистиллатном потоке колонны ЭР (колонна I, рис. 7) практически чистого ТГФ 99.88 мас. % при соотношении F4 : F = 1/2.4 (моль/моль), что соответствует F4 : F = 1/2.42 (кг/кг).

Сравнение вариантов разделения проводили по суммарным нагрузкам кипятильников колонн (табл. 8). Для схемы, представленной на рис. 7а, суммарная нагрузка составляет 6.12 МВт, а для схемы рис. 7б – 5.12 МВт, т.е. на 16% ниже. Для выделения ХЛФ из смеси АЦН–ХЛФ–ДМСО требуется высокое флегмовое число (колонна II, рис. 7а).

В предлагаемом варианте разделения смеси ТГФ–АЦН–ХЛФ (схема на рис. 7б) основной вклад в энергозатраты вносит колонна III ректификации зеотропной смеси (табл. 8). В колонну III подается дистиллатный поток колонны II. При 101.32 кПа относительная летучесть α32 ≈1.3. Изменение давления практически не влияет на ПЖР: α32 ≈1.34 (1.33) при 30 (150) кПа. Для выбора условий разделения смеси АЦН–ХЛФ необходимы дополнительная оптимизация с детализацией текущих и капитальных затрат.

ПЖР бинарных составляющих системы АЦН–ХЛФ и ТГФ–ХЛФ измерены в изотермических условиях, в диапазонах, не совпадающих с температурными режимами ректификации [41–44]. Использование имеющихся в базах данных параметров математических моделей для расчетов в изобарических условиях может быть недостаточно корректным. Поэтому необходимы дальнейшие измерения ПЖР систем, содержащих ХЛФ, при атмосферном давлении.

ЗАКЛЮЧЕНИЕ

Проведены экспериментальные измерения ПЖР для полного диапазона составов системы ТГФ–АЦН при 101.32 кПа. Получены параметры модели NRTL. Экспериментальные исследования фазовых равновесий смесей ТГФ–АЦН–ХЛФ и ТГФ–АЦН–ХЛФ–ДМСО показали, что ДМСО можно использовать в качестве экстрактивного агента для выделения ТГФ. Определена структура диаграммы ПЖР системы ТГФ–АЦН–ХЛФ. Состав тройного азеотропа близок к эквимолярному при атмосферном давлении. Предложена принципиальная схема разделения. Расчеты ректификационного разделения подтвердили селективное действие ДМСО. Определены статические параметры работы колонн схемы экстрактивной ректификации, обеспечивающие возможность получения веществ товарного качества.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 19-19-00620-п).

Авторы заявляют об отсутствии конфликта интересов.

ОБОЗНАЧЕНИЯ

F поток смеси, кг/ч
Т температура, К
N число теоретических тарелок
Q нагрузки кипятильников колонн, МВт
R флегмовое число
S селективности экстрактивных агентов
x состав жидкой фазы, мол. д., мас. %
y состав паровой фазы, мол. д., мас. %
α относительная летучесть компонентов
АЦН ацетонитрил
ДМСО диметилсульфоксид
ПЖР парожидкостное равновесие
ТГФ тетрагидрофуран
ХЛФ хлороформ
ЭА экстрактивный агент
ЭР экстрактивная ректификация

ИНДЕКСЫ

1 тетрагидрофуран
2 ацетонитрил
3 хлороформ
4 диметилсульфоксид
i, j номера компонентов
max максимальное значение
min минимальное значение
exp эксперимент
calc расчет
кип кипение

Список литературы

  1. Serafimov, L.A., Frolkova A.K. Fundamental principle of concentration-field redistribution between separation regions as a basis for the design of technological systems // Theor. Found. Chem. Eng. 1997. V. 31. № 2. P. 159.

  2. Frolkova A.K. Separation of azeotropic mixtures. Physicochemical fundamentals and technological methods / Frolkova A.K. Moscow.: Gumanit. Centr VLADOS, 2010. [Фролкова А.К. Разделение азеотропных смесей. Физико-химические основы и технологические приемы. Монография / А.К. Фролкова. М.: Гуманитар. Центр ВЛАДОС, 2010.]

  3. Mahdi T., Ahmad A., Nasef M.M., Ripin A. State-of-the-art technologies for separation of azeotropic mixtures // Sep. Purif. Review. 2015. V. 44. № 4. P. 308.https://doi.org/10.1080/15422119.2014.963607

  4. Zaretskii M. I., Rusak V.V., Chartov E.M. Extractive distillation in chemical technology: A Review // Coke and Chemistry. 2010. V. 53. № 3. P. 110. [Зарецкий М.И., Русак В.В., Чартов Е.М. Экстрактивная ректификация в химической технологии: Обзор // Кокс и химия. 2010. № 3. С. 36.]https://doi.org/10.3103/S1068364X10030075

  5. Биттрих Г.Й., Гайле А.А., Лемпе Д. Разделение углеводородов с использованием селективных растворителей / Биттрих Г.Й., Гайле А.А., Лемпе Д. и др. Л.: Химия: Ленингр. отд-ние, 1987.

  6. Гайле А.А. N-метилпирролидон: получение, свойства и применение в качестве селективного растворителя / А.А. Гайле, Г.Д. Залищевский. Санкт-Петербург: Химиздат, 2005

  7. Lei Z., Li C., Chen B. Extractive distillation: a Review // Sep. Purif. Review. 2003. V. 32. № 2. P. 121.

  8. Kiss A.A. Distillation: extractive distillation // Molecular Sci. Chem. Eng. 2013. https://doi.org/10.1016/b978-0-12-409547-2.05949-7

  9. Gerbaud V., Rodríguez-Donis I., Hegely L. et al. Review of extractive distillation: Process design, operation optimization and control // Chem. Eng. Res. Des. 2019. V. 141. P. 229. https://doi.org/10.1016/j.cherd.2018.09.020

  10. Teng Z., Zhen S., Xiang Z., Rafiqul G., Kai S. Optimal solvent design for extractive distillation processes: a multiobjective optimization-based hierarchical framework // Ind. Eng. Chem. Res. 2019. V. 58. № 15. P. 5777. https://doi.org/10.1021/acs.iecr.8b04245

  11. Анохина Е.А. Энергосбережение в процессах экстрактивной ректификации. Тонкие химические технологии. 2013. Т. 8. № 5. С. 3.

  12. Momoh S.O. Assessing the accuracy of selectivity as a basis for solvent screening in extractive distillation processes // Sep. Sci. Technol. 1991. V. 26. № 5. P. 729. https://doi.org/10.1080/01496399108049911

  13. Raeva V.M., Sazonova A.Yu. Separation of ternary mixtures by extractive distillation with 1,2-ethandiol and glycerol // Chem. Eng. Res. Des. 2015. V. 99. 2015. P. 125. https://doi.org/10.1016/j.cherd.2015.04.032

  14. Раева В.М., Капранова А.С. Сравнение эффективности экстрактивных агентов при разделении смеси ацетон–метанол // Хим. пром-сть сегодня. 2015. № 3. С. 33.

  15. Myul’khi E.P., Khristenko M.S., Andryukhova M.V. Choice of an extractive separating agent for the 1-pentanol – cyclohexanone binary mixture // Russ. J. Appl. Chem. 2006. V. 79. № 7. P. 1076 [Мюльхи Е.П., Христенко М.С., Андрюхова М.В. Выбор экстрактивного агента для 1-пентанол – циклогексанон бинарной смеси // Журн. прикл. химии. 2006. Т. 79. № 7. С. 1086.]https://doi.org/10.1134/S1070427206070068]

  16. Song Y., Du Y., Wang R., Hongze Y. et al. Vapor–liquid equilibria and conceptual design of extractive distillation for separating ethanol and ethyl propionate // J. Chem. Eng. Data. V. 65. № 7. P. 3428. https://doi.org/10.1021/acs.jced.9b01162

  17. Коган В.Б. Азеотропная и экстрактивная ректификация / Л.: Химия, 1971.

  18. Serafimov L.A., Frolkova A.K., Bushina D.I. Extractive distillation of binary azeotropic mixtures // Theor. Found. Chem. Eng. 2008. V. 42. № 5. P. 507. [Серафимов Л.А., Фролкова А.К., Бушина Д.И. Экстрактивная ректификация бинарных азеотропных смесей // Теорет. основы хим. технологии. 2008. Т. 42. № 5. С. 521.] https://doi.org/10.1134/S0040579508050059

  19. Kossack S., Kraemer K., Gani R., Marquardt W.A. Systematic synthesis framework for extractive distillation processes // Chem. Eng. Res. Des. 2008. V. 86. № 7. P. 781. https://doi.org/10.1016/j.cherd.2008.01.008

  20. Benyounes H., Frolkova A.K. Aspects of multicomponent mixture separation in the presence of selective solvents // Chem. Eng. Communications. 2010. V. 197. № 7. P. 901. https://doi.org/10.1080/00986440903088561

  21. Raeva V.M., Sukhov D.I. Selection of extractive agents for the separation of chloroform–methanol–tetrahydrofuran mixture // Fine Chemical Technologies. 2018. V. 13. № 3. P. 30. [Раева В.М., Сухов Д.И. Выбор экстрактивных агентов для разделения смеси хлороформ–метанол–тетрагидрофуран // Тонкие химические технологии. 2018. Т. 13. № 3. С. 30.] https://doi.org/10.32362/24106593-2018-13-3-30-40

  22. Frolkova A.K., Frolkova A.V., Raeva V.M., Zhuchkov V.I. Features of distillation separation of multicomponent mixtures // Fine Chemical Technologies. 2022. V. 17. № 2. P. 87. [Фролкова А.К., Фролкова А.В., Раева В.М., Жучков В.И. Особенности ректификационного разделения многокомпонентных смесей // Тонкие химические технологии. 2022. Т. 17. № 2. С. 87.] https://doi.org/10.32362/2410-6593-2022-17-2-87-106

  23. Kiva V.N., Hilmen E.K., Skogestad S. Azeotropic phase equilibrium diagrams: a survey // Chem. Eng. Sci. 2003. V. 58. P. 1903. https://doi.org/10.1016/S0009-2509(03)00018-6

  24. Raeva V.M., Sazonova A.Yu. Separation of ternary mixtures by extractive distillation with 1,2-ethandiol and glycerol // Chem. Eng. Res. Des. 2015. V. 99. P. 125. https://doi.org/10.1016/j.cherd.2015.04.032

  25. Wang Yi., Bu G. Geng X., Zhu Z., et al. Design optimization and operating pressure effects in the separation of acetonitrile/methanol/water mixture by ternary extractive distillation // J. Cleaner Production. 2019. V. 218. P. 212. https://doi.org/10.1016/j.jclepro.2019.01.324

  26. Raeva V.M., Dubrovskii A.M. Comparison of extractive distillation flowsheets for methanol–tetrahydrofuran–water mixtures // Fine Chem. Techn. 2020. V. 15. № 3. P. 21. [Раева В.М., Дубровский А.М. Сравнение схем экстрактивной ректификации смесей метанол–тетрагидрофуран–вода // Тонкие химические технологии. 2020. Т. 15. № 3. С. 21.] https://doi.org/10.32362/2410-6593-2020-15-3-21-30

  27. Zhu Z., Wang Y., Hu J., Qi X. et al. Extractive distillation process combined with decanter for separating ternary azeotropic mixture of toluene-methanol-water // Chem. Eng. Transactions. 2017. V. 61. P. 763. https://doi.org/10.3303/CET1761125

  28. Yang A., Su Y., Shi T. et al. Energy-efficient recovery of tetrahydrofuran and ethyl acetate by triple-column extractive distillation: entrainer design and process optimization // Front. Chem. Sci. Eng. 2022. V. 16. P. 303. https://doi.org/10.1007/s11705-021-2044-z

  29. Shi X., Zhu X., Zhao X., Zhang Z. Performance evaluation of different extractive distillation processes for separating ethanol/tert-butanol/water mixture // Process Safety and Environmental Protection. 2020. V. 137. P. 246. https://doi.org/10.1016/j.psep.2020.02.015

  30. Raeva V.M., Gromova O.V. Separation of water–formic acid–acetic acid mixtures in the presence of sulfolane // Fine Chemical Technologies, 2019. V. 14. № 4. P. 24. [Раева В.М., Громова О.В. Разделение смеси вода–муравьиная кислота–уксусная кислота в присутствии сульфолана // Тонкие химические технологии. 2019. Т. 14. № 4. С. 24.] https://doi.org/10.32362/2410-6593-2019-14-4-24-32

  31. Yang A., Zou H., Chien I-L., Wang D. et al. Optimal Design and Effective Control of Triple-Column Extractive Distillation for Separating Ethyl Acetate/Ethanol/Water with Multi-Azeotrope // Ind. Eng. Chem. Res. 2019. V. 58. P. 7265. https://doi.org/10.1021/acs.iecr.9b00466

  32. Jian X., Li J., Qing Ye, Lia X. Intensification and analysis of extractive distillation processes with preconcentration for separating ethyl acetate, isopropanol and water azeotropic mixtures // Sep. Purif. Technol. 2022. V. 287. P. 120499. https://doi.org/10.1016/j.seppur.2022.120499

  33. Ma Z., Yao D., Zhao J., et al. Efficient recovery of benzene and n-propanol from wastewater via vapor recompression assisted extractive distillation based on techno-economic and environmental analysis // Process Safety and Environmental Protection. 2021. V. 148. P. 462. https://doi.org/10.1016/j.psep.2020.10.033

  34. Shan B., Zheng Qi, Chen Z., Shen Y. et al. Dynamic control and performance comparison of conventional and dividing wall extractive distillation for benzene/isopropanol/water separation // J. Taiwan Institute of Chem. Engineers. 2021. V. 128. P. 1. https://doi.org/10.1016/j.jtice.2021.08.005

  35. Yang A., Chun W., Sun S., Shi T. et al. Dynamic study in enhancing the controllability of an energy-efficient double side-stream ternary extractive distillation of acetonitrile/methanol/benzene with three azeotropes // Sep. Purif. Technol. 2020. V. 242. P. 141.https://doi.org/10.1016/j.seppur.2020.116830

  36. Zhao, Y., Zhao, T., Jia, H. et al. Optimization of the composition of mixed entrainer for economic extractive distillation process in view of the separation of tetrahydrofuran/ethanol/water ternary azeotrope // J. Chem. Technol. Biotechnology. 2017. V. 92. № 9. P. 2433. https://doi.org/10.1002/jctb.5254

  37. Zhao Y., Kang Ma, Bai W., Du D. et al. Energy-saving thermally coupled ternary extractive distillation process by combining with mixed entrainer for separating ternary mixture containing bioethanol // Energy. 2018. V. 148. P. 296. https://doi.org/10.1016/j.energy.2018.01.161

  38. Berg L., Yeh An-I., Ratanapupech P. The recovery of ethyl acetate by extractive distillation // Chem. Eng. Communications. 1985. V. 39. P. 193. https://doi.org/10.1080/00986448508911670

  39. Berg L., Yeh An-I. The breaking of ternary acetate-alcohol-water azeotropes by extractive distillation // Chem. Eng. Communications. 1986. V. 48. P. 93. https://doi.org/10.1080/00986448608911779

  40. Raeva V.M., Stoyakina I.E. Selecting extractive agents on the basis of composition – excess Gibbs energy data. // Russian J. Physical Chem. A. 2021. Т. 95. № 9. С. 1779. [Раева В.М., Стоякина И.Е. Выбор экстрактивных агентов с использованием данных состав – избыточная энергия Гиббса // Журн. физ. химии. 2021. Т. 95. № 9. С. 1320.]https://doi.org/10.31857/S004445372109020X.

  41. Solimo H. N., Gomez Marigliano A.C. Excess properties and vapor-liquid equilibrium data for the chloroform + tetrahydrofuran binary system at 30 C // J. Solution Chem. 1993. V. 22. № 10. P. 951. https://doi.org/10.1007/bf00646606

  42. Nagata I., Kawamura Y. Excess thermodynamic functions and complex formation in binary liquid mixtures containing acetonitrile // Fluid Phase Equil. 1979. V. 3. № 1. P. 1. https://doi.org/10.1016/0378-3812(79)80023-0

  43. Govindan A.P., Varma Y.B.G., Ananth M.S. Isothermal (vapor + liquid) equilibria of four binary mixtures // J. Chem. Thermodyn. 1984. V. 16. № 1. P. 1. https://doi.org/10.1016/0021-9614(84)90068-5

  44. Lazarte M., Gomez Marigliano A.C., Solimo H.N. Excess molar volume, viscosity, and molar refraction deviations, and liquid-vapor equilibrium at 303.15 k for chloroform + acetonitrile binary mixture. An infrared study // J. Solution Chemistry. 2004. V. 33. № 12. P. 1549. https://doi.org/10.1007/s10953-004-1393-9

  45. Gmehling J., Bölts R. Azeotropic data for binary and ternary systems at moderate pressures // J. Chem. Eng. Data. 1996. V. 41. № 2. P. 202. https://doi.org/10.1021/je950228f

  46. Огородников С.К., Лестева Т.М. и др. Азеотропные смеси. Справочник / Под ред. В. Б. Когана. Химия, Л., 1971.

  47. Сусарев М.П. Тройные азеотропные системы / Сусарев М.П., Кудрявцева Л.С., Эйзен О.Г. АН ЭССР. Ин-т химии. Таллин: Валгус, 1973.

  48. Frolkova A.V., Fertikova V.G., Rytova E.V., Frolkova A.K. Evaluation of the adequacy of phase equilibria modeling based on various sets of experimental data. Fine Chemical Technologies. 2021. V. 16. № 6. Р. 457. [Фролкова А.В., Фертикова В.Г., Рытова Е.В., Фролкова А.К. Оценка адекватности моделирования фазовых равновесий на основе различных наборов экспериментальных данных. Тонкие химические технологии. 2022. Т. 16. № 6. С. 457.] https://doi.org/10.32362/2410-6593-2021-16-6-457-464

  49. Свентославский В.В. Азеотропия и полиазеотропия / Перевод с англ. Мозжухина А.С.; Под ред. канд. техн. наук Л.А. Серафимова Москва: Химия, 1968.

  50. Yunfei Song, Yuezhan Du, Ruyue Wang et al. Isobaric Vapor-liquid equilibrium data for two binary systems n-hexane + 1,2-dimethoxyethane and methylcyclopentane + 1,2-dimethoxyethane at 101.3 kPa. J. Chem. Eng. Data. 2018. V. 63. № 2. P. 395. https://doi.org/10.1021/acs.jced.7b00802

  51. Yunfei Song, Yuezhan Du, Ruyue Wang et al. Vapor-liquid equilibria and conceptual design of extractive distillation for separating ethanol and ethyl propionate. J. Chem. Eng. Data. 2020. V. 65. № 7. P. 3428. https://doi.org/10.1021/acs.jced.9b01162

  52. Herington E.F.G. Tests for the consistency of experimental isobaric vapour-liquid equilibrium data. J. Inst. Petrol. 1951. V. 37. P. 457.

  53. Уэйлес С. Фазовые равновесия в химической технологии. В 2 ч. / Пер. с англ. под ред. В.С. Бескова. М.: Мир, 1989. [Walas S. Phase Equilibria in Chemical Engineering Butterworth-Heinemann. 1985.]

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал