Теоретические основы химической технологии, 2023, T. 57, № 2, стр. 194-201
Модель экстрагирования из поры в окружающее пространство
Л. Ю. Александрова a, *, А. И. Мошинский a, В. В. Сорокин a, Г. Н. Турманидзе a
a Санкт-Петербургский химико-фармацевтический университет
Санкт-Петербург, Россия
* E-mail: pisce-capricorn@inbox.ru
Поступила в редакцию 09.01.2022
После доработки 11.01.2023
Принята к публикации 17.01.2023
- EDN: EITWJC
- DOI: 10.31857/S0040357123020033
Аннотация
Исследуется задача извлечения целевого компонента из цилиндрической поры. Решение этой задачи положено в основу математической модели массопереноса в пористой среде. Предложенная модель применима для описания ряда процессов, в частности, экстрагирования и промывки осадков. Приведены графические иллюстрации, поясняющие протекание процесса промывки в рамках предложенной модели.
ВВЕДЕНИЕ
При описании извлечения целевого компонента (ЦК) из пористых тел широкое распространение получила диффузионная модель. При этом предполагается, что сплошная среда как бы однородна и перенос ЦК в ней описывается обычным уравнением диффузии. Таким образом внутренняя структура пористого материала практически игнорируется. Иногда она учитывается косвенным образом путем введения некого эффективного коэффициента диффузии, отличного от молекулярного. Фактически основным уравнением процесса является уравнение диффузии, а специфика конкретного процесса извлечения ЦК учитывается граничным и начальным условиями. Решение ряда задач экстрагирования на основе отмеченной модели изложено, например, в работах [1, 2]. В работе [3] предложено учесть влияние структуры пористой среды изменением коэффициента диффузии по координате. Уточнение расчетов по этой модели проведено в работе [4]. Один из подходов моделирования процессов в двухкомпонентных (двухфазных) средах – построение конкретной модели пористой среды, как бы элемента осредненной структуры и далее вывод уравнения процесса традиционными методами на основе выбранной модели пористого материала.
Сочетание конвективного переноса вещества с диффузионным и другими обменными процессами в пористой среде лежит в основе описания ряда природных и технологических процессов [5–7]. В простейшем случае распространение вещества в пористой среде моделируется уравнением конвективной диффузии [7]. Однако эксперименты нередко дают отклонения от решений соответствующих задач, опирающихся на диффузионный закон Фика. Это обычно объясняют наличием определенной структуры пористой среды, отличной от однородного континуума. Для описания массопереноса в подобных средах вводят различные варианты каверн, застойных зон, пор различных масштабов и т.п. (см. например [5–11]). Распространены также двухкомпонентные модели экстрагирования, промывки осадков и т.п. Подразумевается, что пространство, в котором протекает процесс, состоит из двух взаимопроникающих континуумов. Между этими континуумами происходит обмен веществом и другими характеристиками процесса [11]. Наличие дополнительной структуры проявляется как своеобразный релаксационный процесс переноса в дисперсной среде [11]. Отметим, что при описании сорбционных явлений математическая модель выглядит также (аналогично), а в роли застойных зон (и т.п., которых нет) выступает поверхность частиц среды [12]. В то же время отклонение от закона Фика в пористой системе может описываться и в рамках однородного континуума введением более сложного уравнения для потока вещества, например максвелловского типа и т.п. [13–18].
В последнее время проявляется определенный интерес к различного рода нестационарным воздействиям на дисперсные, в частности, пористые среды как импульсного типа [19, 20], так и периодического [21−24, 25 стр. 385].
Нахождение аналитических выражений, которые несложно довести до графических иллюстраций искомых функций – основная цель предложенной работы.
Здесь мы будем полагать, что пористую среду можно смоделировать набором пор (каналов), находящихся на достаточном удалении друг от друга, чтобы можно было бы пренебречь их взаимным влиянием. В простейшем случае (на начальном этапе исследования) будем также пренебрегать движением жидкости вне поры, как и в самой поре. Поры выходят на поверхность образца, откуда целевое вещество переходит во внешнее пространство по диффузионному закону (подчиняется уравнению диффузии).
Рассматриваемая задача состоит из традиционных уравнений диффузии в поре и снаружи ее, граничных условий согласования концентрация ЦК и потоков вещества. Постановка задачи предполагает, что при t < 0 все вещество сосредоточено в поре. При t = 0 пора “открывается” и начинается диффузионный процесс выхода ЦК из поры в окружающее пространство. Будем считать коэффициент диффузии в поре и внешней области совпадающими. Известно, что при наличии циркуляционного течения в поре можно ввести эффективный коэффициент диффузии [26], значения которого выше молекулярного, т.е. отмеченное равенство коэффициентов диффузии может быть нарушено. Схематически структура среды (пора) представлена на рис. 1.
Обычно для описания процесса массопереноса в поре и вне ее предполагаются свои, но взаимосвязанные уравнения. Здесь же анализируется решение без подобного представления, однако в месте контакта поры и внешнего пространства граничные условия четвертого рода были несколько упрощены.
ЗАДАЧА ДЛЯ ЕДИНИЧНОЙ ПОРЫ [27]
Уравнения и дополнительные условия задачи могут быть записаны в следующей форме. В области I (0 ≤ r < ∞), (0 < z < ∞) концентрация C1 (r, z, t) удовлетворяет уравнению
В области II мы имеем одномерное уравнение диффузии
(1)
${{\left. {\frac{{\partial {{C}_{2}}}}{{\partial z}}} \right|}_{{{\text{z}} = 0}}} = f\left( t \right),\,\,\,\,{{\left. {\frac{{\partial {{C}_{2}}}}{{\partial z}}} \right|}_{{{\text{z}} = - l}}} = 0,\,\,\,\,{{\left. {{{C}_{2}}} \right|}_{{{\text{z}} = 0}}} = {{C}_{0}}.$Основной интерес для нас представляет величина полной массы ЦК в поре,
Для функции M(t) приближенное решение сформулированной задачи получено в работе [27] и имеет вид
(2)
$\begin{gathered} \frac{{M\left( {\tau ,\xi } \right)}}{{{{M}_{0}}}} = \frac{2}{\pi }\int\limits_0^\infty {\frac{{(1 - \cos \xi x)\exp \left( { - \tau {{x}^{2}}} \right)}}{{1 + {{{\sin }}^{2}}x - 2\sin x\sin \left[ {\left( {1 + \xi } \right)x} \right]}}} \times \\ \times \,\,\frac{{{{{\sin }}^{2}}x}}{{{{x}^{2}}}}dx, \\ \end{gathered} $Решение в форме (2) непосредственно неудобно (сложно) для практического использования. Поэтому была поставлена задача численного интегрирования выражения (2) и аппроксимации результата формулой достаточно простого вида. Это является одной из главных целей работы. Второй целью было проверить пригодность асимптотических формул (3) при больших и малых значениях времени, сопоставив их с результатом численного интегрирования выражения (2). И, наконец, построение математической модели массопереноса при внешнем обтекании поры.
Заметим, что при $\tau \to \infty $ при подсчете интеграла (2) численным методом, в частности в системе MathCAD возникает неточность, связанная с тем, что область, влияющая на значение интеграла, фактически сосредоточена в окрестности точки x = 0. Поэтому для уточнения поведения функции (2) целесообразно установить ее поведение при больших и малых значениях времени. Этого можно достичь аналитическими методами, которые приводят к асимптотическим формулам для выражения (2)
(3)
$\begin{gathered} \frac{{M\left( {\tau ,\xi } \right)}}{{{{M}_{0}}}} = \frac{{{{\xi }^{2}}}}{{4\tau \sqrt {\pi \tau } }}\,\,\,\,~{\text{для}}~\,\,\,\,\tau \to \infty \,\,\,~{\text{и}}\,\,~~\xi \ne ~~0, \\ \frac{{M\left( {\tau ,\xi } \right)}}{{{{M}_{0}}}} = 1 - \sqrt {\frac{\tau }{\pi }} ~\,\,\,\,{\text{для}}\,\,\,{\text{\;}}\tau \to 0. \\ \end{gathered} $Заметим, что в типичных задачах данного класса расчет кинетических кривых извлечения ЦК при промежуточных значениях времени довольно затруднителен. Поэтому исследователи часто ограничиваются только получением асимптотических зависимостей для количества извлеченного вещества при малых и больших значениях времени, подобных представленных формулами (3).
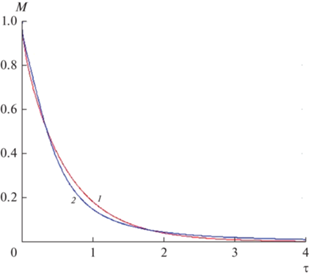
На рис. 2 представлены отдельные кривые, описывающие извлечение ЦК из поры. На этом рисунке показаны три кривые (2 − ξ = 0.15, 3 − ξ = 0.25 и проходящая между ними линия ξ = 0.2), демонстрирующие тенденцию процесса при уменьшении параметра ξ. Там же показана предельная кривая ξ → 0 (линия 1), которая определяется выражением (5).
Результаты расчетов по формуле (2) с достаточной для практики точностью были аппроксимированы зависимостью:
(4)
$M\left( {\tau ,\xi } \right) = ~\,\,\frac{{1 + b\sqrt \tau }}{{1 + \left( {b + \frac{1}{{\sqrt \pi }}} \right)\sqrt \tau + 4b\sqrt \pi \frac{{{{\tau }^{2}}}}{{{{\xi }^{2}}}}}},$В принципе при достаточно тонкой поре ξ = = R/l $ \ll $ 1 можно рассматривать и искривленную пору. При этом уравнение диффузии в поре сохраняет свой вид, а координату z можно считать криволинейной.
При малых значениях параметра относительной толщины ξ = R/l расчет интеграла по формуле (2) осложняется, поскольку знаменатель подынтегрального выражения стремится к нулю в точках xk = π(2k + 1)/2, k = 0, 1, 2 … В этом случае расчеты можно вести по формуле, полученной стандартными методами математической физики
(5)
$\frac{{M\left( \tau \right)}}{{{{M}_{0}}}} = \frac{8}{{{{\pi }^{2}}}}\mathop \sum \limits_{k = 0}^\infty \frac{1}{{{{{\left( {1 + 2k} \right)}}^{2}}}}\exp \left[ { - \frac{{{{\pi }^{2}}\tau {{{\left( {1 + 2k} \right)}}^{2}}}}{4}} \right].$При больших значениях времени в зависимости (5) превалирует первое слагаемое, так что асимптотическое поведение M/M0 при $~{{\tau }} \to \infty $ определяется выражением
(6)
$\frac{{M\left( \tau \right)}}{{{{M}_{0}}}} \cong \frac{8}{{{{\pi }^{2}}}}\exp \left( { - \frac{{{{\pi }^{2}}\tau }}{4}} \right),\,\,\,\,~\tau \to \infty .$При малых значениях времени для соотношения (5) имеет место то же асимптотическое выражение, что и в случае ξ ≠ 0, т.е. вторая формула (3). На рис. 2 формулу (5) представляет кривая 1. Приближенную формулу (4) также можно подкорректировать, учитывая (6).
Формулу (5) можно вывести, если использовать промежуточные результаты работы [27 стр. 368], в которые можно подставить ξ = 0 и далее следовать [27]. Заметим, что указанная процедура сводится к решению следующей задачи для уравнения диффузии:
После решения этой задачи, т.е. определения функции C(z, t), нужно проинтегрировать результат по z в пределах (−l, 0), чтобы получить полное количество вещества в поре. Данная процедура и приводит к зависимости (5).
Обратим внимание на качественное изменение формулы для массы ЦК. Если ранее при больших значениях времени мы имели степенной характер изменения количества извлеченного ЦК (первая формула (3)), то теперь, согласно (6) более быстрое (экспоненциальное) убывание массы ЦК.
ЗАДАЧА ПРИ НАЛИЧИИ КОНВЕКТИВНОГО ДВИЖЕНИЯ В ПРОТОЧНОЙ ЧАСТИ
Рассмотренная выше модель (1)−(6) предполагает отсутствие движения жидкости в области вне поры. В крайнем случае ее можно использовать при малых (в соответствующем масштабе) скоростях движения сплошной среды. При этом можно считать, что суммарная масса ЦК в застойной зоне сохраняется. Это может быть достаточно точным только не начальной стадии процесса, когда допустимо пренебречь веществом, покинувшим пористое тело. Ведь какой бы малой не была скорость переноса вещества, через достаточно большое время остальную часть пористого тела покидает значительная часть ЦК. Однако, данную модель можно положить в основу более общей модели, связанной с учетом конвективного переноса массы в зоне вне поры. В известном смысле предлагаемая модель будет аналогична в рассмотренной работе [8].
Структура пористой среды такова: имеется проточный канал, застойные зоны, между ними происходит массообмен, опирающийся на уравнение диффузии. Обозначим G1 и G2 концентрации целевого компонента соответственно в проточной части и застойной зоне. Уравнение переноса вещества в проточной части запишем в традиционной форме, пренебрегая продольным перемешиванием.
(7)
$\frac{{\partial {{G}_{1}}}}{{\partial t}} + u\frac{{\partial {{G}_{1}}}}{{\partial z}} + K\left( {{{G}_{1}} - {{G}_{2}}} \right) = 0,$Величина G2 в предполагаемой модели будет связана с G1 алгебраическим образом, опираясь на решение для единичной поры (2), а именно:
где G0 – концентрация ЦК в начальный момент времени. Здесь учтено, что движущей силой процесса массопереноса в поре является выражение в скобках в зависимости (8). Во всяком случае так будет при t = 0, когда G1 = 0, M = 1 для рассмотренной выше проблемы (2). В качестве рабочей гипотезы мы распространяем эти положения на любые значения времени. В таком случае, подставляя выражение (8) в уравнение (7), получаем единственное уравнение для определения концентрации ЦК в проточной части:(9)
$\frac{{\partial {{G}_{1}}}}{{\partial t}} + u\frac{{\partial {{G}_{1}}}}{{\partial z}} + K\left( {1 + M} \right){{G}_{1}} = K{{G}_{0}}{{M}^{2}}.$В отличие от работы [8] принимаем, что в начальный момент времени ЦК (извлекаемое вещество) находится не только в застойной части, но и в проточной, т.е. рассматриваем задачу промывки, когда выполняется начальное условие:
Замыкает задачу определения G1 из уравнения (9) граничное условие:
которое соответствует подаче на вход пористого слоя z = 0 промывной жидкости, не содержащей извлекаемого вещества.Целесообразно задачу (9)–(11) привести к безразмерному виду. Удобно ввести следующие безразмерные переменные и параметры:
(12)
$\zeta = Kt;~\,\,\,\,~C = {{{{G}_{1}}} \mathord{\left/ {\vphantom {{{{G}_{1}}} {{{G}_{0}}}}} \right. \kern-0em} {{{G}_{0}}}};~\,\,\,\,x = {{Kz} \mathord{\left/ {\vphantom {{Kz} u}} \right. \kern-0em} u};~\,\,\,\,T = {D \mathord{\left/ {\vphantom {D {K{{l}^{2}}}}} \right. \kern-0em} {K{{l}^{2}}}}.$Теперь эту задачу можно представить так:
(13)
$\frac{{\partial C}}{{\partial \zeta }} + \frac{{\partial C}}{{\partial x}} + \left( {1 + M\left( \zeta \right)} \right)C = {{M}^{2}}\left( \zeta \right),$Мы для краткости записали функцию М, как зависящую только от безразмерного времени ζ, опустив в этой записи два параметра ξ = a/l и T, т.е. следовало бы писать используемое соотношение (2) в виде: M(Tζ, ξ). Фактически функция М зависит от двух безразмерных переменных.
Сформулированную задачу можно решить методом характеристик [29]. Удобно при введении уравнений характеристик рассмотреть два случая.
1) Пусть x ≥ ζ. Будем искать решение уравнения (13) на линиях (характеристиках), определяемых уравнением
(15)
$\frac{{dx}}{{d\zeta }} = 1 = > x = \zeta + {{x}_{{0~}}},\,\,\,\,~~\left( {{{x}_{0}} \geqslant 0} \right).$Тогда производная функции С[x(ζ), ζ] вдоль характеристик равна
(16)
$\frac{{dC}}{{d\zeta }} = \frac{{\partial C}}{{\partial \zeta }} + \frac{{\partial C}}{{\partial x}}\frac{{dx}}{{d\zeta }} = {{M}^{2}}\left( \zeta \right) - \left[ {1 + M\left( \zeta \right)} \right]C.$Согласно уравнениям (13) и (15), в данном варианте функция C будет зависеть только от безразмерного времени ζ. Поле характеристик для уравнения (13) представлено на рис. 4. При ζ = 0, т.е. в точке x0 (рис. 4) значение функции C, согласно первому условию (14) равно единице. Линейное уравнение (16) при отмеченном начальном условии имеет решение
(17)
$\begin{gathered} {{C}_{t}}\left( {x,\zeta } \right) = \exp \left\{ { - \int\limits_0^\zeta {\left[ {1 + M\left( y \right)} \right]} dy} \right\} \times \\ \times \,\,\left[ {\int\limits_0^\zeta {{{M}^{2}}\left( {{\lambda }} \right)} d{{\lambda }}\exp \left\{ {\int\limits_0^\zeta {\left[ {1 + M\left( y \right)} \right]} dy} \right\} + 1} \right]. \\ \end{gathered} $2) Пусть x < ζ. В таком случае уравнение характеристик удобно определить уравнением [фактически соответствующим (15)]
(18)
$\frac{{d\zeta }}{{dx}} = 1 = > \zeta = x + {{\zeta }_{0}},\,\,\,\,~~{{\zeta }_{0}} \geqslant 0.$Хотя все характеристики образуют поле прямых линий с единичными наклоном, мы считаемся с тем, что в данном случае характеристика будет стартовать с границы x = 0 (см. рис. 4). Уравнение (16) заменяется следующим:
(19)
$\frac{{dC}}{{dx}} + \left[ {1 + M\left( {x + {{\zeta }_{0}}} \right)} \right]C = {{M}^{2}}\left( {x + {{\zeta }_{0}}} \right),~\,\,\,\,~x > \zeta .$При интегрировании этого уравнения фиксируем характеристику условием ζ0 = const. После интегрирования решения величину ζ0 следует заменить на ζ0 = ζ – x, согласно соотношению (18). При этом будет осуществлен переход к полю характеристик, лежащих выше (рис. 4) разграничительной характеристики ζ = x. Граничным условием к уравнению (19) будет служить граничное условие (14), т.е. C в точке ζ0 равна нулю. Имеем, после интегрирования уравнения (19), выражение
(20)
$\begin{gathered} {{C}_{x}}\left( {x,\zeta } \right) = {\text{exp}}\left\{ { - \mathop \smallint \limits_0^x \left[ {1 + M\left( {y + \zeta - x} \right)} \right]dy} \right\} \times \\ \times \,\,\mathop \smallint \limits_0^x {{M}^{2}}\left( {{{\lambda }} + \zeta - x} \right)d{{\lambda }} \times \\ \times \,\,\exp \left\{ {\mathop \smallint \limits_0^{{\lambda }} \left[ {1 + M\left( {y + \zeta - x} \right)} \right]dy} \right\},~~x < \zeta . \\ \end{gathered} $Используя функцию Хевисайда: H(z) = 1 (z > 0) и H(z) = 1 (z ≤ 0), решение уравнения (13) в области x > 0, ζ > 0 можно представить следующим образом
(21)
$C\left( {x,\zeta } \right) = {{C}_{t}}\left( \zeta \right)H\left( {x - \zeta } \right) + {{C}_{x}}\left( {x,\zeta ~} \right)H\left( {x - \zeta } \right).$В силу несогласованности начального и граничного условий (14), т.е. C(x → 0, 0) ≠ C(0, ζ → 0) на разделяющей две области характеристике ζ = x будет реализовываться скачок концентраций ЦК, который определяется предельной разностью решений (17) и (20) при x = ζ и будет равен
(22)
$\Delta C = {{\left. {({{C}_{t}} - {{C}_{x}})} \right|}_{{x - {{\zeta }}}}} = \exp \left\{ { - \mathop \smallint \limits_0^\zeta \left[ {1 + M\left( y \right)} \right]dy} \right\}.$Графики этой функции при нескольких значениях параметра ξ представлены на рис. 5. Графики рис. 5 построены при T = 1, что не ограничивает общность, поскольку функция M зависит от времени как от переменной ζK, т.е. при других значениях критерия T кривые рис. 5 простым пересчетом.
Расчеты проводились при ξ = 0,01; 0,05; 0,1; 0,15; 0,2; 0,25; 0,3, поскольку согласно результатам работы [27] параметр ξ должен быть малым, поэтому мы и взяли приведенные значения для параметра ξ. Из графиков рис. 5 видно, что кривые при перечисленных значениях ξ настолько близки, что не имеет смысла их нумеровать.
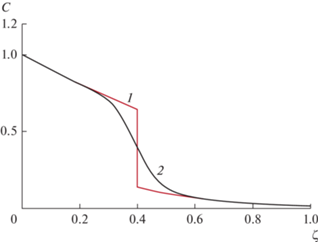
На рис. 6 приведена характерная кривая для решения задачи при ξ = 0.25, T = 1 и значении безразмерной координаты x = 0.4. Пусть L – толщина пористого слоя, значения которого в безразмерных координатах ${{l}_{*}}$ = LK/u. Если ζ < l или t < L/u (L/u – время переноса через слой), то волна концентраций еще не доходит до края слоя z = L и на выходе из слоя скачок не наблюдается.
Скачок концентраций возникает поскольку наша модель не учитывает продольного перемешивания, которое можно представить в уравнении диффузионного переноса (7) слагаемым ${{D}_{*}}$∂2G1/∂z2, где ${{D}_{*}}$– коэффициент продольного перемешивания. В этом случае безразмерное уравнение (13) перепишется так:
(23)
$\begin{gathered} \frac{{\partial C}}{{\partial \zeta }} + \frac{{\partial C}}{{\partial x}} + \left[ {1 + M\left( {\zeta T,\xi } \right)} \right]C = \\ = {{M}^{2}}\left( {\zeta T,\xi } \right) + \varepsilon \frac{{{{\partial }^{2}}C}}{{\partial {{x}^{2}}}},\,\,\,\,\varepsilon = \frac{{{{D}_{*}}K}}{{{{u}^{2}}}}. \\ \end{gathered} $При малых значениях параметра ε влияние продольного перемешивания сказывается в областях с резким изменением концентраций ЦК. В данном случае это в окрестности скачка, то есть линии x = ζ. В работе [30 стр. 297] показано, что в главном приближении учесть роль слагаемого ε∂2С/∂x2 можно заменив функцию Хевисайда в выражении (21) на дополнительную функцию вероятности
(24)
$\begin{gathered} C\left( {x,\zeta } \right) = \\ = \frac{1}{2}\left[ {{{C}_{t}}\left( \zeta \right){\text{erfc}}\left( {\frac{{x - \zeta }}{{2\sqrt {{{\varepsilon }}\zeta } }}} \right) + {{C}_{x}}\left( {x,\zeta } \right){\text{erfc}}\left( {\frac{{x - \zeta }}{{2\sqrt {{{\varepsilon }}\zeta } }}} \right)} \right]. \\ \end{gathered} $ (График зависимости (24) при тех же остальных параметрах приведен на рис. 6. Линия 2 рис. 6 показывает, что данная модель приводит к типичной форме кривых промывки осадков. При этом в модели присутствует два критерия подобия ξ и T. Причем роль критерия T сводится к растяжению или сжатию кривых вдоль временной переменной.
Функция erfc описывает локальное поведение решения в окрестности линии ζ = x, т.е. в движущейся со скоростью u системе координат, когда источники массы вносят в решение пренебрежимый вклад. Зависимость (24) удовлетворяет дополнительным условиям при x → 0 и ζ → 0, когда ε $ \ll $ 1. В окрестности точки x = 0, ζ = 0 локальный анализ решения приводит к соотношению
(25)
$C\left( {x,\zeta } \right) = {\text{erf}}\left( {\frac{x}{{2\sqrt {{{\varepsilon }}\zeta } }}} \right) = {\text{erf}}\left( {\frac{z}{{2\sqrt {{{D}_{*}}{{\tau }}} }}} \right),$– интеграл вероятности. Мы специально записали правую часть формулы (25) в размерных переменных, чтобы показать, что коэффициент массообмена K не влияет на решение в принятом приближении.
ЗАКЛЮЧЕНИЕ
Построены графики кинетических кривых извлечения ЦК из поры при различных значениях относительной ширины поры ξ. Предложена и проверена аппромаксионная формула для описания извлечения ЦК из поры. Приведены также графики асимптотических зависимостей при малых и больших значениях времени и визуальным способом убедились в их пригодности в определенном интервале времени, зависящем от относительной толщины поры. На основе решения задачи массообмена для единичной поры предложена математическая модель для описания процесса при наличии проточного и застойного объемов в пористой среде. Возможно строить и другие модели данного типа. Показано, как учет продольного перемешивания позволяет сглаживать разрывы концентрации. Наличие трех (при учете продольного перемешивания) критериев подобия придает математической модели достаточную гибкость, что позволяет добиваться хорошего соответствия модели экспериментальным данным.
ОБОЗНАЧЕНИЯ
| B | параметр в формуле (4) |
| C1, C2 | концентрация целевого компонента вне поры и внутри ее соответственною |
| D | коэффициент диффузии |
| ${{D}_{*}}$ | коэффициент продольного перемешивания |
| G1, G2 | концентрация целевого компонента в проточной части и застойных зонах соответственно |
| G0 | значение G1 в начальный момент времени |
| K | коэффициент массообмена |
| M | полная масса ЦК в поре |
| M0 | значениеM в начальный момент времени |
| l | глубина поры |
| R | радиус поры |
| T = D/Kl 2 | |
| t | размерное время |
| u | скорость переноса в проточной части системы |
| x = Kz/u | |
| z | размерная координата вдоль капилляра |
| ξ | относительная ширина поры |
| τ, ζ | безразмерное время |
Список литературы
Аксельруд Г.А., Лысянский В.М. Экстрагирование (система твердое тело-жидкость). М.: Химия, 1974.
Романков П.Г., Курочкина М.И. Экстрагирование из твердых материалов. Л.: Химия, 1983.
Бабенко Ю.И., Иванов Е.В. Экстрагирование из капилляра с переменным коэффициентом диффузии // Теор. осн. хим. технол. 2008. Т. 42. № 4. С. 355.
Ганин П.Г., Маркова А.В., Мошинский А.И., Рубцова Л.Н., Сорокин В.В. Расчет выхода вещества из пористой системы при переменном коэффициенте диффузии // Теор. осн. хим. технол. 2020. Т. 54. № 5. С. 565.
Кокотов Ю.А., Золотарев П.П., Елькин Г.Е. Теоретические основы ионного обмена. Сложные ионообменные системы. Л.: Химия, 1986.
Ромм Е.С. Структурные модели порового пространства горных пород. Л.: Недра, 1985.
Развитие исследований по теории фильтрации в СССР 1917–1967) / Под ред. П.Я. Полубариновой-Кочиной и др. М.: Наука, 1969.
Han C.D., Bixler H.J. Washing of the liquid Retained by Granular Solids // Am. Inst. Chem. Eng. J. 1967. V. 13. № 6. P. 1058.
Turner G.A. The frequency response of some illustrative models of porous media // Chem. Eng. Sci. 1959. V. 10. № 1. P. 14.
Aris R. Diffusion and reaction in flow system of Turners’ stracture // Chem. Eng. Sci. 1959. V. 10. № 1/2. P. 80.
Буевич Ю.А. Проблемы переноса в дисперсных средах // Тепломассообмен ММФ. Проблемные доклады. Секция 4, 5. Минск, 1988. С. 100.
Бондаренко А.Г., Колобашкин В.М., Кудряшов Н.А. Диффузия и адсорбция радиоактивного газа в пористой среде // Изв. АН СССР. Механика жидкости и газа. 1976. № 5. С. 85.
Бабенко Ю.И. Иванов Е.В. Экстрагирование из тела с бидисперсной пористой структурой // Теор. осн. хим. технол. 2009. Т. 43. № 4. С. 408.
Мошинский А.И. Математическая модель тепломассопереноса в бидисперсном пористом материале // Прик. мех. техн. физ. 2009. Т. 50. № 5. С. 121.
Мошинский А.И. Описание начальной стадии процессов пропитки и экстрагирования на основе бидисперсной модели // Теор. осн. хим. технол. 2012. Т. 46. № 1. С. 94.
Мошинский А.И. Извлечение вещества из пористого тела в движущуюся жидкость // Прик. мех. техн. физ. 2019. Т. 60. № 4. С. 100.
Мошинский А.И. Тепломассоперенос в пористом материале при учете релаксации потока массы // Мат. модел. 2015. Т. 27. №4. С. 97.
Мошинский А.И. Математическая модель пропитки и экстрагирования в случае бидисперсного пористого материала // Теор. осн. хим. технол. 2009. Т. 43. № 4. С. 401.
Долинский А.А. Использование принципа дискретно-импульсного ввода энергии для создания эффективных энергосберегающих технологий // Инж.-физ. ж. 1996. Т. 69. № 6. С. 885.
Мошинский А.И., Иванов Е.В. Фильтрация жидкости в пористой частице под воздействием импульсов давления на локальных участках ее поверхности // Теор. осн. хим. технол. 2008. Т. 42. № 2. С. 160.
Абиев Р.Ш., Островский Г.М. Моделирование процесса экстрагирования из капиллярно-пористой частицы с бидисперсной структурой // Теор. осн. хим. технол. 2001. Т. 35. № 3. С. 270.
Абиев Р.Ш. Исследование процесса экстрагирования из капиллярно-пористой частицы с бидисперсной структурой // Журн. прикл. химии. 2001. Т. 74. № 5. С. 754.
Малышев Р.М., Кутепов А.М., Золотников А.Н. и др. Влияние наложения поля низкочастотных колебаний на эффективность экстрагирования и математическая модель процесса // Докл. РАН. 2001. Т. 381. № 6. С. 800.
Мошинский А.И. Влияние пульсационного движения жидкости в бидисперсной пористой среде на распространение в ней вещества // Изв. РАН. Механика жидкости и газа. 2010. № 6. С. 109.
Абиев Р. Ш. Вычислительная гидродинамика и теплообмен. Введение в метод конечных разностей. Учебное пособие. СПб. Изд-во НИИ Химия СПбГУ. 2002.
Мошинский А.И. Эффективная диффузия динамически пассивной примеси в узких траншеях // Журн. прикл. мех. и техн. физ. 1987. № 3. С. 62.
Лебедев Н.Н., Скальская И.П., Уфлянд Я.С. Сборник задач по математической физике. М.: ГИТТЛ, 1955.
Малинецкий Г.Г. Математические основы синергетики: Хаос, структуры вычислительный эксперимент. 5-е изд. М.: Изд-во ЛКИ. 2007.
Годунов С.К. Уравнения математической физики. М.: Наука, 1971.
Мошинский А.И. Математическое моделирование химико-технологических и биотехнологических процессов. М.: Изд-во КНОРУС, 2021.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1977.
Мошинский А.И. Теория размерности в проблемах химической технологии. Saarbrücken: Lambert Academiс. 2017.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии