1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 57, № 2, 2023

Теоретические основы химической технологии, 2023, T. 57, № 2, стр. 202-208

Связь коэффициентов диффузии в неидеальных бинарных леннард-джонсовских смесях с энтропией

И. П. Анашкин a, *, С. Г. Дьяконов a, А. В. Клинов a

a ФГБОУ ВПО “Казанский национальный исследовательский технологический университет”
Татарстан, Россия

* E-mail: anashkin.ivan@kstu.ru

Поступила в редакцию 13.10.2022
После доработки 23.12.2022
Принята к публикации 11.01.2023

Полный текст (PDF)

Аннотация

Методом молекулярной динамики проведено моделирование неидеальных леннард-джонсовских смесей. Определены значения давления, внутренней энергии, химического потенциала и коэффициентов диффузии в зависимости от состава и плотности. Неидеальное поведение смесей задавалось параметрами в правилах смешения для потенциала межмолекулярного взаимодействия. Рассмотрено четыре варианта значений таких параметров. Термодинамическая согласованность рассчитанных термодинамических свойств была проверена с использованием выражения Гиббса–Дюгема. Вычислена величина избыточной энтропии, и показана ее связь с эйнштейновскими коэффициентами диффузии. Определен параметр в уравнении регрессии, которое связывает избыточную энтропию с эйнштейновскими коэффициентами диффузии. Его значение получилось 0.8, что близким к значениям в аналогичных выражениях для других веществ.

Ключевые слова: энтропия, коэффициент диффузии, потенциал Леннард–Джонса

ВВЕДЕНИЕ

Физико-химические свойства веществ составляют значительную часть исходной информации, необходимой для моделирования и проектирования процессов химической технологии. Однако экспериментальные данные ограничены и не всегда доступны. Особенно это касается коэффициентов молекулярного переноса массы в жидких растворах. Для многокомпонентных смесей эта ситуация заметно усложняется. Во-первых, увеличение количества компонентов рассматриваемой системы, приводит к росту числа степеней свободы и увеличению трудоемкости экспериментальных исследований. Во-вторых, измеряемые экспериментально коэффициенты диффузии зависят от системы отсчета и имеют вид матрицы, что связано с влиянием на поток одного компонента градиентов концентраций всех компонентов смеси. Так же перекрестные эффекты в межмолекулярном взаимодействии в неидеальных смесях могу существенно влиять на диффузию компонентов смеси.

Рассчитать коэффициенты молекулярной диффузии в многокомпонентных жидких смесях возможно методами молекулярной динамики. В этом случае на основе молекулярного моделирования обычно рассчитываются так называемые эйнштейновские коэффициенты диффузии компонентов смеси, которые по смыслу характеризуют подвижность молекул в равновесных условиях. Далее используя различные теории, например независимых диффузионных потоков можно получить связь между матрицей коэффициентов диффузии и эйнштейновскими коэффициентами [1]. Применение методов молекулярного моделирования оказывается эффективным, но достаточно трудоемким. Поэтому для практических инженерных расчетов желательно иметь полуэмпирические выражения, связывающие диффузионные свойства компонентов смеси со свойствами чистых веществ и их смесей которые несложно измеряются в физическом эксперименте. Известны, например корреляции коэффициентов диффузии с вязкостными свойствами [2, 3]. Одним из таких подходов является установление связи между транспортными свойствами веществ с избыточной энтропией [4]. Использование избыточной энтропии широко рассматривается как фактор масштабирования термодинамических свойств [5] в гипотезе глобального изоморфизма. Связь избыточной энтропии с коэффициентами молекулярного переноса массы была продемонстрирована на множестве чистых веществ [6]: углеводородах [7–11], хладагентах и их смесях [12], модельном леннард-джонсовском флюиде [13–15], металлах [16], веществах имеющих дипольный момент [17]. В статье [18] показана связь коэффициентов диффузии с энтропией для переохлажденных бинарных смесей. Используемые в указанных работах выражения имеют различный вид, однако стоит отметить, что добиться высокой точности описания коэффициентов диффузии широкой области термодинамических состояний (пар, жидкость, сверхкритическая) оказывается возможно с использованием небольшого количества параметров. Для некоторых классов веществ данные параметры получаются универсальными, т.е имеют близкие значения, что очень важно для практического применения.

В данной работе методом молекулярной динамики определены термодинамические свойства и коэффициенты молекулярной диффузии в неидеальных леннард-джонсовских смесях при различной плотности и составе. Рассмотрено несколько вариантов возникновения неидеального поведения смесей, за счет перекрестных параметров межмолекулярного взаимодействия. Для исследуемых систем была показана корреляционная связь коэффициентов диффузии компонентов с избыточной энтропией.

МОЛЕКУЛЯРНОЕ МОДЕЛИРОВАНИЕ

Межмолекулярное взаимодействие в рассматриваемых бинарных смесях, состоящих из компонента А и В описывалось потенциалом Леннарда–Джонса:

(1)
${{\varphi }_{{{\text{АВ}}}}}\left( r \right) = 4{{\varepsilon }_{{{\text{АВ}}}}}\left( {{{{\left( {\frac{{{{\sigma }_{{{\text{АВ}}}}}}}{r}} \right)}}^{{12}}} - {{{\left( {\frac{{{{\sigma }_{{{\text{АВ}}}}}}}{r}} \right)}}^{6}}} \right),$
где $\varepsilon $ – глубина потенциальной ямы, $\sigma $ – расстояние между атомами, где потенциал равен нулю. Для потенциала (1) термодинамические величины удобно представлять в безразмерном виде: энергия $U* = \frac{U}{\varepsilon }$, температура $T* = \frac{{{{k}_{{\text{B}}}}T}}{\varepsilon }$, давление $p* = \frac{{p{{\sigma }^{3}}}}{\varepsilon }$, числовая плотность $n* = n{{\sigma }^{3}} = \frac{N}{V}{{\sigma }^{3}}$, химический потенциал $\mu * = \frac{\mu }{\varepsilon }$, коэффициент диффузии $D* = \frac{D}{\sigma }\sqrt {\frac{m}{\varepsilon }} $, время $t* = t\sqrt {\frac{\varepsilon }{{m{{\sigma }^{2}}}}} $, где ${{k}_{{\text{B}}}}$ – константа Больцмана, N – количество частиц.

Компоненты смеси имели одинаковую массу ${{m}_{{\text{A}}}} = {{m}_{{\text{B}}}}$, размер ${{\sigma }_{{\text{A}}}} = {{\sigma }_{{\text{B}}}}$ и энергию взаимодействия ${{\varepsilon }_{{\text{A}}}} = {{\varepsilon }_{{\text{B}}}}$. Неидеальное поведение данной смеси задавалось параметрами перекрестного взаимодействия в виде εAB/εAA и σAB/σAA. Для идеальной смеси значения этих параметров равны единице. Таким образом, можно представить четыре варианта неидеальных леннард-джонсовых смесей, отличающихся отклонением перекрестных параметров от единицы в большую или меньшую сторону. Значения перекрестных параметров используемых в работе представлены в табл. 1.

Таблица 1.  

Параметры перекрестного взаимодействия

Вариант εAB/εAA σAB/σAA
1 1.2 1
2 0.8 1
3 1 0.933
4 1 1.066

Одинаковые значения параметров потенциала межмолекулярного взаимодействия чистых компонентов позволили сократить количество численных экспериментов, т.к. свойства компонентов будут симметричны относительно 50% состава. Молекулярно-динамическое моделирование проводилось с использованием программного пакета gromacs 2020.1 [19–21]. Исследуемые системы содержали 8000 молекул. Использовался NVT ансамбль, ячейка представляла из себя куб, размеры которого определялись плотностью системы $l* = \sqrt[3]{{\frac{N}{{n{\text{*}}}}}}$. Использовались периодические граничные условия, радиус обрезания потенциала межмолекулярного взаимодействия (1) составлял 8.3σ.

Всего было проведено 9 млн. итераций интегрирования уравнений движения (шаг интегрирования по времени Δt* = 0.0003) из них 1 млн отводился на установление термодинамического равновесия. Температура в системе поддерживалась с использованием термостата Носе–Гувера. Внутренняя энергия системы определялась по следующему выражению:

(2)
$U = \left\langle {\mathop \sum \limits_i^N \mathop \sum \limits_{j > i}^N {{\varphi }_{{ij}}}} \right\rangle ,$
где $\left\langle \ldots \right\rangle $ – усреднение по времени моделирования, нижние индексы соответствуют номеру молекулы.

Давление определялось путем усреднения вириала сил:

(3)
$p = n{{k}_{{\text{B}}}}T + \frac{{\sum\limits_i^N {\sum\limits_{j > i}^N {{{f}_{{ij}}}{{r}_{{ij}}}} } }}{{3V}},$
где $~{{f}_{{ij}}} = - \frac{{d{{\varphi }_{{ij}}}}}{{d{{r}_{{ij}}}}}$ – сила взаимодействия между частицами i и j, r – расстояние между этими частицами.

Коэффициент диффузии для компонента k определялся по уравнению Эйнштейна [22]:

(4)
${{D}_{i}} = \frac{1}{{6{{N}_{i}}}}\mathop {\lim }\limits_{t \to \infty } \frac{d}{{dt}}\left\langle {{{{\left[ {{{{\mathbf{r}}}_{i}}\left( t \right) - {{{\mathbf{r}}}_{i}}\left( 0 \right)} \right]}}^{2}}} \right\rangle ,$
где r – вектор положения частицы в пространстве.

Траектории молекул записывались после каждых 2000 шагов интегрирования уравнения движения. Далее с использованием полученных траекторий определялся химический потенциал каждого из компонентов смеси методом добавления тестовой частицы по выражению [23]:

(5)
$\mu = {{k}_{{\text{B}}}}T~\ln \exp \left( { - \frac{{\Delta U}}{{{{k}_{{\text{B}}}}T}}} \right),$
где $\Delta U$ – изменение энергии системы после добавления тестовой частицы. Для каждой записываемой конфигурации частиц в моделируемой ячейке проводилось 100 000 попыток добавления тестовой молекулы.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

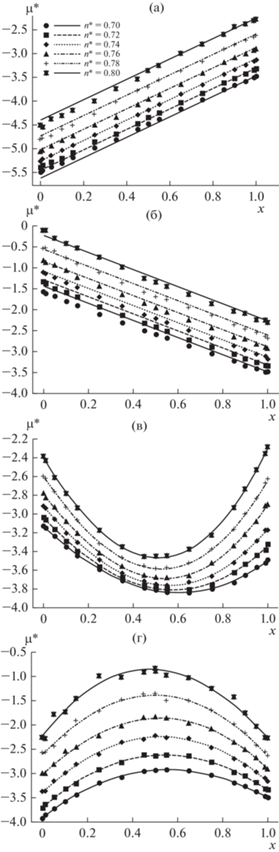
Для всех 4 рассмотренных вариантов неидеальных смесей моделирование проводились при температуре $Т* = 1$. Таблица с рассчитанными значениями коэффициентов диффузии, энергии, давления, химического потенциала от плотности и состава выложены в открытый доступ по ссылке [24]. На рис. 1 представлены зависимости химического потенциала компонента от мольной доли. Видно, что для 1 и 2 вариантов параметров смешения, когда изменяется параметр ${{\varepsilon }_{{{\text{АВ}}}}}$, химический потенциал имеет линейную зависимость от состава. При этом наклон линии не зависит от плотности смеси. В случае, 3 и 4 вариантов, когда изменяется параметр смешения ${{\sigma }_{{{\text{АВ}}}}}$, химический потенциал имеет более сложную зависимость от концентрации. Для удобства обработки результатов моделирования и получения выражения для энтропии химический потенциал для неидеальных смесей вариантов 1 и 2 описывался линейной зависимостью:

(6)
$\mu {\text{*}}\left( {n,x} \right) = \mu _{0}^{*}\left( n \right) + a\left( {1 - x} \right)$
для вариантов 3 и 4 полиномом 3 степени:
(7)
$\begin{gathered} \mu {\text{*}}\left( {n,x} \right) = \mu _{0}^{*}\left( n \right) + a\left( {1 - x} \right) + \\ + \,\,b{{(1 - x)}^{2}} + c{{(1 - x)}^{3}}, \\ \end{gathered} $
где ${{\mu }_{0}}$ – химический потенциал чистого компонента, значение которого было определено по уравнению состояния [25], $a$, $b$ и $c$ – параметры. Используемые аппроксимации представлены на рис. 1 в виде линий.

Рис. 1.

Зависимость химического потенциала от концентрации при различной плотности, геометрические фигуры – численные эксперимент, линии – аппроксимации по выражениям (6) и (7); a – вариант смешения 1, б – вариант смешения 2, в – вариант смешения 3, г – вариант смешения 4.

Корректность результатов моделирования была проверена с использованием уравнения Гиббса–Дюгема:

(8)
$sdT - vdp + \mathop \sum \limits_i {{x}_{i}}d{{\mu }_{i}} = 0,$
где s – удельная энтропия, $v$ – удельный объем. Так как в данной работе температура системы была постоянная $sdT$ = 0. Поставляя производные химических потенциалов из выражений (6) и (7), и интегрируя по $dx$ можно получить выражения давления для вариантов 1 и 2:
(9)
$p{\text{*}}\left( {x,n} \right) = p_{0}^{*}\left( n \right) + n{\text{*}}a(x - {{x}^{2}})$
и вариантов 3 и 4:
(10)
$\begin{gathered} p{\text{*}}\left( {x,n} \right) = p_{0}^{*}\left( n \right) - \frac{{n{\text{*}}x}}{2} \times \\ \times \,\,\left( {ax + 3c{{x}^{3}} - 6c{{x}^{2}} + 3cx + ax - 2a} \right), \\ \end{gathered} $
где $p_{0}^{*}$ – давление чистого леннард-джонсовского флюида при заданной плотности, определяемое по уравнению состояния [25]. На рис. 2 представлено сравнение результатов численного эксперимента где давление определялось по (3) с расчетами, полученными по выражениям (8) и (9). Из рисунка 2 видно хорошее совпадение значений давления, что свидетельствует о термодинамической согласованности полученных результатов.

Рис. 2.

Зависимость давления от концентрации при различной плотности; геометрические фигуры – результаты численного моделирования, линии – результаты по выражениям (8) и (9); a – вариант смешения 1, б – вариант смешения 2, в – вариант смешения 3, г – вариант смешения 4.

Энтропия системы определялась из известного термодинамического выражения:

(11)
$du = Tds - pdv + \sum\limits_i {{{\mu }_{i}}d{{x}_{i}}} ,$
где u – удельная внутренняя энергия. Подставляя в (11) выражения для химических потенциалов (6), (7) и проинтегрировав можно получить зависимость энтропии от состава. В случае описания химического потенциала линейной зависимостью от состава (варианты 1 и 2) полученное выражение выглядит следующим образом:
(12)
$s{\text{*}}\left( {x,n} \right) = s_{0}^{*}\left( n \right) + \frac{{\Delta u{\text{*}}}}{T} + \frac{a}{T}({{x}^{2}} - x)$
для вариантов 3 и 4:
(13)
$\begin{gathered} s{\text{*}}\left( {x,n} \right) = s_{0}^{*}\left( n \right) + \frac{{\Delta u{\text{*}}}}{T} + \frac{{a + b}}{T}\left( {{{x}^{2}} - x} \right) + \\ + \,\,\frac{c}{T}\left( {\frac{{{{x}^{4}}}}{2} - {{x}^{3}} + \frac{{3{{x}^{2}}}}{2} - x} \right), \\ \end{gathered} $
где Δu – разница удельной энергии компонента в смеси и его удельной энергии как чистого вещества.

На рис. 3 представлена зависимость логарифма отношения коэффициента диффузии компонента в смеси к диффузии чистого компонента, рассчитанных по (3) от избыточной энтропии. Последняя определялась по ((12), (13)) как: $\Delta s = s - {{s}_{{id}}}$, где ${{s}_{{id}}} = {{s}_{{\text{A}}}}{{x}_{{\text{A}}}} + {{s}_{{\text{B}}}}{{x}_{{\text{B}}}}$ – удельная идеальная энтропия, в рассмотренном здесь случае она равняется энтропии чистого компонента ${{s}_{{id}}} = {{s}_{0}}\left( n \right)$. Видно, что для всех исследуемых вариантов правил смешения можно выделить общую закономерность близкую к линейной. Наибольшие отклонения от этой зависимости наблюдаются в основном, когда значение избыточной энтропии близко к нулю, что соответствует области малых концентраций одного из компонентов смеси. В этой области, коэффициент диффузии, рассчитываются с наибольшей статистической неопределенностью. Это также видно из рис. 4.

Рис. 3.

Зависимость отношения логарифмов коэффициентов диффузии от избыточной энтропии; геометрическими фигурами показаны различные варианты правила смешения, линия – аппроксимирующая кривая.

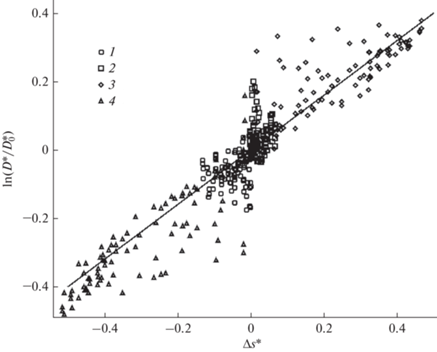
Рис. 4.

Зависимость коэффициентов диффузии от концентрации при различной плотности; геометрические фигуры – численный эксперимент, линии – результаты по выражению (14); a – вариант смешения 1, б – вариант смешения 2, в – вариант смешения 3, г – вариант смешения 4.

В данной работе для описания зависимость коэффициента диффузии от энтропии применялось выражение:

(14)
$D{\text{*}}\left( {x,n} \right) = D_{0}^{*}\left( n \right)\exp \left( {A\Delta s} \right),$
где ${{D}_{0}}$ – коэффициент диффузии чистого компонента, Решая задачу линейного регрессионного анализа, было определено значение параметра A в (14), равное 0.8 (показано на рис. 3 сплошной линией). В работе [14] для описания чистого леннард–джонсовского флюида значение аналогичное параметра в корреляции равнялось 0.7. Также близкие к 0.8 значения параметров были найдены для описания жидкой фазы в работе [17]: для воды – 0.7621, аммиака – 0.6264, метанола – 0.8633, этанола – 0.8387. Это может свидетельствовать о некотором универсальном значении параметра, связывающего коэффициенты диффузии и энтропию как для чистых веществ, так и для смесей.

Сравнение результатов расчетов коэффициентов диффузии полученных по выражению (4) со значениями, полученными по выражению (10) представлено на рис. 4. Видно хорошее качественное и количественное согласование расчетов по полученной здесь корреляционной зависимости с результатами численного моделирования.

ЗАКЛЮЧЕНИЕ

На модельной бинарной леннард–джонсовской неидеальной смеси показана возможность расчета коэффициентов диффузии компонентов по данным о свойствах чистых компонентов и избыточной энтропии смеси. На практике предложенный подход может быть использован совместно с моделями для описания коэффициентов активности [26]. Соотношение, связывающее эйнштейновские коэффициенты диффузии с избыточной энтропией имеет всего один параметр, значение которого может иметь некоторое универсальное значение для широкого круга чистых веществ и смесей. В этом смысле представляется перспективным дальнейшие исследования рассмотренного здесь подхода для описания диффузии в смесях реальных веществ.

БЛАГОДАРНОСТИ

Работа выполнена при финансовой поддержке гранта Министерства науки и высшего образования Российской Федерации № 075-01261-22-00 “Энергоресурсосберегающие процессы разделения жидких смесей для выделения промышленных растворителей”.

ОБОЗНАЧЕНИЯ

ε глубина потенциальной ямы, Дж
μ химический потенциал, Дж/моль
σ расстояние на котором энергия потенциала равна нулю, м
φ потенциал, Дж
f сила взаимодействия, Н
kB константа Больцмана, Дж/К
l длина моделируемой ячейки, м
m масса молекулы, кг
n чистовая плотность 1/м3
p давление, Па
r вектор положения частицы в пространстве
s удельная энтропия, Дж/моль
t время, с
$v$ удельный объем, м–3
T температура, К
u удельная внутренняя энергия, Дж/моль
x мольная доля

ИНДЕКСЫ

* безразмерная величина
0 чистое вещество
A, B компоненты

Список литературы

  1. Taylor R., Krishna R. Multicomponent mass transfer. New York: Wiley, 1993. 579 p.

  2. The Stokes-Einstein law for diffusion in solution // Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character. 1924. V. 106. № 740. P. 724–749.

  3. Shabarova L.V. et al. Modeling Thermal Gas Dynamic Processes of the Production of Silicon from Its Halides // Theor. Found. Chem. Eng. 2020. V. 54. № 4. P. 631–640.

  4. Rosenfeld Y. Relation between the transport coefficients and the internal entropy of simple systems // Phys. Rev. A. 1977. V. 15. № 6. P. 2545–2549.

  5. Dyre J.C. Perspective: Excess-entropy scaling // J. Chem. Phys. 2018. V. 149. № 21. P. 210901.

  6. Dehlouz A. et al. Entropy Scaling-Based Correlation for Estimating the Self-Diffusion Coefficients of Pure Fluids // Ind. Eng. Chem. Res. 2022. V. 61. № 37. P. 14033–14050.

  7. Novak L. Self-Diffusion Coefficient and Viscosity in Fluids // Int. J. Chem. React. Eng. 2011. V. 9. № 1.

  8. Novak L.T. Fluid Viscosity-Residual Entropy Correlation // Int. J. Chem. React. Eng. 2011. V. 9. № 1.

  9. Bell I.H. Entropy Scaling of Viscosity– I: A Case Study of Propane // J. Chem. Eng. Data. 2020. V. 65. № 6. P. 3203–3215.

  10. Bell I.H. Entropy Scaling of Viscosity– II: Predictive Scheme for Normal Alkanes // J. Chem. Eng. Data. 2020. V. 65. № 11. P. 5606–5616.

  11. Nikitiuk B.I. et al. Pair entropy and universal viscosity scaling for molecular systems via molecular dynamics simulations // J. Mol. Liq. 2022. V. 368. P. 120714.

  12. Yang X. et al. Entropy Scaling of Viscosity– III: Application to Refrigerants and Their Mixtures // J. Chem. Eng. Data. 2021. V. 66. № 3. P. 1385–1398.

  13. Bell I.H. et al. Modified Entropy Scaling of the Transport Properties of the Lennard–Jones Fluid // J. Phys. Chem. B. 2019. V. 123. № 29. P. 6345–6363.

  14. Bell I.H. et al. Modified Entropy Scaling of the Transport Properties of the Lennard–Jones Fluid // J. Phys. Chem. B. 2019. V. 123. № 29. P. 6345–6363.

  15. Viet T.Q.Q. et al. Mass effect on viscosity of mixtures in entropy scaling framework: Application to Lennard–Jones mixtures // Fluid Phase Equilibria. 2022. V. 558. P. 113459.

  16. Yokoyama I. A relationship between excess entropy and diffusion coefficient for liquid metals near the melting point // Phys. B Condens. Matter. 1998. V. 254. № 3–4. P. 172–177.

  17. Anashkin I., Dyakonov S., Dyakonov G. Relationship between the Transport Coefficients of Polar Substances and Entropy // Entropy. 2019. V. 22. № 1. P. 13.

  18. Bell I.H., Dyre J.C., Ingebrigtsen T.S. Excess-entropy scaling in supercooled binary mixtures // Nat. Commun. 2020. V. 11. № 1. P. 4300.

  19. Abraham M.J. et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers // SoftwareX. 2015. V. 1–2. P. 19–25.

  20. Van Der Spoel D. et al. GROMACS: Fast, flexible, and free // J. Comput. Chem. 2005. V. 26. № 16. P. 1701–1718.

  21. Pronk S. et al. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit // Bioinformatics. 2013. V. 29. № 7. P. 845–854.

  22. McQuarrie D.A. Statistical mechanics. Sausalito, Calif: University Science Books, 2000. 641 p.

  23. Widom B. Some Topics in the Theory of Fluids // J. Chem. Phys. 1963. V. 39. № 11. P. 2808–2812.

  24. articles [Online]. URL: https://github.com/KSTU/articles/tree/master/entropy-diffusion-mixture.

  25. Johnson J.K., Zollweg J.A., Gubbins K.E. The Lennard-Jones equation of state revisited // Mol. Phys. 1993. V. 78. № 3. P. 591–618.

  26. Demirel Y. Calculation of Excess Entropy for Binary Liquid Mixtures by the NRTL and UNIQUAC Models // Ind. Eng. Chem. Res. 1994. V. 33. № 11. P. 2875–2878.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал