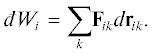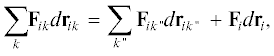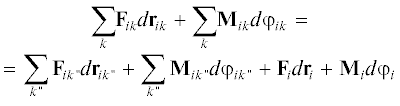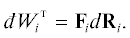Теоретические основы химической технологии, 2023, T. 57, № 3, стр. 346-357

Учет термодинамических закономерностей в химико-технологических расчетах обычно сводится к экстраполяции классической термодинамики за рамки применимости ее концепций равновесности систем и обратимости процессов. Несмотря на то, что закон сохранения и превращения энергии опытным путем был установлен давно [1], на практике обычно используется только закон сохранения энергии без учета ее превращения в виде фундаментального уравнения Гиббса, отражающего первое и второе начала термодинамики для равновесных систем

где внешний энергообмен учитывается теплообменом $TdS$, работой расширения (сжатия) $pdV$ и многокомпонентным массообменом $\sum\limits_k {{{\mu }_{k}}d{{N}_{k}}} $. При учете других возможных видов внешнего энергообмена это уравнение переходит в уравнение энергообмена в открытой равновесной поливариантной системе: где ${{\Psi }_{i}} = {{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial {{\Theta }_{i}}~}}} \right. \kern-0em} {\partial {{\Theta }_{i}}~}}$ – обобщенные потенциалы.

Однако для общего случая реальных неоднородных (внутренне неравновесных) систем до недавнего времени фундаментального энергетического уравнения, аналогичного соотношениям (1) и (2), не существовало. Теплообмен и работа считались разными понятиями, а само понятие энергии разными исследователями трактовалось по-разному [2]. Поэтому корректная аналитическая формулировка и практическое применение закона сохранения и превращения энергии актуальна как в химической технологии, так и в других дисциплинах.

Понятие работы пришло в термодинамику из механики, где она измеряется скалярным произведением вектора результирующей силы F на вызванное ею перемещение dR объекта ее приложения (R – радиус-вектор центра инерции объекта): dW = F ⋅ dR. Понятие работы как количественной меры воздействия одного тела на другое было распространено на немеханические формы движения, в которых проявляются силы электрические, магнитные, гравитационные, химические, ядерные и т.п. Силы – величины аддитивные, т.е. пропорциональные некоторому фактору аддитивности. В механике сплошной среды такими факторами являются масса, объем, поверхность, а силы называются массовыми, объемными, поверхностными. Учет немеханических форм движения расширяет множество факторов аддитивности. В общем случае фактор аддитивности $~{{\Theta }_{i}}$ представляет собой конкретный материальный носитель i-й формы энергии. Так, масса k-го вещества M_k является носителем энергии покоя; энтропия S –носитель тепловой энергии; заряд ${{{{\Theta }}}_{e}}$ − носитель электростатической энергии системы; импульс компонента M_kv_k− носитель кинетической энергии k-го вещества и т.п. Силы также делятся на внутренние и внешние в зависимости от того, действуют ли они между частями (частицами) внутри системы или между системой и окружающей средой.

Однако при рассмотрении реальных, т.е. неравновесных и пространственно неоднородных сред, особое значение приобретает другое свойство тех или иных сил – наличие или отсутствие у них результирующей. В механике работа любой силы есть мера воздействия одного тела или частицы на другое. Учитывая упомянутое выше разнообразие материальных энергоносителей, будем считать, что силы i-го рода действуют на частицы k-го сорта и иерархического уровня материи (ядра, атомы, молекулы, клетки, глобулы, макротела и т.д.). Обозначим силу i-го рода через F_i по природе носителя i-й формы взаимодействия, применяя для обозначения элементарной работы, зависящей от характера (пути) процесса, знак неполного дифференциала đ. Введем в рассмотрение радиус-вектор r_ik этих объектов приложения сил F_ik. Тогда суммарная работа в результате силового воздействия i-го рода на систему в целом будет складываться из элементарных работ 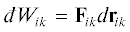такого воздействия на каждую k-ю частицу [2]:

Элементарная работа đW_ik будет различна в зависимости от направления элементарных сил F_ik и вызванных ими элементарных перемещений dr_ik. Система частиц в целом в каждый момент времени характеризуется результирующей силой i-го рода F_i = $\mathop \sum \limits_k {{{\mathbf{F}}}_{{ik}}}$, вызывающей результирующее перемещение системы в целом dR_i= $\mathop \sum \limits_k d{{{\mathbf{r}}}_{{ik}}}.~~$На основе анализа протекания реальных процессов постулируется аксиома неоднородности: по отношению к результирующей сил F_i и перемещений dR_i система всех частиц делится на две части, одна из которых имеет результирующие F_i и dR_i, а другая не имеет, например, из-за хаотичности смещений частиц r_ik под действием сил F_ik. Согласно принятой аксиоме, суммарная работа всех частиц системы всегда удовлетворяет неравенству:

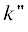где $k{\kern 1pt} '$ – номера тех частиц, для которых существует результирующая векторов смещений и сил. Это значит, что работа всех частиц системы может быть представлена в виде суммы: где – номера тех частиц, для которых отсутствуют результирующие сил и перемещений частиц.

Если учесть, что каждая частица совершает работу не только под действием силы, но и под действием момента этой силы М_ik при повороте частицы на угол φ_ik, то соотношение (4) принимает вид:

Данное соотношение дополняет (4) учетом в аксиоме неоднородности разбиение силовых диполей на упорядоченные и неупорядоченные. Таким образом, аксиома неоднородности приобретает окончательную формулировку: термодинамическая система с макроскопической точки зрения состоит из частиц, участвующих в трех видах движения: беспорядочном (в целом покоя), поступательном и вращательном.

В зависимости от наличия или отсутствия результирующей сил и перемещений частиц может иметь место несколько характерных ситуаций при обсуждении которых для простоты будем опускать упоминание о действии моментов сил (диполей) [2]:

1. Элементарные силы F_ik вызывают перемещения dr_ik одного знака у объектов их приложения, т.е. изменяется положение радиуса-вектора dR_i всей совокупности k-х объектов приложения элементарных сил F_ik. Это возможно, когда система однородна и перемещается как единое целое. Именно такую работу совершают механические системы и технические устройства (машины), предназначенные для целенаправленного преобразования одних видов энергии в другие. Такую работу обычно называют полезной внешней или технической. Однако в общем случае такую работу совершают не только технические устройства, но и химические, биологические, астрофизические и другие системы, поэтому для такой работы удобнее ввести общий термин “упорядоченная работа” и обозначать верхним индексом “Т” – техническая:

2. Упорядоченная работа совершается и в том случае, когда вся система в целом неподвижна, а существует лишь относительное однонаправленное смещение dr_ik ее элементов относительно начального равновесного состояния. Это происходит при перераспределении k-х веществ в многокомпонентной системе, положительных и отрицательных зарядов или полюсов электрических диполей, полюсов магнитных диполей, импульсов, электронов и “дырок” в полупроводниках и других энергоносителей между частями изначально однородной системы. При этом силы F_ik вызывают смещения dr_ik противоположного знака и сумма $\mathop \sum \limits_k {{{\mathbf{F}}}_{{ik}}}d{{{\mathbf{r}}}_{{ik~~}}}$разбивается на две части, имеющие одинаковый знак величин F_ik и dr_ik, что дает отличную от нуля результирующую силу ${{{\mathbf{F}}}_{i}}$. Тогда работа i-го рода над системой в целом определяется тем же соотношением (5), т.е. имеет векторное происхождение. Таким образом, при совершении упорядоченной работы изменяется положение либо центра масс системы в целом, либо центр каждого ее энергоносителя в отдельности (заряда, импульса, энтропии и т.п.), т.е. изменяется лишь внутренняя энергия системы.

3. Элементарные объекты под действием сил F_ik двигаются хаотично, т.е. перемещения dr_ik не однонаправлены. Упорядоченное движение k–х объектов отсутствует, т.е. $d{{{\mathbf{R}}}_{i}} = 0$. Равнодействующей силы нет, однако в целом работа совершается: 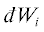= 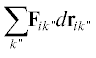$ \geqslant 0.$ Такого рода работа называется неупорядоченной и обозначается W^н. Она не имеет результирующей силы, т.е. для нее не работает правило (6). Можно сказать, что неупорядоченная работа имеет скалярное происхождение. Примером такой работы является работа pdV, совершаемая при всестороннем сжатии или расширении газа в свободное пространство. Локальное давление p можно рассматривать как механическую силу, действующую на элемент df замкнутой поверхности системы по нормали к этому элементу. Очевидно, что результирующая сила давления на всю поверхность однородной системы равна нулю ${{{\mathbf{F}}}_{p}} = 0$, т.к. работа всестороннего расширения (сжатия) не связана с изменением положения тела как целого: $~d{{{\mathbf{R}}}_{f}} = 0$. Эту неупорядоченную работу системы в целом можно выразить как произведение двух скалярных величин, одна из которых характеризует интенсивность ${{\Psi }_{i}}~$ общего хаотического движения i-го рода, а вторая – изменение $~d{{\Theta }_{i}}$ i-й экстенсивной характеристики системы в результате внутреннего силового взаимодействия i-го рода: 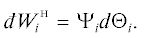Здесь Ψ_i – обобщенный потенциал, являющийся интенсивной величиной (абсолютная величина скорости v, абсолютная температура T, давление p, электрический потенциал φ, химический потенциала k-го вещества μ_k и т.п.); $d{{\Theta }_{i}}$ ${\text{\;}}$– изменение соответствующей экстенсивной координаты состояния системы в целом (количество движения Мv, энтропия S, объем V, заряд ${{{{\Theta }}}_{e}}$, масса k-го компонента M_k и т.п.).

4. Промежуточное положение между этими двумя видами работ занимает работа диссипативного характера ${{W}^{{\text{д}}}}$. Эта работа совершается упорядоченными силами F_i против так называемых “сил рассеяния”, не имеющих результирующей вследствие их хаотической направленности. Диссипативная работа носит смешанное скалярно – векторное происхождение, т.е. сопровождается переходом упорядоченных форм энергии в неупорядоченные (и обратно).

Общим выводом из рассмотренных систуаций является то, что работа одного и того же силового воздействия i-го рода может быть как упорядоченной, так и неупорядоченной в зависимости от того, имеется или нет у преодолеваемых сил результирующая. Она может быть также внешней или внутренней в зависимости от происхождения приложенной силы, полезной или диссипативной в зависимости от целенаправленности процесса. Отсюда следует, что одна и та же i-я форма внутренней энергии U_i (U = $\mathop \sum \limits_i {{U}_{i}}~)$ изменяется в результате совершения над системой как упорядоченной, так и неупорядоченной работы. При этом неупорядоченная работа всегда связана с переносом энергии в одной и той же форме, а упорядоченная – с ее превращением (например, кинетической в потенциальную для механических сил). Таким образом, аксиома неоднородности, выраженная в виде соотношения (5) с учетом 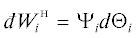и $dU = \sum\limits_i {d{{U}_{i}}~} $, соответствует уравнению сохранения и превращения энергии в виде:

где ${{\Psi }_{i}}$ – аналог обобщенного потенциала (2), а вся внутренняя энергия U становится общей мерой всех видов работы, которые может совершить система (упорядоченных и неупорядоченных). Например, тепловая форма энергии U_т входит одним из слагаемых в сумму (6) изменений различных форм энергии U_i, а соответствующий экстенсивный энергоноситель теплой энергии ${{{{\Theta }}}_{{\text{т}}}}$ = S – энтропия становится обычным термоипульсом, утративший свои векторные свойства в результате хаотического теплового движения. Аналогичные импульсы с утраченными векторными свойствами возникают у всех остальных форм энергии. Следовательно, энтропия характеризует только одну (тепловую) форму движения и никак не может быть обобщенной характеристикой внутренней энергии всей системы, как это обычно принято в классической термодинамике.

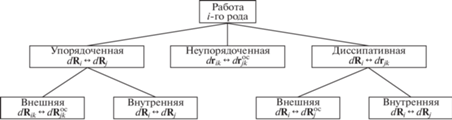
Вышесказанное позволяет ввести классификацию работ, показанную на рис. 1. Видно, что работа одного и того же i-го рода может быть как упорядоченной, так и неупорядоченной (в зависимости от того, имеется или нет у преодолеваемых сил результирующая); она может быть также внешней или внутренней (в зависимости от места приложения силы), полезной или диссипативной (в зависимости от целенаправленности процесса). Факт наличия энергопревращения в процессах совершения упорядоченной работы отражен здесь сменой индекса i на j = 1, 2, …, n в соответствии с изменением природы преодолеваемых сил. Совершение внешней работы (против сил окружающей среды) отмечено верхним индексом “ос”. Эта работа сопровождается передачей части энергии в измененной форме другим телам (окружающей среде). Внутренняя работа оставляет энергию системы неизменной и сопровождается ее превращением из одной формы в другую (как это происходит в колебательных процессах или в циклических химических реакциях типа Белоусова–Жаботинского).

Понимание принципиального различия упорядоченной и неупорядоченной работы приводит к выводу, что одна и та же i-я форма внутренней энергии U_i пространственно неоднородной системы может быть изменена в результате совершения над ней как той, так и другой работы, поэтому число степеней свободы такой системы (т.е. число независимых процессов, которые могут протекать в ней) удваивается по сравнению с однородной (внутренне равновесной) системой. Это явно отражает выражение обобщенного закона сохранения и превращения энергии в виде (7). Такая запись закона сохранения энергии придает ей простой и ясный изначальный смысл способности системы к совершению работы, причем такой смысл был утрачен в прошлом на стадии введения в термодинамику понятий теплоты и внутренней энергии.

В равновесных (однородных) системах выражение (6) естественно переходит в основное уравнение классической термодинамики поливариантных открытых систем в виде обобщенного соотношения Гиббса: dU $ = \sum\limits_i {~{{\Psi }_{i}}d{{\Theta }_{i}}} $. Все процессы такого рода характеризуют перенос энергии в одной и той же i-й форме без ее превращения. Напротив, силы F_i их моменты M_i, смещения поступательные R_i и их углы поворота φ_i в выражении (7) являются дополнительными параметрами, отсутствовавшими в равновесной термодинамике, а суммы $\sum\limits_i {{{{\mathbf{F}}}_{i}}d{{{\mathbf{R}}}_{i}}} \,$ и $\,\sum\limits_i {{{{\mathbf{M}}}_{i}}d{{\varphi }_{i}}} $ характеризуют процесс превращения энергии.

Как видно, соотношение (7) получено на основе аксиомы неоднородности и эвристических (правдоподобных) рассуждений, однако нетрудно показать, что оно переходит в строгое математическое тождество. Для этого достаточно сравнить положение центра какого-либо параметра $~{{\Theta }_{i}}$ в равновесном ${{{\mathbf{R}}}_{{i0}}}$ (с плотностью ${{\rho }_{{i0}}}$) и произвольном неравновесном ${{{\mathbf{R}}}_{i}}$ (с плотностью ${{\rho }_{i}})$ состояниях:

Отсюда ясно, что удаление системы от однородного (внутренне равновесного) состояния сопровождается возникновением смещения $~\Delta {{{\mathbf{R}}}_{{i~}}}$ = ${{{\mathbf{R}}}_{i}}~--~{{{\mathbf{R}}}_{{i0~}}}$ и соответствующего “момента распределения” ${{{\mathbf{Z}}}_{i}}$ параметра $~{{\Theta }_{i}}$:

характеризующего неоднородное состояние системы в целом. Полная производная по времени от этого параметров J_i = dZ_i/dt = ${{\Theta }_{i}}$dR_i/dt = ${{\Theta }_{i}}{{{\mathbf{\bar {v}}}}_{i}},$ называемая обобщенным потоком, имеет смысл импульса энергоносителя ${{\Theta }_{i}}$. Ниже будет показано, что частная производная от внутренней энергии U системы по этому параметру определяет обобщенную силу Х_i = (${{({{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial {\mathbf{Z}}}}} \right. \kern-0em} {\partial {\mathbf{Z}}}}{{~}_{i}})}_{{{{\Theta }_{i}}}}}.$ Важно подчеркнуть, что обобщенные силы X_i и потоки J_i отличаются от таковых в термодинамике необратимых процессов (ТНП) тем, что они реальные, а не полученные на основе “производства энтропии”. Для их определения не надо прибегать к понятию энтропии и их можно измерять непосредственно с помощью контрольно-измерительных приборов.

Появление в неравновесной системе смещения $~\Delta {{{\text{R}}}_{{i~}}}$ = ${{{\mathbf{R}}}_{i}}~--\,~{{{\mathbf{R}}}_{{i0}}}~$ можно наблюдать при возникновении в неподвижной жидкости подвижных элементов из-за механического перемешивания в калориметре Джоуля c мешалкой, приводящего к нагреванию жидкости в результате преобразования механической энергии в тепловую при установления механического эквивалента теплоты (Дж. Джоуль, 1843) [1]. Наблюдение процессов отклонения системы от равновесия ведется в абсолютной системе отсчета, где за начало отсчета принимается равновесное состояние системы, при котором никакие процессы невозможны. При этом сам объект исследования вместе с окружающей средой объединяется в единую систему, которая в таком расширенном состоянии принимается изолированной и замкнутой. В абсолютной системе отсчета для любого объекта исследования ${{{\mathbf{R}}}_{{i0}}} = 0$, а радиус-вектор $~{{{\mathbf{R}}}_{i}}$ смещения центра каждого энергоносителя ${{\Theta }_{i}}$ совпадает с его отклонением от равновесного значения. При этом параметр Z становится произведением количества энергоносителя ${{\Theta }_{i}}$ на вектор смещения R_i$~({{{\mathbf{Z}}}_{i}} = {{\Theta }_{i}}{{{\mathbf{R}}}_{i}})$. Например, для механической системы Z_m = MR, где М – масса системы, R – вектор смещения центра масс. Как видно, параметры неоднородности Z_i (i = 1, 2,… n) определены через интегральный оператор по объему индивидуальной области V и относятся к классу обобщенных функций со специальными свойствами [3–5]. В отличие от однородных обобщенных функций равновесной термодинамики, эта функция позволяют описывать неоднородные (внутренне неравновесные) системы благодаря двум ее замечательным свойствам: 1) неаддитивность по отношению к объему V области в силу зависимости средней плотности ${{\rho }_{{i0}}}$ от V для неоднородной системы; 2) Z_i$ \to 0$ при V $ \to $ 0 (${{\rho }_{i}} \to {{\rho }_{{i0~}}}).$ Это значит, что протекание самопроизвольных природных процессов релаксации соответствуют самопроизвольному обращению в нуль параметров Z_i, так что для характеристики диссипативных процессов излишне прибегать к понятию энтропии и принципу возрастания энтропии.

Обобщенная функция ${\text{\;}}{{{\mathbf{Z}}}_{i}},$ являющаяся функцией области, играет роль, аналогичную дельта–функции Дирака в теоретической физике, построенной на понятии функции области. Последняя была введена Дираком с целью “легализации” понятия точечной массы и точечного заряда. Обобщенная Z – функция и ее дифференциал dZ вводятся для “легализации” понятия протекания равновесного или неравновесного процессов, а также скрытых процессов преобразования энергии в неоднородных (внутренне неравновесных) средах. Параметр неоднородности Z есть функция области Z = Z(V), а определяющий ее интеграл можно понимать не как интеграл Римана, а как интеграл Лебега по областям V с различными значениями ${{\rho }_{{i0}}}$ = ${{\rho }_{{i0}}}$ (V) [3–5].

Если записать полный дифференциал функций ${{{\mathbf{Z}}}_{i}}$ = $~{{{\mathbf{Z}}}_{i}}$(${{\Theta }_{i}}$, ${{{\mathbf{R}}}_{i}})$ в абсолютной системе отсчета $~d{{{\mathbf{Z}}}_{i}}$ = R_id${{\Theta }_{i}}$ + $~{{\Theta }_{i}}d{{{\mathbf{R}}}_{{i~}}}$, то это разложение соответствует разделению всех процессов на равновесные и неравновесные. Более того, оно позволяет различать процессы между собой. В этом нетрудно убедиться, если представить дифференциал смещения $~d{{{\mathbf{R}}}_{i}}$ в виде суммы произведения скаляра ${{{\mathbf{R}}}_{i}}$ на единичный вектор e_i в направлении удлинения вектора ${{{\mathbf{R}}}_{i}},$ и дифференциала de_i как векторного произведения de_i = $d{{{\mathbf{\varphi }}}_{i}}{\mathbf{x}}$e_i, где $~{{{\mathbf{\varphi }}}_{i}}$ – угол поворота вектора e_i. В результате получим

где S_i = e_iR_i – вектор удлинения перемещения. Дифференциал dZ_i, записанный для системы в целом, следует отличать от дифференциала радиус-вектора частицы сплошной среды, определяемого в модели сплошной среды по теореме Коши–Гельмгольца [6]. Согласно (8) полный дифференциал функции Z_i отражает различие между тремя группами независимых процессов: равномерных $d{{\Theta }_{i}}$, перераспределения $d{{{\mathbf{S}}}_{i}}$ и переориентации $d{{{\mathbf{\varphi }}}_{i}}$_i. С учетом (8) внутренняя энергия U системы, как функция ее состояния, в общем случае становится функцией трех независимых аргументов U = U (${{\Theta }_{i}},{\mathbf{~}}{{{\mathbf{S}}}_{i}},{{{\mathbf{\varphi }}}_{i}}$), а ее полный дифференциал выражается как или с учетом обозначений: принимает вид тождества:$~$где $~{{\bar {\Psi }}_{{i~}}}$ – интенсивная величина в виде усредненного обобщенного потенциала (абсолютной температуры Т, давления p, химического потенциала $~{{\mu }_{k}}$, электрического φ, гравитационного ${{\psi }_{g}}$ и др. потенциалов); ${{{\mathbf{F}}}_{i}}$ – силы в их обычном (ньютоновском) понимании; ${{{\mathbf{M}}}_{i}}$ – моменты этих сил, т.е. соответствующие интенсивные характеристики процессов трех типов: равномерных, перераспределения и переориентации.

Аналогия между выражением аксиомы неоднородности (7) и тождеством (10) очевидна. В результате аксиома неоднородности (7) получает аналитическое подтверждение в виде математического тождества (10), которое представляет собой выражение обобщенного закона сохранения и превращения энергии.

С введением времени t в качестве физического параметра, тождество (10) приводится к виду, содержащему полные производные по времени от всех параметров состояния:

где ${{{\mathbf{v}}}_{i}} \equiv {{{{{\mathbf{e}}}_{i}}{{R}_{i}}} \mathord{\left/ {\vphantom {{{{{\mathbf{e}}}_{i}}{{R}_{i}}} {dt}}} \right. \kern-0em} {dt}}$ – поступательная скорость переноса центра энергоносителя ${{\Theta }_{i}}$; ${{{\mathbf{\omega }}}_{i}} \equiv {{~d{{{\mathbf{\varphi }}}_{i}}} \mathord{\left/ {\vphantom {{~d{{{\mathbf{\varphi }}}_{i}}} {dt}}} \right. \kern-0em} {dt}}$ – угловая скорость его переориентации (или вращения). В частном случае, когда параметр ${{\Theta }_{i}}$ имеет смысл массы системы, величины ${\mathbf{v}}$ и $~{\mathbf{\omega }}$ характеризуют ее линейную и угловую скорость ее как целого. В соответствии с аксиомой неоднородности соотношение (11) показывает, что в каждый фиксированный момент времени t неоднородная термодинамическая система всегда включает в себя подсистему в виде «мгновенно твердого» тела, скорость любой точки которого складывается из поступательной скорости и угловой скорости вращения вокруг мгновенного центра инерции тела [7]. Авторы [7] отмечают, что перенос начала координат наблюдателя в центр инерции механической системы предпочтителен для анализа системы в целом. Энергодинамика идет дальше и переносит начало координат наблюдателя в равновесное или стационарное состояние термодинамической системы. Такое рассмотрение системы в целом, в которой действуют обобщенные силы и потоки, особенно полезно тогда, когда целесообразно избежать излишнего переопределения механической системы параметрами состояния элемента сплошной среды, затрудняющего решение поставленной задачи. Заметим, что в ТНП теорию сплошной среды иногда называют “теорией поля” [8], которая на самом деле только привлекается для формулировки модели сплошной среды в качестве удобного формального математического аппарата [6].

Упорядоченной силе ${{{\mathbf{F}}}_{i}}$ в ее общефизическом понимании соответствует обобщенная сила Х_i, которая определяется как частная производная от внутренней энергии U по параметру Z_i при условии постоянства ${{\Theta }_{i}}$, т.е.

Обобщенная сила Х_i имеет смысл удельной силы внутренних напряжений

где $~{{\rho }_{{ui}}} = ~\,\,{{\psi }_{i}} = {{d{{U}_{i}}} \mathord{\left/ {\vphantom {{d{{U}_{i}}} {dM}}} \right. \kern-0em} {dM}}$ – плотность i-й формы энергии U_i или ее локальный потенциал. Связь (12) величин Х_i и F_i позволяет выразить закон сохранения и превращения энергии в свернутом виде, эквивалентном (11) [2]: где ${{J}_{i}} = {{d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}}$ – скалярный поток i-го энергоносителя (обобщенный скалярный поток, соответствующий понятию “расход”); – векторный поток i-го энергоносителя (обобщенный направленный поток, соответствующий понятию его импульса ${{\theta }_{i}}{{{\mathbf{\bar {v}}}}_{{i~}}}$); ${{\bar {v}}_{i}} = {{d{{{\mathbf{R}}}_{i}}} \mathord{\left/ {\vphantom {{d{{{\mathbf{R}}}_{i}}} {dt}}} \right. \kern-0em} {dt}}$ – среднее значение скорости энергоносителя ${{\Theta }_{i}}$ для системы в целом.

Аналитическое выражение закона сохранения и превращения энергии в форме (11) или (14) следует также из представления его в виде, предложенном Н. Умовым (1873) [7]

где V – фиксированный в пространстве объем, ограниченный поверхностью f, ${{{\mathbf{j}}}_{e}}$ – плотность потока энергии через векторный элемент df поверхности с нормалью n. Формулировка закона исходит из принципа близкодействия, согласно которому энергия системы U не просто исчезает в одних точках пространства и возникает в других, а переносится через границы системы какими-либо материальными носителями ${{\Theta }_{i}}$ (i = 1, 2, …, n), число которых определяется уровнем наших знаний о процессе. Под энергоносителем понимается экстенсивный параметр ${{\Theta }_{i}}$: масса М, количество k-го вещества в виде N_k молей (k = 1, 2, …, m), его масса М_k, заряд Q_e, энтропия S, количество движения М$v$, количество движения k-го вещества М_k${{v}_{k}}~$ и т.п. Поток энергии ${{{\mathbf{j}}}_{e}}$ через границы системы складывается из потоков энергии ${{{\mathbf{j}}}_{{ei}}}$ всех i-х энергоносителей ${{\Theta }_{i}}$, каждый из которых, в свою очередь, выражается произведением потока самого i‑го материального энергоносителя ${\mathbf{j}}_{i}^{e} = {{\rho }_{i}}{{{\mathbf{v}}}_{i}}$ на его потенциал ${{\psi }_{i}} = {{d{{U}_{i}}} \mathord{\left/ {\vphantom {{d{{U}_{i}}} {dM}}} \right. \kern-0em} {dM}}$ (удельную энергию) где U_i – парциальная энергия i-й формы движения, ${{\rho }_{i}} = {{d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\Theta }_{i}}} {dV}}} \right. \kern-0em} {dV}}$ – плотность i-го энергоносителя; ${{{\mathbf{v}}}_{i}}$ – локальная скорость его переноса через границы системы. Подставляя (17) в (16) и учитывая, что получим выражение закона сохранения энергии (2) в развернутом виде:

В первой сумме справа вынесем за знак интеграла некоторое среднее значение ${{\bar {\psi }}_{i}}$ локального потенциала ${{\psi }_{i}}$, а во второй – среднее значение ${{{\mathbf{X}}}_{i}}$ градиента потенциала $\nabla {{\psi }_{i}}$. Тогда, сохраняя принятое в термодинамике правило знаков для теплоты и работы (подведенная к системе теплота и совершенная ею работа считаются положительными), интегральную форму закона сохранения энергии (15) можно выразить параметрами неравновесной системы в целом, как это принято в термодинамике:

что эквивалентно соотношению (14). Таким образом, на основании аксиомы неоднородности (7) для закона сохранения и превращения энергии получена аналитическая форма его выражения в виде (11), (14) или (19), которую можно рассматривать как обобщение соотношений Гиббса (1) и (2) на неоднородные (внутренне неравновесные) системы.

Силы F_i или Х_i = F_i/${{\Theta }_{i}}$ выражаются через внутренние параметры состояния системы и поэтому также являются параметрами ее состояния. Этим они отличаются от сил реакции типа сил инерции Ньютона, которые возникают только в процессе ускорения и потому являются функциями процесса, а не состояния. Определенные таким образом силы относятся к внутренним напряжениям, являясь причиной, а не следствием возникновения в системе процессов релаксации, поэтому их можно назвать активными. В этом их отличие от “термодинамических” сил, вводимых в теории необратимых процессов [8], исходя из выражения для скорости возникновения энтропии d_iS/dt. Последние имеют не только иное аналитическое выражение, но и смысл сил реакции, исчезающих при отсутствии процесса релаксации. Введенная здесь сила F_i = ${{\Theta }_{i}}{{{\mathbf{Х}}}_{i}}$ внутренних напряжений i-го рода определена как градиент (14) от энергии системы в целом по отношению к смещению ${{{\mathbf{R}}}_{i}}$ или как полная производная от i-ой парциальной энергии U_i по этому смещению F_i = ${{d{{U}_{i}}} \mathord{\left/ {\vphantom {{d{{U}_{i}}} {d{{{\mathbf{R}}}_{i}}}}} \right. \kern-0em} {d{{{\mathbf{R}}}_{i}}}}$. Тем самым она приобретает обобщенный смысл, т.е. не зависит от выбора той или иной конкретной модели внутренних напряжений, как это делается в модели сплошной среды [6] или в процедуре их определения через производство энтропии [8, 10–11].

Из обобщенного закона сохранения и превращения энергии, аналитически выраженного в виде (11), и связи (12), (13) между силами ${{{\mathbf{X}}}_{i}}~$ и ${{{\mathbf{F}}}_{i}}~$ следует, что в любых реальных системах всегда совершается внутренняя работа, элементарные количества которой определяются двояким образом $dW_{i}^{{\text{т}}} = {{{\mathbf{F}}}_{i}}d{{{\mathbf{R}}}_{i}} = {{{\mathbf{X}}}_{i}}d{{{\mathbf{Z}}}_{i}}$. Такие работы связаны с превращением энергии и называются упорядоченными (полезными или техническими) [2]. На практике они широко применяются и исследуются в механике, энергетике, электродинамике, теплотехнике и во многих других дисциплинах, оперирующих понятием силы. Они являются количественными мерами процессов превращения различных видов энергии из одной формы в другую. Однако при обработке экспериментальных данных обычно исходят из традиционных представлений об однородной (внутренне равновесной) системе, в которой происходит только перенос энергии. Ясно, что корректный анализ и расчет подобных процессов невозможны без учета превращения энергии.

Теперь внутренняя (собственная) энергия U становится количественной мерой всех видов работы, которые может совершить пространственно неоднородная изолированная система. Такое ее понимание очень близко к данному К. Максвеллом определению энергии как “суммы всех действий, которые может оказать система на окружающие ее тела” [12]. Оно позволяет устранить известную неопределенность понятия энергии как “одного из семи интегралов движения” (Л.Д. Ландау, Е.М. Лифшиц) [13], когда “мы не можем сказать об энергии ничего сверх того, что существует нечто, остающееся неизменным” (А. Пуанкаре) [14], а закон ее сохранения – “формулой для расчета определенных численных величин” (Р. Фейнман) [15].

Сформулированные здесь аксиома неоднородности и аналитическая форма обобщенного закона сохранения и превращения энергии имеют далеко идущие последствия при анализе природных и технологических процессов, которые подробно рассмотрены в [2, 3]. Они позволяют корректно учитывать термодинамические закономерности при анализе природных и технологических процессов. Однако, эта форма выражения энергетического закона до сих пор не находила применения в механике сплошной среды, которая традиционно строится на трех законах Ньютона, инерциальной системе отсчета, соотношении Гиббса для открытых равновесных систем и законе сохранения энергии без учета ее превращения в другие формы. В результате оказалось, что многие природные эффекты невозможно описать методами традиционной механики, а все попытки как-то их осмыслить и объяснить отвергались официальной наукой. Поэтому представляет интерес рассмотреть то новое, что вносит сформулированный закон прежде всего в механику.

1. Учет термодинамических закономерностей в механике сплошной среды обычно сводится к формулировке теоремы живых сил, уравнения сохранения энергии для однородных сред в виде уравнения притока тепла и использования гипотезы локального равновесия [6]. Такой учет является неполным, т.к. принимается во внимание только перенос энергии без учета ее превращения, хотя этот закон экспериментально был установлен давно [1]. Поэтому корректное использование закона сохранения энергии с учетом ее превращения актуально как в механике сплошной среды, так и в других дисциплинах. Попытка учесть неоднородность сплошной среды содержится в [10–11], однако она касается только многофазных сред, состоящих из однородных составляющих фаз, и основана на гипотезе локального равновесия и нахождении диссипативной функции в виде производства энтропии. В механике сплошной среды постулируется уравнение движения индивидуального объема V среды, ограниченного замкнутой поверхностью$~~$f и движущегося вдоль пути центра масс [6]:

где F – внешняя дальнодействующая объемная сила; p_n – вектор плотности поверхностной силы, определяемый на основе модели внутренних поверхностных напряжений Коши [16]. Однако постулируемая модель не охватывает все возможные виды внутренних напряжений, возникающих в сплошной среде. Например, явно не учитывается внутренняя сила противодействия действию внешней дальнодействующей силе F. Уравнение (20) исходит из ньютоновского понимания силы, сформировавшегося в те времена, когда понятия энергии вообще не существовало. Здесь принят дедуктивный подход к введению сил в механику сплошной среды, не связанный с постулированием конкретной модели внутренних напряжений и учитывающий закон сохранения и превращения энергии.

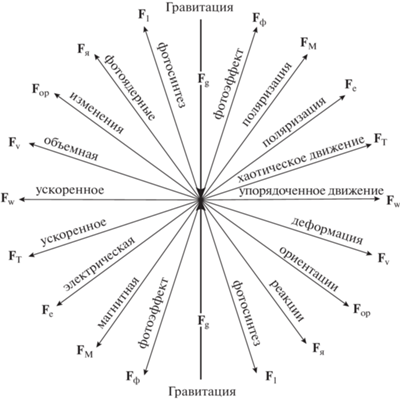
2. Вместо ньютоновской неоднозначной трактовки силы (с одной стороны как функции инерционного процесса, а с другой – как функции состояния системы двух гравитирующих тел) обобщенный энергетический закон, выраженный в виде (11), (14) или (19), дает однозначное определение силы как градиента соответствующей формы энергии (13). Это значит, что напряженность силового поля любого независимого процесса выражается градиентом от энергии U системы в целом по величине ее смещения R_i от равновесия или полной производной по R_i от парциальной энергии U_i системы, т.е. потенциалом ${{\psi }_{i}} = {{d{{U}_{i}}} \mathord{\left/ {\vphantom {{d{{U}_{i}}} {dM}}} \right. \kern-0em} {dM}}$. Другими словами, она целиком определяется пространственной неоднородностью распределения материального энергоносителя ${{\Theta }_{i}},$ определяющего этот процесс. Отсюда следует принципиальное положение, что любые силовые поля порождены не самими массами, зарядами или токами, а их неравномерным распределением в пространстве, т.е. наличие энергоносителей является лишь необходимым, но не достаточным условием возникновения сил и процессов. Необходимым и достаточным условием возникновения сил и природных процессов является именно неравномерность распределения энергоносителя в пространстве. Поэтому любое силовое поле (гравитационное, тепловое, электрическое, магнитное и т.п.) представляет собой не физическую реальность (как это сейчас принято считать), а абстрактное математическое понятие, вводимое для характеристики указанной неравномерности. В данном подходе механические, тепловые, химические, электрические, магнитные, гравитационные, гидродинамические и т.п. силы ${{{\mathbf{F}}}_{i}}$ получают единый смысл, единое математическое выражение и единую размерность, т.е. формулируется единый метод непосредственного нахождения обобщенных сил природных и технологических процессов. Немаловажно и то, что сама процедура нахождения обобщенных сил в виде градиентов парциальных энергий соответствующих степеней свободы системы существенно упрощается: для этого нет необходимости составлять и манипулировать уравнениями баланса массы, импульса и энергии, чтобы выделить члены с производством энтропии, как это делалось до сих пор [8, 10–11]. Тем самым открывается путь к детальной классификации разнообразных обобщенных сил и открытию новых видов сил в природе, например, гравитационной, лучевой (радиантной), электрической, магнитной, гироскопической и др. Всего на сегодня установлено около 30 видов таких сил [2].

3. Совмещение точки отсчета наблюдателя с положением равновесия термодинамической системы меняет обычные представления о механической системе, в которой различаются состояние абсолютного покоя (т.е. всякие процессы вырождены), и состояния движения: поступательного и вращательного. Равновесие поступательного движения характеризуется нулевой скоростью ${\mathbf{v}}$ = = dr/dt = 0; равновесие ускоренного поступательного движения в данном направлении – постоянной ненулевой скоростью ${\mathbf{v}}$ = const $ \ne $ 0; равновесие вращательного движения – нулевой угловой скоростью ${\mathbf{\omega }}$ = d${\mathbf{\varphi }}$/dt = 0; равновесие ускоренного вращательного движения в данном направлении – постоянной ненулевой угловой скоростью ${\mathbf{\omega }}$ = d${\mathbf{\varphi }}$/dt = const $ \ne $ 0 относительно мгновенной оси вращения, ориентируемой в пространстве. В такой абсолютной системе отсчета движение – это изменение состояния покоя (т.е. процесс, протекающий в пространстве переменных смещений R_i), а ускорение – это изменение состояния движения (т.е. процесс, протекающий в пространстве скоростей ${\mathbf{v}}$). Ускорить тело или материальную точку, не изменяя их положения r = r(t) в пространстве, невозможно. При этом ускорение a = a(r, t) должно определяется выражением [2]

где R – смещение центра массы частицы в абсолютной системе отсчета, а первое слагаемое, представляющее локальную составляющую ускорения частицы ${{({{\partial {\mathbf{v}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{v}}} {\partial t}}} \right. \kern-0em} {\partial t}})}_{{\mathbf{R}}}}$ (при неизменном ее положении), не имеет никакого физического смысла и его можно опустить. Из определения (21) следует, что пространство, в котором ускорение возможно в любой точке, не может быть однородным (где $\nabla {\mathbf{v}}$ = 0) и пустым (где $\rho $ = 0), как это принято в современной механике. В случае поступательного движения ускоряющая сила равна и противоположна силе инерции F и определяется как градиент кинетической энергии ${{M{{{\mathbf{v}}}^{2}}} \mathord{\left/ {\vphantom {{M{{{\mathbf{v}}}^{2}}} 2}} \right. \kern-0em} 2}$ такого движения ${{\partial ({{М{{{\mathbf{v}}}^{2}}} \mathord{\left/ {\vphantom {{М{{{\mathbf{v}}}^{2}}} 2}} \right. \kern-0em} 2})} \mathord{\left/ {\vphantom {{\partial ({{М{{{\mathbf{v}}}^{2}}} \mathord{\left/ {\vphantom {{М{{{\mathbf{v}}}^{2}}} 2}} \right. \kern-0em} 2})} {\partial R}}} \right. \kern-0em} {\partial R}}$ = М${\mathbf{v}}\nabla {\mathbf{v}}$ = Ма, что совпадает с (13). Таким образом, ньютоновское определение ускоряющей силы с рассматриваемых позиций представляет собой частный случай обобщенного определения силы как меры действия, направленного на удаление механической системы от равновесного состояния (т.е. от равномерного распределения скоростей по объему системы). То же самое относится и к вращательному ускорению ${{d{\mathbf{\omega }}} \mathord{\left/ {\vphantom {{d{\mathbf{\omega }}} {dt}}} \right. \kern-0em} {dt}}$. Равномерному вращательному движению при ${\mathbf{\omega }}$ = const соответствует неизменная кинетическая энергия E_вр = Iω²/2 = const, где Iω – момент инерции системы как целого, градиент которой равен нулю, т.е. при постоянстве угловой скорости нет затраты работы, как это имеет место при поступательном ускорении.

4. В предлагаемом подходе все силы F_i и их моменты М_i – внутренние, являющиеся следствием напряженного состояния самой системы (т.е. активные) и служащие его мерой. В этом случае имеет значение только наличие или отсутствие результирующей F = $\mathop \sum \limits_i {{{\mathbf{F}}}_{i}}.$ При этом трансформируется и 3-й закон Ньютона, согласно которому “действию всегда соответствует и равная реакция”, причем силы действия и противодействия лежат на одной прямой. Если обозначить активные силы и силы реакции как ${{{\mathbf{F}}}^{a}}~$ и $~{{{\mathbf{F}}}^{r}}$, то это положение имеет вид ${{{\mathbf{F}}}^{a}} = - ~{{{\mathbf{F}}}^{r}}$. Однако в поливариантных системах имеется множество активных сил ${\mathbf{F}}_{i}^{a}$ и сил реакций ${\mathbf{F}}_{j}^{r}$, причем в замкнутых системах их сумма всегда обращается в нуль. Это означает, что каждой активной силе ${\mathbf{F}}_{i}^{a}$ противостоит не одна, а нескольких сил реакции разного рода с результирующей ${\mathbf{F}}_{i}^{r}$ [2]:

где $~{\mathbf{F}}_{{ij}}^{r}~$ – силы реакции j-й природы, противодействующие активной силе ${\mathbf{~F}}_{i}^{a}$ гласно третьему закону Ньютона, равновесие имеет место лишь тогда, когда силы действия ${\mathbf{F}}_{i}^{a}$ и противодействия ${\mathbf{F}}_{i}^{r}$ имеют одну и ту же природу. В противном случае возникает процесс превращения энергии i-го рода в j-ю форму, при котором их сумма остается неизменной: ${{{\mathbf{F}}}_{i}}{{{\mathbf{v}}}_{i}} + {\mathbf{F}}{{{\mathbf{v}}}_{j}} = 0$, что указывает на возможность существования “веера” противодействующих сил ${\mathbf{F}}_{{ij}}^{r}$ (рис. 2).

Наличие таких “разнородных” сил в какой-либо системе предопределяет “ветвление” траектории процесса преобразования энергии в пространстве переменных ${{{{\Theta }}}_{{\text{i}}}}$, что порождает необратимость особого рода. Приходит более общее понимание необратимости как невозможности “вернуть всю природу в начальное состояние” [17]. Необходимо учитывать, что такая необратимость возникает и в том случае, когда механические силы консервативны и допускают обращение во времени. Она обусловлена тем, что одновременно обратить знак всех сил, сохранив при этом и соотношение сил, невозможно хотя бы в связи с повторным ветвлением траектории от каждой такой “обращенной” силы. Это говорит о необходимости принимать во внимание все виды необратимости в механике, несмотря на то, что исследуемые системы консервативны.

5. В механике, базирующейся на законах Ньютона, выпадает из внимания взаимопревращение импульсов. При анализе превращения энергии в законе сохранения энергии в виде (14) или (19) учитываются только члены, содержащее обобщенные силы X_i и потоки J_i, возникающие в системе при ее смещении относительно равновесия:

откуда энергия системы в текущем неравновесном состоянии выражается интегралом: U = $ = \mathop \sum \limits_i \int {{{{\mathbf{X}}}_{i}}{{{\mathbf{J}}}_{i}}dt} + $ U₀, где U₀ – энергия системы в однородном (внутренне равновесном) состоянии.

Слагаемые равенства (23) выражают мощность процесса преобразования одной формы энергии в другую. При этом с исчезновением силы X_i обращается в нуль и поток J_i, являющийся обобщенным импульсом ${{\Theta }_{i}}{{{\mathbf{v}}}_{i}}$. Следовательно, уравнение (23) отражает взаимопревращение не только энергии, но и импульсов в изолированной системе. Из него видно, что импульсы различных форм энергии в общем случае не сохраняются, как и сами энергоносители $~{{\Theta }_{i}}$. Нагляднее всего это проявляется у энтропии, которая возрастает в процессах диссипации в изолированных системах, а также у чисел молей N_k k-х веществ, изменяющихся в ходе химических реакций. Так же ведут себя и импульсы поступательного $P{\kern 1pt} '$ = M${\mathbf{v}}$ и вращательного 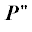= M[ωr] движения как различные составляющие импульса внутреннего движения в системе, которые могут превращаться друг в друга. Традиционное выражение закона сохранения импульса остается в силе, если импульс Р считать состоящим из двух составляющих $P{\kern 1pt} '$ и 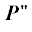, где 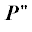является моментом количества движения L = $(I\omega )\omega .~$ В таком случае становится очевидным, что для систем, включающих процессы вращения, в действительности законы Ньютона постулируют постоянство суммарного количества поступательного и вращательного движения: Мv + (Iω)${\mathbf{\omega }}$ = сonst, а не каждого из них в отдельности. Таким образом, обобщенный закон сохранения и превращения энергии обнаруживает возможность нарушения закона сохранения импульса механического движения в случаях превращения энергии в другие ее формы. Это свидетельствует о принципиальной возможности самопроизвольного возникновения внутреннего относительного движения (самодвижения) в механических внутренне неравновесных изолированных (замкнутых) системах, что обычно отвергается и объявляется не соответствующим законам природы.

6. В релаксирующей системе ее смещение относительно равновесия стремится к нулю и при наличии внешнего принуждения принимает минимальное возможное значение, что отражается выражением

Это соотношение представляет собой обобщение вариационного принципа наименьшего действия (ПНД) в механике. Оно отражает то обстоятельство, что релаксирующая система “выбирает” из всех возможных траекторий движения системы ту, при которой она остается наиболее близкой к равновесию (Z_i = min, R_i = min). Например, при движении сплошной среды жидкости X_i = $ - \nabla {\mathbf{v}}$, dZ_i = Pdt. Тогда (24) приобретает смысл минимума кинетической энергии U^k потока, включающей в себя и турбулентную составляющую, что снимает с ПНД покров “таинственности”. Принцип (24) имеет универсальный характер и справедлив не только для механического движения, но для процессов любой другой природы. Он не мог быть получен в рамках представлений, основанных на понятии энтропии, и справедлив для консервативных и неконсервативных систем, поскольку любая необратимость, как показано выше, описывается обобщенными Z-функциями.

7. При новом подходе существенно изменяется организация самого научного исследования на базе изложенного объединения механики и термодинамики. Чтобы в этом убедиться достаточно сравнить этапы решения типовой естественно-научной проблемы традиционной методом и предлагаемым подходом. Традиционная методология: механическое движение → динамика Ньютона → уравнения сохранения массы, импульса, момента импульса, заряда → инженерная задача (инерциальная система отсчета, пустое пространство без эфира как энергоносителя). Новая методология: фиксация условий равновесия системы в целом (в частности, механической) $ \to $ закон сохранения и превращения энергии $ \to ~~$ выделение значимых парциальных энергий с учетом дополнительных условий однозначности $ \to $ вариационный принцип наименьшего действия $U = \mathop \sum \limits_j \int {{{{\mathbf{X}}}_{j}}d{{{\mathbf{Z}}}_{j}}} \to \min $ $ \to $ движущие силы (учет существования реального носителя энергии вместо пустого пространства). Дополнительные условия однозначности включают: 1) уравнения баланса всех энергоносителей ${{\Theta }_{i}}$ и их смещений R_i от равновесия; 2) уравнения состояния; 3) уравнения переноса субстанций; 4) уравнения сохранения массы, импульса, момента импульса энергоносителей с учетом их взаимопревращения в изолированной системе [2, 3].

8. Важным результатом применения новой методологии научного исследования является уяснение того, что энергия может переноситься и преобразовываться не только известными энергоносителями $~{{\Theta }_{i}}$ ($i = 1,~2, \ldots ,~n$), относящимися к видимому нами веществу, но и любыми другими энергоносителями ${{\tilde {\Theta }}_{i}}$, ($i = 1,~2, \ldots ,~k$), относящимися к субстанции, о которой можно судить лишь по косвенным признакам. Примером такого энергоносителя может служить электрический заряд, природа которого до сих пор не ясна. Другим таким энергоносителем может выступать светоносная субстанция, которую так или иначе признавались многими предыдущими теориями, называя ее в разное время “эфиром”, “тонкой материей”, “скрытой массой”, “физическим вакуумом”, “полем”, “темной материей”, “темной энергией”. Обозначая через ${{\tilde {\Theta }}}~$ количество этой скрытой субстанции, можно ввести ее плотность $\tilde {\rho }$ = d${{\tilde {\Theta }}}$/dV. Она всепроницаема, обладает единственной колебательной степенью свободы и соответствующая ей энергия гравитационная [2, 3]. Так как она всепроницаема и занимает 95% Вселенной, то ее взаимодействием с видимым веществом можно пренебречь. Если рассматривать все сущее как изолированную систему, то для нее нетрудно записать закон сохранения и превращения энергии в виде (11), (14) или (19). В принятой системе отсчета $\tilde {\rho }$ – отклонение плотности этой субстанции от ее равновесного значения. Тогда при отсутствии силового взаимодействия этой субстанции с веществом в силу ее всепроницаемости должны выполняться законы сохранения ее количества, импульса и момента импульса [3]:

Совместное решение первых двух уравнений, выполненное Н.А. Магницким, позволило ему построить математическую модель перехода скрытой субстанции в обычную материю в виде основных элементарных частиц (электрона, протона, нейтрона) с их структурными особенностями, а также атомов всех элементов таблицы химических элементов Д.И. Менделеева, не выходя за рамки классической механики [18[.