Теоретические основы химической технологии, 2023, T. 57, № 3, стр. 292-308
Паровой риформинг этана в мембранном реакторе с никелевым катализатором при высоких температурах
В. Н. Бабак a, *, Л. П. Диденко a, Л. А. Семенцова a, Ю. П. Квурт a
a Федеральный исследовательский центр проблем химической физики и медицинской химии РАН
Московская область, г. Черноголовка, Россия
* E-mail: tabor47@mail.ru
Поступила в редакцию 27.03.2023
После доработки 30.03.2023
Принята к публикации 30.03.2023
- EDN: RLNNDC
- DOI: 10.31857/S0040357123030016
Аннотация
Предложена модель парового риформинга чистого этана в мембранном каталитическом реакторе, рабочими элементами которого являются цилиндрические камеры, между которыми помещена водородселективная палладиевая фольга. Верхняя камера вакуумируется, а в нижней находится никелевый катализатор. При равномерной подаче сырья (С2Н6 и Н2О) по периметру нижней камеры задача сводится к нахождению средних потоков С2Н6, СН4, Н2О, СО, СО2 и Н2 в результате решения системы нелинейных обыкновенных дифференциальных уравнений. Исследования проводили в интервале температур 700 $ \leqslant T \leqslant $ 1000 K при допустимых отношениях входных потоков водяной пар/этан более четырех. Найдены оптимальные условия проведения процесса, при которых выход водорода равен 100%. Доказано, что при этих условиях и фиксированной температуре максимальный поток водорода через мембрану наблюдается при минимально допустимых значениях отношений входных потоков пара и этана, равных четырем. Сравнение расчетов с экспериментом подтвердило предположение о существовании двух участков в нижней камере (короткого начального и основного).
ВВЕДЕНИЕ
Водородная энергетика является перспективной и быстро развивающейся отраслью энергетики, основанной на использовании экологически чистого энергоносителя – водорода [1]. В связи с этим потребность в водороде постоянно возрастает. Важным практическим применением водорода является использование в топливных элементах, обеспечивающих наиболее эффективный и экологически чистый способ получения электроэнергии [2]. В настоящее время Н2 в основном получают из природного сырья (природный газ, тяжелые попутные нефтяные газы) [3, 4]. Основным крупномасштабным промышленным способом производства Н2 является паровая конверсия природного газа.
Помимо СН4, для получения Н2 может быть использовано такое ценное сырье, как С2+ углеводороды. В природном газе, помимо метана, содержатся 3–7 об. % С2+ углеводородов. Особенно велико их содержание в попутных нефтяных газах. Гомологи метана более активны в реакции паровой конверсии, и при этом в расчете на моль алкана можно получить больше Н2, чем из метана.
Однако по сравнению с метаном из С2+ углеводородов с более высокой скоростью образуются углеродные отложения (УО), которые могут дезактивировать некоторые катализаторы. В промышленном процессе паровой конверсии природного газа для предотвращения образования УО из гомологов метана используют стадию предриформинга, в которой происходит их паровая конверсия при температурах менее 700 К с образованием смеси СН4, Н2 и оксидов углерода [5]. Использование стадии предриформинга увеличивает капитало- и энергозатраты процесса.
Другой путь предотвращения отравления катализаторов – это использование устойчивых к дезактивации катализаторов. Высокую активность и устойчивость имеют Pt, Rh, Ru, нанесенные на оксидные носители [6]. Такие катализаторы дороги, и более эффективно использовать их в качестве добавок к никелевым, т.е. более дешевым катализаторам. Например, для снижения выхода УО вместо Ni/Al2O3 использовали в качестве носителя СеО2, допированный Cd (Ni/Cd–CeO2) [7].
В работе [3] измеряли скорости паровой конверсии метана, этана, н-бутана на Pd и Pt, нанесенных на CeO2, в температурном интервале 620–770 К. Оба катализатора имели сходную каталитическую активность, которая возрастает при увеличении количества атомов углерода. Введение 14% СеО2 в Ni/Al2O3 повышало устойчивость катализаторов к дезактивации углеродными отложениями при паровой конверсии этана и пропана при 1173 К [8]. Хорошей устойчивостью к образованию УО обладают катализаторы на носителе из диоксида циркония [9]. В работе [10] выполнено сравнительное исследование паровой конверсии метана, этана и этилена на Rh, Pd и Pt, нанесенных на стабилизированный иттрием диоксид циркония (YSZ). Установлено, что в паровой конверсии этана наиболее активен Rh/YSZ, а самая низкая тенденция к образованию УО наблюдается на Pt/YSZ. Исследование паровой конверсии этана при температурах 1073–1171 К на цериевом катализаторе показало, что введение в катализатор 0.15% Cd также увеличивает активность катализатора в основой реакции и снижает образование УО [11].
Высокие температуры паровой конверсии благоприятны для образования УО, которое может происходить по реакциям:
Для снижения этого процесса увеличивают соотношение пар/сырье. В этом случае избыток пара переводит углерод в газообразные продукты:
Несмотря на большое разнообразие активных и устойчивых к образованию УО катализаторов, а также поиск новых гетерогенных каталитических систем [12], в промышленных процессах чаще всего используются катализаторы на основе никеля и меди, нанесенные на оксидные носители (Al2O3, ZnO2, Cr2O3), что обусловлено доступностью и низкой ценой.
Паровую конверсию (риформинг) чаще всего проводят в мембранных каталитических реакторах (трубы, каналы) различных конструкций [13, 14].
Совмещение каталитических и мембранных процессов было впервые предложено академиком В.Я. Грязновым [15].
Основу современных селективных по отношению к водороду мембран составляют палладиевые сплавы с Pt, Y, Ru, Sn, Cu, образующие с Pd твердые растворы, для увеличения механической прочности и водородопроницаемости [16–20].
В данной работе мы использовали фольговые мембраны, получаемые методом холодного проката с промежуточным отжигом в инертной среде [21]. Толщина таких мембран более 10 мкм.
В трубчатых аппаратах с проницаемыми стенками из-за ограниченной пропускной способности фольги (даже при толщине ~10 мкм) высота установок должна быть достаточно большой (~5–10 м). Это усложняет расчет, так как требуется решение уравнений переноса газовой смеси и теплопередачи для пористой среды [14].
В лабораторных условиях широко используются реакторы малых размеров (менее 1 м по высоте), в которых легко поддерживать постоянную температуру и давление [22–24].
В ФИЦ ПХФ и МХ РАН разработан многофункциональный мембранный модуль (ММ), рабочей частью которого являются две цилиндрические камеры, разделенные фольговой перегородкой. С помощью ММ был исследован паровой риформинг чистых метана и пропана на никелевых катализаторах [25, 26].
В настоящей работе проведено исследование конверсии этана, который наряду с пропаном и метаном является основным компонентом, присутствующим в заметном количестве в природном газе и сопутствующих нефтяных газах. Зная известную из литературы кинетику взаимодействия этих газов с водяным паром, нетрудно смоделировать в дальнейшем процессы парового риформинга природного сырья в мембранном модуле в широкой области изменения температур при произвольных отношениях пар/сырье.
ОПИСАНИЕ МЕМБРАННОГО РЕАКТОРА И МЕТОДИКА ЭКСПЕРИМЕНТА
В качестве водородселективной мембраны использовали фольгу толщиной 30 мкм из сплава Pd–6% Ru, предоставленную сотрудниками лаборатории 12 Института металлургии и материаловедения РАН (ИМЕТ РАН, МОСКВА) [21]. Заготовки под фольгу получали плавкой в электродуговой печи в инертной атмосфере. Фольгу заданной толщины получали холодным прокатом с промежуточными вакуумными отжигами. Мембрана из фольги имела форму диска диаметром 56 мм (эффективная площадь поверхности 15.2 см2). Для поддержания механической прочности ее помещали между сетками тонкого плетения из нержавеющей стали. Мембранный реактор включал отделения подвода сырья (ретентат) и отвода Н2 (пермеат), между которыми помещали мембрану (рис. 1). Схема экспериментальной установки представлена в [27]. В отделении ретентата поддерживали атмосферное давление. Движущую силу для отвода Н2 из реакционной смеси через мембрану создавали с помощью вакуумирования отделения пермеата. Для этого использовали безмасляный диафрагменный (мембранный) вакуумный насос MZ 2C NT (Германия).
Рис. 1.
Схематическое изображение мембранного реактора: 1 – верхняя камера; 2 – нижняя камера; 3 – мембрана; $r{\kern 1pt} '$ – радиальная координата; $x$ – безразмерные координаты.
Конверсию сырья (α, %), селективность образования продуктов паровой конверсии этана (${{S}_{{{\text{прод}}}}}$, %) и отвод Н2 через мембрану (φ, %) рассчитывали по формулам:
(1)
$\alpha = \frac{{{{V}^{{{\text{вх}}}}}X_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{{{\text{вх}}}} - {{V}^{{{\text{рет}}}}}X_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{{{\text{рет}}}}}}{{{{V}^{{{\text{вх}}}}}X_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{{{\text{вх}}}}}},$(2)
${{S}_{{{\text{прод}}}}} = \frac{{X_{{{\text{прод}}}}^{{{\text{рет}}}}}}{{X_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{{{\text{рет}}}} + X_{{{{{\text{H}}}_{{\text{2}}}}}}^{{{\text{рет}}}} + X_{{{\text{CO}}}}^{{{\text{рет}}}} + X_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{{{\text{рет}}}} + X_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{{{\text{рет}}}}}},$(3)
$\varphi = \frac{{{{V}^{{{\text{перм}}}}}X_{{{{{\text{H}}}_{{\text{2}}}}}}^{{{\text{перм}}}}}}{{{{V}^{{{\text{перм}}}}}X_{{{{{\text{H}}}_{{\text{2}}}}}}^{{{\text{перм}}}} + {{V}^{{{\text{рет}}}}}X_{{{{{\text{H}}}_{{\text{2}}}}}}^{{{\text{рет}}}}}},$${{V}^{{{\text{вх}}}}}$ – расход газового потока на входе в реактор, см3/мин;
$X_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{{{\text{вх}}}}$ – объемная концентрация С2Н6 в газовом потоке на входе в реактор, об. %;
$X_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{{{\text{рет}}}}$ – объемная концентрация С2Н6 в продуктах реакции на выходе из отделения ретентата, об. %;
${{V}^{{{\text{перм}}}}}$ – скорость газового потока на выходе из отделения пермеата, см3/мин;
$X_{{{{{\text{H}}}_{{\text{2}}}}}}^{{{\text{перм}}}}$ – объемная концентрация Н2 на выходе из отделения пермеата, об. %;
${{V}^{{{\text{рет}}}}}$ – скорость газового потока на выходе из отделения ретентата, см3/мин;
$X_{{{{{\text{H}}}_{{\text{2}}}}}}^{{{\text{рет}}}}$ – объемная концентрация Н2 на выходе из отделения в ретентата, об. %.
В качестве сырья использовали этан 99.95%. В отделение ретентата помещали 2 см3 (3.35 г) промышленного никелевого катализатора марки НИАП–03-01 (производитель ООО “НИАП-КАТАЛИЗАТОР”, г. Новомосковск), содержащего 11.2 мас. % Ni в пересчете на NiO. Сырье смешивали с водяным паром в требуемом соотношении и подавали с заданной скоростью на катализатор через отверстия, расположенные по периферии отделения ретентата, а образующиеся продукты отводили через центральное отверстие и пропускали через холодильник для конденсирования непрореагировавшей воды. Объемную скорость “сухих” газов, содержащих СО2, Н2, СН4 и СО, на выходе из реактора измеряли, используя пенный расходомер, и подавали в хроматограф. Состав продуктов анализировали в режиме реального времени с использованием хроматографа “Кристалл-5000” с ПИД и детектором по теплопроводности. Содержание Н2 в продуктах реакции определяли на колонке с молекулярными ситами 13Х (2 мм × 2 м, 50°С, газ-носитель – аргон). Содержание СН4, СО2 и СО определяли на колонке с активированным углем (2 мм × 2 м, 100°С, газ-носитель – гелий). Для расчета содержания продуктов использовали метод абсолютной калибровки.
Расходы газовых потоков контролировали регуляторами расхода газа РРГ-12 (“Элточприбор”, г. Зеленоград). Реактор помещали внутрь металлического кожуха. Нагрев кожуха осуществляли электрической печью. Для контроля за температурой в реакторе и в печи использовали хромель-алюмелевые термопары.
Катализатор обрабатывали непосредственно в реакторе смесью (60% Н2–40% Ar) – пар в течение 60 мин при температуре эксперимента (предварительные эксперименты показали, что изменение температуры предварительной обработки катализатора в интервале 773–973 К не влияет на его активность). Время реакции 90 мин.
МОДЕЛИРОВАНИЕ ПАРОВОГО РИФОРМИНГА ЭТАНА
Постановка задачи. Рассмотрим движение потоков сырья (этан–водяной пар) и образующихся продуктов в ММ, представленном схематическим на рис. 1. Смесь С2Н6 и Н2О (отношение потоков $m$) подается по периметру цилиндрической нижней камеры. Компоненты реакционной смеси (С2Н6, СН4, СО, СО2, Н2О, Н2) отводятся через центральное отверстие ($r_{0}^{'}$ ≅ 1 мм).
В исследуемой системе могут протекать следующие реакции:
(4)
$1.{\text{ }}\,\,{{{\text{С}}}_{{\text{2}}}}{{{\text{Н}}}_{6}} + 2{{{\text{H}}}_{{\text{2}}}}{\text{O}} \to 2{\text{CO}} + 5{{{\text{H}}}_{2}}\,\,\,\,({{K}_{1}}),$(5)
$2.{\text{ }}\,\,{\text{СО}} + {{{\text{Н}}}_{{\text{2}}}}{\text{О}} \leftrightarrow {\text{С}}{{{\text{О}}}_{2}} + {{{\text{Н}}}_{2}}\,\,({{K}_{2}}),$(6)
$3.\,\,{\text{CO}}\,\,{\text{ + }}\,\,3{{{\text{H}}}_{2}} \leftrightarrow {\text{С}}{{{\text{H}}}_{4}} + {{{\text{H}}}_{{\text{2}}}}{\text{O}}\,\,({{K}_{3}}).$При равномерной подаче сырья концентрации изменяются только в радиальном направлении $r{\kern 1pt} '$. Пренебрегая диффузией в уравнениях переноса и интегрируя их по $z'$ от нуля до $h$, для расчета интегральных мольных потоков ${{\dot {N}}_{i}}$ (моль/с) получим уравнения [25]:
(7)
$\begin{gathered} \frac{{\partial {{{\dot {N}}}_{i}}}}{{\partial r{\kern 1pt} '}} = (2\pi r{\kern 1pt} ')h{{\rho }_{{{\text{кат}}}}}{{\varphi }_{i}} - (2\pi r{\kern 1pt} '){{I}_{{iS}}}, \\ \dot {N}{\kern 1pt} ' = \varepsilon u{\kern 1pt} 'c_{i}^{'}, \\ \end{gathered} $Введем безразмерные координаты $r$ и $y$ (рис. 1):
Уравнения для расчетов интегральных потоков принимают вид:
(8)
$\frac{\partial }{{\partial x}}( - {{\dot {N}}_{i}}) = {{w}_{{{\text{кат}}}}}{{\varphi }_{i}} - {{s}_{{{\text{эфф}}}}}{{I}_{{iS}}},$(9)
${{I}_{{S{\text{,}}{{{\text{H}}}_{{\text{2}}}}}}} = \frac{{{{Q}_{0}}\exp ( - {E \mathord{\left/ {\vphantom {E {RT)}}} \right. \kern-0em} {RT)}}}}{\delta }\sqrt {{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}} ,$Функции источников ${{\phi }_{i}}$ (см. (8)) для компонентов смеси представим в виде:
(10)
$\begin{gathered} {{\phi }_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}} = - {{b}_{1}},\,\,\,\,{{\phi }_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = {{b}_{3}}, \\ {{\phi }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = {{b}_{3}} - {{b}_{2}} - 2{{b}_{1}},\,\,\,\,{{\phi }_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} = {{b}_{2}}, \\ {{\phi }_{{{\text{CO}}}}} = - {{b}_{2}} + 2{{b}_{1}} - {{b}_{3}}, \\ {{\phi }_{{{{{\text{H}}}_{{\text{2}}}}}}} = 5{{b}_{1}} + {{b}_{2}} - 3{{b}_{3}} \\ \end{gathered} $(11)
$\begin{gathered} {{b}_{1}} = \frac{{{{{\tilde {k}}}_{1}}{{w}_{{{\text{кат}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}({{p}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}p_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2} - {{p_{{{\text{CO}}}}^{2}p_{{{{{\text{H}}}_{{\text{2}}}}}}^{5}} \mathord{\left/ {\vphantom {{p_{{{\text{CO}}}}^{2}p_{{{{{\text{H}}}_{{\text{2}}}}}}^{5}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}})}}{{kp_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{3}(1 + {{{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {({{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}k)}}} \right. \kern-0em} {({{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}k)}})}}, \hfill \\ {{b}_{2}} = \frac{{{{{\tilde {k}}}_{2}}({{p}_{{{\text{CO}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} - {{{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{p}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{p}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}} {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}{{{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}{{{[1 + {{k}_{{{\text{CO}}}}}{{p}_{E}} + {{k}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}{{p}_{{{{H}_{{\text{2}}}}O}}}} \mathord{\left/ {\vphantom {{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}{{p}_{{{{H}_{{\text{2}}}}O}}}} {{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}} \right. \kern-0em} {{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}]}}^{2}}}}, \hfill \\ {{b}_{3}} = \frac{{{{{\tilde {k}}}_{3}}(p_{{{\text{H}}{}_{{\text{2}}}}}^{3}{{p}_{{{\text{CO}}}}}{{K}_{3}} - {{p}_{{{\text{CH}}{}_{{\text{4}}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})}}{{p_{{{{{\text{H}}}_{{\text{2}}}}}}^{{2.5}}{{{[1 + {{k}_{{{\text{CO}}}}}{{p}_{{{\text{CO}}}}} + {{k}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}} + {{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \mathord{\left/ {\vphantom {{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}{{p}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} {{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}} \right. \kern-0em} {{{p}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}]}}^{2}}}}. \hfill \\ \end{gathered} $Кинетические и равновесные константы ${{\tilde {k}}_{1}}$, ${{\tilde {k}}_{2}}$, ${{\tilde {k}}_{3}}$ и ${{K}_{2}}$, ${{K}_{3}}$, а также коэффициенты Лэнгмюра для СО, Н2, Н2О известны [28]:
(12)
$\begin{gathered} {{{\tilde {k}}}_{1}} = 7.14 \times {{10}^{3}}\exp [{{ - 4584} \mathord{\left/ {\vphantom {{ - 4584} T}} \right. \kern-0em} T}],\,\,{{{\text{моль}}} \mathord{\left/ {\vphantom {{{\text{моль}}} {{\text{ат}}\,{\text{к}}{{{\text{г}}}_{{{\text{кат}}}}}\,{\text{с}}}}} \right. \kern-0em} {{\text{ат}}\,{\text{к}}{{{\text{г}}}_{{{\text{кат}}}}}\,{\text{с}}}}, \\ {{{\tilde {k}}}_{2}} = 0.54 \times {{10}^{6}}\exp [{{ - 8074.3} \mathord{\left/ {\vphantom {{ - 8074.3} T}} \right. \kern-0em} T}],\,\,{{{\text{моль}}} \mathord{\left/ {\vphantom {{{\text{моль}}} {{\text{ат}}\,{\text{к}}{{{\text{г}}}_{{{\text{кат}}}}}\,{\text{с}}}}} \right. \kern-0em} {{\text{ат}}\,{\text{к}}{{{\text{г}}}_{{{\text{кат}}}}}\,{\text{с}}}}, \\ {{{\tilde {k}}}_{3}} = 1.17 \times {{10}^{{15}}}\exp [{{ - 28867} \mathord{\left/ {\vphantom {{ - 28867} T}} \right. \kern-0em} T}],\,\,{{{\text{мольа}}{{{\text{т}}}^{{1/2}}}} \mathord{\left/ {\vphantom {{{\text{мольа}}{{{\text{т}}}^{{1/2}}}} {{\text{к}}{{{\text{г}}}_{{{\text{кат}}}}}\,{\text{с}}}}} \right. \kern-0em} {{\text{к}}{{{\text{г}}}_{{{\text{кат}}}}}\,{\text{с}}}}, \\ {{K}_{3}} = 1.27 \times {{10}^{{ - 13}}}\exp [{{220\,000} \mathord{\left/ {\vphantom {{220\,000} {RT}}} \right. \kern-0em} {RT}}],\,\,{\text{а}}{{{\text{т}}}^{{--2}}}, \\ {{K}_{2}} = 1.41 \times {{10}^{{ - 2}}}\exp [{{37\,720} \mathord{\left/ {\vphantom {{37\,720} {RT}}} \right. \kern-0em} {RT}}], \\ {{k}_{{{\text{CO}}}}} = 8.23 \times {{10}^{{ - 5}}}\exp [{{70\,650} \mathord{\left/ {\vphantom {{70\,650} {RT}}} \right. \kern-0em} {RT}}],\,\,{\text{а}}{{{\text{т}}}^{{--1}}}, \\ {{k}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = 6.65 \times {{10}^{{ - 4}}}\exp [{{ - 38\,280} \mathord{\left/ {\vphantom {{ - 38\,280} {RT}}} \right. \kern-0em} {RT}}],\,\,{\text{а}}{{{\text{т}}}^{{--1}}}, \\ {{k}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 6.12 \times {{10}^{{ - 9}}}\exp [{{82\,900} \mathord{\left/ {\vphantom {{82\,900} {RT}}} \right. \kern-0em} {RT}}],\,\,{\text{а}}{{{\text{т}}}^{{--1}}}, \\ {{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = 1.77 \times {{10}^{5}}\exp [{{ - 89\,680} \mathord{\left/ {\vphantom {{ - 89\,680} {RT}}} \right. \kern-0em} {RT}}],\,\,{\text{а}}{{{\text{т}}}^{{--1}}}. \\ \end{gathered} $Реакции (1)–(3) в общем случае предполагаются равновесными.
Для нахождения потоков частиц получаем систему из шести обыкновенных дифференциальных уравнений первого порядка:
(13)
$\begin{gathered} \frac{{d{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}}}{{dx}} = - {{b}_{1}}\left( {\frac{{{{w}_{{{\text{кат}}}}}}}{{{{{\dot {N}}}_{{{\text{ВХ}}}}}}}} \right),\,\,\,\,\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dx}} = {{b}_{3}}\left( {\frac{{{{w}_{{{\text{кат}}}}}}}{{{{{\dot {N}}}_{{{\text{ВХ}}}}}}}} \right), \\ \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dx}} = ( - {{b}_{2}} - 2{{b}_{1}} + {{b}_{3}})\left( {\frac{{{{w}_{{{\text{кат}}}}}}}{{{{{\dot {N}}}_{{{\text{BX}}}}}}}} \right), \\ \frac{{d{{n}_{{{\text{CO}}}}}}}{{dx}} = ( - {{b}_{3}} + 2{{b}_{1}} - {{b}_{2}})\left( {\frac{{{{w}_{{{\text{кат}}}}}}}{{{{{\dot {N}}}_{{{\text{BX}}}}}}}} \right), \\ \frac{{d{{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}}}{{dx}} = {{b}_{2}}\left( {\frac{{{{w}_{{{\text{кат}}}}}}}{{{{{\dot {N}}}_{{{\text{BX}}}}}}}} \right), \\ \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{dx}} = (5{{b}_{1}} + {{b}_{2}} - 3{{b}_{3}})\left( {\frac{{{{w}_{{{\text{кат}}}}}}}{{{{{\dot {N}}}_{{{\text{BX}}}}}}}} \right) - \left( {\frac{S}{{{{{\dot {N}}}_{{{\text{BX}}}}}}}} \right){{I}_{{S,{{{\text{H}}}_{{\text{2}}}}}}}, \\ \end{gathered} $Начальные условия на входе ($x = 0$) равны:
(14)
$\begin{gathered} {{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}} = 1,\,\,\,\,{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = m, \\ {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = {{n}_{{{\text{CO}}}}} = {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} = {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 0. \\ \end{gathered} $Здесь ${{\dot {N}}_{{{\text{BX}}}}}$ – поток этана на входе.
Безразмерные потоки ${{n}_{{{\text{CO}}}}}$ и ${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ можно выразить через потоки ${{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}$, ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$:
(15)
$\begin{gathered} {{n}_{{{\text{CO}}}}} = 4(1 - {{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}) - (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}) - 2{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}, \\ {{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}} = (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}) - 2(1 - {{n}_{{{{{\text{C}}}_{{\text{3}}}}{{{\text{H}}}_{{\text{8}}}}}}}) + {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}. \\ \end{gathered} $Суммарный безразмерный поток смеси ${{n}_{\sum }}$ равен:
(16)
${{n}_{\sum }} = \sum\limits_i {{{n}_{i}}} = 1 + (1 - {{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}) + {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}.$В результате система (13) сводится к четырем уравнениям:
(17)
$\begin{gathered} \frac{{d{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}}}{{dx}} = - {{\alpha }_{1}}{{F}_{1}},\,\,\,\,\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dx}} = {{\alpha }_{3}}{{F}_{3}}, \\ \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dx}} = - {{\alpha }_{2}}{{F}_{2}} + {{\alpha }_{3}}{{F}_{3}} - 2{{\alpha }_{1}}{{F}_{1}}, \\ 3\frac{{d{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}}}{{dx}} + 2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dx}} + \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{dx}} + \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{dx}} = \\ = - \beta \sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} . \\ \end{gathered} $Последнее уравнение этой системы можно получить, если выразить функции ${{b}_{i}}\left( {{{{{w}_{{{\text{кат}}}}}} \mathord{\left/ {\vphantom {{{{w}_{{{\text{кат}}}}}} {{{N}_{{{\text{BX}}}}}}}} \right. \kern-0em} {{{N}_{{{\text{BX}}}}}}}} \right)$ из первых трех уравнений (13) и подставить их в шестое.
Выше введены безразмерные функции ${{F}_{i}}$ (i = = 1–3):
(18)
$\begin{gathered} {{F}_{1}} = \frac{{{{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}({{X}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}X_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2} - {{X_{{{\text{CO}}}}^{2}X_{{{{{\text{H}}}_{{\text{2}}}}}}^{5}p_{{{\text{AT}}}}^{4}} \mathord{\left/ {\vphantom {{X_{{{\text{CO}}}}^{2}X_{{{{{\text{H}}}_{{\text{2}}}}}}^{5}p_{{{\text{AT}}}}^{4}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}})}}{{X_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{3}(1 + ...)}} = \\ = \frac{{\left( {\frac{{{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}}}{{{{n}_{\sum }}}}n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2} - {{n_{{{\text{CO}}}}^{2}n_{{{{{\text{H}}}_{{\text{2}}}}}}^{5}p_{{{\text{AT}}}}^{4}} \mathord{\left/ {\vphantom {{n_{{{\text{CO}}}}^{2}n_{{{{{\text{H}}}_{{\text{2}}}}}}^{5}p_{{{\text{AT}}}}^{4}} {n_{\sum }^{4}{{K}_{1}}}}} \right. \kern-0em} {n_{\sum }^{4}{{K}_{1}}}}} \right)}}{{{{n}_{\sum }}n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{3}(1 + ...)}}, \\ {{F}_{2}} = \frac{{{{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}({{X}_{{{\text{CO}}}}}{{X}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} - {{{{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{X}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{X}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}} {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}{{X_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}{{{[1 + ...]}}^{2}}}} = \\ = \frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}({{n}_{{{\text{CO}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} - {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}{{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}} {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}{{n}_{\sum }}{{{[1 + ...]}}^{2}}}}, \\ {{F}_{3}} = \frac{{\left[ {X_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}{{X}_{{{\text{CO}}}}}(p_{{{\text{AT}}}}^{2}{{K}_{3}}) - {{X}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}{{X}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \right]}}{{X_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}X_{{{{{\text{H}}}_{{\text{2}}}}}}^{{1/2}}{{{[1 + ...]}}^{2}}}} = \\ = \frac{{\sqrt {{{n}_{\sum }}} \left[ {n_{{{{{\text{H}}}_{{\text{2}}}}}}^{3}{{n}_{{{\text{CO}}}}}{{{{{(p_{{{\text{AT}}}}^{2}{{K}_{3}})} \mathord{\left/ {\vphantom {{(p_{{{\text{AT}}}}^{2}{{K}_{3}})} {n_{\sum }^{2} - n}}} \right. \kern-0em} {n_{\sum }^{2} - n}}}}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \right]}}{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}\sqrt {{{n}_{{{{H}_{2}}}}}} {{{[1 + ...]}}^{2}}}}. \\ \end{gathered} $Скобки в знаменателях функций ${{F}_{1}}$, ${{F}_{2}}$ и ${{F}_{3}}$ и безразмерные параметры ${{\alpha }_{i}}$ (i = 1–3) и $\beta $ равны:
(19)
$\begin{gathered} (1 + ...) = (1 + {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} k}} \right. \kern-0em} k}{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}), \\ [1 + ...] = 1 + \frac{1}{{{{K}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}\left( {\frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}} \right) + \\ + \,\,{{p}_{{{\text{AT}}}}}\left( {\frac{{{{k}_{{{\text{CO}}}}}}}{{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}} \right)\left( {\frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}} \right)\left( {\frac{{{{n}_{{{\text{CO}}}}}}}{{{{n}_{\sum }}}}} \right) + \\ + \,{{p}_{{{\text{AT}}}}}\left( {\frac{{{{k}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{{{k}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}} \right)\left( {\frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}} \right)\left( {\frac{{{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{{{n}_{\sum }}}}} \right), \\ {{\alpha }_{1}} = \frac{{{{{\tilde {k}}}_{1}}}}{k}\left( {\frac{{{{w}_{{{\text{кат}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right){{p}_{{{\text{AT}}}}},\,\,\,\,{{\alpha }_{2}} = \frac{{{{{\tilde {k}}}_{2}}}}{{k_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}}}\left( {\frac{{{{w}_{{{\text{кат}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right){{p}_{{{\text{AT}}}}}, \\ {{\alpha }_{3}} = \frac{{{{{\tilde {k}}}_{3}}}}{{k_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}}}\left( {\frac{{{{w}_{{{\text{кат}}}}}}}{{{{N}_{{{\text{BX}}}}}}}} \right)\frac{1}{{p_{{{\text{AT}}}}^{{1/2}}}}, \\ \beta = {{s}_{{{\text{эфф}}}}}\left[ {\frac{{{{Q}_{0}}\exp ({{ - E} \mathord{\left/ {\vphantom {{ - E} {RT)}}} \right. \kern-0em} {RT)}}}}{\delta }} \right]\frac{{\sqrt {{{p}_{{{\text{AT}}}}} \times {{{10}}^{5}}} }}{{{{N}_{{{\text{ВХ}}}}}}}. \\ \end{gathered} $Выше мольные доли частиц газовой смеси ${{X}_{i}}$ (i = С2Н6, СН4, Н2О, СО, СО2, Н2) были выражены через потоки ${{n}_{i}}$:
(20)
${{X}_{i}} = {{{{n}_{i}}} \mathord{\left/ {\vphantom {{{{n}_{i}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}},\,\,\,\,{{n}_{\sum }} = \sum\limits_i {{{n}_{i}}} .$Константа равновесия ${{K}_{1}}$ для реакции 1 находится стандартным образом :
где $\Delta S$ и $\Delta H$ – значения энтропии и энтальпии реакции этана с водой.В результате вычислений получаем:
(21)
$\begin{gathered} \ln {{K}_{1}} = \frac{1}{R}\left\{ {441.84 + 135.87\ln ({T \mathord{\left/ {\vphantom {T {298}}} \right. \kern-0em} {298}})} \right. - \\ \left. { - \,\,199(T - 298) \times {{{10}}^{{ - 3}}}} \right\} - \frac{1}{{RT}} \times \\ \times \,\,\left\{ {347\,267 + 135.87(T - 298)} \right. - \\ \left. { - \,\,100({{T}^{2}} - {{{298}}^{2}}) \times {{{10}}^{{ - 3}}}} \right\}. \\ \end{gathered} $Предполагая газовые смеси идеальными, нетрудно показать, что мольный поток этана на входе ${{\dot {N}}_{{{\text{BX}}}}}$ и объемная скорость $G$ связаны соотношением:
(22)
$\begin{gathered} {{{\dot {N}}}_{{{\text{BX}}}}} = \frac{p}{{RT}}{{{\dot {V}}}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}} = \\ = [{{{{p}_{{{\text{AT}}}}}G} \mathord{\left/ {\vphantom {{{{p}_{{{\text{AT}}}}}G} {450(m + 1)}}} \right. \kern-0em} {450(m + 1)}}] \times {{10}^{{ - 5}}},\,\,{{{\text{моль}}} \mathord{\left/ {\vphantom {{{\text{моль}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}, \\ G = {{{{{\dot {V}}}_{\sum }}} \mathord{\left/ {\vphantom {{{{{\dot {V}}}_{\sum }}} {{{V}_{{{\text{кат}}}}}}}} \right. \kern-0em} {{{V}_{{{\text{кат}}}}}}},\,\,\left[ {{1 \mathord{\left/ {\vphantom {1 {\text{ч}}}} \right. \kern-0em} {\text{ч}}}} \right];\,\,\,\,{{{\dot {V}}}_{\sum }} = (1 + m){{{\dot {V}}}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}, \\ \end{gathered} $По порядку величины потоки этана на входе равны ${{\dot {N}}_{{{\text{BX}}}}}$ ~ 10–5–10–4 [моль/с]. Как видно из системы (17), распределения безразмерных потоков ${{n}_{i}}(x)$ внутри нижней камеры зависит от кинетических параметров ${{\alpha }_{1}}$, ${{\alpha }_{2}}$, ${{\alpha }_{3}}$ и безразмерной проницаемости мембраны $\beta $. В табл. 1 приведены некоторые параметры, необходимые для дальнейшего изложения при различных температурах для мембранного модуля (${{w}_{{{\text{кат}}}}}$ = 3.5 г, $s$ = 15.2 см2, $\delta $ = 30 мкм, $h$ = 3.5 мм). В общем случае системы типа (17) решаются численно. Однако, как следует из табл. 1, при допустимых значениях потока этана на входе (22) в рассматриваемой области изменения Т для мембранного модуля кинетические параметры ${{\alpha }_{i}}$ (i = 1–3) удовлетворяют неравенствам ${{\alpha }_{i}} \gg 1$. Последнее означает, что потоки ${{n}_{i}}$ испытывают заметное изменение в узкой области $x$ на входе газовой смеси в нижнюю камеру ($x \cong {1 \mathord{\left/ {\vphantom {1 {\min ({{\alpha }_{i}})}}} \right. \kern-0em} {\min ({{\alpha }_{i}})}} \ll 1$). Это дает возможность свести общую проблему (17) к двум, связанным между собой задачам – решениям на начальном (коротком) участке ($x < {{x}_{{{\text{нач}}}}} \ll 1$) и основном (${{x}_{{{\text{нач}}}}} < x \leqslant 1$).
Таблица 1.
Кинетические и равновесные константы и безразмерные параметры при различных температурах
| $T$, K | 673 | 723 | 773 | 823 | 873 | 973 | 1073 |
|---|---|---|---|---|---|---|---|
| ${{{{\alpha }_{1}}{{{\dot {N}}}_{{{\text{BX}}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}{{{\dot {N}}}_{{{\text{BX}}}}}} {{{p}_{{{\text{AT}}}}}}}} \right. \kern-0em} {{{p}_{{{\text{AT}}}}}}}$, моль/с | 0.06 | 0.079 | 0.098 | 0.141 | 0.194 | 0.334 | 0.517 |
| ${{{{\alpha }_{2}}{{{\dot {N}}}_{{{\text{BX}}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}{{{\dot {N}}}_{{{\text{BX}}}}}} {{{p}_{{{\text{AT}}}}}}}} \right. \kern-0em} {{{p}_{{{\text{AT}}}}}}}$, моль/с | 20.46 | 5.28 | 1.61 | 0.58 | 0.22 | 0.047 | 0.013 |
| ${{{{\alpha }_{3}}{{{\dot {N}}}_{{{\text{BX}}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{3}}{{{\dot {N}}}_{{{\text{BX}}}}}} {p_{{{\text{AT}}}}^{{1/2}}}}} \right. \kern-0em} {p_{{{\text{AT}}}}^{{1/2}}}}$, моль/с | 1.95 × 10–3 | 3.78 × 10–3 | 7.13 × 10–3 | 1.35×10–2 | 2.27×10–2 | 5.3 × 10–2 | 0.083 |
| ${{(\beta {{{\dot {N}}}_{{{\text{BX}}}}})} \mathord{\left/ {\vphantom {{(\beta {{{\dot {N}}}_{{{\text{BX}}}}})} {p_{{{\text{AT}}}}^{{1/2}}}}} \right. \kern-0em} {p_{{{\text{AT}}}}^{{1/2}}}}$, моль/с | 0.8 × 10–4 | 10–4 | 1.15×10–4 | 1.3×10–4 | 1.5×10–4 | 1.8 × 10–4 | 2.1 ×10–4 |
| $({{{{\alpha }_{1}}} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}} {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}})p_{{{\text{AT}}}}^{{3/2}}$ | 30.77 | 20.79 | 13.74 | 10.44 | 8.56 | 6.34 | 6.25 |
| $({{{{\alpha }_{2}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}} {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}})p_{{{\text{AT}}}}^{{3/2}}$ | 1.05 × 104 | 1.4 × 103 | 2.26×102 | 43 | 9.69 | 2 | 0.4 |
| ${{({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}})} \mathord{\left/ {\vphantom {{({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}})} {{{p}_{{{\text{AT}}}}}}}} \right. \kern-0em} {{{p}_{{{\text{AT}}}}}}}$ | 0.041 | 0.026 | 0.016 | 0.96 ×10–2 | 0.66 ×10–2 | 0.34 ×10–2 | 0.002 |
| ${{K}_{3}}$, ат–2 | 1.7 × 104 | 103 | 102 | 12.5 | 2 | 0.085 | 0.0066 |
| ${{K}_{2}}$ | 12 | 7.7 | 5 | 4 | 2.5 | 1.5 | 0.97 |
| ${{K}_{1}}$, ат6 | 2 × 10–3 | 9.1 | 318 | 2 × 104 | 2.7× 106 | 108 | 1010 |
Численное решение на начальном участке. Из табл. 1 видно, что минимальное значение $\mathop {\min }\limits_{i = 1 - 3} ({{\alpha }_{i}})$ равно ${{\alpha }_{3}}$. Разделив уравнения системы (17) на ${{\alpha }_{3}}$ и вводя безразмерную продольную координату $z = {{\alpha }_{3}}x$, перепишем эту систему следующим образом ($\Delta \equiv m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$):
(23)
$\begin{gathered} \frac{{d{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}}}{{dz}} = - \left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right){{F}_{1}},\,\,\,\,\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dz}} = {{F}_{3}}, \\ \frac{{d\Delta }}{{dz}} = \left( {\frac{{{{\alpha }_{2}}}}{{{{\alpha }_{3}}}}} \right){{F}_{2}} - {{F}_{3}} + 3\left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right){{F}_{1}}, \\ 3\frac{{d{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}}}{{dz}} + 2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dz}} - \frac{{d\Delta }}{{dz}} + \frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{dz}} = - \left( {\frac{\beta }{{{{\alpha }_{3}}}}} \right)\sqrt {\frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{{{n}_{\sum }}}}} . \\ \end{gathered} $Начальные условия равны:
Коэффициенты системы (23) зависят только от температуры (${{p}_{{{\text{AT}}}}}$ = 1). Для рассматриваемого ММ они приведены в табл. 1. На начальном участке влияние мембраны незначительно, так как членом в правой части последнего уравнения системы (23) можно пренебречь: $({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}})\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} \leqslant \beta /{{\alpha }_{3}} \ll 1$ (см. табл. 1). Это означает, что это уравнение, учитывая начальные условия, можно заменить равенством:
(24)
${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} = 3(1 - {{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}) + \Delta - 2{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}},\,\,\,\,x < {{x}_{{{\text{нач}}}}},$Безразмерные потоки этана, метана и воды (или $\Delta = m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$) можно найти численным интегрированием трех первых уравнений системы (23). При расчетах использовали разностную схему, аппроксимирующую систему (23) с четвертым порядком точности (метод Рунге–Кутта) [31]. Получим приближенное аналитическое решение при достаточно малых $z$, в непосредственной близости от входа смеси в нижнюю камеру. Нетрудно показать, что в этой области вдали от равновесия реакций (4)–(6) система (23) упрощается:
(25)
$\begin{gathered} \frac{{d{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}}}{{dz}} \cong - \left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)\frac{{{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}}}{{{{n}_{\sum }}n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}, \\ \frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{dz}} \cong {{K}_{3}}\frac{{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{2}\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{n}_{{{\text{CO}}}}}}}{{{{n}_{\sum }}\sqrt {{{n}_{\sum }}} n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}}}, \\ \frac{{d\Delta }}{{dz}} \cong 3\left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)\frac{{{{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}}}{{{{n}_{\sum }}{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}. \\ \end{gathered} $Приближенное решение этой системы, если предположить, что ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} \ll {{n}_{{{\text{CO}}}}}$, равно ($z \to 0$):
(26)
$\begin{gathered} {{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}} \cong \exp \left( { - \frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}\frac{z}{{(1 + m)m}}} \right), \\ \Delta \cong 3\left[ {1 - \exp \left( { - \left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)\frac{z}{{(1 + m)m}}} \right)} \right], \\ {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} \cong {{K}_{3}}\int\limits_0^z {\frac{{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{2}\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{n}_{{{\text{CO}}}}}}}{{{{n}_{\sum }}\sqrt {{{n}_{\sum }}} n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{2}}}dz} , \\ \end{gathered} $При достаточно малых $\left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)\frac{z}{{(1 + m)m}} \leqslant $ $ \leqslant \left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)\frac{{{{z}_{0}}}}{{(1 + m)m}} = 0.1$ можно написать:
(27)
$\begin{gathered} {{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}} \cong 1 - \left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)\frac{z}{{(1 + m)m}}, \\ \Delta \cong 3\left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)\frac{z}{{(1 + m)m}}, \\ {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \cong 6\left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)\frac{z}{{(1 + m)m}}, \\ {{n}_{{{\text{CO}}}}} \cong \left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)\frac{z}{{(1 + m)m}}, \\ {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = \left[ {19.6{{{{K}_{3}}} \mathord{\left/ {\vphantom {{{{K}_{3}}} {\left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)m\sqrt {1 + m} }}} \right. \kern-0em} {\left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}} \right)m\sqrt {1 + m} }}} \right] \times \\ \times \,\,{{\left( {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{3}}}}\frac{z}{{(1 + m)m}}} \right)}^{{4.5}}}. \\ \end{gathered} $На рис. 2 представлены результаты численных расчетов в области $z > {{z}_{0}}$ при $T = 673$ и 873 K. Подобные расчеты были проведены для других температур. Заметим, то при достаточно малых $z < {{z}_{0}}$ потоки ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$ значительно меньше потоков ${{n}_{{{\text{CO}}}}}$, $\Delta $ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$. Это можно объяснить тем, что метанирование является вторичной реакцией (реакция (3)), требующей накопления в системе СО. Показано, что при $z > {{z}_{{{\text{нач}}}}}$ производные ${{d{{n}_{i}}} \mathord{\left/ {\vphantom {{d{{n}_{i}}} {dz \Rightarrow 0}}} \right. \kern-0em} {dz \Rightarrow 0}}$, а безразмерные потоки ${{n}_{i}}$ стремятся к постоянным значениям, причем ${{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}} \Rightarrow 0$ (см. рис. 2). Значения ${{z}_{{{\text{нач}}}}}$ увеличивается с ростом $T$ и не превышает 10. Участок $z < {{z}_{{{\text{нач}}}}}$ (или $x < {{x}_{{{\text{нач}}}}} = {{{{z}_{{{\text{нач}}}}}} \mathord{\left/ {\vphantom {{{{z}_{{{\text{нач}}}}}} {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}}$) в дальнейшем будем называть начальным участком. Можно заметить, что ${{x}_{{{\text{нач}}}}} \ll 1$, так как ${{\dot {N}}_{{{\text{BX}}}}} \leqslant {{10}^{{ - 4}}}$ моль/с (табл. 1 и (22)), то есть размеры начального участка намного меньше радиуса нижней камеры.
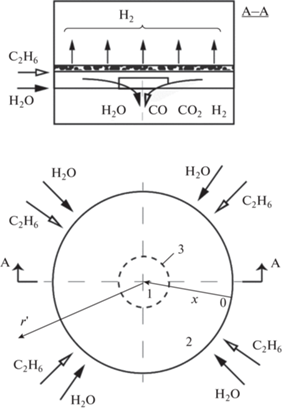
Рис. 2.
Расчет безразмерных потоков ${{n}_{i}}(z)$ на начальном участке при $T = 873$ K (а) и 673 K (б). Кривые 1 – ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}(z)$, 2 – $\Delta (z)$, 3 – ${{n}_{{{\text{СO}}}}}(z)$, 4 – ${{n}_{{{\text{С}}{{{\text{O}}}_{{\text{2}}}}}}}(z)$, 5 – ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(z)$, 6 – ${{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}(z)$.
Как следует из таблицы 1, при $T > 700$ K параметры (${{{{\alpha }_{1}}} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}} {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}}$), (${{{{\alpha }_{2}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}} {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}}$) намного больше единицы. Принимая во внимание, что производные ${{d{{n}_{i}}} \mathord{\left/ {\vphantom {{d{{n}_{i}}} {dz}}} \right. \kern-0em} {dz}}$ при $z > {{z}_{{{\text{нач}}}}}$ малы, можно сделать вывод, что функции ${{F}_{i}}$ (i = 1–3) в этой области также стремятся к нулю. Последнее означает, что реакции (1)–(3). приближаются к равновесию, то есть скорости прямых и обратных реакций становится соизмеримыми (см. (18)). Следовательно, значения потоков ${{n}_{i}}(z)$ на выходе начального участка можно получить не только в результате численных расчетов на участке $z \leqslant {{z}_{{{\text{нач}}}}}$ (см., например, рис. 2), но и с помощью условия (24) и равенств ${{F}_{1}} = {{F}_{2}} = {{F}_{3}} = 0$.
Заметим, что в расчетах распределений потоков ${{n}_{i}}(z)$ на начальном участке нет необходимости, так как величина этого участка мала и не оказывает заметного влияния на поток Н2 через мембрану. Для дальнейшего изложения нам понадобятся только значения потоков ${{n}_{i}}(z)$ на выходе этого участка.
Наряду с использованием палладиевой мембраны были проведены исследования с непроницаемой (из нержавеющей стали) заглушкой. В этом случае в последнем уравнении системы (17) членом $({\beta \mathord{\left/ {\vphantom {\beta {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}})\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} $ можно пренебречь при любом $x$ ($\beta = 0$). Для рассматриваемого немембранного процесса потоки ${{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}(z)$, ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}(z)$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}(z)$ на начальном участке ($z \leqslant {{z}_{{{\text{нач}}}}}$) совпадают с соответствующими потоками для мембранного процесса. На расстоянии от входа $z \geqslant {{z}_{{{\text{нач}}}}}$ производные ${{d{{n}_{i}}} \mathord{\left/ {\vphantom {{d{{n}_{i}}} {dz}}} \right. \kern-0em} {dz}} \Rightarrow 0$, а потоки ${{n}_{i}}$ постоянны, которые, как указано выше, можно получить из условий равновесия ${{F}_{1}} = {{F}_{2}} = {{F}_{3}}$ и уравнения (24). Эти постоянные потоки в дальнейшем обозначим звездочкой (*): ${{n}_{i}} = n_{i}^{*}$. В случае мембранного процесса, в отличии от немембранного, в области $x > {{x}_{{{\text{нач}}}}}$ потоки ${{n}_{i}}(x)$ отклоняются от соответствующих величин $n_{i}^{*}$.
Получим равновесные значения потоков $n_{i}^{*}$ в случае, когда константа равновесия ${{K}_{1}}$ достаточно велика, то есть при $T > 700$ K (Табл. 1). Соответствующую систему уравнений запишем в виде (см. (18)):
(28)
$\begin{gathered} n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{*}n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{*2}} - n_{{{\text{СO}}}}^{{*2}}n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*5}}{{\left( {{{p_{{{\text{AT}}}}^{4}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{4}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{p_{{{\text{AT}}}}^{4}} \mathord{\left/ {\vphantom {{p_{{{\text{AT}}}}^{4}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}} \right)} {n_{\sum }^{{*4}}}}} \right. \kern-0em} {n_{\sum }^{{*4}}}} = 0, \\ n_{{{\text{CO}}}}^{*}n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} - n_{{{\text{С}}{{{\text{O}}}_{{\text{2}}}}}}^{*}n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}) = 0, \\ n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} - {{n_{{{\text{СO}}}}^{*}n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*3}}(p_{{{\text{AT}}}}^{2}{{K}_{3}})} \mathord{\left/ {\vphantom {{n_{{{\text{СO}}}}^{*}n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*3}}(p_{{{\text{AT}}}}^{2}{{K}_{3}})} {n_{\sum }^{2}}}} \right. \kern-0em} {n_{\sum }^{2}}} = 0. \\ \end{gathered} $Предполагая, что $n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{*} \cong 0$ (это будет показано в дальнейшем), равновесные значения потоков $n_{{{\text{CO}}}}^{*}$, $n_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{*}$, $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ и $n_{\sum }^{*}$ можно представить в виде (15, 16, 24):
(29)
$\begin{gathered} n_{{{\text{CO}}}}^{*} = 2(2 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}) - (m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}), \\ n_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{*} = (m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}) - (2 - {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}), \\ n_{\sum }^{*} = 2 + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} + n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}, \\ n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} = (m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}) + 3 - 2{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}. \\ \end{gathered} $Как видно из (29), потоки $n_{{{\text{CO}}}}^{*}$, $n_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{*}$ и $n_{\sum }^{*}$ зависят от $n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$, $n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}$ и $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$.
Для нахождения $n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$, $n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}$ и $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ получаем систему из трех нелинейных алгебраических уравнений:
(30)
$\begin{gathered} \left( {\frac{{n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}}}{{m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}} \right)n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} = \\ = {{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*3}}\left[ {2\left( {\frac{{2 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}}}{{m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}} \right) - 1} \right]\left( {{{K}_{3}}} \right)} \mathord{\left/ {\vphantom {{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*3}}\left[ {2\left( {\frac{{2 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}}}{{m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}} \right) - 1} \right]\left( {{{K}_{3}}} \right)} {n_{\sum }^{{*2}}}}} \right. \kern-0em} {n_{\sum }^{{*2}}}}, \\ \end{gathered} $(31)
$\begin{gathered} \left[ {2\left( {\frac{{2 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}}}{{m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}} \right) - 1} \right]n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} - \\ - \,\,n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}\left[ {1 - \left( {\frac{{2 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}}}{{m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}} \right)} \right]\left( {\frac{1}{{{{K}_{2}}}}} \right) = 0, \\ \end{gathered} $(32)
$\left( {\frac{{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}{{m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}} \right) = 1 + 2\left( {\frac{{2 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}}}{{m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}}} \right).$Выразив из уравнения (31) отношение ${{(2 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*})} \mathord{\left/ {\vphantom {{(2 - n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*})} {(m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*})}}} \right. \kern-0em} {(m - n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*})}}$ через $n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}$ и $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$. В результате получаем:
(33)
$n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*} = \frac{{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{{*4}}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})({{K}_{3}})\Delta {\text{*}}}}{{n_{\sum }^{{*2}}[2n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})]n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}}},$(34)
$n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*} = 2 - \left[ {\frac{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}{{2n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}} \right]\Delta *,$(35)
$n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} + 1 = \left[ {\frac{{4n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + 3n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}{{2n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}} \right]\Delta *,$Из уравнения (35) получаем явную зависимость $\Delta {\text{*}}$ (или $n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}$) от потока водорода $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$:
(36)
$\begin{gathered} 2\Delta * = \frac{{2m + 1 + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} + ({3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2})({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}{2} - \\ - \,\,\sqrt {{{{\left[ {\frac{{2m + 1 + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} + ({3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2})({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}}}{2}} \right]}}^{2}} - (n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} + 1)[2m + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})]} . \\ \end{gathered} $Знак (–) перед радикалом выбран из условия, что $\Delta * \to {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ при $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*} \to 0$ (см. (35)).
Равновесные значения $n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$, $\Delta {\text{*}}$ и $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ находим из условия пересечения кривых $n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$($n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$) (формулы (33) и (34)), где $\Delta {\text{*}}$ определяется из (36).
Результаты численных расчетов в интервале температур $673 < T < 1073$ K для ряда значений $m \geqslant 4$ представлены на рис. 3. Ниже будет показано, что при паровом риформинге этана значение отношения $m$ не может быть менее четырех. В противном случае на основном участке (${{x}_{{{\text{нач}}}}} < x < 1$) поток водяного пара обращается в нуль (пар полностью расходуется) внутри нижней камеры, реакция между С2Н6 и Н2О прекращается и невозможно достичь 100%-ого выхода водорода на выходе нижней камеры.
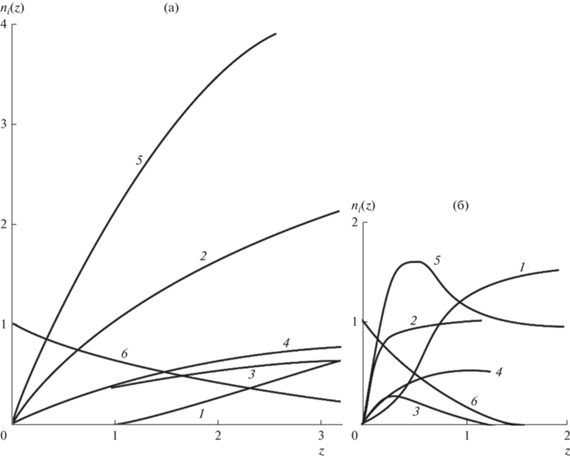
Рис. 3.
Равновесные значения потоков на выходе начального участка при различных $T$ и $m > 4$. Кривые 1 – $m = 4$, 2 – 5, 3 – 7, 4 – $m = 9$. Сплошные линии – $\Delta {\text{*}}(T)$, штриховые – $n_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}^{*}(T)$, штрих-пунктирные – $n_{{{\text{CO}}}}^{*}(T)$, точки – $n_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{*}(T)$.
Равновесные значения $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ для этана в рассматриваемых интервалах температур и отношений потоков на входе $m$ приведены в табл. 2. Для сравнения в этой таблице приведены соответствующие значения $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ для парового риформинга метана [25].
Таблица 2.
Результаты расчета потока $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ на выходе начального участка для парового риформинга метана и этана
| $m$ | $T$, K | ||||
|---|---|---|---|---|---|
| 673 | 773 | 873 | 973 | 1073 | |
| Метан | |||||
| 2 | 0.6 | 1.3 | 2.25 | 3 | 3.18 |
| 2.5 | 0.7 | 1.5 | 2.54 | 3.2 | 3.25 |
| 3 | 0.8 | 1.7 | 2.78 | 3.3 | 3.34 |
| 4 | 0.95 | 2.0 | 3.13 | 3.45 | 3.4 |
| 5 | 1.12 | 2.33 | 3.37 | 3.54 | 3.5 |
| 7 | 1.40 | 2.80 | 3.64 | 3.66 | 3.6 |
| 9 | 1.68 | 3.09 | 3.73 | 3.75 | 3.66 |
| Этан | |||||
| 4 | 0.93 | 2.18 | 3.87 | 5.19 | 5.4 |
| 5 | 1.12 | 2.58 | 4.42 | 5.52 | 5.57 |
| 7 | 1.47 | 3.28 | 5.25 | 5.91 | 5.82 |
| 9 | 1.79 | 3.89 | 5.78 | 6.13 | 5.98 |
Заметим, что на выходе начального участка равновесного значения этана определяются из первого уравнения (28) с учетом (29). В результате несложных вычислений получаем:
(37)
$n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{*} = \frac{{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{7}{{{({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}^{2}}({1 \mathord{\left/ {\vphantom {1 {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}){{\Delta }^{{*2}}}}}{{n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}n_{\sum }^{{*4}}{{{[2n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*} + n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})]}}^{2}}}}.$Нетрудно показать, что $n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{*}$ в рассматриваемых интервалах $T$ и $m$ порядка ~10–5–10–6.
Решение за пределами начального участка. При мембранном процессе на выходе начального участка ($z \cong {{z}_{{{\text{нач}}}}}$) все безразмерные потоки $n_{i}^{{}}$, очевидно, совпадают с равновесными значениями $n_{i}^{*}$ (см. табл. 2).
Допустимые значения потока С2Н6 на входе нижней камеры ${{\dot {N}}_{{{\text{BX}}}}}$ ограничены: ${{\dot {N}}_{{{\text{BX}}}}} \leqslant {{10}^{{ - 4}}}$ (моль/с) (22). Следовательно, безразмерные параметры ${{\alpha }_{i}}$ (i = 1–3) при $T \geqslant 700$ K намного больше единицы (табл. 1). Если предположить, что на основном участке ($x > {{x}_{{{\text{нач}}}}}$) производные ${{\partial {{n}_{i}}} \mathord{\left/ {\vphantom {{\partial {{n}_{i}}} {\partial x}}} \right. \kern-0em} {\partial x}}$ так же ограничены (i = С2Н6, СН4, Н2О, Н2), то несмотря на отток Н2 через мембрану за пределами начального участка условия равновесия реакций (1)–(3) не нарушаются, так как функции ${{F}_{i}}$ (i = 1–3) практически равняются нулю (${{F}_{1}}$ ~ ${1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}} \ll 1$, ${{F}_{2}}$ ~ ${1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{2}}}}} \right. \kern-0em} {{{\alpha }_{2}}}} \ll 1$, ${{F}_{3}}$ ~ ${1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{3}}}}} \right. \kern-0em} {{{\alpha }_{3}}}} \ll 1$, см. (17)). Условия ${{F}_{1}} = {{F}_{2}} = {{F}_{3}} = 0$ позволяют найти потоки ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ и ${{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}}$ как функции ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ за пределами начального участка, где из-за перехода Н2 через мембрану выполняется неравенство ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} < n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$. Это так называемое псевдо-равновесие, при котором из-за слабого оттока Н2 через мембрану химическое равновесие реакций в нижней камере не нарушается.
Очевидно, что на основном участке равенство ${{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}} \cong 0$ сохраняется, следовательно равенства (29) для ${{n}_{{{\text{CO}}}}}$ и ${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ выполняются.
Из условий ${{F}_{i}} = 0$ (i = 2, 3), так же как и выше (см. (33), (34)), можно получить:
(38)
$\begin{gathered} {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = \frac{{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{4}({{{{K}_{3}}} \mathord{\left/ {\vphantom {{{{K}_{3}}} {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})\Delta }}{{n_{\sum }^{2}[2{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})]{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}, \\ {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = 2 - \left[ {\frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}{{2{{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}({1 \mathord{\left/ {\vphantom {1 {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}})}}} \right]\Delta , \\ \end{gathered} $Ранее было отмечено, что на выходе начального участка поток этана ${{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}} = n_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}^{*} = 0$ (см. формулу (37) и табл. 2). Из формулы (37) можно получить, что на основном участке, где ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \leqslant n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$, условие ${{n}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}}}}} \cong 0$ также выполняется.
Получим распределения безразмерных потоков $n_{i}^{{}}(x)$ на основном участке ${{x}_{{{\text{нач}}}}} < x \leqslant 1$.
При отсутствии этана на основном участке четвертое уравнение системы (23) принимает вид:
(39)
$2\frac{{\partial {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{\partial x}} + \frac{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{\partial x}} + \frac{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{\partial x}} = - \beta \sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} .$Зная зависимости ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$(${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$) и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$(${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$), последнее уравнение представим в виде:
(40)
$\left( {2\frac{{\partial {{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + \frac{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + 1} \right)\frac{{\partial {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{\partial x}} = - \beta \sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} ,$Упомянутые выше функции ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$(${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$) и ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$(${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$), находятся с помощью формул (37), (38). Для любого ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \leqslant n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ находим точку пересечения $\Delta $ функций ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}(\Delta )$ (см. (37)) и ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}(\Delta )$ (см. (38)), то есть зависимость ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$(${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$), так как $\Delta = m - {{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$. Соответствующую зависимость ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}$(${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$) находим из любой из формул (37) или (38) при известном $\Delta $ (или ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$).
За пределами температурного интервала 673–1073 K зависимости ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ при любом $m > 4$ можно получить аналитически. Покажем это для высоких температур ($T \geqslant 1000$ K). В этой области потоки $n_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$ на выходе начального участка при любом допустимом $m$ стремятся к нулю (рис. 3), а произведение $p_{{{\text{AT}}}}^{2}({{{{K}_{3}}} \mathord{\left/ {\vphantom {{{{K}_{3}}} {{{K}_{2}}}}} \right. \kern-0em} {{{K}_{2}}}}) \ll 1$ (см. табл. 1). Следовательно, как это видно из уравнения (37), на основном участке сохраняется равенство ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}} \cong 0$. Функцию $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ или ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(\Delta )$ можно найти из уравнения (38), где необходимо произвести замену $\Delta * \to \Delta $. В результате получим:
(41)
${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1/{{K}_{2}}) = {{(m - \Delta )(4 - \Delta )} \mathord{\left/ {\vphantom {{(m - \Delta )(4 - \Delta )} {(\Delta - 2)}}} \right. \kern-0em} {(\Delta - 2)}},$Равновесные значения $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ находим с помощью формул (33), (34) по указанной выше методике (см. например, табл. 2).
Получим зависимости $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ при низких температурах ($T < 700$ K). В этой области константа равновесия ${{K}_{2}} \gg 1$ (табл. 1), следовательно ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}} \cong 2 - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}$ (см. (38)). Приравнивая потоки ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}(\Delta )$ (формулы (37) и (38)), получим аналитическую зависимость ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ от $\Delta $ в области $\Delta \geqslant \Delta {\text{*}}$, ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \leqslant n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$:
(42)
$\begin{gathered} {{\left( {\frac{{4 - \Delta }}{\Delta }} \right)}^{{1/4}}}{{(m - \Delta )}^{{1/2}}}{{(m + 2 - \Delta )}^{{1/2}}} = \\ = \left( {\frac{{{{p}_{{{\text{AT}}}}}{{K}_{3}}}}{{{{K}_{2}}}}} \right){{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}. \\ \end{gathered} $Зависимости $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ в области ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} \leqslant n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ для $T = 673$ и 1073 K и ряда значений $m > 4$ показаны на рис. 4а ($T = 673$ K) и рис. 4б (1073 K). При $T \leqslant 700$ K поток ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}} = 1 - {{\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})} \mathord{\left/ {\vphantom {{\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})} 2}} \right. \kern-0em} 2}$, а при $T > 1000$ K, соответственно, $n_{{C{{H}_{4}}}}^{{}} \cong 0$. Используя равновесные значения $\Delta {\text{*}}(m,T,{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}(m,T,{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$, по формулам (41), (42) нетрудно рассчитать $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ на основном участке нижней камеры за пределами температурного интервала 700–1000 K. Внутри этого интервала необходимы численные расчеты.
Рис. 4.
Зависимости $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ (сплошные), ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ (пунктирные) на основном участке при $T$ = 673 K (a) и $T$ = 973 K (б). Кривые 1 – $m = 4$, 2 – 5, 3 – 7, 4 – $m = 9$
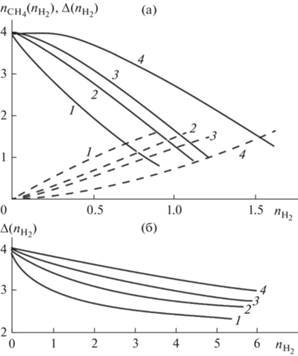
При фиксированной температуре по мере увеличения параметра $m$ поток метана ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$ как функция ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ уменьшается (см. рис. 4а). Увеличение $T$ также способствует уменьшению этой зависимости, причем при $T \geqslant 1000$ K при любом $m > 4$ поток ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}} \cong 0$. Аналогичные закономерности наблюдались и на выходе начального участка (см. рис. 3). Отклонение потока водяного пара $\Delta ({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ от входной величины $m$ увеличивается при возрастании $m$. Очевидно, это связано с ростом скорости химического взаимодействия при увеличении потока водяного пара.
Как видно из рис. 4, отклонение $\Delta $ при любом $m$ и $T$ меньше четырех. Следовательно, если отношение потоков воды и этана на входе $m < 4$, то внутри нижней камеры при некотором ${{x}_{0}} < 1$ выполняется равенство $\Delta = m$. Это означает, что вода полностью расходуется внутри нижней камеры и паровой риформинг невозможен.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЯ
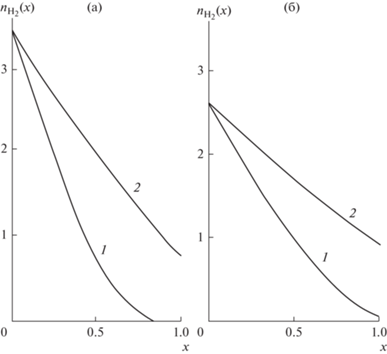
Продифференцировав зависимости ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ по переменной ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$, из уравнения (40) находим распределение потока водорода внутри нижней камеры ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$. Для примера результаты таких расчетов представлены на рис. 5 для температур 773 и 823 K при $m = 5$. Потоки ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ на основном участке в отличие от начального зависят не только от температуры, но и от объемной скорости подачи сырья $G$.
Рис. 5.
Расчет распределения водорода внутри нижней камеры для $m = 5$. (а) $T = $ 823 K, (б) $T = $773 K. Кривые 1 – $G = 1800$ 1/ч, 2 – 3600 1/ч.
В общем случае при любом $m$ значение $G$ находится следующим образом (см. (31)):
(43)
$\begin{gathered} \left( {{G \mathord{\left/ {\vphantom {G {{{{10}}^{3}}}}} \right. \kern-0em} {{{{10}}^{3}}}}} \right) = 4.5(1 + m) \times \\ \times \,\,{{\left[ {\frac{{{{S}_{{{\text{эфф}}}}}Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}}) \times {{{10}}^{6}}\sqrt {10} }}{\delta }} \right]} \mathord{\left/ {\vphantom {{\left[ {\frac{{{{S}_{{{\text{эфф}}}}}Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}}) \times {{{10}}^{6}}\sqrt {10} }}{\delta }} \right]} \beta }} \right. \kern-0em} \beta }. \\ \end{gathered} $Поток водорода ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ достигает своего максимального значения на выходе начального участка и в дальнейшем монотонно уменьшается. Потоки ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}(x)$ и ${{n}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}(x)$ на основном участке ($x > {{x}_{{{\text{нач}}}}}$) монотонно отклоняются от соответствующих значений $n_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}^{*}$ и $n_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{*}$ (см. рис. 4).
Важной характеристикой реактора является отвод водорода φ – отношение потока Н2 через мембрану к суммарному его потоку на выходе из верхней камеры (${{I}_{S}}$) и нижней ${{N}_{{{\text{BX}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)$ (см. (3)):
(44)
$\varphi = \frac{{{{I}_{S}}}}{{{{I}_{S}} + {{N}_{{{\text{BX}}}}}{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)}} = \frac{1}{{1 + \left( {\frac{1}{\beta }} \right)\frac{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)}}{{\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} } dx}}}},$При фиксированной температуре, если объемный поток сырья $G$ “достаточно мал”, то Н2 полностью расходуется внутри нижней камеры на некотором расстоянии от входа ${{x}_{0}}$, при этом потоки ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}({{x}_{0}})$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}({{x}_{0}})$ в точке ${{x}_{0}}$ обращаются в нули (см. рис. 5 и (37)). В этих случаях выход водорода φ равен единице (44). С ростом $G$ заполнение камеры водородом увеличивается и поток ${{I}_{S}}$ через мембрану растет. При некотором $G$ (в дальнейшем обозначим эту величину ${{G}_{{{\text{ОПТ}}}}}$) потоки ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ и ${{n}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$ обращаются в нули на выходе нижней камеры (при $x = 1$). При дальнейшем увеличении $G$ ($G \geqslant {{G}_{{{\text{ОПТ}}}}}$) потоки водорода на выходе становятся больше нуля, а следовательно, выход φ уменьшается, то есть эффективность реактора ухудшается. Сравнение расчетных и экспериментальных значений составов смеси после холодильника, а также выходов φ при $m = 5$ для мембраны Pd–6% Re для различных $T$ и $G$ приведены в табл. 3. В скобках указаны экспериментальные значения соответствующих величин. Несмотря на некоторые расхождения теории и эксперимента основные закономерности процесса риформинга получили теоретическое обоснование. Экспериментальные значения потоков Н2 через мембрану (${{I}_{S}}$) всегда занижены по сравнению с теоретическими (ошибка может достигать 20% и более). Основная причина, по-видимому, связана с утечкой водорода, а также с дезактивацией мембраны окислами углерода и особенно водяными парами, как это отмечено ранее [32].
Таблица 3.
Расходы ${{n}_{i}}(1)$ на выходе нижней камеры ($x = 1$) и состав смеси после холодильника (${{X}_{i}}$) для немембранных и мембранных процессов при $m$ = 5. Потоки Н2 через мембрану
| $T$, K | Процесс | ${{n}_{{{\text{CO}}}}}(1)$ | ${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}(1)$ | ${{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}(1)$ | ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(1)$ | ${{X}_{{{\text{CO}}}}}$ | ${{X}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ | ${{X}_{{{\text{С}}{{{\text{H}}}_{{\text{4}}}}}}}$ | ${{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ | φ |
|---|---|---|---|---|---|---|---|---|---|---|
| 773 | Не мембранн. процесс |
0.133 | 0.80 | 1.07 | 2.58 | 0.03 (0)* |
0.18 (0.42) | 0.22 (0.12) | 0.57 (0.44) | 0 |
| $G = 1800$ 1/ч мембранн. процесс |
0.03 | 1.97 | 0.03 | 0.06 | 0.015 (0) | 0.94 (0.95) | 0.015 (0.05) | 0.03 (0) | 0.99 (0.82) | |
| $G = 3600$ мембранн. процесс |
0.05 | 1.57 | 0.38 | 0.92 | 0.016 (0.02) | 0.54 (0.46) | 0.13 (0.07) | 0.32 (0.41) | 0.82 (0.7) | |
| 823 | Не мембранн. процесс |
0.31 | 0.89 | 0.80 | 3.5 | 0.06 (0) |
0.16 (0.05) | 0.15 (0.12) | 0.63 (0.83) | 0 |
| $G = 1800$ мембранн. процесс | 0 | 2 | 0 | 0 | 0 (0.03) |
1 (0.95) | 0 (0.02) | 0 (0) |
1.0 (0.86) | |
| $G = 3600$ мембранн. процесс |
0.07 | 1.76 | 0.17 | 0.78 | 0.025 (0.012) | 0.64 (0.60) | 0.06 (0.002) | 0.28 (0.38) | 0.86 (0.7) |
* В скобках указаны экспериментальные данные, см. рис. 1, 2, 5.
Оптимальное значение параметра $\beta $ равно (см. (40)):
(45)
$\begin{gathered} {{\beta }_{{{\text{ОПТ}}}}} = \int\limits_0^{n_{E}^{*}} {\left( {2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} - \frac{{d\Delta }}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + 1} \right)} \times \\ \times \,\,\left( {\sqrt {1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + m - \Delta } } \right)\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} }}. \\ \end{gathered} $Распределение потока водорода в нижней камере ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ находим из уравнения (см. (40)):
(46)
$({\text{OT}})\frac{{\int\limits_{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}^{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} {\left( {2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} - \frac{{d\Delta }}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + 1} \right)\left( {\sqrt {1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + m - \Delta } } \right)\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} }}} }}{{\int\limits_0^{n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}} {\left( {2\frac{{d{{n}_{{{\text{C}}{{{\text{H}}}_{{\text{4}}}}}}}}}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} - \frac{{d\Delta }}{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}} + 1} \right)\left( {\sqrt {1 + {{n}_{{{{{\text{H}}}_{{\text{2}}}}}}} + m - \Delta } } \right)\frac{{d{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}}}{{\sqrt {{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} }}} }} = (x - {{x}_{{{\text{нач}}}}}),$Оптимальные значения ${{\beta }_{{{\text{ОПТ}}}}}$ и соответствующие распределения ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ зависят только от температуры и отношения $m$, так как от этих величин зависят $n_{{{{{\text{H}}}_{{\text{2}}}}}}^{*}$ и распределения ${{n}_{i}}({{n}_{{{{{\text{H}}}_{{\text{2}}}}}}})$ (см., например, табл. 2). В табл. 4 приведены расчеты ${{\beta }_{{{\text{ОПТ}}}}}$ в широкой области температур (673–1073 K) при $m$ = 4, 5, 7, 9.
Таблица 4.
Оптимальные значения параметра ${{\beta }_{{{\text{ОПТ}}}}}$ при различных $T$ и $m$
| $T$, K | 673 | 773 | 873 | 973 | 1073 |
|---|---|---|---|---|---|
| $m = 4$ | 26.03 | 17.56 | 13.75 | 12.32 | 11.23 |
| $m = 5$ | 27.40 | 18.51 | 14.65 | 13.45 | 12.60 |
| $m = 7$ | 29.13 | 19.89 | 16.21 | 15.42 | 14.8 |
| $m = 9$ | 30.36 | 20.98 | 17.58 | 17.16 | 16.96 |
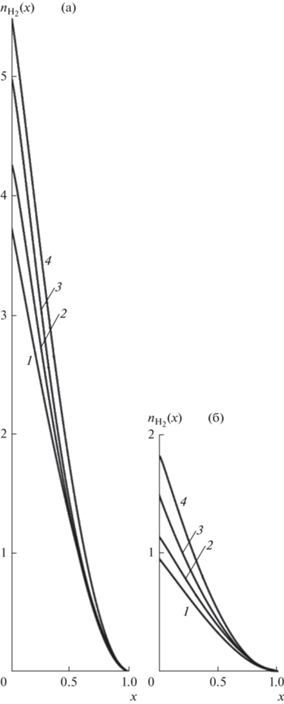
Распределения ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}$, ${{n}_{{{\text{CO}}}}}$, ${{n}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ внутри нижней камеры при оптимальных режимах для двух температур 673, 873 K и различных $m > 4$ представлены на рис. 6. Нетрудно заметить, что безразмерные потоки водорода ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ в нижней камере увеличиваются при возрастании температуры и потока сырья (см. рис. 5), что связано с ростом интенсивности каталитических реакций и увеличением скорости газовой смеси.
Рис. 6.
Распределения потоков ${{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}(x)$ при оптимальных режимах для $T = $ 873 K (а) и $T = $ 673 K (б). Кривые 1 – $m = 4$, 2 – 5, 3 – 7, 4 – $m = 9$.
Потоки Н2 через мембрану ${{I}_{S}}$ (на выходе верхней камеры) и ($G$/103) рассчитываются по формулам (47) и (43), соответственно:
(47)
$\begin{gathered} {{I}_{S}} = \left( {{{N}_{{{\text{ВЫХ}}}}}\beta } \right)\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} dx} = \\ = S\left[ {\frac{{Q\exp ( - {E \mathord{\left/ {\vphantom {E {RT}}} \right. \kern-0em} {RT}}) \times {{{10}}^{2}}\sqrt {10} \sqrt {{{p}_{{{\text{AT}}}}}} }}{\delta }} \right] \times \\ \times \,\,\left( {\int\limits_0^1 {\sqrt {{{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{{\text{H}}}_{{\text{2}}}}}}}} {{{n}_{\sum }}}}} \right. \kern-0em} {{{n}_{\sum }}}}} {\kern 1pt} dx} } \right), \\ \end{gathered} $При увеличении температуры (постоянное $m$) движущая сила увеличивается, что связано с ростом потока водорода в камере. В свою очередь, при увеличении $m$ (постоянная температура) движущая сила падает из-за увеличения избытка пара в смеси, так как в этом случае уменьшается мольная доля водорода ${{X}_{{{{{\text{H}}}_{{\text{2}}}}}}}$.
Для мембраны Pd–6% Ru в табл. 5 приведены расчеты ${{G}_{{{\text{ОПТ}}}}}$ в рассматриваемых интервалах температур и отношений $m$. Значение ${{G}_{{{\text{ОПТ}}}}}$ находится по общей формуле (43), где $\beta = {{\beta }_{{{\text{ОПТ}}}}}$.
Таблица 5.
Расчет оптимального потока сырья ${{G}_{{{\text{ОПТ}}}}}$ (1/ч) для мембраны состава Pd–6% Ru при различных $T$ и $m$
| $T$, K | 673 | 773 | 873 | 973 | 1073 |
|---|---|---|---|---|---|
| $m = 4$ | 0.69 | 1.47 | 2.41 | 3.27 | 3.80 |
| $m = 5$ | 0.79 | 1.68 | 2.71 | 3.59 | 4.44 |
| $m = 7$ | 0.99 | 2.08 | 3.27 | 4.18 | 4.65 |
| $m = 9$ | 1.19 | 2.47 | 3.76 | 4.69 | 5.74 |
Соответствующие потоки на выходе верхней камеры для этой мембраны представлены на рис. 7. С ростом температуры (постоянное $m$) потоки ${{I}_{{S,{\text{ОПТ}}}}}$ растут как за счет увеличения водородопроводимости мембраны, так и движущей силы. При фиксированной температуре потоки ${{I}_{{S,{\text{ОПТ}}}}}$ уменьшаются с увеличением $m$, так как уменьшается движущая сила переноса Н2 через мембрану.
Рис. 7.
Оптимальные потоки ${{I}_{{S,{\text{ОПТ}}}}}$ при различных температурах. Кривые 1 – $m = 4$, 2 – 5, 3 – 7, 4 – $m = 9$.
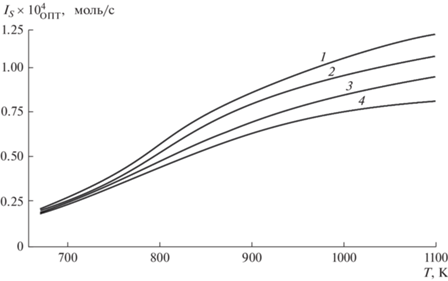
Из рис. 7 следует, что процесс парового риформинга необходимо проводить при достаточно высоких температурах, порядка 900–1000 K, и при как можно меньших отношениях $m$ (~4, 5). При низких температурах поток на выходе верхней камеры становится достаточно малым, а более высокие $T$ являются энергозатратными.
При оптимальных режимах парового риформинга этана на выходе нижней камеры мы получаем газовую смесь СО2 и Н2О, при этом безразмерные потоки компонентов смеси равны (см. (15)):
Соответствующий мольный состав равен:
После прохождения смеси на выходе нижней камеры через холодильник мы получаем практически чистый углекислый газ. На выходе в верхней камере присутствует только водород. Представленные в работе экспериментальные и расчетные величины относятся к фольговой мембране состава Pd–6% Ru, для которой предъэкспоненциальный фактор и энергия активации перехода Н2 через мембрану равны ${{Q}_{0}} = 6.1 \times {{10}^{8}}$ [моль/м с Па] и $E = $ = 13.9 [кДж/моль] соответственно [32].
ЗАКЛЮЧЕНИЕ
Экспериментально исследована паровая конверсия этана в реакторе с мембраной в виде фольги из Pd–6% Ru сплава и промышленным никелевым катализатором при атмосферном давлении в температурном интервале 773–823 К, при объемных скоростях сырья 1800 и 3600 ч–1 при соотношении пар/сырье 5. Ранее выполнены исследования паровой конверсии другого углеводородного сырья (смесей метана с пропаном, пропана, бутана, смесей, моделирующих состав попутного нефтяного газа). Сравнительные эксперименты в мембранном и традиционном реакторах показали, что в мембранном реакторе увеличивается превращение сырья по основным реакциям, приводящим к образованию СО2, СО и Н2, и снижается его превращение в побочных реакциях гидрокрекинга и образования УО. Увеличению этого превращения благоприятствует вакуумирование пермеата. При объемной скорости 1800 ч–1, температуре ~800 K и соотношении пар/сырье, равным пяти, и вакуумировании наблюдается близкая к 100% селективность образования СО2 и целевого продукта Н2. При более высокой объемной скорости сырья (3600 ч–1) уменьшается выход водорода и увеличивается скорость образования УО.
Результаты исследования показывают, что этан является хорошим сырьем для получения водорода высокой чистоты в данном мембранном реакторе. По сравнению с другими С2+ алканами (пропан, н-бутан) при выбранных условиях из этана образуется меньше углеродных отложений и СН4. Таким образом, данный реактор подходит для получения водорода высокой чистоты из различных видов углеводородного сырья.
Наряду с экспериментальными исследованиями проведено моделирование парового риформинга этана в ММ с использованием фольговых палладиевых мембран состава Pd–6% Ru. Доказано, что в нижней камере ММ, заполненной никелевым катализатором, существуют два несоизмеримых участка – начальный, размеры которого намного меньше радиуса камер, и основной. На начальном участке мембрана не оказывает влияние на протекающие химические процессы, причем на выходе этого участка реакции приходят к равновесию, а поток водорода максимален.
Влияние мембраны становится заметной на основном участке, где из-за слабого оттока водорода через мембрану химические равновесия практически не нарушаются.
Теоретически доказано, что при паровом риформинге этана отношение входных потоков Н2О и СН4 не должно быть менее четырех. В противном случае водяной пар полностью расходуется внутри нижней камеры и паровой риформинг прекращается.
Расчеты были проведены в интервале температур ~700–1000 K при отношениях потока воды и метана на входе 4–9.
Для любого фиксированного отношения $m > 4$ в широкой области температур найдены оптимальные значения потока сырья на входе, при которых выход водорода достигает 100%. Показано, что наиболее выгодно проводить риформинг при $m \cong 4{\kern 1pt} - {\kern 1pt} 5$ и температуре в системе порядка 800–900 K.
При оптимальных режимах на выходе нижней камеры смесь практически состоит из водяных паров и СО2. После охлаждения смеси (удаления Н2О) мы получаем чистый углекислый газ. В верхней камере присутствует только водород.
Экспериментальные данные, полученные в указанных выше интервалах изменения температур, при отношении $m = 5$ и объемных скоростях сырья $G$ = 1800, 3600 1/ч, в основном, согласуются с соответствующими теоретическими расчетами. Таким образом, закономерности процесса риформинга получили теоретическое обоснование. Некоторые расхождения теории и экспериментов можно объяснить не учетом в расчетах ряда процессов, таких как реакций метанирования, протекающих наряду с реакцией 3. (например, СО2 + Н2 = СН4 + 2Н2О), а также дезактивацией катализатора, которые в данной работе не учитывались.
Работа выполнена в рамках Программы фундаментальных научных исследований государственных академий наук, тема ИПХФ РАН 0089-2019-0018 (номер госрегистрации АААА-А19-119022690098-3).
ОБОЗНАЧЕНИЯ
| $E$ | энергия активации в уравнении Сивертса, Дж/моль |
| $G$ | объемная скорость подачи сырья, 1/ч |
| $h$ | высота камер, м |
| ${{I}_{{{{H}_{2}}}}}$ | локальный поток Н2 через мембрану, моль/м2 с |
| ${{I}_{S}}$ | интегральный поток Н2 через мембрану, моль/с |
| ${{K}_{1}}$ | константа равновесия реакции (1), ат4 |
| ${{K}_{2}}$ | константа равновесия реакции (2) |
| ${{K}_{3}}$ | константа равновесия реакции (3), ат2 |
| ${{k}_{i}}$ | константы равновесия Лэнгмюра для СО, Н4, Н2, ат–1 |
| $m$ | отношение входных интегральных потоков пар/С2Н6 |
| ${{\dot {N}}_{{{\text{BX}}}}}$ | интегральный поток С2Н6 на входе в нижнюю камеру, моль/с |
| ${{n}_{i}}$ | безразмерный локальный поток компонента смеси |
| $n_{i}^{*}$ | равновесные потоки компонентов на выходе начального участка |
| ${{n}_{\sum }}$ | безразмерный локальный поток смеси |
| $p$ | давление в нижней камере, Па |
| ${{p}_{{{\text{AT}}}}}$ | давление в атмосферах, ат |
| ${{Q}_{0}}$ | предъэкспоненциальный множитель в законе Сиверста, моль/м1/2 кг1/2 |
| $r_{{\max }}^{'}$ | радиус камер, м |
| $R$ | универсальная газовая постоянная, Дж/моль гр |
| ${{b}_{1}}$, ${{b}_{2}}$, ${{b}_{3}}$ | скорости реакций 1–3, моль/кгкат с |
| $r{\kern 1pt} '$, $z{\kern 1pt} '$ | цилиндрические координаты, м |
| ${{s}_{{{\text{эфф}}}}}$ | площадь фольги, м2 |
| $T$ | температура, K |
| ${{w}_{{{\text{кат}}}}}$ | масса засыпки катализатора, кг |
| $x$, $y$ | безразмерные координаты, отсчитываемые от входа сырья |
| ${{X}_{i}}$ | мольная доля i-ого компонента смеси в нижней камере |
| $\Delta $ | безразмерное отклонение потока водяного пара от его входной величины |
| $\beta $ | безразмерный параметр, учитывающий поток Н2 через мембрану |
| φ | отвод водорода |
| ${{\phi }_{i}}$ | источник (сток) компонента i, моль/кгкат |
Список литературы
Saeidi S., Fazlollahi F., Najari S., Iranshahi D., Klemes I.I., Baxter L.L. Hydrogen productions: Perspectives, separation with special emphasis on kinetics of WGS reaction: A state-of-the-art review // J. Ind. and Eng. Chem. 2017. V. 49. P. 1.
Kirillov V.A., Meshcheryakov V.D., Brizitskii O.F., Terent’ev V.Ya. Analysis of a power system based on low-temperature fuel cells and a fuel processor with a membrane hydrogen separator // Theor. Found. Chem. Eng. 2010. V. 44. № 3.P. 227.
Sperle T., Chen D., Lodeng R., Holmen A. Pre-reforming of natural gas on a Ni catalyst: Criteria for carbon free operation // Appl. Catal. A: Gen. 2005. V. 282. P. 195.
Кириллов В.А., Амосов Ю.И., Шигаров А.Б., Кузин Н.А., Киреенков В.В., Пармон В.Н., Аристович Ю.В., Грицай М.А., Светов А.А. Экспериментальное и теоретическое исследование процесса переработок попутного нефтяного газа в нормализованной газ посредством мягкого парового риформинга // Теорет. основы хим. технол. 2017. Т. 51. № 1. С. 15.
Christensen Th.S. Adiabatic prereforming of hydrocarbons an important step in syngas production // Appl. Catal. A: Gen. 1996. V. 138. P. 285.
Avci A.K., Trimm D.L., Aksoylu A.E., Önsan Z.I. Hydrogen production by steam reforming of n-butane over suppoted Ni and Pt-Ni catalysts // Appl. Catal. A: Gen. 2004. V. 258. P. 255.
Wang X., Gorte R.J. Steam reforming of n-butane on Pd/ceria // Catal. Lett. 2001. V. 73. P. 15.
Takeguchi T., Kani Y., Yano T., Kikuchi R., Eguchi K., Tsujimoto K., Uchida Y., Ueno A., Omoshiki K., Aizawa M. Study on steam reforming of CH4 and C2 hydrocarbons and carbon deposition on Ni-YSZ cermets // J. Power Sources. 2002. V. 112. P. 588.
Graf P.O., Mojet B.L., Ommen J.G.V., Lefferts L. Comparative study of steam reforming of methane, ethane and ethylene on Pt, Rh and Pd supported on yttrium-stabilized zirconia // Appl. Catal. A: Gen. 2007. V. 332. P. 310.
Veranitisagul C., Koonsaeng N., Laosiripojana N., Laobuthee A. Preparation of gadolinia doped ceria via metal complex decomposition method: Its application as catalyst for the steam reforming of ethane // J. Ind. Eng. Chem. 2012. V.18. P. 898.
Jeong S., Kim S., Lee B., Ryi S.-K., Lim H. Techno-economic analysis: Ethane steam reforming in a membrane reactor with H2 selectivity effect and profitability analysis // Int. J. Hydrogen Energy. 2018. V. 43. P. 7693.
Волков И.Н. Разработка перспективных катализаторов на основе гетерогенных наноструктур нитрида бора. Автореферат дис. … канд. техн. наук / И.Н. Волков. М. 2022. 39 с.: ил. (на правах рукописи).
Rahimpour M.R., Samimi F., Babapoor A., Tohidian T., Mohebi S. Palladium membranes application in reaction systems for hydrogen separation and purification: A review // Chem. Eng. Proc.: Process Intensification. 2017. V. 121. P. 24.
Tiemersma T., Patil C., van Sint Annaland M., Kuipers I. Modelling of packet bed membrane reactors for autothermal production of ultrapure hydrogen // Chem. Eng. Sci. 2006. V. 61. P. 1602.
Gryaznov V.M. Hydrogen permeable palladium membrane catalyst. An aid to the efficient production of ultra pure chemicals and pharmaceuticals // Platinum Met. Rev. 1986. V. 36. P. 68.
Shirasaki Y., Tsuneki T., Seki T., Yasuda I., Sato T., Iton N. Improvement in hydrogen permeability of palladium membrane by alloying with transition metals // J. Chem. Eng. 2018. V. 51. P. 123.
Holleck G.L. Diffusion and solubility of hydrogen in palladium and palladium-silver alloys // J. Phys. Chem. 1970. V. 74. P. 503.
Fort D., Farr I., Hurris I.A. A comparison of palladium-silver and palladium-yttrium alloys as hydrogen separation membranes // J. Less-Common Met. 1975. V. 39. P. 293.
Sakamoto Y., Chen F.L., Furukawa M., Noguchi M. Permeability and diffusivity of hydrogen in Pd rich Pd–Y(Cd)–Ag ternary allows // J. Allows Comped. 1992. V. 185. P. 191.
Howard B.H., Killmeyer R.P., Rothenberger K., Cugini A.V. Hydrogen permeance of palladium-copper alloy membranes over a wide range of temperatures and pressures // J. Memb. Sci. 2004. V. 241. P. 207.
Burkhanov G.S., Gorina N.B., Kolchugina N.B., Roshan N.R., Slovetsky D.I., Chistov E.M. Palladium-based alloy membranes for separation of high purity hydrogen from hydrogen-containing gas mixtures // Platinum Met. Rev. 2011. V. 55. № 1. P. 3.
Didenko L.P., Babak V.N., Sementsova L.A., Chizhov P.E., Dorofeeva T.V. Steam conversion of propane in a membrane reactor with a industrial nickel catalyst // Petrolium Chemistry. 2021. V. 61. № 1. P. 92.
Boeltken T., Wunsch A., Gietzelt T., Pfeifer P., Dittmeyer R. Ultra-compact microstructured methane steam reforming with integrated palladium membrane for onsite production of pure hydrogen: Experimental demonstration // Int. J. Hydrogen Energy. 2014. V. 30. P. 18058.
Дубинин А.М., Тупоногов В.Г., Иконников И.С. Моделирование процесса производства водорода из метана // Теорет. основы хим. технол. 2013. Т. 47. № 6. С. 634.
Бабак В.Н., Диденко Л.П., Квурт Ю.П., Семенцова Л.А., Закиев С.Е. Моделирование паровой конверсии метана в мембранном реакторе с никелевым катализатором и фольгой из палладиевого сплава // Теорет. основы хим. технол. 2021. Т. 55. № 3. С. 319.
Бабак В.Н., Диденко Л.П., Семенцова Л.А., Квурт Ю.П. Моделирование парового риформинга пропана в каталитическом мембранном реакторе при высоких температурах // Теорет. основы хим. технол. 2022. Т. 56. № 2. С. 167.
Бабак В.Н., Диденко Л.П., Семенцова Л.А., Квурт Ю.П. Оптимизация процесса парового риформинга метана в водородфильтрующем мембранном модуле с никелевым катализатором и фольгой из палладиевых сплавов // Теорет. основы хим. технол. 2022. Т. 56. № 3. С. 282.
Lin Y.M., Liu Sh.I., Chuang Ch.H., Chu Y.T. Effect of incipient removal of hydrogen through palladium membrane on the conversion of methane steam reforming: Experimental and modelling // Catal. Today. 2003. V. 82. № 1. P. 127.
Xu J., Froment G.F. Methane steam refoming, methanation and water-gas shift: I. Intrinsic kinetics // AIChE J. 1989. V. 35. № 1. P. 88.
Мещенко Н.Т., Веселов В.В., Шуб Ф.С., Темкин М.И. Кинетика низкотемпературной паровой конверсии этана на никель-хромовом катализаторе // Кинетика и катализ. 1977. Т. XVIII. Вып. 4. С. 963.
Годунов С.К., Рябенький В.С. Разностные схемы. М.: Наука. 1973. 400 с.
Бабак В.Н., Диденко Л.П., Квурт Ю.П., Семенцова Л.А. Извлечение водорода из бинарных газовых смесей с помощью мембранного модуля на основе палладиевой фольги с учетом дезактивации мембраны// Теорет. основы хим. технол. 2018. Т. 52. № 3. С. 318.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


