Теоретические основы химической технологии, 2023, T. 57, № 3, стр. 273-283

Кинетика ультразвукового растворения порошка оксида металла для разных пространственных сочетаний области кавитации и акустического течения Эккарта

О. М. Градов^a, *, И. В. Зиновьева^a, Ю. А. Заходяева^a, А. А. Вошкин^a

^a Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия

Поступила в редакцию 20.03.2023
После доработки 26.03.2023
Принята к публикации 30.03.2023

EDN: RLPKGQ
DOI: 10.31857/S0040357123030065

Аннотация

Рассмотрены особенности воздействия акустического течения и кавитации, создаваемых бегущей ультразвуковой волной, которые могут быть использованы для эффективного растворения порошка оксида металла. На основе упрощенной схемы, учитывающей, тем не менее, все существенные особенности исследуемой реальности, получены точные выражения для всех параметров стационарного вихревого движения и кавитации, полностью обеспечивающих требования надлежащего регулирования хода реакции. Выведены уравнения, описывающие кинетику растворения для двух типичных режимов: развитой кавитации и докавитационного состояния. Найдены выражения для времени полного завершения процесса. На примере этих двух наиболее типичных видов реакции сформулированы условия, выполнение которых позволяет полностью удовлетворить решению поставленных перед технологией задач. Представлены способы наиболее оптимального применения схемы ультразвукового растворения и отмечены те особенности ее формирования, которые дают возможность осуществлять регулирование процесса. Выполненные расчеты дают возможность выбрать и точно реализовать ту схему акустической стимуляции растворения, которая наиболее полно соответствует ожидаемым выходным результатам и другим особенностям обработки.

Ключевые слова: акустическое течение, ультразвуковая кавитация, растворение, оксиды металлов

ВВЕДЕНИЕ

Во многих технологических производствах получили широкое применение процессы растворения (или выщелачивания) тех или иных компонентов в соответствующем растворителе [1–3]. В настоящее время общее признание получили способности ультразвука (УЗ) многократно сокращать время растворения соединений в растворителях [4–8]. В ряде работ предложены схемы и проанализировано влияние ультразвука на ускоренное извлечение органических и неорганических веществ из различных сред [9–14]. С другой стороны, ультразвуковое воздействие позволяет улучшить характеристики процесса выщелачивания металлов из твердых материалов [1, 15–17]. Так, например, в работе [18] представлены эффективные способы оптимизации времени и температуры экстракции Mo, V и Ni из кислых растворов выщелачивания отработанных катализаторов серной и лимонной кислотой. В то же время применение УЗ воздействия для простого перемешивания в процессе экстракции позволило повысить скорость и степень извлечения (свыше 95%) для всех извлекаемых компонентов. В исследовании [19] по выщелачиванию железа из отходов, накапливающихся при производстве фотоэлектрических модулей, была выявлена способность ультразвука существенно интенсифицировать извлечение металла, сократив время выщелачивания на 37.5%, вследствие разрушения твердой фазы на более мелкие части, что приводит к увеличению контакта твердой и жидкой фаз. Способность ультразвука интенсифицировать огромное количество процессов, реакций, разнообразных взаимодействий в жидкости обусловлена органически присущим ему свойством создавать быстро осциллирующие микропотоки и стационарные акустические течения, что, как правило, существенно изменяет характеристики того явления, которое является объектом внешнего воздействия [20–23].

В настоящей работе детально рассмотрен процесс УЗ растворения порошка оксида металла в растворителе на примере реалистичной схемы взаимодействия, использующей коллимированный пучок УЗ излучения для поддержания и регулирования применяемых реакций. Представленная методика расчета выходных характеристик и рабочих параметров может послужить основой при проектировании и эксплуатации также и других подобных систем, имеющих в своей основе управляемое УЗ воздействие на кинетику растворения. Возможное подключение режима развитой кавитации создает дополнительные существенные возможности для обработки частиц, ускоряя их растворение, как это показано в [24]. Эти и другие свойства ультразвука могут эффективно реализоваться и значительно интенсифицировать работу всей системы УЗ выщелачивания при полном соблюдении всех необходимых режимов и поддержании значений параметров, диапазон изменения которых определяется из детального анализа физико-химической сущности рассматриваемых процессов с учетом индивидуальных особенностей каждой схемы реализации данной технологии. При этом для целей выщелачивания компонентов успешное и полезное внедрение возможно и даже целесообразно практически для всех нелинейных акустических эффектов, включая, как кавитацию и акустическое течение, так и уединенные импульсы, частотную и амплитудную модуляцию, нелинейное взаимодействие волн и т.д.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Расчет связи параметров процесса растворения с характеристиками УЗ

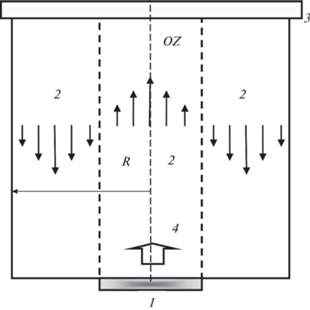
Устройство, использующее бегущую УЗ волну для интенсификации процесса растворения порошка оксида металла, должно содержать ряд обязательных элементов и в простейшем виде представлено схематически на рис. 1. К нижней поверхности рабочего объема цилиндрической формы с радиусом R крепится излучатель УЗ волны 1, которая, согласно [25], создает акустическое течение 2 и становится бегущей при наличии поглотителя 3. Объем заполняется жидкостью, содержащей растворитель, в которой равномерно распределены частицы соединения металла. Воздействуя на звуковые колебания, вязкость жидкости приводит к возникновению стационарных вихревых течений при наличии твердых препятствий или ограничивающих стенок. Эти акустические течения проявляются во втором приближении по амплитуде волны, т.е. относятся к нелинейным явлениям. Они существуют только при наличии вязкости, хотя скорость движения в них и может в определенных условиях иметь слабую зависимость от этого параметра.

Рис. 1.

Схема движения жидкости в акустическом течении Эккарта в плоскости, проходящей через ось цилиндрического объема: 1 – излучатель ультразвука; 2 – направление движения акустического течения; 3 – поглотитель ультразвука; 4 – направление распространения УЗ излучения.

Состояние движущейся жидкости описывается следующей хорошо известной [26] системой гидродинамических уравнений

(1)

$\rho ({{\partial }_{t}}{\mathbf{v}} + {\mathbf{v}}s{\mathbf{v}}) = - \nabla p + \eta \nabla {\mathbf{v}},$

(2)

${{\partial }_{t}}\rho + {\text{div}}(\rho {\mathbf{v}}) = {\text{ }}0,$

(3)

$p = {{A}_{0}}{{\left( {\frac{\rho }{{{{\rho }_{0}}}}} \right)}^{\gamma }} - {{A}_{1}}.$

Здесь функции v(r, t), ρ(r, t) и p(r, t) представляют собой распределение скорости, плотности и давления жидкости по пространственным координатам, описываемым радиус-вектором r, а также изменение их во времени t в условиях, когда константы А₀, А₁ и γ, входящие в уравнение состояния Тэта (3), слабо зависят от температуры среды. Индексом “0” снабжены равновесные значения параметров в отсутствие движения (случай v(r, t) = 0), когда возмущения плотности ρ'(r, t) и давления p'(r, t) равны нулю.

Для получения уравнений нелинейной акустики полная система (1)–(3) записывается в виде разложения по малому параметру М_а = ρ'/ρ₀. где ρ' – возмущение плотности, М_а – акустическое число Маха. Малым предполагается и влияние вязкости η, описываемое последним членом уравнения (1). В звуковой волне изменение состояния среды близко к адиабатическому, т.е. происходит без изменения величины энтропии S, и в этом приближении уравнение состояния жидкости позволяет использовать разложение

(4)

$\begin{gathered} p{\kern 1pt} ' = \rho {\kern 1pt} '{{\left( {\frac{{\partial p}}{{\partial \rho }}} \right)}_{S}} + \frac{1}{2}{{\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{\rho }^{2}}}}} \right)}_{S}}\rho {\kern 1pt} {{'}^{2}} = \\ = c_{0}^{2}\rho {\kern 1pt} '\,\, + {{\left( {\frac{{\partial c_{{}}^{2}}}{{\partial \rho }}} \right)}_{S}}\rho {\kern 1pt} {{'}^{2}};\,\,\,\,c_{0}^{2} = {{\left( {\frac{{\partial p}}{{\partial \rho }}} \right)}_{{S,{{\rho }_{0}}}}}. \\ \end{gathered} $

Здесь ρ = ρ₀ + ρ' + ρ''; p = p₀ + р' + р'', ρ₀ — равновесные значения давления и плотности среды, где р₀ — гидростатическое давление (для воды γ = 7, А₁ = ~300 МПа), ρ'' и р'' – стационарные возмущения плотности и давления, связанные с акустическим течением; А₀ – А₁ = р₀. Поэтому в случае жидкостей из (3) следует

(5)

$c_{0}^{2} = {{A}_{0}}\frac{\gamma }{{{{\rho }_{0}}}};\,\,\,\,{{\left( {\frac{{\partial c_{{}}^{2}}}{{\partial \rho }}} \right)}_{S}} = \frac{{c_{0}^{2}(\gamma - 1)}}{{{{\rho }_{0}}}}.$

Учет нелинейности в выражении (5) для давления позволяет более корректно вычислить коэффициенты в выражениях для компонента скорости акустического течения [22], хотя и не оказывает заметного влияния на характер их зависимостей от параметров задачи.

Определение параметров стационарного потока для целей описания поведения кинетики растворения оксида металла под воздействием ультразвука

Колебательная скорость, связанная с бегущей от излучателя (z = 0) УЗ волной, направлена вдоль оси z и в цилиндрических координатах r, φ, z имеет в линейном приближении следующий вид

(6)

$v_{z}^{'} = U(r){{е}^{ - }}^{{\delta z}}{\text{sin}}(\omega t - kz),$

где δ = 2ηω²/3с₀³ρ₀ – линейный пространственный декремент поглощения звука, k – волновое число.

Значение амплитуды U(r) в плоскости z = 0 определяется граничным условием передачи внешнего УЗ воздействия в рабочий объем и связано с амплитудой акустического давления Р_а в этом месте соотношением U(r = 0) = Р_а/с₀ρ₀, которое вытекает из (1) в линейном приближении [25]. Функция U(r) дает распределение колебательной скорости по фронту волны. Подставляя (6) в (1)–(5), можно найти решение для стационарного потока. В работе [25] это решение найдено при следующих условиях: 1) действительно в пространстве, где есть только z – компонента стационарного потока; 2) звук распространяется в цилиндрической трубе, причем торец, противоположный источнику звука в плоскости z = L_V, закрыт поглотителем так, что в трубе распространяется бегущая волна; 3) в выражении (6) можно считать еxp(–δL_V)~ 1). Интегральный поток массы жидкости через все сечение трубы равен нулю. При этих условиях скорость стационарного акустического течения 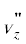имеет вид

(7)

$\begin{gathered} v_{z}^{{''}} = \frac{{{{k}^{2}}}}{{3{{c}_{0}}}}\left\{ {\int\limits_r^R {dss{{U}^{2}}} (s)\ln \frac{R}{s} + \ln \frac{R}{r}\int\limits_0^r {dss{{U}^{2}}} (s)} \right. + \\ \left. { + \,\,\frac{{{{r}^{2}} - {{R}^{2}}}}{{{{R}^{4}}}}\int\limits_0^R {ds{{U}^{2}}} (s)(s{{R}^{2}} - {{s}^{3}})} \right\}. \\ \end{gathered} $

При равномерном распределении колебательной скорости пучка УЗ волн по его сечению с радиусом r₀, когда функция U(r) определяется следующими соотношениями

(8)

$\begin{gathered} U(r) = {{U}_{0}},\,\,\,\,r < {{r}_{0}}; \\ U(r) = {{U}_{0}},\,\,\,\,{{r}_{0}} < r \leqslant R, \\ \end{gathered} $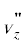

для скорости стационарного акустического течения

из (7) можно записать

(9)

Такое распределение скорости потока показано на рис. 1. В УЗ пучке поток направлен от источника звука, а вблизи стенки рабочего объема – к источнику. Скорость потока максимальна на оси звукового пучка и зависит от R/r₀. При R/r₀ = 1 скорость, согласно (9), обращается в ноль. Из (9) следует, что скорость потока пропорциональна интенсивности звука, квадрату частоты и соотношению радиуса пучка к длине волны.

Описание характеристик области УЗ кавитации, необходимых для оценки параметров кинетики растворения оксида металла в объеме с акустическим течением Эккарта

В любой жидкости обычно образуются небольшие пузырьки, заполненные нерастворенными газами и ее паром. Это явление образования пузырьков называется кавитацией. В условиях равновесия пузырек сохраняет устойчивость, давление в жидкости уравновешивается газовым давлением изнутри. Но когда жидкость в процессе движения попадает из области низкого давления в область более высокого, внутреннее давление в пузырьке, который пришел из области с низким его значением, становится меньше нового, высокого давления в жидкости. Тогда последняя устремляется к центру, захлопывая пузырек. В процессе захлопывания пузырька, как и при фокусировке ударной волны, происходит концентрирование энергии. Скорость захлопывания и давление нарастают по мере уменьшения радиуса пузырька и в стадии фокусировки достигают весьма больших значений. После схлопывания в центральной области образуется пик давления и от центра распространяется ударная волна. Поэтому, когда кавитация протекает вблизи твердых поверхностей, ударная волна может привести к повреждениям поверхности материала [24, 26].

Применение кавитационной УЗ эрозии для растворения крупных частиц соединений металлов показало [24] существенную интенсификацию процесса за счет измельчения объекта в порошок и соответствующего увеличения поверхности взаимодействия фаз. Кроме разрушительного воздействия область кавитации обладает и другими возможностями влиять на процесс растворения. Если акустическое давление Р_а превышает некоторое пороговое значение P_th, то в конце стадии сжатия жидкости под воздействием ультразвука происходит схлопывание кавитационных пузырьков, приводящее к образованию ударных волн, имеющих на фронте существенный перепад давления [24, 26]. Это может приводить не только к изъятию с поверхности соединения металла частичек в виде порошка [24], но и к ускорению молекул растворителя в жидкости, обеспечивая его усиленное перемешивание. Полученные в [24] выражения позволяют рассчитать силовое воздействие, оказываемое отдельной схлопывающейся кавитационной полостью, на плоскую поверхность твердого тела. В предельном случае P_m$ \gg $ p₀ (P_m = max(P_a)) формула для перепада давления P_M на фронте волны имеет вид

(10)

${{P}_{{\text{M}}}} = \frac{{{{P}_{{\text{m}}}}}}{{81}}{{\left( {\frac{{{{P}_{{\text{m}}}}}}{{{{р}_{0}}}}} \right)}^{3}}.$

Движение возникающей сферической ударной волны в жидкости определяется при этом всего двумя параметрами: плотностью жидкости ρ₀ и энергией Е, сосредоточенной первоначально в пузырьке и выделяющейся при распространении ее фронта. Величина такой энергии, как показано в [24], определяется формулой через значение R₀ его равновесного радиуса в отсутствие ультразвука

(11)

$E = \frac{{4\pi R_{0}^{3}}}{9}{{P}_{{\text{m}}}}.$

Процесс распространения волны можно описать, исходя из соображений размерности. Используемые параметры вместе с двумя независимыми переменными – временем t и координатой L(t) от центра пузырька – позволяют составить всего одну независимую безразмерную комбинацию

(12)

$L(t){{\left( {\frac{{{{\rho }_{0}}}}{{E{{t}^{2}}}}} \right)}^{{1/5}}}.$

Ее существование указывает на автомодельность процесса. Поэтому можно утверждать, что положение фронта ударной волны в каждый момент времени должно соответствовать одному и тому же постоянному значению, обозначенному символом β, рассматриваемой безразмерной комбинации. Это дает закон перемещения ударной волны со временем от центра пузырька L(t)

(13)

$L(t) = \beta {{\left( {\frac{{E{{t}^{2}}}}{{{{\rho }_{0}}}}} \right)}^{{1/5}}}.$

Зная расстояние L₀ от центра пузырька до поверхности мишени в начальный момент времени, по формуле (13) можно определить время, за которое фронт ударной волны достигнет намеченной цели.

Необходимо отметить, что формулы (11)–(13) содержат всю детальную информацию, необходимую для вычисления параметров процессов, характеризующих растворение оксида металла в жидкости под воздействием ультразвука.

Описание кинетики процесса растворения оксидов металлов в жидкости под воздействием ультразвука

Растворение оксидов металлов – это комплексный и, в общем случае, многостадийный процесс. Например, растворение твердого тела протекает в три стадии: сначала подвод растворителя к поверхности твердого тела, затем разрушение кристаллической решетки и выход ионов в тонкий слой насыщенного раствора у самой поверхности твердой фазы, а третья стадия – перенос частиц из этого слоя в глубину раствора. Каждая стадия развивается со своей скоростью. Скорость всего процесса определяется скоростью самой медленной стадии, в простейшем случае – это диффузия ионов из насыщенного раствора. Если кинетика процесса определяется диффузией, то имеет место диффузная кинетика.

В общем случае концентрация вещества у поверхности растворения зависит от соотношения скоростей всех трех стадий и находится в диапазоне между концентрацией насыщения С_S и концентрацией в основном объеме растворителя С₁. В большинстве реальных случаев скорости подвода растворителя и собственно межфазного перехода значительно превышают скорость диффузионного отвода вещества в основной объем жидкости, концентрация вещества у поверхности растворения равна при этом концентрации насыщения, а изменение массы M твердого вещества определяется известным кинетическим уравнением [23]

(14)

$ - {{d}_{\tau }}M = {{\beta }_{c}}F({{C}_{S}} - {{C}_{1}}),$

где τ – время; β_с – коэффициент массоотдачи растворенного вещества; F – поверхность растворения.

В случае, если параметры процесса определяются внешним воздействием, например, ультразвуком, можно говорить об УЗ растворении. При этом скорость реакции может определяться различными эффектами, связанными с его взаимодействием с жидкостью, в частности, с акустическим течением, осцилляторными потоками, кавитационными пульсациями и т.д. Упрощенный расчет кинетики растворения порошка оксида металла, можно выполнить на примере процесса с одинаковыми порошинками сферической формы радиуса R_p, равномерно распределенными по рабочему объему с плотностью N_p в растворителе, плотность молекул которого N_r однородна в пространстве. Сам процесс растворения состоит в том, что, когда молекула растворителя сближается с частицей в узле кристаллической структуры оксида металла, то она изолирует последнюю от электромагнитного взаимодействия с другими узлами решетки, и эта частица может свободно перейти в жидкость со скоростью потоков, существующих в ней. Это приводит к разрушению решетки и постепенному переходу ее частиц в раствор.

Количество частиц ∆N(t), перешедших в раствор в любой выбранный момент времени, равно, очевидно, числу молекул растворителя, способных взаимодействовать с узлами кристаллической решетки, т.е. их скоплению, содержащемуся в слое радиуса r_p(t) вблизи поверхности оксида металла и толщиной l, равной расстоянию между узлами решетки, которую для упрощения можно считать кубической

(15)

$\Delta N\left( t \right) = 4\pi r_{{\text{p}}}^{2}\left( t \right)l{\text{ }}{{n}_{{\text{r}}}}\left( t \right),$

где n_r(r, t) – плотность растворителя в момент времени t в точке с радиус-вектором r. Предполагается, что среднее расстояние между молекулами растворителя в жидкости L_r(t) значительно превышает расстояние между узлами кубической кристаллической решетки. Без поступления свежего раствора она уменьшается со временем по мере того, как идет процесс растворения. Расстояние L_r(t) между молекулами растворителя в рабочем объеме определяется количеством этих частиц в нем и тем обстоятельством, что их число уменьшается со временем из-за взаимодействия с соединением металла. Поэтому их плотность n_r связана с первоначальным постоянным в пространстве значением n_r0 соотношением

(16)

${{n}_{{\text{r}}}}\left( {{\mathbf{r}},t} \right)V = V{{n}_{{{\text{r0}}}}} - N\left( {{\mathbf{r}},t} \right){{N}_{{\text{p}}}},$

где N(r, t) – количество молекул оксида металла, перешедших в раствор в заданной точке пространства r и в выбранный момент времени t из одиночной частицы оксида металла.

Если в какой-то момент времени произошло взаимодействие молекул растворителя с узлами решетки, то продукты реакции и новые молекулы растворителя будут перемещаться со скоростью тех потоков, которые доминируют в рабочем объеме. Это может быть связано с внешним воздействием или же диффузионной скоростью u_d. Конечно, взаимодействие происходит непрерывно во времени. Но для упрощения расчетов можно предположить, что оно происходит одномоментно через интервалы времени ∆t, которые определяются временем прохождения со скоростью u_S тех молекул растворителя, которые находились на расстоянии L_r от частицы оксида металла в предыдущий момент реакции, т.е. ∆t = L_r/u_S. Поэтому соотношение (15) можно записать в виде

(17)

$\Delta N(t) = - {\text{ }}4\pi r_{{\text{p}}}^{2}(t)l{{u}_{{\text{S}}}}{{N}_{{\text{r}}}}(t){{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {{{L}_{{\text{r}}}}}}} \right. \kern-0em} {{{L}_{{\text{r}}}}}}.$

Если характерное время растворения частицы оксида металла значительно превышает значение ∆t, то из (17) следует уравнение, описывающее кинетику этой реакции

(18)

${{d}_{{\text{t}}}}N = - 4\pi r_{{\text{p}}}^{2}\left( t \right){{l{{u}_{{\text{S}}}}{{n}_{{\text{r}}}}\left( t \right)} \mathord{\left/ {\vphantom {{l{{u}_{{\text{S}}}}{{n}_{{\text{r}}}}\left( t \right)} {{{L}_{{\text{r}}}}\left( t \right)}}} \right. \kern-0em} {{{L}_{{\text{r}}}}\left( t \right)}}.$

В пределе, когда объем или концентрация растворителя значительно превосходит количество растворяемого материала (N_r0$ \gg $ N), уравнение (18) может быть переписано в форме, совпадающей с феноменологическим соотношением, полученным в начальный период систематического изучения кинетики растворения [23].

В окончательном варианте уравнение (18) можно представить в следующем компактном виде для y = 1 – n, n = N/N₀₀, N₀₀ = 4π(R_p/l)³/3 – количество молекул в частице оксида металла

(19)

$\begin{gathered} {{d}_{{\text{t}}}}y = {{y}^{{2/3}}}{{\left( {q + y} \right)}^{{4/3}}}{{A}_{0}}\left( r \right), \\ {{A}_{0}}\left( r \right) = {{\left( {36\pi } \right)}^{{1/3}}}{{V}_{{\text{p}}}}n_{p}^{{1/3}}{{u}_{{\text{S}}}}. \\ \end{gathered} $

Здесь q = n_r0/(n_pN₀₀) – 1, n_p = N_p/V, V = 4πR²L_V,V_p = ${{ = 4\pi R_{{\text{p}}}^{3}{{n}_{{\text{p}}}}} \mathord{\left/ {\vphantom {{ = 4\pi R_{{\text{p}}}^{3}{{n}_{{\text{p}}}}} 3}} \right. \kern-0em} 3}$.

Если в начальный момент времени t = 0 выполняется n = 0, т.е. y(t = 0) = 1, а для t = τ имеет место n = 1, т.е. y(t = τ) = 0, то из (19) можно получить значение промежутка времени τ, в течение которого в заданной точке пространства частицы оксида металла полностью растворятся в рассматриваемом месте рабочего объема

(20)

${{\tau }} = \frac{{{{I}_{q}}}}{{{{A}_{0}}({\mathbf{r}})}};\,\,\,\,{{I}_{q}} = \int\limits_0^1 {\frac{{{{y}^{{ - 2/3}}}dy}}{{{{{(q + y)}}^{{4/3}}}}}} \equiv 3\int\limits_0^1 {\frac{{dy}}{{{{{(q + {{y}^{3}})}}^{{4/3}}}}}} .$

Таким образом, уравнение (20) позволяет проследить во времени за изменением концентрации растворяемого оксида металла в любой области пространства, предназначенного для реализации этого процесса. На примере докавитационного и кавитационного режимов можно рассмотреть особенности кинетики этой реакции в условиях существования акустического течения Эккарта.

Растворение оксида металла в растворителе с акустическим течением в режиме бегущей УЗ волны без кавитации

Вся зависимость от пространственных координат, содержащаяся в уравнениях (16), (18), (19), заключена в распределении по рабочему объему величины скорости подвода и отвода молекул растворителя к узлам кристаллической структуры оксида металла. В случае, когда кавитация отсутствует, а скорость потока определяет акустическое течение Эккарта, в уравнениях (18), (19) следует использовать выражение u_S = 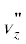+ u_d и соотношения (8), (9). На рис. 2 представлено пространственное распределение и поведение во времени n(t, ρ) для некоторых типичных значений параметров задачи (раздел 2) от радиального аргумента ρ = r/r₀, диапазон изменения величины которого соответствует области, занятой пучком УЗ волн (рис. 1), т.е. 0 < ρ < 1. Аналогичным образом можно рассчитать и поведение этого параметра в области значений радиальной координаты, лежащих в пределах 1 < ρ < R/r₀. Здесь акустическое течение движется в противоположную сторону, но качественно картина сохраняет все те особенности, которые представлены на рис. 2 для соответствующей части схемы УЗ растворения.

Рис. 2.

Распределение концентрации растворяемого оксида металла по радиусу рабочего объема и ее зависимость от времени в области, занятой пучком УЗ волн.

Решение уравнения (19) для промежутка времени τ, в течение которого в заданной точке пространства частица оксида металла полностью растворится в рассматриваемом месте рабочего объема, представлено на рис. 3 для тех же значений параметров, которые были использованы при получении рис. 2. Из этих рисунков видно, что в области замедления потоков растворение идет гораздо медленнее, чем в других местах рабочего объема.

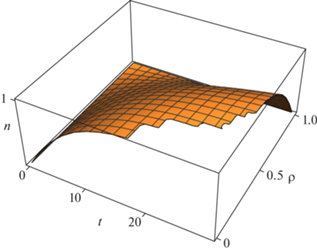
Рис. 3.

Зависимость времени τ_a полного растворения порошка оксида металла в разных точках радиуса рабочего объема и его связь с начальными значениями параметров задачи в области, занятой пучком УЗ волн.

Кроме того, скорость растворения, как это следует из (18), прямо пропорциональна величине акустического давления. При этом для времени растворения, в соответствии с (19), имеет место обратная зависимость. На динамику изменения во времени этих основных параметров реакции имеет существенное влияние начальный радиус R_p частиц оксида металла, представленный на рис. 3 в безразмерном виде через посредство аргумента x = (n_pN₀₀/n_r0)^1/3 ≡ R_p/R_q, где R_q является функцией только начальных параметров задачи. Видно, что усредненное по радиусу рабочего объема время растворения увеличивается с ростом R_p и уменьшается с увеличением скорости потока при ρ = 0.

Следует также обратить внимание на то обстоятельство, что при выводе уравнений (18), (19) было использовано предположение о том, что плотность n_p частиц оксида металла в растворителе не меняется до конца реакции. На самом деле растворение протекает с разной скоростью в разных областях рабочего объема, поэтому в конце процесса не все частицы оксида металла одинаковы по размеру и исчезают они не одновременно, а на протяжении некоторого отрезка времени. Однако в это время частицы очень невелики, поступление растворяемых частиц в раствор мало и нарушение указанного предположения слабо меняет соответствие результатов теории с реальностью на этом этапе.

Кинетика растворения частиц оксида металла в растворителе при комбинированном воздействии кавитации и акустического течения Эккарта

В условиях, когда величина акустического давления P_а, превышает некоторое пороговое значение P_th, в области вблизи УЗ излучателя начинает развиваться кавитация. Размер этой области определяется масштабом этого превышения и пространственным декрементом затухания δ. Находящиеся в ней молекулы растворителя находятся под воздействием ударных волн, генерируемых схлопывающимися пузырьками [24], и приобретают скорость, позволяющую им приближаться к узлам кристаллической решетки и также удаляться, определяя тем самым скорость растворения.

Для определения этой скорости u_S можно использовать уравнение (1), опустив в нем нелинейные и диссипативные слагаемые, которые несущественны в узком слое толщиной L_r вблизи частицы, рассматриваемого в соответствии с предположением относительно величины элементарного отрезка длины, сделанного при выводе уравнений (12), (13), описывающих кинетику УЗ растворения в рассматриваемой схеме реализации реакции. Принимая во внимание сферичность пространственной структуры ударных волн кавитации, необходимо рассмотреть их воздействие на молекулу растворителя вдоль их радиуса L

(21)

${{\rho }_{0}}{{\partial }_{t}}{{u}_{{\text{S}}}} = - {\text{ }}{{\partial }_{L}}p.$

Заменяя в (21) дифференцирование по времени на дифференцирование по координате L с использованием формулы (12), можно приближенно заменить L ~ L_r в этом слое

(22)

${{\partial }_{{\text{t}}}} = {{\partial }_{{\text{t}}}}L{{\partial }_{{\text{L}}}} = ({{2L} \mathord{\left/ {\vphantom {{2L} {5t}}} \right. \kern-0em} {5t}}){{\partial }_{{\text{L}}}} \approx ({{2{{L}_{{\text{r}}}}} \mathord{\left/ {\vphantom {{2{{L}_{{\text{r}}}}} {5{{t}_{{\text{r}}}}}}} \right. \kern-0em} {5{{t}_{{\text{r}}}}}}){{\partial }_{{\text{L}}}},$

где t_r – определяется по формуле (12) через L_r. Дело в том, что L_r является тем минимальным расстоянием от поверхности частицы оксида металла, когда внутри этого слоя гипотетически может не оказаться ни одной молекулы растворителя, кроме вступивших уже во взаимодействие с узлами решетки. Поэтому только те кавитационные пузырьки, которые находятся вне этого слоя, т.е. на расстоянии большем, чем L_r от частицы оксида металла, могут своим ударным воздействием повлиять на скорость движения молекулы растворителя. Таким образом, в очередном элементарном акте рассматриваемой дискретной модели растворения могут принять участие те кавитационные пузырьки, ударные волны от которых, воздействующие на молекулы растворителя, могут достичь поверхности частицы оксида металла за время t_r. Подставляя выражение для t_r в (22) и используя (13), из (21), можно получить для u_S следующее выражение

(23)

${{u}_{{\text{S}}}} = \frac{5}{{108}}\sqrt {\frac{{{{P}_{{\text{m}}}}}}{{{\text{3}}\pi R_{{\text{0}}}^{{\text{3}}}{{n}_{{\text{r}}}}{{\rho }_{{\text{0}}}}}}} {{\left( {\frac{{{{P}_{{\text{m}}}}}}{{{{P}_{{\text{0}}}}}}} \right)}^{3}}{{\beta }^{{ - {\text{5/2}}}}}.$

С помощью (23) уравнение (17), описывающее кинетику реакции в общем случае, может быть записано в виде

(24)

${{d}_{{\text{t}}}}N = - \frac{5}{{27}}\sqrt {\frac{{\pi {{P}_{0}}}}{{3R_{0}^{3}{{\rho }_{0}}{{\beta }^{5}}}}} r_{p}^{2}(t)n_{{\text{r}}}^{{5/6}}l{{\left( {\frac{{{{P}_{{\text{m}}}}}}{{{{P}_{0}}}}} \right)}^{{7/2}}}.$

В безразмерном представлении с использованием обозначений, принятых в уравнении (18), соотношение (24) может быть переписано в следующей форме

(25)

$\begin{gathered} {{d}_{{\text{t}}}}y = {{(q + y)}^{{5/6}}}{{y}^{{2/3}}}{{A}_{0}}({\mathbf{r}}); \\ {{A}_{0}}({\mathbf{r}}) = \frac{4}{5}\sqrt {\frac{{\pi {{P}_{0}}R_{{\text{p}}}^{3}{{l}^{3}}n_{{\text{p}}}^{{5/3}}}}{{3R_{0}^{3}{{\rho }_{0}}{{\beta }^{5}}}}} {{\left( {\frac{{{{P}_{{\text{m}}}}}}{{3{{P}_{0}}}}} \right)}^{{7/2}}}. \\ \end{gathered} $

Уравнение (25) описывает кинетику растворения в условиях развитой УЗ кавитации, когда величина УЗ воздействия превышает пороговое значение. Сравнение с уравнением (18), относящимся к ситуации, когда определяющим фактором является акустическое течение Эккарта, показывает, что в обоих случаях зависимость от амплитуды акустического давления одинакова (квадратичная). Отличия связаны с разными численными выражениями в степенной зависимости и несовпадением коэффициентов, зависящих от начальных условий и характеристик схемы растворения.

На рис. 4 представлена зависимость плотности растворенного вещества в жидкости от времени и радиуса частицы оксида металла в безразмерных координатах, использованных при получении рис. 3.

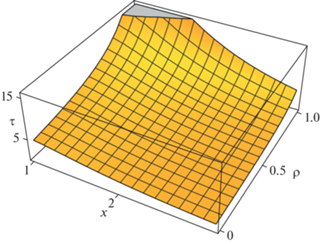
Рис. 4.

Зависимость плотности растворенного вещества в жидкости от времени и радиуса частицы оксида металла в безразмерных координатах в области кавитации, созданной пучком УЗ волн.

Из рис. 4 видно, что количество растворенного вещества растет в каждый момент времени с увеличением радиуса частицы оксида металла по вполне понятной причине роста поверхности взаимодействия в условиях, когда концентрация частиц остается неизменной. В процессе растворения поверхность частицы оксида металла уменьшается, количество поступающего в жидкость растворяемого вещества в единицу времени сокращается и скорость реакции падает.

Из уравнения (25) можно определить время τ полного растворения подобно тому, как это было сделано при получении выражения (19) для амплитуд УЗ воздействия ниже порогового значения, при превышении которого развивается кавитация

(26)

$\begin{gathered} \tau = \frac{{I_{q}^{{}}{{\vartheta }^{{ - 7/2}}}}}{{{{A}_{0}}({\mathbf{r}})}};\,\,\,\,{{I}_{q}} = 3\int\limits_0^1 {\frac{{dy}}{{{{{(q + {{y}^{3}})}}^{{5/6}}}}},} \,\,\,\,\vartheta = \frac{{{{P}_{{\text{m}}}}}}{{{{P}_{{{\text{th}}}}}}}; \\ {{A}_{0}}({\mathbf{r}}) = \frac{4}{5}\sqrt {\frac{{\pi {{P}_{0}}R_{{\text{p}}}^{3}{{l}^{3}}n_{{\text{p}}}^{{5/3}}}}{{3R_{0}^{3}{{\rho }_{0}}{{\beta }^{5}}}}} {{\left( {\frac{{{{P}_{{{\text{th}}}}}}}{{3{{P}_{0}}}}} \right)}^{{7/2}}}. \\ \end{gathered} $

Вариацией начальными параметрами и структурными характеристиками схемы растворения, которые входят в (26), можно проследить влияние тех или иных факторов на кинетику реакции. На рис. 5 показано увеличение времени растворения вдоль оси цилиндрического рабочего объема вследствие диссипативного уменьшения амплитуды УЗ волны и его падение при увеличении последней. Степенная зависимость выходных данных от амплитуды УЗ волны указывают на весьма высокую чувствительность параметров реакции к регулированию внешним воздействием.

Рис. 5.

Изменение времени τ_c полного растворения порошка оксида металла в разных точках оси рабочего объема и его связь с амплитудой акустического давления в области, занятой пучком УЗ волн (ζ = δz).

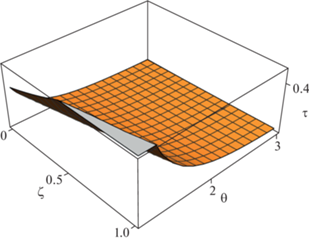
Неоднородность вдоль радиуса цилиндра рабочей камеры целиком определяется свойствами УЗ излучателя и, как правило, практически отсутствует за исключением узкого слоя на границе кавитационной области. Как видно из сравнения (12) и (25), режим растворения с использованием акустического течения отличается от кавитационного величиной степени в слагаемых, содержащих начальные условия и параметры схемы реакции, зависимость от интенсивности ультразвука. Кроме того, в режиме использования кавитации существуют такие характеристики процесса, которых нет в другом режиме. Это пороговое значение интенсивности внешнего УЗ излучения, при превышении которого возникает кавитация, размер радиуса равновесного состояния пузырька, концентрация зародышей кавитации и т.д.

Размер области кавитации определяется величиной пространственного декремента δ, пороговым значением акустического давления P_th, при превышении которого амплитудой P_m внешнего УЗ излучения парогазовые пузырьки начинают схлопываться, создавая характерную картину явления. Протяженность L_c этой области вдоль оси рабочего объема определяется из формулы (6) следующим выражением

${{L}_{{\text{c}}}} = \frac{1}{\delta }\ln \frac{{{{P}_{{\text{m}}}}}}{{{{P}_{{{\text{th}}}}}}}.$

Соответствующим образом можно установить границы этой области и по радиальной координате, используя известное распределение интенсивности ультразвука по сечению излучателя.

Определенный интерес представляет сравнение кинетики растворения под воздействием кавитации, с одной стороны, а с другой стороны, со случаем, когда процесс реализуется в докавитационном режиме с решающим влиянием акустического течения. На рис. 6 приведены зависимости поступления молекул в жидкость от радиуса частиц оксида металла и времени для рассматриваемых режимов растворения в условиях с одинаковыми параметрами, но разными значениями внешнего акустического давления. Необходимо отметить примерно одинаковую динамику поступления в жидкость растворяемого вещества, тогда как зависимость от радиуса частиц оксида металла оказывается более сильной в режиме использования акустического течения.

Рис. 6.

Сравнительная динамика во времени растворения порошка оксида металла в режиме кавитации (верхняя поверхность) и под воздействием акустического течения, а также зависимость от размера частиц оксида металла для одинаковых параметров задачи.

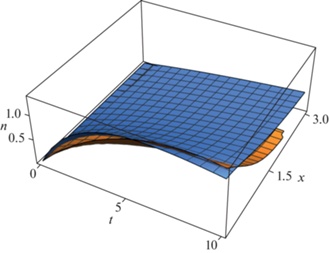
Представленные выше расчеты по определению зависимости кинетики растворения от размера частиц растворяемого вещества не предполагает связь этого параметра с концентрацией порошка. В то же время изучение такой зависимости представляется важным также в условиях, когда на разные по величине частички дробится один и тот же объем материала, т.е. величина ${{n}_{{\text{p}}}}R_{{\text{p}}}^{3}$ = М_с = const. Для кавитационного режима эти два подхода рассмотрены при определении зависимости времени растворения от радиуса частиц оксида металла и от акустического давления в условиях одинаковых значений остальных параметров задачи. На рис. 7 верхняя поверхность связана с дроблением одного и того же образца материала на частицы разного размера, а нижняя показывает зависимость кинетики растворения от радиуса частиц оксида металла при неизменном значении их концентрации в жидкости.

Рис. 7.

Зависимость времени растворения порошка оксида металла в режиме кавитации от радиуса частиц и величины акустического давления в условиях наличия связи размера частиц оксида металла с их концентрацией и при ее отсутствии

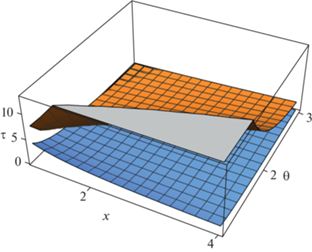
Поведение верхней поверхности с ростом размера частиц можно объяснить следующим образом. Полная площадь поверхности частиц в единице объема жидкости S₀ может быть записана в виде S₀ = $4\pi {{n}_{{\text{p}}}}R_{{\text{p}}}^{2}$ = 4πМ_с/R_p. Таким образом, с ростом радиуса полная поверхность взаимодействия фаз при растворении уменьшается в этом случае, что означает рост продолжительности реакции.

ЗАКЛЮЧЕНИЕ

Применение ультразвука для воздействия на кинетику растворения оксида металла в жидкости рассмотрено в настоящей работе для двух рабочих режимов, использующих кавитацию и стационарное акустическое течение, на примере простой схемы сравнительно редко используемого на практике применения в устройстве бегущей волны (метод Эккарта). Возможно, отсутствие большой популярности в практической реализации связано с кажущимся бесполезным расходованием УЗ энергии, когда существенная ее часть непосредственно подлежит безвозвратному поглощению. На самом деле, в этой схеме используется УЗ энергия в том же долевом размере, что и в других схемах, например, в условиях создания пространственной стоячей волны УЗ колебаний (метод Рэлея). В то же время простота схемы Эккарта может оказаться решающим фактором при ее выборе для ряда важных химических технологий.

Представленные в настоящей работе описания особенностей воздействия кавитации на кинетику растворения порошка оксида металла в жидкости и применения для этой цели стационарного акустического течения позволяет сравнить преимущества и недостатки общих режимов, осознанно использовать тот или другой режим или же применить схему регулируемой эксплуатации обоих методов одновременно. Разная зависимость свойств каждого из режимов от параметров задачи позволяет регулировать, в целом ряде случаев, ход реакции в любой из этих областей независимо друг от друга при одновременном использовании.

Следует отметить, что способ описания кинетики УЗ растворения порошка оксида металлав жидкости на примере акустического течения Эккарта вполне применим также для других схем использования ультразвука с целью интенсификации процесса, поскольку оперирует общими для любого УЗ воздействия понятиями микропотоков, колебательных свойств и нелинейности. Поэтому представленный подход к построению теории УЗ растворения порошков практически не нуждается в серьезной переработке при применении к самым разным практическим схемам реализации этой технологии.

Еще одно свойство кавитации, связанное с эрозионным воздействием на вещество, подробно проанализировано применительно к процессам растворения твердых объектов в работе [20] и проявляется в тех условиях, для которых параметры УЗ силовой обработки превосходят соответствующие значения, характеризующие прочностные свойства объекта воздействия. Кроме того, использование сильно измельченного порошка также делает неактуальным дальнейшее дробление его частичек ударными волнами от схлопывающихся кавитационных пузырьков. В то же время существует широкий диапазон условий, когда одновременным применением эрозионного УЗ воздействия совместно с рассмотренными в настоящей работе режимами УЗ растворения порошка оксида металла в жидкости можно существенно интенсифицировать реакции этой химической УЗ технологии.

Работа выполнена при финансовой поддержке Минобрнауки России в рамках государственного задания ИОНХ РАН.

Список литературы

Narayana K.L., Swamy K.M., Rao K.S., Murty J.S. Leaching of Metals from Ores with Ultrasound // Miner. Process. Extr. Metall. Rev. 1997. V. 16(4). P. 239.
Lei C., Aldous I., Hartley J.M., Thompson D.L., Scott S., Hanson R., Anderson P.A., Kendrick E., Sommerville R., Ryder K.S., Abbott A.P. Lithium ion battery recycling using high-intensity ultrasonication // Green Chem. 2021. V. 23. P. 4710.
Sandilya D.K., Kannan A. Intensification of the Dissolution of a Sparingly Soluble Solid from a Spinning Disk in the Presence of Power Ultrasound // Ind. Eng. Chem. Res. 2020. V. 50(23). P. 13083.
Sandilya D.K., Kannan A. Intensification of the Dissolution of a Sparingly Soluble Solid from a Spinning Disk in the Presence of Power Ultrasound // Ind. Eng. Chem. Res. 2020. V. 50(23). P. 13083.
Xin W., Srinivasakannan C., Xin-hui D., Jin-hui P., Da-jin Y., Shao-hua J. Leaching kinetics of zinc residues augmented with ultrasound // Sep. Purif. Tech. 2013. V. 115. P. 66.
Avvaru B., Roy S.B., Chowdhury S., Hareendran K.N., Pandit A.B. Enhancement of the Leaching Rate of Uranium in the Presence of Ultrasound // Ind. Eng. Chem. Res. 2006. V. 45(22). P. 7639.
Li X., Zhang J., Yang D. Determination of Antiscaling Efficiency and Dissolution Capacity for Calcium Carbonate with Ultrasonic Irradiation // Ind. Eng. Chem. Res. 2012. V. 51(27). P. 9266.
Gui Q., Khan M.I., Wang S., Zhang L. The ultrasound leaching kinetics of gold in the thiosulfate leaching process catalysed by cobalt ammonia // Hydrometallurgy. 2020. V. 196. P. 105426.
Gradov O.M., Voshkin A.A., Zakhodyaeva Y.A. Estimating the parameters of ultrasonically induced mass transfer and flow of liquids in the pseudomembrane method // Chem. Eng. Process. 2017. V. 118. P. 54.
Градов О.М., Зиновьева И.В., Заходяева Ю.А., Вошкин А.А. Кинетика растворения порошка LiCoO₂ в глубоком эвтектическом растворителе хлорид холина–сульфосалициловая кислота под воздействием ультразвука // Теор. осн. хим. техн. 2022. Т. 56. № 6. С. 705–711.
Gradov O.M., Zakhodyaeva Y.A., Voshkin A.A. Breakup of immiscible liquids at the interface using high-power acoustic pulses // Chem. Eng. Process. 2018. V. 131. P. 125.
Gradov O.M., Zakhodyaeva Y.A., Zinov’eva I.V., Voshkin A.A. Some Features of the Ultrasonic Liquid Extraction of Metal Ions // Molecules. 2019. V. 24(19). P. 3549.
Gradov O.M., Zakhodyaeva Yu.A., Zinov’eva I.V., Voshkin A.A. Ultrasonic Intensification of Mass Transfer in Organic Acid Extraction. Processes. 2021. V. 9(1). P. 15.
Gradov O.M., Zakhodyaeva Y.A., Voshkin A.A. Dynamics of Mass Transfer through the Interface between Immiscible Liquids under the Resonance Effect of Ultrasound // Theor. Found. Chem. Eng. 2020. V. 54. P. 1148.
John J.J., De Houwer V., Van Mechelen D., Van Gerven T. Effect of ultrasound on leaching of lead from landfilled metallurgical residues // Ultrasonics Sonochemistry. 2020. V. 69. Article 105239.
Xiao J., Yuan J., Tian Z., Yang K., Yao Z., Yu B., Zhang L. Comparison of ultrasound-assisted and traditional caustic leaching of spent cathode carbon (SCC) from aluminum electrolysis // Ultrasonics Sonochemistry. 2018. V. 40. P. 21–29.
Lei C., Aldous I., Hartley J.M., Thompson D.L., Scott S., Hanson R., Anderson P.A., Kendrick E., Sommerville R., Ryder K.S., Abbott A.P. Lithium ion battery recycling using high-intensity ultrasonication // Green Chem. 2021. V. 23. P. 4710.
Marafi M., Stanislaus A. Waste Catalyst Utilization: Extraction of Valuable Metals from Spent Hydroprocessing Catalysts by Ultrasonic-Assisted Leaching with Acids // Ind. Eng. Chem. Res. 2011. V. 50(16). P. 9495.
Kong J., Xing P., Wei D., Jin X., Zhuang Y. Ultrasound-Assisted Leaching of Iron from Silicon Diamond-Wire Saw Cutting Waste // JOM. 2021. V. 73. P. 791.
Swamy K., Narayana K.L. Intensification of leaching process by dual-frequency ultrasound // Ultrasonics Sonochemistry. 2001. V. 8(4). P. 341–346.
Lupacchini M., Mascitti A., Giachi G., Tonucci L., d’Alessandro N., Martinez J., Colacino E. Sonochemistry in non-conventional, green solvents or solvent-free reactions // Tetrahedron. 2017. V. 73(6). P. 609–653.
Grénman H., Murzina E., Rönnholm M., Eränen K., Mikkola J.-P., Lahtinen M., Salmi T., Murzin D.Y. Enhancement of solid dissolution by ultrasound // Chemical Engineering and Processing: Process Intensification. 2007. V. 46(9). P. 862–869.
Kannan A., Pathan S.K. Enhancement of Solid Dissolution Process // Chem. Eng. J. 2004. V. 102. P. 45.
Gradov O.M., Zinov’eva I.V., Zakhodyaeva Y.A., Voshkin A.A. Modelling of the erosive dissolution of metal oxides in a deep eutectic solvent – choline chloride/sulfosalicylic acid-assisted by ultrasonic cavitation // Metals. 2021. V. 11. Article 1964.
Eckart C. Vortices and streams caused by sound waves // Phys. Rev. 1948. V. 73. № 1. P. 68.
Flynn H.G. Physics of acoustic cavitations in liquids, in: Physical Acoustics; W.P. Mason: New York. 1964. 1B. 57.
Schukarew A. Reaktion geschwindigkeiten zwischen Metallen und Haloiden. Z. Phys. Chem.-Bd. 8. 1891. P. 76–81.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал