Теоретические основы химической технологии, 2023, T. 57, № 4, стр. 399-407
Математическая модель и экспериментальные данные охлаждения воды в противоточных пленочных градирнях
Е. А. Лаптева a, *, А. Г. Лаптев a
a Казанский государственный энергетический университет
Казань, Россия
* E-mail: grivka100@mail.ru
Поступила в редакцию 05.05.2023
После доработки 14.05.2023
Принята к публикации 05.06.2023
- EDN: VJFDSB
- DOI: 10.31857/S0040357123040048
Аннотация
Рассмотрены методы исследования, математического моделирования и расчета тепломассообменных характеристик пленочных блоков оросителей (насадок) в градирнях. Основными методами являются – экспериментальные, численные и приближенные. Отмечено, что для практических целей расчета градирен наибольшее применение находят экспериментальные и приближенные методы. Одним из приближенных методов заключается в применении моделей структуры потоков – диффузионной или ячеечной моделей. Рассмотрено применение ячеечной модели для газовой и жидкой фаз в виде аналитического решения с тепловым числом единиц переноса. В результате вычисляется тепловая эффективность по газовой фазе (нагрева воздуха) и с использованием уравнения теплового баланса определяется эффективность охлаждения воды. Представлены выражения для расчета основных параметров модели – числа ячеек по газовой и жидкой фазам. Даны экспериментальные данные по гидравлическому сопротивлению, объемному коэффициенту массоотдачи и тепловой эффективности в газовой и жидкой фазах, полученные на макете градирни с пакетом труб (блоком оросителей) с дискретно – регулярной шероховатой поверхностью. Показано согласование результатов расчетов по ячеечной модели с экспериментом. Даны результаты расчета мини градирни с регулярными насадками, применяемые в ректификационных и абсорбционных колоннах.
ВВЕДЕНИЕ
Практически на всех промышленных предприятиях химии, нефтехимии, нефтегазопереработки, металлургии и т.д. применяются водооборотные циклы, где вода охлаждается в различных по типам и конструкциям градирнях. Наибольшее применение получили пленочные противоточные градирни, где контакт фаз организуется в блоках оросителей – регулярных или комбинированных насадочных устройствах. Известны сотни различных конструкций насадок [1–3] с интенсификаторами процесса тепломассообмена. Насадки исследуются на стендах различного размера, где получают экспериментальные данные по предельным нагрузкам, гидравлическому сопротивлению, коэффициента тепло- и массоотдачи, эффективности тепломассообмена и брызгоуносу [4–6]. В связи со сложностью и значительной стоимостью исследования перечисленных характеристик представляется целесообразным сокращение уровней (стадий) экспериментов, ограничиваясь в основном гидродинамическими параметрами, т.е. предельными нагрузками, перепадом давления и структурой потоков воды и воздуха. Данные характеристики можно исследовать при нормальных условиях, т.е. без нагрева и охлаждения воды, а определение эффективности охлаждения воды и нагрева воздуха далее выполнять с применением методов математического моделирования на основе частных форм записи законов сохранения импульса, массы и энергии, а именно моделей структуры потока.
Методы математического моделирования в химической технологии подразделяются на точные, численные, асимптотические и приближенные. В двухфазных средах с подвижной межфазной поверхностью получить точное решение практически невозможно, поэтому для расчетов тепломассообменных процессов применяются численные и приближенные методы [7–9]. Численное моделирование основано на компьютерном решении системы дифференциальных уравнений с частными производными и в основном применяется для научно-исследовательских задач и иногда при предпроектной разработке новых контактных устройств, с привлечением экспериментальных данных [10–12]. Например, на основе экспериментов и численной модели исследовано влияние неравномерностей распределение воды и воздуха в блоках оросителей на эффективность тепломассообмена [13, 14].
Аналитические решения, с получением в явном виде расчетных выражений или с итерационными процедурами вычислений для тепломассообменных характеристик двухфазных сред, могут применяться при проектировании или модернизации промышленных градирен. Однако для практических целей при определении эффективности тепломассообмена чаще применяются приближенные методы, а именно теория пограничного слоя гидродинамическая аналогия, модели структуры потоков и другие подходы [15–17].
Для расчета градирен в данной статье применяется приближенный подход, апробированный для насадочных пленочных скрубберов-охладителей газов водой [18]. В основе лежит ячеечная модель структуры потоков для газовой и жидкой фаз с использованием решения, приведенного в монографии [19], полученное для противоточного абсорбера.
Целью данной статьи является определение тепловой эффективности в газовой фазе на основе применения ячеечной модели с числом единиц переноса и далее расчет эффективности охлаждения воды на основе теплового баланса в фазах для различных регулярных насадок в градирнях.
ЯЧЕЕЧНАЯ МОДЕЛЬ
При применении ячеечной модели предполагается условное деление потоков в направлении движения газа и жидкости на ряд ячеек полного перемешивания (одномерная модель). Между ячейками перемешивание отсутствует, поэтому на границах сопряжения ячеек имеется некоторый скачек полей концентраций и температур. Число ячеек по газовой и жидкой фазам чаще всего не совпадает и определяется экспериментально для каждой конструкции контактного устройства различными методами, чаще вводом индикаторов в потоки. В результате обработки экспериментальных данных находятся коэффициенты обратного (продольного) перемешивания каждого потока и обобщаются в виде безразмерных комплексов-модифицированных чисел Пекле ${\text{P}}{{{\text{e}}}_{{{\text{эг}}}}} = {{{{w}_{{\text{г}}}}{{d}_{{\text{э}}}}} \mathord{\left/ {\vphantom {{{{w}_{{\text{г}}}}{{d}_{{\text{э}}}}} {{{D}_{{{\text{пг}}}}}}}} \right. \kern-0em} {{{D}_{{{\text{пг}}}}}}}$ и ${\text{P}}{{{\text{e}}}_{{{\text{эж}}}}} = {{{{u}_{{\text{ж}}}}{{d}_{{\text{э}}}}} \mathord{\left/ {\vphantom {{{{u}_{{\text{ж}}}}{{d}_{{\text{э}}}}} {{{D}_{{{\text{пж}}}}}}}} \right. \kern-0em} {{{D}_{{{\text{пж}}}}}}}.$ Известна приближенная связь между числами Пекле и числом ячеек. Для этого число Пекле записывают относительно высоты насадочного слоя Н, тогда ${\text{P}}{{{\text{e}}}_{{\text{г}}}} = {{Н{\text{P}}{{{\text{e}}}_{{{\text{эг}}}}}} \mathord{\left/ {\vphantom {{Н{\text{P}}{{{\text{e}}}_{{{\text{эг}}}}}} {{{d}_{{\text{э}}}}}}} \right. \kern-0em} {{{d}_{{\text{э}}}}}}$ и ${\text{P}}{{{\text{e}}}_{{\text{ж}}}} = {{Н{\text{P}}{{{\text{e}}}_{{{\text{эж}}}}}} \mathord{\left/ {\vphantom {{Н{\text{P}}{{{\text{e}}}_{{{\text{эж}}}}}} {{{d}_{{\text{э}}}}}}} \right. \kern-0em} {{{d}_{{\text{э}}}}}},$ тогда число ячеек $n = {{({\text{P}}{{{\text{e}}}_{{\text{г}}}} + 1.25)} \mathord{\left/ {\vphantom {{({\text{P}}{{{\text{e}}}_{{\text{г}}}} + 1.25)} {2.5}}} \right. \kern-0em} {2.5}}$ и $m = {{({\text{P}}{{{\text{e}}}_{{\text{ж}}}} + 1.25)} \mathord{\left/ {\vphantom {{({\text{P}}{{{\text{e}}}_{{\text{ж}}}} + 1.25)} {{\text{2}}{\text{.5}}}}} \right. \kern-0em} {{\text{2}}{\text{.5}}}}{\text{.}}$
Поток теплоты в элементарном объеме насадочного слоя запишем в виде
(1)
$dQ = KdF({{T}_{{\text{г}}}} - {{T}_{{\text{ж}}}}) + {{I}_{{\text{п}}}}{\kern 1pt} {{\rho }_{{\text{г}}}}{\kern 1pt} {{\beta }_{{\text{г}}}}{\kern 1pt} dF(х* - х).$Используя подход Меркеля и аналогию Льюиса локальный поток теплоты записывается в форме $dQ = {{\beta }_{х}}dF(I* - I),$ где $I{\text{*}}$ – энтальпия газа вблизи межфазной поверхности при температуре ${{T}_{{\text{ж}}}}{\text{ и }}\varphi \,{\text{ = }}\,{\text{100\% }}$. Тогда полный поток теплоты (Вт) представим в известной форме [20]
Отсюда запишем отношение
(3)
$\frac{{{{\beta }_{х}}F}}{G} = \frac{{{{I}_{{\text{к}}}} - {{I}_{{\text{н}}}}}}{{\Delta {{I}_{{{\text{ср}}}}}}} = {{N}_{{\text{г}}}},$При известных значениям n, m и ${{N}_{{\text{г}}}}$ для противотока решение ячеечной модели представлено в монографии [19] для процесса абсорбции газов, которое после некоторых преобразований для противоточной градирни получено в виде
(4)
$--{\text{ при}}\,\,n > m,\,\,{{Е}_{{\text{г}}}} = 1 - {{\left( {1 + \frac{{{{N}_{{\text{г}}}}m}}{n}} \right)}^{{ - {n \mathord{\left/ {\vphantom {n m}} \right. \kern-0em} m}}}},$(5)
$--{\text{ при}}\,\,m > n,{{Е}_{{\text{г}}}} = 1 - {{\left( {1 + \frac{{{{N}_{{\text{г}}}}n}}{m}} \right)}^{{ - {m \mathord{\left/ {\vphantom {m n}} \right. \kern-0em} n}}}},$(6)
${{Е}_{{\text{г}}}} = \frac{{{{I}_{{\text{к}}}} - {{I}_{{\text{н}}}}}}{{I_{{\text{к}}}^{ * } - {{I}_{{\text{н}}}}}},$Тепловая эффективность охлаждения воды
(7)
${{Е}_{{\text{г}}}} = \frac{{{{Т}_{{{\text{жн}}}}} - {{Т}_{{{\text{жк}}}}}}}{{{{Т}_{{{\text{жн}}}}} - {{Т}_{{{\text{мт}}}}}}}.$Уравнение теплового баланса
(8)
$Q = L{{с}_{{{\text{рж}}}}}({{Т}_{{{\text{жн}}}}} - {{Т}_{{{\text{жк}}}}}) + {{Q}_{u}} = G({{I}_{{\text{к}}}} - {{I}_{{\text{н}}}}),$Из выражений (6)–(8) следует отношение
(9)
$\frac{{{{Е}_{{\text{г}}}}}}{{{{Е}_{{\text{ж}}}}}} = \frac{{L{{с}_{{{\text{рж}}}}}({{Т}_{{{\text{жн}}}}} - {{Т}_{{{\text{мт}}}}}) + {{Q}_{и}}}}{{G(I_{{\text{к}}}^{ * } - {{I}_{{\text{н}}}})}},$АЛГОРИТМ РАСЧЕТА
Таким образом, алгоритм расчета градирни имеет вид:
1. Задаются расходы фаз – L, G, начальная ${{Т}_{{{\text{жн}}}}}$ и требуемая температура воды ${{Т}_{{{\text{жк}}}}};$ начальные параметры воздуха ${{Т}_{{{\text{гн}}}}},$${{х}_{{\text{н}}}},$${{I}_{{\text{н}}}};$ конструктивные характеристики насадки – ${{a}_{{\text{v}}}},$ ${{\varepsilon }_{{{\text{св}}}}},$ ${{d}_{{\text{э}}}}.$ Первое приближение высоты насадочного слоя, например $Н = 1.0{\text{ м}}{\text{.}}$
2. Вычисляется тепловое число единиц переноса (3), которое для насадки представим в более удобной форме
(10)
${{N}_{{\text{г}}}} = \frac{{{{\beta }_{х}}Н{{a}_{{\text{v}}}}{{\psi }_{w}}}}{{{{\rho }_{{\text{г}}}}{{w}_{{\text{о}}}}}}.$Коэффициент массоотдачи ${{\beta }_{х}}$ можно определить экспериментально или вычислить с применением математической модели [22, 23], где основной информацией о насадке является коэффициент гидравлического сопротивления. Коэффициент смачиваемости ${{\psi }_{w}}$ рассчитывается по эмпирическим выражениям в зависимости от материала и конструкции насадки [3, 19].
3. Числа Пекле по жидкой и газовой фазам вычисляются по выражениям для заданного типа насадки [3, 19, 24] и далее находится количество ячеек n и m.
4. По одной из зависимостей (4) или (5) находится эффективность ${{E}_{{\text{г}}}}$ и далее эффективность охлаждения воды по соотношению (9). Находится температура воды на выходе ${{Т}_{{{\text{жк}}}}} = {{Т}_{{{\text{жн}}}}} - $ $ - \,\,{{Е}_{{\text{ж}}}}({{Т}_{{{\text{жн}}}}} - {{Т}_{{{\text{мт}}}}}).$ Если значение ${{Т}_{{{\text{жк}}}}}$ близко к требуемому, то расчет заканчивается, а если нет то изменяются конструктивные характеристики насадки, в первую очередь высота слоя.
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
Для проверки представленных выше выражений использованы экспериментальные данные, полученные авторами на макете градирни с насадкой из вертикальных полиэтиленовых труб с дискретно-регулярной шероховатостью. Диаметр макета градирни 200 мм (внутренний – 190 мм), высота два метра, высота трубчатой насадки Н = = 1.0 м, диаметр труб 50 мм, число труб – 10, удельная поверхность ${{а}_{{\text{v}}}} = 110{\text{ }}{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}};$ ${{\varepsilon }_{{{\text{св}}}}} = 0.95.$
Движение воздуха и воды пленочное противоточное. Начальная температура воды ${{Т}_{{{\text{жн}}}}} = 35{\kern 1pt} - {\kern 1pt} 40^\circ {\text{С}};$ ${{Т}_{{{\text{гн}}}}} = 24{\kern 1pt} - {\kern 1pt} 28^\circ {\text{С}}{\text{.}}$ Плотность орошения от 8.8 до 19.4 м3/(м2 ч), скорость воздуха на поперечное сечение градирни без насадки ${{w}_{{\text{o}}}} = 0.8{\kern 1pt} - {\kern 1pt} 2.5\,\,{\text{м/с}}{\text{.}}$ В эксперименте измерялись температуры воды и воздуха на входе и выходе, влагосодержание на входе и выходе, расходы воздуха и воды, перепад давления. В результате обработки экспериментальных данных получены значения коэффициентов гидравлического сопротивления сухой ${{\xi }_{{{\text{сух}}}}},$ сопротивления орошаемой насадки ${{\xi }_{{{\text{ор}}}}}$ (рис. 1) и объемного коэффициента массоотдачи ${{\beta }_{{x{\text{v}}}}},$ (рис. 2), где
(11)
$\xi = \frac{{2{{d}_{{\text{э}}}}\Delta {{P}_{{\text{г}}}}}}{{H{{\rho }_{{\text{г}}}}{{{({{{{w}_{{\text{о}}}}} \mathord{\left/ {\vphantom {{{{w}_{{\text{о}}}}} {{{\varepsilon }_{{{\text{св}}}}}}}} \right. \kern-0em} {{{\varepsilon }_{{{\text{св}}}}}}})}}^{2}}}};\,\,\,\,{{\beta }_{{хv}}} = \frac{Q}{{{{K}_{r}}{{S}_{{\text{к}}}}H\Delta {{I}_{{{\text{ср}}}}}}},$Рис. 1.
Зависимость коэффициента гидравлического сопротивления вертикальных орошаемых шероховатых пучков труб (насадки) от скорости воздуха: 1 – qж = 8.8 м3/(м2 ч), 2 – qж = 19.4 м3/(м2 ч), 3 – qж = 0; точки экспериментальные данные авторов, сплошные линии – осредненные данные эксперимента.
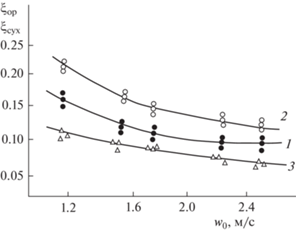
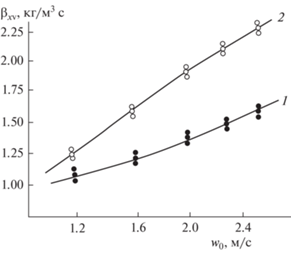
Рис. 2.
Зависимость объемного коэффициента массоотдачи от скорости воздуха. Обозначения на рис. 1. Линии 1, 2 – расчет по выражению (13).
На рис. 1 представлены экспериментальные данные по коэффициентам гидравлического сопротивления насадки из шероховатых труб.
Кривые 1, 2 ${{\xi }_{{{\text{ор}}}}} = f({{q}_{{\text{ж}}}},{{w}_{{\text{о}}}})$ и кривая 3 ${{\xi }_{{{\text{сух}}}}} = f({{w}_{{\text{о}}}})$ аппроксируются эмпирическими зависимостями (±10%)
(12)
${{\xi }_{{{\text{сух}}}}} = \frac{{2.2}}{{\operatorname{Re} _{{{\text{эг}}}}^{{0.38}}}},\,\,\,\,{{\xi }_{{{\text{ор}}}}} = {{\xi }_{{{\text{сух}}}}} + 0.23\frac{{\operatorname{Re} _{{\text{ж}}}^{{0.5}}}}{{\operatorname{Re} _{{{\text{эг}}}}^{{0.45}}}},$Средний поверхностный коэффициент массоотдачи можно вычислить по выражению, полученному на основе теории пограничного слоя и модификации гидродинамической аналогии для шероховатых поверхностей [23]
(13)
${\text{S}}{{{\text{h}}}_{{\text{г}}}} = 0.158\operatorname{Re} _{{\text{ж}}}^{{0.85}}{{\left( {{{{{\xi }_{{{\text{ор}}}}}} \mathord{\left/ {\vphantom {{{{\xi }_{{{\text{ор}}}}}} 8}} \right. \kern-0em} 8}} \right)}^{{0.429}}}{\text{Sc}}_{{\text{г}}}^{{0.33}}.$Выражение (13) применяется для регулярных насадок, как с гладкой поверхностью $({{\operatorname{Re} }_{{{\text{ог}}}}} > 3000),$ так и с поверхностными интенсификаторами $({{\operatorname{Re} }_{{{\text{ог}}}}} > (500{\kern 1pt} - {\kern 1pt} 1000)).$ Объемный коэффициент массоотдачи ${{\beta }_{{х{\text{v}}}}} = {{\rho }_{{\text{г}}}}{{\beta }_{{\text{г}}}}{{a}_{{\text{v}}}}{{\psi }_{w}},$ вычисленный с применением выражению (13) удовлетворительно согласуется с экспериментальными данными (рис. 2), с расхождением ±12–16%.
Экспериментальные данные по структуре потоков не получены, поэтому воспользуемся эмпирическими выражениями для трубчатой насадки из работ [16, 24]. В жидкой фазе (в пленке) выражение для модифицированного числа Пекле имеет вид [19]
(14)
${\text{P}}{{{\text{e}}}_{{\text{ж}}}} = \frac{{{{u}_{{\text{ж}}}}H}}{{{{D}_{{{\text{пж}}}}}}} = A\operatorname{Re} _{{\text{ж}}}^{m}{\text{Ga}}_{d}^{{0.1}}{{({H \mathord{\left/ {\vphantom {H \theta }} \right. \kern-0em} \theta })}^{{0.68}}}.$Коэффициенты A и m зависят от ${{\operatorname{Re} }_{{\text{ж}}}}$
| ${{\operatorname{Re} }_{{\text{ж}}}}$ | A | m |
| 50–340 | 0.0171 | –0.36 |
| 340–1200 | 3.88 × 10–3 | 0.66 |
| 1200–2500 | 0.0367 | –0.24 |
В газовой фазе для регулярной трубчатой насадки [24]
РЕЗУЛЬТАТЫ РАСЧЕТА
При скорости воздуха ${{w}_{{{\text{о}}}}} = 1.2{\text{ м/с}}$ и плотности орошения ${{q}_{{{\text{ж}}}}} = 8.8{\text{ }}{{{{{\text{м}}}^{{\text{3}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{3}}}}} {{\text{(}}{{{\text{м}}}^{{\text{2}}}}\,{\text{ч)}}}}} \right. \kern-0em} {{\text{(}}{{{\text{м}}}^{{\text{2}}}}\,{\text{ч)}}}}$ экспериментально получено: ${{\beta }_{{x{\text{v}}}}} = 1.14{\text{ кг/(}}{{{\text{м}}}^{{\text{3}}}}\,{\text{с);}}$ ${{\xi }_{{{\text{ор}}}}} = 0.168;$ ${{E}_{{\text{ж}}}} = 0.251;$ ${{E}_{{\text{г}}}} = 0.464;$ ${{I}_{{\text{н}}}} = 43.19{\text{ кДж/кг;}}$ ${{Т}_{{{\text{жн}}}}} = 35.0^\circ {\text{С;}}$ ${{Т}_{{{\text{мт}}}}} = 15.4^\circ {\text{С}}{\text{.}}$
Результаты расчета: ${{\operatorname{Re} }_{{\text{ж}}}} = 97;$ ${\text{G}}{{{\text{a}}}_{d}} = 223\,941;$ $\theta = 4.4 \times {{10}^{{ - 5}}},{\text{м;}}$ число ${\text{P}}{{{\text{e}}}_{{\text{ж}}}} = 10.33$ при Н = 1.0 м. Число ${\text{P}}{{{\text{e}}}_{{\text{г}}}} = 30$ при ${{d}_{{\text{э}}}} = 0.035{\text{ м;}}$ Н = 1.0 м. Число ячеек m = 5; n = 15.
Тепловое число единиц переноса
Тепловая эффективность (4) ${{E}_{{\text{г}}}} = 0.49.$ Экспериментально полученное значение ${{E}_{{\text{г}}}} = 0.464.$ Расхождение около 5%, что вполне допустимо для двухфазных сред.
При ${{q}_{{\text{ж}}}} = 19.4{\text{ }}{{{\text{м}}}^{{\text{3}}}}{\text{/(}}{{{\text{м}}}^{{\text{2}}}}\,{\text{ч);}}$ ${{w}_{{\text{о}}}} = 1.2{\text{ м/с}}$ получаем ${{E}_{{\text{г}}}} = 0.523;$ экспериментальное значение ${{E}_{{\text{г}}}} = 0.535.$ Расхождение около 2%.
Далее приведены результаты расчетов ${{E}_{{\text{г}}}}$ для сетчатой трубчатой насадки из полиэтилена в колонке диаметром 200 мм с числом элементов – 18 и высотой слоя Н = 0.4 м, dэ = 0.027 м [25]. При скорости воздуха wо = 1.07 м/с и qж = 4.93 м3/(м2 ч) экспериментально получено тепловое число единиц переноса Nг = 0.542. Расчет числа ячеек показывает n = 6, m = 5. Тогда из (4) имеем ${{E}_{{\text{г}}}} = 0.35.$ Экспериментальное значение ${{E}_{{\text{г}}}} = 0.31.$ Согласование удовлетворительное.
Таким образом, подтверждена адекватность представленной выше математической модели тепловой эффективности для двух типов регулярных трубчатых насадок в интервале wо = = 1.07–2.5 м/с и qж = 4.93–19.8 м3/(м2 ч), т.е. практически во всем рабочем режиме работы пленочных градирен.
Рис. 3.
Зависимость эффективности теплообмена в газовой фазе от скорости воздуха: 1 – qж = 8.8 м3/(м2 ч), 2 – qж = 19.4 м3/(м2 ч). Точки – эксперимент. Сплошные лини – расчет по формулам (4), (5).
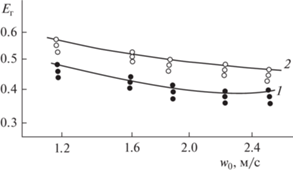
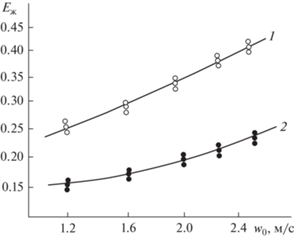
Рис. 4.
Зависимость эффективности охлаждения воды от скорости воздуха при 1 – qж = 8.8 м3/(м2 ч), 2 – qж = 19.4 м3/(м2 ч). Точки – эксперимент; линии расчет по формуле (9) с Ег (4) или (5).
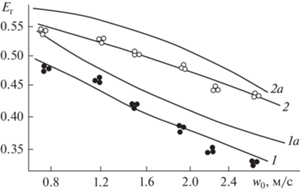
На рис. 5 представлено сравнение экспериментальных и расчетных значений тепловой эффективности исследованной насадки из полиэтиленовых труб с шероховатой поверхностью. Расчеты сделаны по выражениям ячеечной модели (4), (5) и модели идеального вытеснения газа ${{E}_{{\text{г}}}} = 1 - ( - \exp {{N}_{{\text{г}}}}).$ Из расчетов следует, что не учет структуры потока дает завышенные результаты по значениям тепловой эффективности ${{E}_{{\text{г}}}}$ на 8–15% (кривые 1а и 2а) по сравнению с расчетом по ячеечной модели.
Рис. 5.
Зависимость тепловой эффективности в воздушной фазе от скорости воздуха 1 – ${{q}_{{\text{ж}}}} = 8.8$ м3/(м2 ч); 2 – ${{q}_{{\text{ж}}}} = 19,4$ м3/(м2 ч). Точки экспериментальные данные; 1, 2 – расчет по выражениям (4), (5); 1а, 2а – расчет по модели идеального вытеснения.
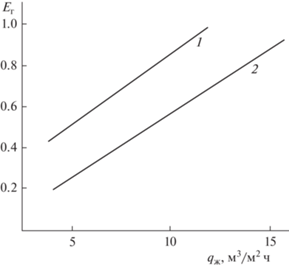
На рис. 6 представлены результаты расчетов по требуемой тепловой эффективности градирни Ег для рекомендуемых в справочниках летних условий эксплуатации в г. Казани. Начальная температура воздуха ${{Т}_{{\text{н}}}} = 26.8^\circ {\text{С;}}$ относительная влажность φ = 43%; температура мокрого термометра ${{Т}_{{{\text{мт}}}}} = 18.7^\circ {\text{С}}{\text{.}}$ Энтальпия воздуха на входе ${{I}_{{\text{н}}}} = 51\,100$ Дж/кг. Начальная температура воды, подаваемая на охлаждение ${{Т}_{{\text{н}}}} = 40^\circ {\text{С;}}$ требуемая конечная температура воды ${{Т}_{{{\text{жк}}}}} = 28^\circ {\text{С}}$ и ${{Е}_{{\text{ж}}}} = 0.56.$ Из рисунка видно, что при увеличении плотности орошения требуемая тепловая эффективность в газовой фазе повышается при заданных температурах воды на выходе ${{Т}_{{{\text{жк}}}}}$ и входе ${{Т}_{{{\text{жн}}}}}.$
Рис. 6.
Зависимость требуемой эффективности охлаждения воды в газовой фазе от плотности орошения при Еж = 0.56: 1 – скорость воздуха wo = 1 м/с; 2 – wo = 2 м/с.
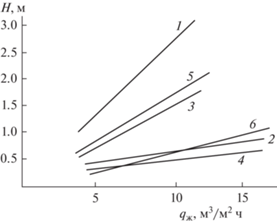
На рис. 7 даны зависимости высоты блоков оросителей для трех конструкций регулярных насадок, которые обеспечивают требуемую тепловую эффективность Ег для заданных выше условий процесса охлаждения воды. Рассмотрены насадки из полиэтиленовой сетки в виде трубок (диаметром 50 мм), насадка из полиэтиленовых элементов 2К МГУИЭ [2] и насадка исследованная авторами в данной работе.
Рис. 7.
Зависимость высоты блока оросителей от режимных параметров градирни для достижения требуемой эффективности Ег при Еж = 0.56; 1, 2 – трубчатая насадка из полиэтиленовой сетки; 3, 4 – насадка 2 КР МГУИЭ [2]; насадка из шероховатых полиэтиленовых труб, исследованная в данной работе. 1, 3, 5 – скорость воздуха ${{w}_{{\text{o}}}} = 1$ м/с; 2, 4, 6 – скорость воздуха ${{w}_{{\text{o}}}} = 2$ м/с.
Насадка из полиэтиленовой сетки имеет удельную поверхность ${{a}_{{\text{v}}}} \approx 140{\text{ }}{{{{{\text{м}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{2}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ и исследована в работе [25].
Регулярная насадка 2КР МГУИЭ (ун-т инженерной экологии) представляет собой пакеты размером 1.0 × 0.5 × 0.5 м, разделение по высоте приставками размером по 1.0 × 0.5 × 0.21 м, выполненных в виде блока регулярно уложенных винтовых элементов из полиэтилена с условным диаметром 70 мм и шагом винта 100 мм. Удельная поверхность насадки 115.2 м2/м3; свободный объем 0.95. Перепад давления сухой и орошаемой насадки дан в работе [2]. Так, пример при скорости воздуха ${{w}_{{\text{o}}}} = 1.0{\text{ м/с}}$ значение ${{\Delta Р} \mathord{\left/ {\vphantom {{\Delta Р} Н}} \right. \kern-0em} Н} = 12{\text{ Па;}}$ при ${{w}_{{\text{o}}}} = 2{\text{ м/с;}}$ ${{\Delta Р} \mathord{\left/ {\vphantom {{\Delta Р} Н}} \right. \kern-0em} Н} = 40{\text{ Па;}}$ при плотности орошения от 5 до 15 м3/(м2 ч). Для сравнения перепад давления исследованной насадки из шероховатых труб при ${{w}_{{\text{o}}}} = 2{\text{ }}{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{c}}}} \right. \kern-0em} {\text{c}}}$ и ${{q}_{{\text{ж}}}} = 8.8{\text{ }}{{{{{\text{м}}}^{3}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{3}}} {({{{\text{м}}}^{2}}{\text{ч}})}}} \right. \kern-0em} {({{{\text{м}}}^{2}}{\text{ч}})}}$ составляет ${{\Delta P} \mathord{\left/ {\vphantom {{\Delta P} H}} \right. \kern-0em} H} = 14{\text{ Па}}{\text{.}}$
Из рис. 6 следует преимущество по тепловой эффективности насадки 2КР МГУИЭ и насадки из шероховатых труб, исследованная авторами в данной работе.
РЕЗУЛЬТАТЫ РАСЧЕТА МИНИ ГРАДИРНИ
На промышленных предприятиях все чаще стали применятся мини градирни, которые характеризуются большими удельными нагрузками по воде и воздуху, а также небольшими габаритами. Тепловая и гидравлическая нагрузки мини градирен могут 2–5 раз превышать нагрузки крупномасштабных градирен. Так как объемы мини градирен относительно небольшие, то в них могут использоваться более конструктивно сложные и дорогостоящие контактные устройства с повышенной эффективностью за счет различных интенсификаторов [1–3, 26–28].
На основе применения представленной математической модели показаны примеры расчетов некоторых современных металлических регулярных насадок [2, 3], для мини градирни, которые в химической технологии в основном применяются в колоннах ректификации и абсорбции.
Примем термодинамические параметры воды и воздуха: ${{T}_{{{\text{жн}}}}} = 38.4$°С; ${{T}_{{{\text{мт}}}}} = 16.7^\circ {\text{С;}}$ ${{I}_{{\text{н}}}} = 47.1$ кДж/кг; $I_{{\text{к}}}^{*} = 147.27$ кДж/кг; ${{Е}_{{\text{ж}}}} = 0.39$. Плотность орошения ${{q}_{{\text{ж}}}} = 22.0$ м3/(м2 ч), скорость воздуха ${{w}_{{\text{о}}}} = 2.2{\text{ м/с}}{\text{.}}$ Требуемая тепловая эффективность (9) ${{Е}_{г}} = 0.791$ при заданной ${{Е}_{{\text{ж}}}} = 0.39.$
Рассмотрим три вида регулярных насадок:
1. Вертикальная металлическая насадка ПИРАПАК (вариант G) [2]. Насадка ПИРАПАК благодаря специальному расположению слоев, создает условия для зигзагообразного движения жидкости и газа. Удельная поверхность ${{а}_{{\text{v}}}} = 180$ м2/м3 (${{d}_{{\text{э}}}} = 0.021$ м).
Из расчетов получаем высоту насадки Н = 0.45 м и перепад давления $\Delta {{Р}_{{{\text{ор}}}}}$ = 55 Па.
2. Сегментная регулярная рулонная насадка “Инжехим” [3], образована сдвоенными листами, один из которых имеет гофры треугольной формы, на сторонах гофров выполнены лепестки в виде круговых сегментов, при этом хорды сегментов смежных сторон гофров расположенных под углом друг к другу. Насадка изготавливается в виде круглого пакета из перфорированных сплошных лент шириной 40 мм методом штамповки с удельной поверхностью 180–480 м2/м3 (в зависимости от размера гофр).
Примем удельную поверхность ${{а}_{{\text{v}}}} = 180$ м2/м3 при свободном объеме ${{\varepsilon }_{{{\text{св}}}}} = 0.95$ (${{d}_{{\text{э}}}} = 0.021$ м). При ${{Е}_{г}} = 0.791$ требуемая высота насадки Н = 0.5 м, перепад давления $\Delta {{Р}_{{{\text{ор}}}}}$ = 50 Па.
3. Регулярная рулонная гофрированная насадка с шероховатой поверхностью (Инжехим) [3], в зависимости от высоты гофры может иметь удельную поверхность 180–350 м2/м3. Для расчетов примем ${{а}_{{\text{v}}}} = 180$ м2/м3. Необходимая высота насадки Н = 0.54 м. Перепад давления имеется значение $\Delta {{Р}_{{{\text{ор}}}}}$ = 43 Па.
Как следует из расчетов все три рассмотренные современные регулярные насадки примерно равнозначные.
В качестве примера в табл. 1 приведены подробные результаты расчетов сегментно-регулярной рулонной насадки “Инжехим” при различной скорости воздуха.
Таблица 1.
Результаты расчета гидравлических и тепломассообменных характеристик мини градирни (qж = 22 м3/м2 ч)
| ${{w}_{{\text{о}}}}{{,}_{{}}}{\text{м/с}}$ | ${{Е}_{{\text{ж}}}}$ | ${{Е}_{{\text{г}}}}$ | ${{\xi }_{{{\text{ор}}}}}$ | ${{\beta }_{х}},\,\,{\text{кг/}}{{{\text{м}}}^{{\text{2}}}}\,{\text{с}}$ | $H,{\text{ м}}$ | $\Delta {{Р}_{{{\text{ор}}}}},\,{\text{Па}}$ |
|---|---|---|---|---|---|---|
| 1.8 | 0.39 | 0.99 | 0.756 | 0.047 | 1.05 | 75 |
| 2.0 | 0.39 | 0.87 | 0.77 | 0.053 | 0.61 | 90 |
| 2.2 | 0.39 | 0.791 | 0.7 | 0.054 | 0.5 | 50 |
| 2.5 | 0.39 | 0.696 | 0.63 | 0.058 | 0.4 | 45 |
| 2.25 | 0.5 | 0.994 | 0.7 | 0.054 | 1.65 | 170 |
| 2.4 | 0.5 | 0.932 | 0.68 | 0.057 | 0.88 | 100 |
| 2.6 | 0.5 | 0.86 | 0.6 | 0.058 | 0.68 | 80 |
| 2.8 | 0.5 | 0.798 | 0.56 | 0.06 | 0.57 | 75 |
Из приведенных расчетов следует, что при ${{Е}_{{\text{ж}}}} = 0.39$ целесообразно проводить охлаждение воды при ${{w}_{{\text{о}}}} = 2.2{\kern 1pt} - {\kern 1pt} 2.5$ м/с, а при заданной эффективности ${{Е}_{{\text{ж}}}} = 0.5$, целесообразная требуемая скорость воздуха в интервале ${{w}_{{\text{о}}}} = 2.6{\kern 1pt} - {\kern 1pt} 2.8$ м/с.
В рассмотренных насадках при ${{w}_{{\text{о}}}} \geqslant 3$ м/с резко возрастает перепад давления, поэтому скорость воздуха в насадочной мини градирне должна быть не выше 2.8 м/с.
ВЫВОДЫ
Повышение эффективности тепломассообменных процессов возможно за счет применения как поверхностных, так и объемных интенсификаторов. В пленочных контактных устройствах наибольшее применение получили поверхностные интенсификаторы в виде различных выступов, накаток, просечек и других завихрителей потоков. При решении таких задач важное значение имеет достоверное определение гидравлического сопротивления, коэффициентов тепломассоотдачи и эффективности явлений межфазного переноса теплоты и массы. Если гидравлическое сопротивление контактных устройств с интенсификаторами практически всегда исследуется экспериментально, как и предельные нагрузки, то методы определения эффективности тепломассообмена имеют как полуэмпирический характер, так и с применением численных или приближенных математических моделей. К приближенным математическим методам относятся модели структуры потоков, активное применение которых началось во второй половине прошлого столетия для насадочных и тарельчатых колонн. Причем применение таких моделей в инженерных расчетах аппаратов обеспечивает достаточно высокую точность определения режимных и конструктивных характеристик при заданных требованиях к проведению процесса. В данной статье наглядно показано применение решения ячеечной модели структуры потока для расчета тепловой эффективности в газовой фазе пленочных блоков градирни, а на основе теплового баланса и определение эффективности охлаждения воды. Причем основными параметрами применяемых выражений являются объемной коэффициент массоотдачи, число единиц переноса и количество ячеек полного перемешивания в газовой и жидкой фазах, которые связаны с числами Пекле обратного перемешивания потоков. Определение данных параметров может выполняться как экспериментальными, так и теоретическими методами. В статье представлены результаты экспериментальных исследований регулярной насадки из вертикального пучка труб с шероховатой поверхностью и показано удовлетворительное согласование результатов расчета тепловой эффективности по ячеечной модели с экспериментом. Таким образом, применение ячеечной модели позволяет учесть структуру потоков в газовой и жидкой фазах в расчетах эффективности пленочных контактных устройств с интенсификаторами и находить рациональные режимные и конструктивных характеристики процесса охлаждения воды в градирнях.
Представленные экспериментальные данные и алгоритм расчета пленочных градирен могут применяться при решении задач их проектирования или модернизации.
Исследование выполнено в рамках научного проекта РНФ 21-79-10406.
УСЛОВНЫЕ ЗНАЧЕНИЯ
| ${{a}_{{\text{v}}}}$ | удельная поверхность насадки, м2/м3 |
| ${{d}_{{\text{э}}}}$ | эквивалентный диаметр насадки, м |
| ${{D}_{{{\text{пг}}}}},{{D}_{{{\text{пж}}}}}$ | коэффициенты обратного перемешивания в газовой и жидкой фазах, м2/с |
| $G$ | массовый расход воздуха, кг/с |
| $dF$ | площадь контакта фаз в элементарном объеме, м2 |
| ${{D}_{{\text{г}}}}$ | коэффициент молекулярной диффузии влаги в воздухе, м2/с |
| ${{I}_{{\text{п}}}}$ | удельная энтальпия пара, Дж/кг |
| $I$ | удельная энтальпия газа, Дж/кг |
| ${{I}_{{\text{н}}}},{\text{ }}{{I}_{{\text{к}}}}$ | начальное и конечное значения удельных энтальпий воздуха, Дж/кг |
| $\Delta {{I}_{{{\text{ср}}}}}$ | средняя движущая вила теплообмена в виде разности энтальпий на входе и выходе насадки, Дж/кг |
| $I_{{\text{к}}}^{ * }$ | значение энтальпии влажного воздуха на выходе из слоя насадки градирни на линии насыщения при начальной температуре воды на входе ${{Т}_{{{\text{жн}}}}}$ |
| $K$ | коэффициент теплопередачи, Вт/(м2 К) |
| $L$ | массовый расход воды, кг/с |
| ${{с}_{{{\text{рж}}}}}$ | удельная теплоемкость воды, Дж/(кг К) |
| $F$ | площадь поверхности контакта фаз, м2 |
| n, m | число ячеек в газовой и жидкой фазах |
| ${{T}_{{\text{г}}}},{\text{ }}{{T}_{{\text{ж}}}}$ | температуры газа и жидкости, °С |
| ${{Т}_{{{\text{мт}}}}}$ | температура окружающего воздуха по смоченному термометру, °С |
| ${{Т}_{{{\text{жн}}}}},{{Т}_{{{\text{жк}}}}}$ | начальная (на входе) и конечная температура воды, °С |
| ${{N}_{{\text{г}}}}$ | тепловое число единиц переноса |
| ${{Q}_{u}}$ | поток теплоты с испарившейся жидкостью, Вт |
| r | удельная теплота парообразования, Дж/кг |
| $\Delta {{P}_{{\text{г}}}}$ | перепад давления, Па |
| ${{S}_{{\text{к}}}}$ | площадь поперечного сечения градирни (макета), м2 |
| ${{w}_{{\text{г}}}}{\text{, }}{{u}_{{\text{ж}}}}$ | средние скорости газа и жидкости, м/с |
| ${{w}_{{\text{о}}}}$ | скорость воздуха на полное сечении градирни (т.е. без насадки), м/с |
| ${{x}_{{\text{н}}}},{\text{ }}{{x}_{{\text{к}}}}$ | начальное и конечное влагосодержание воздуха, кг/кг |
| ${{\beta }_{х}}$ | средний коэффициент массоотдачи, кг/(м2 с) |
| ${{\beta }_{{\text{г}}}}$ | коэффициент массоотдачи в газовой фазе, м/с |
| ${{\rho }_{{\text{г}}}}$ | плотность газа, кг/м3 |
| $\varphi $ | относительное влагосодержание |
| ${{\psi }_{w}}$ | коэффициент смачиваемости поверхности насадки |
| ${{\varepsilon }_{{{\text{св}}}}}$ | свободный объем насадки |
| $\sigma $ | поверхностное натяжение, Н/м |
КОМПЛЕКСЫ
| ${\text{S}}{{{\text{h}}}_{{\text{г}}}} = {{{{\beta }_{{\text{г}}}}{{d}_{{\text{э}}}}} \mathord{\left/ {\vphantom {{{{\beta }_{{\text{г}}}}{{d}_{{\text{э}}}}} {{{D}_{{\text{г}}}}}}} \right. \kern-0em} {{{D}_{{\text{г}}}}}}$ | число Шервуда |
| ${\text{S}}{{{\text{c}}}_{{\text{г}}}} = {{{{v}_{{\text{г}}}}} \mathord{\left/ {\vphantom {{{{v}_{{\text{г}}}}} {{{D}_{{\text{г}}}}}}} \right. \kern-0em} {{{D}_{{\text{г}}}}}}$ | число Шмидта |
| ${{\operatorname{Re} }_{{\text{ж}}}} = {{4{{q}_{{\text{ж}}}}} \mathord{\left/ {\vphantom {{4{{q}_{{\text{ж}}}}} {({{a}_{{\text{v}}}}{{v}_{{\text{ж}}}})}}} \right. \kern-0em} {({{a}_{{\text{v}}}}{{v}_{{\text{ж}}}})}}$ | число Рейнольдса в жидкой фазе |
| ${{\operatorname{Re} }_{{{\text{эг}}}}} = {{{{w}_{{\text{o}}}}{{d}_{{\text{э}}}}} \mathord{\left/ {\vphantom {{{{w}_{{\text{o}}}}{{d}_{{\text{э}}}}} {{{v}_{{\text{г}}}}}}} \right. \kern-0em} {{{v}_{{\text{г}}}}}}$ | число Рейнольдса в газовой фазе |
| ${\text{G}}{{{\text{a}}}_{d}} = {{g{{\chi }^{3}}} \mathord{\left/ {\vphantom {{g{{\chi }^{3}}} {v_{{\text{ж}}}^{2}}}} \right. \kern-0em} {v_{{\text{ж}}}^{2}}}$ | число Галилея |
| ${{K}_{r}} = 1 - {{с}_{{{\text{рж}}}}}{{{{Т}_{{{\text{жн}}}}}} \mathord{\left/ {\vphantom {{{{Т}_{{{\text{жн}}}}}} r}} \right. \kern-0em} r}$ | поправка Меркеля |
| $\chi = \sqrt {{\sigma \mathord{\left/ {\vphantom {\sigma {g{{\rho }_{{\text{ж}}}}}}} \right. \kern-0em} {g{{\rho }_{{\text{ж}}}}}}} $ | капилярная постоянная, м |
| $\theta = {{({{v_{{\text{ж}}}^{2}} \mathord{\left/ {\vphantom {{v_{{\text{ж}}}^{2}} g}} \right. \kern-0em} g})}^{{1/3}}}$ | приведенная толщина пленки, м |
НИЖНИЕ ИНДЕКСЫ
Список литературы
Пушнов А.С., Цурикова Н.П., Шинкунас С. и др. Совершенствование конструкций контактных устройств для градирен / Под об. ред. А.С. Пушнова, А. Сакалаускаса. Санкт-Петербург: ПОЛИТЕХ-ПРЕСС, 2020. 382 с.
Сокол Б.А., Чернышев А.К., Баранов Д.А. Насадки массообменных колонн. Москва: Галилея-принт, 2009. 358 с.
Каган А.М., Лаптев А.Г., Пушнов А.С., Фарахов М.И. Контактные насадки промышленных тепломассообменных аппаратов: Казань: Отечество, 2013. 454 с.
Laptev A.G., Farakhov T.M., Basharov M.M. Processes and apparatuses of chemical technol ogies: modeling and modernization of industrial desulfurizing packed columns at refineries // Chemistry and Technology of Fuels and Oils. 2016. T. 52. № 5. C. 472–479.
Скачков И.В., Бальчугов А.В., Рыжов С.О. Гидродинамические исследования технологии газожидкостных процессов на новой регулярной насадке // Современные технологии. Системный анализ. Моделирование. 2012. № 3(35). С. 147–150.
Ramkumar R., Ragupathy A. Optimization of cooling tower performance with different types of packings using Taguchi approach. J. Braz. Soc. Mech. Sci. Eng. 37. (2015). 929–36.
Rahmati M., Alavi S.R., Tavakoli M.R. Experimental investigation on 486 performance enhancement of forced draft wet cooling towers with special emphasis on the role of stage numbers. Energy Conv Manag. 126. (2016). 971–81.
Raj G., Chandra P., Pathak P.K. Comparative analysis of two different types of fills used in wet cooling tower for higher-scale water with conventional film type fill. Heat Transf-Asian Res. 48. (2019). 493. 4000-15. Г. Радж, П. Чандра, П.К. Патак.
Naik B.K., Muthukumar P. A novel approach for performance assessment of mechanical draft wet cooling towers. Appl. Therm. Eng. 121. (2017). 14–26.
Boyadjiev C.H.R.B., Dzhonova D.B., Popova-Krumova P.G., Stefanova K.V., Pavlenko A.N., Zhukov V.E., Slesareva E.Yu. Liquid wall flow in counter-current column apparatuses for absorption processes with random packings // Bulgarian Chemical Communications. 2020. V. 52. P. 74–79.
Cioncolini A. Pressure drop prediction in annular two-phase flow in macroscale tubes and channels / A. Cioncolini, J.R. Thome // International J. Multiphase Flow. 2017. № 89. P. 321–330.
Ван Л., Ван С., Лу Дж. Исследование модели теплопередачи и влияющих факторов для градирен с поперечным потоком // Журн. прикладных наук и технологий. 14 (2015). 278–82.
Витковская Р.Ф., Пушнов А.С., Шинкунас С. Аэрогидродинамика и тепломассообмен насадочных аппаратов: Лань-Пресс. 2019. 288 с.
Лаптева Е.А., Столярова Е.Ю., Лаптев А.Г. Численное определение эффективности тепломассообмена в пленочной градирне с учетом неравномерности распределения воды и воздуха // Теплоэнергетика. 2020. № 4. С. 52–59.
Дмитриев А.В., Мадышев И.Н., Харьков В.В., Дмитриева О.С., Зинуров В.Е. Экспериментальное исследование влияния наполнителя на теплогидравлические характеристики испарительной градирни. ThermSciEngProg. 22 (2021). 9.
Федяев В.Л., Снигерев Б.А., Моренко И.В., Гайнуллин Р.Ф., Гайнуллина Р.Ф. О модернизации градирен СК-1200 // Известия высших учебных заведений. Проблемы энергетики. 2009. № 5–6. С. 43–51.
Ramkrishnan R., Arumugam R. Experimental study of cooling tower performance using ceramic tile packing // Processing and Application of Ceramics. 7. (2013). 21–7. 15.
Laptev A.G., Lapteva E.A. Mathematical model and thermohydraulic characteristics of packed scrubbers of condensation cooling of a gas // J. Engineering Physics and Thermophysics. 2022. T. 95. № 1. C. 257–265.
Рамм В.М. Абсорбция газов. М.: Химия, 1976.
Пономаренко В.С., Арефьев Ю.И. Градирни промышленных и энергетических предприятий. Москва: Энергоатомиздат, 1998.
Кафаров В.В., Винаров А.Ю., Гордеев Л.С. Моделирование и системный анализ биохимических производств. М.: Лесн. Пром-сть, 1985. 280 с.
Laptev A.G., Lapteva E.A. Mathematical models of friction on the surface of phase separation and heat and mass transfer in film units of cooling-tower sprinklers with intensifiers // Theoretical Foundations of Chemical Engineering. 2021. T. 55. № 5. C. 906–913.
Laptev A.G., Lapteva E.A. Mathematical models and calculation of the coefficients of heat and mass transfer in the packings of mechanical-draft towers // J. Engineering Physics and Thermophysics. 2017. T. 90. № 3. C. 644–650.
Лаптев А.Г., Лаптева Е.А. Определение коэффициентов турбулентного перемешивания в одно- и двухфазных средах по модели Тейлора // Фундаментальные исслед. 2015. № 2–13. С. 2810–2814.
Лаптев А.Г., Ведьгаева И.А. Устройство и расчет промышленных градирен: Казань: КГЭУ, 2004. 180 с.
Bagomedov M.G.-G., Pushnov A.S., Berengarten M.G. Effect of packing type on hydraulic resistance of contact devices // Chemical and Petroleum Engineering. 2019. T. 55. № 5–6. C. 379–383.
Бондарь К.Е. и др. Повышение эффективности тепломассообменных процессов в малогабаритных аппаратах охлаждения воды // Фундаментальные исследования. 2017. № 9. 1. С. 25–29.
Боев Е.В., Афанасенко В.Г., Николаев Е.А., Иванов С.П. Повышение эффективности тепломассообменных насадок промышленных градирен // Газовая промышленность. 2010. № 7(648). С. 85–88.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


