1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 57, № 4, 2023

Теоретические основы химической технологии, 2023, T. 57, № 4, стр. 379-388

Методика расчета предельных и оптимальных режимов химико-энерготехнологического процесса прокалки кускового и окомкованного рудного фосфатного сырья на колосниковой решетке обжиговой конвейерной машины

В. П. Мешалкин a, В. А. Орехов b, М. И. Дли b, В. И. Бобков b, *, Т. Б. Чистякова c

a Российский химико-технологический университет имени Д.И. Менделеева, Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия

b Национальный исследовательский университет “МЭИ”
г. Смоленск, Россия

c Санкт-Петербургский государственный технологический институт (технический университет)
Санкт-Петербург, Россия

* E-mail: vovabobkoff@mail.ru

Поступила в редакцию 22.02.2023
После доработки 26.03.2023
Принята к публикации 20.04.2023

Полный текст (PDF)

Аннотация

В данной работе предложена методика и математическая модель для расчета химико-энерготехнологического процесса обжига рудного фосфатного сырья в движущемся плотном слое на колосниковой решетке обжиговой конвейерной машины. По результатам проведенных вычислительных экспериментов на разработанной компьютерной модели, представлен анализ предельных и оптимальных режимов процессов сушки и обжига кускового и окомкованного рудного фосфатного сырья на конвейере обжиговой машины. Определены предельные условия прокалки кускового и окомкованного рудного сырья при засыпке в виде монослоя кусков, совместном обжиге и в виде слоя фосфоритовых окатышей, с учетом технологических ограничений функционирующих обжиговых конвейерных машин. Для фосфатного рудного сырья установлено, что предельно достижимая степень декарбонизации при высокотемпературном обжиге в виде кусков в обжигово-конвейерной машине составляет 60%. Обжиг в виде окатышей, позволяет обеспечить степень декарбонизации в 80%. Предложенная в настоящей работе методика теплофизических и кинетических исследований может быть распространена на изучение закономерностей термически активируемых эндотермических химико-металлургических процессов прокалки в широком классе железорудных сырьевых материалов. Представленная компьютерная модель для расчета предельных и оптимальных условий функционирования обжиговых конвейерных машин используется для оперативной адаптации промышленных установок, к периодически изменяющимся свойствам рудных сырьевых материалов, поступающих на термическую обработку.

Ключевые слова: температура, рудное сырье, фосфорит, окатыши, прокалка, обжиг, сушка, химико-энерготехнологический процесс, обжиговая конвейерная машина

ВВЕДЕНИЕ

В данной работе предлагается методика численного поиска предельных параметров химико-энерготехнологических процессов сушки и высокотемпературного обжига фосфатного рудного сырья в плотном слое на колосниковой решетке с целью определения оптимальных режимов реализации указанных энергоемких процессов в обжигово-конвейерных технологических аппаратах [1, 2]. Под предельными, понимаются такие режимные условия протекания химико-энерготехнологического процесса прокалки, которые обеспечивают его максимальную эффективность и производительность обжигово-конвейерных технологических аппаратов, работающих на заданном рудном сырье, при высоте и фракционном составе засыпки, учитывающие выполнение технологических ограничений [3, 4]. Так как скорости процессов сушки, высокотемпературного обжига и спекания при термической подготовке возрастают с повышением температуры, предельные условия будут достигаться, если нагрев плотного слоя рудного сырья до требуемой или предельно допустимой температуры происходит наикратчайшим путем и при этой температуре материал выдерживается в течении времени, необходимого для завершения термически активируемых химико-энерготехнологических процессов обжига [5, 6]. При этом температура газов на входе в слой $T_{g}^{*}$ не должна превышать предельно допустимых для данного аппарата значений $T_{g}^{{*\,\max }}$. Ограничения накладываются и на температуру газов, покидающих слой $T_{g}^{{*{\kern 1pt} *}}$ согласно условиям безаварийной работы колосниковой решетки. Максимальные скорости прососа газов в предельных режимах должны обеспечиваться производительностью тяго-дутьевых установок – эксгаустеров обжиговой конвейерной машины [7, 8].

Определенные ограничения на предельный режим функционирования обжигово-конвейерной машины накладывают специфические особенности обрабатываемого фосфатного рудного сырья [9, 10]. В частности, температура, поступающего в зону сушки, греющего газа, не должна превышать некоторого заданного значения – $T_{d}^{*}$, во избежание разрушения зерен кускового или окомкованного рудного сырья парами воды, образующимися при дегидрации кристаллогидратов и испарения физической влаги [11, 12]. То есть, повышение $T_{g}^{{*\,\max }}$ выше $T_{d}^{*}$, может осуществляться при достижении заданной степени сушки ${{\alpha }}_{w}^{z}$. Перепад температур в зернах дисперсного рудного материала, вызванный нестационарными условиями нагрева и протеканием эндотермических химико-энерготехнологических процессов, не должен превышать, допустимых условиями термической прочности значений [13, 14].

ПОСТАНОВКА ЗАДАЧИ ПОИСКА ОПТИМАЛЬНЫХ УСЛОВИЙ ОБЖИГА

Таким образом, определение предельных условий реализации процессов прокалки сводится к поиску таких зависимостей $T_{g}^{*}\left( {{\tau }} \right)$ и ${{\omega }_{g}}\left( \tau \right)$, которые удовлетворяли бы следующим условиям:

(1)
$\frac{{dT_{g}^{*}}}{{d\tau }} \to \max ,$
(2)
$T_{g}^{{*{\kern 1pt} *}} \to T_{r}^{{\max }},$
(3)
${{\omega }_{g}} \to \omega _{g}^{{\max }},$
при выполнении ограничений:
(4)
$T_{g}^{*} \leqslant T_{r}^{{*\,\max }},$
(5)
$T_{g}^{{*{\kern 1pt} *}} \leqslant T_{r}^{{\max }},$
(6)
$\Delta T_{m}^{{}} \leqslant \Delta T_{m}^{{\max }},$
(7)
${{\omega }_{g}} \leqslant \omega _{g}^{{\max }},$
где: $\omega _{g}^{{\max }}$ – максимальная скорость прососа газов, $T_{r}^{{\max }}$ – предельная температура газов на колосниковой решетке, $\Delta T_{m}^{{}},\;\;\Delta T_{m}^{{\max }}$ – текущий и предельный перепады температур в зерне рудного материала.

Учитывая, что плотный слой по каналу воздействия – скорость газов – температура газов на выходе из слоя характеризуется распределенностью параметров и значительной инерционностью, условие (2) с ограничением (5) сформируется следующим образом в уравнение:

(8)
$\Theta \frac{{dT_{g}^{{*{\kern 1pt} *}}}}{{d\tau }} + \left( {T_{g}^{{*{\kern 1pt} *}} - T_{r}^{{\max }}} \right) = 0,$
где: $\Theta $ – постоянная времени процесса прокалки – может быть определена если задаться длительностью процесса ${{{{\tau }}}_{p}}$ и относительной величиной недогрева:
(9)
$\Delta = {{\left. {\frac{{T_{r}^{{\max }} - T_{g}^{{*{\kern 1pt} *}}}}{{T_{r}^{{\max }} - T_{m}^{0}}}} \right|}_{{{{\tau }} = {{{{\tau }}}_{p}}}}},$
где: $T_{m}^{0}$ – начальная температура рудного материала.

Тогда из условия (8), можно определить $\Theta = - \frac{{{{{{\tau }}}_{p}}}}{{\ln \Delta }}$.

При постановке численного поиска, с целью упрощения задачи скорость повышения температуры газа на входе в слой, условие (1), задавалась постоянной. Ее значение определялось на основании допущения о том, что скорость повышения температуры зерен рудного материала не превышает температуры газа теплоносителя [15, 16]. Тогда с учетом ограничений, функция $T_{g}^{*}\left( {{\tau }} \right)$ примет вид:

(10)
$T_{g}^{*}\left( {{\tau }} \right) \leqslant T_{d}^{*},\,\,\,\,{\text{при}}\,\,\,\,{\text{0 < }}\,\,\alpha _{w}^{{}} \leqslant \alpha _{w}^{z},$,
(11)
$\begin{gathered} \frac{{dT_{g}^{*}}}{{d\tau }} = \frac{{\Delta T_{m}^{{\max }} \cdot 6{{a}^{{\min }}}}}{{{{X}^{2}}}} = {\text{const,}} \\ {\text{при}}\,\,\,\,T_{d}^{*} < T_{g}^{*} < T_{g}^{{*\,\max }}, \\ \end{gathered} $
где: ${{a}^{{\min }}}$ – минимальное значение коэффициента температуропроводности в интервале температур обжига.

С учетом принятых допущений, определение предельных режимов сводится к определению момента времени, в который выполняется условие (10) и определение вида функции ${{\omega }}_{g}^{{}}\left( {{\tau }} \right)$, при котором процесс обжига протекает с минимальным отклонением от функции (8).

Поиск предельных режимов осуществлялся путем численных решений системы дифференциальных уравнений в частных производных вида:

(12)
$\left\{ \begin{gathered} \rho {{C}_{p}}\left( {{{T}_{m}},{{\alpha }_{W}},{{\alpha }_{1}},{{\alpha }_{2}}} \right)\frac{{\partial {{T}_{m}}}}{{\partial \tau }} = \frac{\partial }{{\partial x}}\left( {\lambda \left( {{{T}_{m}}} \right)\frac{{\partial {{T}_{m}}}}{{\partial x}}} \right) - \hfill \\ - \,\,\left( {C_{1}^{0}Q_{1}^{0}\frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }} + C_{2}^{0}Q_{2}^{0}\frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }} + {{W}^{0}}Q_{W}^{0}\frac{{\partial {{\alpha }_{W}}}}{{\partial \tau }}} \right); \hfill \\ \frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }} = {{k}_{{01}}}\exp \left( { - \frac{{{{E}_{1}}}}{{R{{T}_{m}}}}} \right){{f}_{1}}\left( {{{\alpha }_{1}}} \right); \hfill \\ \frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }} = {{k}_{{02}}}\exp \left( { - \frac{{{{E}_{2}}}}{{R{{T}_{m}}}}} \right){{f}_{2}}\left( {{{\alpha }_{2}}} \right); \hfill \\ \frac{{\partial {{\alpha }_{W}}}}{{\partial \tau }} = {{k}_{{0W}}}\exp \left( { - \frac{{{{E}_{W}}}}{{R{{T}_{m}}}}} \right){{f}_{W}}\left( {{{\alpha }_{W}}} \right). \hfill \\ \end{gathered} \right.$

При этом начальные условия принимают вид:

(13)
$\begin{gathered} {{T}_{m}}\left( {x,0} \right) = T_{m}^{0};\,\,\,\,{{\alpha }_{1}}\left( {x,0} \right) = 0; \hfill \\ {{\alpha }_{2}}\left( {x,0} \right) = 0;\,\,\,\,{{\alpha }_{W}}\left( {x,0} \right) = 0; \hfill \\ \end{gathered} $
граничные условия принимают вид:

(14)
$\begin{gathered} \lambda \left( {{{Т}_{m}}} \right){{\left( {\frac{{\partial {{Т}_{m}}}}{{\partial x}}} \right)}_{{x = X}}} = {{K}_{F}}{{\left( {{{T}_{g}} - {{Т}_{m}}} \right)}_{{x = X}}}, \\ {{\left( {\frac{{\partial {{T}_{m}}}}{{\partial x}}} \right)}_{{x = 0}}} = 0. \\ \end{gathered} $

Здесь: α – степень превращения, а именно отношение $\alpha = 1 - {{G\left( \tau \right)} \mathord{\left/ {\vphantom {{G\left( \tau \right)} {{{G}_{0}}}}} \right. \kern-0em} {{{G}_{0}}}}$, где G0 – количество карбонатного вещества, вступающего в реакцию, G(τ) – количество не прореагировавшего вещества за время τ, α1 – степень превращения MgCO3, α2 – степень превращения СаСО3. MgCO3 → MgO + + CO2 – $Q_{1}^{0}$ и СаСО3 → CaO + CO2 – $Q_{2}^{0}$, где $Q_{1}^{0}$ = = 1.21 × 105 Дж/моль – тепловой эффект реакции разложения MgCO3, $Q_{2}^{0}$ = 1.78 × 105 Дж/моль – тепловой эффект реакции разложения CaCO3. $C_{1}^{0}$, $C_{2}^{0}$ – начальные концентрации карбонатов магния и кальция соответственно, кг/м3, E1, E2 – энергии активации диссоциации карбонатов, Дж/моль, k01, k02 – предэкспоненциальные множители. Аналогично, для процесса сушки, представленным уравнением Арениуса: ${{{{\alpha }}}_{W}}$ – степень сушки, ${{W}^{0}}$ – начальное влагосодержание, кг/м3, $Q_{W}^{0}$ – удельная теплота парообразования, ${{k}_{{0W}}}$ и ${{E}_{W}}$ – предэкспоненциальный множитель и энергия активации процесса сушки. Вид функций ${{f}_{1}}\left( {{{\alpha }_{1}}} \right)$, ${{f}_{2}}\left( {{{\alpha }_{2}}} \right)$, ${{f}_{W}}\left( {{{\alpha }_{W}}} \right)$ также считается известным. x – координата по толщине пластины с полутолщиной X, $x \in \left[ { - X;X} \right]$, R – универсальная газовая постоянная, T – температура, ${{\lambda }}$ – удельная теплопроводность, $\rho $ – плотность. В настоящей работе предполагается известной зависимость объемной теплоемкости от температуры и степеней превращения, она имеет вид:

(15)
$\begin{gathered} \rho {{C}_{p}}\left( {{{T}_{m}},{{\alpha }_{W}},{{\alpha }_{1}},{{\alpha }_{2}}} \right) = \rho {{C}_{p}}{{\left( {{{Т}_{m}}} \right)}^{o}} + \\ + \,\,\left[ {\rho {{C}_{p}}{{{\left( {{{Т}_{m}}} \right)}}^{c}} - \rho {{C}_{p}}{{{\left( {{{Т}_{m}}} \right)}}^{o}}} \right]\left( {1 - {{\alpha }_{\Sigma }}} \right) + \\ + \,\,\rho {{C}_{p}}\left( {{{Т}_{m}}} \right)\left( {1 - {{\alpha }_{W}}} \right), \\ \end{gathered} $
где ${{{{\alpha }}}_{\Sigma }} = 0.5\left( {{{{{\alpha }}}_{1}} + {{{{\alpha }}}_{2}}} \right)$ – суммарная степень превращения (декарбонизации), ${{\rho }}{{C}_{p}}{{\left( {{{Т}_{m}}} \right)}^{c}}$, ${{\rho }}{{C}_{p}}{{\left( {{{Т}_{m}}} \right)}^{o}}$ – температурные зависимости объемной теплоемкости необожженного $\left( {{{{{\alpha }}}_{1}}\,\,{\text{ = }}\,\,{{{{\alpha }}}_{2}} = 0} \right)$ и нацело обожженного $\left( {{{{{\alpha }}}_{1}}\,\,{\text{ = }}\,\,{{{{\alpha }}}_{2}} = 1} \right)$ рудного материала, соответственно. Выбор линейного вида функции (15) основывается на свойстве аддитивности теплоемкости смеси [17, 18].

Условия нагрева плотного слоя рудного фосфатного сырья в обжиговой машине могут быть воспроизведены заданием переменных во времени температур газа-теплоносителя на входе в слой ${{\left( {{{T}_{g}}} \right)}_{{y = 0}}} = {{T}_{g}}\left( {{\tau }} \right)$ и скорости газа-теплоносителя на полное сечение аппарата ${{{{\omega }}}_{g}} = {{{{\omega }}}_{g}}\left( {{\tau }} \right)$.

Для расчета распределения температуры газа-теплоносителя по высоте слоя использовалась зависимость

(16)
${{\omega }_{g}}\left( \tau \right){{\rho }_{g}}\left( Т \right){{С}_{{р\,g}}}\left( Т \right)\frac{{d{{T}_{g}}}}{{dy}} = Q,$
где: Q – тепло, воcпринимаемое слоем рудного материала, включает в себя тепловые потоки, расходуемые на нагрев материала и покрытие эндотермических эффектов гетерогенных превращений. Значение определяется из решения внутренней задачи теплообмена пластины, толщиной 2X

$\begin{gathered} Q = \int\limits_0^{2X} {\left( {\rho {{С}_{р}}\left( Т \right)\frac{{dT}}{{d\tau }} + Q_{1}^{0}C_{1}^{0}\frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }}} \right.} + \\ + \,\,\left. {Q_{2}^{0}C_{2}^{0}\frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }} + Q_{W}^{0}{{W}^{0}}\frac{{\partial {{\alpha }_{W}}}}{{\partial \tau }}} \right)dx. \\ \end{gathered} $

В конечных разностях уравнение (16) имеет вид:

(17)
${{\omega }_{g}}\left( \tau \right){{\rho }_{g}}\left( Т \right){{С}_{{р\,g}}}\left( Т \right)\frac{{\left( {{{T}_{g}}_{i} - {{T}_{g}}_{{i - 1}}} \right)}}{{\Delta {{Y}_{i}}}} = {{Q}_{i}},$
где ${{Q}_{i}}$ определяется с учетом принятой физической модели

$\begin{gathered} {{Q}_{i}} = \frac{{\Delta {{Y}_{i}}}}{{2X}}\left( {1 - \varepsilon } \right)\int\limits_0^{2X} {\left( {\rho {{С}_{р}}\left( Т \right)\frac{{dT}}{{d\tau }} + Q_{1}^{0}C_{1}^{0}\frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }}} \right. + } \hfill \\ \left. { + \,\,Q_{2}^{0}C_{2}^{0}\frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }} + Q_{W}^{0}{{W}^{0}}\frac{{\partial {{\alpha }_{W}}}}{{\partial \tau }}} \right)dx. \hfill \\ \end{gathered} $

Выражение (17) используется для определения температур газа-теплоносителя в плотном слое:

${{T}_{g}}_{i} = {{T}_{g}}_{{i - 1}} + \frac{{{{Q}_{i}}\Delta {{Y}_{i}}}}{{{{{{\omega }}}_{g}}\left( {{\tau }} \right){{{{\rho }}}_{g}}\left( Т \right){{С}_{{р\,g}}}\left( Т \right)}}.$

МЕТОДИКА ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ

Для вычислительного поиска бала создана компьютерная модель на языке Borland C++. Вид зависимости ${{\omega }_{g}}\left( \tau \right)$ определялся путем минимизации отклонения от функции, определяемой уравнением (8). Для этого изменения скорости газа теплоносителя в каждый момент времени определялись из условия:

$\Theta \frac{{dT_{g}^{{*{\kern 1pt} *}}}}{{d\tau }} + \left( {T_{g}^{{*{\kern 1pt} *}} - T_{r}^{{\max }}} \right) = K\frac{{d\omega _{g}^{{}}}}{{d\tau }},$
где: K – коэффициент, определяемый опытным путем.

Вычислительные эксперименты проводились с использованием разработанной компьютерной модели, на основе представленной методики численного поиска, проводились вычислительные эксперименты. Анализ результатов многочисленных вычислительных экспериментов показал влияние на эффективность энергоемкого процесса обжига монослоя кускового рудного сырья: температуры греющего газа и высоты слоя засыпки рудного сырья на колосниковую решетку обжиговой конвейерной машины [19, 20]. Определены оптимальные условия реализации химико-энерготехнологического процесса обжига монослоя, а также сушки и прокалки окомкованного рудного фосфатного сырья на постели кускового фосфорита, в плотном слое на конвейере обжиговой машины [21, 22]. Обоснованы также, оптимальные условия сушки и обжига окомкованного рудного фосфатного сырья на постели из обожженных фосфоритовых окатышей, применительно к обжиговой машине ОК-108. Все варианты расчетов проведены для слоя со средним размером зерен 0.025 м. В вычислительных экспериментах использовались теплофизические, кинетические закономерности процессов сушки и обжига, полученные ранее авторами [23, 24] для кускового и окомкованного фосфорита, из рудной породы – фосфатно-глинисто-кремнистого сланца, химический состав которого представлен в табл. 1.

Таблица 1.

Химический анализ образца – фосфатно-глинисто-кремнистого сланца, содержание компонентов, %

P2O5 CaO MgO CO2 SiO Al2O3 K2O Na2O Fe2O3 Прочие ρ, кг/м3
21.7 44.2 8.0 19.1 2.9 0.3 0.2 0.5 0.7 2.4 2850 до обжига
2300 после обжига

Анализ результатов экспериментов. Результаты вычислительных экспериментов представлены графически.

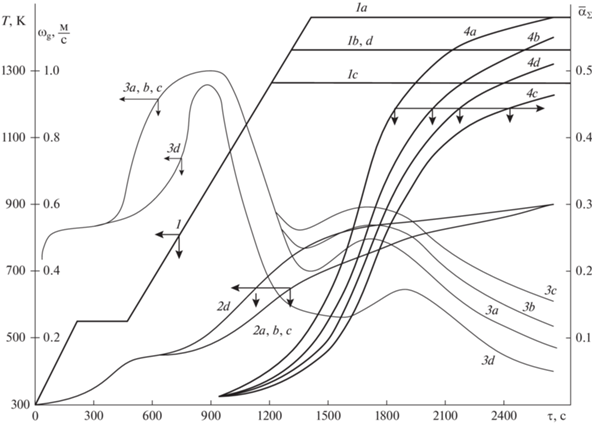
На рис. 1 приведены результаты четырех вычислительных экспериментов по определению предельных режимов обжига монослоя кускового фосфорита в зависимости от высоты слоя засыпки и температуры греющего газа [25, 26]. Кривые 1 и 2 соответствуют расчетным температурам газа-теплоносителя на входе и выходе из слоя, соответственно. Кривая 3 соответствует расчетным значениям скорости прососа нагревающих газов. Средние значения по слою степени декарбонизации сырья, соответствующие вычислительным экспериментам, отмечены кривыми 4.

Рис. 1.

Предельные режимы обжига кускового фосфорита – фосфатно-глинисто-кремнистого сланца. 1, 2 – температуры греющих газов на входе и выходе из слоя, соответственно; 3 – скорость подачи газа теплоносителя; 4 – средняя по слою степень декарбонизации; варианты a, b, c – соответствуют температурам газа на входе в слой: 1473 К, 1373 К, 1273 К, соответственно, при высоте засыпки 0.5 м; вариант d – соответствует температуре газа теплоносителя 1373 К, при высоте засыпки 0.35 м.

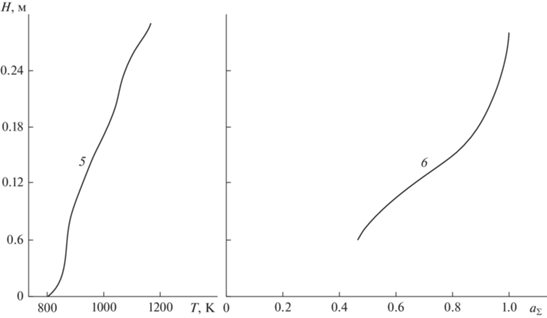
На рис. 2 приведены распределения температур рудного материала и степеней превращения по высоте слоя, соответствующие окончанию процесса обжига τ = 2650 с. Обжиг считался законченным при достижении температурой уходящих газов значения: $T_{g}^{{*{\kern 1pt} *}}\left( {{\tau }} \right) = T_{r}^{{\max }} - \Delta $, где Δ = 20 К, $T_{r}^{{\max }}$ = 923 К.

Рис. 2.

Распределение температуры и степени декарбонизации по высоте слоя в конце процесса обжига τ = 2650 с. 5 – температура материала, 6 – степень декарбонизации, буквенные индексы соответствуют рис. 1.

Вычислительные эксперименты показывают, что предельно достижимые степени декарбонизации для принятых условий и при предельных параметрах, соответствующих функционирующим обжиговым машинам составляют около 60%. Установлено, что увеличение высоты засыпки незначительно повышает качество обожженного рудного материала. Повышение температуры греющего газа в пределах 1273–1473 К позволяет интенсифицировать химико-энерготехнологический процесс обжига. Предельные степени декарбонизации возрастают при этом на 15%. Из числа приведенных режимов, наиболее эффективным следует считать режим 1a, соответствующий обжигу слоя рудного материала, высотой 0.5 м, нагреваемым газом теплоносителем с предельной температурой 1474 К. Он позволяет получать наиболее качественно обожженный рудный материал при максимальной производительности аппарата. Зависимости температуры и скорости прососа газов от времени, соответствующие этому режиму, могут рассматриваться как оптимальные для принятого в вычислительных экспериментах рудного фосфатного сырья.

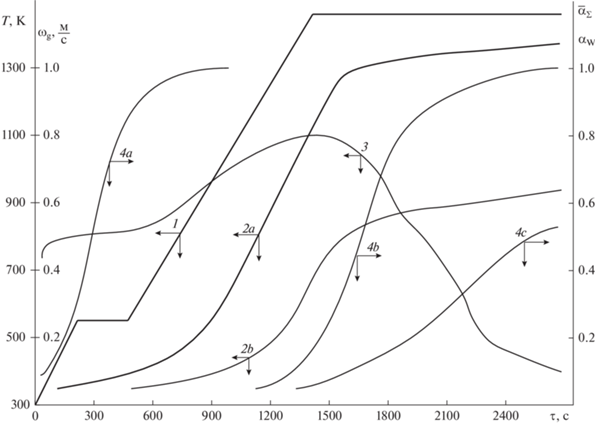
На рис. 3 приведены результаты расчетов оптимальных условий сушки и обжига окомкованного сырья – фосфоритовых окатышей (высота засыпки 0.4 м) и постели кускового фосфорита (высота засыпки 0.1 м) при технологических ограничениях, соответствующих действующим обжиговым конвейерным машинам.

Рис. 3.

Оптимальный режим обжига фосфоритовых окатышей на “постели” кускового фосфорита. 1, 2a, 2b – температуры греющих газов на входе, границы окатышей и на выходе из слоя, соответственно; 3 – скорость подачи газа теплоносителя; 4a, 4b и 4c – кривые сушки, средней по слою степени декарбонизации фосфоритовых окатышей и “постели”, соответственно.

Распределения температур материала по высоте слоя и степени декарбонизации, по окончании процесса обжига τ = 2650 с, показаны на рис. 4. Реализация расчетного режима на обжиговой машине позволит получать практически нацело обожженные и упрочненные окатыши. При этом средняя степень декарбонизации кускового фосфатного сырья составит 50%.

Рис. 4.

Распределение температуры материала и степени декарбонизации по высоте слоя в конце процесса обжига τ = = 2650 с. Совместный обжиг. 5 – температура материала, 6 – степень декарбонизации.

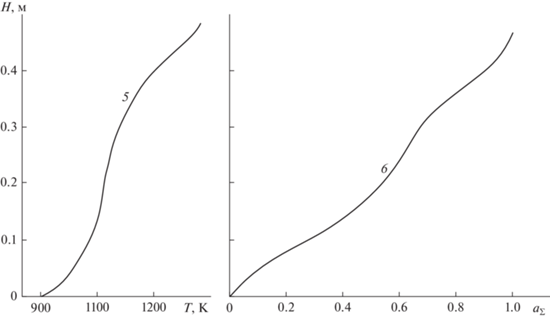
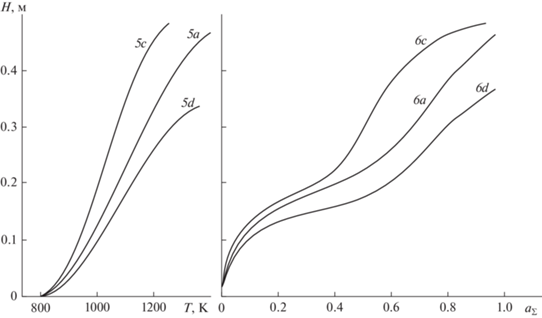
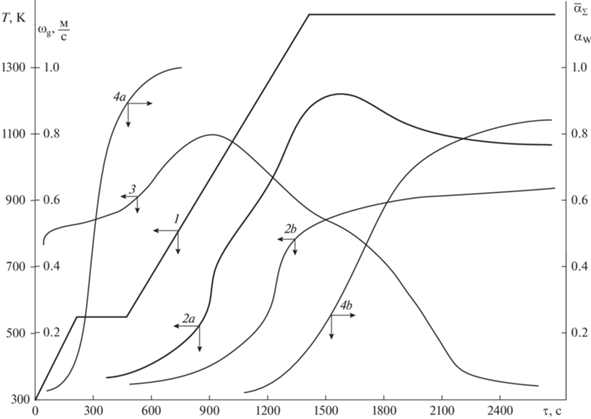
Результаты расчетов оптимальных условий сушки и обжига окомкованного рудного фосфатного сырья (высота засыпки 0.24 м) на постели обожженных окатышей (высота засыпки 0.06 м) приведены на рис. 5, 6. В расчетах предельная температура газов, покидающих слой, принималась равной 1073 К, что соответствует технологическим ограничениям действующих обжиговых конвейерных машин [24]. Расчеты показывают, что реализация оптимального режима позволяет получать фосфоритовые окатыши со средней степенью декарбонизации около 80%. При этом только 65% окатышей прокаливается до температуры выше 1150 К, соответствующей началу спекания. Таким образом, 35% готовых фосфоритовых окатышей будет иметь неудовлетворительное качество.

Рис. 5.

Оптимальный режим обжига фосфоритовых окатышей на “постели” из отожженных окатышей в машине типа ОК. 1, 2a, 2b – температуры греющих газов на входе, на границе сырых окатышей и на выходе из слоя, соответственно; 3 – скорость подачи газа теплоносителя; 4a, 4b – кривые степени сушки, средней по слою степени декарбонизации окатышей соответственно.

Рис. 6.

Распределение температуры материала и степени декарбонизации по высоте слоя в конце процесса обжига фосфоритовых окатышей. 5 – температура материала, 6 – степень декарбонизации.

ЗАКЛЮЧЕНИЕ

Разработана методика и компьютерная модель вычислительного поиска предельных и оптимальных режимов сложного химико-энерготехнологического процесса прокалки. Определены оптимальные режимы обжига кускового рудного фосфатного сырья и окатышей на постели кускового материала применительно к современным обжиговым машинам конвейерного типа.

Научно обосновано, что наиболее высокая степень декарбонизации фосфатного рудного сырья достигается прокалкой в обжиговой машине конвейерного типа в полученном оптимальном режиме. Следует отметить, что измельчение и последующее окомкование фосфоритового рудного сырья, а также присадки связующих материалов, способствуют снижению температур размягчения рудного сырья, что может в дальнейшей переработке отрицательно повлиять на работу верхней зоны фосфорной рудотермической печи.

Методика численного поиска и разработанная компьютерная модель могут использоваться для оперативной режимной адаптации промышленных установок обжига к теплофизическим, реакционным и прочностным свойствам рудного фосфатного сырья.

Исследование проведено при финансовой поддержке РНФ в рамках научного проекта № 21-79-30029.

ОБОЗНАЧЕНИЯ

α степень реагирования реакции декарбонизации
${{\omega }}$ скорость газа-теплоносителя, м/с
λ коэффициент теплопроводности, Вт/м К
ρ плотность, кг/м3
τ время, с
ε порозность плотного слоя
Т температура, К
x координата
${{C}_{p}}$ удельная теплоемкость, Дж/(кг K)
$C_{i}^{0}$ начальная концентрация карбонатов
$Q$ количество теплоты, Дж
$Q_{i}^{0}$ тепловой эффект декарбонизации, Дж/моль
X полутолщина пластины, м
H высота плотного слоя, м
G количество прореагировавшего вещества, моль
k0 предэкспоненциальный множитель, с–1
${{{{\alpha }}}_{W}}$ степень сушки
${{W}^{0}}$ начальное влагосодержание, кг/м3
$Q_{W}^{0}$ удельная теплота парообразования, Дж/моль

ИНДЕКСЫ

i номер компонента в смеси карбонатов
g газ
m рудный материал
W процесс сушки

Список литературы

  1. Самарский А.П. Динамическое моделирование непрерывных технологических процессов в среде LABVIEW // Российский химический журн. (Журн. Рос. хим. об-ва). 2022. Т. 66. № 2. С. 8–15.

  2. Meshalkin V.P., Dovì V.G., Bobkov V.I., et al. State of the art and research development prospects of energy and resource-efficient environmentally safe chemical process systems engineering // Mendeleev Communications, 2021. 31(5). P. 593–604.

  3. Самотылова С.А., Торгашов А.Ю. Применение физически обоснованной математической модели массообменного технологического процесса для повышения точности оценивания качества конечного продукта // Теоретические основы химической технологии. 2022. Т. 56. № 3. С. 379–396.

  4. Zhu X., Ji Y. A digital twin–driven method for online quality control in process industry // International J. Advanced Manufacturing Technology. 2022. 119(5–6). P. 3045–3064.

  5. Егоров А.Ф., Савицкая Т.В., Михайлова П.Г. Современное состояние в области анализа, синтеза и оптимального функционирования многоассортиментных цифровых химических производств: аналитический обзор // Теоретические основы химической технологии. 2021. Т. 55. № 2. С. 154–187.

  6. Орехов В.А., Бобков В.И. Особенности исследования термической деструкции карбонатов в окомкованных фосфоритах при высокотемпературном обжиге // Тепловые процессы в технике. 2022. Т. 14. № 12. С. 555–562.

  7. Акулич П.В., Слижук Д.С. Тепломассоперенос в плотном слое при дегидратации коллоидных и сорбционных капиллярно-пористых материалов в условиях нестационарного радиационно-конвективного энергоподвода // Теоретические основы химической технологии. 2022. Т. 56. № 2. С. 148–157.

  8. Zhu X., Ji Y. A digital twin–driven method for online quality control in process industry // International J. Advanced Manufacturing Technology. 2022. 119(5–6). P. 3045–3064.

  9. Борисов В.В., Курилин С.П., Луферов В.С. Нечеткие реляционные когнитивные темпоральные модели для анализа и прогнозирования состояния сложных технических систем // Прикладная информатика. 2022. Т. 17. № 1(97). С. 27–38.

  10. Трушин А.М., Носырев М.А., Равичев Л.В., Фролова С.И., Яшин В.Е., Ильина С.И. Сочетание вариационного и эмпирического методов определения порозности при осаждении сферических частиц // Теоретические основы химической технологии. 2022. Т. 56. № 2. С. 205–208.

  11. Meshalkin V., Bobkov V., Dli M., Dovì V. Optimization of energy and resource efficiency in a multistage drying process of phosphate pellets // Energies. 2019. T. 12. № 17. C. 3376.

  12. Пучков А.Ю., Лобанева Е.И., Култыгин О.П. Алгоритм прогнозирования параметров системы переработки отходов апатит-нефелиновых руд // Прикладная информатика. 2022. Т. 17. № 1(97). С. 55–68.

  13. Буткарев А.А., Вербыло С.Н., Бессмертный Е.А., Буткарева Е.А. Совершенствование и практическое использование методологии ВНИИМТ для оптимизации теплотехнических схем обжиговых конвейерных машин с рабочими площадями 278, 306 и 552 м2 // Сталь. 2020. № 5. С. 7–13.

  14. Wang S., Guo Y., Zheng F., Chen F., Yang L. Improvement of roasting and metallurgical properties of fluorine-bearing iron concentrate pellets // Powder Technology. 2020. 376. P. 126–135.

  15. Цирлин А.М., Гагарина Л.Г., Балунов А.И. Синтез теплообменных систем, интегрированных с технологическим процессом // Теоретические основы химической технологии. 2021. Т. 55. № 3. С. 347–358.

  16. Matyukhin V.I., Yaroshenko Y.G., Bragin V.V. Sintered iron-ore manufacturing capabilities when using combined fuel // Steel in Translation. 2019. T. 49. № 11. C. 771–777.

  17. Ming Yan, Xinnan Song, Jin Tian, Xuebin Lv, Ze Zhang, Xiaoyan Yu and Shuting Zhang. Construction of a new type of coal moisture control device based on the characteristic of indirect drying process of coking coal // Energies 2020. 13(16), 4162.

  18. Деревянко М.С., Кондратьев А.В. Исследование фазовых превращений и термодинамических свойств оксидных систем // Известия высших учебных заведений. Черная металлургия. 2022. Т. 65. № 3. С. 188–189.

  19. Nayak D., Ray N., Dash N., et al. Induration aspects of low-grade ilmenite pellets: Optimization of oxidation parameters and characterization for direct reduction application // Powder Technology. 2021. 380. P. 408–420.

  20. Савельев С.Г., Кондратенко М.Н. Системное исследование технологических параметров, определяющих интенсивность агломерационного процесса // Известия высших учебных заведений. Черная металлургия. 2021. Т. 64. № 3. С. 184–191

  21. Belyakov N.V., Nikolina N.V. Plant protection technologies: From advanced to innovative // J. Physics: Conference Series. 2021. 1942(1), 012072.

  22. Meshalkin V.P., Bobkov V.I., Dli M.I., Orekhov V.A., Garabadzhiu A.V. Heat Conductivity of a Composite Phosphate Ore Material with Reacting Carbonate Inclusions // Theoretical Foundations of Chemical Engineering, 2022. V. 56. № 6. P. 971–977.

  23. Meshalkin V.P., Bobkov V.I., Dli M.I., Fedulov A.S., Shinkevich A.I. Computer-assisted decision-making system of optimal control over the energy and resource efficiency of a chemical energotechnological system for processing apatite-nepheline ore wastes // Theoretical Foundations of Chemical Engineering. 2021. V. 55. № 1. P. 62–69.

  24. Пучков А.Ю., Дли М.И., Прокимнов Н.Н., Шутова Д.Ю. Многоуровневые алгоритмы оценки и принятия решений по оптимальному управлению комплексной системой переработки мелкодисперсного рудного сырья // Прикладная информатика. 2022. Т. 17. № 6. С. 102–121.

  25. Дмитриев А.Н., Смирнова В.Г., Вязникова Е.А., Долматов А.В., Витькина Г.Ю. Влияние структуры обожженных окатышей на прочность и разрушение при испытании на статическое сжатие // Известия высших учебных заведений. Черная металлургия. 2021. Т. 64. № 11. С. 785–792.

  26. Пучков А.Ю., Соколов А.М., Федотов В.В. Нейросетевой метод анализа процессов термической обработки окомкованного фосфатного рудного сырья // Прикладная информатика. 2022. Т. 17. № 5. С. 62–76.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал