1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 57, № 4, 2023

Теоретические основы химической технологии, 2023, T. 57, № 4, стр. 363-370

Оценка эффективности разделения пылегазовых потоков в прямоточных циклонах

В. С. Топталов a, *, Ю. Г. Чесноков a, В. П. Мешалкин a, b, Н. Н. Кулов c, О. М. Флисюк a, Н. А. Марцулевич a, И. Г. Лихачев a

a Санкт-Петербургский государственный Технологический институт (Технический университет)
Санкт-Петербург, Россия

b Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия

c Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия

* E-mail: ixumuk@mail.ru

Поступила в редакцию 15.05.2023
После доработки 26.05.2023
Принята к публикации 05.06.2023

Полный текст (PDF)

Аннотация

В статье приводится модель для определения эффективности фракционного разделения прямоточного циклона. Модель включает параметры, характеризующие движение частицы в циклоне, влияющие на степень сепарации: расстояние, которое проходит частица, двигаясь по спирали, и ее траекторию. Представлены результаты экспериментального исследования эффективности разделения в прямоточном циклоне новой конструкции. Эксперименты проводились с кварцевой мукой четырех дисперсных составов – 15, 20, 30 и 50 мкм. При работе с частицами малой дисперсности циклон показал высокую эффективность для аппаратов такого типа. Приведен анализ кривых эффективности разделения.

Ключевые слова: прямоточный циклон, пылеулавливание, закрученный поток, эффективность улавливания прямоточного циклона

ВВЕДЕНИЕ

Циклоны используют для отделения дискретной фазы – твердых частиц – от газовой фазы. Они широко применяются для очистки газов из-за их простой конструкции, низких затрат на техническое обслуживание, безопасности и стабильности [1]. Ряд этих преимуществ вместе с достаточно высокой степенью улавливания делает циклоны хорошим инструментом для осуществления инженерной защиты окружающей среды от пылевых выбросов промышленных предприятий в атмосферу. Уловленный из газовых потоков материал может быть возвращен обратно в производство, что позволяет осуществлять рециклинг ресурсов и ресурсосбережение [2].

Существует два основных типа конструкций циклонных сепараторов. Первый тип – прямоточные циклоны – это циклоны с осевым потоком и направляющими лопатками для создания вращения. Известен ряд исследований таких циклонных сепараторов с осевым потоком [3]. Второй тип – циклоны с тангенциальным подводом газа, которые являются основой для различных конструкций и новых разработок [4].

Исследователи активно занимаются разработкой новых и совершенствованием имеющихся конструкций газоочистителей. Так, в работе Джанфей Сонг и др. [5] проведено экспериментальное и численное исследование циклонного сепаратора с тангенциальным подводом газа. Основной задачей работы являлось определение угла подачи газа в аппарат, обеспечивающего наибольшую эффективность. Опыты проводились на тальке дисперсностью 1–10 мкм. Для проведения опытов исследователями была собрана экспериментальная установка, включающая в себя циклон, дозатор, вентилятор и ряд вспомогательных устройств. В.С. Асламова и др. [6] разработали прямоточный циклон для использования на производстве минеральной ваты. Опыты показали, что аппарат хорошо улавливает волокна минеральной ваты. Особенностью конструкции является наличие биконического вытеснителя, снабженого оребрением, при этом ребра представляют собой пластины с осями, направленными вдоль траектории движения газа. Лингзи Ванг и др. [7] описывают циклон с многослойным центральным каналом. Особенностью циклона является многоступенчатая и многократная закрутка входящего потока газа. Конструкция позволила увеличить наиболее эффективную скорость входящего загрязненного газового потока в аппарат и при этом увеличить максимальную эффективность. Ик-Хуан Ан и др. [8] разработали миниатюрный циклонный сепаратор, который можно устанавливать на входном отверстии в приборах для определения концентрации сажи в газовом потоке, работающих при скорости потока менее 200 мл/мин. Был изготовлен прототип для экспериментальной оценки его характеристик, а предельный размер циклонного сепаратора определен посредством численного анализа с использованием различных моделей турбулентности.

Помимо работ по разработке новых конструкций аппаратов, можно отметить ряд статей с изучением гидродинамики закрученных газовых потоков. В работе [9] было проведено комплексное численное и экспериментальное исследование нестационарных режимов вихревого течения в модельной вихревой камере. В исследовании [10] рассматриваются гидро- и аэродинамические закономерности двухфазного закрученного потока в аппарате вихревого типа. Выполнено экспериментальное исследование структуры завихренного однофазного и двухфазного течения на системе воздух-вода в моделях вихревого полого аппарата. На основе измерения поля скоростей и статического давления выявлено совпадение профилей относительных осевой и окружной составляющих скорости газового потока на любом расстоянии от завихрителя при различных скоростях газа. Исследователями [11] установлено, что введение в закрученный поток дисперсной фазы приводит к значительному снижению тангенциальной составляющей скорости газа, а профиль осевой скорости газа при увеличении расхода дисперсной фазы изменяется постепенно и приближается к форме, характерной для осевого течения в кольцевом канале.

В настоящее время не существует четкой теории разделения, точно описывающей различные факторы, участвующие в разделении. Известно, что силы, влияющие на частицы, являются определяющим процесс разделения фактором. Однако механическое поведение частиц в циклонных сепараторах до конца не изучено [12]. Е. Сеиыед Гхасеми и др. [13] исследовали движение сферической частицы, выпущенной в закрученном потоке. Для этого применяется метод наименьших квадратов и метод моментов. Рассмотрено влияние различных параметров, а именно начального радиуса, начальной радиальной скорости, начальной угловой скорости и отношения сопротивления к инерции, на безразмерные профили скорости и распределение положения частиц. В работе [14] проведено моделирование закрученного двухфазного потока газ-твердое тело в трехмерной цилиндрической трубе промышленных габаритов с установленным в ней винтовым завихрителем. Авторами доказано, что распределение частиц по поперечному сечению всегда соответствует нормальному закону распределения, а компоненты скорости частиц у стенки значительно больше, чем частиц в центре. Жангхао Ван и др. [15] исследовали проанализировали влияние геометрических параметров завихрителя на азимутальную скорость частиц и критерий Рейнольдса частиц. Результаты показывают, что наличие завихрителя усиливает как турбулентное возмущение, так и завихренность газа. Увеличение угла наклона лопасти и диаметра завихрителя благотворно влияет на дисперсию частиц. Венбин Ли и др. [16] изучили траектории движения частиц в цилиндрической трубе с многосекционным винтовым завихрителем. Приведенная в исследовании аналитическая модель показывает, что при использовании такого завихрителя траектории частиц становятся более предсказуемыми и турбулентность оказывает на них значительно меньшее влияние. Ма и др. [17] и Соуза и др. [18] смоделировали движение частиц в циклонных сепараторах. Их результаты показали, что турбулентность вызывает унос частиц, которые могли быть уловлены аппаратом, и, следовательно, снижает эффективность сепарации. Ванг и др. [19] протестировали траектории частиц разного размера и обнаружили, что крупные частицы в основном остаются на стенке конической части циклона, при условии, что их размеры превышают критическое значение. Он объяснил это явление анализом трех сил, которые действовали на частицы в конической части. Ван и Юи [20] обнаружили, что на внешней стенке завихрителя образуется статическое электричество, которое приводит к снижению эффективности сепарации, и также, что стабилизатор завихрителя небольшого диаметра приводит к лучшей эффективности сепарации, особенно для крупных частиц. Кроме того, Ли и соавт. [21] показали, что подъемная сила Саффмана ускоряет процесс разделения и сокращает время пребывания мелких частиц в камере разделения. Куи и др. [22] пришли к выводу, что радиальное распределение частиц становится неравномерным из-за действия центробежной силы.

Математические модели циклонов, описывающие движение газовой фазы и дисперсных частиц, а также лабораторные исследования позволяют определить эффективность аппаратов, не прибегая к эксплуатационным затратам. Таким образом, разработка и изучение новых конструкций циклонных сепараторов и математических моделей к ним является актуальной задачей.

Целью настоящей работы является теоретическое и экспериментальное определение эффективности улавливания мелкодисперсной пыли в прямоточном циклоне новой конструкции.

РАСЧЕТ ЭФФЕКТИВНОСТИ УЛАВЛИВАНИЯ ТВЕРДЫХ ЧАСТИЦ В ПРЯМОТОЧНОМ ЦИКЛОНЕ

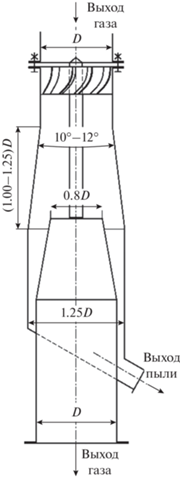
Описание конструкции исследуемого циклона. Прямоточный циклон состоит из соосно расположенных патрубков для входа и выхода газа. Во входном патрубке установлен лопастной завихритель с профилированными лопатками.

Профиль лопаток обеспечивает безударный вход и выход газового потока из завихрителя, что уменьшает его турбулентность. Завихритель имеет удлиненный стабилизатор в форме цилиндра, который доходит до патрубка для выхода газа. После прямого участка с завихрителем расположен участок, имеющий расширение в форме усеченного конуса. Входной диаметр этого участка равен 150 см (D), а усеченный конус длину 185 (1–1.25D) см и конусность 12°. После прохождения входного патрубка газ проходит в выхлопной патрубок для выхода газа. Первой частью патрубка для выхода газа является усеченный конус с диаметрами оснований 120 (0.8D) см и 150 (D) см. Схема циклона представлена на рис. 1. На описанную выше конструкцию, включающую в себя приведенные на рис. 1 соотношения, получен патент [23].

Рис. 1.

Схема прямоточного циклона.

Оценочный расчет эффективности улавливания. Будем считать, что скорость движения частиц в тангенциальном и осевом направлениях совпадает со скоростью газа, а скорость движения частицы в радиальном направлении определим из условия баланса сил. Иными словами, будем рассматривать движение частицы в радиальном направлении как квазистационарное. Если частицы имеют сферическую форму, диаметр частиц d, плотность частиц ρp, а плотность газа ρ, то равнодействующая центробежной силы и центростремительной силы (силы давления) будет равна:

(1)
$\frac{{\pi {{d}^{3}}}}{6}({{\rho }_{p}} - \rho )\frac{{{{w}^{2}}}}{r}.$

Здесь w – тангенциальная составляющая скорости газа, которая вычисляется при помощи разработанной ранее модели, r – радиальная координата. Сумма этих сил должна уравновешиваться силой сопротивления движению частицы в радиальном направлении со стороны газа. Обозначим через vp скорость движения твердой частицы в радиальном направлении. В том случае, если для расчета силы сопротивления можно применить формулу Стокса, условие баланса сил будет иметь вид:

(2)
$\frac{{\pi {{d}^{3}}}}{6}({{\rho }_{p}} - \rho )\frac{{{{w}^{2}}}}{r} = 3\pi \mu d{{v}_{p}}.$

Здесь µ – вязкость газа. Обобщить это выражение на случай, когда формула Стокса неприменима, не представляет никакого труда. Если частица первоначально на входе в циклон) находилась на расстоянии R от оси циклона, а радиус циклона R2, то расчет промежутка времени τ, в течение которого частица будет двигаться до стенки, можно осуществить по формуле:

(3)
$\tau = \int\limits_R^{{{R}_{2}}} {\frac{{18\mu }}{{({{\rho }_{p}} - \rho ){{d}^{2}}{{w}^{2}}}}rdr} .$

За это время частица в осевом направлении пройдет расстояние z, которое вычисляется следующим образом:

(4)
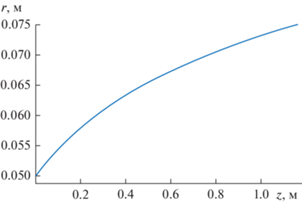
$z = \int\limits_R^{{{R}_{2}}} {\frac{{18\mu u}}{{({{\rho }_{p}} - \rho ){{d}^{2}}{{w}^{2}}}}rdr} .$

В рассматриваемом соотношении u – осевая составляющая скорости газа. Если в качестве R взять радиус втулки R1, к которой крепятся лопасти завихрителя, при помощи полученной формулы вычислим такую длину циклона, что все частицы данного диаметра окажутся у наружной стенки и будут уловлены. На рис. 2 построен график зависимости этой величины от диаметра частиц. Вычисления проведены при следующих значениях параметров: ρp = 2320 кг/м3, ρ = 1.205 кг/м3, µ = 18.15 Па с. При расчетах составляющих скорости газа среднее значение осевой составляющей в кольцевом зазоре между двумя цилиндрами принималось 12 м/с.

Рис. 2.

Расстояние, которое проходит частица в осевом направлении при перемещении в радиальном направлении от поверхности втулки до стенки в зависимости от диаметра частицы.

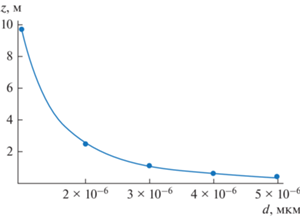
Разумеется, подобные расчеты будут завышать эффективность циклона по следующим причинам. Во-первых, по направлению движения газа в циклоне у его стенок происходит торможение газа. В первую очередь здесь речь идет о тангенциальной составляющей скорости. В итоге уменьшается центробежная сила и эффективность пылеулавливания снижается. Во-вторых, осевая составляющая скорости описывается при помощи модели довольно грубо. По данным численных расчетов осевая составляющая сильнее изменяется по сечению и, поскольку есть изменение составляющих скорости в осевом направлении, появляется небольшая радиальная составляющая скорости. В-третьих, в рамках упрощенной модели не учитывается турбулентное перемешивание, которое безусловно приводит к уменьшению эффективности пылеулавливания. Учет всех этих факторов возможен при использовании для расчетов компьютерных программ.

По формуле:

(5)
$z = \int\limits_{{{R}_{1}}}^R {\frac{{18\mu u}}{{({{\rho }_{p}} - \rho ){{d}^{2}}{{w}^{2}}}}rdr} $
можно определить осевую координату частицы, радиальная координата которой R, и которая за завихрителем находится у поверхности внутреннего цилиндра. Если в формуле (5) в качестве R взять ряд значений радиальной координаты, вычисляя интеграл можно определить соответствующее значение осевой координаты. Таким путем находим координаты точек, лежащих на траектории в меридиональной плоскости, которые непосредственно за завихрителем находятся у поверхности внутреннего цилиндра. На рис. 3 такая траектория построена для частиц диаметром 3 мкм. В том случае, когда движение твердых частиц происходит только под действием центробежной силы, а турбулентное перемешивание отсутствует, эта траектория в меридиональной плоскости будет отделять прилегающую к внутреннему цилиндру область, где твердые частицы данного диаметра отсутствуют, от той области, где концентрация твердых частиц данного диаметра постоянна и равна концентрации до циклона. Аналогичным образом можно построить траектории частиц в меридиональной плоскости, которые за завихрителем находятся на другом расстоянии от стенки. Для этого в формуле (5) надо взять какое-либо иное значение вместо R1.

Рис. 3.

Проекция траектории частицы диаметром 3 мкм на меридиональную плоскость.

Рис. 4.

Зависимость эффективности пылеулавливания от диаметра частиц.

Если отвод твердых частиц осуществляется на расстоянии L от завихрителя, по формуле:

(6)
$L = \int\limits_R^{{{R}_{2}}} {\frac{{18\mu u}}{{({{\rho }_{p}} - \rho ){{d}^{2}}{{w}^{2}}}}rdr} $
вычисляется такое значение радиальной координаты R, что все частицы, которые находятся на входе в циклон на расстояниях до оси, больших чем R, будут уловлены.

Для расчета такого значения R необходимо использовать метод последовательных приближений. Для частиц сравнительно больших диаметров, траектории в меридиональной плоскости, которые начинаются у поверхности внутреннего цилиндра, достигают стенки на расстояниях от завихрителя, меньших чем L. Все такие частицы полностью улавливаются. Например, если L = 0.6 м, полностью будут улавливаться частицы, диаметр которых превышает 4.171 мкм. В том случае, когда диаметр частицы меньше такого предельного значения, улавливаться будет только часть частиц. Поскольку будут улавливаться те частицы, которые за завихрителем находятся в кольцевой области R < r < R2, степень улавливания для частиц данного диаметра можно определить как отношение площади этого кольца к полному поперечному сечению циклона:

(7)
$\eta = \frac{{R_{2}^{2} - {{R}^{2}}}}{{R_{2}^{2} - R_{1}^{2}}}.$

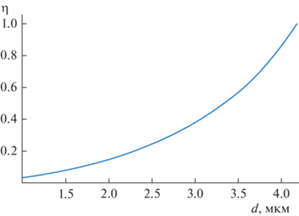
Проделав подобные расчеты при ряде значений диаметра частиц, можно построить график зависимости фракционной эффективности от диаметра частиц. На рис. 4 такой график построен при L = 0.6 м.

Разумеется, все эти расчеты следует рассматривать как ориентировочные, поскольку целый ряд важных факторов, указанных выше, при расчете не учитывается.

ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ЦИКЛОНА

Эффективность пылеулавливания рассматриваемого циклона определялась на лабораторной установке, схема которой приведена на рис. 5.

Рис. 5.

Схема экспериментальной установки. 1 – шнековый дозатор; 2 – завихритель; 3 – лопасть завихрителя; 4 – корпус прямоточного циклона; 5 – дифманометр; 6 – диафрагма с присоединенным к ней дифманометром; 7 – шиберная заслонка; 8 – рукавный фильтр; 9 – центробежный вентилятор

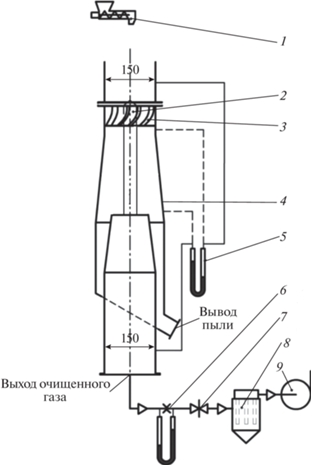
Установка работает следующим образом. С помощью центробежного вентилятора 9 создается необходимый расход воздуха. Шнековым питателем 1 мелкодисперсный материал дозируется в поток воздуха, входящего в циклон. За счет возникшей центробежной силы частицы пыли относятся к стенкам циклона и попадают в нижнюю часть циклона, предназначенную для сбора пыли. Гидравлическое сопротивление всего аппарата измерялось дифманометром 5. Расход воздуха измерялся с помощью диафрагмы 6 и присоединенного к ней дифманометра, и регулировался шиберной заслонкой 7 в пределах от 200 до 1300 м3/ч. Тканевый фильтр 8, установленный перед центробежным вентилятором улавливал частицы, которые не уловил циклон. Диапазон запыленности газа варьировался в пределах от 100 до 400 г/м3. Уловленная пыль извлекалась из пылеприемной камеры и взвешивалась на электронных весах. Погрешностью данных измерений являлась погрешность весов и составляла ±0.5 г, что давало относительную погрешность измерений менее 0.5%.

В качестве модельного материала для проведения экспериментов была выбрана кварцевая мука – перемолотый на шаровых мельницах оксид кремния. Она обладает довольно большой насыпной плотностью и низкой образивностью. Эксперименты проводились на кварцевой муке четырех дисперсных составов 15, 20, 30 и 50 мкм. Ее краткие технические характеристики приведены в табл. 1.

Таблица 1.  

Технические характеристики кварцевой муки

Характеристики Дисперсность 
15 мкм 20 мкм 30 мкм 50 мкм
1. Насыпная плотность, г/см3 0.85 0.9 0.97 1
2. Массовая доля SiO2, % 99.7 99.7 99.7 99.48
3. Массовая доля влаги, % 0.2 0.2 0.2 0.2
4. Диаметр частиц, мкм. Средний D50 17 23 34 43
5. Диаметр частиц, мкм. Максимальный D90 44 62 92 123

Постановка эксперимента осуществлялась в следующей последовательности.

1. Навеска кварцевой муки, используемая для проведения опыта, насыпалась в приемный бункер шнекового дозатора.

2. Запускался центробежный вентилятор и при помощи шиберной заслонки устанавливался требуемый расход воздуха.

4. Включался электропривод дозатора, и кварцевая мука подавалась во входящий в циклон поток воздуха.

5. После окончания опыта, уловленная пыль извлекалась из пылеприемной камеры и взвешивалась. На основе значений массы уловленной пыли определялась эффективность разделения циклона.

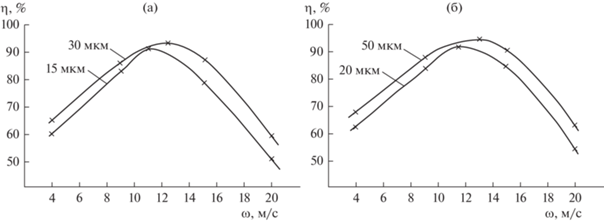
На рис. 6 приведен график зависимости эффективности улавливания частиц от скорости газового потока для четырех дисперсных составов. Кривые имеет явно выраженный максимум, соответствующий скорости потока порядка 12 м/с. Это обуславливается возрастанием значения тангенциальной составляющей скорости газового потока при увеличении расхода газа и, следовательно, центробежной силы, действующей на частицы. При дальнейшем увеличении расхода газа определяющим становиться турбулентное перемешивание в потоке.

Рис. 6.

Эффективность улавливания кварцевой муки дисперсностью: (а) – 15 и 30 мкм; (б) – 20 и 50 мкм; угол закрутки лопастей заверителя 60°.

ЗАКЛЮЧЕНИЕ

В работе предложена модель движения частиц в разделительной камере прямоточного циклона новой конструкции и на ее основе проведена оценка эффективности пылеулавливания. Проведенные эксперименты по оценке степени пылеулавливания циклона показали, что аппарат с такими конструктивными соотношениями имеет хорошую эффективность даже при очистке газов, содержащих частицы до 15 мкм. Предложенный подход к оценке эффективности разделения может быть использован и для оценки эффективности разделения в прямоточных циклонах других конструкций.

ФИНАНСИРОВАНИЕ РАБОТЫ

Исследование выполнено за счет гранта Российского научного фонда, проект 21-79-30029.

Авторы заявляют, что у них нет конфликта интересов.

СПИСОК ОБОЗНАЧЕНИЙ

d диаметр частиц, м
r радиальная координата, м
L расстояние от завихрителя до патрубка отвода твердых частиц, м
R расстояние от оси циклона до рассматриваемой частицы во входном сечении, м
R1 радиус втулки, к которой крепятся лопасти завихрителя, м
R2 радиус циклона (цилиндрической части циклона), м
u осевая скорость газа, м/с
vp радиальная скорость частицы, м/с
w тангенциальная составляющая скорости газа;
z осевая координата, м
µ вязкость газа, Па с
τ время, с
ρ плотность газа, кг/м3
ρp плотность твердых частиц, кг/м3

Список литературы

  1. Мешалкин В.П. Введение в проектирование энергосберегающих химико-технологических систем. М.: РХТУ им. Д.И. Менделеева, 2020.

  2. Long Huang, Songsheng Deng, Zhi Chen, Jinfa Guan, Ming Chen. Numerical analysis of a novel gas-liquid pre-separation cyclone // Separation and Purification Technology. 2018. V. 194. P. 470–479. https://doi.org/10.1016/j.seppur.2017.11.066

  3. Zheng-Wei Zhang, Qing Li, Yan-Hong Zhang, Hua-Lin Wang. Simulation and experimental study of effect of vortex finder structural parameters on cyclone separator performance // Separation and Purification Technology. 2022. V. 286. 120394. https://doi.org/10.1016/j.seppur.2021.120394

  4. Mohamadali Mirzaei et al. A hybrid multiphase model accounting for particle agglomeration for coarse-grid simulation of dense solid flow inside large-scale cyclones // Powder Technology. 2022. V. 399. 117186. https://doi.org/10.1016/j.powtec.2022.117186

  5. Jianfei Song, Yaodong Wei, Guogang Sun, Jianyi Chen. Experimental and CFD study of particle deposition on the outer surface of vortex finder of a cyclone separator // Chemical Engineering J. 2017. V. 309. P. 249–262. https://doi.org/10.1016/j.cej.2016.10.019

  6. Асламова В.С., Асламов А.А., Ляпустин П.К., Мусева Т.Н., Брагин Н.А. Прямоточный циклон для производства минеральной ваты // Экология и промышленность России. 2007. № 6. С. 26–27.

  7. Lingzi Wang, Biyuan Liu, Jianmei Feng, Xueyuan Peng. Experimental study on the separation performance of a novel oil–gas cyclone separator // Powder Technology. 2023. V. 415. 118124. https://doi.org/10.1016/j.powtec.2022.118124

  8. Ik-Hyun An, Chang-Hoon Lee, Jun-Hyung Lim, Hyo-Young Lee, Se-Jin Yook. Development of a miniature cyclone separator operating at low Reynolds numbers as a pre-separator for portable black carbon monitors // Advanced Powder Technology. 2021. V. 32. I. 12. P. 4779–4787. https://doi.org/10.1016/j.apt.2021.10.027

  9. Guoyin Yu, Sijie Dong, Linna Yang, Di Yan, Kejun Dong, Yi Wei, Bo Wang. Experimental and numerical studies on a new double-stage tandem-nesting cyclone // Chem. Eng. Sci. 2021. V. 236. https://doi.org/10.1016/j.ces.2021.116537

  10. Турубаев Р.Р., Шваб А.В. Численное исследование аэродинамики закрученного потока в вихревой камере комбинированного пневматического аппарата // Вестник Томского государственного университета. Математика и механика. 2017. № 47. С. 87–98. https://doi.org/10.17223/19988621/47/9

  11. Николаев А.Н., Харьков В.В. Описание профилей окружной и осевой компонент скорости в полом вихревом аппарате // Вестник Казанского технологического университета. 2016. № 17. С. 71–74.

  12. Chengming Song, Binbin Pei, Mengting Jiang, Bo Wang, Delong Xu, Yanxin Chen. Numerical analysis of forces exerted on particles in cyclone separators // Powder Technology. 2016. V. 294. P. 437–448. https://doi.org/10.1016/j.powtec.2016.02.052

  13. Seiyed E., Ghasemi M., Vatani D.D., Ganji. Efficient approaches of determining the motion of a spherical particle in a swirling fluid flow using weighted residual methods // Particuology. 2015. V. 23. P. 68–74. https://doi.org/10.1016/j.partic.2014.12.008

  14. Wenbin Li, Feng Wu, Liuyun Xu, Jipeng Sun, Xiaoxun Ma. CFD-DEM investigation of gas–solid swirling flow in an industrial-scale annular pipe // Chinese Journal of Chemical Engineering. V. 461. 141975. https://doi.org/10.1016/j.cjche.2023.03.011

  15. Zhanghao Wan, Shiliang Yang, Duzuo Tang, Haibin Yuan, Jianhang Hu, Hua Wang. Particle-scale modeling study of coaxial jets of gas-solid swirling flow in an industrial-scale annular pipe via CFD-DEM // Powder Technology. V. 419. 118307. https://doi.org/10.1016/j.powtec.2023.118307

  16. Wenbin Li, Feng Wu, Liuyun Xu, Jipeng Sun, Xiaoxun Ma. Numerical and experimental study on the particle erosion and gas–particle hydrodynamics in an integral multi-jet swirling spout-fluidized bed // Chinese J. Chemical Engineering. 2023. 159655. https://doi.org/10.1016/j.cjche.2023.03.011

  17. Ma L., Ingham D.B., Wen X. Numerical modelling of the fluid and particle penetration through small sampling cyclones // J. Aerosol Sci. 2004. V. 31. P. 1097–1119.

  18. Francisco José de Souza, Ricardo de Vasconcelos Salvo, Diego Alves de Moro Martins. Large eddy simulation of the gas–particle flow in cyclone separators // Sep. Purif. Technol. 2012. V. 94. P. 61–70. https://doi.org/10.1016/j.seppur.2012.04.006

  19. Wang B., Xu D.L., Chu K.W., Yu. A.B. Numerical study of gas–solid flow in a cyclone separator // Appl. Math. Model. 2006. V. 30 P. 1326–1342. https://doi.org/10.1016/j.apm.2006.03.011

  20. Wang B., Yu A.B. Numerical study of the gas–liquid–solid flow in hydrocyclones with different configuration of vortex finder // Chem. Eng. J. 2008. V. 135. P. 33–42. https://doi.org/10.1016/j.cej.2007.04.009

  21. Xiaodong Li, Jianhua Yan, Yuchun Cao, Mingjiang Ni, Kefa Cen. Numerical simulation of the effects of turbulence intensity and boundary layer on separation efficiency in a cyclone separator // Chem. Eng. J. 2003. V. 95. P. 235–240. https://doi.org/10.1016/S1385-8947(03)00109-8

  22. Cui J., Chen X., Gong X., Yu. G. Numerical study of gas–solid flow in a radial-inlet structure cyclone separator // Ind. Eng. Chem. Res. 2010. V. 49. P. 5450–5460. https://doi.org/10.1016/j.apm.2006.03.011

  23. Флисюк О.М., Топталов В.С., Марцулевич Н.А., Муратов О.В. Прямоточный циклон. Пат. 195672U1 РФ 2020.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал