Теоретические основы химической технологии, 2023, T. 57, № 5, стр. 563-580
Место энергодинамики в научных основах химической технологии
И. Н. Дорохов *
Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
* E-mail: indorokhov@yandex.ru
Поступила в редакцию 28.06.2023
После доработки 11.07.2023
Принята к публикации 23.07.2023
- EDN: MDTTUC
- DOI: 10.31857/S004035712305007X
Аннотация
Дано компактное и исчерпывающее толкование основ энергодинамики и показано, что она существенно раздвигает горизонты естествознания и открывает новые пути совершенствования научных основ химической технологии.
ВВЕДЕНИЕ
Методологический аппарат химической технологии строится на базе таких дисциплин, как физико-химическая гидродинамика, механика, равновесная термодинамика, термодинамика необратимых процессов (ТНП), тепломассообмен и др. В последнее время наблюдается привлечение идей системного анализа и энергодинамики [1–4]. Особенность энергодинамики состоит в том, что она требует пересмотра ряда положений как равновесной термодинамики, так и термодинамики необратимых процессов (ТНП). Задача настоящего сообщения – дать компактное и в то же время исчерпывающее толкование энергодинамики с целью ее более широкого использования специалистами в области химической технологии.
Термин “энергодинамика” был введен А.И. Вейником [5], научное направление создал и изложил в своих фундаментальных монографиях В.А. Эткин [3, 4]. Энергодинамика – это термодинамика, распространенная на нестатические процессы и любые формы энергии. Ее объект исследования – реальные природные и технологические процессы, а метод – термодинамический, т.е. феноменологический и системный. Процесс в энергодинамике – это любое пространственно – временное изменение макрофизических свойств объекта исследования, формулируемого как энергодинамическая система. Одна из основных сущностей системы состоит в том, она есть нечто большее, чем сумма ее частей.
Универсальной характеристикой энергодинамической системы является энергия, представляющая собой наиболее общую функцию ее состояния. Производные от нее по независимым аргументам определяют все другие свойства системы. Энергия играет роль связующего звена между различными процессами, протекающими в этой системе, – механическими, тепловыми, химическими, электромагнитными, ядерными и т.д. В основе энергодинамики лежит закон сохранения и превращения энергии, не имеющий ограничений. Система в термодинамическом смысле может быть простой или сложной, открытой или закрытой, равновесной или неравновесной, замкнутой или незамкнутой, изолированной или неизолированной и т.п.
Анализ носит дедуктивный характер (от общего к частному) и опирается исключительно на подтвержденные опытом данные о природных явлениях, т.е. феноменологию. Системный подход не исключает из рассмотрения те внутренние (скрытые от наблюдателя) системообразующие связи, благодаря которым система в целом приобретает новые свойства, которых не было у отдельных ее частей (элементов) и без которых система не может функционировать полноценно [1, 2]. Дедуктивный анализ сложнее для наблюдателя, однако позволяет критически оценивать (верифицировать) результаты индуктивного анализа и тем самым приближает его к реальности. Например, энергодинамика не исключает исследования внутренних (в том числе диссипативных) процессов, которыми классическая механика обычно пренебрегает, изучая “консервативные” системы.
Энергодинамическая система отличается от механической. Элементы механической системы – это материальные точки, а элементы энергодинамической – это реальные процессы, координатами которых являются материальные носители различных форм энергии – так называемые энергоносители. Если в механике обобщенными координами состояния системы служат координаты положения и скоростей отдельных материальных точек, то в энергодинамике координаты – это числовые характеристики материальных энергоносителей Θi и смещений Ri их центров относительно равновесия, которые характеризуют систему в целом. Энергия Е, является экстенсивной характеристикой системы и представляет собой однозначную функцию экстенсивных координат Е = Е(Θi, Ri). Например, механический процесс характеризуется в энергодинамике массой и смещением центра масс, тепловой процесс – энтропией и смещением ее центра; химический процесс – количеством компонента и смещением его центра; электростатический процесс – зарядом и смещением его центра и т.д.
Построение механики в курсах теоретической физики тоже принято дедуктивным, но при этом исходят из постулатов однородности и изотропности пространства и однородности времени, а также вариационного принципа наименьшего действия Лагранжа – частного случая более общего принципа наименьшего принуждения Гаусса [6]. Авторы [6] признают, что по отношению к произвольной системе отсчета пространство не является однородным и изотропным. Так, если какое-либо тело не взаимодействует ни с какими другими телами, то это еще не значит, что различные положения и различные ориентации его в пространстве в механическом отношении эквивалентны. Эта неэквивалентность наглядно проявляется, когда речь идет о пространственно неоднородных средах, являющихся анизотропными в силу того, что ряд свойств, зависящих от градиентов каких-либо потенциалов, различен в разных направлениях.
Переход к энергетическим координатам состояния (Θi, Ri), дополненный аксиоимой различимости процессов, с необходимостью приводит к абсолютной системе отсчета [1–4]. Понятие энергодинамической системы, свободное от постулатов однородности и изотропности пространства и принципа относительности Галилея, ограниченного прямолинейным и равномерным движением, шире понятия механической системы и делает механическую систему частным случаем энергодинамической. Для энергодинамики механика является “равноправным” представителем наряду с другими, в том числе, немеханическими формами движения материи. Такой взгляд на механику требует не только коррекции всех ее законов, но и позволяет естественным путем доказать принцип наименьшего принуждения в механике, упомянутый выше.
Энергодинамика, являясь последовательно феноменологической теорией, не исходит из модельных представлений о структуре систем и механизме протекающих в них процессов. Для конкретизации ее исходных принципов все необходимые сведения о частных свойствах исследуемых систем (в том числе законы Ньютона, Кулона, Ампера, уравнения состояния, переноса, баланса массы, заряда, импульса, момента импульса и т.д.) она привлекает извне (из опыта) в качестве дополнительных условий однозначности для замыкания ее уравнений. Ее уравнения опираются на формализм дифференциального и интегрального исчисления и математические свойства энергии системы как характеристической функции определенного числа переменных состояния, отражающих количественную и качественную сторону исследуемых форм движения. Поэтому следствия такой теории приобретают характер непреложных истин в пределах применимости условий однозначности, а сама энергодинамика становится теорией принципов.
ОБОБЩЕНИЕ ПОНЯТИЙ РАВНОВЕСНОЙ ТЕРМОДИНАМИКИ
Расширение сферы применимости равновесной термодинамики на реальные (неравновесные) процессы выполняется так, чтобы сохранить главное достоинство классической термодинамики – максимум получаемых следствий при минимуме принимаемых допущений. Для этого необходимо обобщение ряда понятий равновесной термодинамики [3, 4]. Ниже приводятся важнейшие из них.
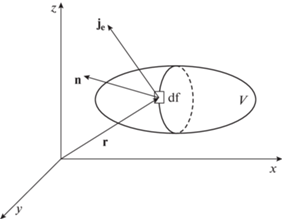
Внешние и внутренние параметры системы. Одни и те же параметры системы (например, объем системы V) могут относиться как к внешним, так и внутренним, что требует уточнения этих понятий. Внешние параметры – это параметры, определяющие взаимное положение частей системы или ее положение в целом относительно других тел. Если система как целое движется относительно окружающих тел, т.е. положение центра объема V системы изменяется в пространстве, то этот параметр относится к внешним. Тот же объем V следует считать внутренним параметром, если система в целом не изменяет своего положения относительно окружающих тел.
Обобщение понятия процесс. Процесс – это любое пространственно-временное изменение макрофизических свойств объекта исследования, т.е. последовательность смены состояний системы в сопутствующей системе отсчета от начального состояния, соответствующего равновесию системы.
Равновесие реальной системы. Равновесным считается состояние реальной системы, в котором прекращаются любые процессы при отсутствии причин, их подавляющих. Реальная система, находящаяся под действием внешних силовых полей и имеющая постоянные параметры состояния, называется стационарной, если после прекращения действия этих полей она изменяются (релаксируют к равновесию), т.е. различают полное и частичное равновесие. Разновидностью стационарного состояния является внешнее равновесие, характеризующееся прекращением внешнего энергообмена при сохранении пространственной неоднородности системы, а заторможенное равновесие – это разновидность стационарного состояния, характеризующегося прекращением внутренних процессов под действием внешних ингибиторов. С принятой точки зрения позиций в природе нет “равновесных процессов”, т.е. все реальные процессы в ней в той или иной мере неравновесны.
Число степеней свободы системы. По Гиббсу число степеней свободы равновесной системы равно числу параметров состояния, которые могут быть произвольно изменены без нарушения равновесия гетерогенной системы. Однако изменить состояние системы без нарушения ее равновесия невозможно. Поэтому за число степеней свободы реальной (неравновесной) системы принимается число процессов, различимых феноменологически и несводимых к другим процессам, протекающим в системе [3.4].
Уточнение понятия теплоты и работы. Термин “теплота” обычно употребляется в двух смыслах: 1) как функция процесса, являющаяся количественной мерой теплообмена и называемой кратко “теплотой процесса”; 2) как функция состояния, являющаяся количественной мерой внутренней тепловой энергии и называемой кратко “теплотой тела”. Для первой применяется обозначение Q, а для второй Uт. Для обозначения бесконечно малого приращения любой функции состояния используется знак полного дифференциала d (dUт), а для элементарных количеств теплоты Q или работы W как функций процесса – знак δ (δW, δQ).
При изучении процессов, связанных с переносом вещества, т.е. энергомассообмена, классическое понимание теплоты и работы как двух единственно возможных способов энергообмена системы с окружающей средой становится ограниченным, т.к. не учитывает массообмен. Поэтому приходится отнести понятия работы и теплоты исключительно к способам энергообмена, не связанными с переносом вещества.
Невозможность считать теплоту и работу формами любого внешнего энегообмена требует введения новых понятий внутреннего теплообмена и внутренней работы. При этом в связи с рассмотрением сложных систем, совершающих помимо работы расширения другие виды работ, целесообразно обобщить понятие работы как количественной меры процесса, связанного с преодолением каких-либо сил. Такой “силовой подход” позволяет различать не только термическую, механическую, электрическую магнитную и др. виды работ (в зависимости от природы преодолеваемых сил), но и работу упорядоченную и неупорядоченную (в зависимости от наличия или отсутствия результирующих этих сил); внешнюю и внутреннюю (против внешних и внутренних сил); полезную и диссипативную (против полезных сил и сил рассеяния).
Сделанных обобщений исходных понятий равновесной термодинамики достаточно для создания концептуальной базы новой термодинамики реальных процессов. При этом фундаментом новой термодинамики становятся два нижеследующих принципа.
ПРИНЦИП РАЗЛИЧИМОСТИ РЕАЛЬНЫХ ПРОЦЕССОВ
Классическая термодинамика, изучающая равновесные процессы, различает их не по причинам, их вызывающим, и не по механизму переноса энергии, а по их последствиям, т.е. по особым, феноменологическим отличимым и несводимым к другим изменениям состояния, которые они вызывают. Таковы, в частности, изохорный, изобарный, изотермический и адиабатический процессы. Например, если состояние системы изменяется так, что ее объем V = const, то такой процесс так и называется – изохорический. Такой способ классификации процессов принимается не только для равновесных, но и для реальных процессов. Это предъявляет соответствующие требования к выбору координат реальных процессов. Координата состояния реального процесса – это параметр состояния, который не изменяется при одновременном изменении других независимых параметров. Такая классификации вытекает из аксиомы различимости процессов: реальные процессы можно различать, пользуясь всем доступным арсеналом экспериментальных средств. Возможность такой классификации представляет собой непреложный факт, подтвержденный всем накопленным опытом становления и развития естествознания человечества и принимается исходной аксиомой термодинамики реальных процессов. С помощью ее обосновывается фундаментальное положение, согласно которому число независимых координат, определяющих состояние любой (равновесной или неравновесной) термодинамической системы равно числу ее независимых процессов [4]. Это положение равносильно тому, что любому независимому процессу соответствует единственная независимая координата состояния. Такие координаты в общем случае являются величинами экстенсивными, поскольку каждая из них определяет энергию системы – величину экстенсивную.
Данный принцип приводит к двум важным следствиям. Первое касается нахождения необходимого и достаточного числа координат состояния для конкретной исследуемой системы, что позволяет избежать как “недоопределения”, так и “переопределения” ее состояния (что снижает вероятность ошибок в исследованиях реальных процессов). Второе разделяет все реальные процессы исходя из понятия равновесия: в природе есть только два вида процессов – равномерные и перераспределения. Первые напоминают выпадение осадков на неровную (в общем) поверхность (рельеф) и характеризуются одинаковым по величине изменением свойств во всех частях системы, т.е. имеют скалярный характер. Вторые – это процессы, подобные перераспределению осадков на неровной поверхности, т.е. имеют направленный (векторный) характер. Другими словами, первые связаны с потоками типа “расход” или “наполнение”, вторые – с направленными потоками. Такое разделение реальных процессов на две категории требует расширения пространства переменных состояния термодинамической системы.
ПРОТИВОНАПРАВЛЕННОСТЬ РЕАЛЬНЫХ ПРОЦЕССОВ
Из предыдущего принципа вытекает концептуальное положение о существовании в неоднородных системах противоположно направленных процессов, что является причиной появления у системы новых свойств. Чтобы в этом убедиться, достаточно представить величину любого экстенсивного параметра системы Θi (массы М, энтропии S, электрического заряда Θe, импульса P, его момента L и т.п.) интегралами от его локальной ${{\rho }_{i}}$ = d${{{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{{{\Theta }_{i}}} {dV~}}} \right. \kern-0em} {dV~}}$ и средней ${{\bar {\rho }}_{i}}$ = Θi/V плотности выражением ${{\Theta }_{i}} = \int\limits_V {{{\rho }_{i}}dV = } \,\int\limits_V {{{{\bar {\rho }}}_{i}}dV} .$ Отсюда непосредственно следует тождество:
(1)
$\int\limits_V {{{d({{\rho }_{i}} - {{{\bar {\rho }}}_{i}})} \mathord{\left/ {\vphantom {{d({{\rho }_{i}} - {{{\bar {\rho }}}_{i}})} {dt}}} \right. \kern-0em} {dt}}} dV \equiv 0,$которое соблюдается только в том случае, если знак скорости какого-либо процесса d(ρi – ${{\bar {\rho }}_{i}}$)/dt противоположен хотя бы в некоторых элементах ее объема dV, т.е. когда эти процессы противонаправлены. Такая противонаправленность процессов носит общефизический характер, т.е. среди процессов, протекающих в пространственно неоднородных системах, всегда имеются такие, которые вызывают противоположные изменения ее свойств. Это говорит о существовании естественной поляризации природы в самом общем понимании этого слова. Этот принцип можно считать физическим подтверждением закона единства и борьбы противоположностей. Если свойства энергодинамической системы всюду не отличаются от среднего, то никакие процессы в такой системе невозможны. Противоположности возникают только в результате количественного отличия от среднего значения каких-либо свойств системы. В этом ключ эмерджентности энергодинамической системы. Это свойство присуще всем природным явлениям в большом и малом от микро- до мегамира и является одним основных принципов мироздания, выполняя роль ограничителя для многочисленных фантазий о существовании в природе материи и антиматерии, частиц и античастиц, положительной и отрицательной энергии, положительных и отрицательных зарядов, темной энергии и темной материи и т.д. и т.п. [4].
РАСШИРЕНИЕ ПРОСТРАНСТВА ПЕРЕМЕННЫХ СОСТОЯНИЯ
В равновесной термодинамике координатами пространства состояний системы являются так называемые термостатические экстенсивные переменные ${{\Theta }_{i}}$ (масса, объем, число молей компонента, заряд, энергия, энтропия и т.д.), характеризующие систему в целом. Эти скалярные величины служат координатами природных процессов первого типа (равномерных). Для описания процессов второго типа (перераспределения) необходимы свои экстенсивные координаты, характеризующие неоднородное (внутренне неравновесное) состояние системы в целом, т.е. позволяющие отражать протекание направленных (векторных) процессов.
Природный объект в термодинамике характеризуется массой М и объемом V, для которых, как и других экстенсивных величин, вводится общее обозначение А. Экстенсивной величине А соответствуют интенсивная объемная характеристика ${{\alpha }_{v}}$ = А/V и удельная массовая характеристика ${{\alpha }_{m}}$ = А/М, которые удовлетворяют очевидному соотношению ${{\alpha }_{V}}$ = ${{\rho }}{{\alpha }_{m}}$, где$~~{{\rho }}$ = М/V – плотность материала объекта. Чтобы пользоваться формализмом дифференциального и интегрального исчисления, предполагается непрерывность производных $\rho = {{\partial М} \mathord{\left/ {\vphantom {{\partial М} {\partial V}}} \right. \kern-0em} {\partial V}}$, ${{\alpha }_{v}}$ =$~{{\partial А} \mathord{\left/ {\vphantom {{\partial А} {\partial V}}} \right. \kern-0em} {\partial V}}$ и ${{\alpha }_{m}}$ = ${{\partial А} \mathord{\left/ {\vphantom {{\partial А} {\partial М}}} \right. \kern-0em} {\partial М}}.~$ Это значит, что природный объект подчиняется континуальной (непрерывной) модели сплошной среды (в отличие от корпускулярной модели), т.е. $~{{\alpha }_{v}}$ и $~{{\alpha }_{m}}$ принимаются непрерывными функциями радиус-вектора r точки пространства и времени t [7]. При А = ${{\Theta }_{i}}~$ сказанное относится и к энергоносителям ${{\Theta }_{i}}$, для которых $~{{\alpha }_{{vi}}}$ = $~{{\rho }_{i}} = $ ${{\partial {{\Theta }_{i}}} \mathord{\left/ {\vphantom {{\partial {{\Theta }_{i}}} {\partial V}}} \right. \kern-0em} {\partial V}}.~$ Непрерывное (полевое) распределением плотности энергоносителя ${{\rho }_{i}}\left( {{\mathbf{r}},t} \right)$ связано c положением его центра в объеме V соотношением, аналогичным определению положения центра масс механической системы
(2)
$\begin{gathered} ~{{{\mathbf{R}}}_{i}}\left( {{\mathbf{r}},t} \right) = \left( {{1 \mathord{\left/ {\vphantom {1 {{{\Theta }_{i}}}}} \right. \kern-0em} {{{\Theta }_{i}}}}} \right) \cdot \int\limits_V {{{\rho }_{i}}\left( {{\mathbf{r}},t} \right){\mathbf{r}}dV} , \\ \left( {{\text{ }}i = 1,2,3 \ldots ,n} \right).~ \\ \end{gathered} $Среднее его значение, соответствующее равновесию системы, имеет вид
(3)
${{{\mathbf{\bar {R}}}}_{i}} = \left( {{1 \mathord{\left/ {\vphantom {1 {{{\Theta }_{i}}}}} \right. \kern-0em} {{{\Theta }_{i}}}}} \right) \cdot \int\limits_V {{{{\bar {\rho }}}_{i}}\left( t \right){\mathbf{r}}dV} ,$(4)
$~{{{\mathbf{Z}}}_{i}} = {{\Theta }_{i}}\left( {{{{\mathbf{R}}}_{i}} - ~{{{{\mathbf{\bar {R}}}}}_{i}}} \right) = \int\limits_V {\left( {{{\rho }_{i}} - {{{\bar {\rho }}}_{i}}} \right)} {\kern 1pt} {\mathbf{r}}dV,$ОБОБЩЕНИЕ ФУНДАМЕНТАЛЬНОГО УРАВНЕНИЯ ГИББСА
Фундаментальное уравнение Гиббса, выражает объединенное первое и второе начала термодинамики равновесных открытых систем
(5)
$\begin{gathered} dЕ = TdS - pdV + \sum\limits_k {{{\mu }_{k}}d{{N}_{k}}} , \\ (k = 1,2, \ldots ,K), \\ \end{gathered} $Представим себе систему, которая в квазиравновесном состоянии пополняет свою энергию “n” независимыми способами (путем теплообмена, массообмена, работы и т.д.). Тогда ее равновесное состояние определяется (согласно принципу различимости процессов) “n” независимыми термостатическими координатами ${{\Theta }_{i}}$. При отклонении от состояния равновесия она будет обладать в общем случае “n” дополнительными степенями свободы, обусловленными протеканием в ней векторных процессов релаксации. В соответствии с принципом различимости ее состояние в данном случае представляет собой набор значений “n” скалярных ${{\Theta }_{i}}$ и “n” векторных экстенсивных координат Zi, определенных выше. Этого достаточно, чтобы записать полный дифференциал энергии системы как функции этих переменных E = E(${{\Theta }_{i}}$, Zi) в виде
(7)
$dЕ = \mathop \sum \limits_i \left( {{{\partial Е} \mathord{\left/ {\vphantom {{\partial Е} {\partial {{\Theta }_{i}}}}} \right. \kern-0em} {\partial {{\Theta }_{i}}}}} \right)d{{\Theta }_{i}} + \mathop \sum \limits_i ({{\partial Е} \mathord{\left/ {\vphantom {{\partial Е} {\partial {{{\mathbf{Z}}}_{i}}}}} \right. \kern-0em} {\partial {{{\mathbf{Z}}}_{i}}}})~d{{{\mathbf{Z}}}_{i}}.$Поскольку производные от одних параметров состояния (в данном случае энергии Е) по другим (${{\Theta }_{i}}$ и ${{{\mathbf{Z}}}_{i}}$) также являются параметрами состояния, то, обозначая их соответственно
(8)
$\overline {{{\Psi }_{i}}} \equiv ({{\partial E} \mathord{\left/ {\vphantom {{\partial E} {\partial {{\Theta }_{i}}}}} \right. \kern-0em} {\partial {{\Theta }_{i}}}});\,\,\,\,{{{\mathbf{X}}}_{i}} \equiv --\left( {{{\partial E} \mathord{\left/ {\vphantom {{\partial E} {\partial {{{\mathbf{Z}}}_{i}}}}} \right. \kern-0em} {\partial {{{\mathbf{Z}}}_{i}}}}} \right),$(9)
$dЕ \equiv \mathop \sum \limits_i {{\bar {\Psi }}_{i}}d{{\Theta }_{i}} - \mathop \sum \limits_i {{{\mathbf{X}}}_{i}}d{{{\mathbf{Z}}}_{i}},\,\,\,\,~\left( {~i = 1,~2, \ldots ,~n} \right).$Это тождество представляет собой обобщение фундаментального уравнения Гиббса (6) на неоднородные системы. Оно есть результат учета совместного влияния на состояние системы двух пар “глобальных” (для системы в целом) сопряженных переменных $~{{\Psi }_{i}}$,$~{{\Theta }_{i}}$ и Хi, Zi. В сравнении с (6) уравнение (9) содержит удвоенное число переменных состояния, что отражает наличие у пространственно распределенных сред дополнительных степеней свободы. связанных с векторными процессами (перераспределения).
В однородных системах, где Zi = 0, а интенсивные переменные (абсолютная температура Т, давление р, химические потенциалы ${{\mu }_{k}}$ и т.д.) не зависят от пространственных координат r, уравнение (9) переходит в уравнение Гиббса (6), где ${{\Theta }_{i}}$ = S, –V, Mk и т.д., а параметры $\overline {{{\Psi }_{i}}} $ переходят в $~{{\Psi }_{i}}$. Иного рода члены второй суммы выражения (9), соответствующие процессам перераспределения. Смысл их проясняется, если учесть, что выведение системы из состояния внутреннего равновесия требует затраты определенной работы. Тогда, сопоставляя эту работу с общим определением элементарной работы i-го рода Wi как произведения результирующей Fi сил i-го рода на вызванное ею перемещение dr объекта ее приложения, можно записать
(10)
$\delta {{W}_{{i~}}} = {{{\mathbf{F}}}_{i}}d{{{\mathbf{r}}}_{i}} = ({{{{{\mathbf{F}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\mathbf{F}}}_{i}}} {{{\Theta }_{i}}}}} \right. \kern-0em} {{{\Theta }_{i}}}}){{\Theta }_{i}}d{{{\mathbf{r}}}_{i}} = {{{\mathbf{X}}}_{i}}d{{{\mathbf{Z}}}_{i}}.~$Видно, что термодинамические силы Хi представляют собой результирующую движущую силу процесса совершения полезной работы, отнесенную к единице переносимой величины Хi = Fi/${{\Theta }_{i}}$. Это значит, что силы Хi аналогичны удельным массовым, объемным, поверхностным и т.п. силам в их обычном (ньютоновском) понимании.
Обобщение (9) соотношения Гиббса (6) свидетельствует о том, что все реальные системы, являясь неоднородными, относятся к так называемым сложным системам [11]. В них каждая i-я форма неравновесного энергообмена, будь то теплообмен, массобмен или работа, вызывает изменения состояния двоякого рода. Так, неравномерная объемная деформация порождает не только изменение плотности системы в целом (что характеризуется членом pdV), но и перераспределение плотности в пространстве системы, т.е. изменения состояния, характерные для процесса выравнивания давления (“барической релаксации”) или, напротив, перекачки газа из одной части системы в другую, что характеризуется членом XvdZv. Аналогичным образом, неравномерный нагрев системы вызывает не только повышение средней температуры (что характеризуется членом TdS), но и перераспределением энтропии по системе (что наблюдается при термической релаксации или работе тепловых насосов и характеризуется членом ХsdZs). По тем же причинам в соотношениях (7) и (9) наряду с членами ${{\mu }_{k}}d{{N}_{k}}$ появляются члены ХkdZk, описывающие процессы смесеобразования или разделения смесей (в том числе процессы диффузии или диализа). Иными словами, неоднородная система совершает наряду с работой расширения другие виды работ (называемые обычно полезными внешними или техническими).
Для характеристики скорости протекания упомянутых выше процессов, достаточно перейти в соотношении (9) к полным производным от энергии системы Е по времени t:
(11)
$\begin{gathered} {{dЕ} \mathord{\left/ {\vphantom {{dЕ} {dt}}} \right. \kern-0em} {dt}} \equiv \sum\limits_i {\overline {{{\Psi }_{i}}} } d{{{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}} - \\ - \,\,\sum\limits_i {{{{{{\mathbf{X}}}_{i}}d{{{\mathbf{Z}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\mathbf{X}}}_{i}}d{{{\mathbf{Z}}}_{i}}} {dt}}} \right. \kern-0em} {dt}}} ,\,\,\,(~i = 1,~2, \ldots ,~n). \\ \end{gathered} $Скорость равномерного пополнения системы энергией определяется слагаемыми $\overline {{{\Psi }_{i}}} {{d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}}$, в которых производные ${{d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}}$, представляют скалярный поток энергоносителя Ji$ \equiv $ $d{{\Theta }_{i}}$/dt (типа равномерного выпадения осадков на поверхность с неровным рельефом). Слагаемые XidZi представляют скорость пополнения системы энергией за счет работы сил Xi на перемещенях dZi согласно соотношению (10). Им соответствует векторный поток Ji = dZi/dt (направленный поток через ориентируемые участки поверхности). Скалярный поток соответствует представлению о потоке как количестве k-го вещества, заряда и т.п., проходящего в единицу времени через всю контрольную поверхность f, и имеет размерность кг/с, м3/с, Кл/с и т.д. Векторные потоки Ji согласно с выражению (9) представляет собой произведение переносимой полевой величины ${{\Theta }_{i}}$ на скорость wi = = dri/dt ее переноса относительно начального положения центра этой величины
(12)
${{{\mathbf{J}}}_{i}} = {{d{{{\mathbf{Z}}}_{i}}} \mathord{\left/ {\vphantom {{d{{{\mathbf{Z}}}_{i}}} {dt}}} \right. \kern-0em} {dt}} = {{\Theta }_{i}}{{{\mathbf{w}}}_{i}} = {{\Theta }_{i}}({{{\mathbf{v}}}_{i}}--{\mathbf{v}}){\text{ }},$Видно, что термодинамические силы (как удельные движущие силы процесса переноса материального энергоносителя) и соответствующие им потоки вводятся в качестве исходных понятий без привлечения громоздких уравнений баланса массы, заряда, импульса и производства энтропии, уравнений для кинетической и потенциальной энергии, как это принято в неравновесной термодинамике [12–22 ]. Стало возможным обнаружить новые, неизвестные до сих пор виды сил: силы избирательного массообмена, силы лучистого энергообмена, гироскопические силы, силы продольного магнитного поля, а также вскрыть решающую роль гравитационных сил в природе [4]. Итак, соотношения (9) или (11), описывающие состояние неравновесной системы в пространстве переменных ${{\Theta }_{i}}$ и Zi, по–существу, представляют собой обобщенное уравнение сохранения энергии для реальных природных и технологических процессов.
МАТЕМАТИЧЕСКИЙ АППАРАТ ЭНЕРГОДИНАМИКИ
При переходе от термостатики к энергодинамике пространство координат системы в виде термостатических переменных $~{{\Theta }_{i}}$ дополняется параметрами неоднородности Zi, порождаемыми смещениями Ri центров этих параметров относительно равновесного состояния. Описание смещения Ri ведется в координатах r и скоростей v материальных точек. Тем самым состояние энергодинамической системы задается на пространстве как скалярных ${{\Theta }_{i}},$ так и векторных Zi величин. Обобщенной характеристикой такой системы служит скалярная функция состояния – ее энергия Е(${{\Theta }_{i}}$, Zi). По существу, энергодинамическая система порождается объединением двух систем – термостатической и механической, а усложнение структуры обусловлено строением параметров неоднородности Zi.
Классификация реальных процессов. Если записать полный дифференциал ${{{\mathbf{Z}}}_{i}}$ =$~~{{{\mathbf{Z}}}_{i}}$(${{\Theta }_{i}}$,$~{{{\mathbf{R}}}_{i}})$ в абсолютной системе отсчета d$~{{{\mathbf{Z}}}_{i}}$ = Rid${{\Theta }_{i}}$ +$~{{\Theta }_{i}}d{{{\mathbf{R}}}_{{i~}}}$, то, во-первых, это разложение соответствует разделению всех процессов на равновесные и неравновесные. Во-вторых, оно разделяет процессы по типу связанного с ними движения. Действительно, представим дифференциал смещения $~d{{{\mathbf{R}}}_{i}}$ в виде суммы произведения скаляра ${{R}_{i}}$ на единичный вектор ei в направлении удлинения вектора ${{{\mathbf{R}}}_{i}},$ и дифференциала dei как векторного произведения dei = dφi × ei, где φi – угол поворота вектора ei. В результате получим
(14)
$d{{{\mathbf{Z}}}_{i}} = {{{\mathbf{R}}}_{i}}d~{{\Theta }_{i}} + {{\Theta }_{i}}d{{{\mathbf{S}}}_{i}} + \,\,~{{\Theta }_{i}}{{R}_{i}}[d{{{\mathbf{\varphi }}}_{i}} \times {\mathbf{~}}{{{\mathbf{e}}}_{i}}],$Из (14) видно, что энергия Е системы, как функция ее состояния, в общем случае становится функцией трех независимых аргументов Е = Е (${{\Theta }_{i}},~{{{\mathbf{S}}}_{i}}$,φi), а ее полный дифференциал выражается как
(15)
$\begin{gathered} dE = \sum\limits_i {\left( {{{\partial Е} \mathord{\left/ {\vphantom {{\partial Е} {\partial {{\Theta }_{i}}}}} \right. \kern-0em} {\partial {{\Theta }_{i}}}}} \right)} d{{\Theta }_{i}} + \sum\limits_i {\left( {{{\partial Е} \mathord{\left/ {\vphantom {{\partial Е} {\partial {{{\mathbf{S}}}_{i}}}}} \right. \kern-0em} {\partial {{{\mathbf{S}}}_{i}}}}} \right)} d{{{\mathbf{S}}}_{i}} + \\ + \,\,\sum\limits_i {\left( {{{\partial Е} \mathord{\left/ {\vphantom {{\partial Е} {\partial {{{\mathbf{\varphi }}}_{i}}}}} \right. \kern-0em} {\partial {{{\mathbf{\varphi }}}_{i}}}}} \right)} d{{{\mathbf{\varphi }}}_{i}} \\ \end{gathered} $(16)
$dЕ \equiv \sum\limits_i {{{{\bar {\Psi }}}_{i}}d{{\Theta }_{i}}} ~\,\, + \sum\limits_i {{{{\mathbf{F}}}_{i}}d{{{\mathbf{S}}}_{i}}} + \sum\limits_i {{{{\mathbf{M}}}_{i}}d{{{\mathbf{\varphi }}}_{i}}} ,$(17)
${{dЕ} \mathord{\left/ {\vphantom {{dЕ} {dt}}} \right. \kern-0em} {dt}} \equiv \sum\limits_i {{{{\bar {\Psi }}}_{i}}{{d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}}} + \sum\limits_i {{{{\mathbf{F}}}_{i}}{{{\mathbf{\upsilon }}}_{i}}} + \sum\limits_i {{{{\mathbf{M}}}_{i}}{{{\mathbf{\omega }}}_{i}}} ,$Из соотношения (17) видно, что в каждый фиксированный момент времени t неоднородную термодинамическую систему можно представить как идеальное “мгновенно твердое” тело, у которого скорость любой точки складывается из поступательной скорости ${{{\mathbf{\upsilon }}}_{i}}$ и угловой скорости $~{{{\mathbf{\omega }}}_{i}}~$ вращения вокруг мгновенного центра инерции этого тела. Авторы [6] отмечают, что перенос начала координат наблюдателя в центр инерции механической системы предпочтителен для анализа системы в целом. Энергодинамика идет дальше и переносит начало координат наблюдателя в равновесное или стационарное состояние термодинамической системы. Такое рассмотрение системы в целом, в которой действуют обобщенные силы и потоки, предпочтительнее, когда надо избежать излишнего переопределения механической системы параметрами состояния элемента сплошной среды, что затрудняет решение поставленной задачи. Для решения задач в такой постановке необходим соответствующий математический аппарат, позволяющий описывать процессы не только переноса, но и преобразования энергии.
Расширение пространства переменных с введением векторных координат смещения Ri(или пары S и ${{{\mathbf{\varphi }}}_{i}}$) отражает не только количественные, но и качественные изменения различных форм энергии. Протекание в системах наряду со скалярными процессами (с координатами ${{{{\Theta }}}_{i}})~$ векторных процессов (с координатами Ri) означает, что в таких системах совершается как неупорядоченная Wн, так и упорядоченная We работа (соответственно). Необратимость реальных процессов, связанная с диссипацией энергии (т.е. способностью к совершению неупорядоченной работы), проявляется в скаляризации процесса, т.е. утрате им векторной природы. Появляется возможность различать процессы энергопереноса (переноса энергии между телами в одной и той же форме) и процессы энергопревращения (превращения энергии из одной формы в другую), что связано с совершением неупорядоченной и упорядоченной работы.
Глобальная и локальная форма обобщенного закона сохранения энергии. Переход от глобальной формы (17) обобщенного закона сохранения энергии к его локальной формулировке для любого элемента сплошной среды (континуума) требует обоснования. Известно, что математическая модель сплошной среды базируется на трех постулатах: 1) сплошность (или непрерывность) материальной среды; 2) эвклидова метрика пространства; 3) абсолютность времени. Рабочим инструментом такой модели служит математическая теория скалярных, векторных и тензорных полей, используемых для описания пространственных распределений параметров состояния сплошной среды [7].
Математический аппарат термодинамики необратимых процессов строится на математической модели механики сплошной среды, дополненной фундаментальным соотношением равновесной термодинамики – уравнением Гиббса (5) [12–16 ]. Существенным ограничением такого подхода является допущение о локальном равновесии (гипотеза локального равновесия), т.е. о справедливости всех понятий равновесной термодинамики для элементарного объема континуума. При этом соотношение Гиббса (5) записывается относительно изменения энтропии S
(18)
$dS = {{T}^{{--1}}}dE + {{T}^{{--1}}}pdV + {{T}^{{--1}}}\sum\limits_k {{{\mu }_{k}}d{{N}_{k}}} ,$На основе этого скорость роста энтропии (“производство энтропии”) представляется в виде [12]
(19)
${{dS} \mathord{\left/ {\vphantom {{dS} {dt}}} \right. \kern-0em} {dt}} = \mathop \sum \limits_i \left( {{{\partial S} \mathord{\left/ {\vphantom {{\partial S} {\partial {{\alpha }_{i}}}}} \right. \kern-0em} {\partial {{\alpha }_{i}}}}} \right)\left( {{{d{{\alpha }_{i}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{i}}} {dt}}} \right. \kern-0em} {dt}}} \right) = \mathop \sum \limits_i {{X}_{i}}{{J}_{i}},$В энергодинамике математический аппарат строится аналогично, но теперь уже путем объединения модели сплошной среды с обобщенным уравнением сохранения энергии (17), что позволяет учитывать неоднородность системы в любом элементарном объеме системы. Первая особенность такого подхода состоит в том, что, как отмечалось выше, отпадает процедура поиска выражений для термодинамических потоков и сил через производство энтропии, поскольку они изначально присутствуют в исходном энергетическом соотношении (17). Во-вторых, надо учитывать, что энергия – экстенсивная характеристика термодинамической системы в целом. В связи с этим необходимо уточнить смысл, который вкладывается в понятие локальной энергии сплошной среды и дифференциальное уравнение баланса этой величины.
Впервые дифференциальную форму баланса энергии Е предложил Н. Умов (1873) [23]
(20)
$\rho {{de} \mathord{\left/ {\vphantom {{de} {dt}}} \right. \kern-0em} {dt}} + \nabla {{{\mathbf{j}}}_{e}} = 0,$(21)
$\rho {{ds} \mathord{\left/ {\vphantom {{ds} {dt}}} \right. \kern-0em} {dt}} + \nabla {{{\mathbf{j}}}_{s}} = {{\sigma }_{s}},$И. Дьярмати (1974) обобщил подход к составлению дифференциальных уравнений для экстенсивных свойств сплошной среды в ТНП [15 ] . Он допустил, что сплошная среда может характеризоваться экстенсивными свойствами, такими как энергия или ее энергоносители. Если некоторая экстенсивная полевая величина А c удельной характеристикой αm = ${{\partial А} \mathord{\left/ {\vphantom {{\partial А} {\partial M~}}} \right. \kern-0em} {\partial M~}}$ непрерывно распределена в материале континуума, занимающего объем V, ограниченный замкнутой поверхностью f, и плотность материального континуума есть ρ то полное изменение этой величины
в объеме V в зависимости от времени t(22)
$~{{dA} \mathord{\left/ {\vphantom {{dA} {dt}}} \right. \kern-0em} {dt}} = \frac{d}{{dt}}\int\limits_V {{{\alpha }_{V}}} dV = \,\,~\frac{d}{{dt}}\int\limits_V {\rho {{\alpha }_{m}}dV} $Локальное (пространственное) уравнения баланса. В данном случае нас интересует, что происходит в разные моменты времени в данной геометрической точке пространства, связанного с системой отсчета наблюдателя, т.е. наше внимание концентрируется на точке пространства, в которую приходят разные частицы движущейся сплошной среды. В этом случае объем V, для которого необходимо выразить изменение величины А, покоится в пространстве. Для такого способа наблюдения соотношение (22) принимает вид
(23)
${{dA} \mathord{\left/ {\vphantom {{dA} {dt}}} \right. \kern-0em} {dt}} = \frac{d}{{dt}}\mathop \smallint \limits_V^{} \rho {{a}_{m}}dV = \mathop \smallint \limits_V^{} \frac{\partial }{{\partial t}}(\rho {{a}_{m}})dV,$(24)
${\mathbf{j}}_{a}^{0} = \rho {{\alpha }_{m}}{{{\mathbf{v}}}_{a}} = {{\alpha }_{v}}{{{\mathbf{v}}}_{a}},$(25)
$\int\limits_V {\frac{\partial }{{\partial t}}} (\rho --{{\alpha }_{m}})dV = - \oint\limits_f {{{{\mathbf{j}}}_{a}}d{\kern 1pt} \operatorname{f} } ~\,\, + \int\limits_V {{{\sigma }_{a}}dV} ,$(26)
$\mathop \smallint \limits_{\text{V}}^{} \left( {\frac{\partial }{{\partial {\text{t}}}}({{\rho }}{{\alpha }_{m}})dV + \nabla {\mathbf{j}}_{a}^{0} - {{\sigma }_{a}}} \right) = 0.$В силу произвольности фиксированного объема V из (26) следует равенство нулю подынтегрального выражения, т.е.
(27)
$\begin{gathered} {{\partial \left( {{{\rho }}{{\alpha }_{m}}} \right)} \mathord{\left/ {\vphantom {{\partial \left( {{{\rho }}{{\alpha }_{m}}} \right)} {\partial t}}} \right. \kern-0em} {\partial t}} + \nabla {\mathbf{j}}_{a}^{0} = {{\sigma }_{a}} \\ {\text{или}}\,\,\,\,{{\partial {{\alpha }_{v}}} \mathord{\left/ {\vphantom {{\partial {{\alpha }_{v}}} {\partial t}}} \right. \kern-0em} {\partial t}} + \nabla ({{\alpha }_{v}}{{{\mathbf{v}}}_{a}}) = {{\sigma }_{a}}. \\ \end{gathered} $Полученное дифференциальное уравнение (27) называется локальной формой дифференциального уравнения баланса для полевой величины А. Из него следует локальная форма баланса массы континуума в отсутствии источников (σа = 0), для чего надо положить αm = 1 и ${\mathbf{j}}_{a}^{0}$ = $\rho {\mathbf{v}}$. В результате из (27) получаем
(28)
${{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } {\partial t}}} \right. \kern-0em} {\partial t}} + \nabla (\rho {\mathbf{v}}) = 0.$Заметим, что в каждой геометрической точке фиксированного объема V помимо потока массы континуума ${\mathbf{j}}_{a}^{0}$ = $\rho {\mathbf{v}}$ определяется и поток свойства А этого континуума ${\mathbf{j}}_{a}^{0}$ = ραmva = αvva. Это полезно иметь в виду, когда речь идет о таких абстрактных экстенсивных свойствах, как энергия Е, энтропия S и т.п.
Субстанциональное (материальное) уравнение баланса. В этом случае система координат наблюдателя связана с частицами сплошной среды. Она как бы “вморожена” в среду и деформируется вместе с ней. Все точки сплошной среды покоятся относительно подвижной (сопутствующей) системы координат. Это значит, что субстанциональный поток массы равен нулю j = 0. Если сравнить субстанциональный поток масcы j и его локальный поток j0 относительно внешней системы координат, то должно выполняться очевидное условие
Однако, из этого не следует, что при субстанциональном описании обращается в нуль плотность потока любого экстенсивного свойства А:
(30)
${{{\mathbf{j}}}_{a}} = {\mathbf{j}}_{a}^{0} - \rho {{\alpha }_{m}}{\mathbf{v}} = \rho {{\alpha }_{m}}({{{\mathbf{v}}}_{a}} - {\mathbf{v}}) = {{\alpha }_{{\text{v}}}}({{{\mathbf{v}}}_{a}} - {\mathbf{v}}).$При А = М величина ja становится плотностью потока массы ${\mathbf{j}}_{a}^{0}$ и соотношение (29) обращается в нуль, что соответствует уравнению (28).
При субстанциональном описании в сопутствующей системе координат выделенный объем материальной среды V движется вместе со средой, т.е. V = сonst, М = сonst и ρ = сonst, поэтому соотношение (22) принимает вид
(31)
${{dA} \mathord{\left/ {\vphantom {{dA} {dt}}} \right. \kern-0em} {dt}} = \frac{d}{{dt}}\int\limits_V {\rho {{\alpha }_{m}}dV} = \int\limits_V {\rho ({{d{{\alpha }_{m}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{m}}} {dt)dV}}} \right. \kern-0em} {dt)dV}}} .$Принимая во внимание (30), можно записать субстанциональное интегральное уравнение баланса
(32)
$\mathop \smallint \limits_V^{} \rho ({{d{{\alpha }_{m}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{m}}} {dt}}} \right. \kern-0em} {dt}})dV = - \oint\limits_f {{{{\mathbf{j}}}_{a}}d{\mathbf{f}}} + \int\limits_V {{{\sigma }_{a}}dV} ,$(33)
$\rho ({{d{{\alpha }_{m}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{m}}} {dt}}} \right. \kern-0em} {dt}}) + \nabla {{{\mathbf{j}}}_{a}} = {{\sigma }_{a}}\,\,\,\,{\text{или}}\,\,\,\,{{d{{\alpha }_{v}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{v}}} {dt}}} \right. \kern-0em} {dt}} + \nabla {{{\mathbf{j}}}_{a}} = {{\sigma }_{a}}.$Связь между субстациональным и локальным изменением удельной полевой величины αm дается соотношением [15 ] :
(34)
$\rho ({{d{{\alpha }_{m}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{m}}} {dt}}} \right. \kern-0em} {dt}}) = \partial {{(\rho {{\alpha }_{m}})} \mathord{\left/ {\vphantom {{(\rho {{\alpha }_{m}})} \partial }} \right. \kern-0em} \partial }t + \nabla \rho {{\alpha }_{m}}{\mathbf{v}}$(35)
$\rho ({{d{{\alpha }_{m}}} \mathord{\left/ {\vphantom {{d{{\alpha }_{m}}} {dt}}} \right. \kern-0em} {dt}}) = \partial {{{{\alpha }_{v}}} \mathord{\left/ {\vphantom {{{{\alpha }_{v}}} \partial }} \right. \kern-0em} \partial }t + \nabla {{\alpha }_{v}}{\mathbf{v}}.$Здесь αm может быть любой удельной полевой величиной, в том числе скаляром, компонентом вектора или тензора второго ранга и т.д. Если в частном случае удельная масса αm = 1, то соотношение (34) и (35) сводится к локальному уравнению баланса массы (28).
Дифференциальные уравнения баланса энергоносителя. Переходя от обозначений αv = dA/dV, αm = dA/dM к соответствующим обозначениям плотности i-го энергоносителя ρi = ${{d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\Theta }_{i}}} {dV}}} \right. \kern-0em} {dV}}$ и его удельной величины $\rho _{i}^{'}$ = ${{d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\Theta }_{i}}} {dM}}} \right. \kern-0em} {dM}}$, а также учитывая связь $~\rho {{\alpha }_{m}}$ = αv, можно записать $~$субстанциональное дифференциальное уравнение баланса энергоносителя${\text{\;}}{{{{\Theta }}}_{{\text{i}}}}$ на основе соотношения (33)
(36)
${{d{{\rho }_{i}}} \mathord{\left/ {\vphantom {{d{{\rho }_{i}}} {dt}}} \right. \kern-0em} {dt}} + \nabla {{\rho }_{i}}{{{\mathbf{w}}}_{i}} = {{\sigma }_{i}}\,\,\,\,{\text{или}}\,\,\,\,{{d{{\rho }_{i}}} \mathord{\left/ {\vphantom {{d{{\rho }_{i}}} {dt}}} \right. \kern-0em} {dt}} + \nabla {{{\mathbf{j}}}_{i}} = {{\sigma }_{i}},$Локальное дифференциальное уравнение баланса энергоносителя ${{\Theta }_{{i~}}}$ на основе соотношения (27) примет вид
(37)
${{\partial {{\rho }_{i}}} \mathord{\left/ {\vphantom {{\partial {{\rho }_{i}}} {\partial t}}} \right. \kern-0em} {\partial t}} + \nabla {{\rho }_{i}}{{{\mathbf{v}}}_{i}} = {{\sigma }_{i}}\,\,\,\,{\text{или}}\,\,\,\,{{\partial {{\rho }_{i}}} \mathord{\left/ {\vphantom {{\partial {{\rho }_{i}}} {\partial t}}} \right. \kern-0em} {\partial t}} + \nabla {\mathbf{j}}_{i}^{0} = {{\sigma }_{i}}.$Из (36) и (37) видно, что какая-либо экстенсивная величина ${{\Theta }_{i}}$ в изолированной системе (где $\nabla {{{\mathbf{j}}}_{i}}$ = 0 или $\nabla {\mathbf{j}}_{i}^{0}$ = 0) остается постоянной, если в системе отсутствует ее источник (σi = 0). Решение вопроса о том, подчиняется ли этому закону какой-либо энергоноситель, решается исключительно экспериментальным путем [15 ] .
Связь потока энергии с потоками энергоносителей. Если за А принять энергию системы Е, то для нее справедливо соотношение (22) в виде
(38)
${{dE} \mathord{\left/ {\vphantom {{dE} {dt}}} \right. \kern-0em} {dt}} = ~~~\frac{d}{{dt}}\mathop \smallint \limits_V^{} {{\alpha }_{e}}dV = ~~\frac{d}{{dt}}\mathop \smallint \limits_V^{} \rho edV = - {{J}_{e}},$(39)
${{J}_{e}} = {{dE} \mathord{\left/ {\vphantom {{dE} {dt}}} \right. \kern-0em} {dt}} = - \oint\limits_f {{{{\mathbf{j}}}_{e}}{\mathbf{n}}df} ,$(40)
$~{{dЕ} \mathord{\left/ {\vphantom {{dЕ} {dt}}} \right. \kern-0em} {dt}} = ~--\oint\limits_f {{{{\mathbf{j}}}_{e}}d{\mathbf{f}}} ~ = - \int\limits_V {\nabla {{{\mathbf{j}}}_{e}}dV} .$Такую же форму предложил Н. Умов (1837) [23] для механической системы в виде упругого тела, однако в рассматриваемом случае она имеет более общий характер, т.к. не ограничивается понятием механической энергии. Уравнение (40) отражает принятую концепцию близкодействия, согласно которой энергия системы Е не просто исчезает в одних точках пространства и возникает в других, а переносится через границы системы df потоком энергии с плотностью $~~~{{{\mathbf{j}}}_{{\text{e}}}}~$ материальным носителем. Как показано выше, от интегрального уравнения (40) нетрудно перейти к его дифференциальной субстанциональной форме
(41)
${{d{{\rho }_{e}}} \mathord{\left/ {\vphantom {{d{{\rho }_{e}}} {dt}}} \right. \kern-0em} {dt}} + \nabla {{{\mathbf{j}}}_{e}} = 0,$Для дальнейшего важно установить связь между плотностью потока энергии je и потоками ее энергоносителей ji. Для этого представим каждую i-ю составляющую jei плотности потока энергоносителя ${{\Theta }_{i}}$, в виде произведения удельного значения энергии (потенциала) ${{\psi }_{i}} = ~\,\,{{\partial E} \mathord{\left/ {\vphantom {{\partial E} {\partial ~{{\Theta }_{i}}}}} \right. \kern-0em} {\partial ~{{\Theta }_{i}}}}$ на плотность потока импульса энергоносителя ji = ρivi, где ρi = ${{\partial ~{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{\partial ~{{\Theta }_{i}}} {~\partial V}}} \right. \kern-0em} {~\partial V}},$ vi – скорость переноса i-го энергоносителя во внешней (неподвижной) системе отсчета. При этом искомая связь принимает вид:
(42)
$~{{{\mathbf{j}}}_{e}} = \mathop \sum \limits_i {{{\mathbf{j}}}_{{ei}}} = \mathop \sum \limits_i {{\psi }_{i}}~{{{\mathbf{j}}}_{i}},\,\,(i = 1,2, \ldots ,n).$Теперь дивергенция потока $\nabla {{{\mathbf{j}}}_{e}}$, входящая в уравнение (40), становится дивергенцией произведения скаляра $~{{\psi }_{i}}$ на вектор ji, так что можно записать
(43)
$\nabla {{{\mathbf{j}}}_{e}} = \mathop \sum \limits_i \nabla {{{\mathbf{j}}}_{a}}_{i} = \sum\limits_i {\nabla {{\psi }_{i}}{{{\mathbf{j}}}_{i}}} = \sum\limits_i {{{\psi }_{i}}\nabla {{{\mathbf{j}}}_{i}}} + \sum\limits_i {{{{\mathbf{j}}}_{i}}\nabla {{\psi }_{i}}} .$Подставляя (43) в (40), получаем выражение закона сохранения энергии в развернутом виде:
(44)
${{dЕ} \mathord{\left/ {\vphantom {{dЕ} {dt}}} \right. \kern-0em} {dt}} = - \sum\limits_i {\int\limits_V {{{\psi }_{i}}\nabla {{{\mathbf{j}}}_{i}}} } {\kern 1pt} {\kern 1pt} dV - \sum\limits_i {\int\limits_V {{{{\mathbf{j}}}_{i}}\nabla {{\psi }_{i}}dV} } {\kern 1pt} ,$Нетрудно показать, что развернутая форма (44) эквивалентна глобальной форме (11) закона сохранения энергии. Для этого в первой сумме справа вынесем за знак интеграла некоторое среднее значение $\overline {{{\psi }_{i}}} $ локального потенциала ${{\psi }_{i}}$, а во второй вынесем за знак интеграла среднее значение ${{{\mathbf{X}}}_{i}}$ градиента потенциала $\nabla {{\psi }_{i}}$. Тогда, сохраняя принятое в термодинамике правило знаков для теплоты и работы (подведенная к системе теплота и совершенная ею работа считаются положительными) закон сохранения энергии (44) можно выразить параметрами неравновесной системы в целом:
(46)
${{dE} \mathord{\left/ {\vphantom {{dE} {dt}}} \right. \kern-0em} {dt}} = \mathop \sum \limits_i {{\bar {\psi }}_{i}}{{J}_{i}} + \mathop \sum \limits_i {{{\mathbf{X}}}_{i}}{{{\mathbf{J}}}_{i}},\,\,\,\,(i = 1,2, \ldots ,n),$${{{\mathbf{J}}}_{i}} = \int\limits_V {{{{\mathbf{j}}}_{i}}dV} = \int\limits_V {{{\rho }_{i}}{{{\mathbf{\upsilon }}}_{i}}dV} = ~~{{\Theta }_{i}}{{{\mathbf{\bar {\upsilon }}}}_{i}}$ – векторный поток i-го энергоносителя (обобщенный направленный поток, соответствующий понятию его импульса ${{\theta }_{i}}{{{\mathbf{\bar {\upsilon }}}}_{{i~}}}$);
${{{\mathbf{\bar {\upsilon }}}}_{i}} = {{d{{{\mathbf{R}}}_{i}}} \mathord{\left/ {\vphantom {{d{{{\mathbf{R}}}_{i}}} {dt}}} \right. \kern-0em} {dt}}$ – среднее значение скорости энергоносителя $~~{{\Theta }_{i}}$ для системы в целом;
${{{\mathbf{X}}}_{i}} = - \overline {\nabla {{\psi }_{i}}} = {{{{{\mathbf{F}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\mathbf{F}}}_{i}}} {{{\Theta }_{i}}}}} \right. \kern-0em} {{{\Theta }_{i}}}}~$ – усредненный по объему системы градиент соответствующего потенциала, взятый с обратным знаком, представляет собой обобщенный вектор напряженности или удельную величину силы (аналог понятия массовой, объемной, поверхностной и т.п. силы в механике). Эквивалентность (46) и (11) очевидна.
Глобальные и локальные переменные энергодинамической системы. Для дальнейшего важно установить связь между глобальными и локальными переменными энергодинамической системы. Она устанавливается путем сравнения между собой двух форм выражения обобщенного закона сохранения энергии (44) и (11). С этой целью рассмотрим частный случай идеальной равновесной системы, для которой ее полная энергия совпадает с внутренней (Е = U), а сама система пространственно однородна $({{\psi }_{i}}$ = ${{\Psi }_{i}}).$ В этом случае в уравнении (44) справа остается только первая сумма:
(47)
${{dЕ} \mathord{\left/ {\vphantom {{dЕ} {dt}}} \right. \kern-0em} {dt}} = - \sum\limits_i {\int\limits_V {{{\psi }_{i}}\nabla {{{\mathbf{j}}}_{i}}} } {\kern 1pt} dV = - \sum\limits_i {{{\Psi }_{i}}} \int\limits_V {\nabla {{{\mathbf{j}}}_{i}}} {\kern 1pt} dV.$Для выражения дивергенции потоков энергоносителей $\nabla {{{\mathbf{j}}}_{i}}$ через термостатические переменные воспользуемся дифференциальным субстанциональным уравнением баланса (36), где σi = 0:
(48)
$\nabla {{{\mathbf{j}}}_{i}} = ~ - {{d{{\rho }_{i}}} \mathord{\left/ {\vphantom {{d{{\rho }_{i}}} {dt}}} \right. \kern-0em} {dt}}.$Подставляя (48) в (47), получим
(49)
${{dЕ} \mathord{\left/ {\vphantom {{dЕ} {dt}}} \right. \kern-0em} {dt}} = \mathop \sum \limits_i {{\Psi }_{i}}\mathop \smallint \limits_V^{} \left( {{{d{{\rho }_{i}}} \mathord{\left/ {\vphantom {{d{{\rho }_{i}}} {dt}}} \right. \kern-0em} {dt}}} \right)~dV = \mathop \sum \limits_i {{\Psi }_{i}}d{{{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}},$В случае реальной неоднородной (внутренне неравновесной) системы рассмотренный идеальный случай соответствует равномерному процессу при нулевом смещении (Zi = 0). В этом случае потенциал ${{\psi }_{i}}~$ распределен произвольно по объему системы, а изменение dρi/dt совпадает с изменением общего количества энергоносителя ${{\Theta }_{i}}$ в объеме V, т.е. dρi/dt = $~{{{{(d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{(d{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}})} \mathord{\left/ {\vphantom {{{{(d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{(d{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}})} M}} \right. \kern-0em} M}$. Поэтому для данного случая уравнение (44) примет вид
(50)
$~{{dЕ} \mathord{\left/ {\vphantom {{dЕ} {dt}}} \right. \kern-0em} {dt}} = - \sum\limits_i {\int\limits_V {{{\psi }_{i}}\nabla {{{\mathbf{j}}}_{i}}dV} } \, = \,\mathop \sum \limits_{i~} \left( {{{d~{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d~{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}}} \right)\frac{1}{M}\mathop \smallint \limits_M^{} {{\psi }_{i}}dM,$Перейдем к рассмотрению членов второй суммы уравнения (44). Видно, что они выражают ту часть потока энергии через границы системы, которая независима от членов первой суммы (теплообмена, работы расширения и энергомассообмена). Определенные как произведение xiji локальной силы хi = –$\nabla {{\psi }_{i}}$ и локального потока энергоносителя ji, они выражают локальную производительность (мощность) i-го процесса. Из свойства аддитивности энергии следует очевидное свойство инвариантности мощности процесса N = XiJi, что выражается как
(52)
${{{\mathbf{X}}}_{i}}{{{\mathbf{J}}}_{i}} = \int\limits_V {{{{\mathbf{x}}}_{i}}{{{\mathbf{j}}}_{i}}dV} ~,$(53)
${{{\mathbf{X}}}_{i}} = {\mathbf{J}}_{i}^{{ - 1}}\mathop \smallint \limits_V^{} {{{\mathbf{x}}}_{i}}{{{\mathbf{j}}}_{i}}{\kern 1pt} dV.$Установленная таким образом связь между локальными переменными, которыми оперируют полевые теории, в том числе, механика сплошной среды, и термодинамическими параметрами, характеризующими состояние континуальной системы в целом, открывает возможность описания их свойств с позиций энергодинамики. Введение понятий потоков Ji (глобального) и ji (локального), как обобщенных скоростей процессов переноса и мощности (производительности) процесса преобразования энергии в системе в целом Ni = = XiJi и в единице объема системы xiji имеет важное значение для всего естествознания в целом. Отметим, что понятие производительности относится только к процессам полезного преобразования энергии и поэтому в принципе не могло возникнуть в ТНП, которая ограничивается рассмотрением исключительно релаксационных (диссипативных) явлений.
Критерий противонаправленности процессов (безэнтропийный критерий эволюции системы). Преобразуем уравнение (44) с учетом субстанционального дифференциального уравнения баланса энергоносителя (36), в результате получим
(54)
$\begin{gathered} ~{{dЕ} \mathord{\left/ {\vphantom {{dЕ} {dt}}} \right. \kern-0em} {dt}} = \mathop \sum \limits_i {{\Psi }_{i}}\left( {{{d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}}} \right) - \\ - \,\,\mathop \sum \limits_i {\kern 1pt} \mathop \smallint \limits_V^{} {{\psi }_{i}}{{\sigma }_{i}}dV + \mathop \sum \limits_i {\kern 1pt} \mathop \smallint \limits_V^{} {{{\mathbf{x}}}_{i}}{{{\mathbf{j}}}_{i}}dV. \\ \end{gathered} $Поскольку в равновесии $dЕ = \mathop \sum \limits_i {{\Psi }_{i}}{{\Theta }_{i}},$ то из (54) следует важная связь источников энергоносителей ${{\sigma }_{i}}$ с локальными термодинамическими силами $~{{{\mathbf{x}}}_{i}}$:
(55)
$\mathop \sum \limits_i {{\psi }_{i}}{{\sigma }_{i}} = \mathop \sum \limits_i {{{\mathbf{x}}}_{i}}{{{\mathbf{j}}}_{i}},$(56)
$T{{\sigma }_{s}} = T\left( {{{{{d}_{i}}S} \mathord{\left/ {\vphantom {{{{d}_{i}}S} {dt}}} \right. \kern-0em} {dt}}} \right) = \mathop \sum \limits_i {{X}_{i}}{{J}_{i}},$Таблица. 1.
Согласно принципу компенсации (55) в процессе релаксации неравновесных систем ($\mathop \sum \limits_i {{{\mathbf{x}}}_{i}}{{{\mathbf{j}}}_{i}} > 0$) возможно возникновение как источников (${{\sigma }_{i}} > 0$), так и стоков (${{\sigma }_{i}} < 0$) различных энергоносителей. В частности, такие источники или стоки имеются у числа молей ${{N}_{k}}$ любого k-го вещества, которое возникает или исчезает в ходе химических реакций. Существуют они и у поляризационных зарядов, возникающих под влиянием внешнего поля. Источники появляются у различных фаз вещества. Сюда же относится возрастание энтропии в изолированных системах. Однако существуют процессы, в которых приложенная работа лишь частично превращается в тепло, а остальная часть переходит в другие (нетепловые) формы энергии. Например, в процессах резания металлов или дробления материалов количество выделившегося тепла диссипации всегда меньше затраченной работы из-за перехода части упорядоченной энергии в другие формы внутренней энергии (например, энергию формирования поверхности раздела фаз). Таким образом, соотношение (55) свидетельствует о том, что внутренние источники (стоки) действительно существуют не только у энтропии S, но и у всех остальных энергоносителей.В классической термодинамике отсутствуют строгие доказательства принципа возрастания энтропии. На самом деле, в рамках равновесной термодинамики таких доказательств и быть не может. Действительно, пусть мы имеем равновесную систему, обладающую двумя степенями свободы: термической (характеризующейся энтропией S) и деформационной (характеризующейся объемом V). Внутренняя энергия изолированной системы ${{U}_{{{\text{из\;}}}}}$ как функция ее состояния имеет вид $~{{U}_{{{\text{из}}}}} = U\left( {S,~V} \right)$. В таком случае, рассматривая энтропию S как обратную функцию ${{S}_{{{\text{из}}}}} = S\left( {U,~V} \right)$, находим, что в изолированных системах (где $U,~V = {\text{const}}$) энтропия остается неизменной:
С физической точки зрения такой вывод очевиден: в равновесной системе никакие процессы, в том числе и процессы диссипации, возникнуть не могут. Они возможны только в отсутствие равновесия, когда в число параметров, характеризующих энергию системы ${{U}_{{{\text{из}}}}}$, входят и параметры неравновесности, например, силы ${{{\mathbf{X}}}_{i}}$, способные изменяться в изолированных системах, т.е. ${{U}_{{{\text{из}}}}} = U\left( {S,{{{\mathbf{X}}}_{i}},~V} \right)$. Тогда и энтропия такой системы может изменяться вместе с ${{{\mathbf{X}}}_{i}}$. Однако в этом случае и сам принцип возрастания энтропии становится не нужным, поскольку сами параметры ${{{\mathbf{X}}}_{i}}$ могут выполнять роль критериев эволюции, притом намного более простых, понятных, легко вычислимых и информативных, поскольку они способны отразить не только инволюцию, но эволюцию системы, и не только системы в целом, но и каждой степени ее свободы в отдельности:
(57)
$d{{{\mathbf{X}}}_{i}} < 0\,\,\left( {{\text{инволюция}}} \right);~\,\,d{{{\mathbf{X}}}_{i}} > 0\left( {{\text{эволюция}}} \right).$При необходимости выяснить поведение системы в целом, то альтернативой энтропии может служить критерий:
(58)
$\begin{gathered} \mathop \sum \limits_i {{{\mathbf{X}}}_{i}}{{{\mathbf{J}}}_{i}} < 0\,\,\left( {{\text{инволюция}}} \right); \\ ~~\mathop \sum \limits_i {{{\mathbf{X}}}_{i}}{{{\mathbf{J}}}_{i}} > 0\,\,\left( {{\text{эволюция}}} \right). \\ \end{gathered} $Критерии (57) и (58) позволяют установить причину необратимости и оценить вклад в процесс диссипации каждого реального процесса, что важно при анализе возможностей его совершенствования.
Выявленные безэнтропийные критерии эволюции имеют далеко идущие последствия в становлении современного мировоззрения. В термодинамике это приводит к утверждению идей тепловых машин Карно и ошибочности термодинамики Клаузиуса, основанной на понятии энтропии, что привело к выявленному И. Пригожиным вопиющему противоречию термодинамики с биологической эволюцией. В биологии это приводит к доказательству принципа выживаемости, согласно которому более продолжительным репродуктивным периодом обладают более развитые системы с большим числом процессов, противонаправленным релаксационным. Такие системы дольше живут и, естественно, приобретают преимущество. Это не борьба за выживание, а приобретение преимуществ при усложнении системы. В космологии это приводит к необходимости деления материи на структурированную (барионную) и неструктурированную (эфироподобную), что позволяет обосновать существование ее кругооборота во Вселенной и возможности функционирования неограниченно во времени и пространстве, вопреки теории Большого взрыва. В электростатике и электродинамике это привело к утверждению новых представлений о распространении света [4].
Противонаправленность процессов в сочетании с понятием локальной производительности (мощности) физико-химической системы порождает новое направление в технике – техническую энергодинамику как науку о преобразовании энергии в любых машинах [4]. Данное направление не могло родиться в рамках ТНП, которая ограничивалась рассмотрением исключительно релаксационных (диссипативных) явлений. При переходе к анализу реальных процессов известные соотношения взаимности Л. Онзагера Lij = Lji уступают место энергодинамическим соотношениям взаимности $\left( {{{\partial {{J}_{i}}} \mathord{\left/ {\vphantom {{\partial {{J}_{i}}} {\partial {{X}_{j}}}}} \right. \kern-0em} {\partial {{X}_{j}}}}} \right) = - ~\left( {{{\partial {{J}_{j}}} \mathord{\left/ {\vphantom {{\partial {{J}_{j}}} {\partial {{X}_{i}}}}} \right. \kern-0em} {\partial {{X}_{i}}}}} \right)$, имеющим универсальный характер [4].
НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ЭНЕРГОДИНАМИКИ
Избирательное взаимодействие. Как показано выше, в энергодинамике термодинамические силы Xi выражаются отрицательными градиентами обобщенных потенциалов ${{\psi }_{i}}$ (температуры, давления, химического, электрического, гравитационного и т.п.). т.е. Хi = $ - \nabla {{\psi }_{i}}$. В настоящее время найдены аналитические выражения около трех десятков движущих сил различных физико-химических процессов переноса [4]. При этом выяснилось, что многочисленные термомеханические, термохимические, термоэлектрические, термомагнитные, электрокинетические и т.п. эффекты, наблюдаемые при протекании реальных процессов, обусловлены суперпозицией каких-либо двух разнородных сил из числа действующих в неоднородной системе. Накладываясь в разных соотношениях, зависящих от условий протекания того или иного процесса, эти силы порождают то разнообразие процессов, которое мы наблюдаем в различных макросистемах.
В энергодинамике показано, что любая волна (акустическая, гидравлическая, электромагнитная, эфирная и т.п.) подобна диполю, что обусловливает силовой характер ее взаимодействия с веществом. При этом сила проявляется как градиент специфического амплитудно-частотного потенциала [25]. Благодаря этому любые взаимодействия, осуществляемые посредством осциллирующей промежуточной среды, как бы ее ни называли (эфиром или полем), также приобретают силовой характер. При этом характер такого взаимодействия определяется не какой-либо особой природой действующих сил, а резонансным усилением энергообмена на частотах собственных колебаний различных структурных элементов взаимодействующих тел. Такое взаимодействие названо избирательным.
Убедительным подтверждением такой природы взаимодействия являются многочисленные явления резонансного поглощения или излучения, наблюдаемые во всех областях естествознания. Показано, что избирательное силовое взаимодействие с веществом может осуществляться полем любой осциллирующей скалярной величины, т.е. это поле не обязательно электромагнитное. Таково, в частности, резонансное поглощение энергии упругих или электромагнитных волн; “безразличие” к атомам иного “сорта”, выражающееся в понятии парциального давления; взаимодействие различных химических реагентов в определенных для каждого из них кратных соотношениях; явления катализа в химических реакциях; селективная проводимость мембран по отношению к различным веществам и растворам; избирательная абсорбция определенных веществ поверхностью тел; диффузия, осмос, фильтрация веществ через полупроводниковые мембраны; синхронизация частот излучения в лазерах; избирательное взаимодействие белков с РНК и избирательное воздействие фармацевтических средств на организм; преимущественное воспроизведение одних из них и уничтожение других в процессах эволюции и т.д. и т.п. [26].
Законы превращения вместо законов сохранения. Весомым вкладом энергодинамики в естествознание является возможность описывать и объяснять такие явления природы, которые до сих пор не поддавались описанию и объяснению c позиций фундаментальных законов сохранения энергии, массы, заряда, количества движения и его момента. Появление многочисленных запатентованных самодвижущихся устройств, работающих с нарушением законов Ньютона, а также обнаружение ускоренного расширения Вселенной, свидетельствующее о самопроизвольном возрастании количества движения в ней, приводят к необходимости пересмотра вышеперечисленных “фундаментальных” законов с позиций энергодинамики.
Известно, что механика Ньютона не рассматривала внутренние процессы, протекающие в ускоряющихся телах, полагая, что они остаются в состоянии внутреннего равновесия. Внутреннее равновесие означает равенство нулю дивергенции потока любого энергоносителя $\nabla {{{\mathbf{j}}}_{i}} = 0$ в уравнении (25), где для механической системы принимается А = ${{\Theta }_{i}}$, в частности $~{{\Theta }_{i}}$ = $P = M\upsilon $, Р – количество движения механической системы (скаляр). Поэтому интегральное уравнение
(59)
${{d{{\Theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\Theta }_{i}}} {dt}}} \right. \kern-0em} {dt}} = \int\limits_V {{{\partial {{\rho }_{i}}} \mathord{\left/ {\vphantom {{\partial {{\rho }_{i}}} {\partial t}}} \right. \kern-0em} {\partial t}}} dV = - \oint\limits_f {{{{\mathbf{j}}}_{i}}} d{\mathbf{f}} + \int\limits_V {{{\sigma }_{p}}dV} $(60)
$F = {{dP} \mathord{\left/ {\vphantom {{dP} {dt}}} \right. \kern-0em} {dt}} = \int\limits_V {{{\sigma }_{p}}} dV,$Таким образом, закона сохранения импульса ${\mathbf{P}} = M{\mathbf{\upsilon }}$ при ${\mathbf{F}} = {{d{\mathbf{P}}} \mathord{\left/ {\vphantom {{d{\mathbf{P}}} {dt}}} \right. \kern-0em} {dt}}$ в природе не существует. Формально это становится ясным при применении уравнений (59) или (60) к компонентам ${{P}_{\alpha }} = M{{\upsilon }_{\alpha }}$ ($\alpha = 1,2,3$) импульса $M{\mathbf{\upsilon }}$, в котором при этом условии появляются слагаемые $\sigma _{\alpha }^{e}$ внешнего источника импульса. То же самое справедливо в отношении компонента момента импульса ${\mathbf{M}} = {{I}_{\omega }}{\mathbf{\omega }}$, выраженного произведением момента инерции $~{{I}_{\omega }}$ и угловой скорости $~{\mathbf{\omega }}$.
Нетрудно показать, что законы сохранения любых энергоносителей, включая количество движения и его момент, уступают место принципу их взаимопревращения. Вектор скорости ${\mathbf{\upsilon }}$ может быть разложен на поступательную ${\mathbf{w}}~$ и вращательную u = ${\mathbf{\omega }}~{\text{ }} \times {\mathbf{r}}$ составляющие:
Соответственно этому и импульс ${\mathbf{J}} = M{\mathbf{\upsilon }}$ включает в себя наряду с поступательной ${{{\mathbf{J}}}^{{\text{w}}}} = {\text{M}}{\mathbf{w}}$ вращательную составляющую ${{{\mathbf{J}}}^{{{\omega }}}} = M({\mathbf{\omega }} \times {\mathbf{r}})$ (момент количества движения). Поэтому закон сохранения импульса
При учете колебательного движения энергоносителей число процессов взаимопревращения импульсов существенно расширяется. Простейшим из таких процессов является волнообразование. С учетом плотности импульса волнового движения плотность импульса i-го энергоносителя ${{{\mathbf{j}}}_{i}} = {{{\mathbf{\upsilon }}}_{i}}$ теперь будет включать в себя уже три составляющих: поступательную ${\mathbf{j}}_{i}^{w} = {{\rho }_{i}}{{{\mathbf{w}}}_{i}}$, вращательную ${\mathbf{j}}_{i}^{\omega } = {{\rho }_{i}}{{{\mathbf{r}}}_{i}} \times {{{\mathbf{\omega }}}_{i}}$ и колебательную ${\mathbf{j}}_{i}^{\nu } = \rho _{i}^{\nu }{\mathbf{\upsilon }}_{i}^{\nu }$. Тогда, переходя от локальных к глобальным переменным, закон сохранения внутренней энергии закрытой неоднородной системы примет вид [27]:
Видно, что при ${{{\mathbf{X}}}_{i}} \ne 0$ в нуль обращается сумма потоков всех i-х энергоносителей замкнутой неоднородной системы, но не каждый из них в отдельности. Это значит, что имеет место взаимное превращение не только различных форм энергии, но и импульсов одной и той же ее формы (в данном случае механической). В частности, имеет место взаимное превращение импульсов поступательного, вращательного и колебательного движения. Отсюда следует, что закон сохранения любого энергоносителя должен уступить место общему принципу взаимопревращения энергоносителей ${{\Theta }_{i}} \to {{\Theta }_{j}}$, ($i,j = 1,2, \ldots ,n$). Это значит, что импульс является эмерджентным свойством системы, допускающим возможность как его возникновения или исчезновения, так и взаимного превращения подобно различным формам энергии. Многочисленные экспериментальные подтверждения этого принципа придают ему статус закона природы.
Практика показывает, что создание реальных “самодвижущихся” устройств вполне возможно [28–30]. В частности, основным процессом, приводящим к возникновению локальной неоднородности в любой среде, является волнообразование. Именно это приводит к появлению в космической среде сил гравитации и инерции, создающих благодаря их всепроникающему характеру “опору” для кажущихся “самодвижущимися” устройств, якобы нарушающих законы механики. Энергодинамика приводит к пониманию возможности создания движения за счет любых внутренних сил при наличии их результирующей. Это открывает новые возможности создания установок длительного космического транспорта. Примером может служить действующая модель космического двигателя, развивающего тягу за счет направленного микроволнового излучения, созданная российским ученым и изобретателем В.С. Леоновым [30].
Восстановление первоначального варианта таблицы химических элементов Д.И. Менделеева. Обобщенный закон сохранения энергии (11) говорит о том, что энергия может переноситься и преобразовываться не только известными нам энергоносителями ${{\Theta }_{i}}$ ($i = 1,~2, \ldots ,~n$), относящимися к видимому нами веществу, но и любыми другими энергоносителями ${{\tilde {\Theta }}_{i}}$, ($i = 1,~2, \ldots ,~k$), относящимися к субстанции, о которой можно судить лишь по косвенным признакам. Таким энергоносителем может быть электрический заряд, природа которого до сих пор не ясна. Другим таким энергоносителем может выступать светоносная субстанция, которую признавали многие предыдущие теории, называя ее “эфиром”, “тонкой материей”, “скрытой массой”, “физическим вакуумом”, “полем”, “темной материей”, “темной энергией”. Обозначим через ${{\tilde {\Theta }}}~$ количество этой скрытой субстанции с плотностью ${{\tilde {\rho }}}$ = d${{\tilde {\Theta }}}$/dV. Она всепроницаема, обладает единственной колебательной степенью свободы упорядоченного движения и соответствующая ей энергия гравитационная [31]. В каждое мгновение каждая ее колебательная мода ${{\tilde {\Theta }}_{i}}~$, число которых бесконечно и счетно, ведет себя как твердое тело, участвуя в упорядоченном движении. Так как она всепроницаема и занимает 95% Вселенной, то ее взаимодействием с видимым веществом можно пренебречь. В принятой абсолютной системе отсчета $\tilde {\rho }$ – отклонение плотности этой субстанции от равновесной. Тогда при отсутствии силового взаимодействия этой субстанции с веществом в силу ее всепроницаемости должны выполняться законы сохранения ее количества, импульса и момента импульса [2]:
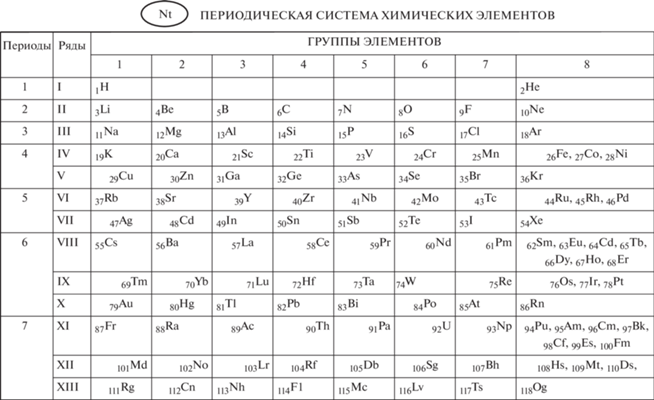
Совместное решение первых двух уравнений, выполненное Н.А. Магницким, позволило ему при определенных допущениях построить математическую модель перехода скрытой субстанции в обычную материю в виде основных элементарных частиц (электрона, протона, нейтрона) с отражением их внутренних структурных особенностей, а также атомов всех элементов таблицы химических элементов Д.И. Менделеева, не выходя при этом за пределы классической механики [32]. Одним из важных результатов такого подхода является аналитическое обоснование достоверности первоначального варианта таблицы Д.И. Менделеева, содержащей семь периодов и восемь групп, который оказался наиболее близким к описанию существа происходящих в атомах периодических процессов (табл. 1 ). В частности, расчеты показали, что каждая из групп содержит не две, а три подгруппы. Вместо рассмотрения лантаноидов и актиноидов как выпадающих элементов из таблицы химических элементов, должна присутствовать третья подгруппа в каждой из восьми групп. Д.И. Менделеев обозначил физический вакуум элементом ньютонием Nt и поместил его в нулевую группу нулевого ряда своей таблицы. Однако Nt не является химическим элементом, поэтому он помещен в строку заголовка над табл. 1 [32].
ЗАКЛЮЧЕНИЕ
Компактное изложение важнейших положений энергодинамики и ее практических результатов показывает, что она существенно раздвигает горизонты естествознания и, в частности, обогащает методологическую базу химической технологии, открывая новые способы и приемы решения практических задач.
ОБОЗНАЧЕНИЯ
| А | произвольная экстенсивная физическая величина |
| $\alpha $ | произвольная интенсивная физическая величина |
| M | масса |
| V | объем |
| F | сила |
| Х | обобщенная сила |
| W | работа |
| U | энергия |
| S, s | энтропия |
| N | число молей |
| T | температура |
| R | радиус-вектор центра инерции |
| Z | момент распределения |
| J,J | поток, импульс |
| P | импульс-вектор |
| M | момент импульса |
| ${{{{\Psi }}}_{{}}}$, ${{\psi }}$ | обобщенный потенциал |
| ${{\Theta }}$ | энергоноситель |
| I | момент инерции |
| f | поверхность |
| n | нормаль к поверхности |
| ${{{\mathbf{\upsilon }}}_{{}}}$ | скорость |
| w | скорость переноса системы в целом |
| n | число форм энергии |
| р | давление |
| ${{\rho }}$ | плотность |
| $~{{\mu }}$ | химический потенциал |
| r | радиус-вектор частицы |
| ${\mathbf{\varphi }}$ | угол поворота вектора |
| ω | угловая скорость |
ИНДЕКСЫ
Список литературы
Дорохов И.Н. Аксиома неоднородности и обобщенный закон сохранения и превращения энергии // Теорет. основы хим. технологии. 2023. Т. 57. № 3. С. 346.
Дорохов И.Н. Системно-энергодинамический анализ природных и технологический процессов. М.: ЛЕНАНД, 2023.
Эткин В.А. Термокинетика (термодинамика неравновесных процессов переноса и преобразования энергии). Тольятти: Акад. бизнеса, 1999.
Эткин В.А. Энергодинамика (синтез теорий переноса и преобразования энергии). СПб.: Наука, 2008.
Вейник А.И. Термодинамика реальных процессов. Мн.: Навука i тэхника, 1991.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 1. Механика. М.: Наука, 1973.
Седов Л.И. Механика сплошной среды. Т. 1. М.: Наука, 1970.
Дорохов И.Н. Обобщенная Z – функция и системно – энергодинамический подход к анализу природных и технологических процессов // Вестник Международной академии системных исследований. Информатика, экология, экономика. 2022. Т. 24. С. 4.
Гюнтер Н.М. О постановке некоторых задач математической физики // Уч. зап. Ленингр. Гос. унив. 1940. Вып.10. № 55. С. 12.
Гельфанд И.М., Шилов Г.Е. Обобщенные функции и действия над ними. 2-е изд. М.: Наука, 1959.
Сычев В.В. Сложные термодинамические системы. М.: Энергия, 1970.
Onsager L. Reciprocal relations in irreversible processes // Phys. Rev., 1931. 237 (14). P. 405; 238(12). P. 2265.
Пригожин И. Введение в термодинамику необратимых процессов. М.: Изд-во иностр. лит., 1969.
Де Гроот С., Мазур П. Неравновесная термодинамика. М.: Мир, 1964.
Дьярмати И. Неравновесная термодинамика. Теория поля и вариационные принципы. М.: Мир, 1974.
Хаазе Р. Термодинамика необратимых процессов. М.: Мир, 1967.
Нигматулин Р.И. Некоторые соотношения неравновесной термодинамики для двухтемпературного и двухскоростного газа с фазовыми переходами // МЖГ. 1968. № 5. С. 111.
Дорохов И.Н., Кафаров В.В., Нигматулин Р.И. Методы механики сплошной среды для описания многофазных многокомпонентных смесей с химическими реакциями и процессами тепло- и массопереноса // ПММ, 1975. Т. 39. № 3. С. 485.
Дорохов И.Н., Кафаров В.В., Нигматулин Р.И. Общие уравнения движения многофазных многокомпонентных монодисперсных систем с химическими реакциями и процессами тепло- и массопереноса // Теорет. основы хим.технологии. 1977. Т. 11. № 2. С. 163.
Дорохов И.Н., Кафаров В.В., Нигматулин Р.И. Термодинамический анализ двухфазной многокомпонентной дисперсной системы с химическими реакциями и процессами тепло- и массопереноса // Теорет. основы хим.технологии. 1977. Т. 11. № 3. С. 343.
Дорохов И.Н., Кафаров В.В., Кольцова Э.М. Уравнения термогидромеханики двухфазной полидисперсной среды с фазовыми переходами при непрерывном распределении частиц по размерам // ПМТФ. 1978. № 1. С. 103.
Дорохов И.Н., Кафаров В.В., Кольцова Э.М. (1982) Термодинамический анализ движущей силы массопереноса в процессе кристаллизации из растворов // ИФЖ. 1982. Т. XLII. № 2. С. 260.
Умов Н.А. Избранные сочинения. М.-Л., 1950.
Яуман Густав. Замкнутая система физических и химических дифференциальных законов // Акад. Wiss. Вена, Nat.–Naturwiss. Класс IIА. 1911. С. 385.
Эткин В.А. О потенциале и движущей силе лучистого теплообмена // Вестник Дома ученых Хайфы. 2010. Т. ХХ. С. 2.
Эткин В.А. Об избирательном взаимодействии / Вестник Дома Ученых Хайфы. 2012. Т. 29. С. 2.
Эткин В.А. О несовместимости законов сохранения энергии и импульса // Annali d Italia, P. 41.
Колтовой Н.А. Научные исследования аномальных явлений. Т. 1–14. www.koltovoi.nethous.ru
Фролов А.В. Новые источники энергии. 9-е изд. Тула.: Изд-во ТулГУ, 2017.
Леонов В.С. Способ создания тяги в вакууме и полевой (квантовый) двигатель для космического корабля (варианты). Патент РФ № 2185526 // Б.И. 2002. № 20.
Etkin V.A. On Wave Nature of Matter // World Scientific News 69.2017. P. 220–235.
Магницкий Н.А. Теория сжимаемого осциллирующего эфира. М.: ЛЕНАНД, 2021.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии