Теоретические основы химической технологии, 2023, T. 57, № 6, стр. 661-667
Анализ процесса течения нефти на основе вихревых дорожек Кармана
В. А. Налетов a, *, М. Б. Глебов a, Л. В. Равичев a
a Российский химико-технологический университет имени Д.И. Менделеева
Москва, Россия
* E-mail: jacen23@yandex.ru
Поступила в редакцию 27.09.2023
После доработки 29.09.2023
Принята к публикации 01.10.2023
- EDN: ECQYDQ
- DOI: 10.31857/S0040357123060167
Аннотация
В работе проводится анализ локальных вихревых течений нефти при ее транспортировке по магистральным продуктопроводам на основе дорожек Кармана. Анализ вихревых течений базируется на моделировании гидродинамики с применением программного комплекса Ansys Fluent. Моделирование локальных вихревых течений основано на использовании модели SST (Shear Stress Transport), представляющей комбинацию двух моделей турбулентности: k-ε и k-ω. Доказано, что при заданных параметрах течения нефти и ее характеристиках возможна организация локальных вихревых течений в центре трубопровода. Оценка гидравлических сопротивлений в зоне вихревых дорожек Кармана указывает на возможность их уменьшения. С другой стороны, анализ общих потерь давления свидетельствует, что при обтекании вихреобразователей доминируют потери от лобового сопротивления, что требует поиска иных способов организации локальных вихревых течений или способов преодоления потерь от лобового сопротивления на основе использования ресурсов мультифункциональных установок в процессах транспорта нефти.
ВВЕДЕНИЕ
Актуальность исследования вихревых течений обусловлена необходимостью поиска энергосберегающих технических решений в технологиях трубопроводного транспорта сырья и продуктов. Например, гидравлические потери при перекачке жидких сред по магистральным продуктопроводам большой протяженности требует существенных затрат электроэнергии на приводы насосного оборудования. Так согласно данным Публичного Акционерного Общества (ПАО) “Транснефть”, являющегося оператором большинства магистральных продуктопроводов Российской Федерации, затраты электроэнергии на транспортировку нефти и нефтепродуктов составляют около 1.3% от общего электропотребления страны, в силу чего ПАО “Транснефть” входит в десятку наиболее энергозатратных компаний.
Необходимо также учесть, что в связи с постепенным исчерпанием запасов нефти малой и средней вязкости нефтегазодобывающие компании вынуждены переходить к добыче трудноизвлекаемых запасов сырья, в первую очередь высоковязкой нефти (ВВН) и природных битумов (ПБ), которые по различным оценкам превышают запасы нефти малой и средней вязкости примерно в пять раз [1]. Особенности реологических свойств ВВН обуславливают повышенные силы внутреннего трения и соответственно дополнительные энергозатраты [2].
В природе подавляющее число течений являются вихревыми. Вихревым называют течение потока жидкости или газа, в котором частицы помимо поступательного движения совершают вращательное движение вокруг мгновенной оси [3].
Примеры вихревых течений мы наблюдает в различных природных комплексах: в атмосфере – циклоны, антициклоны, смерчи; в океане – синоптические вихри, имеющие диаметры до нескольких сотен километров и глубину до нескольких километров; в реках – водовороты и мелкомасштабные вихри, образующиеся при обтекании ям, препятствий и тому подобное [4].
Одним из первых, кто обратил внимание на то, что естественной (природной) формой потока является вихревая или винтовая структура, был Виктор Шаубергер. Он доказал, что такая форма потока является наиболее эффективной и обеспечивает минимальное сопротивление при его движении в трубопроводе [5]. Для этого Шаубергер предложил использовать трубы не стандартного (круглого), а винтового сечения, повторяющего движение потока.
В работе [6] обсуждаются результаты по организации вихревых течений за счет определенной конструкции труб, на внутренней поверхности которых имеется спиральный профиль для закручивания потока. Отмечено, что при перекачке смеси нефти с водой, центробежные силы увлекают более плотную, но менее вязкую среду (воду) к стенкам, вследствие чего затраты на перекачку флюида уменьшаются. Однако изготовление сложных профилированных труб для организации вихревых течений является затратным мероприятием.
В развитие организации вихревых течений в работе [7] предложен способ, позволяющий за счет вставки в трубу круглого профиля пружины также обеспечить завихрение потока нефти.
В работе [8] представлен анализ применения вихреобразователя движущейся среды для снижения гидравлических потерь в трубопроводах. Авторами было разработано и представлено устройство, способное закручивать поступающий в трубчатый корпус поток вязкой жидкости. Анализ эффективности устройства производился на основе моделирования процесса течения нефти через вихреобразователь с использованием программного комплекса Ansys Fluent. Полученные в ходе моделирования данные подтвердили, что вихреобразователь, который был установлен перед участком трубопровода, приводит к снижению гидравлических потерь.
В работах [9, 10] представлены экспериментальные данные по гидравлике вращательного движения жидкости, которое обеспечивалось, в частности, вращением собственно трубы как по, так и против часовой стрелки. Результаты исследования также показали, что вихревые течения являются предпочтительными.
Анализ представленных работ свидетельствует о том, что рассматривались в основном варианты “закрутки” всего потока нефти, начиная от его периферии к центру, что безусловно требует больших затрат энергии, чем организация локальных вихревых течений.
В данной работе проводилось исследование локальных вихревых течений нефти исключительно в центральной части трубопровода, основанных на “вихревых дорожках” Кармана, который в 1911 г. обнаружил образование особой последовательности вихрей при обтекании кругового цилиндра, ось которого перпендикулярна встречному потоку, и описал условия ее формирования [11].
Изучению вихревых течений Кармана посвящены ряд работ [12, 13], из которых следует, что можно выделить 4 фазы (зоны) развития вихревого течения: зона формирования дорожки (неустановившаяся зона), зона дорожки Кармана (установившаяся зона), зона затухания дорожки, а также, в ряде случаев, зона вторичной вихревой дорожки.
Для организации вихревых течений нефти в работе использовался неподвижный вихреобразователь, условно размещенный в центре трубного участка.
Целями настоящего исследования является анализ локальных вихревых течений нефти на основе оценки как относительных потерь давления в зоне дорожек Кармана, то есть без учета лобового сопротивления при обтекании вихреобразователя, так и общих потерь давления с учетом лобового сопротивления и вязкого трения при обтекании вихреобразователей.
Анализ локальных вихревых течений нефти проводился на основе моделирования гидродинамики.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
На первом этапе исследования проводилось моделирование гидродинамики вихревых течений нефти с применением программного комплекса Ansys Fluent.
На основании сравнительного анализа четырех наиболее известных моделей гидродинамики, а именно: k-ε; k-ω; SST и SAS, входящих в программный комплекс Ansys Fluent, приведенного в работе [14], было принято решение об использовании для моделирования вихревых течений модели SST (Shear Stress Transport), которая на достаточно немногочисленных по количеству узлах сетки способна адекватно воспроизводить и моделировать вихри.
Модель SST – это комбинация двух моделей турбулентности: k-ε и k-ω. Для расчета течения во внешнем потоке используются уравнения k-ε модели, а в пристеночной области – уравнения k-ω модели [15].
Модель SST использовалась в модификации Transition SST, также известной как модель γ-Reθ. Данная модификация применена для более точного описания вихревых течений.
Общий вид используемой математической модели представляется следующим образом. В ней записываются уравнения для кинетической энергии турбулентности k и удельной скорости диссипации кинетической энергии турбулентности ω:
(1)
$\begin{gathered} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \,\,~\frac{{\partial \left( {\rho {{U}_{j}}k} \right)}}{{\partial {{x}_{j}}}} = \, \\ = {{P}_{k}} - \beta {\text{*}}\rho k\omega + \frac{\partial }{{\partial {{x}_{j}}}}\left[ {\left( {\mu + \frac{{{{\mu }_{T}}}}{{{{\sigma }_{k}}}}} \right)\frac{{\partial k}}{{\partial {{x}_{j}}}}} \right], \\ \end{gathered} $(2)
$\begin{gathered} \frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {{U}_{j}}\omega } \right)}}{{\partial {{x}_{j}}}} = {{P}_{\omega }} - \beta \rho {{\omega }^{2}} + \\ + \,\,\frac{\partial }{{\partial {{x}_{j}}}}\left[ {\left( {\mu + \frac{{{{\mu }_{T}}}}{{{{\sigma }_{\omega }}}}} \right)\frac{{\partial \omega }}{{\partial {{x}_{j}}}}} \right] + \frac{{2\rho \left( {1 - {{F}_{1}}} \right)}}{{{{\sigma }_{{\omega 2}}}\omega }}\frac{{\partial k}}{{\partial {{x}_{i}}}}\frac{{\partial \omega }}{{\partial {{x}_{i}}}}, \\ \end{gathered} $Также вводятся два дополнительных уравнения переноса, одно для перемежаемости турбуленции $~\gamma $, а второе для критерия начала перехода в единицах толщины потери импульса чисел Рейнольдса.
Уравнение переноса для фактора перехода потока в турбулентный режим γ имеет вид:
(3)
$\begin{gathered} \frac{{\partial \left( {\rho \gamma } \right)}}{{\partial t}} + ~\frac{{\partial \left( {\rho {{U}_{j}}\gamma } \right)}}{{\partial {{x}_{j}}}} = \\ = ~{{P}_{{\gamma 1}}} - {{E}_{{\gamma 1}}} + {{P}_{{\gamma 2}}} - {{E}_{{\gamma 2}}} + \frac{\partial }{{\partial {{x}_{j}}}}\left[ {\left( {\mu + \frac{{{{\mu }_{T}}}}{{{{\sigma }_{\gamma }}}}} \right)\frac{{\partial \gamma }}{{\partial {{x}_{j}}}}} \right]~, \\ \end{gathered} $Уравнение критерия начала перехода в единицах толщины потери импульса чисел Рейнольдса $R{{\tilde {e}}_{{\theta t}}}$ имеет вид:
(4)
$\begin{gathered} \frac{{\partial \left( {\rho R{{{\tilde {e}}}_{{\theta t}}}} \right)}}{{\partial t}} + ~\frac{{\partial \left( {\rho {{U}_{j}}R{{{\tilde {e}}}_{{\theta t}}}} \right)}}{{\partial {{x}_{j}}}} = \\ = ~{{P}_{{\theta t}}} + \frac{\partial }{{\partial {{x}_{j}}}}\left[ {{{\sigma }_{{\theta t}}}\left( {\mu + {{\mu }_{T}}} \right)\frac{{\partial R{{{\tilde {e}}}_{{\theta t}}}}}{{\partial {{x}_{j}}}}} \right]~, \\ \end{gathered} $Граничным условием у стенки для $R{{\tilde {e}}_{{\theta t}}}$ является нулевой поток, а условие для $R{{\tilde {e}}_{{\theta t}}}$ на входе рассчитывается на основе эмпирической корреляции интенсивности на входе. Начальным условием по времени является равенство нулю скорости потока.
Преимуществами принятой модели являются устойчивость и хорошая сходимость, благодаря сочетанию k-ω и k-ε моделей. Так, в свободном турбулентном потоке SST модель ведет себя как k-ε, что ведет к снижению чувствительности начальных условий, которой подвержена модель k-ω, и повышается стабильность решения. В свою очередь, k-ω модель обеспечивает корректное описание пристеночной турбулентности при обтекании вихреобразователей. Модификация модели Transition SST дает более точные результаты в описании турбулентности, но требует больше расчетного времени.
На втором этапе исследования был проведен анализ относительных потерь давления как в зоне дорожек Кармана по мере удаления от вихреобразователя, так и общих потерь давления с учетом, в частности, лобового сопротивления и вязкого трения при обтекании вихреобразователей.
РАСЧЕТНАЯ ЧАСТЬ
Задачей первого этапа моделирования было установление возможности организации локальных вихревых течений нефти при заданных параметрах течения нефти и ее характеристиках. Исследования проводились на горизонтальном участке нефтепровода длиной, не превышающей 10 м и диаметром 1.2 м (фрагмент магистрального нефтепровода 1-го класса).
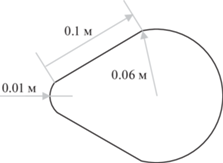
Для организации вихревых течений нефти был выбран вихреобразователь каплевидной формы, имеющий наименьшее значение лобового сопротивления по отношению к другим формам, с исходными (номинальными) размерами согласно рис. 1.
В качестве исходных данных были приняты следующие: скорость потока нефти принята равной 3.1 м/с (соответствует штатному значению скорости в нефтепроводе); плотность нефти – 931.1 кг/м3; вязкость нефти – 0.1792 Па с. Шероховатость стенок трубопровода принята равной 0.002 м.
Расчетная сетка имела следующие характеристики: количество узлов – 90427, число элементов – 89416.
В зоне вихреобразователя сетка детализирована как показано на рис. 2.
В ходе моделирования относительные размеры вихреобразователя изменялись как в меньшую, так и большую стороны.
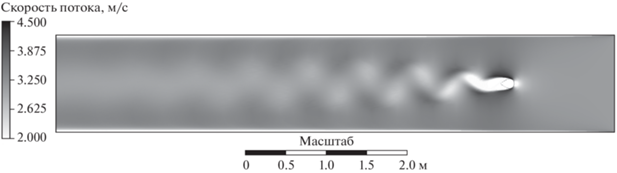
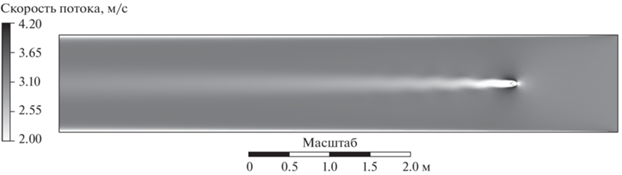
На рис. 3–5 в качестве примера представлены вихревые дорожки Кармана для номинального, уменьшенного и увеличенного соответственно в 2 раза размеров вихреобразователей.
Как следует из результатов моделирования, при заданном режиме течения нефти в трубопроводе и заданных ее характеристиках можно наблюдать образование локальных вихревых течений в виде дорожек Кармана для всех трех размеров вихреобразователей. При этом зона неустановившегося вихревого течения (зона формирования дорожки) тем больше, чем больше размер вихреобразователя. Одновременно можно наблюдать и большую амплитуду вихря при большем размере вихреобразователя.
На втором этапе исследования проводилась оценка гидравлических потерь (потерь давления) при организации локальных вихревых течений нефти.
Вначале для анализа эффективности локальных вихревых течений оценка проводилась исключительно в зоне дорожек Кармана. За точку отсчета (условно нулевые потери давления) было принято расстояние от вихреобразователя, равное 1 м. Относительные потери давления на больших расстояниях от вихреобразователя рассчитывались дискретно по отношению к данной точке отсчета вплоть до контрольной точки, равной 5.6 м.
В табл. 1 представлены относительные потери давления в зоне дорожек Кармана для вихреобразователей различных размеров.
Таблица 1.
Относительные потери давления при различных размерах вихреобразователей
| Расстояние от вихреобразователя, м | Относительные потери давления ΔP, Па | |||
|---|---|---|---|---|
| без вихреобразователя | вихреобразователь в 2 раза меньше | вихреобразователь номинального размера | вихреобразователь в 2 раза больше | |
| 1.00 | 0 | 0 | 0 | 0 |
| 2.50 | 106.85 | 64.41 | 6.94 | –197.05 |
| 4.00 | 202.30 | 118.30 | 44.53 | –300.32 |
| 5.50 | 290.98 | 161.72 | 90.07 | –210.67 |
| 5.60 | 297.11 | 164.24 | 91.20 | –168.47 |
Как следует из данных табл. 1, для выбранных размеров вихреобразователей в зоне дорожек Кармана наблюдается снижение гидравлических потерь при течении нефти в трубном участке нефтепровода, что подтверждает эффективность локальных вихревых течений.
В дальнейшем проводилась оценка общих потерь давления с учетом потерь как от лобового сопротивления, так и потерь на трение при обтекании вихреобразователей.
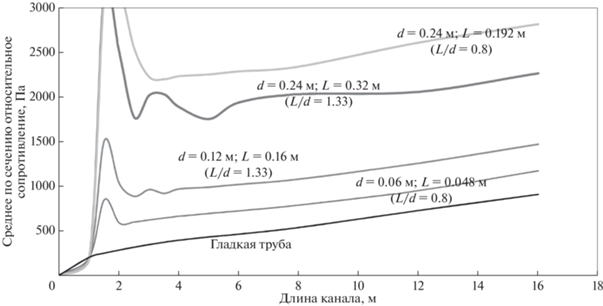
Результаты расчетов приведены на рис. 6.
Как следует из данных на рис. 6, общие потери давления при обтекании вихреобразователей представленных относительных размеров выше, чем для гладкой трубы.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Анализ вихревых течений в зоне дорожек Кармана при заданных параметрах течения и характеристиках нефти показал, что наибольшего снижения гидравлических потерь возможно достичь для номинального и увеличенного в 2 раза размера вихреобразователей, что обусловлено большей энергией, которую запасет вихрь при обтекании тела большего диаметра.
В ходе вычислительных экспериментов было установлено, что вихревые дорожки Кармана практически полностью затухают на расстоянии порядка 7.0 м, что корреспондируется с выводами, приведенными в работе [13] о конечной протяженности вихревой дорожки Кармана в вязкой среде.
На диаграмме (рис. 6) наблюдается несколько пиков повышения гидравлических потерь. Самые большие пики идентифицируется с максимальными значениями коэффициентов лобового сопротивления при обтекании вихреобразователей, которые тем больше, чем больше диаметр вихреобразователя. Менее значительные пики связаны с вязким трением при течении нефти вдоль поверхности вихреобразователей.
Анализ суммарных гидравлических потерь показывает, что в общих потерях доминируют потери от лобового сопротивления при обтекании вихреобразователей, что не позволяет при выбранном способе организации локальных вихревых течений путем обтекания неподвижного тела достичь подтвержденного эффекта снижения гидравлических потерь на основе дорожек Кармана.
ЗАКЛЮЧЕНИЕ
На основании анализа локальных вихревых течений нефти в виде дорожек Кармана можно сделать следующие общие выводы:
1. Моделированием течений нефти при обтекании вихреобразователей каплевидной формы в программной среде Ansys Fluent было доказано, что в центральной части трубопровода возможна организация локальных вихревых течений в виде дорожек Кармана, что является альтернативой способу закрутки всего потока нефти от периферии к центру, априори требующему больших затрат энергии.
2. Для моделирования вихревых течений нефти было обосновано применение математической модели SST, представляющей комбинацию двух моделей турбулентности: k-ε и k-ω в модификации Transition SST, входящую в программный комплекс Ansys Fluent.
3. Показано, что в зоне дорожек Кармана возможно снижение гидравлических потерь при перекачке нефти трубопроводным транспортом, что позволяет достичь эффекта энергосбережения, не прибегая к закручиванию всего потока нефти.
4. Было установлено, что вихревые дорожки Кармана при течении нефти в трубопроводе имеет конечную протяженность, в частности, для исходных параметров течения нефти и размеров вихреобразователей – порядка 7 м. В дальнейшем вихревая дорожка затухает.
5. Было установлено, что при обтекании неподвижных вихреобразователей, размещенных в центре трубы, в общих гидравлических потерях доминируют потери давления от лобового сопротивления, что указывает на необходимость поиска иных способов и устройств для организации локальных вихревых течений. В качестве одной из альтернатив для преодоления лобового сопротивления можно предложить интеграцию данного способа с мультифункциональными системами подогрева нефти на магистральных нефтепроводах (пунктами подогрева нефти), способными, помимо подогрева нефти попутно вырабатывать электроэнергию в качестве продукта [16].
ОБОЗНАЧЕНИЯ
| ΔP | потери давления |
| β, β*, σω2, σγ, σθt | постоянные коэффициенты модели |
| γ | перемежаемость турбуленции |
| μ | динамическая вязкость среды |
| μT | турбулентная вязкость |
| ρ | плотность среды |
| σω, σk | функции от параметров потока |
| ω | удельная скорость диссипации кинетической энергии турбулентности |
| d | диаметр вихреобразователя |
| E | составляющая, определяющая возникновение (источник) |
| F1 | стыковочная (“весовая” функция) |
| k | кинетическая энергия турбулентности |
| L | длина вихреобразователя |
| P | составляющая, определяющая рост (генерацию) |
| $R\tilde {e}{{{\kern 1pt} }_{{\theta t}}}$ | критерий начала перехода в единицах толщины потери импульса чисел Рейнольдса |
| t | время |
| U | скорость потока |
| x | координата |
ИНДЕКСЫ
Список литературы
Щепалов А.А. Тяжелые нефти, газовые гидраты и другие перспективные источники углеводородного сырья: Учебно-методическое пособие. Нижний Новгород: Нижегородский госуниверситет, 2012. 93 с.
Газизов Р.Э., Солодова Н.Л., Вагапов Б.Р. Трубопроводный транспорт тяжелой нефти и битумов // Вестник технологического университета. 2017. Т. 20. № 10. С. 17–21.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. 3-е изд. М.: Наука, 1986. 736 с.
Etling D., Brown R.A. Roll vortices in the planetary boundary layer: A review // Boundary-Layer Meteorology. 1993. V. 65. P. 215–248.
Шаубергер В. Энергия воды. М.: Эксмо. 2008. 320 с.
Новоселов В.В., Прохоров А.Д. Трубопроводный транспорт нефти / под общ. ред. С.М. Вайштока: Недра-Бизнецентр, 2008. 621с.
Голованчиков А.Б., Ильина Л.А., Ильин А.В., Дулькина Л.А., Дулькин А.Б., Каращук Д.С. Устройство для уменьшения гидравлических потерь в трубопроводе. Патент RU 2285198 С1 от 10.10.2006.
Иншаков Р.С., Балабуха А.В., Анисимова Е.Ю., Цырендашиев Н.Б., Панасенко Н.Л., Цыбуля И.И. Применение завихрителя потока движущейся среды для снижения гидравлических потерь в трубопроводах // Вестник Евразийской науки. 2018. Т. 10. № 3. С. 52–62.
Коноплёв Н.Г., Коробков Г.Е. Экспериментальные исследования энергетических процессов потока жидкости в трубопроводе // Транспорт и хранение нефтепродуктов и углеводородного сырья. 2019. № 1. С. 28–33.
Алексеенко С.В., Куйбин П.А., Окулов В.Л. Введение в теорию концентрированных вихрей. Институт теплофизики им. С.С. Кутателадзе. Новосибирск. 2003. 504 с.
Karman T. von, Rubach H. L. Über den Mechanismus des Fliissigkeits- und Luft-widerstands // Phys. Zeit. 1912. № 13. P. 49–59.
Фомин Г.М. О циркуляции вихрей и скорости перемещения дорожки Кармана // Ученые записки ЦАГИ. 1971. Т. II. № 4. С. 99–102.
Алексюк А.И., Шкадова В.П., Шкадов В.Я. Возникновение, развитие и затухание вихревой дорожки в следе за обтекаемым телом // Вест. моск. ун-та. Сер. 1, математика. механика. 2012. № 3. С. 24–32.
Вальгер С.А., Фёдоров А.В., Фёдорова Н.Н. Моделирование несжимаемых турбулентных течений в окрестности плохообтекаемых тел с использованием ПК ANSYS Fluent // Вычислительные технологии. 2013. Т. 18. № 5. С. 27–40.
ANSYS Fluent Theory Guide: Release 15.0 // Canonsburg.: ANSYS, Inc. 2013. 814 p.
Налетов В.А., Глебов М.Б. Оптимальная организация процесса подогрева нефти при транспортировке по магистральным нефтепроводам // Наука и технологии трубопроводного транспорта нефти и нефтепродуктов. 2022. Т. 12. № 3. С. 284–291.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии