Вестник Военного инновационного технополиса «ЭРА», 2022, T. 3, № 1, стр. 68-74
ПРИМЕНЕНИЕ АЛГОРИТМОВ ДИСКРЕТНОЙ ОПТИМИЗАЦИИ ДЛЯ ПОСТРОЕНИЯ ПРОСТРАНСТВЕННОГО МАРШРУТА ГРУППЫ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
А. В. Заяра 1, *, М. А. Набиев 1
1 Военный инновационный технополис “ЭРА”
Анапа, Россия
* E-mail: era_1@mil.ru
Поступила в редакцию 23.12.2021
После доработки 10.01.2022
Принята к публикации 10.01.2022
Аннотация
Проведены анализ и выбор алгоритмов дискретной оптимизации для построения оптимального пространственного сплайн-маршрута группы беспилотных летательных аппаратов в различных порядках построения. С этой целью применялись две разновидности жадного алгоритма, метод ветвей и границ, венгерский и муравьиный. Апробация проводилась методом статистического моделирования с использованием программ на языке Python. Получение эталонного результата с целью оценки корректности выбора лучшего алгоритма осуществлено методом полного перебора вариантов, реализация которого оказалась возможной на основании небольшого объема выборки (n = 4). Путем селекции, проводимой по критериям кратчайшего маршрута и наименьшего машинного времени, выбран наиболее эффективный венгерский алгоритм.
ВВЕДЕНИЕ
Роботизация военного дела определила необходимость применения беспилотных летательных аппаратов (БпЛА) в составе группы для полетов аппаратов в невозможных для пилотируемой авиации боевых порядках со сложными пространственными эволюциями [1]. Прежде всего это касается боевых действий на урбанистической местности, которые считаются одними из наиболее сложных, что обусловлено рядом факторов:
– ограниченность применения танков и артиллерии;
– повышенная сложность сценариев применения частей и подразделений;
– динамичность боевых действий (необходимость организации оперативного перехода от наступательных действий к оборонительным и обратно, высокая степень неопределенности местоположения противника из-за сложности разведки в городской инфраструктуре);
– перенос боевых действий с “плоской” 2D-карты на “объемную” 3D-карту с учетом городской застройки [2].
При управлении группой летательных аппаратов полетное задание будет составляться таким образом, чтобы обеспечить кратчайший путь между промежуточными точками для каждого БпЛА с целью экономии заряда аккумуляторной батареи. Маршрут будет представлять собой кусочно-линейную функцию с учетом рельефа и инфраструктуры местности. Пример такого маршрута для группы из восьми БпЛА представлен на рис. 1.
Для решения этой задачи необходимо выбрать траекторию полета, обходящую препятствия, и порядок построения группы БпЛА в пространстве. Для оптимизации будет использоваться целевая функция – минимальное значение суммы расстояний между точками в соседних геометрических фигурах, определяющих боевой порядок группы дронов. В зависимости от урбанистического рельефа и выполняемых в течение полета задач эти фигуры могут видоизменяться. Если полную траекторию для каждого аппарата из начальной до целевой точки вычислять однократно, то потребуется значительный объем вычислений [3]. Поэтому предлагается решать задачу оптимизации полетного задания постепенно по ходу построения маршрута.
Несмотря на то что существуют примеры организации совместного маневрирования большого числа дронов для выполнения задач шоу-бизнеса [4], в настоящее время методики управления движением БпЛА военного назначения в составе группы находятся в стадии разработки. В связи с этим задача выбора кратчайшего маршрута при перестроении группы в геометрические фигуры различной формы и размера в промежуточных точках маршрута представляется актуальной.
Таким образом, целью исследования является выбор алгоритма оптимизации набора путей для группы из n аппаратов между опорными рубежами составного маршрута в форме линейного сплайна. Для достижения цели необходимо:
– определить перечень алгоритмов дискретной оптимизации, которые применимы для решения поставленной задачи – выбора набора кратчайших путей для группы дронов;
– провести анализ и оценить степень их применимости;
– подготовить исходные данные и реализовать статистическое моделирование, по результатам которого обоснованно выбрать наиболее оптимальный алгоритм.
При этом определяются следующие допущения.
1. Кривизна траекторий БпЛА в расчете длины пути для каждого отдельного дрона не учитывается.
2. Возможность столкновения соседних аппаратов не рассматривается.
3. Оценка кратчайшего пути определяется как минимальная сумма путей всех аппаратов только на одном участке линейно-кусочной траектории, т.е. целевая функция, которую предстоит минимизировать
где n – количество БпЛА, wij – путь i-го дрона из исходного положения до j-го места в заданном порядке, а xij – коэффициент, засчитывающий путь wij в общее расстояние, если ребро выбирается (xij = 1), и не засчитывающий в противоположном случае (xij = 0).РЕШЕНИЕ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ
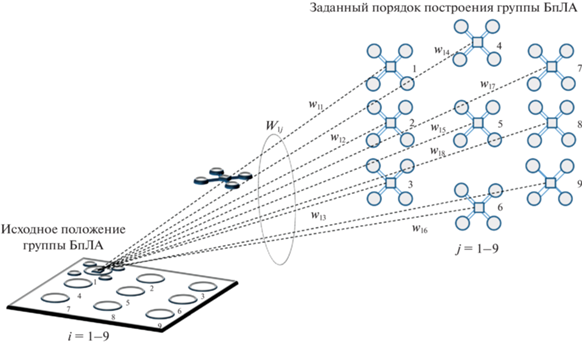
Задача выбора кратчайшего из возможных вариантов путей между двумя местами в заданных порядках построения дронов в промежуточных точках маршрута поясняется схемой на рис. 2.
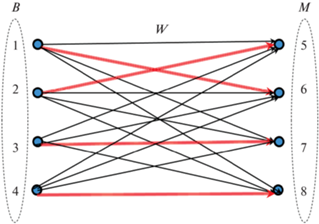
В качестве предмета исследования используется модель в виде двудольного ориентированного графа (рис. 3):
Рис. 2.
Возможные маршруты движения отдельного БпЛА при перемещении из одного установленного порядка размещения в другое.
где D = B ⊕ M – множество вершин, состоящее из двух равных по мощности подмножеств; B – подмножество вершин (каждая имеет полустепень исхода n) соответствует БпЛА (bi – отдельный дрон с номером i); M – подмножество вершин (каждая имеет полустепень захода n), место в установленном построении.
Граф G можно представить в виде матрицы смежности 2n × 2n. Пример матрицы орграфа для звена из четырех БпЛА (рис. 3) представлен в табл. 1.
Таблица 1.
Матрица смежности ориентированного графа
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | w15 | w16 | w17 | w18 |
| 2 | 0 | 0 | 0 | 0 | w25 | w26 | w27 | w28 |
| 3 | 0 | 0 | 0 | 0 | w35 | w16 | w17 | w18 |
| 4 | 0 | 0 | 0 | 0 | w45 | w16 | w17 | w18 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Для задания двудольного графа вместо всей матрицы смежности достаточно взять ее подматрицу, в которой строки соответствуют вершинам одной доли, а столбцы – вершинам другой [5]. В табл. 1 упомянутая подматрица выделена по контуру двойной линией. Матрицу смежности можно считать малоинформативной, так как ¾ ее содержания занимают нули. Для дальнейшего упрощения следует пронумеровать столбцы с 1 до n, а также изменить нумерацию весов ребер орграфа (элементов матрицы) wij, где $j = ~\overline {1 \ldots n} $ (табл. 2).
Таблица 2.
Подматрица двудольного графа
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | w11 | w12 | w13 | w14 |
| 2 | w21 | w22 | w23 | w24 |
| 3 | w31 | w32 | w33 | w34 |
| 4 | w41 | w42 | w43 | w44 |
В ориентированном графе (2) необходимо определить n паросочетаний, инциндентых вершинам из подмножества B и подмножества M, с таким расчетом, чтобы выполнялось условие (1). Другими словами, сформулированное условие соответствует классической задаче комбинаторной оптимизации – задаче о назначениях.
Для определения минимального паросочетания предлагается использовать алгоритмы, применяемые при решении задач линейного программирования: жадный, венгерский, метод ветвей и границ и муравьиный. Далее последовательно рассмотрим применение каждого из перечисленных алгоритмов для решения поставленной задачи.
Основываясь на парадигме жадного алгоритма [6], хотя в данном случае его корректнее было назвать “экономным”, предложены два его варианта: просто “экономный” и “экономный с элементами полного перебора”. Оба варианта основываются на лемме, что ребро с минимальным весом двудольного ориентированного графа обязательно входит в минимальный остов этого графа, где ребро с минимальным весом, инцидентное вершине, wimin – одно из ребер, исходящих из вершины и имеющее наименьший вес, а остов графа – дерево, содержащее все вершины [5]. Результатом решения должен быть минимальный граф Gmin – двудольный ориентированный граф, имеющий минимальный суммарный вес ребер.
Первый вариант (классический жадный) заключается в анализе элементов матрицы (табл. 2) на предмет поиска элемента с минимальным весом wij min. После чего строка и столбец, соответствующие wij min, удаляются из матрицы. Процедура повторяется до тех пор, пока в матрице не останется единственный элемент. Это – самый простой алгоритм. Результат будет достигнут всего за (n + 1)2/2 итераций.
Суть второго варианта “экономного” алгоритма заключается в частичном внедрении в жадный элементов полного перебора. Начиная с первой строки (вершины из подмножества B), выбирается ребро с минимальным весом. После выбора ребра wi min строка, соответствующая вершине, и столбец, соответствующий этому ребру, удаляются из матрицы. Процедура повторяется до тех пор, пока в матрице не останется единственный элемент. После этого определяется суммарный вес выбранных ребер, осуществляется переход ко второй вершине и повторяется поиск ребер с минимальным весом. В результате получается n значений сумм $\sum\nolimits_{i = 1}^{i = n} {{{w}_{{ij}}}} ~~$, из которых выбирается минимальная, соответствующая минимальному графу Gmin. Объем вычислений будет определяться (n + 1)2n/2.
Применение разновидностей экономного алгоритма полностью подтвердило особенности и недостатки жадной парадигмы [6]:
– легко придумать один или несколько вариантов жадных алгоритмов;
– трудно установить их правильность.
Применение метода ветвей и границ возможно только для решения задачи коммивояжера на основе исходных данных в виде неориентированного графа, в котором необходимо найти гамильтонов цикл минимальной длины. Для адаптации задачи о назначении к исходным данным задачи коммивояжера необходимо двудольный ориентированный граф (2) преобразовать в неориентированный с дополнительными ребрами, соединяющими вершины подмножества B с вершинами подмножества M. Это позволит для оптимизации применить готовые программы из библиотек языков программирования. Всем дополнительным ребрам присваиваются веса с одинаковыми значениями “0”, остальным – заведомо больше реальных “∞”. Необходимые изменения в исходных данных поясняются примером в табл. 3.
Таблица 3.
Матрица смежности графа задачи о назначениях, адаптированная для решения задачи коммивояжера
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | ∞ | ∞ | ∞ | ∞ | w15 | w16 | w17 | w18 |
| 2 | ∞ | ∞ | ∞ | ∞ | w25 | w26 | w27 | w28 |
| 3 | ∞ | ∞ | ∞ | ∞ | w35 | w16 | w17 | w18 |
| 4 | ∞ | ∞ | ∞ | ∞ | w45 | w16 | w17 | w18 |
| 5 | 0 | 0 | 0 | 0 | ∞ | ∞ | ∞ | ∞ |
| 6 | 0 | 0 | 0 | 0 | ∞ | ∞ | ∞ | ∞ |
| 7 | 0 | 0 | 0 | 0 | ∞ | ∞ | ∞ | ∞ |
| 8 | 0 | 0 | 0 | 0 | ∞ | ∞ | ∞ | ∞ |
Венгерский алгоритм, который предлагается применить, основан на двух идеях:
– если из всех элементов некой строки или столбца вычесть одно и то же число y, общая стоимость уменьшится на y, а оптимальное решение не изменится;
– если есть решение нулевой стоимости, то оно оптимально.
Алгоритм ищет значения, которые надо вычесть из всех элементов каждой строки и каждого столбца (разные для разных строк и столбцов), такие, что все элементы матрицы останутся неотрицательными, но появится нулевое решение [6]. Для его реализации используется готовая программа из библиотек языков программирования.
Заключительным алгоритмом в списке, который рассматривается в настоящей работе, является муравьиный. В связи с тем что его применение сильно зависит от настроечных параметров, классическую задачу решения задачи коммивояжера необходимо адаптировать применительно к задаче о назначениях. Исходными данными будет являться матрица (табл. 2), которая записывается в виде
(3)
$W = ~\left( {\begin{array}{*{20}{c}} {{{w}_{{11}}}}& \cdots &{{{w}_{{1n}}}} \\ \vdots & \ddots & \vdots \\ {{{w}_{{n1}}}}& \cdots &{{{w}_{{nn}}}} \end{array}} \right)$.В строках указывается номер дрона – i = 1…n. В столбцах – номер места в конечном построении – j = 1…n. Значение wij соответствует расстоянию от первоначального расположения БпЛА до определенного места в конечном порядке построения. Затем необходимо определить для каждого БпЛА степень близости от исходного места до возможных мест в конечном построении
и заполнить матрицу близости(5)
$H = \left( {\begin{array}{*{20}{c}} {{{\eta }_{{11}}}}& \cdots &{{{\eta }_{{1n}}}} \\ \vdots & \ddots & \vdots \\ {{{\eta }_{{n1}}}}& \cdots &{{{\eta }_{{nn}}}} \end{array}} \right)$.Далее оцениваются постоянные, необходимые для последующей оптимизации с применением муравьиного алгоритма. Другими словами, необходимо составить перечень исходных констант, который формируется в результате анализа условий задачи.
В классической постановке задачи муравьиного алгоритма ключевыми являются две формулы оценки вероятности выбора муравьем пути
(6)
${{P}_{{ij}}} = \frac{{{{\tau }}_{{ij}}^{\alpha }~{{\eta }}_{{ij}}^{{{\beta }}}}}{{\sum\limits_{i = 1}^{i = n} {{{\tau }}_{{ij}}^{\alpha }~{{\eta }}_{{ij}}^{{{\beta }}}} }}$.(7)
$\Delta {{{{\tau }}}_{{i,j}}} = \left\{ \begin{gathered} \frac{Q}{{{{D}_{k}}}},\quad {\text{если\;}}k{\text{ - й\;муравей\;прошел\;по\;ребру\;}}i,j,~ \hfill \\ 0,\quad \;\;{\kern 1pt} {\text{если\;иначе}}. \hfill \\ \end{gathered} \right.$В формуле (6) с большой долей субъективности назначаются три константы:
α – показатель, определяющий приоритет запаха феромона;
β – показатель, усиливающий влияние близости вершины ηij на выбор маршрута;
n – количество муравьев.
Для решения рассматриваемой задачи предлагается на всех итерациях не учитывать влияние α и β, приравняв их к “1”. Количество условных муравьев принимается равным n, количество итераций – n!/2. Затем определяется маршрут для каждого k-го насекомого как последовательное прохождение по ребрам двудольного графа G. Начиная с первой вершины, принадлежащей подмножеству B, условный муравей выбирает более “предпочтительный” путь из n вариантов (ребер) в выбранную вершину, принадлежащую подмножеству M, а первая строка и столбец с номером выбранной вершины удаляются из исходной матрицы. Процедура повторяется до тех пор, пока в графе не останется последнее ребро (в матрице – единственный элемент).
Вершины из подмножества B следуют по порядку от 1 до n. Последовательность выбранных путей одного условного насекомого
рассчитывается как сумма весов выбранных муравьем ребер. На этом итерация завершается.Следующим шагом оптимизации является определение количества феромона на маршрутах муравьев τ. Первоначальное количество феромона предлагается принять равным τ0 = 0.1 на каждом ребре. По ходу работы алгоритма количество будет обновляться с каждой итерацией и определяться по формуле
(9)
${{{{\tau }}}_{{ij}}} = \rho {{{{\tau }}}_{{i - 1,j - 1}}} + \sum\limits_{k = 1}^{k = K} {\Delta {{{{\tau }}}_{{i,j}}}} ,$Коэффициент, определяющий испарение феромона ρ, как правило, принимается меньше “1”. Он необходим для того, чтобы подчеркнуть увеличивающуюся с каждой итерацией разность между количеством феромона на ребрах, по которым “муравьи” прошли, и количеством феромона на ребрах, которые муравьи не выбрали. Предлагается принять ρ = 0.9.
Таким образом, каждая итерация будет включать следующие действия:
1. Поиск вероятностей перехода из вершины в вершину для каждого муравья по формуле (6).
2. Определение методом статистического моделирования ребер, выбранных муравьями, сопровождаемое последовательным удалением из матрицы строк и выбранных столбцов.
3. Оценка суммарной продолжительности маршрута Dk.
4. Расчет и обновление уровня феромона на ребрах.
Затем пересчет вероятностей (6) повторяется в соответствии с установленным числом итераций n!/2. Далее определяется наиболее повторяемое размещение вариантов и сравнивается с оптимальным результатом.
Применение всех перечисленных алгоритмов, кроме жадных, превращает исследуемую задачу в NP-полную [9]. Поэтому для выбора наиболее эффективного алгоритма предлагается провести статистическое моделирование облета одного здания группой из четырех БпЛА на примере технополиса “ЭРА”. Траектория моделируемого полета представляет собой неправильный пятиугольник. Построение дронов в поворотных точках маршрута задается простыми геометрическими фигурами, которые поясняются рис. 4. Исходными данными для моделирования являются пять матриц вида (3). В них собраны все возможные расстояния между промежуточными токами фигур построений.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Все предложенные алгоритмы реализованы на языке Python. Для метода ветвей и границ и венгерского алгоритма были использованы готовые подпрограммы из библиотеки языка программирования. Для реализации остальных были составлены программы.
Моделирование проводили на процессоре I-ntel Core-i7-800x, частота 3.5 ГГц, 12 ядер, ОЗУ 32 ГБ. Эффективность применяемых алгоритмов оценивали по двум критериям: выполнение условия (1) и временные затраты на поиск оптимального решения. Результаты представлены в табл. 4. В качестве эталона планируется использование решения, полученного методом полного перебора.
Таблица 4.
Результаты моделирования показателей группового полета БпЛА
| Алгоритм оптимизации | F(x), м | Время выпол- нения, с × 10–4 |
|---|---|---|
| Полный перебор | 1499.741 | 3 |
| Экономный | 1502.18 | 2.65 |
| Экономный с элементами перебора | 1499.766 | 6.18 |
| Муравьиный | 1499.760 | 300 |
| Метод ветвей и границ | 1499.741 | 190 |
| Венгерский | 1499.741 | 40 |
Для моделирования использован пример с элементарными условиями:
– короткий маршрут полета в форме пятиугольника (~377 м);
– численность подразделения БпЛА – всего четыре аппарата;
– для определения боевого порядка использованы простейшие геометрические фигуры (три четырехугольника и две прямые линии).
Полученные результаты расчетов подтвердили достижение поставленной в начале исследования цели.
ВЫВОДЫ
Задача выбора кратчайшего из возможных вариантов путей между двумя местами в заданных порядках построения дронов в промежуточных точках маршрута решалась с использованием шести алгоритмов (табл. 4). Полный перебор всех вариантов предоставил эталонное значение и показал вполне приемлемое время, затраченное на проведение расчета. Тем не менее уже при увеличении n до 10 существующие вычислительные мощности не справятся с решением задачи полного перебора, поскольку ее продолжительность составит больше одного часа. Поэтому ориентируясь на результат в 1499.741 м, выбираем алгоритм, реализация которого показывает наименьшие временные затраты. Таким будет являться венгерский алгоритм, который был разработан специально для решения задачи о назначениях. Результат, полученный с использованием простого экономного алгоритма, предоставил возможность численно оценить погрешность оптимизации Δ. Применение венгерского алгоритма при продолжительности маршрута всего 377.15 м точнее простого экономного, который является самым быстрым
(11)
${{\Delta }_{{{\text{венгр}}}}}~ = ~\left| {\frac{{1502.18 - 1499.741}}{{1499.741}}~\, \times 100\% } \right| \approx 0.4\% ~$.Если рассматривать применение экономного алгоритма с элементами перебора, то в этом случае подкупают время выполнения, близкое к минимальному, и погрешность всего в тысячную долю процента
(12)
$\begin{gathered} {{\Delta }_{{{\text{эконом\;с\;переб}}}}} = \\ = \left| {\frac{{1499.766 - 1499.741}}{{1499.741}} \times 100\% } \right| \approx 0.001\% . \\ \end{gathered} $Применение метода ветвей и границ, муравьиного алгоритма признаются нецелесообразными по причине значительных временных затрат на их реализацию. Учитывая то что в настоящее время наметилась тенденция усложнения условий применения дронов (увеличение их количества и продолжительности полета, изменение форм боевых порядков), однозначно можно сделать вывод о правильности выбора венгерского алгоритма для оптимизации построения пространственного маршрута группы БпЛА. Тем более, что сравнительно небольшие временные затраты на оптимизацию позволяют распределить командные функции (проведение расчетов) между отдельными аппаратами внутри группы, что потенциально улучшит боевые возможности всей группы БпЛА.
Список литературы
Барабанов М.С., Бендетт С., Денисенцев С.А. и др. Роботизация и военное дело будущего / Под ред. Бондарева В.Н. М.: Центр анализа стратегий и технологий, 2021. 232 с.
Дайджест № 3 по теме “Технологии формирования типовых сценариев группового применения РТК ВН” // Целевая поисковая лаборатория прорывных интеллектуальных технологий группового управления РТК Фонда перспективных исследований. Февраль 2021. 84 с.
Тань Лиго, Фомичёв А.В. // Вестн. МГТУ им. Н.Э. Баумана. Сер. “Приборостроение”. 2016. № 2. С. 53.
China is making 1.000-UAV drone swarms now. https://www.popsi.com/china-drone-swarms/
Алексеев В.Е., Захарова Д.В. Теория графов. Нижний Новгород: Нижегородский госуниверситет, 2017. 119 с.
Рафгарден Тим. Совершенный алгоритм. Жадные алгоритмы и динамическое программирование. СПб: Питер, 2020. 256 с.
Венгерский алгоритм решения задачи о назначениях. https://neerc.ifmo.ru/wiki/index.php?title
Чураков М., Якушев А. Муравьиные алгоритмы. http://rain.ifmo.ru/cat
Базеева Н.А. Теория алгоритмов / Под общ. ред. проф. Ломшина М.И. Саранск: Изд-во Мордов. ун-та, 2019. 136 с.
Дополнительные материалы отсутствуют.
Инструменты
Вестник Военного инновационного технополиса «ЭРА»