Водные ресурсы, 2021, T. 48, № 2, стр. 233-235

Хорошо известна важная роль брызгообмена во взаимодействии атмосферы и больших водоемов [4, 5]. Известны различные механизмы генерации брызг у поверхности воды, которыми обусловлены широкий спектр размеров брызг, скорость и направление их движения. Один из важных механизмов образования брызг при сильных ветрах связан с разрывом пленки жидкости при всплывании пузырей воздуха. При этом могут образовываться мелкие брызги, взлетающие с очень высокой скоростью. Например, в [4] (с. 59) упоминаются начальные скорости подъема брызг – 50 и даже 100 м/c. Значения числа Рейнольдса Re в таких случаях могут достигать нескольких сотен. Этому соответствует нелинейный закон сопротивления, что затрудняет описание движения таких брызг.

Это движение в поле силы тяжести описывается уравнением

здесь $t$ – время; $w$ – вертикальная скорость (вертикальная ось $z$ направлена вверх); ${\text{g}}$ – ускорение свободного падения; $c$ – коэффициент сопротивления, вообще говоря, существенно зависящий от $\operatorname{Re} $. Например, формула Клячко–Мазина: в интервале $3 < \operatorname{Re} < 400$ приводит к силе сопротивления, отличающейся от экспериментальных данных на ≤2% [1, 3]. Здесь $\rho $ – плотность среды; $\eta ,\nu $ – коэффициенты ее динамической и кинематической вязкости; ${\mathbf{v}}$ – вектор скорости частицы относительно среды; $R$ – радиус движущейся частицы (рассматриваются капли сферической формы); ${{\rho }_{p}}$ – плотность вещества частицы; индекс $S$ относится к “стоксовым” частицам (малых размеров, для которых число Re мало и справедлив линейный закон сопротивления: ${{c}_{S}} = {{9\eta } \mathord{\left/ {\vphantom {{9\eta } {2{{R}^{2}}{{\rho }_{p}}}}} \right. \kern-0em} {2{{R}^{2}}{{\rho }_{p}}}}$). Отметим, что вместо диаметра частицы $2R$ в выражении для числа Re можно, разумеется, использовать радиус. Поэтому, например, в [1] и [3] числа Re при прочих равных условиях различаются в два раза.

В случае вертикального движения брызг уравнение (1) решается в квадратурах:

где ${{w}_{0}}$ – начальная скорость частицы (капли). Но такой неявный вид решения не позволяет выразить явные зависимости таких важных параметров, как высота подъема брызг $h$ и время их пребывания в воздухе $\tau $, от начальной скорости и размеров брызг, а также от вязкости и плотности среды. Предлагается эффективный метод приближенного решения.

Идея используемого приближения заключается в следующем. На начальной стадии подъема частиц скорость и сопротивление очень велики, и это позволяет сделать два упрощения. В уравнении (1) можно пренебречь силой тяжести, которая на этой стадии мала по сравнению с силой сопротивления. В выражении (2) при больших значениях Re, очевидно, можно пренебречь единицей в скобках. В этом случае интеграл в (4) легко вычисляется аналитически; решение имеет следующий вид:

где $z\left( t \right)$ – вертикальная координата частицы. На этой стадии скорость подъема быстро убывает со временем (при $t = 1.5{{\tau }_{1}}$ уже почти в 4 раза). Далее следует переходный период, в течение которого подъем окончательно прекращается и начинается оседание; скорость установившегося оседания ${{w}_{ \downarrow }}$ хорошо изучена и для брызг малых размеров мала по сравнению с рассмотренной выше скоростью подъема. Таким образом, можно предположить, что высота подъема брызг приближенно определяется решением (5) при упоминавшемся выше ориентировочном времени подъема порядка $1.5{{\tau }_{1}}$: Затем следует вышеупомянутый переходный период, когда медленный уже подъем сменяется медленным оседанием. За этот период высота положения брызг не успевает существенно измениться. По сравнению со временем дальнейшего оседания он в случае капель малых размеров длится недолго. Поэтому, хотя указанный переходный период трудно поддается аналитическому исследованию, он не вносит существенного вклада ни в высоту подъема брызг, ни в искомую продолжительность их пребывания в воздухе.

Согласно приведенным соображениям, порядок высоты подъема быстродвижущихся брызг определяется выражением (6), а время пребывания в воздухе – того же порядка, что и время оседания:

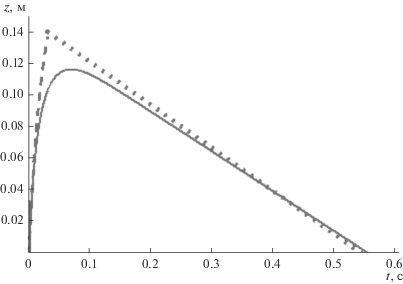
Если ${{{{\rho }_{p}}} \mathord{\left/ {\vphantom {{{{\rho }_{p}}} \rho }} \right. \kern-0em} \rho } = {{10}^{3}},\nu = 1.5 \times {{10}^{{ - 5}}}$ м²/с, то при ${{w}_{0}} = 10$ м/с [6], $R = 0.5 \times {{10}^{{ - 4}}}$ м получаем ${{\left. {\operatorname{Re} } \right|}_{{t = 0}}} \approx 70$, ${{\tau }_{1}} \approx 0.02$ с, $h \approx 0.15$ м. Скорость установившегося оседания брызг таких размеров – порядка 0.27 м/с [2]. Таким образом, согласно (7), время пребывания таких брызг в воздухе ~0.6 с.

Выше использовано предположение о том, что переходный период между быстрым подъемом и установившимся оседанием не вносит большого вклада как в высоту перемещения брызг, так и в продолжительность их пребывания в воздухе. Поскольку этот период плохо поддается аналитическому исследованию, справедливость указанного предположения проверена численным решением системы (1)–(2). На рис. 1 представлена вычисленные таким образом величины $z\left( t \right)$ для рассмотренных выше значений параметров. Видно, что порядок численных значений $h$ и $\tau $ и приведенных выше аналитических оценок хорошо согласуется. Как и предполагалось, бóльшую часть времени пребывания капли в воздухе происходит ее оседание с постоянной скоростью; начальная стадия подъема хорошо описывается приближенным решением (5). Для смыкания двух рассмотренных асимптотик выбран вышеупомянутый момент времени $t = 1.5{{\tau }_{1}}$. Высота $h$, вообще говоря, существенно зависит от этого выбора, так что полученное приближенное решение претендует лишь на правильные порядки величин.