Водные ресурсы, 2023, T. 50, № 5, стр. 602-612

ВВЕДЕНИЕ

Обменные процессы на границе вода–воздух – ключевой фактор гидродинамических и экологических процессов в водных экосистемах, формирования погоды и климата, образования течений, поверхностных волн и турбулентного перемешивания, которое напрямую влияет на перенос примесей [51], характеристики стратификации [64], кислородный режим и газообмен [38]. Основные характеристики взаимодействия – вертикальные турбулентные потоки импульса, тепла и влаги (явного и скрытого тепла). Знание о величинах этих потоков необходимо для численного прогноза погоды, моделирования Земной системы, интерпретации данных дистанционного зондирования и других геофизических приложений.

Недостаточное знание o структурe приводного слоя атмосферы и его обменe импульсом, теплом и влагой сo взволнованной водной поверхностью при разных фоновых условиях является в настоящее время основным препятствием для правильного функционирования оперативных, глобальных и региональных моделей прогноза погоды и экспертных моделей изменения климата.

Перенос импульса между атмосферой и водной поверхностью во многом определяется параметрами шероховатости для импульса, температуры и влажности. Кроме того, на поток импульса влияют скорость ветра, атмосферная стратификация, размер, крутизна и фазовая скорость ветровых волн и зыби. Вопрос о свойствах параметров шероховатости поверхности мелководных акваторий остается во многом открытым, несмотря на многочисленные исследования. Особенно это касается небольших акваторий, где параметры ветрового волнения перестают зависеть от разгона и определяются направлением ветра и характеристиками топографии.

При численном моделировании пограничного слоя для расчетов осредненных потоков используются так называемые аэродинамические балк-формулы [24]:

где C_D, C_H, C_E – безразмерные коэффициенты обмена (коэффициент сопротивления, число Стентона и число Дальтона соответственно); c_p и ρ – теплоемкость и плотность воздуха, L_s – удельная теплота испарения, τ, H и LH – турбулентные потоки импульса, тепла и влаги соответственно; U_z, T_z и q_z – скорость ветра, температура и влажность на высоте z; T_s и q_s – температура и влажность у поверхности. Коэффициенты обмена, как правило, относятся к стандартной высоте измерений z = 10 м и к условиям нейтральной стратификации.

Этот метод позволяет использовать данные стандартных метеорологических измерений, но основная трудность заключается в определении коэффициентов обмена.

Из уравнений теории подобия Монина–Обухова (ТПМО) [4] можно получить выражения:

где ${{\alpha }_{T}} = {{{{K}_{T}}} \mathord{\left/ {\vphantom {{{{K}_{T}}} {{{K}_{m}}}}} \right. \kern-0em} {{{K}_{m}}}}$ и ${{\alpha }_{q}} = {{{{K}_{q}}} \mathord{\left/ {\vphantom {{{{K}_{q}}} {{{K}_{m}}}}} \right. \kern-0em} {{{K}_{m}}}}$ – отношения турбулентных коэффициентов теплопроводности и диффузии к вязкости, или обратные турбулентные числа Прандтля и Шмидта соответственно; z – высота измерений; ${{z}_{{0u}}}$ – параметр динамической (или аэродинамической) шероховатости; ${{z}_{{0T}}}$ и ${{z}_{{0q}}}$ – параметры шероховатости для температуры и удельной влажности, т. е. высоты, на которых скорость ветра, температура и влажность достигают приземных значений, если экстраполировать профиль соответствующих метеорологических величин до поверхности. Интегральные универсальные функции ${{\Psi }_{а}}$ определяются так: ${{\Psi }_{a}} = \int_0^\zeta {\frac{{1 - {{\phi }_{a}}(\zeta )}}{\zeta }} {\kern 1pt} d\zeta $, ${{\phi }_{a}}(\zeta )$ – универсальные функции, описывающие профили метеовеличин, $\zeta = \frac{z}{L}$ – безразмерный параметр устойчивости, $L = \frac{{u_{*}^{3}}}{{\kappa \left( {\frac{{\text{g}}}{{{{T}_{0}}}}} \right)\left( {\frac{H}{{{{c}_{p}}\rho }}} \right)}}$ – масштаб Обухова.

Параметризации для определения универсальных функций разработаны на основе многочисленных специализированных экспериментов при различных условиях стратификации [16, 23, 32, 53] и достаточно надежно описывают профили метеовеличин в условиях стационарности и однородного рельефа. Параметры шероховатости ${{z}_{{0u}}}$, ${{z}_{{0T}}}$ и ${{z}_{{0q}}}$ – не напрямую измеряемые физические величины. Их введение в формулы подобия позволяет избежать детального описания профилей скорости ветра и температуры в непосредственной близости к подстилающей поверхности, т. е. в вязком подслое. В ТПМО параметры шероховатости определяют взаимодействие вязкого подслоя, в котором перенос импульса и скалярных величин осуществляется силами молекулярной теплопроводности, диффузии и вязкости, с шероховатой поверхностью [14, 30]. В вязком подслое перенос импульса через поверхность осуществляется в основном за счет разности давлений на противоположных гранях элементов шероховатости, а перенос тепла – за счет молекулярной теплопроводности. Этот контраст приводит к разнице масштабов шероховатости для скорости ветра ${{z}_{{0u}}}$ (динамическая шероховатость) и для скаляров (в частности температуры и влажности) [79]. Параметр динамической шероховатости различных поверхностей суши в развитом турбулентном течении определяется прежде всего размерами и формой элементов шероховатости [14, 30] (за исключением случая, когда высота элементов шероховатости сравнима с масштабом длины Обухова, например в условиях городской застройки [80]), т. е. может быть определен исходя из структуры поверхности. Параметры шероховатости для температуры и влажности более изменчивы и зависят от большего количества факторов, включая молекулярную вязкость и теплопроводность [6, 66].

В случае морской поверхности определение параметра динамической шероховатости усложняется тем, что состояние поверхности зависит от скорости ветра. Несмотря на многочисленные работы в этой области, до сих пор нет четкого понимания характера зависимости параметра динамической шероховатости и связанного с ним сопротивления водной поверхности от средней скорости ветра, характера и возраста волнения, динамического и температурного состояния морской поверхности. Шероховатость водной поверхности вызывается движением соприкасающегося с ней слоя воздуха и поддерживается в основном за счет передачи потока импульса и энергии к поверхности. Мелкомасштабные шероховатости морской поверхности представляют собой сложную совокупность гравитационных волн и капиллярной ряби, происхождение и структура которых зависят не только от ветра, но и от течений, внутренних волн в море и атмосфере, глубины водоема, рельефа дна, воздействия движущихся и стационарных объектов, антропогенных поверхностных загрязнений и других факторов [21, 25].

Среди водных объектов с точки зрения их воздействия на климатическую систему особый интерес вызывают внутренние водоемы – озера и водохранилища [19, 56]. Поверхность озер отличается от поверхности окружающего ландшафта небольшим альбедо, значительно меньшей шероховатостью, высокой теплопроводностью и большой теплоемкостью: следовательно, они влияют на процессы в пограничном слое атмосферы, на локальную циркуляцию атмосферы и тепловой и водный баланс регионального масштаба [31, 46], что необходимо учитывать при региональном и климатическом моделировании.

Но в большинстве моделей озер схемы параметризации процессов обмена по-прежнему основаны на океанских данных [33, 47, 68, 79]. Из-за различий в процессах волнообразования в океане и озере, связанных с глубиной водоема и ограниченным разбегом волн, этот подход может привести к значимым ошибкам [62]. Так, установлено, что поверхность озера может быть аэродинамически более шероховатой, чем открытый океан, при одинаковой скорости ветра; использование океанских параметризации может привести к ошибке годовой оценки испарения над озером на 40% [44]. Поэтому необходимо обратить внимание на параметризацию коэффициентов обмена и показателей шероховатости для озерных моделей. Работы в этом направлении проводились и ранее [13, 34, 35, 52, 67], но вопрос о свойствах параметра шероховатости поверхности мелководных акваторий, в частности озер, остается во многом открытым.

Основным критерием для определения ветрового волнения на мелководье выбирается параметр $H \leqslant {\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. \kern-0em} 2}$ (H – глубина водоема, а λ – характерная длина волн) [2]. Для условий глубокой воды наибольшее сопротивление ветру оказывают высокочастотные составляющие спектра морского волнения, поскольку их фазовые скорости намного меньше фазовых скоростей составляющих в окрестности спектрального максимума волн ${{\omega }_{0}}$, следовательно – и скорости воздушного потока. Длинные и пологие волны, соответствующие максимуму спектра морского волнения и имеющие фазовые скорости, близкие к скорости ветра, не оказывают заметного тангенциального сопротивления воздушному потоку, но могут вносить волновое сопротивление. Волны на мелководье имеют сравнительно небольшие фазовые скорости из-за ограничивающего влияния глубины водоема при относительно большой крутизне, которая связана с нелинейными взаимодействиями длинных и коротких волн. По этой причине вклад составляющих волнового спектра в общее сопротивление водной поверхности вблизи максимума спектра с частотой ${{\omega }_{0}}$ оказывается соизмеримым с вкладом высокочастотных составляющих и даже преобладающим. Этот эффект усиливается с уменьшением глубины водоема, т. е. значения параметра динамической шероховатости растут с увеличением скорости ветра или с уменьшением глубины. Кроме того, на небольших озерах происходят несинхронные взаимодействия между изменениями характеристик поверхностного волнения и поля скорости ветра. Важное различие формирования волн в озере и океане – короткий разгон. В результате, волновое поле характеризуется молодыми и высокочастотными волнами, а измеренные значения возраста волн превышают литературные данные. Следовательно, оценки, полученные в открытом океане и даже в мелководных прибрежных зонах, неприменимы для параметрзации процессов обмена в условиях внутренних водоемов.

Также не учитывается тот факт, что условия слабых ветров более типичны для внутренних водоемов, чем для открытого океана [77], а в этом случае на параметры шероховатости влияют неоднородности поверхностного натяжения и мелкомасштабные капиллярные волны [48, 75].

С учетом того, что чувствительность определения турбулентных потоков на границе атмосфера – водная поверхность к выбору схемы определения параметров шероховатости велика [74], необходима разработка надежных схем расчета этих параметров, в том числе для мелководных водоемов.

СПОСОБЫ ОПРЕДЕЛЕНИЯ ПАРАМЕТРА ШЕРОХОВАТОСТИ

Согласно ТПМО, параметры шероховатости ${{z}_{{0u}}}$, ${{z}_{{0T}}}$ и ${{z}_{{0q}}}$ определяются как высоты, на которых профили соответствующих метеопараметров равны нулю.

Для температуры (и аналогично для влажности)

${{T}_{*}} = \frac{H}{{{{u}_{*}}}}$, T_s – температура поверхности или аэродинамическая температура (температура воздуха на высоте шероховатости).

Из формул (4)–(6) и (7), (8) параметры шероховатости определяются так:

В данной работе используются универсальные функции в следующем виде [16, 23, 27, 32, 36]:

неустойчивая стратификация $\zeta < - 0.05$:

нейтральная стратификация: $ - 0.05 < \zeta < 0.05$:

устойчивая стратификация $\zeta > 0.05$:

Для определения коэффициентов обмена и масштаба Обухова (параметра устойчивости) в этом методе необходимы прямые пульсационные измерения характеристик атмосферной турбулентности. Несмотря на то, что при расчетах используются эмпирические универсальные функции, данный метод – единственный прямой способ определения параметра шероховатости.

При наличии профильных измерений для расчета параметра динамической шероховатости возможно использование формулы для определения логарифмического профиля ветра при нейтральной стратификации $u = \frac{{{{u}_{*}}}}{\kappa }\left[ {\ln \left( {\frac{z}{{{{z}_{{0u}}}}}} \right)} \right]$. В этом случае ${{z}_{{0u}}}$ легко определить по измерениям на двух уровнях:

${{z}_{1}}$ и ${{z}_{2}}$ – верхний и нижний уровни, на которых измеряются скорости ветра ${{u}_{1}}$ и ${{u}_{2}}$.

Если учитывать тот факт, что при взаимодействии атмосферы с шероховатой поверхностью существует глубина смещения (“displacement”) D, на которую смещается атмосферный поток по вертикали [80], формулы для логарифмического профиля ветра и (18) должны быть переписаны в виде:

Формула (20) требует дополнительной информации о динамической скорости. Но глубина вытеснения D водной поверхности незначительна, особенно при слабых и умеренных ветрах, и ее можно не учитывать.

Вычисление параметра шероховатости из формулы (18) в реальных условиях может приводить к ошибкам из-за несоответствия реального профиля скорости ветра логарифмическому закону при стратификации атмосферы, отличной от нейтральной. Использование профильного метода правомерно, если брать невысокие уровни измерений метеопараметров, применим он только для неподвижных оснований и требует измерений скорости ветра однотипными датчиками с высокой точностью. Значения z_0u, полученные таким образом из логарифмического профиля, построенного по данным $u(z)$ на двух уровнях, различаются несущественно даже при сильно устойчивой и сильно неустойчивой стратификации, если измерения выполнены на уровнях над поверхностью до ~5 м [42]. Поправки на стратификацию за счет функций ${{\Psi }_{u}}\left( \zeta \right)$ и ${{\Psi }_{T}}\left( \zeta \right)$ также малы при сильных ветрах, когда $L \to \pm \infty $ и ${{\Psi }_{u}}\left( \zeta \right)$, ${{\Psi }_{T}}\left( \zeta \right) \to 0$.

За последние несколько десятилетий разработаны разные схемы параметризации параметра шероховатости водных поверхностей [25, 45, 57, 68], в том числе учитывающие стратификацию атмосферы [79].

В моделях взаимодействия атмосферы и океана для параметризации условий шероховатости на границе вода–воздух, как правило, используется формула Чарнока [18]:

где a – эмпирический коэффициент, называемый параметром Чарнока. Экспериментальные данные [12] показали, что в зависимости от условий значения коэффициента Чарнока могут различаться более чем на порядок и существенно зависят от характеристик поверхностного волнения и глубины водоема. Предпринимались различные попытки связать параметр шероховатости с параметрами морского волнения. На основании многочисленных лабораторных и натурных экспериментов, а также теоретических расчетов в качестве параметра, определяющего шероховатость морской поверхности, выбран возраст волн, определяемый как $\left( {\frac{{{{c}_{{ph}}}}}{{{{u}_{*}}}}} \right)$ или $\left( {\frac{{{{c}_{{ph}}}}}{{{{u}_{z}}}}} \right)$, c_ph – фазовая скорость волн. В качестве дополнительных параметров используются частота спектрального пика ветрового волнения [63], высота волн.

В ряде работ [22, 26, 39, 40, 49, 58] предложена обобщающая формула зависимости коэффициента шероховатости от параметра возраста волн в следующем виде:

Для предельного развития волн на мелководных водоемах, когда характеристики поверхностной шероховатости перестают зависеть от разгона, а также при трансформации волн, приходящих со стороны открытого моря (большие разгоны), используется уравнение [5]

где h – глубина водоема. Из соображений размерности зависимость (23) можно аппроксимировать формулой

Значение коэффициента m выбирается исходя из тех условий, что при развитом волнении и глубоком море параметр Чарнока $a = \frac{{{\text{g}}{{z}_{{0u}}}}}{{u_{*}^{2}}} \to 0.011$, он меняется от 25 до 50 в зависимости от глубины водоема и близости берега. Как показывают данные измерений, этот подход применим для прибрежных зон, но не всегда подходит для замкнутых внутренних водоемов.

Для океанической поверхности, как и предположил в своих теоретических исследованиях Чарнок, параметр a имеет порядок 10⁻² ([17, 18], a = = 0.0123). Это подтверждено и более поздними исследованиями (в [57] a = 0.011). Для случая мелководных водоемов, согласно [7], значения параметра Чарнока могут существенно отличаться от значений для океана. Например, более высокие значения a найдены в работах [29] (a = 0.0144), [76] (a = 0.018) и [55] (на порядок выше – а = = 0.110). В ряде публикаций для озер и прибрежных зон обосновано значение а = 0.03 [12, 29, 59, 70].

При слабых ветрах водная поверхность может быть представлена как гладкая твердая стенка, которую вязкий подслой отделяет от пристеночного потока. Преобладание вязкого механизма формирования параметра шероховатости морской поверхности наблюдается при скоростях ветра <5 м/с. Поэтому в схемах параметризации аэродинамической шероховатости обычно рассматриваются две ситуации: течение, связанное с напряжением ветра [18, 57], и течение, связанное с вязкостью.

С учетом вязкости формулу Чарнока можно переписать в виде:

где ν – кинематическая вязкость воздуха (м²/с), величина которой составляет ⁓1.5 × 10^–5 м²/с для атмосферы на уровне моря. Параметр c связан с числом Рейнольдса Re и в океанических условиях принимается равным 0.11, а для озер может увеличиваться до 0.54 [72].

Для оценки параметров шероховатости для температуры и влажности применяется подход, впервые предложенный С.С. Зилитинкевичем [1], где параметризуется их зависимость от Re и параметра динамической шероховатости. В общем виде эта зависимость выражается в виде:

Коэффициенты a и b зависят от типа поверхности и определяются по данным измерений, показатель степени n соответствует различным упрощениям в уравнениях переноса-диффузии скалярной величины (температуры, влажности) в вязком подслое [43]. В различных параметризациях используются значения n = 1; 0.5; 0.25 [66]. Формула (26) может быть записана в виде [62]: где $\kappa $ постоянная Кармана, Pr =  0.71 – молекулярное число Прандтля для воздуха, Sc  =  0.66 молекулярное число Шмидта для водяного пара.

Обзоры параметризаций параметров шероховатости для различных поверхностей можно найти в работах [6, 14]. Для морской поверхности используется параметризация, предложенная в работе С.С. Зилитинкевича [79]. Для озер параметризации параметров шероховатости проверены в работах [20, 59, 62, 67, 71]. Но в озерных моделях, как и прежде, в основном используются параметризации, разработанные для открытого моря.

ИСПОЛЬЗУЕМЫЕ ДАННЫЕ И МЕТОДЫ ОБРАБОТКИ

Для анализа параметризаций параметра шероховатости использованы данные измерений характеристик атмосферной турбулентности на оз. Большой Вилюй [61], Можайском и Горьковском водохранилищах. Средняя глубина оз. Большой Вилюй – 4 м, Можайского и Горьковского водохранилищ – 20 м. На озере и Можайском водохранилище измерительный комплекс располагался на достаточном удалении от берегов на заякоренном плавучем основании. На Горьковском водохранилище для измерений использовался катамаран “Геофизик” [3]. Направление ветра во время измерений обеспечивало достаточную длину разгона волн и позволило не учитывать влияние берегов. Определение параметров шероховатости проводилось по формулам (9)–(11), где использовались значения коэффициентов обмена, динамической скорости ${{u}_{*}}$, потоков тепла и влаги и параметра устойчивости $\zeta = \frac{z}{L}$. В формулах (24) и (25) значения ${{u}_{*}}$ также брались измеренные. Измерения проводились в летний период 2015 г. на Большом Вилюе, в 2017 г. на Можайском водохранилище и в 2016–2018 гг. на Горьковском.

Измерительный комплекс состоял из акустического анемометра (марка “WindMaster 3D”, производство “Gill Instruments”) и инфракрасного газоанализатора CO₂/H₂O открытого типа (марка “LI 7500”, производство “LI-COR, Inc.”). На оз. Большой Вилюй газоанализатор не использовался – определялись только параметр динамической шероховатости и параметр шероховатости для температуры. Данные акустического анемометра синхронизировались с данными газоанализатора и использовались для вычисления турбулентных потоков тепла, импульса и метана. Для вычисления потоков использовался метод турбулентных пульсаций (“Eddy-covariance”) [15].

Согласно этому методу, потоки вычисляются по ковариациям между измеряемыми пульсациями метеопараметров и концентраций газов:

Обозначения соответствуют обозначениям в формулах (1)–(3); u', v', w' – пульсации трех компонент скорости ветра: продольной, поперечной и вертикальной соответственно; T ' – пульсации температуры; q' – пульсации влажности. При вычислении потоков использовались спектральная коррекция [50], коррекция флуктуаций плотности [73], коррекция акустической температуры [65], коррекция наклона анемометра, а также статистические тесты [69]. Для контроля качества данных были применены методы, предложенные в [28]. Футпринт (область формирования потока на поверхности) оценивался на основе аналитической модели [41]. Был взят период осреднения 20 мин.

Но даже при всех коррекциях данные о турбулентных потоках обычно имеют большой случайный разброс. И, соответственно, получаемые по формулам (9)–(11) параметры шероховатости тоже имеют сильный разброс. Единственный способ преодолеть этот разброс — использовать дополнительные коррекции [9–11, 78]. При отборе данных использовались ограничения по скорости ветра ${{u}_{*}} > 0.05$ м/с, по значениям потоков $\left| {H,LH} \right| \geqslant 10$ Вт/м². Использовались только данные, соответствующие области формирования потоков над водной поверхностью. При дополнительной проверке данные отбраковывались, если они соответствовали следующим критериям [44]:

Критерий (31) применялся соответственно предположению, что масштаб шероховатости не превышает одной десятой высоты наблюдения (максимум 3.0 м в данном исследовании). Критерии (32), (33) взяты с учетом переноса тепла и влаги в вязком подслое [60]. Предполагается, что при масштабах, меньших этого уровня, поверхностный обмен теплом и влагой не может происходить [8, 11].

В результате фильтраций для анализа было отобрано 645 значений параметра динамической шероховатости, 572 значения параметра шероховатости для температуры и 489 для влажности.

РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ

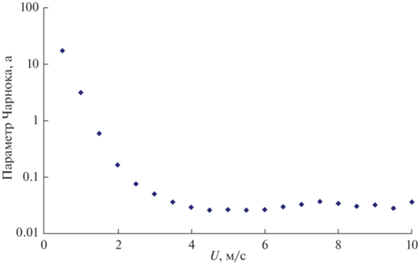
На рис. 1 показан полученный из измерений (формулы (9), (21)) параметр Чарнока. Для скоростей ветра >5 м/с Параметр Чарнока равен 0.03, что согласуется с предыдущими данными [71]. Измерения подтверждают преобладание вязкого механизма формирования шероховатости при ветрах <4 м/с, когда расчет по формуле (21) некорректен и необходим учет эффектов вязкости. Большой разброс экспериментальных данных о параметре шероховатости при слабых ветрах может быть связан со стратификацией, нестационарностью поля ветра, влиянием направления и малыми скоростями ветра [54].

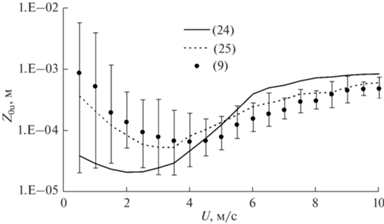
На рис. 2 показано сравнение параметров динамической шероховатости, полученных по формулам (9), (25) (с = 0.11, a = 0.03), (24) (m = 25). При средних скоростях ветра расчеты по формуле Чарнока совпадают с результатами наблюдений. Завышенные результаты расчетов по формуле (24), вероятно, связаны с тем, что данная параметризация проводилась для прибрежных районов при трансформации волн, приходящих со стороны открытого моря. Значения параметра шероховатости при отсутствии ветра ${{z}_{0}} = 0.001$ м соответствуют данным модельных расчетов для режима свободной конвекции в работе [37]. В целом, параметр динамической шероховатости меняется от 0.00007 до 0.0009 м.

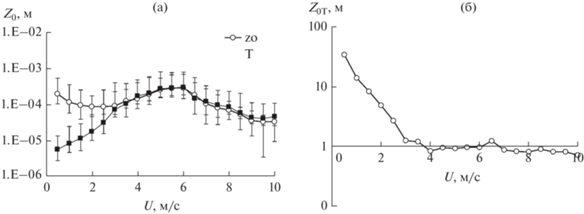
Параметры шероховатости для импульса, тепла и влаги при средних ветрах в среднем составляли 0.0006, 0.000073 и 0.000069 м соответственно. На рис. 3a показана зависимость параметров шероховатости для температуры и импульса от скорости ветра. Следует заметить, что при малых ветра параметры шероховатости для температуры и влажности не равны (рис. 3б). Cooтношение масштабов шероховатости для температуры и для влаги намного больше единицы для слабого ветра и уменьшается до значений, близких к единице, для ветра выше порогового значения ⁓3.0 м/с. Более эффективный перенос явного тепла, чем скрытого, при слабых ветрах ${{z}_{{0H}}} > {{z}_{{oT}}}$ вызван тем, что в формировании потока плавучести большую роль играет термический поток.

Полученные из измерений авторами данного исследования параметризации выглядят следующим образом:

Коэффициенты в формулах (34)–(36) близки к полученным ранее коэффициентам [62], что свидетельствует о проявлении единого механизма процессов переноса в вязком подслое замкнутых водоемов.

ВЫВОДЫ

В настоящем исследовании параметров шероховатости мелководных водоемов использованы данные пульсационных наблюдений на различных акваториях. Результаты показали возможность использования формулы Чарнока для расчета параметра динамической шероховатости для мелководных замкнутых водоемов. При средних скоростях ветра результаты расчетов по формуле Чарнока совпадают с результатами наблюдений, при этом параметр Чарнока в три раза выше, чем для условий открытого океана. При слабых ветрах шероховатость создается поверхностным натяжением или мелкомасштабными капиллярными волнами и соотношение Чарнока в виде (21) неприменимо, так как влияние гравитационных волн уменьшается. Причем переход от вязкого механизма к волновому происходит при бóльших скоростях ветра, чем в океане. При средних ветрах в озере динамическая шероховатость больше, чем в открытом океане. Связано это, видимо, с тем, что в озере волны не достигают больших возрастов и сохраняют параметры молодых волн и при усилении ветра.

Параметры шероховатости для температуры и влажности при скорости ветра <3 м/с не равны. Более эффективный перенос явного тепла, чем скрытого, при слабых ветрах обусловлен тем, что в формировании потока плавучести большую роль играет термический поток. Числовые коэффициенты в зависимостях отношения динамической шероховатости к параметру шероховатости для температуры (влажности) от числа Рейнольдса близки к полученным ранее значениям для других замкнутых водоемов, что свидетельствует о едином механизме формирования процессов переноса в вязком подслое. Полученные параметризации могут быть использованы в климатических и озерных моделях для расчета турбулентных потоков над водными объектами суши.