Водные ресурсы, 2023, T. 50, № 5, стр. 585-601
Применимость различных педострансферных функций к описанию гидрофизических характеристик почв (грунтов)
А. А. Рязанова a, b, *, В. Ю. Богомолов a, b, c, d, e, А. И. Медведев e, f
a Институт мониторинга климатических и экологических систем СО РАН
634055 Томск, Россия
b Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Россия
c Научно-исследовательский Томский государственный университет
634050 Томск, Россия
d Научно-исследовательский вычислительный центр,
Московский государственный университет им. М.В. Ломоносова
119234 Москва, Россия
e Институт водных проблем РАН
119333 Москва, Россия
f Гидрометеорологический научно-исследовательский центр Российской Федерации
123376 Москва, Россия
* E-mail: r.ann.1194@gmail.com
Поступила в редакцию 01.02.2023
После доработки 05.04.2023
Принята к публикации 05.04.2023
- EDN: LHPGZL
- DOI: 10.31857/S0321059623600114
Аннотация
Проведен сравнительный анализ гидрофизических характеристик, полученных с помощью педотрансферных функций, и гидрофизических характеристик из глобального почвенного набора.
ВВЕДЕНИЕ
Почва играет важную роль в энергетическом и водном обмене между земной поверхностью и атмосферой, поэтому блоки деятельного слоя суши входят в состав всех систем прогноза погоды и моделей Земной системы, независимо от пространственных и временных масштабов воспроизводимых процессов. Они, в частности, описывают водный и энергетический балансы, включающие осадки, испарение, поверхностный сток, инфильтрацию, питание подземных вод и фазовые переходы. Для адекватного воспроизведения влажности и температуры почвы в моделях деятельного слоя суши требуется набор параметров, представляющих гидравлические, термические и радиационные свойства почвы. При математическом описании тепловлагопереноса в почве все физические процессы, как правило, предполагаются одномерными по вертикали, поскольку вертикальная компонента градиентов температуры и влаги в различных ее состояниях обычно значительно превосходит горизонталìьные компоненты.
МАТЕРИАЛЫ И МЕТОДЫ
Уравнения тепловлагопереноса в почве с учетом корневой системы растительности для модели деятельного слоя суши ИВМ РАН−МГУ записываются в виде [2–5]:
(1)
$\rho C\frac{{\partial T}}{{\partial t}} = \frac{\partial }{{\partial z}}{{\lambda }_{T}}\frac{{\partial T}}{{\partial z}} + {{L}_{i}}{{F}_{i}} - {{L}_{{v}}}{{F}_{{v}}},$(2)
$\frac{{\partial W}}{{\partial t}} = \frac{\partial }{{\partial z}}{{\lambda }_{W}}\frac{{\partial W}}{{\partial z}} + \frac{{\partial \gamma }}{{\partial z}} - {{F}_{i}} - {{F}_{{v}}} - {{R}_{f}} - {{R}_{r}},$(3)
$\frac{{\partial V}}{{\partial t}} = \frac{\partial }{{\partial z}}{{\lambda }_{V}}\frac{{\partial V}}{{\partial z}} + {{F}_{{v}}},$(5)
$~T\left( {z,{{t}_{0}}} \right) = {{T}_{0}}\left( z \right),~\,\,\,\,W\left( {z,{{t}_{0}}} \right) = {{W}_{0}}\left( z \right),$(6)
$T\left( {0,t} \right) = {{T}_{s}}\left( t \right),\,\,\,\,~{{\left. {\frac{{\partial T}}{{\partial z}}} \right|}_{{z{\kern 1pt} = {\kern 1pt} H}}} = 0,$(7)
${{\lambda }_{w}}{{\left. {\frac{{\partial W}}{{\partial z}}} \right|}_{{z{\kern 1pt} = {\kern 1pt} 0}}} = {{B}_{w}},\,\,\,\,{{\lambda }_{w}}{{\left. {\frac{{\partial W}}{{\partial z}}} \right|}_{{z{\kern 1pt} = {\kern 1pt} H}}} = 0,$Коэффициент теплопроводности в модели задается по формулам Пильке, Йохансена или Коте–Конрада [15]. Для задания гидрофизических характеристик λW и γ в модели реализованы параметризации Брукса–Кори (Клаппа–Хорнбергера) [10, 12] и Муалема–ван Генухтена [18, 29]. В данной работе будем рассматривать только параметризацию Клаппа–Хорнбергера как часто используемую в моделях деятельного слоя суши:
(8)
$\begin{gathered} \psi = {{\psi }_{{{\text{max}}}}}{{\left( {\frac{{{{W}_{{{\text{max}}}}}}}{W}} \right)}^{b}},\,\,\,\,{{\lambda }_{w}} = {{\lambda }_{{{\text{max}}}}}{{\left( {\frac{W}{{{{W}_{{{\text{max}}}}}}}} \right)}^{{b{\kern 1pt} + {\kern 1pt} 2}}}, \\ \gamma = {{\gamma }_{{{\text{max}}}}}{{\left( {\frac{W}{{{{W}_{{{\text{max}}}}}}}} \right)}^{{2b{\kern 1pt} + {\kern 1pt} 3}}}, \\ \end{gathered} $(9)
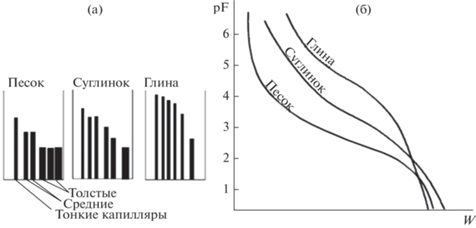
${{\lambda }_{{{\text{max}}}}} = \frac{{b{{\gamma }_{{{\text{max}}}}}\left( { - {{\psi }_{{{\text{max}}}}}} \right)}}{{{{W}_{{{\text{max}}}}}}},$Таким образом, при моделировании профиля температуры и влаги возникает вопрос, как задавать гидрофизические параметры Ψmax, λmax, γmax, b, Wmax. Изначально в модели реализован подход, при котором по заданному гранулометрическому составу и пористости определяется тип почвы по классификации почв USDA [26], а затем для выбранного типа почвы из имеющейся таблицы [1] выбираются средние значения гидрофизических параметров. Такой подход не всегда дает надежные результаты: например, при попадании параметров гранулометрического состава в границы типов почвы по какой-либо классификации гидрофизические параметры могут сильно отличаться от средних значений для типов почвы в силу того, что непрерывные педотрансферные функции при данном подходе заменяются кусочно-постоянными зависимостями. На значимость подобных эффектов указывает большая разность средних по типам почвы значений гидрофизических параметров, хорошо заметная на примере основной гидрофизической характеристики (ОГХ) (рис. 1 ). Также в описанном выше подходе не учитывается влияние органического вещества почв на гидрофизические параметры.
Для устранения недостатков используемого в модели подхода существует несколько вариантов.
Первый вариант – это проведение прямых in situ измерений требуемых гидрофизических характеристик при наличии почвенных образцов, что трудоемко, сопряжено с ошибками измерений и не обеспечивает регулярного по горизонтали покрытия в региональном и глобальном масштабe. Такой вариант применим в случае запусков модели для одиночной ячейки или локального почвенного профиля.
Второй вариант предполагает использование педотрансферных функций (ПТФ) [8]. По Е.В. Шеину [6], ПТФ – это эмпирические зависимости, позволяющие восстанавливать основные гидрофизические функции почв, в том числе ОГХ, по известным из материалов Почвенных служб и массово определяемым базовым свойствам почв, таким как гранулометрический состав, пористость, плотность и содержание органического вещества. Использование ПТФ позволяет получить гидрофизические параметры с тем же пространственным охватом и разрешением, что и базовые свойства.
Существует множество ПТФ, они условно делятся на три большие группы: классовые, непрерывные и полученные на основе нейронных сетей. В классовых ПТФ гидрофизические параметры определяются только текстурным классом почвы (к текстурным классам относятся, например, песок, глина, супесь и др.) в предположении, что почвы близких классов имеют схожие гидравлические свойства. Непрерывные ПТФ в качестве аргументов принимают объемное содержание глины Vclay, ила Vsilt, песка Vsand, т. е. компоненты гранулометрического состава, и в некоторых случаях органического вещества VSOM, а также пористости θs, что дает значения для гидрофизических характеристик для всего множества типов почв. В качестве примера непрерывной ПТФ приведем ПТФ Косби [13]:
(10)
${{\psi }_{{{\text{max}}}}} = {{10}^{{\left( {1.54{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.0095{{V}_{{{\text{sand}}}}}{\kern 1pt} \,\, + \,\,{\kern 1pt} 0.0063{{V}_{{{\text{silt}}}}}} \right)}}},$(12)
${{\gamma }_{{{\text{max}}}}} = {{10}^{{\left( { - 0.6{\kern 1pt} \,\, + \,\,{\kern 1pt} 0.0126{{V}_{{{\text{sand}}}}}{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.0064{{V}_{{{\text{clay}}}}}} \right)}}},$Третий вариант подхода – использование глобальных наборов данных почвенного состава и гидрофизических характеристик. Пример такого набора – глобальный почвенный набор (ГПН) почвенных гидравлических и термических характеристик для моделирования деятельного слоя суши [14]. Почвенные характеристики этого набора данных приведены в табл. 1 . Все характеристики представлены глобальными полями с пространственным разрешением 30'', имеют четыре варианта распределения по горизонтальным слоям (максимум 8 слоев до глубины 3.8 м) и доступны для свободной загрузки.
Таблица 1.
Основные свойства почвы
| Vgravel, VSOM, Vsand, Vsilt, Vclay, θs | Объемные фракции гравия, органического веществa почв, песка, ила и глины, а также содержание насыщенной воды, эквивалентное пористости (Vgravel + VSOM + Vsand + Vsilt + Vclay + θs = 100%) |
|---|---|
| Гидрофизические характеристики для параметризации Клаппа–Хорнбергера | |
| ψmax | Потенциал влаги при максимальном насыщении, см |
| b | Безразмерный параметр |
| γmax | Гидравлическая проводимость при максимальном насыщении, см/д |
Таким образом, вопрос исследования можно переформулировать следующим образом: будет ли обеспечена приемлемая точность моделирования при использовании внутри модели деятельного слоя суши какой-то одной, в некотором смысле оптимальной, ПТФ для расчета гидрофизических характеристик по внешним данным о составе почвы, либо необходимо использовать глобальные наборы информации и по гранулометрическому составу, и по гидрофизическим характеристикам? Для ответа на этот вопрос в настоящей работе проведен анализ наиболее часто используемых в научной литературе и исследованиях ПТФ, на основе которого можно выбрать оптимальную (одну) ПТФ для включения ее в модель деятельного слоя.
Для расчета потенциала влаги насыщенной почвы и безразмерного показателя Клаппа–Хорнбергера часто используются следующие ПТФ: Сакстона [24], Кэмпбелла [11], Ролза [9], Остервельда [21], Уильямса [30], Майра [19], Сакстона и Ролза [23], Косби [13]. Для расчета гидравлической проводимости часто используют ПТФ: Сакстона [24], Ролза [9], Косби [13], Востена [31, 32], Джабро [18], Оттони [22], Швета–Прасана [25], Немеса [20], Томасселы [28]. Формулы для этих ПТФ представлены в табл. 2.
Таблица 2.
Непрерывные ПТФ
| ПТФ | Формула |
|---|---|
| Сакстон [24] | $A = 100{\kern 1pt} {\text{exp}}\left[ {a + b{{V}_{{{\text{clay}}}}} + cV_{{{\text{sand}}}}^{2} + dV_{{{\text{sand}}}}^{2}{{V}_{{{\text{clay}}}}}} \right]$ $B = e + fV_{{{\text{clay}}}}^{2} + gV_{{{\text{sand}}}}^{2}{{V}_{{{\text{clay}}}}}$ ψmax = A$\theta _{s}^{B}$ b = B ${{\gamma }_{{{\text{max}}}}} = {\text{exp}}\left( {p + q{{V}_{{{\text{sand}}}}} + \frac{{r + t{{V}_{{{\text{sand}}}}} + u{{V}_{{{\text{clay}}}}} + {v}V_{{{\text{clay}}}}^{2}}}{{{{\theta }_{s}}}}} \right)$ a, b, c, d, e, f, g, r, t, u, v – заданные константы |
| Кэмпбелл [11] | ${{f}_{{{\text{clay}}}}} = {{V}_{{{\text{clay}}}}}{\kern 1pt} /{\kern 1pt} 100;\,\,\,\,~{{f}_{{{\text{sand}}}}} = {{V}_{{{\text{sand}}}}}{\kern 1pt} /{\kern 1pt} 100$ ${{d}_{g}} = {\text{exp}}\left[ { - 0.80 - 3.17{{f}_{{{\text{sand}}}}} - 7.61{{f}_{{{\text{clay}}}}}} \right]$ ${{\sigma }_{g}} = {\text{exp}}{{\left[ {13.32{{f}_{{{\text{sand}}}}} + 47.7{{f}_{{{\text{clay}}}}} - {\text{l}}{{{\text{n}}}^{2}}{{d}_{g}}} \right]}^{{0.5}}}$ ${{\Psi }_{{{\text{es}}}}} = - 0.05d_{g}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}{\kern 1pt} }}$ $b = - 20{{\Psi }_{{{\text{es}}}}} + 0.2{{\sigma }_{g}}~$ ${{\Psi }_{{{\text{max}}}}} = 100.0{{\left( {{{{{\rho }_{b}}} \mathord{\left/ {\vphantom {{{{\rho }_{b}}} {1.3}}} \right. \kern-0em} {1.3}}} \right)}^{{0.67b}}}$, ${{\rho }_{b}}$ – плотность почвы, г/м3 |
| Ролз [9] | ${{\Psi }_{{{\text{max}}}}} = {\text{exp}}(5.3396738 + 0.1845038{{V}_{{{\text{clay}}}}} - 2.48394546$ $\begin{gathered} \overline {{{\theta }_{s}}} = 0.00213853V_{{{\text{clay}}}}^{2} - 0.04356349{{V}_{{{\text{sand}}}}}{{\theta }_{s}} - 0.61745089{{V}_{{{\text{clay}}}}}{{\theta }_{s}} + \hfill \\ + \,\,0.00143598V_{{{\text{sand}}}}^{2}\theta _{s}^{2} - 0.00855375V_{{{\text{clay}}}}^{2}\theta _{s}^{2} - \,\,0.00001282V_{{{\text{sand}}}}^{2}{{V}_{{{\text{clay}}}}} + ~\,\,0.00895359V_{{{\text{clay}}}}^{2}{{\theta }_{s}} - \hfill \\ - \,\,0.00072472V_{{{\text{sand}}}}^{2}{{\theta }_{s}} + 0.0000054V_{{{\text{clay}}}}^{2}{{V}_{{{\text{sand}}}}} + 0.50028060\theta _{s}^{2}{{V}_{{{\text{clay}}}}}) \hfill \\ b = 1{\kern 1pt} /{\kern 1pt} ({\text{exp}}( - 0.7842831 + 0.0177544{{V}_{{{\text{sand}}}}} - 1.062498{{{{\theta }}}_{s}} - 0.00005304V_{{{\text{sand}}}}^{2} - \hfill \\ - \,\,0.00273493V_{{{\text{clay}}}}^{2} + 1.11134946{{\theta }}_{s}^{2}\,\, - \,\,0.03088295{{V}_{{{\text{sand}}}}}{{\theta }_{s}} + \,\,0.00026587V_{{{\text{sand}}}}^{2}\theta _{s}^{2} - \hfill \\ - \,\,0.00610522V_{{{\text{clay}}}}^{2}\theta _{s}^{2} - 0.00000235V_{{{\text{sand}}}}^{2}{{V}_{{{\text{clay}}}}} + 0.00798746V_{{{\text{clay}}}}^{2}{{\theta }_{s}} - 0.00674491\theta _{s}^{2}{{V}_{{{\text{clay}}}}})\,\,\,\, \hfill \\ {{\gamma }_{{{\text{max}}}}} = {\text{exp}}(19.52348{{\theta }_{s}} - 8.96847 - 0.028212{{V}_{{{\text{clay}}}}} + 0.00018107V_{{{\text{sand}}}}^{2} - 0.0094125V_{{{\text{clay}}}}^{2} - \hfill \\ - \,\,8.395215\theta _{s}^{2} + 0.077718{{V}_{{{\text{sand}}}}}{{\theta }_{s}}\,\, - \,\,0.00298V_{{{\text{sand}}}}^{2}\theta _{s}^{2} - \,\,0.019492V_{{{\text{clay}}}}^{2}\theta _{s}^{2} + 0.0000173V_{{{\text{sand}}}}^{2}{{V}_{{{\text{clay}}}}} + \hfill \\ + \,\,0.02733V_{{{\text{clay}}}}^{2}{{\theta }_{s}} + 0.001434V_{{{\text{sand}}}}^{2}{{\theta }_{s}} - 0.0000035V_{{{\text{clay}}}}^{2}{{V}_{{{\text{sand}}}}})\,\,\,\,\,\,\, \hfill \\ \end{gathered} $ |
| Остервельд [21] | $A = \frac{{{{\rho }_{b}}}}{{100}}\left( {35.36 + 0.644{{V}_{{{\text{clay}}}}} - 0.251{{V}_{{{\text{sand}}}}} + 0.675} \right)$ $b = \frac{1}{{0.19}}$ ${{\Psi }_{{{\text{max}}}}} = 10{{\left( {{A \mathord{\left/ {\vphantom {A {{{\theta }_{s}}}}} \right. \kern-0em} {{{\theta }_{s}}}}} \right)}^{b}}$ |
| Уильямс 1 [30] | $A = 1.839 + 0.257\ln \left( {{{V}_{{{\text{clay}}}}}} \right) + 0.7624 - 0.0001V_{{{\text{sand}}}}^{2}$ $B = - 0.303 + 0.093\ln \left( {{{\rho }_{b}}} \right) + 0.0565\ln \left( {{{V}_{{{\text{clay}}}}}} \right) - 0.00003V_{{{\text{sand}}}}^{2}$ $b = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} B}} \right. \kern-0em} B}$ ${{\Psi }_{{{\text{max}}}}} = 1000{\kern 1pt} {\text{exp}}\left( {\frac{{\ln \left( {100{{\theta }_{s}}} \right) - A}}{B}} \right)$ |
| Уильямс 2 [30] | $A = 2.57 + 0.238\ln \left( {{{V}_{{{\text{clay}}}}}} \right) - 0.000192V_{{{\text{sand}}}}^{2} - 0.0926\ln \left( {{{V}_{{{\text{SOM}}}}}} \right) + 0.0412{{V}_{{{\text{SOM}}}}}$ $B = - 0.403 + 0.0871\ln \left( {{{V}_{{{\text{clay}}}}}} \right) - 0.00077{{V}_{{{\text{sand}}}}}$ $b = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} B}} \right. \kern-0em} B}$ ${{\Psi }_{{{\text{max}}}}} = 1000{\text{exp}}\left( {\frac{{\ln \left( {100{{\theta }_{s}}} \right) - A}}{B}} \right)$ |
| Майр [19] | $\begin{gathered} {{\Psi }_{{{\text{max}}}}}~ = {\text{exp}}( - 4.9840297533 + 0.0509226283{{V}_{{{\text{sand}}}}} + 0.1575152771{{V}_{{{\text{silt}}}}} + \hfill \\ + \,\,0.1240901644{{\rho }_{b}} - 0.1640033143{{V}_{{{\text{OC}}}}} - 0.0021767278V_{{{\text{silt}}}}^{2} + \hfill \\ + \,\,0.0000143822~V_{{{\text{silt}}}}^{3} + 0.0008040715V_{{{\text{clay}}}}^{2} + 0.0044067117V_{{{\text{OC}}}}^{2}) \hfill \\ b = {{1.0} \mathord{\left/ {\vphantom {{1.0} {{\text{exp}}}}} \right. \kern-0em} {{\text{exp}}}}( - 0.8466880654 - 0.0046806123{{V}_{{{\text{sand}}}}} + 0.0092463819{{V}_{{{\text{silt}}}}} - 0.4542769707{{\rho }_{b}} - \hfill \\ - \,\,0.0497915563~{{V}_{{{\text{OC}}}}} + 0.0003294687V_{{{\text{sand}}}}^{2} - \hfill \\ - \,\,0.000001689056V_{{{\text{sand}}}}^{3} + 0.0011225373V_{{{\text{OC}}}}^{2}) \hfill \\ \end{gathered} $ где ${{V}_{{{\text{OC}}}}} = {{{{V}_{{{\text{SOM}}}}}} \mathord{\left/ {\vphantom {{{{V}_{{{\text{SOM}}}}}} {~1.724}}} \right. \kern-0em} {~1.724}}$ |
| Сакстон и Ролз [23] | $\begin{gathered} x = ( - 0.00251{{V}_{{{\text{sand}}}}} + 0.00195{{V}_{{{\text{clay}}}}} + 0.011{{V}_{{{\text{SOM}}}}} + 0.00006{{V}_{{{\text{sand}}}}}{{V}_{{{\text{SOM}}}}} - 0.00027{{V}_{{{\text{clay}}}}}{{V}_{{{\text{SOM}}}}} + \hfill \\ + \,\,0.0000452~{{V}_{{{\text{sand}}}}}{{V}_{{{\text{clay}}}}} + 0.299) \hfill \\ \end{gathered} $ $y = x + \left( {1.283~{{x}^{2}} - 0.374x - 0.015} \right)$ $\begin{gathered} z = - 0.02 + 1.14( - 0.00024{{V}_{{{\text{sand}}}}} + 0.00487{{V}_{{{\text{clay}}}}} + 0.006{{V}_{{{\text{SOM}}}}} + 0.00005{{V}_{{{\text{sand}}}}}{{V}_{{{\text{SOM}}}}} - \hfill \\ - \,\,0.00013{{V}_{{{\text{clay}}}}}{{V}_{{{\text{SOM}}}}} + 0.0000068{{V}_{{{\text{sand}}}}}{{V}_{{{\text{clay}}}}} + 0.031) \hfill \\ \end{gathered} $ $\begin{gathered} \overline {{{\theta }_{s}}} = y - 0.064 - 0.00097{{V}_{{{\text{sand}}}}} + \,\,1.636\,(0.00278~{{V}_{{{\text{sand}}}}} + 0.00034{{V}_{{{\text{clay}}}}} + 0.022{{V}_{{{\text{SOM}}}}} - \hfill \\ - \,\,0.00018{{V}_{{{\text{sand}}}}}{{V}_{{{\text{SOM}}}}} - 0.00027{{V}_{{{\text{clay}}}}}{{V}_{{{\text{SOM}}}}} - 0.0000584{{V}_{{{\text{sand}}}}}{{V}_{{{\text{clay}}}}} + 0.078) \hfill \\ \end{gathered} $ $b~ = \frac{{\ln 1500 - ~\ln 33}}{{\ln y - ~\ln z}}$ ${{\Psi }_{{{\text{max}}}}} = 10{{\overline {{{\theta }_{s}}} }^{{ - b}}}{\text{exp}}\left( {\ln 33 + b\ln y} \right)$ |
| Косби 1 [13] | ${{\Psi }_{{{\text{max}}}}} = {{10}^{{\left( {1.54{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.0095{{V}_{{{\text{sand}}}}}{\kern 1pt} \,\, + \,\,{\kern 1pt} 0.0063{{V}_{{{\text{silt}}}}}} \right)}}}$ $b = 3.10 + 0.157{{V}_{{{\text{clay}}}}} - 0.003{{V}_{{{\text{sand}}}}}$ ${{\gamma }_{{{\text{max}}}}} = 2.54 \times {{10}^{{\left( { - 0.6~{\kern 1pt} + {\kern 1pt} ~0.0126{{V}_{{{\text{sand}}}}}{\kern 1pt} \,\, - {\kern 1pt} \,\,0.0064{{V}_{{{\text{clay}}}}}} \right)}}}$ |
| Косби 2 [13] | ${{\Psi }_{{{\text{max}}}}} = {{10}^{{\left( {1.88{\kern 1pt} \,\, - {\kern 1pt} \,\,0.0131{{V}_{{{\text{sand}}}}}} \right)}}}$ $b = 2.91 + 0.159{{V}_{{{\text{clay}}}}}$ |
| Востен 1 [31] | ${\text{topsoil}} = 1$ $\begin{gathered} {{\gamma }_{{{\text{max}}}}} = 0.04167{\text{exp(}}7.755 + 0.0352{{V}_{{{\text{silt}}}}} + 0.93{\text{topsoil}} - 0.967\rho _{b}^{2} - 0.000484V_{{{\text{clay}}}}^{2} - \hfill \\ ~ - \,\,0.000322V_{{{\text{silt}}}}^{2} + 0.001{\kern 1pt} /{\kern 1pt} {{V}_{{{\text{silt}}}}} - 0.0748{\kern 1pt} /{\kern 1pt} {{V}_{{{\text{SOM}}}}} - 0.643\ln {{V}_{{{\text{silt}}}}} - 0.01398{{\rho }_{b}}{{V}_{{{\text{clay}}}}} - \hfill \\ - \,\,0.1673{{\rho }_{b}}{{V}_{{{\text{SOM}}}}} + 0.02986{\text{topsoil}}{{V}_{{{\text{clay}}}}} - 0.03305{\text{topsoil}}{{V}_{{{\text{silt}}}}}) \hfill \\ \end{gathered} $ |
| Востен 2 [32] | $\begin{gathered} {{\gamma }_{{{\text{max}}}}} = 0.04167{\text{exp(}} - 42.6 + 8.71{{V}_{{{\text{SOM}}}}} + 61.9{{\rho }_{b}} - 20.79\rho _{b}^{2} - 0.2107V_{{{\text{SOM}}}}^{2} - \hfill \\ - \,\,0.0162{{V}_{{{\text{clay}}}}}{{V}_{{{\text{SOM}}}}} - 5.382{{\rho }_{b}}{{V}_{{{\text{SOM}}}}}{\text{)}} \hfill \\ \end{gathered} $ |
| Джабро [18] | ${{\gamma }_{{{\text{max}}}}} = {{10}^{{\left( {9.56{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.81{\text{ln}}10\left( {{{V}_{{{\text{silt}}}}}} \right){\kern 1pt} \,\, - \,\,{\kern 1pt} 1.09{\text{ln}}10\left( {{{V}_{{{\text{clay}}}}}} \right){\kern 1pt} \,\, - {\kern 1pt} \,\,4.64{{\rho }_{b}}} \right)}}}$ |
| Оттони 1 [22] | ${{\gamma }_{{{\text{max}}}}} = {{{{{10}}^{{\left( {2.039{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.00874{{V}_{{{\text{silt}}}}}{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.00723{{V}_{{{\text{clay}}}}}} \right)}}}} \mathord{\left/ {\vphantom {{{{{10}}^{{\left( {2.039{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.00874{{V}_{{{\text{silt}}}}}{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.00723{{V}_{{{\text{clay}}}}}} \right)}}}} {24}}} \right. \kern-0em} {24}}$ |
| Оттони 2 [22] | ${{\gamma }_{{{\text{max}}}}} = {{{{{10}}^{{\left( {3.998{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.0101{{V}_{{{\text{silt}}}}}{\kern 1pt} \,\, - {\kern 1pt} \,\,0.0152{{V}_{{{\text{clay}}}}}{\kern 1pt} \,\, - \,\,{\kern 1pt} 1.163{{\rho }_{b}}} \right)}}}} \mathord{\left/ {\vphantom {{{{{10}}^{{\left( {3.998{\kern 1pt} \,\, - \,\,{\kern 1pt} 0.0101{{V}_{{{\text{silt}}}}}{\kern 1pt} \,\, - {\kern 1pt} \,\,0.0152{{V}_{{{\text{clay}}}}}{\kern 1pt} \,\, - \,\,{\kern 1pt} 1.163{{\rho }_{b}}} \right)}}}} {24}}} \right. \kern-0em} {24}}$ |
| Швета– Прасана 1 [25] | $\begin{gathered} {{\gamma }_{{{\text{max}}}}} = - 1.272 - 0.0433{{V}_{{{\text{silt}}}}} + 0.693{{V}_{{{\text{SOM}}}}} + 13.04{{\theta }_{s}} + 0.0009V_{{{\text{silt}}}}^{2} - 0.0074{{V}_{{{\text{silt}}}}}{{V}_{{{\text{SOM}}}}}\,\, - \hfill \\ - \,\,0.091{{V}_{{{\text{silt}}}}}{{\theta }_{s}} - 0.0036V_{{{\text{SOM}}}}^{2} - 1.128{{V}_{{{\text{SOM}}}}}{{\theta }_{s}} - 3.204\theta _{s}^{2} \hfill \\ \end{gathered} $ |
| Швета– Прасана 2 [25] | $\begin{gathered} {{\gamma }_{{{\text{max}}}}} = 80.16 + 0.81{{V}_{{{\text{sand}}}}} - 143.57{{\rho }_{b}} + 21.99{{V}_{{{\text{SOM}}}}} + 0.002V_{{{\text{sand}}}}^{2} - 0.687{{V}_{{{\text{sand}}}}}{{\rho }_{b}} - \hfill \\ - \,\,0.0022{{V}_{{{\text{sand}}}}}{{V}_{{{\text{SOM}}}}} + 63.33\rho _{b}^{2} - 13.63{{\rho }_{b}}{{V}_{{{\text{SOM}}}}} - 0.219V_{{{\text{SOM}}}}^{2} \hfill \\ \end{gathered} $ |
| Немес [20] | ${{x}_{1}} = - 3.663 + 0.046{{V}_{{{\text{sand}}}}}$ ${{x}_{2}} = - 0.887 + 0.083{{V}_{{{\text{clay}}}}}$ ${{x}_{3}} = - 9.699 + 6.451{{\rho }_{b}}$ ${{x}_{4}} = - 0.807 + 1.263{{V}_{{{\text{SOM}}}}}$ ${{z}_{1}} = - 0.428 + 0.998{{x}_{1}} + 0.651x_{1}^{2} + 0.130x_{1}^{3}$ ${{z}_{2}} = 0.506{{x}_{1}} - 0.188{{x}_{2}} - 0.327{{x}_{3}} - 0.094{{x}_{4}}$ $\begin{gathered} {{z}_{3}} = - 0.268 + 0.885{{z}_{1}} + 0.544z_{1}^{2} - 0.682z_{1}^{3} + 0.320{{z}_{2}} - 0.134{{z}_{1}}{{z}_{2}} + 1.119z_{1}^{2}{{z}_{2}} + 0.050z_{2}^{2} - \hfill \\ - \,\,0.645{{z}_{1}}z_{2}^{2} + 0.160z_{2}^{3} + 0.126{{x}_{4}} - 0.144{{z}_{1}}{{x}_{4}}~ - \,\,0.372z_{1}^{2}{{x}_{4}} + 0.247{{z}_{2}}{{x}_{4}} + 0.795{{z}_{1}}z2{{x}_{4}} - \hfill \\ - \,\,0.344z_{2}^{2}{{x}_{4}} + 0.038x_{4}^{2} - 0.071{{z}_{1}}x_{4}^{2} + 0.020{{z}_{2}}x_{4}^{2} - 0.015x_{4}^{3} \hfill \\ \end{gathered} $$\begin{gathered} {{z}_{4}} = 0.102 + 1.383{{z}_{3}} + 0.302z_{3}^{2} + 0.103z_{3}^{3} + 0.331{{x}_{2}} + 0.693{{z}_{3}}{{x}_{2}} + 0.541z_{3}^{2}{{x}_{2}} + 0.198x_{2}^{2} + \hfill \\ + \,\,0.429{{z}_{3}}x_{2}^{2} + 0.092x_{2}^{3} + 0.060{{x}_{3}} + 0.277{{z}_{3}}{{x}_{3}} + \,\,~0.417z_{3}^{2}{{x}_{3}} + 0.242{{x}_{2}}{{x}_{3}} + 0.929{{z}_{3}}{{x}_{2}}{{x}_{3}} + \hfill \\ + \,\,0.319x_{2}^{2}{{x}_{3}} + 0.026x_{3}^{2} + 0.094{{z}_{3}}{{x}_{3}}^{2} + 0.116{{x}_{2}}x_{3}^{2} \hfill \\ \end{gathered} $ ${{\gamma }_{{{\text{max}}}}} = 0.04167\,\,~ \times \,\,{{10}^{{\left( {0.571{\kern 1pt} \,\, + \,\,{\kern 1pt} 0.956{{z}_{4}}} \right)}}}$ |
| Томассела [28] | ${{\gamma }_{{{\text{max}}}}} = 0.1\left( { - 4.994 + 0.56728{{V}_{{{\text{sand}}}}} - 0.131{{V}_{{{\text{clay}}}}} - 0.0127{{V}_{{{\text{SOM}}}}}} \right)$ |
На базе языка программирования Python был создан программный модуль, реализующий набор функций, требуемых для расчета выбранных ПТФ, а также предоставляющий возможность получения результатов в графическом виде для их анализа.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
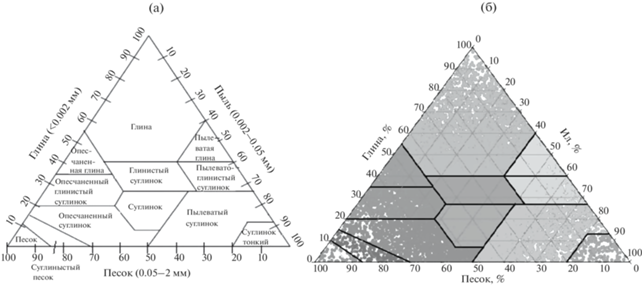
На первом этапе работы для расчета гидрофизических характеристик с применением ПТФ использовались смоделированные показатели состава почвы. Для моделирования содержания песка, глины и ила авторы данной работы придерживаются классификации почв USDA (США, “Department of agriculture”), разработанной Министерством сельского хозяйства США и Национальным объединением исследователей почв [26]. Данная классификация наглядно демонстрируется с помощью треугольника Ферре [27] (рис. 2 ). Случайным образом на основе равномерного распределения былo сгенерировано множество значений объемного содержания песка, ила и глины с учетом того, что всегда выполняется следующее выражение: Vclay + Vsilt + Vsand = 100%. В качестве значений θs и VSOM на основе данных из ГПН рассчитаны средние значения этих характеристик для каждого типа почвы, который определялся согласно методике [7] по треугольнику Ферре.
Рис. 2.
Треугольник Ферре для классификации типов почвы по USDA [27] (а) и распределение статистической выборки значений почвенных фракций (гранулометрического состава; белый цвет на треугольнике означает отсутствующие комбинации почвенных фракций, если увеличивать размер выборки, то площадь белого цвета будет сокращаться) (б).
Для начала был проведен тестовый расчет ПТФ из программного модуля на Python. Результаты расчета сравнивались с результатами расчета PTF Calculator для MS Excel, разработанный в 2010 г. А. Губером и Я. Пачепски [16]. Тест был пройден успешно, результаты тестового расчета совпали с результатами PTF Calculator.
После этого был проведен основной расчет гидрофизических характеристик с помощью выбранных ПТФ с использованием ранее сгенерированного множества значений объемного содержания песка, ила и глины (рис. 3, 4 ).
Рис. 3.
Потенциал влаги при максимальном насыщении почвы (см), рассчитанный с использованием сгенерированной выборки значений гранулометрического состава по треугольнику Ферре. Значения осей x и y: Vsand и Vclay ∈ (0; 100).

Рис. 4.
Гидравлическая проводимость при максимальном насыщении почвы (см/ч), рассчитанная с использованием сгенерированной выборки значений гранулометрического состава по треугольнику Ферре. Значения осей x и y: Vsand и Vclay ∈ (0; 100).
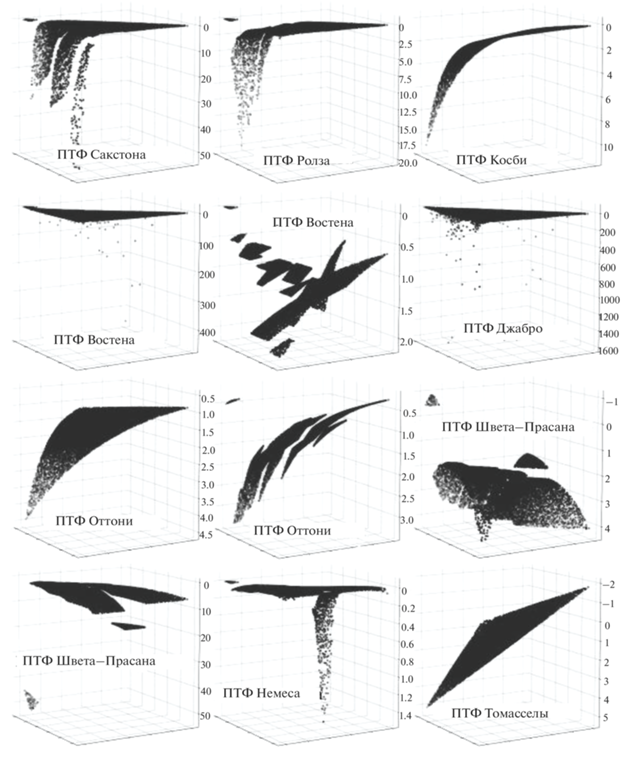
Некоторые ПТФ дают сильно завышенные значения относительно других, что объясняется тем, что эти ПТФ могут давать ошибочные граничные гидрофизические характеристики, в некоторых оригинальных публикациях даются границы применимости ПТФ (например ПТФ Ролза применима только тогда, когда 5% < Vclay < 60% и 5% < Vsand < 70%), что сразу же накладывает ограничения на их использование. Также на графиках гидрофизических характеристик, при расчете которых использовались ПТФ, зависящие не только от гранулометрического состава, но и от пористости/содержания органического вещества почв, наблюдаются линии разрыва. Возможно, это объясняется тем, что для сгенерированной выборки по треугольнику Ферре в качестве пористости/содержания органического вещества почв использовались средние значения для каждого типа почвы. Поэтому анализ поведения ПТФ только на смоделированных данных не может быть полным.
Таким образом, выполнен второй этап работ – расчет гидрофизических характеристик с использованием выбранных ПТФ по данным из ГПН, описанного выше. Для этого исходный ГПН был переведен на пространственное разрешение 0.1° на 0.1° с учетом площади каждой ячейки, так как исходное пространственное разрешение набора очень мелкое и, соответственно, размер файлов очень велик, что вызывает некоторые затруднения при расчетах. Для анализа брался только первый уровень (0–0.0451 м) глубины почвы, что соответствует поверхности. На рис. 5 представлено распределение почвенных фракций (гранулометрический состав) на поверхности по типам почв, полученных из этого набора. Отметим, что пористость и содержание органического вещества почв в ГПН имеют свои уникальные значения для всего множества величин гранулометрических параметров.
Рис. 5.
Распределение почвенных фракций (гранулометрический состав) по треугольнику Ферре, взятых из глобального набора почвенных характеристик с пространственным разрешением 0.1° × 0.1°.
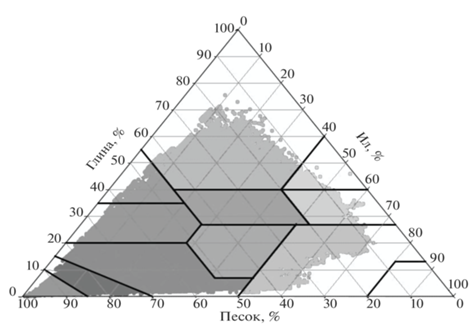
На рис. 6, 7 представлены рассчитанные значения потенциала влаги гидравлической проводимости при максимальном насыщении почвы с использованием ПТФ по данным из ГПН.
Рис. 6.
Потенциал влаги при максимальном насыщении почвы (см), рассчитанный по данным из ГПН. Значения осей x и y: Vsand и Vclay ∈ (0; 100).
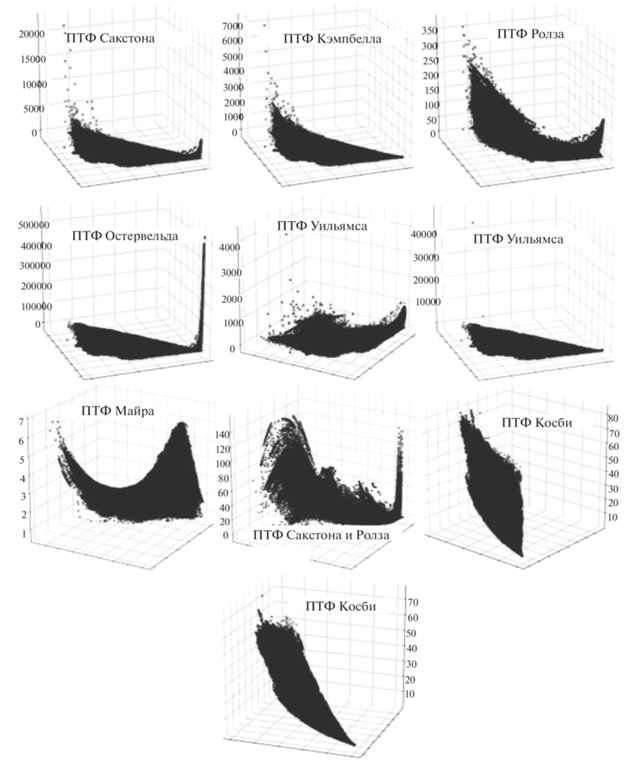
Рис. 7.
Гидравлическая проводимость при максимальном насыщении почвы (см/ч), рассчитанная по данным из ГПН. Значения осей x и y: Vsand и Vclay ∈ (0; 100).
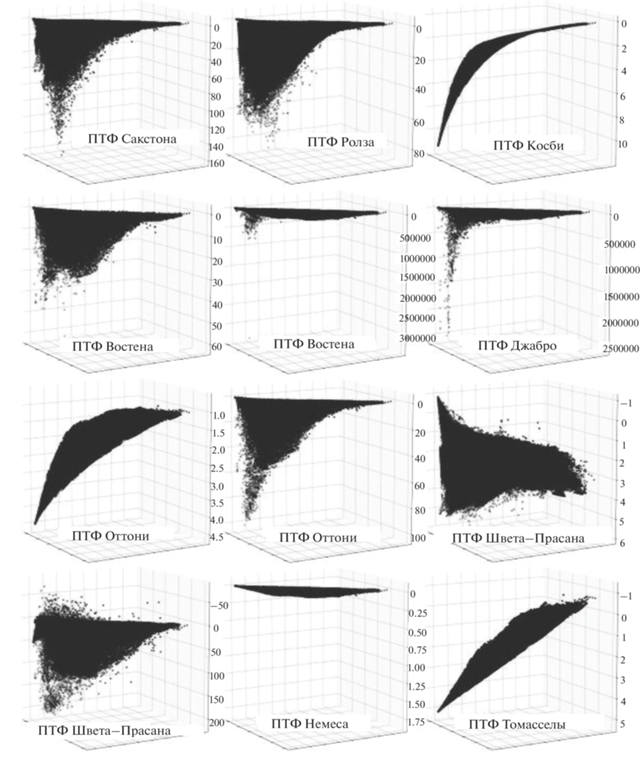
При сравнении результатов (потенциал влаги – рис. 3 и 6 ; гидравлическая проводимость – рис. 4 и 7 ) можно сделать следующие ниже выводы.
1. Прежде всего видно, что в первом варианте (рис. 3 и 4 ) графики гидрофизических характеристик, где ПТФ зависят не только от гранулометрического состава, но и от пористости/органического вещества почв, имеют линии разрыва. Возможно, это объясняется тем, что пористость/ плотность и органическое вещество почв являются кусочно-разрывными функциями, так как представляют собой набор средних, определенных по треугольнику Ферре, для разных типов почв, при этом другие независимые аргументы для ПТФ (песок, глина, ил) являются непрерывными функциями во всей области определения. Графики ПТФ (рис. 6, 7 ), рассчитанные по данным ГПН, не имеют таких разрывов, так как пористость/органическое вещество почв представляют собой непрерывные функции, соответствующие изменению области определения других аргументов.
2. В первом и во втором случаях формы ПТФ (рис. 3, 6 ; рис. 4, 7 ) близки между собой, но шкалы и порядок значений различаются. Это может объясняться тем, что не все крайние значения гранулометрического состава есть в ГПН (рис. 2, 5 ).
3. Как в первом, так и во втором случаях ПТФ Сакстона, Кэмпбэлла, Остервельда, Уильмса, Сакстона и Ролза (рис. 3, 6 ); Востена (только во втором случае), Джабро (рис. 4, 7 ) в крайних точках дают очень высокие значения гидрофизических характеристик по сравнению с другими ПТФ.
4. Графики для одной и той же гидрофизической характеристики имеют разную форму. В группу наиболее схожих по форме графиков можно отнести ПТФ Сакстона, Кэмпбелла, Ролза, Остервельда, Уильямса и Косби. Формы ПТФ Майра и Сакстона/Ролза отличаются от остальных. Оси на графиках по ПФТ Косби ориентированы по-другому для наглядности формы. Формы графиков для гидравлической проводимости более неоднородны. Наиболее схожи формы по ПТФ Сакстона, Ролза, Востена 1, Джабро, Оттони 2, Шветта–Прасана 2; Косби и Оттони 1. Графики по ПТФ Шветта–Прасана 1, Немеса, Томасселы отличаются от всех.
На основании проведенного анализа можно заключить, что не представляется возможности выбрать какую-либо одну ПТФ для расчета гидрофизических характеристик и использования ее в модели деятельного слоя суши. Поэтому проведем еще сравнение рассчитанных гидрофизических характеристик по ПТФ с данными гидрофизических характеристик, которые представлены в ГПН.
На рис. 8 представлены графики потенциала влаги и гидравлической проводимости при максимальном насыщении по данным из ГПН. Если сравнить их со значениями, полученными по различным ПТФ по данным ГПН, то можно отметить, что форма некоторых ПТФ совпадает (ПТФ Сакстона, Ролза, Востена 1, Оттони 2 для гидравлической проводимости и ПТФ Сакстона, Кэмпбелла, Ролза, Уильямса и Косби 1, 2 для потенциала влаги). Но при сравнении значений различия достаточно большие, для потенциала влаги схожие по форме ПТФ дают очень высокие значения (например, максимальная величина по ПТФ Сакстона – 20000 см), в то же время потенциал влаги из ГПН ≤ 100 см. Для гидравлической проводимости схожие по форме ПТФ также дают завышенные значения по сравнению со значениями из ГПН (например, максимальная величина по ПТФ Востена 60 см/ч).
Рис. 8.
Потенциал влаги (см) (а) и гидравлическая проводимость (см/ч) (б) при максимальном насыщении из ГПН.
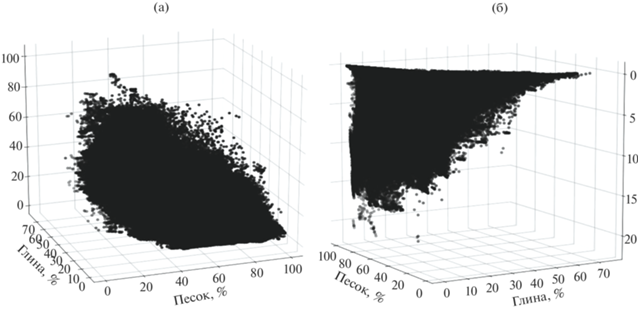
В качестве дополнения приведем статистические характеристики (табл. 3, 4 ) для гидрофизических характеристик, полученных с использованием выбранных ПТФ по сгенерированной выборке и по данным из ГПН, и для гидрофизических характеристик непосредственно из ГПН. Для сравнения двух статистических характеристик в качестве основных используются ME (средняя ошибка), MAE (средняя абсолютная ошибка), MRE (средняя относительная ошибка), RMSE (среднеквадратичная ошибка), CC (коэффициент корреляции Пирсона) и KGE (эффективность Клинга–Гупты). Аналогичные статистические характеристики для гидравлической проводимости представлены в табл. 5, 6.
Таблица 3.
Статистические характеристики для потенциала влаги, рассчитанного с помощью выбранных ПТФ по сгенерированной выборке и по данным из ГПН
| ПТФ | Среднее значение Ψmax (выборка) | Среднее значение Ψmax (ГПН) | ско Ψmax (выборка) | ско Ψmax (ГПН) | ME | MAE | MRE | RMSE | KGE |
|---|---|---|---|---|---|---|---|---|---|
| Сакстон | 1151.3 | 2791.7 | 1641.7 | 47796.4 | 1640.5 | 3757.2 | 142.5 | 4.79E + 04 | –10.1 |
| Кэмпбелл | 48.1 | 228.6 | 63.4 | 788.2 | 180.5 | 198.9 | 375.4 | 811.1 | –3.2 |
| Ролз | 59.8 | 63.8 | 50.0 | 63.0 | 4.0 | 56.8 | 6.7 | 80.6 | 0.0 |
| Остервельд | 1.68E+5 | 742.8 | 2.48E+5 | 1.01E+04 | –1.67E+05 | 1.68E+05 | –99.6 | 2.99E+05 | –7.3 |
| Уильямс | 213.1 | 28.3 | 253.6 | 123.8 | –184.8 | 199.1 | –86.7 | 337.4 | –2.0 |
| Уильямс | 132.4 | 17.3 | 174.6 | 38.5 | –115.1 | 128.5 | –86.9 | 212.7 | –0.5 |
| Майр | 2.6 | 3.4 | 0.9 | 1.9 | 0.8 | 1.5 | 29.1 | 2.2 | –0.2 |
| Сакстон и Ролз | 18.5 | 50.3 | 18.9 | 38.5 | 31.8 | 39.0 | 172.0 | 53.4 | –1.0 |
| Косби | 13.2 | 31.8 | 10.2 | 18.7 | 18.5 | 21.5 | 139.8 | 28.2 | –0.7 |
| Косби | 12.6 | 31.8 | 9.7 | 16.4 | 19.3 | 21.7 | 153.3 | 27.1 | –0.9 |
Таблица 4.
Статистические характеристики для потенциала влаги, рассчитанного с помощью выбранных ПТФ по данным из ГПН, и для потенциала влаги из ГПН
| ПТФ | Среднее значение Ψmax (ГПН) | ско Ψmax (ГПН) | ME | MAE | MRE | RMSE | CC | KGE |
| Сакстон | 2791.7 | 47 796.4 | 1125.0 | 1138.2 | 4292.0 | 2000.6 | –0.7 | –42.0 |
| Кэмпбелл | 228.6 | 788.2 | 21.9 | 23.6 | 83.4 | 58.8 | 0.6 | –0.2 |
| Ролз | 63.8 | 63.0 | 33.5 | 46.8 | 128.0 | 69.6 | –0.4 | –0.9 |
| Остервельд | 742.8 | 1.01E+04 | 1.7E+05 | 1.7E+05 | 6.4E+05 | 3.0E+05 | –0.7 | –6.4E+03 |
| Уильямс | 28.3 | 123.8 | 186.9 | 196.5 | 712.9 | 325.1 | –0.6 | –6.3 |
| Уильямс | 17.3 | 38.5 | 106.2 | 133.2 | 405.1 | 214.9 | –0.6 | –3.4 |
| Майр | 3.4 | 1.9 | –23.6 | 23.6 | –90.0 | 29.9 | 0.7 | –0.1 |
| Сакстон и Ролз | 50.3 | 38.5 | –16.8 | 20.8 | –63.9 | 24.8 | 0.4 | 0.2 |
| Косби | 31.8 | 18.7 | –13.0 | 13.3 | –49.5 | 18.2 | 0.8 | 0.5 |
| Косби | 31.8 | 16.4 | –13.6 | 14.1 | –52.1 | 19.1 | 0.8 | 0.4 |
| Среднее значение Ψmax из ГПН | 26.2 | |||||||
| ско Ψmax из ГПН | 19.1 | |||||||
Таблица 5.
Статистические характеристики для гидравлической проводимости, рассчитанной с помощью выбранных ПТФ по сгенерированной выборке и по данным из ГПН
| ПТФ | Среднее значение γmax (выборка) | Среднее значение γmax (ГПН) | ско γmax (выборка) | ско γmax (ГПН) | ME | MAE | MRE | RMSE | KGE |
|---|---|---|---|---|---|---|---|---|---|
| Сакстон | 1.8 | 1.2 | 5.7 | 3.9 | –0.6 | 2.6 | –34.7 | 6.9 | –0.1 |
| Ролз | 1.9 | 0.4 | 5.0 | 1.2 | –1.5 | 2.0 | –77.5 | 5.3 | –0.3 |
| Косби | 5.6 | 1.3 | 4.2 | 1.1 | –4.3 | 4.6 | –76.5 | 6.1 | –0.3 |
| Востен | 1.2 | 2.6E+11 | 1.9 | 3.7E+14 | 2.6E+11 | 2.6E+1 | 2.1E+13 | 3.7E+14 | –2.1E+11 |
| Востен | 47.7 | 1.1 | 4222.5 | 0.3 | –46.6 | 47.9 | –97.8 | 4222.7 | –0.7 |
| Джабро | 419.9 | 3.3 | 13141.9 | 806.9 | –416.6 | 422.4 | –99.2 | 13173.2 | –6.0 |
| Оттони | 2.8 | 1.4 | 1.3 | 0.5 | –1.4 | 1.6 | –50.1 | 2.0 | –0.1 |
| Оттони | 1.6 | 1.1 | 2.9 | 0.5 | –0.5 | 1.1 | –29.2 | 3.0 | –0.3 |
| Швета–Прасана | 1.1 | 2.2 | 1.4 | 0.7 | 1.1 | 1.4 | 99.2 | 1.9 | –0.6 |
| Швета–Прасана | 20.8 | 4.4 | 23.0 | 3.9 | –16.3 | 18.2 | –78.7 | 28.5 | –0.3 |
| Немес | 8.4E+24 | 0.0 | 1.2E+28 | 0.1 | –8.4E+24 | 8.4E+24 | –100.0 | 1.2E + 28 | –0.7 |
| Томассела | 3.2 | 1.0 | 1.6 | 1.2 | –2.3 | 2.5 | –70.6 | 3.0 | –0.9 |
Таблица 6.
Статистические характеристики для гидравлической проводимости, рассчитанной с помощью выбранных ПТФ по данным из ГПН, и для гидравлической проводимости из ГПН
| ПТФ | Среднее значение γmax (ГПН) | cко γmax (ГПН) | ME | MAE | MRE | RMSE | CC | KGE |
|---|---|---|---|---|---|---|---|---|
| Сакстон | 1.2 | 3.9 | 0.6 | 1.3 | 53.6 | 4.6E+00 | 0.7 | –0.3 |
| Ролз | 0.4 | 1.2 | 0.8 | 1.2 | 65.9 | 4.0E+00 | 0.7 | 0.0 |
| Косби | 1.3 | 1.1 | 4.5 | 4.5 | 387.1 | 6.5E+00 | –0.1 | –3.1 |
| Востен | 2.6E+11 | 3.7E+14 | 0.0 | 0.8 | 4.1 | 1.9E+00 | 0.5 | 0.5 |
| Востен | 1.1 | 0.3 | 46.6 | 48.0 | 4048.1 | 4.2E+03 | 0.0 | –70.1 |
| Джабро | 3.3 | 806.9 | 418.7 | 419.7 | 3.6E+04 | 1.3E+04 | 0.0 | –363.6 |
| Оттони | 1.4 | 0.5 | 1.7 | 2.2 | 147.0 | 2.8E+00 | –0.1 | –0.9 |
| Оттони | 1.1 | 0.5 | 0.5 | 0.9 | 40.8 | 2.8E+00 | 0.4 | 0.2 |
| Швета–Прасана | 2.2 | 0.7 | 0.0 | 1.1 | –4.3 | 1.5E+00 | 0.6 | 0.5 |
| Швета–Прасана | 4.4 | 3.9 | 19.6 | 20.2 | 1706.3 | 3.1E+01 | –0.4 | –16.1 |
| Немес | 0.0 | 0.1 | 8.4E+24 | 8.4E+24 | 7.3E+26 | 1.2E+28 | 0.0 | –7.3E+24 |
| Томассела | 1.0 | 1.2 | 2.1 | 2.4 | 182.5 | 3.1E+00 | 0.0 | –1.2 |
| Среднее значение γmax из ГПН | 1.2 | |||||||
| ско γmax из ГПН | 1.7 | |||||||
ЗАКЛЮЧЕНИЕ
В случае расчета ПТФ по сгенерированному множеству гранулометрического состава и средним значениям пористости и содержания органического вещества почв для каждого типа почвы по треугольнику Ферре вид ПТФ (наличие разрывов на графике) отличается от ПТФ, рассчитанных по данным, взятым из ГПН. Отсюда можно сделать вывод, что использование средних значений пористости или содержания органического вещества почв при расчете ПТФ может давать ошибку (недооценку) в значениях как потенциала влаги (соответственно и безразмерного показателя Клаппа–Хорнбергера), так и гидравлической проводимости.
ПТФ могут в принципе давать сильно завышенные значения как при каких-то крайних значениях гранулометрического состава, так и в общем. Отсюда можно сделать вывод, что использовать какую-то одну ПТФ в модели для расчета требуемых характеристик некорректно. Оптимальное решение – использование готовых и проверенных глобальных наборов почвенных характеристик, например ГПН, авторы которого используют специальные методики ансамблевого осреднения и минимизации для получения глобального поля гидрофизических характеристик.
Авторы выражают благодарность В.М. Степаненко (НИВЦ МГУ) и И.А. Репиной (ИФА РАН) за помощь в работе над статьей.
Список литературы
Алексеев В.А., Володин Е.М., Галин В.Я., Дымников В.П., Лыкосов В.Н. Описание модели общей циркуляции атмосферы ИВМ РАН – версия 1997 года. М.: ИВМ РАН, 1997. 78 с.
Володин Е.М., Дианский Н.А., Гусев А.В. Воспроизведение современного климата с помощью совместной модели общей циркуляции атмосферы и океана INMCM4.0 // Изв. РАН. Физика атмосферы и океана. 2010. Т. 46. С. 448–466.
Лыкосов В.Н., Палагин Э.Г. Динамика взаимосвязанного переноса тепла и влаги в системе атмосфера–почва // Метеорология и гидрология. 1978. № 8. С. 48–56.
Палагин Э.Г. Математическое моделирование агрометеорологических условий перезимовки озимых культур. Л.: Гидрометеоиздат, 1981. 191 с.
Травова С.В., Степаненко В.М., Медведев А.И., Толстых М.А., Богомолов В.Ю. Качество воспроизведения состояния почвы моделью деятельного слоя суши ИВМ РАН−МГУ в составе модели прогноза погоды ПЛАВ // Метеорология и гидрология. 2022. № 3. С. 5–24. https://doi.org/10.52002/0130-2906-2022-3-5-24
Шеин Е.В. Курс физики почв. М.: Изд-во МГУ, 2005. 432 с.
Benham E., Ahrens R.J., Nettleton W.D. Clarification of Soil Texture Class Boundaries // National Soil Survey Center. L.: USDA-NRCS, 2009.
Bouma J., van Lanen H.A.J. Transfer functions and threshold values: from soil characteristics to land qualities. Washington: Int. Workshop Quantified Land Evaluation Procedures, 1986. P. 106.
Brakensiek D.L., Rawls W.J., Stephenson G.R. Modifying SCS hydrologic soil groups and curve numbers for rangeland soils // St. J. ASAE Paper. 1984. PNR-84-203.
Campbell G.S. A simple method for determining unsaturated conductivity from moisture retention data // Soil Scinc. 1974. 117 (6). P. 311–314. https://doi.org/10.1097/00010694-197406000-00001
Campbell G.S., Shiozawa S. Prediction of hydraulic properties of soils using particle-size distribution and bulk density data ed. M.Th. van Genuchten et al // Proc. Int. Workshop on Indirect methods for Estimating the Hydraulic Properties of Unsaturated Soils. Riverside: Univ. California, 1992. P. 317–328.
Clapp R.B., Hornberger M.G. Empirical equations for some soil hydraulic properties // Water Resour. Res. 1978. V. 14. № 4. P. 601–604.
Cosby B.J., Hornberger G.M., Clapp R.B., Ginn T.R. A statistical exploration of the relationships of soil moisture characteristics to the physical properties of the soil // Water Resour. Res. 1984. V. 20. № 6. C. 682–690.
Dai Y., Xin Q., Wei N., Zhang Y., Shangguan W., Yuan H. et al. A global high-resolution data set of soil hydraulic and thermal properties for land surface modeling // Advances Modeling Earth Systems. 2019. V. 11. № 9. P. 2996–3023. https://doi.org/10.1029/2019MS001784
Drozdov E.D., Stepanenko V.M., Voropay N.N., Dyukarev E.A., Kokoreva A.A., Cherkashina A.A., Bogomolov V.Yu. Parametrization of soil thermal conductivity in the INM RAS-MSU land surface model // IOP Conf. Ser.: Earth Environ. Sci. 2020. V. 611. P. 1–5. https://doi.org/10.1088/1755-1315/611/1/012022
Guber A.K., Pachepsky Ya.A. Multimodeling with Pedotransfer Functions. Documentation and User Manual for PTF Calculator (CalcPTF). Version 3.0. Environmental Microbial and Food Safety Laboratory Beltsville Agricultural Research Center. USDA-ARS. 2010.
Jabro J.D. Estimation of saturated hydraulic conductivity of soils from particle size distribution and bulk density data // Trans ASAE. 1992. V. 35. P. 557–560.
Mayr T., Jarvis N.J. Pedotransfer functions to estimate soil water retention parameters for a modified Brooks–Corey type model // Geoderma. 1999. V. 91. P. 1–9.
Mualem Y. A new model for predicting the hydraulic conductivity of unsaturated porous media // Water Resour. Res. 1976. V. 12 (3). P. 513–522. https://doi.org/10.1029/WR012i003p00513
Nemes A., Rawls W.J., Pachepsky Y.A. Influence of organic matter on the estimation of saturated hydraulic conductivity // Soil Sci. Soc. Am. J. 2005. V. 69. P. 1330–1337. https://doi.org/10.2136/sssaj2004.0055
Osterveld M., Chang C. Empirical relations between laboratory determination of soil texture and moisture characteristic // Can. Agric. Eng. 1980. V. 22. P. 149–151.
Ottoni M.V., Ottoni Filho T.B., Lopes-Assad M.L.R.C., Rotunno Filho O.C. Pedotransfer functions for saturated hydraulic conductivity using a database with temperate and tropical climate soils // J. Hydrol. 2019. V. 575. P. 1345–1358. https://doi.org/10.1016/j.jhydrol.2019.05.050
Saxton K.E., Rawls W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions // Soil Sci. Soc. 2006. V. 70. № 5. P. 1569–1578. https://doi.org/10.2136/sssaj2005.0117
Saxton K.E., Rawls W.J., Romberger J.S., Papendic R.I. Estimating generalized soil- water characteristics from texture // Soil Sci. Soc. 1986. V. 50. № 4.
Shwetha P., Prasanna K. Pedotransfer functions for the estimation of saturated hydraulic conductivity for some Indian sandy soils // Eurasian Soil Sci. 2018. V. 51. P. 1042–1049. https://doi.org/10.1134/S1064229318090119
Soil Science Division Staff. Soil survey sand / Eds C. Ditzler, K. Scheffe, H.C. Monger. Washington: Government Printing Office, 2017.
Soil survey manual. Washington: United States Department of Agriculture, 2018. P. 63–65.
Tomasella J., Hodnett M.G. Estimating unsaturated hydraulic conductivity of Brazilian soils using soil-water retention data // Soil Sci. 1997. V. 162. P. 703–12. https://doi.org/10.1097/00010694-199710000-00003
van Genuchten M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils // Soil Sci. Soc. 1980. V. 44 (5). P. 892–898. https://doi.org/10.2136/sssaj1980.03615995004400050002x
Williams J., Ross P., Bristow K. Prediction of the Campbell water retention function from texture, structure, and organic matter / Eds M.Th. van Genuchten et al. // Proc. Int. Workshop on Indirect methods for Estimating the Hydraulic Properties of Unsaturated Soils. Riverside: Univ. California, 1992. P. 427–442.
Wösten J.H.M., Lilly A., Nemes A., Bas C Le. Development and use of a database of hydraulic properties of European soils // Geoderma. 1999. V. 90. I. 3–4. P. 169–185. ISSN 0016-7061. https://doi.org/10.1016/S0016-7061(98)00132-3
Wösten J.H.M., Pachepsky Y.A., Rawls W.J. Pedotransfer functions: bridging the gap between available basic soil data and missing soil hydraulic characteristics // J. Hydrol. 2001. V. 251. P. 123–150. https://doi.org/10.1016/S0022-1694(01)00464-4
Дополнительные материалы отсутствуют.