Вулканология и сейсмология, 2022, № 2, стр. 66-73

ВВЕДЕНИЕ

В физике землетрясений широко используются три эмпирических закона, а именно, закон Омори [Omori, 1894], закон Гутенберга–Рихтера [Gutenberg, Richter, 1956] и закон Бата [Bath, 1965]. Этим законам посвящена богатейшая энциклопедическая, монографическая и обзорная литература (см. например, [Richter, 1958; Kasahara, 1981; Гульельми, 2015, 2017; Завьялов и др., 2020]). Во многих оригинальных научных статьях эти три закона используются при систематизации наблюдений, при поиске вариантов теоретической интерпретации законов, а также при поиске новых законов, закономерностей и свойств землетрясений – этого исключительно сложного и опасного природного явления.

В данной статье мы сосредоточили внимание на двух законах, а именно, на законе Омори и законе Бата, описывающих свойства афтершоков сильных землетрясений. Мы попытались взглянуть на законы с необычной точки зрения. Вполне понятно, что каждый закон был открыт в процессе работы, в которой ставилась конкретная исследовательская задача, а сам закон был сформулирован в определенных физико-математических терминах [Omori, 1894; Bath, 1965]. Мы попытались, преследуя исключительно методические цели, варьировать постановку задачи и/или переформулировать закон. Иногда попытки такого рода дают интересные результаты.

Наш подход оказался особенно успешным в отношении закона Омори. Мы переформулировали закон, записали его в виде дифференциального уравнения, и ввели представление о коэффициенте деактивации очага землетрясения. Модифицированная теория предсказала уменьшение коэффициента деактивации с увеличением магнитуды главного удара землетрясения. Экспериментальное исследование полностью подтвердило теоретическое предсказание.

В случае закона Бата мы определили величину разности между магнитудой главного удара и магнитудой сильнейшего афтершока на начальном этапе эволюции афтершоков. Кроме того, мы видоизменили постановку задачи, ввели представление о так называемых “зеркальных” форшоках и установили, что они подчиняются закону, аналогичному закону Бата.

ЗАКОН ОМОРИ

Эксперимент

Для экспериментальной проверки неравенства (6) мы использовали данные о землетрясениях, которые произошли на Земле с 1973 по 2019 гг. и были представлены в мировом каталоге землетрясений USGS/NEIC (https://earthquake. usgs.gov).

Было найдено 2508 главных ударов с магнитудой ${{M}_{0}} \geqslant 6$ и глубиной гипоцентра, не превышающей 250 км. Для каждого главного удара была определена круговая эпицентральная зона с радиусом R. Если принять, что характерный размер очаговой зоны L = 2R, то тогда величина L определяется по формуле

(7)

$L = 0.43{{M}_{0}} - 1.27.$

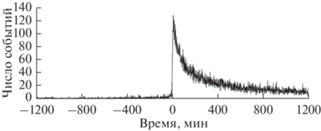
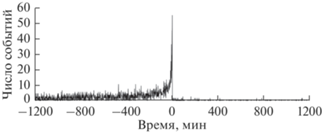
Здесь L выражена в километрах [Завьялов, Зотов, 2021]. Событие по определению есть подземный толчок с магнитудой $M < {{M}_{0}}$, который произошел в эпицентральной зоне в интервале $ \pm {\kern 1pt} 20$ ч относительно момента главного удара. Всего было накоплено 1618 событий до, и 30837 событий после главного удара. Рис. 1 дает представление о распределении событий во времени.

Рис. 1.

Распределение событий во времени. График построен методом наложения эпох. Время отсчитывается от момента главного удара.

Мы проверили, выполняется ли неравенство (5). Результат проверки представлен на рис. 2. Формула

(8)

${\text{lg}}N = - \alpha + \beta {{M}_{0}}$

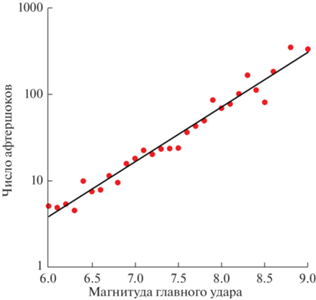
аппроксимирует найденную зависимость. Здесь $\alpha = 3.7$, $\beta = 0.7$. Коэффициент детерминации весьма высокий (${{R}^{2}} = 0.92$), так что неравенство (5), которое вытекает из (8), можно считать вполне обоснованным.

Рис. 2.

Зависимость количества афтершоков от магнитуды главного удара на интервале от 0 до 20 ч.

Рис. 3 показывает результат измерений $\sigma $ при различных значениях ${{M}_{0}}$. Для измерений $\sigma $ мы воспользовались методикой, разработанной при составлении Атласа Афтершоков [Гульельми и др., 2019; Завьялов и др., 2020; Guglielmi et al., 2020].

Рис. 3.

Зависимость коэффициента деактивации очага землетрясения от магнитуды главного удара.

Мы видим, что в среднем $\sigma $ монотонно уменьшается с ростом величины ${{M}_{0}}$. Зависимость $\sigma \left( {{{M}_{0}}} \right)$ аппроксимируется формулой

(9)

$\sigma = A - B{{M}_{0}},$

где $A = 0.64$, $B = 0.07$ при достаточно высоком коэффициенте детерминации (${{R}^{2}} = 0.82$). Таким образом, неравенство ${{d\sigma } \mathord{\left/ {\vphantom {{d\sigma } {d{{M}_{0}}}}} \right. \kern-0em} {d{{M}_{0}}}} < 0$ надежно подтверждается прямыми измерениями.

ЗАКОН БАТА

Классическая триада

В систематике землетрясений особый класс образуют последовательности событий, которые образуют своеобразное триединство: форшоки–главный удар–афтершоки. Магнитуда главного удара ${{M}_{0}}$ всегда превышает магнитуды форшоков ${{M}_{ - }}$ и афтершоков ${{M}_{ + }}$, причем ${{M}_{ + }} > {{M}_{ - }}$ и ${{N}_{ + }} > {{N}_{ - }}$, где ${{N}_{ - }}$ и ${{N}_{ + }}$ – количества форшоков и афтершоков на одинаковых интервалах времени до и после главного удара соответственно. Такого рода последовательности предложено называть классической триадой [Гульельми, 2015].

Закон Бата гласит, что разность между магнитудой главного удара и магнитудой сильнейшего афтершока $\Delta M = {{M}_{0}} - {{M}_{{ + {\text{max}}}}}$ в классической триаде приблизительно постоянна в том смысле, что почти не зависит от ${{M}_{0}}$. В литературе обычно приводится значение $\Delta M = 1.1{\kern 1pt} - {\kern 1pt} 1.2$ (см. например [Richter, 1958]). Укажем здесь на содержательные работы [Lombardi, 2002; Helmstetter, Sornette, 2003; Apostol, 2020], посвященные экспериментальной проверке и поиску теоретической интерпретации закона.

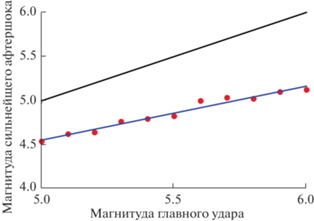
Мы предприняли пилотный анализ закона Бата, используя материал наблюдений, отобранный для исследования зависимости $\sigma \left( {{{M}_{0}}} \right)$. Рис. 4 прекрасно иллюстрирует сущность закона. Синяя линия

(10)

${{M}_{{ + {\text{max}}}}} = - C + D{{M}_{0}}$

аппроксимирует экспериментальные точки. Здесь ${{M}_{{ + {\text{max}}}}}$ – магнитуда сильнейшего афтершока на интервале от 0 до 20 ч, C = 0.53, D = 0.85, ${{R}^{2}} = 0.84$. Черная линия ${{M}_{{ + {\text{max}}}}} = {{M}_{0}}$ проведена для наглядности. Мы видим стабильную величину разности между синей и черной линиями, которая, возможно, немного увеличивается с ростом ${{M}_{0}}$. Для проверки указанной возможности мы построили график зависимости $\Delta M = {{M}_{0}} - {{M}_{{ + {\text{max}}}}}$ от ${{M}_{0}}$. Однако коэффициент детерминации ${{R}^{2}} = 0.13$ слишком мал. Таким образом, мы не можем утверждать, что $\Delta M$ зависит от ${{M}_{0}}$.

Рис. 4.

Сопоставление магнитуд сильнейших афтершоков и магнитуд главных ударов (точки). Синяя линия аппроксимирует экспериментальные точки. Черная линия проведена для наглядности.

В среднем по всем нашим измерениям $\Delta M = 1.6$. Эта величина примерно в полтора раза выше, чем та, которая обычно указывается в связи с законом Бата. Расхождение между нашими измерениями $\Delta M$ и литературными данными, вероятно, связано с тем, что наша выборка афтершоков ограничена интервалом времени 0–20 ч после главного удара. В этой связи мы хотим обратить внимание на неполноту стандартной формулировки закона Бата. А именно, в дополнение к указанию величины $\Delta M = 1.1{\kern 1pt} - {\kern 1pt} 1.2$ следовало бы указывать вероятное время ожидания появления сильнейшего афтершока. Недостаточно сказать, что рано или поздно возникнет сильнейший афтершок с магнитудой, не превышающей определенной величины. Необходимо ответить хотя бы ориентировочно на естественный вопрос о том, когда это произойдет. В этом направлении предстоит еще дополнительная работа. Судя по нашей оценке, сильнейший афтершок чаще всего появляется на интервале от недели до месяца после главного удара.

Зеркальная триада

В соответствии с нашей методологической установкой, указанной во Введении, попытаемся переформулировать постановку задачи, которую в свое время решил Бат. Во-первых, произведем селекцию землетрясений по следующему признаку: ${{M}_{ + }} < {{M}_{ - }}$, ${{N}_{ + }} < {{N}_{ - }}$. Другими словами, пусть форшоки будут более сильными и более многочисленными, чем афтершоки. Во-вторых, найдем зависимость от ${{M}_{0}}$ разности $\Delta M = {{M}_{0}} - {{M}_{{ - {\text{max}}}}}$ для такой разновидности редких, но весьма интересных триад. Будем называть их зеркальными триадами.

На рис. 5 представлено распределение событий во времени в зеркальных триадах. На интервале времени с 1973 по 2019 гг. было найдено 2430 реперов (главных толчков) с магнитудами $5 \leqslant M \leqslant 6$, 4183 форшоков и 201 афтершок. Мы видим, что в качественном отношении распределение является зеркальным по отношению к тому, что показано на рис. 1.

Рис. 5.

Распределение событий во времени для зеркальных триад. График построен методом наложения эпох.

Таким образом, мы обнаружили, что для форшоков в зеркальных триадах выполняется закон, аналогичный закону Бата для афтершоков в классических триадах (рис. 6). Зависимость магнитуды сильнейшего форшока от магнитуды репера аппроксимируется формулой

(11)

${{M}_{{ - {\text{max}}}}} = 1.5 + 0.61{{M}_{0}},$

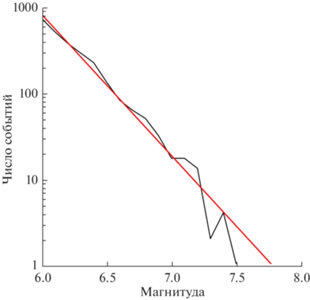
причем коэффициент детерминации весьма велик: ${{R}^{2}} = 0.97$. Величина разности $\Delta M$ в данном случае увеличивается от 0.45 при ${{M}_{0}} = 5$ до 0.84 при ${{M}_{0}} = 6$.

Рис. 6.

Закон Бата для форшоков в зеркальных триадах.

При исследовании закона Бата для зеркальных триад мы обнаружили, что заметная часть реперов не имеет афтершоков. Естественно возникает вопрос, не существуют ли достаточно сильные уединенные землетрясения, не имеющие на заданном интервале времени ни афтершоков, ни форшоков. Пилотный анализ показал, что такие уединенные события действительно происходят. Мы назвали их Grande terremoto solitario (итальянский яз.) (Большое уединенное землетрясение) или сокращенно GTS. В период с 1973 по 2019 гг. обнаружено 2498 GTS (на интервале 20 ч до репера и 20 ч после него землетрясения не наблюдались). На рис. 7 показано распределение числа GTS по магнитудам. Оно хорошо аппроксимируется распределением Гутенберга–Рихтера

(12)

${\text{lg}}N = a - bM$

со следующими параметрами: a = 11.3, b = 1.4.

Рис. 7.

Распределение по магнитудам сильных уединенных землетрясений. Прямая линия соответствует распределению Гутенберга–Рихтера.

ОБСУЖДЕНИЕ

По закону Бата совокупность магнитуд афтершоков конкретного события образует множество чисел $\left\{ {{{M}_{ + }}} \right\}$, не превышающих числа ${{M}_{{ + {\text{max}}}}} = {{M}_{0}} - \Delta M$. У нас возник вопрос, что можно сказать о минимальной магнитуде в совокупности $\left\{ {{{M}_{ + }}} \right\}$, и как она соотносится с магнитудой главного удара? Мы не знаем ответа. Да и сам вопрос может показаться надуманным. Но, строго говоря, если конечная минимальная магнитуда существует, то с формальной точки зрения закон Омори [Omori, 1894] противоречит закону сохранения энергии. В самом деле, если $W$ есть мощность потока афтершоков и выполняется закон Омори $n = k/t$, то полная энергия афтершоков

Формулировка закона в виде уравнения эволюции (1) позволяет избежать противоречия. В самом деле, достаточно предположить, что коэффициент деактивации $\sigma \left( t \right)$ зависит от времени. Тогда вместо формулы Омори будем иметь

Итак, мы предполагаем, что $\sigma $ зависит от времени. Не противоречит ли это линейной зависимости $g\left( t \right) = {{g}_{0}} + \sigma t$, которую мы использовали в двух предыдущих разделах статьи, и которая выполняется лишь в том случае, если $\sigma = {\text{const}}$? Дело здесь в следующем. Опыт составления Атласа Афтершоков [Гульельми и др., 2019; Завьялов и др., 2020; Guglielmi et al., 2020] показал, что коэффициент деактивации действительно испытывает сложные вариации в процессе релаксации очага после образования магистрального разрыва. Однако на первом этапе эволюции $\sigma = {\text{const}}$. Интервал времени, на котором $\sigma = {\text{const}}$, мы называем эпохой Омори. Продолжительность эпохи Омори изменяется от нескольких дней до многих десятков дней. Измерения $\sigma $, результат которых использован при построении рис. 5, в этом отношении вполне корректны, поскольку производились на интервале от 0 до 15 ч после главного удара, т.е. заведомо в эпоху Омори.

Заметим, что в работе [Завьялов и др., 2020] указана тенденция к увеличению продолжительности эпохи Омори с ростом магнитуды главного удара. По нашему мнению, указанная тенденция заслуживает дальнейшего изучения.

Запись закона Омори в форме уравнения (1) открывает интересные возможности для обобщений теории. Естественным обобщением уравнения (1) является логистическое уравнение:

Более широкое обобщение мы находим при поиске моделей пространственно-временного распределения $n\left( {x,t} \right)$ афтершоков. Интересный результат был получен при добавлении члена 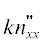в правую часть уравнения (16):

Уравнение (18) имеет решения в виде медленных нелинейных волн [Колмогоров и др., 1937], которые напоминают волнообразную структуру пространственно-временного распределения афтершоков, обнаруженную в работе [Zotov et al., 2018]. Трехпараметрическую модель (18) иногда называют $\gamma \sigma $k–моделью.

В связи с законом Омори нелишне также будет упомянуть работу [Flannigan et al., 2020]. В этой работе авторы обратили внимание на аналогию между эффектом Баркгаузена в ферроэлектрике и таким явлением, как релаксация очага землетрясения за счет переупаковки структурных элементов литосферы и потрескивание в виде афтершоков, сопровождающем релаксацию.

Говоря о законе Омори $n = {k \mathord{\left/ {\vphantom {k t}} \right. \kern-0em} t}$, нельзя не сказать о двухпараметрическом законе $n = {k \mathord{\left/ {\vphantom {k {{{t}^{p}}}}} \right. \kern-0em} {{{t}^{p}}}}$ Хирано–Утсу [Hirano, 1924; Hirano et al., 1995]. Многочисленные измерения свидетельствуют, что параметр $p$ изменяется от случая к случаю и от места к месту от 0.7 до 1.5, причем в среднем $p = 1.1$ (см. обзор [Гульельми, 2017] и указанную в нем литературу). Сделаем замену переменной $n \to g = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}$. Закон Хирано–Утсу предстанет в форме $g = {{{{t}^{p}}} \mathord{\left/ {\vphantom {{{{t}^{p}}} k}} \right. \kern-0em} k}$. Коэффициент деактивации $\sigma = {{dg} \mathord{\left/ {\vphantom {{dg} {dt}}} \right. \kern-0em} {dt}}$ в этом случае равен $\sigma = \left( {{p \mathord{\left/ {\vphantom {p k}} \right. \kern-0em} k}} \right){{t}^{{p - 1}}}$. Следовательно, при $p \ne 1$ не существует эпохи Омори, что резко противоречит наблюдениям [Гульельми и др., 2019; Завьялов и др., 2020; Guglielmi et al., 2020]. Таким образом, закон Хирано–Утсу неприемлем. В эпоху Омори выполняется закон Омори в оригинальной формулировке [Omori, 1894], или в форме уравнения эволюции (1) при $\sigma = {\text{const}}$.

При исследовании закона Бата мы обнаружили зеркальные триады – особую разновидность последовательности подземных толчков. Предварительный анализ зеркальных триад указывает на возможное существование GTS – изолированных (уединенных) землетрясений достаточно большой магнитуды (M > 6). Происхождение GTS пока что не вполне ясно. Возможно, система разломов в окрестности гипоцентра GTS характеризуется необычным распределением порогов разрушения, в котором единичный разлом достаточно большой площади обладает аномально низким порогом. После образования магистрального разрыва, проявившегося в форме GTS, остаточное напряжение в окрестности гипоцентра недостаточно велико для того, чтобы активизировались другие разломы.

В заключении данного раздела статьи мы хотим со всеми необходимыми оговорками высказать осторожное суждение по вопросу о происхождении зеркальных триад. Допустим, что система разломов в некотором объеме горных пород находится под воздействием медленно растущего напряжения сдвига $\tau $. Пороговое напряжение ${{\tau }_{*}}$, при котором происходит разрыв (разрушение) и борта разлома испытывают взаимное перемещение друг относительно друга, вообще говоря, тем ниже, чем больше линейные размеры разлома $l$: ${{\tau }_{*}} = {C \mathord{\left/ {\vphantom {C {{{l}^{m}}}}} \right. \kern-0em} {{{l}^{m}}}}$, где m > 0, а C – размерный коэффициент пропорциональности, зависящий от свойств горных пород в выделенном объеме. Тогда пороговое значение ${{\tau }_{*}}$ первым будет достигнуто у самого крупного разлома. Его разрушение проявляется в виде главного удара землетрясения с магнитудой ${{M}_{0}}$. Если параметр C равномерно распределен по объему очага, то форшоков не возникает. Но при этом афтершоки появляются по той причине, что после главного удара общее внешнее напряжение частично снимается. Оставшееся напряжение перераспределяется по очагу, возникают локальные перенапряжения, причем таким образом, что более мелкие разломы, чем тот, который породил главный удар, могут активизироваться и дать повторные подземные толчки. Так можно представить появление укороченной классической триады, в которой форшоки отсутствуют.

В ряде случаев специфическое распределение разломов по величине $l$ и распределение локальных напряжений могут оказаться такими, что ни один афтершок не возбудится. Возможно такая ситуация возникает при появлении GTS.

Появление зеркальной триады можно понять, если допустить, что параметр C распределен неоднородно по объему, а точнее, что существует сильный разброс значений $C\left( l \right)$. Тогда возможна ситуация, когда перед тем, как будет разрушен самый крупный разлом, могут активизироваться более мелкие разломы и возникнут форшоки. Появится триада тектонических землетрясений. Будет она классической, или зеркальной зависит от распределения разломов по величине $l$, от дисперсии коэффициента $C\left( l \right)$, и от мозаики локальных напряжений, возникших после главного удара.

ЗАКЛЮЧЕНИЕ

Богатейший опыт изучения классических законов физики землетрясений можно с успехом использовать для развития теории и для поиска новых подходов к анализу экспериментального материала. Примененный нами методический прием прост и состоит в том, что при исследовании закона Омори мы переформулировали закон, представив его в виде уравнения эволюции афтершоков. Это дало возможность поставить вопрос о зависимости коэффициента деактивации очага от магнитуды главного удара. Результат состоит в том, что теоретически предсказано и экспериментально обнаружено монотонное уменьшение коэффициента деактивации при увеличении магнитуды главного удара. Мы уверены, что обнаружение других зависимостей такого рода приблизит нас к физической интерпретации коэффициента деактивации.

При анализе закона Бата мы переформулировали постановку задачи и в результате обнаружили малочисленную, но исключительно интересную разновидность последовательности подземных толчков, названную нами зеркальной триадой. Для форшоков зеркальной триады установлен закон, аналогичный закону Бата для афтершоков. Обнаружено, что величина разности между магнитудой главного удара и магнитудой сильнейшего форшока увеличивается с ростом магнитуды главного удара.