Журнал вычислительной математики и математической физики, 2019, T. 59, № 1, стр. 87-101
ОБ эффективности двух подходов к расчету обтекания крыла с выпущенной механизацией при наличии отрывных зонС. М. Босняков, В. В. Власенко, М. Ф. Енгулатова, С. В. Матяш, С. В. Михайлов, С. С. Молев
С. М. Босняков 1, 2, *, В. В. Власенко 2, М. Ф. Енгулатова 2, С. В. Матяш 2, С. В. Михайлов 2, С. С. Молев 2
1 МФТИ
141701 М.о., Долгопрудный, Институтский пер., 9, Россия
2 ЦАГИ
140180 М.о., Жуковский, ул. Жуковского, 1, Россия
* E-mail: bosnyakov@tsagi.ru
Поступила в редакцию 13.03.2017
Аннотация
На примере модельных уравнений, описывающих конвективный перенос, проведен анализ ошибок аппроксимации явной численной схемы и различных неявных схем с одинаковым способом аппроксимации пространственных производных. Показано, что при выполнении ограничения на шаг по времени, определяемого условием Куранта–Фридрихса–Леви, неявная схема уступает по точности явной, а при дальнейшем увеличении шага по времени точность описания конвективных процессов существенно снижается. Рассмотрено два способа организации маршевой процедуры по времени – дробный шаг в случае явной схемы и дуальный шаг в случае неявной схемы. Показано, что метод дробного шага эффективен только на сетках с разбросом размеров ячеек 100–1000. Для численного решения задач с условием прилипания на твердых стенках (разброс размеров ячеек 104–105) рассмотрены два подхода – неявная схема с дуальным шагом во всех ячейках и зональный подход, при котором дуальный шаг используется в тонкой пристеночной области (около 3% от толщины развитого турбулентного пограничного слоя), а в остальной области применяется дробный шаг. Эти два подхода применены к задаче обтекания крыла с отклоненной механизацией. Дано сопоставление расчетных и экспериментальных данных. Проведена оценка точности расчета. Исследованы причины возникновения ошибок. Определены области эффективного применения каждого из указанных подходов. Библ. 24. Фиг. 9. Табл. 1.
ВВЕДЕНИЕ
На больших углах атаки обтекание крыла с выпущенной взлетно-посадочной механизацией происходит с образованием отрывных зон. Этот тип течения подробно изучен многими исследователями, например, в рамках рабочих совещаний High Lift Workshop (см. [1], [2]). Было отмечено, что в подавляющем числе случаев расчетные данные дают завышенные значения максимальной подъемной силы и критического угла атаки [3] по сравнению с представленными экспериментальными данными. Среди прочих причин отмечено, что отрывное течение в области выпущенных предкрылков и закрылков является нестационарным и для корректного расчета необходимо применять нестационарные методы типа URANS [4]. Оценки показывают, что затраты компьютерных ресурсов в нестационарном случае на порядок превосходят затраты, характерные для стационарных расчетов. Следовательно, вопрос эффективности и точности расчета приобретает первостепенное значение. При этом главная проблема расчетной методологии заключается в том, чтобы получить качественное решение за разумное время.
Для достижения поставленной цели можно использовать различные подходы, основанные на явных и неявных численных схемах. Явные схемы обеспечивают высокое качество описания нестационарных процессов, но требуют соблюдения ограничений типа Куранта–Фридрихса–Леви в каждой ячейке (в том случае, когда задача решается с учетом вязкости и турбулентности потока, следует говорить об условии устойчивости, которое учитывает не только конвекцию, но и эти эффекты). Это приводит к тому, что минимальная по размеру ячейка определяет размер расчетного шага по времени во всей расчетной области. По этой причине явные схемы применяются в тех случаях, когда протекающие процессы имеют единый масштаб. Например, такая ситуация имеет место во многих задачах аэроакустики (при условии, что расчет ведется на квазиравномерных сетках). На практике мономасштабные проблемы встречаются редко. Как правило, задачи имеют несколько масштабов. Например, рассматриваемое отрывное течение с кромки крыла на фоне нестационарного обтекания всего самолета. Это приводит к необходимости учета как локальных, так и глобальных процессов. Многомасштабность решаемых задач является основным источником роста потребляемых компьютерных ресурсов. Добиться экономии можно путем повышения порядка точности численной схемы [5], [6] или применением эффективных сеточных подходов, например, адаптации сетки (Adaptive Mesh Refinement [7], [8]) с учетом физических факторов задачи. Адаптация обеспечивает концентрацию мелких ячеек в ограниченных зонах, которые слабо влияют на процесс развития крупномасштабных явлений. Такой подход хорошо реализуется в задачах с несколькими масштабами и невозможен в задачах с большим набором характерных масштабов. Следует учитывать, что пропуск всего одного ключевого масштаба приводит к искажению всей физической картины течения. Следовательно, расчетная сетка должна отслеживать все основные масштабы и выдерживать условия “однородности” с целью выполнения условия Куранта–Фридрихса–Леви (условия устойчивости). На практике это удается не всегда и, как следствие, приходится использовать наименьший масштаб и вести расчет с глобальным шагом по времени, который рассчитан с учетом этого масштаба. Именно такая ситуация типична для многих приложений. В этом случае неизбежно локальное применение неявной схемы, которая позволяет вести расчет с большими шагами по времени, но при неизбежной потере точности. Наибольшие проблемы возникают в пристеночных областях пограничного слоя. Именно здесь образуются чрезвычайно маленькие ячейки (с неблагоприятным соотношением сторон). Они серьезно тормозят скорость расчета. Известно, что (в основном) нестационарные процессы развиваются не во внутренней, а во внешней части пограничного слоя и невязком ядре потока. Это дает основание для “загрубления” расчета в тонкой пристеночной области. Таким образом, расчетный шаг по времени выбирается с учетом особенностей течения во внешней части пограничного слоя (удовлетворяет условию устойчивости), а непосредственно у стенки (во внутренней части пограничного слоя) расчет ведется по неявной схеме с коэффициентом устойчивости ${{C}_{{{\text{stab}}}}}\sim 1000$ или более. (Коэффициентом устойчивости будем называть отношение шага по времени к локальному ограничению, определяемому условием устойчивости.) Качество решения в окрестности стенки понижается, но в целом нестационарный процесс описывается с хорошим приближением за счет внешних областей.
В современной литературе по вычислительной аэродинамике можно найти примеры применения неявных схем для решения нестационарных задач (см., например, [9], [10]). Для повышения качества решения обычно используются “точные по времени” алгоритмы. В этих алгоритмах схемный оператор не упрощается (т.е. оператор не линеаризуется и не расщепляется по пространственным направлениям или физическим процессам). Другими словами, приходится решать нелинейные системы уравнений, построенные с охватом всех ячеек расчетной сетки. Для решения таких систем используются итерационные методы. Одним из наиболее удачных итерационных методов для точного решения нелинейных систем является метод дуального шага по времени [11], где вводится понятие псевдо-времени. В идеале итерационный процесс по псевдо-времени нужно доводить до полной сходимости, но на практике ограничиваются наперед заданной точностью [12]. Следует отметить, что даже при высоком порядке аппроксимации по времени и при точном решении возникающей системы нелинейных уравнений, увеличение числа Куранта (коэффициента устойчивости) при решении нестационарной задачи приводит к быстрому росту погрешностей схемы. Согласно результатам [13], в задачах конвекции уже при числах Куранта $CFL\sim 10$ теряется смысл использования схем высокого порядка аппроксимации по времени, так как они порождают большие погрешности.
В данной работе проведен анализ и представлены расчеты, которые демонстрируют преимущества и недостатки упомянутых ранее подходов.
1. ТОЧНОСТЬ ЯВНОЙ И НЕЯВНОЙ СХЕМ ДЛЯ ЗАДАЧ КОНВЕКЦИИ НА ПРИМЕРЕ МОДЕЛЬНОГО УРАВНЕНИЯ
В данном разделе рассмотрена модельная задача конвекции, которая поможет исследовать различные схемы для решения системы уравнений движения газа в нестационарной постановке.
На первом этапе рассмотрим линейное уравнение переноса. Согласно теории дифференциального приближения к численной схеме [14], из-за ошибок аппроксимации вместо исходного уравнения (с нулевой правой частью) мы решаем уравнение вида
(1)
$\frac{{\partial u}}{{\partial t}} + a\frac{{\partial u}}{{\partial x}} = \sum\limits_{n = 2}^\infty {{{\alpha }_{n}}{{h}^{{n - 1}}}\frac{{{{\partial }^{n}}u}}{{\partial {{x}^{n}}}}} ,$Теперь рассмотрим “невязкое” уравнение Бюргерса
В отличие от уравнения переноса, оно описывает процессы с переменной скоростью конвекции. Для численного расчета можно выбрать явную или неявную схемы. Начнем с явной схемы, реализованной на равномерной сетке. Рассмотрим случай u > 0 и запишем схему Годунова, которая в этом случае имеет шаблон “левый уголок” [15]:
Разложив компоненты уравнения в ряды Тейлора относительно точки (i; n), получим
Теперь возьмем неявную схему с такой же аппроксимацией пространственного оператора, но на неизвестном слое
“Cглаживающий” неявный член можно упростить, если заменить квадратичную функцию $f(u) = {{u}^{2}}{\text{/}}2$ кусочно-линейной функцией так, что при ${{x}_{{i - 1}}} \leqslant x < {{x}_{i}}$ $f(u) \approx \left( {(u_{{i - 1}}^{n} + u_{i}^{n})u - u_{{i - 1}}^{n}u_{i}^{n}} \right){\text{/}}2$, а при ${{x}_{i}} \leqslant x < {{x}_{{i + 1}}}$ $f(u) \approx \left( {\left( {u_{i}^{n} + u_{{i + 1}}^{n}} \right)u - u_{i}^{n}u_{{i + 1}}^{n}} \right){\text{/}}2$. К такой линеаризации в случае уравнения Бюргерса сводится метод Роу (см. [16]). Получим
Разложив компоненты уравнения в ряды Тейлора около точки (i; n), получим
Видно, что “численная вязкость” $D > 0$ при любых значениях числа Куранта, что означает абсолютную устойчивость схемы. Но в области применимости явной схемы ($CFL \leqslant 1$) для каждого значения CFL ошибки аппроксимации по неявной схеме больше по сравнению с явной схемой, а при $CFL > 1$ ошибки быстро растут вместе с CFL.
Этот вывод сохраняется и для схем со смешанной аппроксимацией пространственного оператора. Для примера можно взять схему из семейства Кранка–Николсона с таким же способом аппроксимации пространственной производной, как и в схеме Годунова (далее – “вторая неявная схема”):
2-е дифференциальное приближение к этой схеме имеет следующий вид:
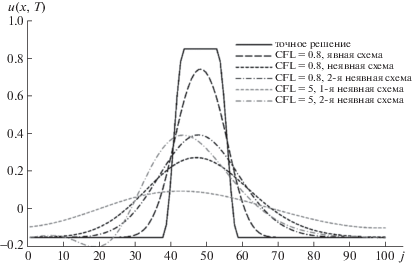
Это важно учитывать при решении нестационарных задач, где отсутствует эффект “установления” решения. Рассмотрим модельную нестационарную задачу для линейного уравнения переноса, см. фиг. 1. Отрезок покрывается равномерной сеткой из 100 ячеек, на его краях ставятся периодические граничные условия. В начальный момент задается решение в виде сглаженной “шапочки”. Рассматривается момент времени, когда “шапочка” проходит всю область и возвращается к исходному положению. Точное решение уравнения переноса представлено на рисунке сплошной черной линией. Черные штриховые кривые показывают решения, полученные с использованием описанных выше явной и неявных схем при одинаковом СFL = 0.8. Серым цветом показаны решения, полученные по неявным схемам с числом CFL = 5. Результат очевидным образом подтверждает проведенный выше анализ. Видно, что неявные схемы «размазывают» решение сильнее, чем явная схема. При этом с увеличением числа Куранта этот эффект усугубляется: кроме сглаживания, появляются ошибки в скорости переноса и нефизичные осцилляции. Таким образом, при описании нестационарных процессов конвективной природы для повышения точности следует выполнять условие $CFL\sim 1$ даже при использовании неявной схемы.
2. ДВА ПОДХОДА К ПОСТРОЕНИЮ ЧИСЛЕННОЙ СХЕМЫ ДЛЯ РЕШЕНИЯ НЕСТАЦИОНАРНОЙ ЗАДАЧИ
В предыдущем разделе отмечено, что явная схема при определенных условиях имеет преимущество по точности перед неявной схемой, но может проигрывать по быстродействию. На практике не удается проводить расчет с ячейками одного размера. Расчетная сетка претерпевает существенные сгущения и, как следствие, наименьшие по размеру ячейки определяют величину расчетного шага по времени. Другими словами, для большинства ячеек расчетной области выполняется условие $CFL \ll 1$, что отрицательно влияет не только на быстродействие, но и на точность. Для задачи поиска решения методом установления проблема частично решается путем применения процедуры интегрирования с локальным шагом по времени. При этом каждая расчетная ячейка считается таким образом, что локальное значение числа Куранта CFL (или коэффициента устойчивости Cstab в случае наличия диффузии) близко к единице [17]. Этот подход можно применять для задач, имеющих гарантированное стационарное решение. В случае “выхода решения на стационар” различие временных слоев нивелируется, и результат считается пригодным для практического использования. При решении нестационарных задач данный способ ускорения расчета непригоден. Вместо него можно предложить две другие процедуры – дробный и дуальный шаг по времени.
Первая процедура ускорения расчета заключается в проведении интегрирования по времени специальным образом, когда в каждой ячейке организуется необходимое число шагов по явной схеме с коэффициентом устойчивости, близким к максимально возможному для этой ячейки (${{C}_{{{\text{stab}}}}} = 0.5{\kern 1pt} - {\kern 1pt} 1$) и последующим выходом всех ячеек на один и тот же временной слой. При таком подходе большая по размеру ячейка делает один большой шаг по времени и ждет, пока маленькая ячейка делает несколько шагов вплоть до полного выравнивания по времени. Процессы в ячейках с разной величиной шага по времени синхронизируются при помощи интерполяции по времени. Достижение одного и того же временного уровня будем называть завершением глобального шага по времени. Например, если в ячейке А локальный шаг по времени равен ${{\tau }_{{\max }}}$, в ячейке B – ${{\tau }_{{\max }}}{\text{/}}2$, а в ячейке С – ${{\tau }_{{\max }}}{\text{/}}4$, то в течение одного глобального шага в ячейке А следует сделать один локальный шаг по времени, в ячейке B – два локальных шага по времени, а в ячейке С – четыре локальных шага по времени. Таким образом, в каждой ячейке мы разбиваем (дробим) глобальный шаг по времени на мелкие шаги. Это дает название процедуры – дробный шаг по времени [17] (в дальнейшем для краткости “дробная схема”).
Рассмотрим организацию описанного алгоритма. Перед началом расчета в каждой ячейке оценивается максимально возможное значение шага по времени – $\tau _{{ijk}}^{{{\text{stab}}}}$, определяемое локальным условием устойчивости. Затем вычисляется максимально возможный шаг для всей расчетной области – ${{\tau }_{{\max }}} = \mathop {\max }\limits_{i,j,k} \tau _{{ijk}}^{{{\text{stab}}}}$ и определяется локальный шаг для каждой ячейки. В ячейке с номером $(i,j,k)$ величина локального шага по времени берется равной ${{\tau }_{{ijk}}} = {{\tau }_{{\max }}}{\text{/}}{{2}^{l}}$, где l – наименьшее целое число, при котором ${{\tau }_{{ijk}}} \leqslant \tau _{{ijk}}^{{{\text{stab}}}}$. В результате этой процедуры все множество ячеек расчетной области подразделяется на несколько подмножеств, которые называются уровнями. Во всех ячейках уровня m величина локального шага по времени равна ${{\tau }_{{ijk}}} = {{\tau }_{{\max }}}{\text{/}}{{2}^{{M - m}}}$, где M – количество уровней. В ячейках 1-го уровня локальный шаг по времени минимален, а в ячейках уровня M соответственно максимален.
Расчет ведется по схеме Годунова–Колгана–Родионова (см. [17]), имеющей 2-й порядок аппроксимации по всем переменным. В этой схеме для достижения 2-го порядка аппроксимации по времени используется процедура “предиктор-корректор”. Поэтому каждый локальный шаг состоит из двух внутренних шагов. Первый внутренний шаг (предиктор) служит для определения параметров на временном слое $({{t}_{0}} + \tau {\text{/}}2)$, а 2-й шаг (корректор) соответственно для определения параметров на слое $({{t}_{0}} + \tau )$. Особую важность приобретает процедура синхронизации ячеек, находящихся на разных уровнях. Рассмотрим для примера случай, когда имеется три уровня ячеек. В ячейках 1-го уровня величина локального шага по времени равна ${{\tau }_{{\max }}}{\text{/}}4$, в ячейках 2-го уровня – ${{\tau }_{{\max }}}{\text{/}}2$, а на 3-м уровне – ${{\tau }_{{\max }}}$. Порядок вычислений в течение одного глобального шага по времени представлен в таблице. Если полное количество уровней равно M, то в течение одного глобального шага совершается ${{2}^{M}}$ “проходов” по расчетной области. При “проходе” структура вычислений в каждой ячейке зависит от номера уровня m. Если r – номер “прохода” и (r – 1) делится нацело на ${{2}^{m}}$, то в ячейке совершается предварительный шаг‑предиктор; если $(r - 1 - {{2}^{{m - 1}}})$ делится нацело на ${{2}^{m}}$, то в ячейке совершается шаг–корректор. В остальных случаях ячейка является “пассивной”, т.е. вычисления в ней не производятся.
Таблица.
Порядок вычислений в ходе одного глобального шага при дробном шаге по времени в задаче с тремя уровнями ячеек
| Номер прохода | Момент времени | 1-й уровень $\tau = {{\tau }_{{\max }}}{\text{/}}4$ | 2-й уровень $\tau = {{\tau }_{{\max }}}{\text{/}}2$ |
3-й уровень $\tau = {{\tau }_{{\max }}}$ |
|---|---|---|---|---|
| 1 | ${{t}_{0}}$ | 1-й внутренний шаг | 1-й внутренний шаг | 1-й внутренний шаг |
| 2 | ${{t}_{0}} + {{\tau }_{{\max }}}{\text{/}}8$ | 2-й внутренний шаг | ||
| 3 | ${{t}_{0}} + {{\tau }_{{\max }}}{\text{/}}4$ | 1-й внутренний шаг | 2-й внутренний шаг | |
| 4 | ${{t}_{0}} + 3{{\tau }_{{\max }}}{\text{/}}8$ | 2-й внутренний шаг | ||
| 5 | ${{t}_{0}} + {{\tau }_{{\max }}}{\text{/}}2$ | 1-й внутренний шаг | 1-й внутренний шаг | 2-й внутренний шаг |
| 6 | ${{t}_{0}} + 5{{\tau }_{{\max }}}{\text{/}}8$ | 2-й внутренний шаг | ||
| 7 | ${{t}_{0}} + 3{{\tau }_{{\max }}}{\text{/}}4$ | 1-й внутренний шаг | 2-й внутренний шаг | |
| 8 | ${{t}_{0}} + 7{{\tau }_{{\max }}}{\text{/}}8$ | 2-й внутренний шаг |
Для вычислений в “активных” ячейках нужно знать параметры потока в ячейках-соседях. Если соседние ячейки “пассивны”, то параметры в них находятся при помощи линейной интерполяции по времени. В каждой ячейке хранятся значения параметров потока на двух временных слоях – на последнем достигнутом временном слое и на предыдущем. Например, во время 6-го “прохода” в ячейках 2-го уровня хранятся параметры на временном слое ${{t}_{0}} + {{\tau }_{{\max }}}{\text{/}}2$ и на временном слое ${{t}_{0}} + 3{{\tau }_{{\max }}}{\text{/}}4$. Линейная интерполяция между этими слоями дает значения на временном слое, который рассматривается на данном “проходе” – ${{t}_{0}} + 5{{\tau }_{{\max }}}{\text{/}}8$.
Очевидным недостатком описанного алгоритма является его неконсервативность. Потоки через общие грани ячеек, например, (i, j, k) и (i + 1, j, k), вычисляются отдельно для каждой из этих ячеек по независимым формулам и в разные моменты времени. Консервативный алгоритм также возможен (см. [18]). Он необходим при решении задач с сильными разрывами.
Второй способ ускорения расчета связан с построением “точной по времени” (т.е. аппроксимирующей нестационарную задачу) неявной схемы, имеющей 2-й порядок аппроксимации. Рассматривается пример одномерного скалярного гиперболического уравнения $\frac{{\partial u}}{{\partial t}} + \frac{{\partial F(u)}}{{\partial x}} = 0$. Схема может быть представлена в следующем виде:
Потоки ${{F}_{{i + 1/2}}}$ и ${{F}_{{i - 1/2}}}$ рассчитаны по параметрам на новом временном слое (n + 1) и обеспечивают 2-й порядок аппроксимации по пространству. Шаг по времени ${{\tau }_{n}}$ формально неограничен, другими словами, возможен расчет с $CFL \gg 1$. При реализации такой схемы возникают технические проблемы. Пространственные потоки рассчитываются на неизвестном временном слое и ячейки связаны друг с другом. Это приводит к нелинейной алгебраической системе, в которой число уравнений равно количеству ячеек. Возможны различные подходы к решению указанной системы, например, применение метода дуального шага по времени (в дальнейшем для краткости “дуальная схема”). К дискретному оператору приписывается фиктивный член, зависящий от псевдо-времени $\xi $:
Идея заключается в том, что стационарное решение этой задачи при $\xi \to \infty $ совпадает с искомым решением физической задачи на слое $u = {{u}^{{n + 1}}}$. Другими словами, сложная нестационарная задача заменяется серией более простых подзадач, каждая из которых решается методом установления по псевдо-времени. Это позволяет применять такие известные методы ускорения сходимости по псевдо-времени, как локальный шаг по времени [17] или линеаризованные неявные схемы [19], пример которых был представлен в предыдущем разделе (первая неявная схема).
На фиг. 2 приведен пример сравнения вычислительной эффективности методов дробного и дуального шагов по времени. Рассматривается обтекание профиля крыла NACA0012 (M = 0.8, угол атаки 2.26°, хорда 1 м). Расчет ведется на базе уравнений Рейнольдса, замкнутых моделью турбулентности q–ω (см. [20]). Используется расчетная сетка, которая ориентирована на применение пристеночных функций [20], [21]. Так, на поверхности профиля высота первой пристеночной ячейки в окрестности середины хорды позволяет сделать оценку ${{y}^{ + }}\sim 10$. При этом разброс относительных размеров максимальных и минимальных ячеек в пределах пограничного слоя не превышает 1000. По горизонтальной оси на графике (см. фиг. 2) отложена величина “глобального шага по времени” $\Delta t$. По вертикальной оси отложен параметр эффективности $R$, который равен отношению величины процессорного времени ЭВМ, необходимого для описания заданного интервала физического времени по явной схеме с одинаковым минимальным шагом по времени во всей расчетной области, к соответствующему значению процессорного времени, затраченному на расчет этой же задачи с применением “дуальной” или “дробной” схем. Чем больше величина $R$, тем эффективнее исследуемая схема. Следует отметить, что при использовании описанной выше “дуальной” схемы величина шагов $\Delta t$ одинакова во всех ячейках. В том случае, когда расчет идет с применением “дробной” схемы, ситуация меняется. В каждой ячейке используется собственное значение шага $\tau = \Delta t{\text{/}}{{2}^{l}}$, $l \in Z$, которое удовлетворяет локальному условию устойчивости. Тем не менее существует максимальное значение $\Delta {{t}_{{\max }}}$ (в рассматриваемом случае $\Delta {{t}_{{\max }}} \approx 8 \times {{10}^{{ - 6}}}$), которое соответствует ограничению на шаг по времени для явной схемы в невязкой части потока непосредственно над внешней границей пограничного слоя в центральной части профиля. Считается, что при развитии течения именно в этой области наиболее интенсивно проистекают конвективные процессы, определяющие структуру течения в окрестности всего профиля. Этот шаг $\Delta {{t}_{{\max }}}$ рекомендуется в данном тесте как максимальный для неявной схемы. Анализ графиков на фиг. 2 показывает, что в данном примере метод дробного шага превосходит по эффективности метод дуального шага при всех значениях $\Delta t$ из выбранного диапазона. Однако наблюдается эффект “насыщения”. Так, при увеличении $\Delta t$ рост эффективности дробного шага замедляется и выходит на “полку”. Это связано с тем, что увеличиваются “накладные расходы” на обработку “малых” ячеек, в которых приходится делать большое количество локальных шагов. С другой стороны, эффективность “дуальной” схемы растет практически линейно по $\Delta t$.
Фиг. 2.
Сравнение эффективности дробного и дуального шага по времени на сетке с отношением размеров ячеек порядка 1000.
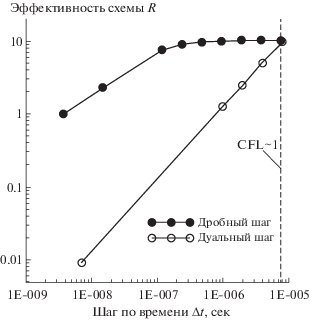
Обе схемы можно использовать за пределами исследуемого диапазона. При этом “дробная” схема работает вплоть до значений $\Delta t$, определяемых условием устойчивости в очень больших ячейках сетки вдали от профиля, а для “дуальной” схемы формального ограничения вообще нет. Тем не менее применяется ограниченный диапазон $\Delta t$, так как есть основания полагать, что при $\Delta t > \Delta {{t}_{{\max }}}$ эффективность дробного шага не увеличится или даже понизится, а “дуальная” схема даст завышенные ошибки.
Следует отметить, что в случае применения метода дробного шага коэффициент R сильно зависит от структуры расчетной сетки. В данном примере использованы пристеночные функции, что позволило избежать построения чрезвычайно маленьких ячеек. В общем случае, при расчете с условием прилипания на поверхности тела, высота первой ячейки выбирается исходя из условия ${{y}^{ + }}\sim 0.1 - 1$. На такой сетке соотношение относительных размеров максимальных и минимальных ячеек становится равным 104–105, а эффективность дробного шага заметно падает. С другой стороны, эффективность метода дуального шага по-прежнему остается высокой. Это позволяет предложить альтернативный подход к решению нестационарных задач с условием прилипания на твердых стенках. Расчетная область делится на две зоны, в каждой из которых расчет ведется независимо друг от друга с обменом информацией через граничные условия. При этом в тонкой пристеночной зоне расчет проводится по неявной схеме с дуальным шагом, а в остальной части – по явной схеме с дробным шагом. В дальнейшем для краткости такой подход называется зональным.
3. РАСЧЕТЫ ОБТЕКАНИЯ ПРОФИЛЯ И КРЫЛА С МЕХАНИЗАЦИЕЙ
Рассмотрим в качестве примера расчет обтекания профиля крыла с предкрылком и закрылком. Указанный профиль был исследован экспериментально (см. [22]) в проекте EUROPIV2 шестой рамочной программы Европейского Союза. Фактически рассматривалось прямое крыло (размах – 2.1 м) с трехэлементным профилем RA16SC1. Углы отклонения предкрылка и закрылка устанавливались в одной позиции и были равны 30° и 40° соответственно. Хорда базовой части крыла равнялась c = 0.5 м. Число ${{M}_{\infty }} = 0.15$ соответствовало посадочному режиму полета, число Re, рассчитанное по скорости свободного потока и базовой хорде, равнялось $1.7 \times {{10}^{6}}$. В эксперименте были получены распределения статического давления и измерены поля скорости. Использован метод PIV.
Для расчетов использовалась модификация программы, описанной в [17], [23]. В программу добавлены специальные блоки, реализующие описанную выше неявную схему с дуальным шагом по времени. Для итераций по псевдо-времени применена линеаризованная неявная схема (см. [19]). Для замыкания уравнений Рейнольдса использовалась модификация модели SST, описанная в [20]. Метод дробного шага по времени реализован в базовой программе и описан в [17]. Дополнительно подготовлены блоки программы с целью реализации зонального подхода.
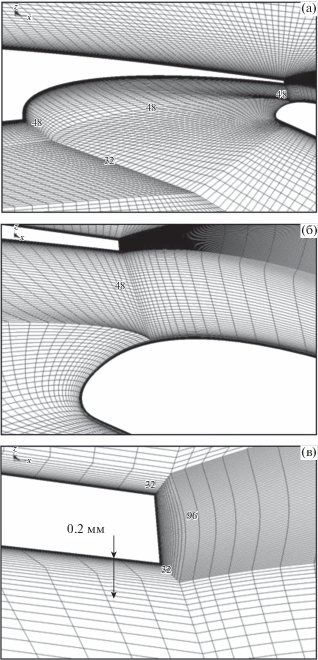
Для проведения расчета вокруг профиля построена специальная сетка, см. фиг. 3. Каждый элемент профиля (предкрылок, базовый элемент, закрылок) окружен тонкой зоной. Например, вокруг базового элемента крыла толщина “пристеночной” зоны равна приблизительно 0.2 мм, что составляет 3% толщины пограничного слоя в середине базовой части профиля. Толщина блоков сетки в районе закрылка и предкрылка в два раза меньше – около 0.1 мм. В случае использования зонального подхода в “пристеночной” зоне расчет ведется по неявной схеме с дуальным шагом, а в остальных блоках сетки – с дробным шагом по времени. Общее количество ячеек в расчете равно 45 888, из них 21 120 размещены в “пристеночной” зоне. Внешние границы расчетной области отдалены от поверхности профиля на расстояние порядка 40 длин его суммарной хорды. Все твердые поверхности считаются теплоизолированными. На них выполняется условие прилипания. Коэффициенты сопротивления и подъемной силы рассчитываются в системе координат, связанной с продольной осью x, ориентированной вдоль вектора скорости набегающего потока, и осью y, перпендикулярной этому вектору.
Сначала проанализируем структуру течения. Результаты расчета представлены на фиг. 4, где изображены линии тока в окрестности всех элементов профиля. Они позволяют визуализировать зоны отрыва потока. Например, при угле атаки α = 5° наблюдаются три отрывные зоны. Одна зона размещена у нижней поверхности предкрылка, вторая – под базовым элементом профиля; третья расположена над закрылком и вызвана сходом потока с его задней кромки. За базовым элементом крыла пограничный слой становится турбулентным на расстоянии порядка одной шестой хорды от передней кромки. Вниз по потоку от задней кромки базового элемента крыла возникает слой смешения потоков с его верхней и нижней поверхностей, который является турбулентным с самого начала. Аналогичный слой смешения образуется за предкрылком. При угле атаки α = 9° отрыв над закрылком практически исчезает (наблюдается только у задней кромки). Картина течения при α = 12° указывает на те же особенности, что мы наблюдали при α = 9°. Перестройка течения начинается при угле атаки α = 17.5°. Над верхней поверхностью закрылка в застойной зоне начинает формироваться интенсивный вихрь. Структура течения при α = 19° в целом повторяет структуру, описанную ранее, но интенсивность вихря за закрылком в застойной зоне возрастает. При дальнейшем увеличении угла атаки до величин порядка α = 24° эти тенденции приводят к срыву потока с верхней поверхности базового элемента крыла. Срыв потока сопровождается падением подъемной силы, потерей устойчивости течения и возникновением крупномасштабных нестационарных процессов [3].
Анализ эффективности различных схем расчета проводится по графикам на фиг. 5–7. Коэффициент устойчивости ${{C}_{{{\text{stab}}}}}$ рассчитан по параметрам потока в области существенных конвективных нестационарных процессов (у внешней границы пограничного слоя). Профиль обтекается с углом атаки α = 19°. Из предыдущего анализа следует, что на указанном режиме наблюдаются три зоны отрыва потока. При этом наиболее интенсивный отрыв образуется при сходе потока с верхней поверхности основного элемента крыла и закрылка.
Фиг. 5.
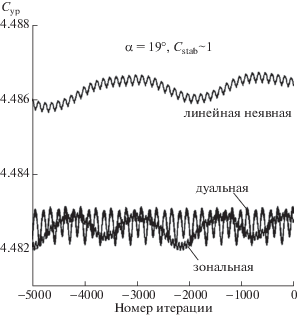
Сравнение качества схем при решении задачи обтекания трехзвенного профиля: а) зональная, дуальная и линейная неявная схемы, последние 5000 итераций каждого расчета.
Фиг. 6.
Влияние шага интегрирования по времени на результат расчета обтекания трехзвенного профиля при помощи линейной неявной схемы.

Фиг. 7.
Влияние шага интегрирования по времени на результат расчета обтекания трехзвенного профиля при помощи “дуальной” схемы.

На первом этапе расчет выполнен с применением “зональной”, “дуальной” и линейной неявных схем с одинаковым значением глобального шага по времени $\Delta t = 5 \times {{10}^{{ - 6}}}$ с (${{C}_{{{\text{stab}}}}}\sim 1$). На фиг. 5 приведено решение, полученное указанными методами за последние 5000 шагов (${{C}_{{{\text{yp}}}}}$ – коэффициент подъемной силы по давлению). Несмотря на заметные осцилляции решения можно заключить, что “дуальная” и “зональная” схемы дают в среднем близкие результаты. Отличие заключается в том, что “зональное” решение имеет четко выраженную низкочастотную волну с высокочастотной рябью, а “дуальное” решение напоминает “пилу” с постоянным шагом. Результат, полученный с помощью линейной неявной схемы, несколько завышен ($0.1\% $). С точки зрения практических приложений, отличия можно считать несущественными.
Оценка амплитуды осцилляций решения дает величину порядка $0.02\% $, что указывает на практически стационарный характер обтекания профиля. Возникает естественное желание выполнить расчет методом установления по времени с применением эффективной линейной неявной схемы. На фиг. 6 представлены результаты такого решения, полученного при разных значениях величины ${{C}_{{{\text{stab}}}}}$. Для наглядности на график нанесены две линии, представленные на фиг. 5. Первая линия соответствует решению, полученному по зональному подходу, а вторая получена по линейной неявной схеме при ${{C}_{{{\text{stab}}}}} \approx 1$. Как упоминалось выше, они близки друг к другу. Кроме того, на график нанесены линии, полученные по линейной неявной схеме при ${{C}_{{{\text{stab}}}}} \approx 100$ и ${{C}_{{{\text{stab}}}}} \approx {{10}^{6}}$. Случай ${{C}_{{{\text{stab}}}}} \approx {{10}^{6}}$ является характерным для решения задачи методом установления. Видно, что с увеличением ${{C}_{{{\text{stab}}}}}$ возрастает как абсолютное значение ошибки, так и амплитуда осцилляций решения. Например, при ${{C}_{{{\text{stab}}}}} \approx {{10}^{6}}$ величина коэффициента подъемной силы завышена по сравнению с уровнем “зональной” схемы приблизительно на $2\% $, а амплитуда осцилляций решения относительно среднего достигает 0.2%. Напомним, что подавляющее большинство участников тестирования крыла с механизацией в рамках рабочих совещаний High Lift Workshop [1], [2] отметило факт завышения значения подъемной силы на отрывных режимах обтекания. Из материалов совещания [1], [2] следует, что расчет велся методами установления.
На фиг. 7 приведен результат расчета с применением “дуальной” схемы при разных значениях ${{C}_{{{\text{stab}}}}}$. График построен в зависимости от физического времени. Использован обратный отсчет, при котором за ноль принимается время прекращения расчета. Это позволяет нанести на один график результаты, полученные за разные временные промежутки. Ранее на фиг. 5 проведено сопоставление уровней средних величин, полученных по разным схемам для ${{C}_{{{\text{stab}}}}} \approx 1$, что может служить ориентиром для оценки величин отклонения решений на фиг. 7. Сопоставление показывает, что в случае “дуальной” схемы (также, как и в случае “линейной”) просматривается влияние шага интегрирования по времени на результат. Например, при ${{C}_{{{\text{stab}}}}} \approx 1000$ среднее значение коэффициента подъемной силы занижено на $0.1\% $, но такие отклонения считаются незначительными с точки зрения практических приложений. Дальнейшее увеличение ${{C}_{{{\text{stab}}}}}$ при проведении нестационарного расчета нецелесообразно.
На фиг. 8 сопоставляются эффективности “зональной” и “дуальной” схем. Используются те же обозначения, что и на фиг. 2. Штриховой линией показано максимальное значение глобального шага по времени $\Delta t$, при котором по мнению авторов обеспечивается качественное описание нестационарных процессов (${{C}_{{{\text{stab}}}}}\sim 1$ в невязком ядре потока вокруг профиля). Следует отметить, что при $\Delta t = 5 \times {{10}^{{ - 5}}}$ с (${{C}_{{{\text{stab}}}}}\sim 10$) “дуальная” схема в 3 раза эффективнее “зональной”. С увеличением шага интегрирования по времени вплоть до ${{C}_{{{\text{stab}}}}} \approx 1000$ преимущество дуальной схемы не вызывает сомнений. Тут следует вспомнить предыдущий анализ, где показано, что точность расчета при таких ${{C}_{{{\text{stab}}}}}$ уменьшается несущественно. С другой стороны, при расчете с небольшими шагами по времени ${{C}_{{{\text{stab}}}}} < 10$ “зональная” схема в разы эффективнее, чем “дуальная”. Указанный вывод подтверждается при исследовании эффективности “зональной” и “дуальной” схем на примере обтекания трехмерного крыла с выпущенными закрылками и предкрылками [24], см. фиг. 9.
Фиг. 8.
Сопоставление эффективности зонального подхода и схемы с дуальным шагом во всей расчетной области при решении задачи обтекания трехзвенного профиля.
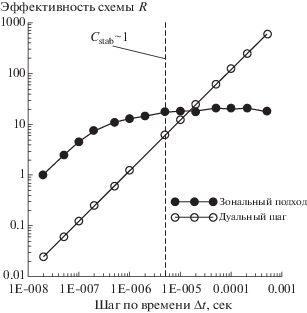
Фиг. 9.
Сопоставление эффективности зонального подхода и схемы с дуальным шагом во всей расчетной области при решении задачи обтекания крыла.

В заключение следует отметить, что в рассмотренных примерах эффективнее применять “дуальную” схему с большими шагами по времени (${{C}_{{{\text{stab}}}}} \approx 1000$). Однако в тех случаях, когда имеются существенные нестационарные конвективные процессы, целесообразно вести расчет с ${{C}_{{{\text{stab}}}}}\sim 1$. При выполнении указанного условия зональный подход дает выигрыш.
Список литературы
Slotnick J., Hannon J., Chaffin M. Overview of the 1st AIAA CFD High Lift Prediction Workshop // 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. 2011. P. 862.
Rumsey C.L., Slotnick J.P. Overview and Summary of the Second AIAA High-Lift Prediction Workshop // J. of Aircraft. 2014. V. 52. № 4. P. 1006–1025.
Ericsson L.E., Reding J.P. Fluid dynamics of unsteady separated flow. P. II. Lifting surfaces // Progress in Aerospace Sciences. 1987. V. 24. № 4. P. 249–356.
Blazek J. Computational fluid dynamics: principles and applications.New York: Elsevier, 2001.
Vlasenko V., Bosniakov S., Mikhailov S., Morozov A., Troshin A. Computational approach for investigation of thrust and acoustic performances of present-day nozzles // Progr. Aerospace Sci. 2010. V. 46. P. 141–197.
Wang Z.J. High-order methods for the Euler and Navier–Stokes equations on unstructured grids // Progr. Aerospace Sci. 2007. V. 43. P. 1–41.
Berger M.J., Oliger J. Adaptive mesh refinement for hyperbolic partial differential equations // J. of Comput. Phys. 1984. V. 53. P. 484.
Plewa T., Linde T., Weirs V.G. Adaptive mesh refinement – theory and applications. Lecture Notes in Computational Science and Engineering // Proc. of the Chicago Workshop on Adaptive Mesh Refinement Meth. Sept. 3–5, 2003. V. 41.
Timofeev E., Norouzi F. Hybrid, explicit-implicit, finite-volume schemes on unstructured grids for unsteady compressible flows // AIP Conference Proc. AIP Publishing. 2016. V. 1738. № 1. P. 030002.
Башкин В.А., Егоров И.В. Численное моделирование динамики вязкого совершенного газа. М.: Физматлит, 2012.
Jameson A. Time Dependent Calculations Using Multigrid, with Applications to Unsteady Flows Past Airfoils and Wings // AIAA 10th Comput. Fluid Dynamics. Conference June 24–26 1991, Honolulu, Hi. AIAA 91–1596.
Chiew J., Thomas H. Stability Analysis of Dual-Time Stepping // AIAA Aviation. 13–17 June 2016, Washington, D.C. 46th AIAA Fluid Dynamics Conference.
Кажан Е.В. О возможности использования неявной схемы в рамках пакета EWT–ЦАГИ // Тр. ЦАГИ. 2007. Вып. 2617. С. 201–211.
Шокин Ю.И., Яненко Н.Н. Метод дифференциального приближения. Применение к газовой динамике // Новосибирск: Наука, 1985.
Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001.
Roe P.L. Approximate Riemann solvers, parameter vectors, and difference schemes // J. of Comput. Phys. 1981. V. 43. P. 357–372.
Bosnyakov S., Kursakov I., Lysenkov A., Matyash S., Mikhailov S., Vlasenko V., Quest J. Computational Tools for Supporting the Testing of Civil Aircraft Configurations in Wind Tunnels // Progr. Aerospace Sci. 2008. V. 44. P. 67–120.
Молев С.С. Повышение качества моделирования нестационарных процессов при использовании явной схемы с дробным шагом по времени // Уч. зап. ЦАГИ. 2015. Т. 46. № 8. С. 53–70.
Кажан Е.В. Повышение устойчивости явной схемы ГКР локальным введением неявного сглаживателя // Уч. зап. ЦАГИ. 2012. № 6.
Бабулин А.А., Босняков С.М., Власенко В.В., Енгулатова М.Ф., Матяш С.В., Михайлов С.В. Опыт валидации и настройки моделей турбулентности применительно к задаче об отрыве пограничного слоя на клине конечной ширины // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 6. С. 1034–1048.
Goncalves E., Houdeville R. Reassessment of the wall functions approach for RANS computations // Aerospace Sci. and Technology. 2001. V. 5. № 1. P. 1–14.
Arnott A., Neitzke K., Agocs J., Sammer G., Schneider G., Schroeder A. Detailed Characterisation Using PIV of the Flow Around an Aerofoil in High Lift Configuration // EUROPIV2 Workshop on Particle Image Velocimetry. Berlin: Springer, 2003. P. 31–42. ISBN 3-540-21423-2.
Михайлов С.В. Объектно ориентированный подход к созданию эффективных программ, реализующих параллельные алгоритмы расчета // Тр. ЦАГИ. 2007. Вып. 2617. С. 86–108.
Rudnik R., Germain E. Re-No. Scaling Effects on the EUROLIFT High Lift Configurations // 45th AIAA Aerospace Sci. Meeting and Exhibit, 2007, AIAA paper 2007–0752.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики