Журнал вычислительной математики и математической физики, 2019, T. 59, № 1, стр. 118-127
Влияние квантовых эффектов на оптические свойства парных плазмонных частиц с субнанометровым зазоромЮ. А. Еремин, А. Г. Свешников
Ю. А. Еремин 1, *, А. Г. Свешников 1
1 МГУ ВМК
119991 Москва, Ленинские горы, Россия
* E-mail: eremin@cs.msu.ru
Поступила в редакцию 04.07.2018
Аннотация
В данной статье на основе метода Дискретных источников исследуется влияние эффекта нелокального экранирования на оптические свойства линейного кластера несферических плазмонных наночастиц с субнанометровом зазором. Показано, что деформация частиц и уменьшение зазора между ними приводят к усилению влияния эффекта нелокального экранирования. Оказалось, что возрастание интенсивности как рассеянного, так и ближнего полей блокируется эффектом нелокальности, и альтернативой усиления полей может служить увеличение деформации составляющих элементов. Библ. 35. Фиг. 5.
1. ВВЕДЕНИЕ
Один из наиболее интересных и актуальных разделов нанофотоники посвящен изучению физических явлений, связанных с возможностью управления световым излучением и получения сильных сфокусированных электромагнитных полей в масштабах нескольких атомов [1]–[3]. Такая фокусировка достигается посредством использования эффекта плазмонного резонанса (ПР). Важнейшим свойством плазмонов является их способность манипулировать светом, а именно – направлять его вдоль металлических полос или фокусировать его в отверстиях, сужениях, зазорах между частицами или вблизи участков поверхностей с резким изменением профиля. В этом случае концентрация поля происходит в объемах, имеющих размеры в сотни раз меньше длины волны излучения, но интенсивность электрического поля может достигать нескольких порядков величин [3], [4]. Практика моделирования поведения ПР основана на классической электромагнитной теории Максвелла, в которых коллективное поведение электронов описывается в рамках эмпирических диэлектрических постоянных [1], [2], а распределение электромагнитного поля описывается решением системы уравнений Максвелла. Подобный подход предсказывает монотонное возрастание электрического поля по мере уменьшения зазора между частицами, что побуждает исследователей к разработке нанотехнологий для практической реализации плазмонных структур с субнаноразмерными зазорами [5], [6].
Кроме прочего, кластеры плазмонных частиц с субнанометровыми зазорами оказываются весьма привлекательными в качестве составляющих элементов плазмонных систем, поскольку они позволяют манипулировать положением ПР и его амплитудой в широком диапазоне длин волн. В ряде работ было показано, что квантовомеханические эффекты, такие как нелокальное экранирование и туннелирование электронов, приобретают существенное значение, по мере того, как размеры зазора приближаются к шкале субнанометра. Учет возникающих при этом квантовых эффектов в значительной степени разрушает классическое описание поведения полей в подобных системах. Вместе с тем недавние теоретические и экспериментальные исследования [7]–[9] показывают, что по мере того, как размер зазора попадает в нанометровую и субнанометровую шкалу, квантовая природа электронов и нелокальное экранирование могут значительно изменять плазмонный отклик рассматриваемой структуры [10], [11]. В этом квантовом режиме оказывается, что классическое описание не учитывает фактическую локализацию поверхностных зарядов, вызванных внешним электромагнитным полем [12], [13]. Сдвиг наведенных поверхностных зарядов относительно геометрических границ металла тесно связан явлением нелокальности и приводит к экранированию зарядов внутри структуры [14], [15]. Этот эффект может быть описан с использованием концепции нелокальных диэлектрических функций с различными уровнями сложности в имеющихся теоретических построениях [16], [17].
Можно схематически проиллюстрировать влияние квантовых эффектов на электромагнитные свойства ПР наноструктур с различными зазорами. Размеры зазора до 2–5 нм (в зависимости от материала структуры) соответствуют классическому режиму, для которого система уравнений Максвелла правильно описывает смещение ПР в длинноволновую область и величину его амплитуды при уменьшении зазора. Как только размер зазора становится меньше 2–5 нм, система переходит в квантовый режим, что требует более детального исследования. В данном диапазоне эффект нелокального экранирования (ЭНЭ) выступает как доминирующий квантовый эффект. В этом случае поведение ПР качественно сходно с предсказаниями локальной классической модели, но возникают существенные количественные различия как в амплитуде ПР, так и его положении. Таким образом, для правильного количественного описания происходящих процессов и связанных с ними изменений в плазмонном отклике в диапазоне размеров 0.5–2 нм необходимо существенно учитывать ЭНЭ [7], [17]. По мере дальнейшего уменьшения зазоров <0.5 нм преобладающий вклад вносит эффект туннелирования электронов, который полностью изменяет поведение плазмонного отклика [18]–[20].
В данной работе метод Дискретных источников (МДИ) модифицируется применительно к исследованию линейного кластера плазмонных частиц с наноразмерным зазором, обеспечивающим переход в квантовый режим, с учетом ЭНЭ [7], [17]. Одним из проявлений ЭНЭ является появление продольных электромагнитных полей. Когда размер элементов структуры становится существенно меньше свободного пробега электронов в веществе, внутри формируется объемный заряд, который под действием внешнего поля образует ток. В этом случае внутреннее электрическое поле Е перестает быть чисто поперечным (div E = 0), и для адекватного описания происходящих процессов возникает необходимость привлечения дополнительно продольных полей (rot E = 0) [21]. При этом учет наличия продольных полей может осуществляться на основе различных теорий, в данной работе учет осуществляется на основе наиболее востребованной в настоящее время модели обобщенного нелокального отклика (ОНО) (Generalized Nonlocal Optical Response (GNOR)) [17], [22], [23]. В рамках GNOR проводится обобщение гидродинамической теории нелокального отклика посредством учета диффузии электронов [23]. Именно это обстоятельство позволило модели GNOR оказаться наиболее подходящим инструментом описания процессов, происходящих в кластере наночастиц с квантовым зазором [24]. На основе компьютерной модели МДИ проведен сравнительный анализ классической и модели ОНО, по их влиянию, как на величину ПР, так и его положение в спектральной области. Исследовано поведение интенсивности поля в зазоре между частицами в спектральном диапазоне.
2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБОБЩЕННОГО НЕЛОКАЛЬНОГО ОТКЛИКА
Сразу отметим, что введение продольных компонент поля для описания ЭНЭ в рамках ОНО проводится на основе обобщения закона Ома для тока проводимости внутри [23], то есть с осуществлением перехода следующего вида:
Будем рассматривать рассеяние поля электромагнитной плоской волны $\{ {{{\mathbf{E}}}_{0}},\;{{{\mathbf{H}}}_{0}}\} $ линейным кластером, состоящим из двух проницаемых осесимметричных частиц с внутренними областями${{D}_{{1,2}}}$, расположенных в ${\text{ }}{{R}^{3}}$. Пусть частицы имеют гладкие поверхности $\partial {{D}_{{1,2}}} \in {{С }^{{(2,\alpha )}}}$ (пространство Гёльдера), а плоская волна распространяется под углом $\pi - {{\theta }_{0}}$ по отношению к оси симметрии OZ. Тогда математическая постановка задачи рассеяния в рамках ОНО может быть записана в следующем виде, включая систему уравнений Максвелла для внешнего и внутреннего полей
(1)
$\begin{gathered} {{{\mathbf{n}}}_{{1,2}}} \times \left( {{{{\mathbf{E}}}_{{1,2}}}\left( P \right) - {{{\mathbf{E}}}_{e}}\left( P \right)} \right) = {{{\mathbf{n}}}_{{1,2}}} \times {{{\mathbf{E}}}_{0}}\left( P \right),{\text{ }} \\ {{{\mathbf{n}}}_{{1,2}}} \times \left( {{{{\mathbf{H}}}_{{1,2}}}\left( P \right) - {{{\mathbf{H}}}_{e}}\left( P \right)} \right) = {{{\mathbf{n}}}_{{1,2}}} \times {{{\mathbf{H}}}_{0}}\left( P \right),\quad P \in {\text{ }}\partial {{D}_{{1,2}}}, \\ {{\varepsilon }_{L}}{{{\mathbf{n}}}_{{1,2}}} \cdot {{{\mathbf{E}}}_{{1,2}}}(P) = {{\varepsilon }_{e}}{{{\mathbf{n}}}_{{1,2}}} \cdot \left( {{{{\mathbf{E}}}_{0}}(P) + {{{\mathbf{E}}}_{e}}(P)} \right) \\ \end{gathered} $Параметры $\eta $ и ${{\varepsilon }_{L}}$ описывают продольную составляющую внутреннего поля ${\mathbf{E}}_{i}^{L}$ и будут определены в соответствии с моделью ОНО ниже. Следует отметить, что из формулировки задачи (1) непосредственно вытекает, что продольная компонента поля, во-первых, локализована строго внутри частицы, и, во-вторых, не вносит вклад в магнитное поле ${{{\mathbf{H}}}_{i}}$, так как $\operatorname{rot} (\operatorname{grad} \Psi ) = 0$. Введение в рассмотрение дополнительно продольного поля ${\mathbf{E}}_{i}^{L}$, подлежащего определению, требует наличия дополнительного граничного условия. Оно формулируется как обращение в нуль нормальной компоненты тока проводимости $\left( {{\mathbf{J}} \cdot {\mathbf{n}}} \right) = 0$ на поверхностях $\partial {{D}_{{1,2}}}$. В силу непрерывности тангенциальных компонент полного поля ${\mathbf{H}}$ (1) на поверхностях $\partial {{D}_{{1,2}}}$ легко показать, что в этом случае нормальная компонента ${\mathbf{n}} \cdot \operatorname{rot} {\mathbf{H}} = 0$ также непрерывна, отсюда из первого уравнения Максвелла (1) получается искомый скачок нормальной компоненты поля ${\mathbf{E}}$, который и выступает в качестве дополнительного граничного условия (1) на $\partial {{D}_{{1,2}}}$ [23].
3. ВЫЧИСЛИТЕЛЬНАЯ СХЕМА МЕТОДА ДИСКРЕТНЫХ ИСТОЧНИКОВ
Для решения задачи дифракции (1) будем использовать МДИ [25, 26]. Он обладает определенными преимуществами перед другими методами: МДИ не требует ни генерации сеток, ни использования процедур интегрирования по поверхности рассеивателя. Позволяет в аналитическом виде получать как ближнее, так и дальнее поля, причем решая задачу одновременно для всего набора углов падения плоской волны и поляризаций. Позволяет проводить анализ рассеивателей, обладающих большими значениями диэлектрической проницаемости, посредством выбора различного числа дискретных источников для представления внешнего и внутреннего полей, что оказывается весьма существенным применительно к данному случаю. Отличительной особенностью метода является то обстоятельство, что он дает возможность получать апостериорную оценку погрешности полученного решения, что позволяет контролировать реальную сходимость приближенного решения к точному.
В нашем случае поле P/S поляризованной волны может быть записано в виде
(2)
$\begin{gathered} {\mathbf{E}}_{0}^{P} = \left( {{{{\mathbf{e}}}_{x}}\cos {{\theta }_{0}} + {{{\mathbf{e}}}_{z}}\sin {{\theta }_{0}}} \right) \cdot \gamma ,\quad {\mathbf{H}}_{0}^{P} = - {{{\mathbf{e}}}_{y}}{{n}_{e}} \cdot \gamma ;\quad \gamma = \exp \left\{ { - j{{k}_{e}}\left( {x\sin {{\theta }_{0}} - z\cos {{\theta }_{0}}} \right)} \right\}, \\ {\mathbf{H}}_{0}^{S} = \left( {{{{\mathbf{e}}}_{x}}\cos {{\theta }_{0}} + {{{\mathbf{e}}}_{z}}\sin {{\theta }_{0}}} \right) \cdot \gamma ,\quad {\mathbf{E}}_{0}^{S} = {{{\mathbf{e}}}_{y}}{{n}_{e}} \cdot \gamma , \\ \end{gathered} $При построении приближенного решения на основе МДИ будем существенно учитывать осевую симметрию и поляризацию плоской волны [25]. В основу представления для внешнего $\{ {{{\mathbf{E}}}_{e}},\;{{{\mathbf{H}}}_{e}}\} $ и внутреннего поперечного поля $\left\{ {{\mathbf{E}}_{i}^{T},\;{{{\mathbf{H}}}_{i}}} \right\}:\operatorname{div} {\mathbf{E}}_{i}^{T} = 0$ положим следующие векторные потенциалы
(3)
$\begin{gathered} {\mathbf{A}}_{{mn}}^{{1,e,i}} = \left\{ {Y_{m}^{{e,i}}\left( {\xi ,z_{n}^{{e,i}}} \right)\cos (m + 1)\varphi ;\; - {\kern 1pt} Y_{m}^{{e,i}}\left( {\xi ,z_{n}^{{e,i}}} \right)\sin (m + 1)\varphi ;\;{\text{0}}} \right\}, \\ {\mathbf{A}}_{{mn}}^{{2,e,i}} = \left\{ {Y_{m}^{{e,i}}\left( {\xi ,z_{n}^{{e,i}}} \right)\sin (m + 1)\varphi ;\;Y_{m}^{{e,i}}\left( {\xi ,z_{n}^{{e,i}}} \right)\cos (m + 1)\varphi ;\;{\text{0}}} \right\},\quad {\mathbf{A}}_{n}^{{3,e,i}} = \left\{ {0;\;0;\;Y_{0}^{{e,i}}\left( {\xi ,z_{n}^{{e,i}}} \right)} \right\}, \\ \end{gathered} $Для построения приближенного решения необходимо определить значения диэлектрической проницаемости ${{\varepsilon }_{L}}$ и продольного волнового числа ${{k}_{L}}$. В рамках ОНО ${{\varepsilon }_{L}}$ определяется как ${{\varepsilon }_{L}} = {{\varepsilon }_{i}}(\omega ) - {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} {\left( {j\gamma \omega - {{\omega }^{2}}} \right)}}} \right. \kern-0em} {\left( {j\gamma \omega - {{\omega }^{2}}} \right)}}$, где ${{\varepsilon }_{i}}(\omega )$ – диэлектрическая проницаемость металла с учетом частотной дисперсии, ${{\omega }_{p}}$ – плазменная частота для данного металла, $\gamma $ – коэффициент затухания в среде [17]. Скалярный потенциал для продольного поля удовлетворяет следующему уравнению Гельмгольца: $\left( {{{\nabla }^{2}} + k_{L}^{2}} \right)\Psi (M) = 0$, а величина продольного волнового числа определяется через значение $\eta $, как $k_{L}^{2} = {{\varepsilon }_{i}}(\omega ){\text{/}}{{\eta }^{2}}$. При этом в рамках ОНО $\eta $ представляется в следующем виде ${{\eta }^{2}} = {{{{\varepsilon }_{L}}\left( {{{\beta }^{2}} + D\left( {\gamma + j\omega } \right)} \right)} \mathord{\left/ {\vphantom {{{{\varepsilon }_{L}}\left( {{{\beta }^{2}} + D\left( {\gamma + j\omega } \right)} \right)} {\left( {{{\omega }^{2}} - j\gamma \omega } \right)}}} \right. \kern-0em} {\left( {{{\omega }^{2}} - j\gamma \omega } \right)}}$. Здесь β – гидродинамическая скорость в плазме, связанная со скоростью Ферми ${{v}_{F}}$ соотношением ${{\beta }^{2}} = 3{\text{/}}5v_{F}^{2}$, D – коэффициент диффузии электронов [23]. Отметим, что при $\beta \to 0,\;D \to 0$ поле внутри частицы становится чисто поперечным, так как ${{k}_{L}} \to \infty {\text{ }} \Rightarrow \Psi \to 0$.
Для случая Р-поляризации продольное поле строится на основе следующих скалярных потенциалов, представляющих собой частные решения уравнения Гельмгольца с нелокальным волновым числом $\left( {{{\nabla }^{2}} + k_{L}^{2}} \right){{\Psi }_{{mn}}}(M) = 0$
(4)
$\begin{gathered} \Psi _{{mn}}^{P}(M) = {{j}_{{m + 1}}}({{k}_{L}}{{R}_{{\xi {{z}_{n}}}}}){{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{R}_{{\xi {{z}_{n}}}}}}}} \right. \kern-0em} {{{R}_{{\xi {{z}_{n}}}}}}}} \right)}^{{m + 1}}}\cos (m + 1)\varphi ,\quad m = 0,1, \ldots ,M, \\ {{\Psi }_{n}}(M) = {{j}_{0}}({{k}_{L}}{{R}_{{\xi {{z}_{n}}}}}),\quad n = 1,2, \ldots ,{{N}_{L}}. \\ \end{gathered} $(5)
$\begin{gathered} {\mathbf{E}}_{{e,i}}^{N} = \sum\limits_{m = 0}^M {{\text{ }}\sum\limits_{n = 1}^{N_{{e,i}}^{m}} {\left\{ {p_{{mn}}^{{e,i}}\frac{j}{{k{{\varepsilon }_{{e,i}}}{{\mu }_{{e,i}}}}}\operatorname{rot} \operatorname{rot} {\mathbf{A}}_{{mn}}^{{1,e,i}} + q_{{mn}}^{{e,i}}\frac{1}{{{{\varepsilon }_{{e,i}}}}}{\text{rot}}{\mathbf{A}}_{{mn}}^{{2,e,i}}} \right\}} } + \sum\limits_{n = 1}^{N_{{e,i}}^{0}} {r_{n}^{{e,i}}\frac{j}{{k{{\varepsilon }_{{e,i}}}{{\mu }_{{e,i}}}}}\operatorname{rot} \operatorname{rot} {\mathbf{A}}_{n}^{{3,e,i}};} \\ {\mathbf{E}}_{i}^{{LN}} = \sum\limits_{m = 0}^M {\sum\limits_{n = 1}^{N_{L}^{m}} {p_{{mn}}^{{L,i}}\nabla \Psi _{{mn}}^{P}(M) + \sum\limits_{n = 1}^{N_{L}^{0}} {r_{n}^{{L,i}}\nabla {{\Psi }_{n}}(M)} } } ;\quad i = 1,2;\quad {\mathbf{H}}_{{e,i}}^{N} = \frac{j}{{k{{\mu }_{e}}}}\operatorname{rot} {\mathbf{E}}_{{e,i}}^{N}. \\ \end{gathered} $В случае S-поляризации скалярный потенциал для продольного поля будет иметь вид
(6)
$\Psi _{{mn}}^{S}(M) = {{j}_{{m + 1}}}({{k}_{L}}{{R}_{{\xi {{z}_{n}}}}}){{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{R}_{{\xi {{z}_{n}}}}}}}} \right. \kern-0em} {{{R}_{{\xi {{z}_{n}}}}}}}} \right)}^{{m + 1}}}\sin (m + 1)\varphi ,$(7)
$\begin{gathered} {\mathbf{E}}_{{e,i}}^{N} = \sum\limits_{m = 0}^M {{\text{ }}\sum\limits_{n = 1}^{N_{{e,i}}^{m}} {\left\{ {p_{{mn}}^{{e,i}}\frac{j}{{k{{\varepsilon }_{{e,i}}}{{\mu }_{{e,i}}}}}\operatorname{rot} \operatorname{rot} {\mathbf{A}}_{{mn}}^{{2,e,i}} + q_{{mn}}^{{e,i}}\frac{1}{{{{\varepsilon }_{{e,i}}}}}\operatorname{rot} {\mathbf{A}}_{{mn}}^{{1,e,i}}} \right\}} } + \sum\limits_{n = 1}^{N_{{e,i}}^{0}} {r_{n}^{{e,i}}\frac{1}{{{{\varepsilon }_{{e,i}}}}}\operatorname{rot} {\mathbf{A}}_{n}^{{3,e,i}};} \\ {\mathbf{E}}_{i}^{{LN}} = \sum\limits_{m = 0}^M {\sum\limits_{n = 1}^{N_{L}^{m}} {p_{{mn}}^{{L,i}}\nabla \Psi _{{mn}}^{S}(M)} } ;\quad {\mathbf{H}}_{{e,i}}^{N}{\text{ }} = \frac{j}{{k{{\mu }_{e}}}}\operatorname{rot} {\mathbf{E}}_{{e,i}}^{N}. \\ \end{gathered} $Подставляя представления для полей (5), (7) в (1), легко убедиться, что они аналитически удовлетворяют всем условиям граничной задачи (1), за исключением условий сопряжения на поверхностях частиц $\partial {{D}_{{1,2}}}$. Используя условия сопряжения для полей, получаем для определения неизвестных амплитуд ДИ следующие соотношения:
(8)
$\begin{gathered} {{{\mathbf{n}}}_{{1,2}}} \times \int\limits_0^{2\pi } {\left( {{\mathbf{E}}_{{1,2}}^{{N \bot }}\left( {{{\xi }_{l}},\varphi } \right) + {\mathbf{E}}_{{1,2}}^{{NL}}\left( {{{\xi }_{l}},\varphi } \right) - {\mathbf{E}}_{e}^{N}\left( {{{\xi }_{l}},\varphi } \right)} \right){{e}^{{ - jm\varphi }}}} d\varphi = {{{\mathbf{n}}}_{{1,2}}} \times \int\limits_0^{2\pi } {{{{\mathbf{E}}}_{0}}\left( {{{\xi }_{l}},\varphi } \right)} {{e}^{{ - jm\varphi }}}d\varphi ,{\text{ }} \\ {{{\mathbf{n}}}_{{1,2}}} \times \int\limits_0^{2\pi } {\left( {{\mathbf{H}}_{{1,2}}^{N}\left( {{{\xi }_{l}},\varphi } \right) - {\mathbf{H}}_{e}^{N}\left( {{{\xi }_{l}},\varphi } \right)} \right)} {{e}^{{ - jm\varphi }}}d\varphi = {{{\mathbf{n}}}_{{1,2}}} \times \int\limits_0^{2\pi } {{{{\mathbf{H}}}_{0}}\left( {{{\xi }_{l}},\varphi } \right){{e}^{{ - jm\varphi }}}d\varphi } ,{\text{ }}l = 1, \ldots ,K;\quad m = 1, \ldots ,M, \\ {{{\mathbf{n}}}_{{1,2}}} \cdot \int\limits_0^{2\pi } {\left( {{{\varepsilon }_{L}}{\mathbf{E}}_{{1,2}}^{{N \bot }}\left( {{{\xi }_{l}},\varphi } \right) + {{\varepsilon }_{L}}{\mathbf{E}}_{{1,2}}^{{NL}}\left( {{{\xi }_{l}},\varphi } \right) - {{\varepsilon }_{e}}{\mathbf{E}}_{e}^{N}\left( {{{\xi }_{l}},\varphi } \right)} \right){{e}^{{ - jm\varphi }}}d\varphi } = {{\varepsilon }_{e}}{{{\mathbf{n}}}_{{1,2}}} \cdot \int\limits_0^{2\pi } {{{{\mathbf{E}}}_{0}}({{\xi }_{l}},\varphi ){{e}^{{ - jm\varphi }}}d\varphi } . \\ \end{gathered} $Схема вычислительного алгоритма определения амплитуд ДИ $\left\{ {p_{{mn}}^{{e,i}};p_{{mn}}^{{L,i}};q_{{mn}}^{{e,i}};r_{n}^{{e,i}};r_{n}^{{L,i}}} \right\}$ заключается в использовании обобщенного метода коллокаций [27]. Точки коллокаций $\left\{ {{{\xi }_{l}}} \right\}_{{l = 1}}^{K}$ равномерно покрывают образующие поверхностей частиц, а число источников выбирается так, чтобы линейная система для каждой Фурье гармоники оказывалась переопределенной $5K > 2\left( {{{N}_{e}} + {{N}_{i}}} \right) + {{N}_{L}}$. Далее, проводится QR-факторизация матриц и последовательное псевдорешение систем для каждой гармоники для всего набора углов падения волны ${{\theta }_{0}}$ [28]. При необходимости вычисляется невязка граничных условий в промежуточных точках по отношению к точкам коллокаций [25].
Определив амплитуды ДИ, легко вычислить θ, φ компоненты диаграммы направленности рассеянного поля ${\mathbf{F}}(\theta ,\varphi )$ на единичной сфере $\Omega = \left\{ {0 \leqslant \theta \leqslant \pi ;\;0 \leqslant \varphi \leqslant 2\pi } \right\}$
(9)
$\begin{gathered} F_{\theta }^{{\text{P}}}\left( {\theta {\text{,}}\varphi } \right) = j{{k}_{e}}\sum\limits_{m = 0}^M {{{{\left( {j\sin \theta } \right)}}^{m}}{\text{co}}s\left\{ {\left( {m + 1} \right)\varphi } \right\} \sum\limits_{n = 1}^{N_{e}^{m}} { \left\{ { p_{{mn}}^{e}\cos \theta + q_{{nm}}^{e}} \right\}} } {\text{ exp}}\left\{ { - j{{k}_{e}}w_{n}^{e}\cos \theta } \right\} - \\ - \;j{{k}_{e}}\sin \theta \sum\limits_{n = 1}^{N_{e}^{0}} {{\text{ }}r_{n}^{e}{\text{ exp}}\left\{ { - j{{k}_{e}}w_{n}^{e}\cos \theta } \right\}{\text{, }}} \\ F_{\varphi }^{{\text{P}}}\left( {\theta {\text{,}}\varphi } \right){\text{ }} = - j{{k}_{e}}\sum\limits_{m = 0}^M {{{{\left( {j\sin \theta } \right)}}^{m}}{\text{sin}}\left\{ {\left( {m + 1} \right)\varphi } \right\}\sum\limits_{n = 1}^{N_{e}^{m}} { \left\{ { p_{{mn}}^{e} + q_{{nm}}^{e}\cos \theta } \right\}} } {\text{ exp}}\left\{ { - j{{k}_{e}}w_{n}^{e}\cos \theta } \right\}. \\ \end{gathered} $(10)
$\begin{gathered} F_{\theta }^{S}\left( {\theta {\text{,}}\varphi } \right) = j{{k}_{e}}\sum\limits_{m = 0}^M {{{{\left( {j\sin \theta } \right)}}^{m}}\sin \left\{ {\left( {m + 1} \right)\varphi } \right\} \sum\limits_{n = 1}^{N_{e}^{m}} { \left\{ { p_{{mn}}^{e}\cos \theta - q_{{nm}}^{e}} \right\}} } {\text{ exp}}\left\{ { - j{{k}_{e}}w_{n}^{e}\cos \theta } \right\}, \\ F_{\varphi }^{S}\left( {\theta {\text{,}}\varphi } \right) = j{{k}_{e}}\sum\limits_{m = 0}^M {{{{\left( {j\sin \theta } \right)}}^{m}}{\text{co}}s\left\{ {\left( {m + 1} \right)\varphi } \right\} \sum\limits_{n = 1}^{N_{e}^{m}} { \left\{ { p_{{mn}}^{e}\cos \theta - q_{{nm}}^{e}} \right\}} } {\text{ exp}}\left\{ { - j{{k}_{e}}w_{n}^{e}\cos \theta } \right\} - \\ + \;j{{k}_{e}}\sin \theta \sum\limits_{n = 1}^{N_{e}^{0}} {{\text{ }}r_{n}^{e}{\text{ exp}}\left\{ { - j{{k}_{e}}w_{n}^{e}\cos \theta } \right\}{\text{.}}} \\ \end{gathered} $4. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
Нас будет интересовать сечение рассеяния, которое представляет собой суммарную интенсивность рассеянного поля
(11)
$\sigma _{{scs}}^{{P,S}}({{\theta }_{0}}) = \int\limits_{{{\Omega }_{{}}}} {DSC_{{}}^{{P,S}}{\text{ (}}{{\theta }_{0}},\theta ,\varphi {\text{)}}} d\omega {\kern 1pt} ,$(12)
$\sigma _{{ext}}^{P}({{\theta }_{0}}) = - \frac{{4\pi }}{{{{k}_{e}}}}\operatorname{Im} F_{\theta }^{P}(\pi - {{\theta }_{0}},\pi );\quad \sigma _{{ext}}^{S}({{\theta }_{0}}) = \frac{{4\pi }}{{{{k}_{e}}}}\operatorname{Im} F_{\varphi }^{S}(\pi - {{\theta }_{0}},\pi ).$В качестве формы частиц будем рассматривать вытянутые сфероиды, эквиобъемный диаметр каждого D = 12 нм, задавая в качестве исходных параметров соотношение осей сфероидов $r = a{\text{/}}b > 1$ и величину расстояния между частицами – d, т.е. величину зазора. Прежде чем переходить к описанию численных результатов, отметим, что основной вычислительной проблемой при учете продольных волн является весьма существенное различие величин продольного ${{k}_{L}}$ и поперечного волновых ${{k}_{e}}$ чисел. Например, в рассматриваемом ниже диапазоне длин волн это различие доходило до значения ${{\left| {{{k}_{L}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{k}_{L}}} \right|} {{{k}_{e}}}}} \right. \kern-0em} {{{k}_{e}}}} \approx 200$, что определяет существенно различный характер поведения полей. В то время, как для поперечного волнового числа отношение ${{\left| {{{k}_{i}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{k}_{i}}} \right|} {{{k}_{e}}}}} \right. \kern-0em} {{{k}_{e}}}}$на превышало 20. Таким образом, оказывается, что продольная волна осциллирует в 10 раз чаще, чем поперечная, что влечет за собой существенное возрастание необходимого для достижения приемлемой точности числа точек коллокаций K по сравнению с локальным случаем [25].
В нашей предыдущей публикации [35], посвященной классической модели линейного кластера плазмонных частиц, было установлено, что можно управлять положением и амплитудой ПР в оптическом диапазоне, варьируя три основных параметра: D – эквиобъемный диаметр частиц, r – вытянутость, d – величину зазора. За счет этого можно обеспечить нужное расположение ПР в широком диапазоне длин волн.
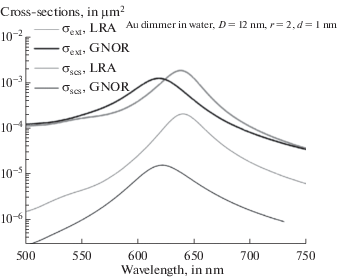
Перейдем к описанию результатов моделирования. На фиг. 1 приведены спектральные оптические характеристики: сечение экстинкции $\sigma _{{ext}}^{P}{\text{ }}$ и рассеяния $\sigma _{{scs}}^{P}$ для сфероидов с соотношением осей $r = 2$ и зазором d = 1 нм при направлении падения плоской волны перпендикулярно оси сфероидов (${{\theta }_{0}} = 90^\circ $). Из рисунка видно, что максимумы ПР для GNOR сдвинуты в коротковолновую область (blue shift) по сравнению с локальным случаем (LRA). Кроме того, очевидно существенное увеличение различия в амплитудах ПР между сечением экстинкции и сечением рассеяния для GNOR по сравнению с локальным случаем.
Фиг. 1.
$\sigma _{{ext}}^{P}(\lambda )$ и $\sigma _{{scs}}^{P}(\lambda )$ с учетом ОНО (GNOR) и без учета (LRA) для золотых (Au) сфероидов $D = 12$ нм, $r = 2$, d = 1 нм, при угле падения плоской волны перпендикулярно оси сфероидов ${{\theta }_{0}} = 90^\circ $.
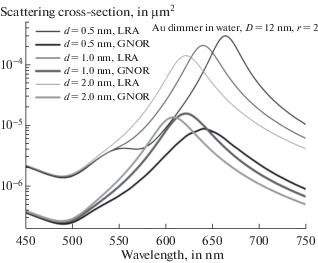
Фиг. 2 посвящена анализу сечения рассеяния (11) для сфероидов с $r = 2$ при различных значениях размеров зазора d. Как видно из рисунка, при уменьшении зазора различие между локальным и нелокальным ПР усиливается, при этом возрастают как величина сдвига максимума, так и различие в амплитудах. На фиг. 3 приведены значения $\sigma _{{scs}}^{P}$ при зазоре d = 1 нм для различных значений вытянутости сфероидов $r$. Из рисунка явствует, что увеличение вытянутости ведет к возрастанию амплитуды ПР. Таким образом, следует заключить, что альтернативным уменьшению зазора может служить путь по увеличению вытянутости составляющих элементов, который может привести к лучшим результатам в смысле возрастания интенсивности рассеяния. Аналогичные предыдущему результаты, но для относительной интенсивности поля ${{\left| {{{{\mathbf{E}}}_{e}} + {{{\mathbf{E}}}_{0}}} \right|}^{2}}{\text{/}}{{\left| {{{{\mathbf{E}}}_{0}}} \right|}^{2}}$ в центре зазора между частицами, можно видеть на фиг. 4, 5. Здесь также видна альтернатива уменьшению зазора для усиления ближнего поля (т.н. hot spot), которая состоит в увеличении вытянутости сфероидов.
Фиг. 2.
$\sigma _{{scs}}^{P}(\lambda )$ с учетом и без учета ОНО для Au сфероидов $D = 12$ нм, $r = 2$, при угле падения ${{\theta }_{0}} = 90^\circ $, для различных расстояний между сфероидами $d = 0.{\text{5, 1}}{\text{.0, 2}}{\text{.0}}\;{\text{н м }}$.
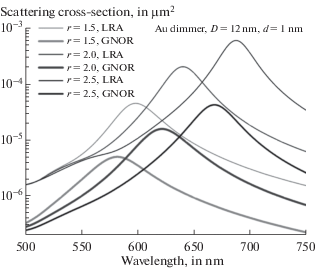
Фиг. 3.
$\sigma _{{scs}}^{P}(\lambda )$ с учетом и без учета ОНО. $D = 12$ нм, d = 1 нм, ${{\theta }_{0}} = 90^\circ $ для сфероидов различной вытянутости $r = {\text{1}}{\text{.5, 2}}{\text{.0, 2}}{\text{.5}}$.
Фиг. 4.
Относительная интенсивность полного поля ${{\left| {{{{\mathbf{E}}}_{e}} + {{{\mathbf{E}}}_{0}}} \right|}^{2}}{\text{/}}{{\left| {{{{\mathbf{E}}}_{0}}} \right|}^{2}}$ в точке посередине между сфероидами с учетом и без учета ОНО. $D = 12$ нм, $r = 2$, ${{\theta }_{0}} = 90^\circ $ для различных расстояний между сфероидами $d = 0.{\text{5, 1}}{\text{.0, 2}}{\text{.0н м }}$.

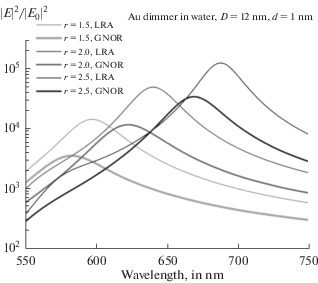
Фиг. 5.
${{\left| {{{{\mathbf{E}}}_{e}} + {{{\mathbf{E}}}_{0}}} \right|}^{2}}{\text{/}}{{\left| {{{{\mathbf{E}}}_{0}}} \right|}^{2}}$с учетом и без учета ОНО. $D = 12$ нм, $r = 2$, d = 1 нм, ${{\theta }_{0}} = 90^\circ $ для сфероидов различной вытянутости $r = {\text{1}}{\text{.5, 2}}{\text{.0, 2}}{\text{.5}}$.
5. ЗАКЛЮЧЕНИЕ
Метод дискретных источников был модифицирован применительно к анализу влияния эффекта нелокального экранирования на рассеивающие свойства линейного кластера несферических плазмонных наночастиц с субнанометровом зазором. Показано, что деформация частиц и уменьшение зазора приводят к усилению влияния эффекта нелокальности, что вызывает сдвиг плазмонного резонанса в коротковолновую область и уменьшение его амплитуды. При этом оказывается, что усиление интенсивности как рассеянного, так и ближнего полей блокируется эффектом нелокального экранирования и альтернативой уменьшению зазора может служить увеличение линейного размера составляющих элементов. Полученные результаты могут использоваться при проектировании перспективных устройств нанофотоники, в частности применительно к исследованию процессов флюоресценции и рамановской спектроскопии.
Список литературы
Майер С.А. Плазмоника. Теория и приложения. М.–Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2011.
Климов В.В. Наноплазмоника. Физматлит, 2009.
Duan H., Fernàndez-Domínguez A.I., Bosman M., Maier S.A., Yang J.K.W. // Nano Lett., Nanoplasmonics: classical down to the nanometer scale. Nano Lett. 2012. V. 12. P. 1683–1689.
Kern J. Großmann S., Tarakina N.V., Häcke T. et al. Atomic-scale confinement of resonant optical fields // Nano Lett. 2012. V. 12. P. 5504–5509.
Manfrinato V.R., Zhang L., Su D., Dua H. et al. Resolution limits of electron-beam lithography toward the atomic scale // Nano Lett. 2013. V. 13. P. 1555–1558.
Mertens J., Eiden A.L., Sigle D.O., Huang F. et al. Controlling subnanometer gaps in plasmonic dimers using graphene // Nano Lett. 2013. V. 13. P. 5033–5038.
García de Abajo, F.J.J. Nonlocal effects in the plasmons of strongly interacting nanoparticles, dimers, and waveguides // Phys. Chem. C. 2008. V. 112. P. 17983–17987.
Toscano G., Raza S., Jauho A., Mortensen N.A., Wubs M. Modified field enhancement and extinction by plasmonic nanowire dimers due to nonlocal response // Opt. Express, 2012. V. 20. P. 4176–4188.
Stella L., Zhang P., García-Vidal F.J., Rubio A., García-Gonzàlez P. Performance of nonlocal optics when applied to plasmonic nanostructures // J. Phys. Chem. C. 2013. V. 117. P. 8941–8949.
Cirací C., Hill R.T., Mock J.J., Urzhumov Y. et al. Probing the ultimate limits of plasmonic enhancement // Science. 2012. V. 337. P. 1072–1074.
Bochterle J., Neubrech F., Nagao T., Pucci A. Angstrom-scale distance dependence of antenna-enhanced vibrational signals // ACS Nano. 2012. V. 6. P. 10917–10923.
Fuchs R., Claro F. Multipolar response of small metallic spheres: nonlocal theory // Phys. Rev. B. 1987. V. 35. P. 3722–3727.
Pitarke J.M., Silkin V.M., Chulkov E.V., Echenique P.M. Theory of surface plasmons and surface-plasmon polaritons // Rep. Prog. Phys. 2007. V. 70. P. 1–87.
Teperik T.V., Nordlander P., Aizpurua J., Borisov A.G. Robust subnanometric plasmon ruler by rescaling of the nonlocal optical response // Phys. Rev. Lett. 2013. V. 110. № 263901.
Toscano G., Straubel J., Kwiatkowski A., Rockstuhl C. et al. Resonance shifts and spill-out effects in self-consistent hydrodynamic nanoplasmonics // Nat. Commun. 2015. V. 6. № 7132.
Pelton M., Bryant G. Introduction to Metal-Nanoparticle Plasmonics. Wiley. 2013.
Raza S., Bozhevolnyi S.I., Wubs M., Mortensen A.N. Nonlocal optical response in metallic nanostructures // J. Phys. Condens. Matter. 2015. V. 27. № 183204.
Esteban R., Zugarramurdi A., Zhang P., Nordlander P. et al. A classical treatment of optical tunneling in plasmonic gaps: extending the quantum corrected model to practical situations // Faraday Discuss. 2015. V. 178. P. 151–183.
Zhu W., Esteban R., Borisov A.G., Baumberg J.J. et al. Quantum mechanical effects in plasmonic structures with subnanometre gaps. Review // Natur Commun. 2016. V. 7. № 11495.
Savage K.J., Hawkeye M.M., Esteban R. Borisov A.G. et al. Revealing the quantum regime in tunnelling plasmonics // Nature. 2012. V. 491. P. 574–577.
Лифшиц Е.М., Питаевский Л.П. Физическая кинетика. М.: Наука, 1978. 167 c.
Mortensen N.A. Nonlocal formalism for nanoplasmonics: phenomenological and semi-classical considerations // Phot. Nanostr. 2013. V. 11. P. 303–316.
Wubs M., Mortensen A. Nonlocal Response in Plasmonic Nanostructures/Quantum Plasmonics. S.I. Bozhevolnyi (eds.), Springer, Switzerland. 2017. P. 279–302.
Tserkezis Ch., Yan W., Hsieh W., Sun G. et al. On the origin of nonlocal dumping in plasmonic monomers and dimmers // Int. J. Mod. Phys. B. 2017. V. 31. № 17400005.
Еремин Ю.А., Свешников А.Г. Компьютерная технология анализа задач рассеяния на основе метода дискретных источников // ЖВМиМФ. 2000. Т. 40. № 12. С. 1842–1856.
Еремин Ю.А., Свешников А.Г. Математическая модель учета эффекта нелокальности плазмонных структур на основе метода дискретных источников // ЖВМиМФ. 2018. Т. 58. № 4. С. 586–594.
Бахвалов Н.С. Численные методы. М.: Наука, 1975.
Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.
Newton R.G. Scattering Theory of Waves and Particles. McGraw Hill, 1966.
http://www.refractiveindex.info.
Raza S., Wubs M., Bozhevolnyi S.I., Mortensen N.A. Nonlocal study of ultimate plasmon hybridization // Opt. Lett. 2015. V. 40. № 5. P. 839–842.
Cacciola A., Iatí M.A., Saija R., Borghese F. et al. How nonlocal damping reduces plasmon-enhanced fluorescence in ultranarrow gaps // J. Quantit. Spectr. Radiat. Trans. 2017. V. 195. P. 97–106.
Tserkezis C., Mortensen N.A., Wubs M. How nonlocal damping reduces plasmon-enhanced fluorescence in ultranarrow gaps // Phys. Rev. B. 2017. V. 96. № 085413.
Roller E.-M. Besteiro L.V., Pupp C., Khorashad L.K. et al. Hotspot-mediated non-dissipative and ultrafast plasmon passage // Nat. Phys. 2017. V. 13. P. 761–765.
Гришина Н.В., Еремин Ю.А., Свешников А.Г. Анализ плазмонных резонансов близко расположенных частиц методом дискретных источников // Оптика и спектроскопия. 2012. Т. 113. № 4. С. 484–489.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики


