Журнал вычислительной математики и математической физики, 2019, T. 59, № 12, стр. 2077-2085

О методах, основанных на решении вариационных и краевых задач для уравнений в частных производных для аккуратной аппроксимации функции расстояния до поверхности

А. Г. Беляев^1, 2, *, П.-А. Файоль^1, 2, **

¹ Computer Graphics Laboratory, University of Aizu
Aizu-Wakamatsu, Japan

² Institute of Sensors, Signals and Systems, School of Engineering & Physical Sciences Heriot-Watt University
Edinburgh, UK

^* E-mail: a.belyaev@hw.ac.uk
^** E-mail: fayolle@u-aizu.ac.jp

Поступила в редакцию 01.07.2019
После доработки 01.07.2019
Принята к публикации 05.08.2019

DOI: 10.1134/S0044466919120068

Полный текст (PDF)

Аннотация

В статье рассматривается новая вариационная задача для аппроксимации функции расстояния до поверхности (кривой в двумерном случае), ограничивающей область. Показано, что задача может быть эффективно решена методом переменных направлений множителей Лагранжа. Проанализированы связи между рассматриваемой задачей и задачами степенной диффузии ($p$-Laplacian diffusion). Преимущества предложенного метода для аппроксимации функции расстояния продемонстрированы численно. Библ. 24. Фиг. 5.

Ключевые слова: вариационная задача, аппроксимация функции расстояния до поверхности, задача степенной диффузии, метод переменных направлений множителей Лагранжа.

ВВЕДЕНИЕ

Быстрая и аккуратная аппроксимация функции расстояния до поверхности (до кривой в двумерном случае) важна для многих прикладных задач, включая задачи, возникающие при применении метода линий уровня (пересчет функции расстояния до эволюционирующей линии/поверхности уровня) [1], модели турбулентности, использующие так называемое расстояние до стенки [2], [3], задачи моделирования неоднородных материалов в вычислительной механике [4], задачи нахождения срединных осей (скелетов) фигур и их применения в построении сеток [5], задачи, связанные с методами конечных элементов [6], [7], задачи навигации роботов [8], а также различные задачи, возникающие в исследованиях по компьютерной графике и геометрическому моделированию [9]–[11]. В настоящие время аппроксимация функции расстояния при помощи вариационных методов и методов, основанных на решении уравнений в частных производных, получает все большее распространение [12]–[16].

В настоящей работе мы развиваем вариационные методы и методы, основанные на уравнениях в частных производных, для аккуратной аппроксимации функции расстояния. В частности, мы предлагаем новый простой вариационный принцип для функции расстояния. Соответствующая вариационная задача решается численно методом переменных направлений множителей Лагранжа (ADMM) [17]. Мы также показываем, что похожая вариационная задача может быть сформулирована для $p$-лапласиана и численно решена при помощи ADMM. Решение этой задачи для $p$-лапласиана также доставляет аппроксимацию функции расстояния.

Мы исследуем и оцениваем предложенные вариационные задачи и рассматриваем их применение для оценки функции расстояния до полигональных кривых на плоскости и полиэдрических поверхностей в пространстве.

Настоящая статья является расширенной версией нашей работы [18], представленной на конференции NUMGRID 2018.

1. ВАРИАЦИОННАЯ АППРОКСИМАЦИЯ ФУНКЦИИ РАССТОЯНИЯ

Рассмотрим ограниченную область $\Omega \subset {{\mathbb{R}}^{m}}$ (на практике мы имеем дело с $m = 2$ или $m = 3$) с границей $\partial \Omega $, ориентированной при помощи внешней нормали $n$. Обозначим $\left| q \right|$ длину вектора $q = {{({{q}_{1}}, \ldots ,{{q}_{m}})}^{ \top }}$, $\left| q \right| = \sqrt {q_{1}^{2} + \ldots + q_{m}^{2}} $. Пусть $d(x)$ обозначает функцию расстояния до $\partial \Omega $. Известно, что функция расстояния удовлетворяет уравнению эйконала

(1)

$\left| {\nabla d} \right| = 1\quad {\text{на}}\quad \Omega $

и краевым условиям на границе

(2)

$d = 0,\quad \partial d{\text{/}}\partial n = 1\quad {\text{и}}\quad {{\partial }^{k}}d{\text{/}}\partial {{n}^{k}} = 0,\quad k = 2,3, \ldots \quad {\text{на}}\quad \partial \Omega .$

Обычно (1) используется с первым из краевых условий (условие Дирихле), упомянытых в (2), поскольку уравнение эйконала (1) вместе с условием Дирихле на границе $d = 0$ на $\partial \Omega $ влекут остальные краевые условия (2).

1.1. Предложенная аппроксимация функции расстояния

Наше главное наблюдение можно сформулировать следующим образом.

Предложение 1. Функция расстояния $d(x)$ является решением для следующей вариационной задачи минимизации

(3)

$\int\limits_\Omega {\phi dx} \; \to \;max,\quad где\quad \mathop {max}\limits_{{\mathbf{x}} \in \Omega } \left| {\nabla \phi } \right| \leqslant 1\quad и\quad \phi = 0\quad на\quad \partial \Omega .$

Доказательство. Действительно, для того, чтобы максимизировать $\int_\Omega \,\phi dx$, фукция $\phi (x)$ должна расти как можно быстрее, и, значит, ее градиент $\left| {\nabla \phi } \right|$ в каждой точке $x$ достигает своего максимального допустимого значения. Таким образом, решение (3) удовлетворяет

$\left| {\nabla \phi } \right| = 1\quad {\text{в}}\quad \Omega \quad {\text{и}}\quad \phi = 0\quad {\text{на}}\quad \partial \Omega .$

Это означает, что решение является функцией расстояния $d(x)$.

Для того чтобы решить (3) численно, мы сначала переформулируем эту задачу в следующую задачу без ограничений:

(4)

$F(\phi ) + G(\nabla \phi ) \to min,$

где

$F(\phi ) = - \int\limits_\Omega {\phi dx} ,\quad \phi = 0\quad {\text{на}}\quad \partial \Omega ,\quad G(q) = \left\{ \begin{gathered} 0,\quad {\text{если}}\quad {{\left\| q \right\|}_{{{{L}^{\infty }}}}} \leqslant 1, \hfill \\ + \infty \quad {\text{иначе}}{\text{.}} \hfill \\ \end{gathered} \right.$

Задача минимизации (4) решается численно при помощи ADMM. Соответствующий лагранжиан может быть записан в виде

(5)

$L(\phi ,q,\sigma ) = \int\limits_\Omega {\left( { - \phi + G(q) + \sigma (\nabla \phi - q) + \frac{r}{2}{{{\left| {\nabla \phi - q} \right|}}^{2}}} \right)} {\kern 1pt} dx,$

где $\sigma $ обозначает вектор множителей Лагранжа, а $r > 0$ является параметром регуляризации. Применение ADMM к (5) ведет к следующим итерациям:

repeat

(1) Minimize (5) w.r.t. $\phi (x)$ by solving

$ - r(\Delta {{\phi }_{{k + 1}}} - {\text{div}}{{q}_{k}}) = 1 + {\text{div}}\mathop \sigma \nolimits_k \quad {\text{in}}\quad \Omega ,\quad {{\phi }_{{k + 1}}} = 0\quad {\text{on}}\quad \partial \Omega ;$

(2) Perform the projection ${{q}_{{k + 1}}} = {{P}_{B}}\left( {\nabla {{\phi }_{{k + 1}}} + \mathop \sigma \nolimits_k {\text{/}}r} \right)$, where

${{P}_{B}}({\text{z}}) = \left\{ \begin{gathered} z,\quad {\text{if}}\quad \left\| z \right\| \leqslant 1, \hfill \\ z{\text{/}}\left\| z \right\|,\quad {\text{otherwise;}} \hfill \\ \end{gathered} \right.$

(3) Update the Lagrange multipliers by

$\mathop \sigma \nolimits_{k + 1} = \mathop \sigma \nolimits_k + r\left( {\nabla {{\phi }_{{k + 1}}} - {{q}_{{k + 1}}}} \right)$;

until convergence

1.2. Аппроксимация функции расстояния через $p$-лапласиан диффузии

Результаты, полученные в [19], [20], показывают, что $d(x)$ может быть приближена решением следующей задачи для $p$-лапласиана:

(6)

$ - {{\Delta }_{p}}u = 1\quad {\text{в}}\quad \Omega ,\quad u = 0\quad {\text{на}}\quad \partial \Omega ,$

где ${{\Delta }_{p}}u = \nabla \cdot ({{\left| {\nabla u} \right|}^{{p - 2}}}\nabla u)$ обозначает $p$-лапласиан, $p \geqslant 2$, и $p$ выбрано достаточно большим. Численные эксперименты, выполненные в [14], [21], показывают, что решения (6) доставляют достаточно аккуратные аппроксимации функции расстояния. Наша цель сейчас состоит в установлении связи между (6) для больших значений $p$ и вариационной задачей (3).

Напишем вариационную задачу минимизации, соответствующую (6),

(7)

$E(v) \equiv \frac{1}{p}{{\int\limits_\Omega {\left| {\nabla v} \right|} }^{p}}dx - \int\limits_\Omega {vdx} \to min,\quad v = 0\quad {\text{на}}\quad \partial \Omega .$

Предложение 2. Вариационная задача (7) эквивалентна следующей задаче минимизации

(8)

$\int\limits_\Omega {\phi dx} \to max,\quad где\quad {{\left\| {\nabla \phi } \right\|}_{{{{L}^{p}}(\Omega )}}} = 1\quad и\quad \phi = 0\quad на\quad \partial \Omega .$

Доказательство. Рассмотрим $E(tv)$ как функцию от действительного числа $t$ и минимизируем ее по $t$ (легко видеть, что это соответствует методу Ритца, примененного в случае только одной базисной функции $v({\text{x}})$). Получаем

$E(tv) = \frac{{{{t}^{p}}}}{p}{{\int\limits_\Omega {\left| {\nabla v} \right|} }^{p}}dx - t\int\limits_\Omega {vdx} ,$

$\frac{{dE(tv)}}{{dt}} = {{t}^{{p - 1}}}{{\int\limits_\Omega {\left| {\nabla v} \right|} }^{p}}dx - \int\limits_\Omega {vdx} = 0,\quad {{t}_{0}} = \mathop {\left( {{{\int\limits_\Omega {vdx} } \mathord{\left/ {\vphantom {{\int\limits_\Omega {vdx} } {{{{\int\limits_\Omega {\left| {\nabla v} \right|} }}^{p}}dx}}} \right. \kern-0em} {{{{\int\limits_\Omega {\left| {\nabla v} \right|} }}^{p}}dx}}} \right)}\nolimits^{\tfrac{1}{{p - 1}}} ,$

$E({{t}_{0}}v) = - \frac{{p - 1}}{p}{{\mathop {\left( {\int\limits_\Omega {vdx} } \right)}\nolimits^{\tfrac{p}{{p - 1}}} } \mathord{\left/ {\vphantom {{\mathop {\left( {\int\limits_\Omega {vdx} } \right)}\nolimits^{\tfrac{p}{{p - 1}}} } {\mathop {\left( {{{{\int\limits_\Omega {\left| {\nabla v} \right|} }}^{p}}dx} \right)}\nolimits^{\tfrac{1}{{p - 1}}} }}} \right. \kern-0em} {\mathop {\left( {{{{\int\limits_\Omega {\left| {\nabla v} \right|} }}^{p}}dx} \right)}\nolimits^{\tfrac{1}{{p - 1}}} }}.$

Заметим, что минимизация $E(tv)$ сначала по $t$, а затем по $v$ эквивалентна (7). Другими словами, (7) эквивалентно следующей вариационной задаче:

(9)

${{\mathop {\left( {\int\limits_\Omega {vdx} } \right)}\nolimits^p } \mathord{\left/ {\vphantom {{\mathop {\left( {\int\limits_\Omega {vdx} } \right)}\nolimits^p } {{{{\int\limits_\Omega {\left| {\nabla v} \right|} }}^{p}}dx \to max,}}} \right. \kern-0em} {{{{\int\limits_\Omega {\left| {\nabla v} \right|} }}^{p}}dx \to max,}}\quad v = 0\quad {\text{на}}\quad \partial \Omega ,$

которая в свою очередь может быть записана в виде (8), если положить $\phi = v{\text{/}}{{\left\| {\nabla v} \right\|}_{{{{L}^{p}}(\Omega )}}}$.

Для случая $p = 2$ похожий результат получен в [22, § 5.2] в связи с исследованием жесткости кручения стрежня.

Поскольку (8) эквивалентно следующей задаче

(10)

$\int\limits_\Omega {\phi dx} \to max,\quad {\text{где}}\quad {{\left\| {\nabla \phi } \right\|}_{{{{L}^{p}}(\Omega )}}} \leqslant 1\quad {\text{и}}\quad \phi = 0\quad {\text{на}}\quad \partial \Omega ,$

то становится ясно, что функция расстояния аппроксимируется решением задачи для $p$-лапласиана: если устремить $p$ к $\infty $, то (10) превратится в (3).

Решение задачи (6) доставляет минимум в следующей вариационной задаче минимизации:

(11)

$\int\limits_\Omega {\frac{1}{p}} {{\left| {\nabla \phi } \right|}^{p}}dx - \int\limits_\Omega {\phi dx} \to min.$

Для численного решения (11) при помощи ADMM введем лагранжиан

(12)

$L(\phi ,q,\sigma ) = \int\limits_\Omega \,\left( { - \phi + \frac{1}{p}{{{\left| q \right|}}^{p}} + \sigma \cdot (q - \nabla \phi ) + \frac{r}{2}{{{\left| {\nabla \phi - q} \right|}}^{2}}} \right)dx{\text{,}}$

где $r > 0$ является регуляризационным параметром, а $\sigma $ обозначает вектор множителей Лагранжа.

Аналогично тому, как мы уже это делали, применим ADMM минимизацию (12). Первый и последний шаги в каждой итерации остаются без изменения. Второй шаг состоит в минимизации по $\sigma $ в то время как $\phi $ и $\sigma $ зафиксированы. В этом случае оптимальное значение $q$ пропорционально $\nabla \phi - \sigma {\text{/}}r$ и легко может быть найдено в виде $q(x) = c(x)(\nabla \phi (x) - \sigma (x){\text{/}}r)$, где $c(x)$ – некоторая функция от $x$. Это приведет нас к следующей простой задаче минимизации:

$\frac{1}{p}{{c}^{p}}\mathop {\left| {\nabla \phi - \frac{\sigma }{r}} \right|}\nolimits^p + \frac{r}{2}\mathop {\left| {\nabla \phi - \frac{\sigma }{r}} \right|}\nolimits^2 {{(c - 1)}^{2}} \to min,$

которая в свою очередь сводится к решению уравнения при фиксированном $x$

(13)

$f(c) \equiv {{c}^{{p - 1}}}\mathop {\left| {\nabla \phi - \frac{\sigma }{r}} \right|}\nolimits^{p - 2} + r(c - 1) = 0.$

Для любого фиксированного $x$ многочлен $f(c)$ в (13) имеет корень $[0,1]$, поскольку $f(0) < 0$ и $f(1) > 0$. В [23] использовались простые итерации метода Ньютона, которые начинались с некоторого ${{c}_{0}}(x)$ выбранного эвристически. В настоящей работе мы используем уточнения ньютоновских итераций, предложенные Чебышёвым (см., например, [24])

(14)

${{c}_{{k + 1}}} = {{c}_{k}} - \frac{{f({{c}_{k}})}}{{f{\kern 1pt} '({{c}_{k}})}} - \frac{{f{\kern 1pt} '{\kern 1pt} '({{c}_{k}}){{f}^{2}}({{c}_{k}})}}{{2{{{[f{\kern 1pt} '({{c}_{k}})]}}^{3}}}}$

или

(15)

${{c}_{{k + 1}}} = {{c}_{k}} - \frac{{f({{c}_{k}})}}{{f{\kern 1pt} '({{c}_{k}})}} - \frac{{f\left( {{{c}_{k}} - f({{c}_{k}}){\text{/}}f{\kern 1pt} '({{c}_{k}})} \right)}}{{f{\kern 1pt} '({{c}_{k}})}}$

и начинаем с ${{c}_{1}} = 1$ (или 0). Для численного решения (13) применение этих чебышевских итераций ведет к улучшению сходимости по сравнению с классическим методом Ньютона.

Таким образом, приходим к следующей итеративной схеме для аппроксимации функции расстояния путем численного решения задачи (6)

repeat

(1) Minimize (12) w.r.t. $\phi (x)$ by solving

$ - r(\Delta {{\phi }_{{k + 1}}} - {\text{div}}{{q}_{k}}) = 1 + {\text{div}}\mathop \sigma \nolimits_k \quad {\text{in}}\quad \Omega ;\quad {{\phi }_{{k + 1}}} = 0\quad {\text{on}}\quad \partial \Omega ;$

(2) Compute numerically the root in $[0,1]$ to

${{c}^{{p - 1}}}\mathop {\left| {\nabla \phi - \tfrac{\sigma }{r}} \right|}\nolimits^{p - 2} + r(c - 1) = 0\quad {\text{by either }}({\text{14}}){\text{ or }}({\text{15}}){\text{;}}$

(3) Update the Lagrange multipliers by

$\mathop \sigma \nolimits_{k + 1} = \mathop \sigma \nolimits_k + r(\nabla {{\phi }_{{k + 1}}} - {{q}_{{k + 1}}});$

until convergence

Отметим схожесть между двумя предложенными алгоритмами. Оба они основаны на ADMM. Разница состоит в том, что для второго шага в минимизации (12) при помощи ADMM требуется численно найти корень уравнения (13), в то время как соответствующий шаг в численном решении (4) использует простую проекцию.

Аппроксимацию функции расстояния посредством решения ${{u}_{p}}(x)$ задачи (6) можно существенно улучшить около границы $\partial \Omega $. Рассмотрим следующую процедуру нормализации:

(16)

${{v}_{p}}(x) = - {{\left| {\nabla {{u}_{p}}} \right|}^{{p - 1}}} + \mathop {\left[ {\frac{p}{{p - 1}}{{u}_{p}} + {{{\left| {\nabla {{u}_{p}}} \right|}}^{p}}} \right]}\nolimits^{\tfrac{{p - 1}}{p}} ,$

для которой получаем

(17)

${{v}_{p}} = 0\quad {\text{и}}\quad \partial {{v}_{p}}{\text{/}}\partial n = 1\quad {\text{на}}\quad \partial \Omega .$

Нормализация (16) была предложена в [14] и недавно успешно использовалась в [21] для расчета эффектов турбулентности.

2. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

2.1. Дискретизация

Рассмотренные итеративные схемы для минимизации (4) и (11) базируются на численном решении задачи Дирихле для уравнения Пуассона

(18)

$ - \Delta \phi (x) = f(x)\quad {\text{в}}\quad \Omega ,\quad \phi = 0\quad {\text{на}}\quad \partial \Omega ,$

где $f(x)$ – некоторая заданная функция. Численное решение (18) сводится к решению системы линейных уравнений

(19)

$A\Phi = F,$

где матрица $A$, доставляющая дискретную аппроксимацию Лапласиана $\Delta $, является разреженной и остается одной и той же для каждой итерации ADMM. Таким образом, обе рассмотренные схемы достаточно эффективны численно, поскольку $A$ в (19) должна быть факторизована лишь однажды (в наших вычислениях мы используем разложение Холецкого для факторизации $A$).

В наших экспериментах мы рассматривавем двумерные области, ограниченные ломаными, и трехмерные области, ограниченные треугольными сетками. Соответственно мы оцениваем функцию расстояния до ломаной в двумерном случае и до треугольной сетки в трехмерном случае. Задача Пуассона, возникающая при решении (4) при помощи ADMM, решается с помощью метода конечных элементов с линейными базисными функциями.

2.2. Сравнение с точной функцией расстояния

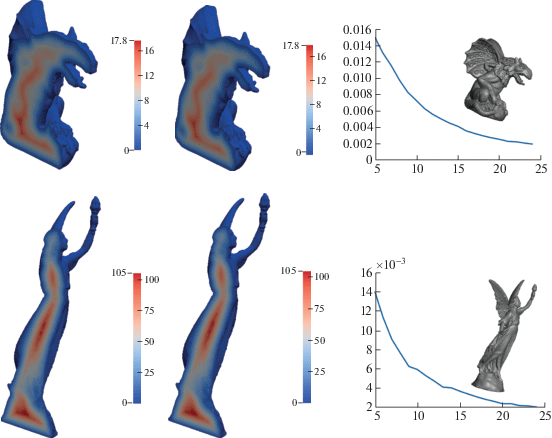
Фиг. 1 и 2 демонстрируют результаты, полученные для двумерных и трехмерных областей с относительно сложной геометрией. На фигурах левые изображения соответствуют точной функции расстояния, полученной путем вычисления минимального расстояния от данной точки до граничных отрезков (треугольников в трехмерном случае). Средние изображения представляют функцию расстояния, полученную посредством применения ADMM итераций к (4). В трехмерном случае левые и средние изображения демонстрируют линии уровня функции расстояния на двумерных срезах трехмерных областей. Правые изображения показывают как графики относительной ошибки

${{\left\| {{{\phi }_{{k + 1}}} - {{\phi }_{k}}} \right\|}_{2}}{\text{/}}{{\left\| {{{\phi }_{k}}} \right\|}_{2}}$

уменьшаются с каждой итерацией ADMM. Таким образом, мы можем заключить, что численное решение (4) при помощи ADMM итераций демонстрирует хорошую сходимость и ведет к аккуратной аппроксимации функции расстояния.

Фиг. 1.

Слева: точная функция расстояния до границы области, полученная путем вычисления минимального расстояния от данной точки до граничных отрезков. В середине: функция расстояния, полученная посредством применения ADMM итераций к (4). Справа: график зависимости относительной ошибки от количества ADMM итераций.

Фиг. 2.

Сравнение точной функции расстояния и ее аппроксимации на примере двух тетраэдрических сеток, представляющих трехмерные модели Горгулья и Люси. Слева: точная функция расстояния до границы области, полученная путем вычисления минимального расстояния от данной точки до граничных треугольников. В середине: функция расстояния, полученная посредством применения ADMM итераций к (4). Справа: график зависимости относительной ошибки от количества ADMM итераций.

2.3. Сравнение с аппроксимацией функции расстояния при помощи $p$-лапласиана

Фиг. 3 демонстрирует аппроксимацию функции расстояния внутри двумерной области при помощи решения (6), а также нормализации (16) для различных значений $p$ (одинаковая цветовая карта используется для различных значений параметра $p$).

Фиг. 3.

Верхний ряд: аппроксимация функции расстояния решениями задачи (6) для $p$-Лапласиана при $p = 2,5$ и $15$; чем больше значение $p$, тем более аккуратная аппроксимация получается. Нижний ряд: применение нормализации (16) к решениям (6) ведет к улучшению аппроксимации функции расстояния (используются те же значения $p = 2,5$ и $15$).

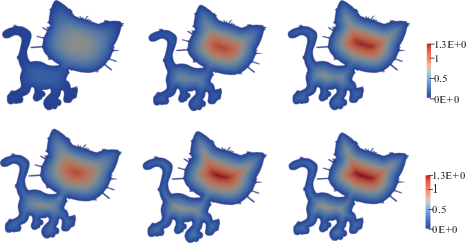
Отметим, что для малых значений $p$-нормализация (16) существенно улучшает аппроксимацию функции расстояния. Это можно увидеть, сравнивая, например, верхний и нижний левые изображения фиг. 3.

На фиг. 4 дано сравнение функции расстояния, полученной при помощи (4) с аппроксимациями, соответствующими решениям задачи Дирихле для $p$-лапласиана (6). Среднее изображение фиг. 4 соответствует численному решению (6) при помощи ADMM для $p = 15$ (см. разд. 2). Решение уже само по себе хорошо аппроксимирует функцию расстояния. Как продемонстрировано на правом изображении фиг. 4, нормализация (16) улучшает аппроксимацию. Левое изображение соответствует функции расстояния, полученной посредством решения (4) при помощи ADMM.

Фиг. 4.

Слева: решение задачи (4). В середине: решение задачи (6) для $p$-Лапласиана при $p = 15$; Справа: после применения нормализации (16).

Как показано на фиг. 5, аналогичные результаты получаются в трехмерном случае. Численные решения вариационной задачи (4) для двух областей показаны на левых изображениях. Средние изображения соответствуют решению (6) для $p = 15$. Решения (6), нормализированные при помощи (16), представлены правыми изображениями. Линии уровней всех представленных аппроксимаций даны при использовании двумерных срезов трехмерных областей.

Фиг. 5.

Аппроксимация функции расстояния для двух трехмерных моделей. Слева: решение задачи (4). В середине: решение задачи Дирихле для $p$-Лапласиана (6) при $p = 15$. Справа: после нормализации при помощи (16).

ЗАКЛЮЧЕНИЕ

В настоящей работе рассмотрена новая вариационная задача для функции расстояния до границы области (4) и показано, как эта задача может быть решена при помощи ADMM итераций. Мы также показали, как ADMM может быть использован для численного решения задачи Дирихле для $p$-лапласиана, которая, в свою очередь, приближает функцию расстояния. Рассмотренные методы протестированы для двумерных и трехмерных полигональных областей. Перенесение полученных результатов на случай анизотропных функций расстояний представляется интересным направлением для будущих исследований.

Авторы благодарны AIM@SHAPE репозиторию за возможность использования модели Горгулья и лаборатории компьютерной графики Стэнфордского университета за возможность использования модели Люси.

Список литературы

Gibou F., Fedkiw R., Osher S. A review of level-set methods and some recent applications. Journal of Computational Physics. 2017. V. 353. P. 82–109.
Tucker P.G. Hybrid Hamilton-Jacobi-Poisson wall distance function model. Computers & Fluids. 2011. V. 44 (1). P. 130–142.
Roget B., Sitaraman J. Wall distance search algorithm using voxelized marching spheres. Journal of Computational Physics.2013. V. 241. P. 76–94.
Biswas A., Shapiro V., Tsukanov I. Heterogeneous material modeling with distance fields. Comput. Aided Geom. Des. 2004. V. 21. P. 215–242.
Xia H., Tucker P.G. Fast equal and biased distance fields for medial axis transform with meshing in mind. Applied Mathematical Modelling. 2011. V. 35. P. 5804–5819.
Babuška I., Banerjee U., Osborn J.E. Survey of meshless and generalized finite element methods: A unified approach. Acta Numerica. 2003. V. 12. P. 1–125.
Freytag M., Shapiro V., Tsukanov I. Finite element analysis in situ. Finite Elem. Anal. Des. 2011. V. 47 (8). P. 957–972.
Cadena C., Carlone L., Carrillo H., Latif Y., Scaramuzza D., Neira J., Reid I., Leonard J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Transactions on Robotics. 2016. V. 32. P. 1309–1332.
Calakli F., Taubin G. SSD: Smooth signed distance surface reconstruction. Computer Graphics Forum. 2011. V. 30 (6). P. 1993–2002.
Zollhöfer M., Dai A., Innmann M., Wu C., Stamminger M., Theobalt C., Nieβner M. Shading-based refinement on volumetric signed distance functions. ACM Transactions on Graphics. 2015. V. 34 (4). P. 96:1–96:14.
Zhu B., Skouras M., Chen D., Matusik W. Two-scale topology optimization with microstructures. ACM Transactions on Graphics. 2017. V. 36 (5). P. 36:1–36:14.
Belyaev A., Fayolle P.-A., Pasko A. Signed L_p-distance fields. Computer-Aided Design. 2013. V. 45. P. 523–528.
Crane K., Weischedel C., Wardetzky M. Geodesics in heat: A new approach to computing distance based on heat flow. ACM Transactions on Graphics. 2013. V. 32. P. 152:1–152:11.
Belyaev A., Fayolle P.-A. On variational and PDE-based distance function approximations. Computer Graphics Forum. 2015. V. 34 (7). P. 104–118.
Lee B., Darbon J., Osher S., Kang M. Revisiting the redistancing problem using the Hopf-Lax formula. Journal of Computational Physics. 2017. V. 330. P. 268–281.
Royston M., Pradhana A., Lee B., Chow Y.T., Yin W., Teran J., Osher S. Parallel redistancing using the Hopf-Lax formula. Journal of Computational Physics. 2018. V. 365. P. 7–17.
Glowinski R. On alternating direction methods of multipliers: A historical perspective. In W. Fitzgibbon, Y.A. Kuznetsov, P. Neittaanmäki, and O. Pironneau, editors, Modeling, Simulation and Optimization for Science and Technology, pages 59–82. Springer, 2014.
Belyaev A., Fayolle P.-A. A variational method for accurate distance function estimation. In Numerical Geometry, Grid Generation and Scientific Computing, NUMGRID 2018 / Voronoi 150. Springer, 2019.
Bhattacharya T., DiBenedetto E., Manfredi J. Limits as $p \to \infty $ of ${{\Delta }_{p}}{{u}_{p}} = f$ and related extremal problems. Rend. Sem. Mat. Univ. Pol. Torino, Fascicolo Speciale Nonlinear PDEs, pages 15–68. 1989.
Kawohl B. On a family of torsional creep problems. Journal für die reine und angewandte Mathematik. 1990. V. 410 (1). P. 1–22.
Wukie N.A., Orkwis P.D. A p-Poisson wall distance approach for turbulence modeling. In 23rd AIAA Computational Fluid Dynamics Conference, 2017.
Pólya G., Szegö G. Isoperimetric Inequalities in Mathematical Physics. Princeton University Press, 1951.
Fayolle P.-A., Belyaev A. p-Laplace diffusion for distance function estimation, optimal transport approximation, and image enhancement. Computer Aided Geometric Design. 2018. V. 67. P. 1–20.
Butzer P., Jongmans F., Chebyshev P.L. (1821–1894): A guide to his life and work. Journal of Approximation Theory. 1999. V. 96. P. 111–138.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал