Журнал вычислительной математики и математической физики, 2019, T. 59, № 2, стр. 217-234
Оптимизационный метод в осесимметричных задачах электрической маскировки материальных тел
Г. В. Алексеев *, Д. А. Терешко
ИПМатем ДВО РАН
690041 Владивосток, ул. Радио, 7, Россия
* E-mail: alekseev@iam.dvo.ru
Поступила в редакцию 25.04.2018
Аннотация
Исследуются обратные задачи дизайна сферических оболочек, предназначенных для маскировки материальных тел в стационарном электрическом поле. С помощью оптимизационного метода указанные обратные задачи сводятся к экстремальным задачам, в которых роль управлений играют компоненты диагонального тензора электропроводности анизотропного материала оболочки. Доказывается разрешимость прямой и экстремальной задач. Предлагается численный алгоритм решения экстремальных задач, основанный на методе роя частиц, обсуждаются результаты вычислительных экспериментов. Библ. 32. Фиг. 5. Табл. 3.
1. ВВЕДЕНИЕ
В последние годы интенсивно развивается новое направление в технической физике, связанное с разработкой технологий дизайна специальных функциональных устройств, служащих для управления физическими полями. Одним из важнейших таких функциональных устройств является материальная оболочка, имеющая вид шарового слоя (или кольца на плоскости ${{\mathbb{R}}^{2}}$), заполненная неоднородной и анизотропной в общем случае средой. В зависимости от поставленной цели указанная оболочка может служить для защиты любого объекта, помещенного внутрь ее, от обнаружения с помощью волнового или статического (электрического, магнитного или теплового) поля либо, наоборот, для концентрирования соответствующего поля в ее внутренности (см. [1], [2]). О других возможных целях проектируемых материальных оболочек можно прочитать, например, в [3]–[5].
Отметим, что первые работы в этой области были посвящены исследованию задач дизайна устройств невидимости относительно электромагнитных полей на основе предложенного в [6] метода оптических преобразований. Затем основные результаты из теории электромагнитной маскировки были перенесены на случай акустической маскировки (см. [7]), а далее на случай маскировки от статических полей (см. [2], [3], [8]–[11]).
Нужно отметить, что построенные в цитируемых статьях решения задачи маскировки обладают рядом недостатков. Во-первых, указанные решения получены при жестких упрощающих предположениях на исходные данные, обеспечивающих построение в явном виде точного либо приближенного решения соответствующей прямой задачи. В случае маскировки от статических полей их роль обычно играет требование однородности внешне приложенного поля, в котором требуется замаскировать объект. Во-вторых, техническая реализация решений, полученных в цитируемых статьях, связана с существенными трудностями. Один из способов преодоления указанных недостатков состоит в замене исходной задачи точной маскировки задачей приближенной маскировки и применении для ее решения метода оптимизации решения обратных задач.
В этой статье мы преследуем две цели. Первая цель состоит в том, чтобы сформулировать точные постановки обратных задач для статической осесимметричной модели электропроводности, возникающих при проектировании специальных маскировочных устройств сферической формы, и выполнить их краткий теоретический анализ. Для реализации этой цели мы применим оптимизационный метод решения обратных задач, к классу которых относятся задачи маскировки. Начиная с основополагающих работ А.Н. Тихонова [12], этот метод широко используется при исследовании обратных задач электромагнетизма и теплопроводности (см., например, монографии [13]–[16] и оригинальные работы [17]–[22]). Отметим также статьи [23]–[25], в которых оптимизационный метод используется при теоретическом анализе задач электромагнитной, акустической или тепловой маскировки.
Второй целью являются разработка эффективного численного алгоритма решения осесимметричных задач электрической маскировки и анализ результатов проведенных вычислительных экспериментов. Разрабатываемый алгоритм основывается на численном решении экстремальных задач, возникающих при применении оптимизационного метода к рассматриваемым обратным задачам. В качестве процедуры численной оптимизации используется метод роя частиц по схеме, предложенной и кратко описанной в заметках [26], [27] для решения 2D задач тепловой маскировки.
2. ПОСТАНОВКА И АНАЛИЗ ПРЯМОЙ ЗАДАЧИ
Сформулируем и изучим в этом разделе прямую задачу электропроводности, рассматриваемую в ограниченной трехмерной области $D$, имеющей вид цилиндра
при некоторых заданных числах ${{z}_{0}} > 0$ и $c > 0$ (см. фиг. 1). Начнем с введения внешне приложенного поля электрического потенциала ${{U}^{e}}$, являющегося составной частью задачи дизайна электрических функциональных устройств. Будем считать, что поле ${{U}^{e}}$ создается при помощи двух горизонтальных оснований ${{\Gamma }_{1}}$: $z = - {{z}_{0}}$ и ${{\Gamma }_{2}}$: $z = {{z}_{0}}$, поддерживаемых при разных значениях ${{u}_{1}}$ и ${{u}_{2}}$ электрического потенциала, тогда как боковая поверхность $\Gamma $ цилиндра $D$ электрически изолирована, причем основная среда, заполняющая область $D$, однородна и изотропна, а ее электропроводные свойства описываются постоянным коэффициентом электропроводности ${{\sigma }_{0}} > 0$. В таком случае искомое поле ${{U}^{e}}$ является решением в области $D$ уравнения Лапласа $\Delta U = 0$, удовлетворяющим следующим краевым условиям:
(2.1)
${{\left. U \right|}_{{z = - {{z}_{0}}}}} = {{u}_{1}},\quad {{\left. U \right|}_{{z = {{z}_{0}}}}} = {{u}_{2}},\quad {{\left. {\frac{{\partial U}}{{\partial n}}} \right|}_{\Gamma }} = 0.$(2.2)
${{U}^{e}}(z) = {{u}_{1}} + \frac{{z + {{z}_{0}}}}{{2{{z}_{0}}}}({{u}_{2}} - {{u}_{1}}) \equiv {{u}_{0}}\frac{z}{{{{z}_{0}}}} + \frac{{{{u}_{1}} + {{u}_{2}}}}{2},\quad {{u}_{0}} \equiv \frac{{{{u}_{2}} - {{u}_{1}}}}{2}.$Предположим теперь, что в цилиндр $D$ вноcится некоторый объект, заполненный средой, обладающей электропроводящими свойствами, отличающимися от свойств основной среды. Тогда поле ${{U}^{e}}$ изменяется и принимает вид $U = {{U}^{e}} + {{u}^{s}}$. Здесь ${{u}^{s}}$ – возмущение поля ${{U}^{e}}$, вызванное внесением объекта в область $D$, которое будем называть электрическим откликом объекта в области $D$.
Нахождение электрического отклика ${{u}^{s}}$ сводится к решению прямой задачи электропроводности. Чтобы ее сформулировать, предположим, что вносимый объект представляет собой пару $(\Omega ,\sigma )$, где $\Omega = \left\{ {{\mathbf{x}} \in D:a < \left| {\mathbf{x}} \right| < b} \right\}$ – сферический слой с внутренним и внешним радиусами $a$ и $b$, заполненный неоднородной анизотропной средой, а $\sigma $ – тензор электропроводности, описывающий ее электропроводящие свойства. Будем ссылаться на пару $(\Omega ,\sigma )$ как на электрическую оболочку. Введем внутренность ${{\Omega }_{i}} = \left\{ {{\mathbf{x}} \in D:\left| {\mathbf{x}} \right| < a} \right\}$ и внешность ${{\Omega }_{e}} = \left\{ {{\mathbf{x}} \in D:\left| {\mathbf{x}} \right| > b} \right\}$ слоя $\Omega $ в $D$ (см. фиг. 1) и обозначим через ${{u}_{i}}$, $u$ либо ${{u}_{e}}$ сужения искомого электрического поля соответственно на ${{\Omega }_{i}}$, $\Omega $ либо ${{\Omega }_{e}}$. Отметим, в частности, что ${{u}_{e}} \equiv {{U}^{e}} + u_{e}^{s}$, где на поле $u_{e}^{s} = {{\left. {{{u}^{s}}} \right|}_{{{{\Omega }_{e}}}}}$ будем ссылаться как на внешний электрический отклик объекта $(\Omega ,\sigma )$ в ${{\Omega }_{e}}$.
С учетом введенных обозначений исходная прямая задача электропроводности сводится к нахождению тройки функций: ${{u}_{i}}$ во внутренности ${{\Omega }_{i}}$ области $\Omega $, $u$ в области $\Omega $ и ${{u}_{e}}$ во внешности ${{\Omega }_{e}}$, удовлетворяющих уравнениям
(2.3)
${{\sigma }_{0}}\Delta {{u}_{i}} = 0\quad {\text{в }}\;{{\Omega }_{i}},\quad {\text{div}}(\sigma \operatorname{grad} u) = 0\quad {\text{в }}\;\Omega ,\quad {{\sigma }_{0}}\Delta {{u}_{e}} = 0\quad {\text{в }}\;{{\Omega }_{e}},$(2.4)
${{u}_{i}} = u,\quad {{\sigma }_{0}}\frac{{\partial {{u}_{i}}}}{{\partial n}} = \left( {\sigma \nabla u} \right) \cdot {\mathbf{n}}\quad {\text{н а }}\;{{\Gamma }_{i}},\quad {{u}_{e}} = u,\quad {{\sigma }_{0}}\frac{{\partial {{u}_{e}}}}{{\partial n}} = (\sigma \nabla u) \cdot {\mathbf{n}}\quad {\text{н а }}\;{{\Gamma }_{e}}.$Наряду с прямой задачей важную роль в приложениях играют обратные задачи электропроводности. Первая из обратных задач, рассматриваемых в этой статье, заключается в нахождении параметров среды, заполняющей оболочку $(\Omega ,\sigma )$, исходя из следующих двух условий:
1) внешний электрический отклик $u_{e}^{s} = {{\left. {{{u}^{s}}} \right|}_{{{{\Omega }_{e}}}}}$ равен нулю, так что ${{u}_{e}} = {{U}^{e}}$ в ${{\Omega }_{e}}$; и
2) полное электрическое поле ${{u}_{i}}$ во внутренней области ${{\Omega }_{i}}$ постоянно: ${{u}_{i}} = u_{i}^{0} = {\text{const}}$ (см. [3]). Для краткости на указанные условия 1 и 2 будем ниже ссылаться как на условия внешней либо внутренней маскировки, а на саму обратную задачу будем ссылаться как на задачу полной маскировки, причем искомую оболочку, обеспечивающую точное выполнение указанных двух условий, будем называть идеальной или универсальной маскировочной оболочкой. Кроме задачи полной маскировки, на практике также рассматривают задачи частичной (внешней или внутренней) маскировки. Они отвечают ситуации, когда параметры среды выбираются так, чтобы выполнялось введенное выше условие 1 (в случае задачи внешней маскировки) либо условие 2 (в случае задачи внутренней маскировки). Задачи внешней маскировки обычно возникают в ситуации, когда требуется замаскировать от обнаружения конкретное материальное тело.
В свою очередь, приведенную обратную задачу полной маскировки можно усложнить, сформулировав задачу нахождения параметров среды, заполняющей область $\Omega $, из того условия, что ее внешний электрический отклик $u_{e}^{s}$ совпадает с электрическим откликом заранее заданного объекта (либо нескольких объектов) и выполняется введенное выше условие 2. На указанную задачу часто ссылаются как на задачу электрического камуфляжа или электрического иллюзиона (см. [2], [3]).
При исследовании задачи 1 и экстремальных задач будем существенно использовать ряд функциональных пространств. К ним относятся пространство ${{H}^{1}}(\tilde {\Omega })$, где $\tilde {\Omega }$ – одна из областей $D$, ${{\Omega }_{i}}$, $\Omega $, ${{\Omega }_{e}}$, а также пространства ${{L}^{\infty }}(\Omega )$, ${{H}^{s}}(\Omega )$, ${{L}^{2}}(Q)$, ${{H}^{{1/2}}}({{\Gamma }_{l}})$, $l = 1,2$. Здесь $Q \subset {{\Omega }_{i}} \cup {{\Omega }_{e}}$ – непустое открытое подмножество. Скалярные произведения и нормы в ${{L}^{2}}(\Omega )$ и ${{H}^{s}}(\Omega )$ будем обозначать через ${{( \cdot , \cdot )}_{\Omega }}$, ${{\left\| {\, \cdot \,} \right\|}_{\Omega }}$ и ${{( \cdot , \cdot )}_{{s,\Omega }}}$, ${{\left\| {\, \cdot \,} \right\|}_{{s,\Omega }}}$. Нормы в ${{H}^{1}}(\tilde {\Omega })$, ${{L}^{2}}(Q)$, ${{H}^{{1/2}}}({{\Gamma }_{l}})$ будут обозначаться через ${{\left\| {\, \cdot \,} \right\|}_{{1,\tilde {\Omega }}}}$, ${{\left\| {\, \cdot \,} \right\|}_{Q}}$ и ${{\left\| {\, \cdot \,} \right\|}_{{1/2,{{\Gamma }_{l}}}}}$. Положим $L_{{{{\lambda }_{0}}}}^{\infty }(\Omega ) = \left\{ {\lambda \in {{L}^{\infty }}(\Omega ):\lambda ({\mathbf{x}}) \geqslant {{\lambda }_{0}}} \right\}$, $H_{{{{\lambda }_{0}}}}^{s}(\Omega ) = \left\{ {\lambda \in {{H}^{s}}(\Omega ):\lambda ({\mathbf{x}}) \geqslant {{\lambda }_{0}}} \right\}$, ${{\lambda }_{0}} = {\text{const}} > 0$. Хорошо известно в силу теоремы вложения, что имеет место непрерывное и компактное вложение ${{H}^{s}}(\Omega ) \subset {{L}^{\infty }}(\Omega )$ при $s > 3{\text{/}}2$ и справедлива следующая оценка:
Подчеркнем, что каждая из двух введенных выше областей: цилиндр $D$ и сферический слой $\Omega $ обладают осевой симметрией в том смысле, что сечения их вертикальной полуплоскостью, проходящей через ось $z$, не зависят от азимутального угла $\varphi $. Это позволяет надеяться на то, что решение прямой задачи также не будет зависеть от полярного угла $\varphi $ в случае осесимметричных исходных данных. Указанное свойство решения будет существенно использоваться в дальнейшем вместе со следующим предположением:
(i) тензор $\sigma $ диагонален в сферических координатах $r = \left| {\mathbf{x}} \right|$, $\theta $, $\varphi $, а его диагональные компоненты (радиальный, полярный и азимутальный коэффициенты электропроводности) ${{\sigma }_{r}} \equiv \lambda $, ${{\sigma }_{\theta }} \equiv \mu $ и ${{\sigma }_{\varphi }} \equiv \tau $ не зависят от $\varphi $ и удовлетворяют условиям:
(2.5)
$\lambda \in L_{{{{\lambda }_{0}}}}^{\infty }(\Omega ),\quad \mu \in L_{{{{\mu }_{0}}}}^{\infty }(\Omega ),\quad {{\lambda }_{0}} = {\text{const}} > 0,\quad {{\mu }_{0}} = {\text{const}} > 0,\quad \tau = \mu .$С учетом условия (i) ниже, наряду с декартовыми координатами в областях ${{\Omega }_{i}}$, $\Omega $ и ${{\Omega }_{e}}$, в области $\Omega $ будем также использовать сферические координаты $r$, $\theta $, $\varphi $. Напомним в связи с этим, что вектор ${\text{grad}}\,u$ и произведение диагонального в сферических координатах тензора $\sigma = {\text{diag}}(\lambda ,\mu ,\mu )$ на ${\text{grad}}\,u$ определяются в сферических координатах формулами
Присутствующее в (2.5) условие ${{\sigma }_{\varphi }} = {{\sigma }_{\theta }}$ широко используется при исследовании трехмерных задач дизайна сферических электрических (функциональных) устройств. Более того, в случае, когда параметры $\lambda $, $\mu $, а также ${{u}_{1}}$ и ${{u}_{2}}$, постоянны, причем выполнятся условие $2\lambda \mu = \sigma _{0}^{2} + {{\sigma }_{0}}\lambda $, можно показать, рассуждая как в [4, гл. 4], что существует точное решение задачи (2.1), (2.3), (2.4), которое является осесимметричным, т.е. не зависит от угла $\varphi $, и, как нетрудно проверить непосредственной подстановкой, описывается следующими формулами:
(2.6)
$\begin{gathered} {{u}_{i}}(r,\theta ) = \frac{{{{u}_{0}}}}{{{{z}_{0}}}}\mathop {\left( {\frac{a}{b}} \right)}\nolimits^{q(s) - 1} rcos\theta + \frac{{{{u}_{1}} + {{u}_{2}}}}{2}\quad {\text{в }}\;{{\Omega }_{i}},\quad u(r,\theta ) = \frac{{{{u}_{0}}}}{{{{z}_{0}}}}\mathop {\left( {\frac{r}{b}} \right)}\nolimits^{q(s) - 1} rcos\theta + \frac{{{{u}_{1}} + {{u}_{2}}}}{2}\quad {\text{в }}\;\Omega , \\ {{u}_{e}}(r,\theta ) = \frac{{{{u}_{0}}}}{{{{z}_{0}}}}rcos\theta + \frac{{{{u}_{1}} + {{u}_{2}}}}{2}\quad {\text{в }}\;{{\Omega }_{e}},\quad q(s) \equiv \frac{{ - 1 + \sqrt {1 + 8s} }}{2},\quad s = \frac{\mu }{\lambda },\quad {{u}_{0}} = \frac{{{{u}_{2}} - {{u}_{1}}}}{2}. \\ \end{gathered} $(2.7)
$q(s) > 0\quad {\text{н а }}\;(0,\infty ),\quad q(0) = 0,\quad q(1) = 1,\quad q(s) \to \infty \quad {\text{п р и }}\quad s \to \infty .$Из (2.6) и (2.2) следует, что градиенты $\nabla {{u}_{e}}$ и $\nabla {{u}_{i}}$ постоянны, причем
(2.8)
${{u}_{e}} = {{U}^{e}},\quad \left| {\nabla {{u}_{e}}} \right| = \left| {\nabla {{U}^{e}}} \right| = \frac{{{{u}_{0}}}}{{{{z}_{0}}}}\quad {\text{в }}\;{{\Omega }_{e}},\quad \left| {\nabla {{u}_{i}}} \right| = \frac{{{{u}_{0}}}}{{{{z}_{0}}}}\mathcal{K}(s)\quad {\text{в }}\;{{\Omega }_{i}},\quad \mathcal{K}(s) \equiv \mathop {\left( {\frac{a}{b}} \right)}\nolimits^{q(s) - 1} .$Как уже указывалось выше, мы будем предполагать, что решение $U \equiv ({{u}_{i}},u,{{u}_{e}})$ задачи 1 не зависит от угла $\varphi $. Чтобы формализовать это условие, введем в функциональном пространстве ${{H}^{1}}(D)$ его подпространство $X \subset {{H}^{1}}(D)$, состоящее из функций $u:D \to \mathbb{R}$, не зависящих от полярного угла $\varphi $. Норму в $X$ введем с учетом формулы для $\operatorname{grad} U$ в (2.8) и независимости $U$ от $\varphi $ формулами
(2.9)
$\left\| U \right\|_{X}^{2} = \left\| U \right\|_{D}^{2} + \left\| {\nabla U} \right\|_{D}^{2},\quad \left\| {\nabla U} \right\|_{D}^{2} \equiv \left\| {\nabla U} \right\|_{{{{\Omega }_{i}} \cup {{\Omega }_{e}}}}^{2} + \left\| {\frac{{\partial U}}{{\partial r}}} \right\|_{\Omega }^{2} + \mathop {\left\| {\frac{1}{r}\frac{{\partial U}}{{\partial \theta }}} \right\|}\nolimits_\Omega ^2 .$(2.10)
$\left\| {\nabla U} \right\|_{D}^{2} \geqslant \delta \left\| U \right\|_{X}^{2}\quad \forall U \in {{X}_{0}}.$Введем еще одно предположение, касающееся граничных функций ${{u}_{1}}$ и ${{u}_{2}}$:
(ii) ${{u}_{1}} \in {{H}^{{1/2}}}({{\Gamma }_{1}})$, ${{u}_{2}} \in {{H}^{{1/2}}}({{\Gamma }_{2}})$ и существует функция ${{U}^{0}} \in X$ такая, что
(2.11)
${{\left. {{{U}^{0}}} \right|}_{{{{\Gamma }_{1}}}}} = {{u}_{1}},\quad {{\left. {{{U}^{0}}} \right|}_{{{{\Gamma }_{2}}}}} = {{u}_{2}},\quad {{\left\| {{{U}^{0}}} \right\|}_{X}} \leqslant {{M}_{u}} \equiv {{C}_{D}}\left( {{{{\left\| {{{u}_{1}}} \right\|}}_{{1/2,{{\Gamma }_{1}}}}} + {{{\left\| {{{u}_{2}}} \right\|}}_{{1/2,{{\Gamma }_{2}}}}}} \right).$Анализ задачи 1 начнем с вывода ее слабой формулировки. Пусть $\Phi \in {{X}_{0}}$ – произвольная тестовая функция. Умножим каждое из уравнений, входящих в (2.3), рассматриваемых, соответственно, в областях ${{\Omega }_{i}}$, $\Omega $ и ${{\Omega }_{e}}$, на $\Phi $, проинтегрируем соответственно по ${{\Omega }_{i}}$, $\Omega $ и ${{\Omega }_{e}}$ и применим соответствующие формулы Грина. Складывая полученные тождества, используя граничные условия в (2.1), (2.4), приходим с учетом (2.8) к слабой формулировке задачи 1. Она заключается в нахождении тройки $U = ({{u}_{i}},u,{{u}_{e}}) \in X$, равной ${{u}_{i}}$ в ${{\Omega }_{i}}$, $u$ в $\Omega $ и ${{u}_{e}}$ в ${{\Omega }_{e}}$, из условий:
(2.12)
${{a}_{\sigma }}(U,\Phi ) \equiv {{a}_{0}}(U,\Phi ) + a(\lambda ,\mu ;U,\Phi ) = 0\quad \forall \Phi \in {{X}_{0}},\quad {{\left. {{{u}_{e}}} \right|}_{{{{\Gamma }_{1}}}}} = {{u}_{1}},\quad {{\left. {{{u}_{e}}} \right|}_{{{{\Gamma }_{2}}}}} = {{u}_{2}}.$(2.13)
${{a}_{0}}(U,\Phi ) = {{\sigma }_{0}}\int\limits_{{{\Omega }_{i}} \cup {{\Omega }_{e}}} {\nabla U} \cdot \nabla \Phi d{\mathbf{x}},\quad a(\lambda ,\mu ;U,\Phi ) = {{a}_{1}}(\lambda ;U,\Phi ) + {{a}_{2}}(\mu ;U,\Phi ),$Пусть $\lambda \in {{L}^{\infty }}(\Omega )$, $\mu \in {{L}^{\infty }}(\Omega )$. Используя стандартные неравенства Коши либо Гельдера и формулу (2.9) для нормы ${{\left\| {\, \cdot \,} \right\|}_{X}}$, выводим следующие оценки:
(2.14)
$\begin{gathered} \left\| {{{a}_{0}}} \right\| \leqslant {{\sigma }_{0}},\quad \left\| {a(\lambda ,\mu ; \cdot , \cdot )} \right\| \leqslant {{\left\| \lambda \right\|}_{{{{L}^{\infty }}(\Omega )}}} + {{\left\| \mu \right\|}_{{{{L}^{\infty }}(\Omega )}}}, \\ \left\| {{{a}_{\sigma }}} \right\| \leqslant {{\sigma }^{0}} = max\left( {{{\sigma }_{0}},{{{\left\| \lambda \right\|}}_{{{{L}^{\infty }}(\Omega )}}},{{{\left\| \mu \right\|}}_{{{{L}^{\infty }}(\Omega )}}}} \right). \\ \end{gathered} $Предположим, более того, что $\lambda $ и $\mu $ удовлетворяют условиям (2.5). Тогда имеем
(2.15)
${{a}_{\sigma }}(U,U) \geqslant {{\sigma }_{ * }}\left\| {\nabla U} \right\|_{D}^{2} \geqslant \delta {{\sigma }_{ * }}\left\| U \right\|_{X}^{2}\quad \forall U \in {{X}_{0}},\quad {{\sigma }_{ * }} = min({{\sigma }_{0}},{{\lambda }_{0}},{{\mu }_{0}}).$Будем искать решение ${{U}_{\sigma }}$ задачи (2.12), т.е. слабое решение задачи 1, в виде ${{U}_{\sigma }} = {{U}^{0}} + {{\tilde {U}}_{\sigma }}$, где ${{U}^{0}}$ – введенная в условии (ii) функция, ${{\tilde {U}}_{\sigma }} \in {{X}_{0}}$ – новая неизвестная функция. Из (2.12) следует, что ${{\tilde {U}}_{\sigma }}$ является решением задачи
(2.16)
${{a}_{\sigma }}({{\tilde {U}}_{\sigma }},\Phi ) = \left\langle {{{F}_{\sigma }},\Phi } \right\rangle \equiv - {{a}_{\sigma }}({{U}^{0}},\Phi )\quad \forall \Phi \in {{X}_{0}}.$Поскольку форма ${{a}_{\sigma }}:X \times X \to \mathbb{R}$ линейна, непрерывна и коэрцитивна на ${{X}_{0}}$ с константой $\delta {{\sigma }_{ * }}$ согласно (2.15), то в силу теоремы Лакса-Мильграма решение ${{\tilde {U}}_{\sigma }}$ задачи (2.16) существует, единственно и для него с учетом (2.15) выполняется оценка
(2.17)
$\begin{gathered} {{\left\| {{{U}_{\sigma }}} \right\|}_{X}} \leqslant {{\left\| {{{U}^{0}}} \right\|}_{X}} + {{\left\| {{{{\tilde {U}}}_{\sigma }}} \right\|}_{X}} \leqslant {{M}_{u}} + {{(\delta {{\sigma }_{ * }})}^{{ - 1}}}{{\sigma }^{0}}{{M}_{u}} = \left[ {1 + {{{(\delta {{\sigma }_{ * }})}}^{{ - 1}}}{{\sigma }^{0}}} \right]{{M}_{u}} = \\ = \;{{(\delta {{\sigma }_{ * }})}^{{ - 1}}}\left( {\delta {{\sigma }_{ * }} + {{\sigma }^{0}}} \right){{M}_{u}} = {{C}_{0}}{{C}_{\sigma }}{{M}_{u}},\quad {{C}_{0}} = {{(\delta {{\sigma }_{ * }})}^{{ - 1}}},\quad {{C}_{\sigma }} = \delta {{\sigma }_{ * }} + {{\sigma }^{0}}. \\ \end{gathered} $Подчеркнем, что константа ${{C}_{0}}$ не зависит от пары $(\lambda ,\mu )$, хотя и зависит от ${{\sigma }_{0}}$, ${{\lambda }_{0}}$ и ${{\mu }_{0}}$ в силу (2.15), тогда как константа ${{C}_{\sigma }}$, как и ${{\sigma }^{0}}$ в (2.14), зависит от $\lambda $, $\mu $. Однако, если $\lambda $ и $\mu $ могут изменяться лишь в некоторых ограниченных множествах ${{K}_{1}} \subset L_{{{{\lambda }_{0}}}}^{\infty }(\Omega )$ и ${{K}_{2}} \subset L_{{{{\mu }_{0}}}}^{\infty }(\Omega )$, то для решения ${{U}_{\sigma }}$ задачи (2.12), наряду с (2.17), справедлива оценка
(2.18)
${{\left\| {{{U}_{\sigma }}} \right\|}_{X}} \leqslant {{C}_{0}}{{C}_{1}}{{M}_{u}},\quad {{C}_{1}} = sup{{C}_{\sigma }},\quad \sigma \equiv (\lambda ,\mu ) \in {{K}_{1}} \times {{K}_{2}},$Теорема 2.1. Пусть при выполнении условий (i), (ii) ${{K}_{1}} \subset L_{{{{\lambda }_{0}}}}^{\infty }(\Omega )$ и ${{K}_{2}} \subset L_{{{{\mu }_{0}}}}^{\infty }(\Omega )$ – непустые ограниченные множества. Тогда для произвольной пары $(\lambda ,\mu ) \in {{K}_{1}} \times {{K}_{2}}$ решение ${{U}_{\sigma }}$ задачи (2.12) существует, единственно и удовлетворяет оценке (2.18), где константа ${{C}_{0}}$ определена в (2.17), а константа ${{C}_{1}}$ не зависит от $(\lambda ,\mu )$, но зависит от множеств ${{K}_{1}}$ и ${{K}_{2}}$.
3. ПРИМЕНЕНИЕ ОПТИМИЗАЦИОННОГО МЕТОДА. ФОРМУЛИРОВКА И АНАЛИЗ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
Напомним, что наша цель состоит в теоретическом и численном исследовании обратных задач, возникающих при разработке технологий дизайна устройств маскировки относительно электрических полей. Для достижения указанной цели мы применим метод оптимизации. Этот метод основан на минимизации функционала, который точно соответствует обратной задаче дизайна функционального устройства, служащего для приближенной маскировки. В результате исходная обратная задача сводится к исследованию экстремальной задачи, на которую принято ссылаться как на обратную экстремальную задачу. В качестве функционала качества выберем один из следующих:
(3.1)
${{I}_{i}}(U) = \frac{1}{{I_{i}^{0}}}{{\int\limits_{{{Q}_{i}}} {\left| {\nabla U} \right|} }^{2}}d{\mathbf{x}},\quad {{Q}_{i}} \subset {{\Omega }_{i}},\quad I_{i}^{0} = {{\int\limits_{{{Q}_{i}}} {\left| {\nabla {{U}^{e}}} \right|} }^{2}}d{\mathbf{x}},$Выбирая то или иное подмножество ${{Q}_{e}}$ в ${{\Omega }_{e}}$ либо ${{Q}_{i}}$ в ${{\Omega }_{i}}$ и заданное в ${{Q}_{e}}$ поле ${{U}^{d}}$, мы можем сформулировать и исследовать несколько различных классов обратных экстремальных задач для рассматриваемой модели электропроводности. В частном случае, когда ${{U}^{d}} = {{U}^{e}}$, функционал ${{I}_{e}}(U)$ имеет смысл относительной среднеквадратичной нормы внешнего электрического отклика $u_{e}^{s} = {{u}_{e}} - {{U}^{e}}$ по области ${{Q}_{e}} \subset {{\Omega }_{e}}$. Поэтому минимизация функционала ${{I}_{e}}(U)$ направлена в этом случае на нахождение приближенного решения задачи внешней маскировки. Точно так же минимизация функционала ${{I}_{i}}(U)$ (либо функционала $I(U)$ при ${{U}^{d}} = {{U}^{e}}$) направлена на решение задачи внутренней (либо полной) маскировки. В частности, параметр ${{\sigma }^{{{\text{opt}}}}} = ({{\lambda }^{{{\text{opt}}}}},{{\mu }^{{{\text{opt}}}}})$, на котором достигается минимум функционала $I(U)$, описывает приближенное решение задачи полной маскировки. В том же случае, когда ${{U}^{d}} = {{U}^{e}} + u_{0}^{s}$, где $u_{0}^{s}$ – рассеянный отклик некоторого объекта, задача минимизации функционала $I(U)$ имеет своей целью нахождение приближенного решения соответствующей задачи электрического иллюзиона.
Будем предполагать ниже, что управления $\lambda $ и $\mu $ могут изменяться в некоторых множествах ${{K}_{1}}$ и ${{K}_{2}}$, удовлетворяющих следующему условию:
(j) ${{K}_{1}} \subset H_{{{{\lambda }_{0}}}}^{s}(\Omega )$, ${{K}_{2}} \subset H_{{{{\mu }_{0}}}}^{s}(\Omega )$ – непустые выпуклые замкнутые множества, где ${{\lambda }_{0}} = {\text{const}} > 0$, ${{\mu }_{0}} = {\text{const}} > 0$, $s > 3{\text{/}}2$.
Полагая $K = {{K}_{1}} \times {{K}_{2}}$, $\sigma = (\lambda ,\mu )$, введем оператор $G = ({{G}_{0}},{{G}_{1}},{{G}_{2}}):$ $X \times K \to Y \equiv X_{0}^{ * } \times {{H}^{{1/2}}}({{\Gamma }_{1}}) \times $ $ \times \;{{H}^{{1/2}}}({{\Gamma }_{2}})$, действующий по формулам $\left\langle {{{G}_{0}}(U,\sigma ),\Phi } \right\rangle = {{a}_{\sigma }}(U,\Phi )$ $\forall \Phi \in {{X}_{0}}$, ${{G}_{1}}(U) = {{\left. U \right|}_{{{{\Gamma }_{1}}}}} - {{u}_{1}}$, ${{G}_{2}}(U) = {{\left. U \right|}_{{{{\Gamma }_{2}}}}} - {{u}_{2}}$.
Рассмотрим следующую экстремальную задачу:
(3.2)
$\tilde {I}(U,\sigma ) \equiv \frac{{{{\alpha }_{0}}}}{2}I(U) + \frac{{{{\alpha }_{1}}}}{2}\left\| \lambda \right\|_{{s,\Omega }}^{2} + \frac{{{{\alpha }_{2}}}}{2}\left\| \mu \right\|_{{s,\Omega }}^{2} \to {\text{inf}},\quad G(U,\sigma ) = 0,\quad (U,\sigma ) \in X \times K.$(jj) ${{\alpha }_{0}} > 0$; ${{\alpha }_{1}} \geqslant 0$, ${{\alpha }_{2}} \geqslant 0$ и ${{K}_{1}}$, ${{K}_{2}}$ – ограниченные множества, либо ${{\alpha }_{1}} > 0$, ${{\alpha }_{2}} > 0$ и функционал $I(U)$ ограничен снизу.
Теорема 3.1. Пусть при выполнении условий (ii), (j), (jj) $I:X \to \mathbb{R}$ – слабо полунепрерывный снизу функционал и ${{Z}_{{ad}}}$ – непустое множество. Тогда задача (3.2) имеет, по крайней мере, одно решение $(U,\sigma ) \in X \times K$.
Доказательство. Обозначим через $({{U}^{m}},{{\sigma }^{m}}) \in X \times K$, ${{\sigma }^{m}} = ({{\lambda }^{m}},{{\mu }^{m}})$, $m \in \mathbb{N} = \left\{ {1,\;2,\; \ldots } \right\}$ минимизирующую последовательность для функционала $\tilde {I}$, для которой выполняются соотношения $li{{m}_{{m \to \infty }}}\tilde {I}({{U}^{m}},{{\sigma }^{m}}) = in{{f}_{{(U,\sigma ) \in {{Z}_{{ad}}}}}}\tilde {I}(U,\sigma ) \equiv \tilde {I}{\text{*}}$ и
(3.3)
${{a}_{0}}({{U}^{m}},\Phi ) + {{a}_{1}}({{\lambda }^{m}};{{U}^{m}},\Phi ) + {{a}_{2}}({{\mu }^{m}};{{U}^{m}},\Phi ) = 0\quad \forall \Phi \in {{X}_{0}}.$(3.4)
${{\left\| {{{\lambda }^{m}}} \right\|}_{{s,\Omega }}} \leqslant {{c}_{1}},\quad {{\left\| {{{\mu }^{m}}} \right\|}_{{s,\Omega }}} \leqslant {{c}_{2}}.$Переходя далее к пределу в (3.3) при $m \to \infty $ и рассуждая, как в [25], выводим с учетом свойств форм ${{a}_{1}}$ и ${{a}_{2}}$, что
Замечание 1. Отметим, что утверждения теоремы 3.1 остаются справедливыми для всех трех функционалов ${{I}_{e}}$, ${{I}_{i}}$ и $I$, введенных в (3.1), поскольку они неотрицательны и слабо полунепрерывны снизу, причем для каждого из них множество ${{Z}_{{ad}}}$ не пусто при выполнении условий (i), (ii), (j), (jj) в силу теоремы 2.1.
Замечание 2. Отметим, что теорема 3.1 касается существования решения. Что касается единственности и устойчивости решения задачи (3.2), то, в общем случае, единственность решения можно доказать лишь при выполнении малости исходных данных либо “великости” параметров ${{\alpha }_{1}}$, ${{\alpha }_{2}}$, имеющих смысл параметров регуляризации. Для доказательства этого факта удобно воспользоваться математическим аппаратом, основанным на анализе системы оптимальности для задачи (3.2), которая может быть выведена, как в [25], с использованием общей теории экстремальных задач, приведенной, например, в [14]. Однако на этом мы не будем останавливаться.
4. ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В СЛУЧАЕ СЛОИСТОЙ ОБОЛОЧКИ. ПРИМЕНЕНИЕ МЕТОДА РОЯ ЧАСТИЦ
Хорошо известно, что техническая реализация маскировочных оболочек, заполненных неоднородными анизотропными средами с переменными параметрами, связана с большими трудностями (см. [4]). Один из способов преодоления этих трудностей состоит в том, чтобы в качестве искомой оболочки использовать слоистую оболочку, состоящую из $M$ концентрических слоев ${{\Omega }_{j}} = \left\{ {{{r}_{{j - 1}}} < r < {{r}_{j}}} \right\}$, $j = 1,\; \ldots ,\;M$, $a = {{r}_{0}} < {{r}_{1}} < \ldots \; < {{r}_{M}} = b$, каждый из которых заполнен однородной анизотропной (или изотропной) средой с постоянными параметрами электропроводности ${{\lambda }_{j}} > 0$ и ${{\mu }_{j}} > 0$, $j = 1,\; \ldots ,\;M$. В этом случае решение как прямой, так и обратной, задач существенно упрощается, так как параметры $\lambda $ и $\mu $ среды, заполняющей область $\Omega $, описываются формулами
(4.1)
$\lambda ({\mathbf{x}}) = \sum\limits_{j = 1}^M \,{{\lambda }_{j}}{{\chi }_{j}}({\mathbf{x}}),\quad \mu ({\mathbf{x}}) = \sum\limits_{j = 1}^M \,{{\mu }_{j}}{{\chi }_{j}}({\mathbf{x}}).$Обратимся теперь к экстремальным задачам. Будем предполагать ниже, что компоненты $2M$-мерного вектора ${\mathbf{s}} \equiv ({{\lambda }_{1}},{{\mu }_{1}},\; \ldots ,\;{{\lambda }_{M}},{{\mu }_{M}})$, составленного из коэффициентов ${{\lambda }_{j}}$ и ${{\mu }_{j}}$, входящих в представления (4.1), могут изменяться в ограниченном множестве
(4.2)
$S = \left\{ {{\mathbf{s}} = ({{\lambda }_{1}},{{\mu }_{1}},\; \ldots ,\;{{\lambda }_{M}},{{\mu }_{M}})} \right.:{{\lambda }_{0}} \leqslant {{\lambda }_{j}} \leqslant {{\lambda }^{0}},\;{{\mu }_{0}} \leqslant {{\mu }_{j}} \leqslant {{\mu }^{0}},\;\left. {j = 1,\; \ldots ,\;M} \right\}$(4.4)
$J({\mathbf{s}}) = \frac{{{{J}_{e}}({\mathbf{s}}) + {{J}_{i}}({\mathbf{s}})}}{2} \to inf,\quad {\mathbf{s}} \in S.$(4.5)
${{J}_{e}}({\mathbf{s}}) = \frac{{{{{\left\| {U[{\mathbf{s}}] - {{U}^{e}}} \right\|}}_{{{{L}^{2}}({{\Omega }_{e}})}}}}}{{{{{\left\| {{{U}^{e}}} \right\|}}_{{{{L}^{2}}({{\Omega }_{e}})}}}}},\quad {{J}_{i}}({\mathbf{s}}) = \frac{{{{{\left\| {\nabla U[{\mathbf{s}}]} \right\|}}_{{{{L}^{2}}({{\Omega }_{i}})}}}}}{{{{{\left\| {\nabla {{U}^{e}}} \right\|}}_{{{{L}^{2}}({{\Omega }_{i}})}}}}},$Так как множество $S$ является замкнутым и ограниченным в пространстве ${{\mathbb{R}}^{{2M}}}$, а функции ${{J}_{e}}({\mathbf{s}})$ и ${{J}_{i}}({\mathbf{s}})$ непрерывны на $S$, то решение каждой из задач (4.3) и (4.4) существует. Однако, поскольку обе экстремальные задачи (4.3) и (4.4) получены фактически путем дискретизации рассматриваемых обратных задач, то они относятся к классу плохо обусловленных задач. Это означает, в частности, что решение каждой их них может не обладать свойствами единственности и устойчивости.
Существует несколько способов решения указанных плохо обусловленных задач. Первый способ, предложенный в работах А.Н. Тихонова [12], основан на регуляризации рассматриваемых задач. Именно этой цели служит внесение в минимизируемый функционал качества регуляризирующих добавок в виде квадратов норм управлений, выполненное в разд. 3. Однако регуляризация, хотя и улучшает обусловленность рассматриваемой экстремальной задачи, но одновременно искажает ее физический смысл и вносит погрешности в ее решение. Альтернативный подход основан на использовании для решения плохо обусловленных задач типа (4.3), (4.4) эволюционных алгоритмов глобальной минимизации (типа генетического алгоритма) либо на применении методов поиска минимума на основе коллективного поведения децентрализованной самоорганизующейся системы (типа метода роя частиц, муравьиного алгоритма, алгоритма пчелиной колонии).
Для решения экстремальных задач (4.3), (4.4) ниже будем использовать численный алгоритм, основанный на методе роя частиц (см. [28]). Этот метод был предложен в 1995 г. в работе [29]. Указанный метод не использует значений производных от минимизируемого функционала, является достаточно простым и универсальным при численной реализации. Поэтому в последнее время этот подход применяется при решении широкого класса обратных задач и задач управления в различных областях науки и техники. Одно из важных направлений использования этого метода связано с оптимизацией формы летательных аппаратов (см, например, [30]). Другое направление связано с решением обратных задач механики и физики (см., например, [26], [27], [31]).
В методе роя частиц искомые параметры, определяющие значение минимизируемого функционала $J$, представляются в виде координат радиус-вектора ${\mathbf{s}} = ({{\lambda }_{1}},{{\mu }_{1}},\; \ldots ,\;{{\lambda }_{M}},{{\mu }_{M}})$ некоторой абстрактной частицы. Роем частиц называют любой конечный набор частиц ${{{\mathbf{s}}}_{1}},\; \ldots ,\;{{{\mathbf{s}}}_{N}}$. В этом методе задается начальное положение роя и запускается итерационная процедура перемещения частиц, использующая значения функционала для каждого положения частицы таким образом, что через конечное число шагов все они оказываются в окрестности некоторой точки ${{{\mathbf{s}}}_{ * }}$. При этом на каждой итерации определяются вектор скорости смещения ${{{\mathbf{v}}}_{j}}$ и персональное наилучшее положение ${{{\mathbf{p}}}_{j}}$ $j$-й частицы, $j = 1,\; \ldots ,\;N$, а также глобальное наилучшее положение ${{{\mathbf{p}}}_{g}}$. Они отвечают минимальным значениям функционала для $j$-й частицы и для всего роя за все предыдущие итерации. По завершении итерационного процесса точка ${{{\mathbf{s}}}_{ * }} = {{{\mathbf{p}}}_{g}}$ и выбирается за решение задачи минимизации. Таким образом, алгоритм поиска вектора ${\mathbf{s}} = ({{\lambda }_{1}},{{\mu }_{1}},\; \ldots ,\;{{\lambda }_{M}},{{\mu }_{M}})$, решающего задачу (4/4), можно записать в виде следующих шагов:
Шаг 0. Задать значения параметров алгоритма и начальные положения ${\mathbf{s}}_{j}^{0}$, $j = 1,\; \ldots ,\;N$ всех частиц. Положить ${\mathbf{v}}_{j}^{0} = 0$, ${\mathbf{p}}_{j}^{0} = {\mathbf{s}}_{j}^{0}$. Вычислить значения $J({\mathbf{s}}_{j}^{0})$ функционала $J$ для всех частиц. Найти их минимум и определить глобальное наилучшее положение ${{{\mathbf{p}}}_{g}}$, отвечающее минимуму. Положить $i = 0$.
Шаг 1. Для каждой частицы ${\mathbf{s}}_{j}^{i}$, $j = 1,\; \ldots ,\;N$ вычислить новое значение вектора скорости ${\mathbf{v}}_{j}^{{i + 1}}$ и новое положение ${\mathbf{s}}_{j}^{{i + 1}}$ по формулам
(4.6)
${\mathbf{v}}_{j}^{{i + 1}} = w{\mathbf{v}}_{j}^{i} + {{c}_{1}}{{d}_{1}}\left( {{\mathbf{p}}_{j}^{i} - {\mathbf{s}}_{j}^{i}} \right) + {{c}_{2}}{{d}_{2}}\left( {{{{\mathbf{p}}}_{g}} - {\mathbf{s}}_{j}^{i}} \right),\quad {\mathbf{s}}_{j}^{{i + 1}} = {\mathbf{s}}_{j}^{i} + {\mathbf{v}}_{j}^{{i + 1}}.$Шаг 2. Если условие выхода из цикла не выполняется, то положить $i: = i + 1$ и перейти на шаг 1.
Условие выхода из цикла может определяться достижением достаточно малого значения ${{J}^{{opt}}}$ функционала $J$ либо максимального числа итераций $L$. Нижний индекс $j \in \left\{ {1,\; \ldots ,\;N} \right\}$ в (4.6) обозначает номер частицы, а верхний индекс $i \in \left\{ {0,\; \ldots ,\;L} \right\}$ – номер итерации. Числа $w$, ${{c}_{1}}$ и ${{c}_{2}}$ являются постоянными параметрами алгоритма. Коэффициенты ${{d}_{1}}$ и ${{d}_{2}}$ являются случайными величинами, равномерно распределенными на интервале $(0,\;1)$. Из описания алгоритма следует, что центральное место в методе роя частиц занимает выбор числа $N$ частиц роя и параметров $w$, ${{c}_{1}}$, ${{c}_{2}}$, входящих в формулу (4.6) для ${\mathbf{v}}_{j}^{{i + 1}}$. Достаточно подробно об этом написано в [28].
В заключение этого раздела исследуем свойства функционалов ${{J}_{e}}$, ${{J}_{i}}$ и $J$ в простейшем случае однослойной оболочки, отвечающем ситуации, когда множество $S$ в (4.2) определяется соотношением
(4.8)
${{J}^{{{\text{min}}}}} \leqslant \mathop {inf}\limits_{({{\lambda }_{ * }},{{\mu }_{ * }}) \in S*} J({{\lambda }_{ * }},{{\mu }_{ * }}) \leqslant J({{\lambda }_{ * }},{{\mu }_{ * }})\quad \forall ({{\lambda }_{ * }},{{\mu }_{ * }}) \in S{\text{*}}{\text{.}}$(4.9)
${{J}_{e}}({{\lambda }_{ * }},{{\mu }_{ * }}) = 0,\quad \int\limits_{{{\Omega }_{i}}} {{{{\left| {\nabla {{U}^{e}}} \right|}}^{2}}} d{\mathbf{x}} = \mathop {\left( {\frac{{{{u}_{0}}}}{{{{z}_{0}}}}} \right)}\nolimits^2 \int\limits_{{{\Omega }_{i}}} {d{\mathbf{x}}} ,\quad \int\limits_{{{\Omega }_{i}}} {{{{\left| {\nabla {{u}_{i}}} \right|}}^{2}}} d{\mathbf{x}} = \mathop {\left( {\frac{{{{u}_{0}}}}{{{{z}_{0}}}}} \right)}\nolimits^2 {{\mathcal{K}}^{2}}(s)\int\limits_{{{\Omega }_{i}}} {d{\mathbf{x}}} .$(4.10)
${{J}_{i}}({{\lambda }_{ * }},{{\mu }_{ * }}) = \mathcal{K}(s) = \mathop {\left( {\frac{a}{b}} \right)}\nolimits^{q(s) - 1} \quad \forall ({{\lambda }_{ * }},{{\mu }_{ * }}) \in S*,\quad s = {{\mu }_{ * }}{\text{/}}{{\lambda }_{ * }}.$Полученное соотношение (4.10) позволяет придать физический смысл значению ${{J}_{i}}({{\lambda }_{ * }},{{\mu }_{ * }})$ функционала ${{J}_{i}}$ на любой допустимой паре $({{\lambda }_{ * }},{{\mu }_{ * }}) \in S* \subset S$ как мере видимости $\mathcal{K}(s)$ оболочки $(\Omega ,{{\lambda }_{ * }},{{\mu }_{ * }})$, отвечающей паре $({{\lambda }_{ * }},{{\mu }_{ * }})$, которая, как указывалось раньше, стремится к нулю при $s \to \infty $. Учитывая (4.10) и (4.8), приходим к следующей оценке значения ${{J}^{{{\text{min}}}}}$:
(4.11)
${{J}^{{{\text{min}}}}} \leqslant J({{\lambda }_{ * }},{{\mu }_{ * }}) = 0.5{{J}_{i}}({{\lambda }_{ * }},{{\mu }_{ * }}) = 0.5\mathcal{K}(s)\quad \forall ({{\lambda }_{ * }},{{\mu }_{ * }}) \in S*,\quad s = \mu {\text{*/}}\lambda {\text{*}}{\text{.}}$Исходя из приведенных результатов, маскировочную эффективность проектируемой маскировочной оболочки $(\Omega ,\lambda ,\mu )$ будем оценивать при помощи величины
5. АНАЛИЗ РЕЗУЛЬТАТОВ ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
Обсудим здесь первые результаты по численному решению рассматриваемых задач маскировки с использованием метода роя частиц. Полученные результаты имеют, с одной стороны, самостоятельное значение, а с другой стороны, они могут использоваться при выборе начальных приближений при применении итерационных методов, сходимость которых зависит от удачного выбора начальных приближений. Отметим прежде всего, что наиболее затратной частью описанного выше алгоритма является вычисление значений $J({\mathbf{s}}_{j}^{i})$ минимизируемого функционала $J({\mathbf{s}})$ для положения ${\mathbf{s}}_{j}^{i}$ частицы при разных значениях $i$ и $j$. Эта процедура состоит из двух этапов. На первом этапе вычисляется решение $U({\mathbf{s}}_{j}^{i})$ прямой задачи 1. Для этого мы используем пакет программ FreeFEM++ (www.freefem.org), предназначенный для численного решения двумерных и трехмерных краевых задач методом конечных элементов. После нахождения $U({\mathbf{s}}_{j}^{i})$ далее вычисляются среднеквадратичные интегральные нормы, входящие в выражения функционалов ${{J}_{e}}$ либо ${{J}_{i}}$ в (4.5), при помощи численного интегрирования по сечению области ${{\Omega }_{e}}$ либо ${{\Omega }_{i}}$ плоскостью $y = 0$.
При проведении вычислительных экспериментов предполагалось, что область $D$, оболочка $\Omega $ и граничные условия определяются при помощи следующих размерных величин:
Приближенно замаскировать тело, помещенное в подобласть ${{\Omega }_{i}}$, можно при помощи однослойной универсальной оболочки $(\Omega ,{\mathbf{s}})$, где ${\mathbf{s}} = (\lambda ,\mu )$, искомые параметры которой $(\lambda ,\mu )$ определяются путем решения задачи минимизации (4.4) при $M = 1$. При этом важную роль играет выбор ограничений ${{\lambda }_{0}}$, ${{\lambda }^{0}}$, ${{\mu }_{0}}$, ${{\mu }^{0}}$ множества управлений $S$ в (4.2). Из анализа свойств точного решения (2.6) следует, что материалы с малым значением параметра $\lambda $ и большим значением параметра $\mu $ (т.е. с высокой анизотропией $s$) обеспечивают малость значения ${{J}_{i}}(\lambda ,\mu )$ функционала ${{J}_{i}}$, равного $\mathcal{K}(s)$ при $s = \mu {\text{/}}\lambda $, поскольку $\mathcal{K}(s) = {{(a{\text{/}}b)}^{{q(s) - 1}}} \to 0$ при $s = \mu {\text{/}}\lambda \to \infty $. С учетом этого при проведении расчетов для однослойных оболочек выбирались малые значения ${{\lambda }_{0}} = 0.01{{\sigma }_{0}}$ и ${{\lambda }^{0}} = 0.5{{\sigma }_{0}}$ для границ параметра $\lambda $ и относительно большие (возрастающие) значения границ ${{\mu }_{0}}$ и ${{\mu }^{0}}$ для второго параметра $\mu $ (см. ниже).
Полученные путем минимизации функционала $J$ оптимальные значения $({{\lambda }^{{{\text{opt}}}}}$, ${{\mu }^{{{\text{opt}}}}})$ управляющих параметров, соответствующие им значения параметра анизотропии $s = {{\mu }^{{{\text{opt}}}}}{\text{/}}{{\lambda }^{{{\text{opt}}}}}$ и оптимальные значения ${{J}^{{{\text{opt}}}}} \equiv J({{\lambda }^{{{\text{opt}}}}},{{\mu }^{{{\text{opt}}}}})$, $J_{i}^{{{\text{opt}}}} \equiv {{J}_{i}}({{\lambda }^{{{\text{opt}}}}},{{\mu }^{{{\text{opt}}}}})$, $J_{e}^{{{\text{opt}}}} \equiv {{J}_{e}}({{\lambda }^{{{\text{opt}}}}},{{\mu }^{{{\text{opt}}}}})$ функционалов качества $J$, ${{J}_{i}}$ и ${{J}_{e}}$ представлены в табл. 1 для четырех разных сценариев, отвечающих четырем разным возрастающим парам $({{\mu }_{0}},{{\mu }^{0}})$. Как и следовало ожидать, увеличение параметра анизотропии $s$ материала оболочки приводит к уменьшению значений $J({{\lambda }^{{{\text{opt}}}}},{{\mu }^{{{\text{opt}}}}})$ и ${{J}_{i}}({{\lambda }^{{{\text{opt}}}}},{{\mu }^{{{\text{opt}}}}})$.
Таблица 1.
Результаты вычислительных экспериментов для однослойной анизотропной маскировочной оболочки при разном выборе границ множества управлений
| ${{\mu }_{0}}{\text{/}}{{\sigma }_{0}}$ | ${{\mu }^{0}}{\text{/}}{{\sigma }_{0}}$ | ${{\lambda }^{{{\text{opt}}}}}{\text{/}}{{\sigma }_{0}}$ | ${{\mu }^{{{\text{opt}}}}}{\text{/}}{{\sigma }_{0}}$ | $s$ | ${{J}^{{{\text{opt}}}}}$ | $J{{_{i}^{{{\text{opt}}}}}^{{}}}$ | $J_{e}^{{{\text{opt}}}}$ |
|---|---|---|---|---|---|---|---|
| 0.1 | 5 | $4.2 \times {{10}^{{ - 2}}}$ | 5 | 119 | $9.65 \times {{10}^{{ - 3}}}$ | $4.91 \times {{10}^{{ - 3}}}$ | $1.44 \times {{10}^{{ - 2}}}$ |
| 5 | 10 | $4.1 \times {{10}^{{ - 2}}}$ | 10 | 244 | $5.47 \times {{10}^{{ - 4}}}$ | $4.23 \times {{10}^{{ - 4}}}$ | $6.71 \times {{10}^{{ - 4}}}$ |
| 10 | 15 | $3.5 \times {{10}^{{ - 2}}}$ | 11.1 | 317 | $4.19 \times {{10}^{{ - 4}}}$ | $1.37 \times {{10}^{{ - 4}}}$ | $7.03 \times {{10}^{{ - 4}}}$ |
| 15 | 20 | $1.9 \times {{10}^{{ - 2}}}$ | 16.3 | 858 | $3.76 \times {{10}^{{ - 4}}}$ | $3.81 \times {{10}^{{ - 7}}}$ | $7.52 \times {{10}^{{ - 4}}}$ |
Для оболочки с сильной анизотропией, отвечающей последней строке табл. 1, вычисленное внешнее поле ${{u}_{e}}[{{\lambda }^{{{\text{opt}}}}},{{\mu }^{{{\text{opt}}}}}]$, отвечающее оптимальным значениям
(5.1)
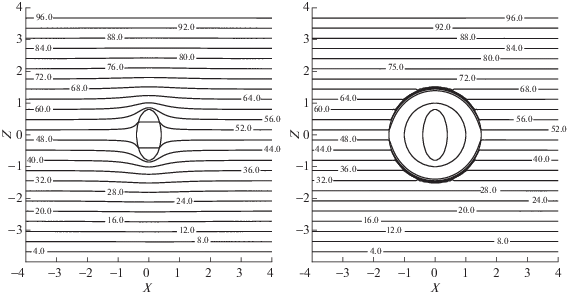
${{\lambda }^{{{\text{opt}}}}} = 1.9 \times {{10}^{{ - 2}}}{{\sigma }_{0}},\quad {{\mu }^{{{\text{opt}}}}} = 16.3{{\sigma }_{0}},$Фиг. 3.
Линии уровня в сечении плоскостью $y = 0$ внешнего поля ${{U}^{e}}(x,0,z)$ (а) и поля $U(x,0,z)$ при наличии универсальной оболочки без тела (б).

Предположим теперь, что в область $D$, заполненную внешней средой с коэффициентом электропроводности ${{\sigma }_{0}} = 1$, помещается шар радиуса ${{r}_{0}} = 0.8$ м, заполненный однородным изотропным материалом с коэффициентом электропроводности $\sigma = 10$σ0. Внесение данного тела в область $D$ приводит (в отсутствие оболочки) к возмущению внешнего поля ${{U}^{e}}$, которое проявляется геометрически на фиг. 4а искривлением первоначально прямых линий уровня поля ${{U}^{e}}$, представленных на фиг. 3а. Количественно указанное возмущение определяется значением меры внешнего возмущения поля ${{\Delta }_{e}} = {{{{{\left\| {U - {{U}^{e}}} \right\|}}_{{{{\Omega }_{e}}}}}} \mathord{\left/ {\vphantom {{{{{\left\| {U - {{U}^{e}}} \right\|}}_{{{{\Omega }_{e}}}}}} {{{{\left\| {{{U}^{e}}} \right\|}}_{{{{\Omega }_{e}}}}}}}} \right. \kern-0em} {{{{\left\| {{{U}^{e}}} \right\|}}_{{{{\Omega }_{e}}}}}}}$, принимающей в данном случае значение $1.02 \times {{10}^{{ - 2}}}$. Именно указанное возмущение поля позволяет обнаружить присутствие тела. Для маскировки внесенного шара его следует окружить универсальной маскировочной оболочкой с параметрами ${{\lambda }^{{{\text{opt}}}}}$ и ${{\mu }^{{{\text{opt}}}}}$, приведенными в (5.1). Полученное в результате решения соответствующей прямой задачи поле ${{U}^{{{\text{opt}}}}} = U({{\lambda }^{{{\text{opt}}}}},{{\mu }^{{{\text{opt}}}}})$, которому отвечает значительно меньшее значение меры внешнего возмущения поля $\Delta _{e}^{{{\text{opt}}}} = {{{{{\left\| {{{U}^{{{\text{opt}}}}} - {{U}^{e}}} \right\|}}_{{{{\Omega }_{e}}}}}} \mathord{\left/ {\vphantom {{{{{\left\| {{{U}^{{{\text{opt}}}}} - {{U}^{e}}} \right\|}}_{{{{\Omega }_{e}}}}}} {{{{\left\| {{{U}^{e}}} \right\|}}_{{{\text{opt}}}}}}}} \right. \kern-0em} {{{{\left\| {{{U}^{e}}} \right\|}}_{{{\text{opt}}}}}}}$, равное $1.14 \times {{10}^{{ - 3}}}$, представлено в виде изолиний на фиг. 4б.
Фиг. 4.
Линии уровня поля $U(x,0,z)$ в сечении плоскостью $y = 0$ для сферического тела без оболочки (а) и при ее наличии (б).

В качестве второго возмущающего тела выберем эллипсоид вращения с горизонтальной полуосью ${{a}_{x}} = 0.4$ м и вертикальной полуосью ${{a}_{z}} = 0.8$ м, заполненный однородным изотропным материалом с коэффициентом электропроводности $\sigma = 10$σ0. Наличие эллипсоида в области $D$ проявляется на фиг. 5а искривленными линиями уровня возмущенного поля и определяется количественно значением ${{\Delta }_{e}} = 6.76 \times {{10}^{{ - 3}}}$. Последующее помещение в область $D$ оболочки $(\Omega ,{{\lambda }^{{{\text{opt}}}}},{{\mu }^{{{\text{opt}}}}})$ опять приводит в значительному уменьшению возмущения поля ${{U}^{e}}$, вызванного указанным эллипсоидом. Это вытекает из фиг. 5б, где представлены изолинии соответствующего поля ${{U}^{{{\text{opt}}}}}$, для которого соответствующее значение $\Delta _{e}^{{{\text{opt}}}}$ равно $1.14 \times {{10}^{{ - 3}}}$. Таким образом, использование маскировочной оболочки для обоих тел приводит к существенному уменьшению внешнего возмущения ${{\Delta }_{e}}$ поля ${{U}^{e}}$, вызванного помещением маскируемого тела (шара или эллипсоида) в область ${{\Omega }_{i}}$.
Фиг. 5.
Линии уровня поля $U(x,0,z)$ в сечении плоскостью $y = 0$ для эллипсоидального тела без оболочки (а) и при ее наличии (б).
Отметим, что, в отличие от статьи [27], посвященной решению задачи маскировки конкретного тела путем решения задачи (4.3), в данной статье была решена задача дизайна универсальной оболочки, служащей для маскировки материальных тел, помещаемых внутрь подобласти ${{\Omega }_{i}}$. Указанная универсальность достигается за счет высокой анизотропии используемого в оболочке материала. Подчеркнем, что каждое из указанных выше тел можно замаскировать при помощи своей персонально подобранной оболочки с существенно меньшим показателем анизотропии путем решения задачи внешней маскировки (4.3). В частности, для шара радиуса $r = 0.8$ м решение экстремальной задачи (4.3) для однослойной однородной изотропной маскировочной оболочки при $S = \left\{ {{\mathbf{s}} = (\lambda ,\mu ):\;0.01{{\sigma }_{0}} \leqslant \lambda ;\;\mu \leqslant 15{{\sigma }_{0}}} \right\}$ дает следующие значения:
Для этого можно применить подход, основанный на проектировании многослойных оболочек с использованием двух однородных изотропных материалов, чередующихся по слоям (см., например, [9]). Предполагая, что число слоев $M$ четно, обозначим коэффициенты электропроводности $j$-го слоя через ${{\sigma }_{j}}$, $j = 1,\; \ldots ,\;M$, а коэффициенты электропроводности используемых материалов через ${{\sigma }_{A}}$ и ${{\sigma }_{B}}$. Распределим материалы по слоям таким образом, что ${{\sigma }_{1}} = {{\sigma }_{3}} = \; \ldots \; = {{\sigma }_{{M - 1}}} = {{\sigma }_{A}}$, ${{\sigma }_{2}} = {{\sigma }_{4}} = \; \ldots \; = {{\sigma }_{M}} = {{\sigma }_{B}}$, и решим задачу минимизации (4.4), в которой под вектором управляющих параметров ${\mathbf{s}}$ будем понимать пару $({{\sigma }_{A}},{{\sigma }_{B}})$, а под $S$ – множество $S = \left\{ {({{\sigma }_{A}},{{\sigma }_{B}}){\text{:}}\;0.01{{\sigma }_{0}} \leqslant {{\sigma }_{A}},\;{{\sigma }_{B}} \leqslant 15{{\sigma }_{0}}} \right\}$. Полученные путем минимизации функционала $J$ оптимальные значения $\sigma _{A}^{{{\text{opt}}}}$ и $\sigma _{B}^{{{\text{opt}}}}$ управляющих параметров ${{\sigma }_{A}}$ и ${{\sigma }_{B}}$ и соответствующие им оптимальные значения ${{J}^{{{\text{opt}}}}}$, $J_{i}^{{{\text{opt}}}}$ и $J_{e}^{{{\text{opt}}}}$ функционалов качества $J$, ${{J}_{i}}$ и ${{J}_{e}}$ представлены в табл. 2 для пяти различных сценариев, отвечающих значениям $M = 2,\;4,\;6,\;8,\;10$. Отчетливо видно, что минимальное значение ${{J}^{{{\text{opt}}}}}$ функционала $J$ (а также $J_{i}^{{{\text{opt}}}}$) уменьшается с ростом числа $M$, достигая при $M = 10$ значения ${{J}^{{{\text{opt}}}}} = 3.31 \times {{10}^{{ - 4}}}$, отвечающего достаточно высокой маскировочной эффективности соответствующей оболочки $(\Omega ,{{{\mathbf{s}}}^{{{\text{opt}}}}})$.
Таблица 2.
Результаты вычислительных экспериментов для многослойной оболочки с чередующимися изотропными слоями для разного числа слоев $M$
| $M$ | $\sigma _{A}^{{{\text{opt}}}}{\text{/}}{{\sigma }_{0}}$ | $\sigma _{B}^{{{\text{opt}}}}{\text{/}}{{\sigma }_{0}}$ | ${{J}^{{{\text{opt}}}}}$ | $J{{_{i}^{{{\text{opt}}}}}^{{}}}$ | $J_{e}^{{{\text{opt}}}}$ |
|---|---|---|---|---|---|
| 2 | 0.01 | 3.07 | $4.01 \times {{10}^{{ - 2}}}$ | $8.01 \times {{10}^{{ - 2}}}$ | $1.24 \times {{10}^{{ - 4}}}$ |
| 4 | 0.01 | 5.83 | $8.14 \times {{10}^{{ - 3}}}$ | $1.61 \times {{10}^{{ - 2}}}$ | $1.81 \times {{10}^{{ - 4}}}$ |
| 6 | 0.01 | 7.66 | $4.25 \times {{10}^{{ - 3}}}$ | $8.31 \times {{10}^{{ - 3}}}$ | $1.91 \times {{10}^{{ - 4}}}$ |
| 8 | 0.01 | 9.61 | $7.81 \times {{10}^{{ - 4}}}$ | $1.54 \times {{10}^{{ - 3}}}$ | $2.91 \times {{10}^{{ - 5}}}$ |
| 10 | 0.01 | 11.28 | $3.31 \times {{10}^{{ - 4}}}$ | $6.37 \times {{10}^{{ - 4}}}$ | $2.42 \times {{10}^{{ - 5}}}$ |
Можно добиться еще большей маскировочной эффективности многослойной оболочки, если предположить, что проектируемая оболочка состоит из $M$ различных однородных изотропных слоев, обладающих разными в общем случае проводимостями ${{\sigma }_{1}},{{\sigma }_{2}},\; \ldots ,\;{{\sigma }_{M}}$, выбрав в качестве $S$ множество $\left\{ {({{\sigma }_{1}},{{\sigma }_{2}}, \ldots ,{{\sigma }_{M}})} \right.{\text{:}}\;0.01{{\sigma }_{0}} \leqslant {{\sigma }_{k}} \leqslant 15{{\sigma }_{0}},\;\left. {k = 1,\; \ldots ,\;M} \right\}$. Расчеты показали, что в этом случае оптимальные значения всех управляющих параметров с нечетным индексом совпадают и равны нижней границе $0.01{{\sigma }_{0}}$, все четные управления, кроме последнего, принимают максимально возможное значение $15{{\sigma }_{0}}$, а $\sigma _{M}^{{{\text{opt}}}}$ растет с ростом числа слоев $M$. Полученные путем минимизации функционала $J$ оптимальные значения $\sigma _{1}^{{{\text{opt}}}}$, $\sigma _{2}^{{{\text{opt}}}}$, $\sigma _{M}^{{{\text{opt}}}}$ управляющих параметров и соответствующие им оптимальные значения ${{J}^{{{\text{opt}}}}}$, $J_{i}^{{{\text{opt}}}}$ и $J_{e}^{{{\text{opt}}}}$ представлены в табл. 3 для тех же пяти различных сценариев $M = 2,\;4,\;6,\;8,\;10$. Сравнительный анализ табл. 2 и 3 показывает, что увеличение числа управлений за счет перехода от чередующихся слоев к независимым слоям оболочки позволяет уменьшить оптимальное значение ${{J}^{{{\text{opt}}}}}$ функционала $J$ и, следовательно, увеличить маскировочную эффективность соответствующей оболочки $(\Omega ,{{\sigma }^{{{\text{opt}}}}})$ примерно в два раза за счет уменьшения значения $J_{i}^{{{\text{opt}}}}$.
Таблица 3.
Результаты вычислительных экспериментов для многослойной оболочки с независимыми изотропными слоями для разного числа слоев $M$
| $M$ | $\sigma _{1}^{{{\text{opt}}}}{\text{/}}{{\sigma }_{0}}$ | $\sigma _{2}^{{{\text{opt}}}}{\text{/}}{{\sigma }_{0}}$ | $\sigma _{M}^{{{\text{opt}}}}{\text{/}}{{\sigma }_{0}}$ | ${{J}^{{{\text{opt}}}}}$ | $J{{_{i}^{{{\text{opt}}}}}^{{}}}$ | $J_{e}^{{{\text{opt}}}}$ |
|---|---|---|---|---|---|---|
| 2 | 0.01 | 3.07 | 3.07 | $4.01 \times {{10}^{{ - 2}}}$ | $8.01 \times {{10}^{{ - 2}}}$ | $1.24 \times {{10}^{{ - 4}}}$ |
| 4 | 0.01 | 15 | 5.74 | $3.55 \times {{10}^{{ - 3}}}$ | $6.93 \times {{10}^{{ - 3}}}$ | $1.76 \times {{10}^{{ - 4}}}$ |
| 6 | 0.01 | 15 | 7.48 | $1.58 \times {{10}^{{ - 3}}}$ | $2.98 \times {{10}^{{ - 3}}}$ | $1.94 \times {{10}^{{ - 4}}}$ |
| 8 | 0.01 | 15 | 9.43 | $3.09 \times {{10}^{{ - 4}}}$ | $5.88 \times {{10}^{{ - 4}}}$ | $3.03 \times {{10}^{{ - 5}}}$ |
| 10 | 0.01 | 15 | 11.03 | $1.77 \times {{10}^{{ - 4}}}$ | $2.92 \times {{10}^{{ - 4}}}$ | $6.23 \times {{10}^{{ - 5}}}$ |
Отмеченная выше закономерность, заключающаяся в том, что оптимальные значения параметров всех слоев, кроме последнего, чередуются, принимая минимальное и максимальное из возможных значений, наблюдалась и при расчетах других сценариев маскировочных оболочек. Это позволяет сводить решение задачи минимизации (4.4) к нахождению электропроводности ${{\sigma }_{M}}$ последнего слоя. Отмеченную закономерность можно использовать для значительного снижения вычислительных затрат при решении задач проектирования маскировочных оболочек.
При дальнейшем увеличении числа слоев $M$ наступает эффект насыщения, в том смысле, что последующее увеличение $M$ не приводит к заметному увеличению маскировочной эффективности для фиксированного выбора множества $S$. Тем не менее дальнейшего улучшения маскировочного эффекта можно добиться за счет специального расширения множества $S$, как это вытекает из разд. 4. Указанный эффект насыщения с увеличением числа слоев отмечался и в близких работах по электромагнитной маскировке (см., например, [32]).
Проведенные численные расчеты подтвердили принципиальную возможность создания универсальных маскировочных оболочек, снижающих заметность материального тела для систем обнаружения, основанных на регистрации внешних возмущений электрического поля. Как и было предсказано на основе анализа точных решений в некоторых частных случаях, для достижения указанной универсальности при построении оболочки требуется использовать материалы с высокой анизотропией. Так как материалы с указанными свойствами в природе практически не встречаются, то вместо них можно использовать многослойные оболочки, собранные из оптимально подобранных однородных изотропных материалов. Анализ результатов вычислительных экспериментов продемонстрировал увеличение маскировочной эффективности многослойных оболочек с ростом числа слоев.
Предложенный в статье подход к решению задач дизайна маскировочных оболочек является достаточно универсальным и может быть использован без существенных изменений при решении задач маскировки в магнитостатике и теплопереносе. По аналогичной схеме могут быть рассмотрены более общие задачи управления стационарными физическими полями различной природы за счет создания специальных конструкций с оптимально выбранными физическими и геометрическими свойствами.
Список литературы
Narayana S., Sato Y. Heat flux manipulation with engineered thermal materials // Phys. Rev. Lett. 2012. V. 108. 214303.
Guenneau S., Amra C., Veynante D. Transformation thermodynamics: cloaking and concentrating heat flux // Opt. Express. 2012. V. 20. 8207.
Han T., Qiu C.-W. Transformation Laplacian metamaterials: recent advances in manipulating thermal and dc fields // J. Opt. 2016. V. 18. 044003.
Алексеев Г.В. Проблема невидимости в акустике, оптике и теплопереносе. Владивосток: Дальнаука, 2016. 224 с.
Guenneau S., Petiteau D., Zerrad M., Amra C., Puvirajesinghe T. Transformed Fourier and Fick equations for the control of heat and mass diffusion // AIP Advances. 2015. V. 5. 053404.
Pendry J.B., Schurig D., Smith D.R. Controlling electromagnetic fields // Science. 2006. V. 312. P. 1780–1782.
Cummer S.A., Schurig D. One path to acoustic cloaking // New J. Phys. 2007. V. 9. P. 45.
Sanchez A., Navau C., Prat-Camps J., Chen D.X. Antimagnets: controlling magnetic fields with superconductor-metamaterial hybrids // New J. Phys. 2011. V. 13. 093034.
Han T., Yuan T., Li B., Qiu C.W. Homogeneous thermal cloak with constant conductivity and tunable heat localization // Sci. Rep. 2013. Vol. 3. P. 1593.
Yang F., Zhong Mei Z.L., Jin T.Y., Cui T.J. DC electric invisibility cloak // Phys. Rev. Lett. 2012. V. 109. 053902.
Zeng L. Bi-layer steady state current cloak // Phys. Lett. A. 2014. V. 378. P. 923–926.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1986. 288 с.
Алифанов О.М., Артюхин Е.А., Румянцев С.В. Экстремальные решения некорректных задач и их приложения к обратным задачам теплообмена. М.: Наука, 1988. 288 с.
Фурсиков А.В. Оптимальное управление распределенными системами. Теория и приложения. Новосибирск: Научная книга, 1999. 352 с.
Короткий А.И., Стародубцева Ю.В. Моделирование прямых и обратных граничных задач для стационарных моделей тепломассопереноса. Екатеринбург: Издательство Уральского университета, 2015. 168 с.
Самарский А.А., Вабишевич П.Н. Численные методы решения обратных задач математической физики. М.: Эдиториал УЗСС. 2004. 480 с.
Алексеев Г.В., Вахитов И.С., Соболева О.В. Оценки устойчивости в задачах идентификации для уравнения конвекции-диффузии-реакции // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 12. С. 2190–2205.
Исмаил-заде А.Т., Короткий А.И., Наймарк Б.М., Цепелев И.А. Трехмерное численное моделирование обратной задачи тепловой конвекции // Ж. вычисл. матем. и матем. физ. 2003. Т. 43. № 4. С. 614–626.
Терешко Д.А. Численное восстановление граничного потока тепла для стационарных уравнений тепловой конвекции // Сиб. журн. индустр. матем. 2014. Т. 17. № 4. С. 111–119.
Бризицкий Р.В., Савенкова А.С. Обратные экстремальные задачи для уравнений Максвелла // Ж. вычисл. матем. и матем. физ. 2010. Т. 50. № 6. С. 1038–1046.
Бризицкий Р.В., Сарицкая Ж.Ю. Оценки устойчивости решений экстремальных задач для нелинейного уравнения конвекции–диффузии–реакции // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 12. С. 60–71.
Бризицкий Р.В., Сарицкая Ж.Ю. Обратные коэффициентные задачи для нелинейного уравнения конвекции–диффузии–реакции // Изв. РАН. Сер. матем. 2018. Т. 82. № 1. С. 17–33.
Алексеев Г.В. Управление граничным импедансом в двумерной задаче маскировки материальных тел методом волнового обтекания // Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 12. С. 2044–2061.
Алексеев Г.В., Лобанов А.В., Спивак Ю.Э. Оптимизационный метод в задачах акустической маскировки материальных тел // Ж. вычисл. матем. и матем. физ. 2017. Т. 57. № 9. С. 1477–1493.
Алексеев Г.В. Анализ двумерной задачи тепловой маскировки на основе оптимизационного метода // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 4. С. 504–519.
Алексеев Г.В., Левин В.А., Терешко Д.А. Оптимизационный анализ задачи тепловой маскировки цилиндрического тела // Докл. АН. 2017. Т. 472. № 4. С. 398–402.
Алексеев Г.В., Левин В.А., Терешко Д.А. Оптимизационный метод в задачах дизайна сферических слоистых тепловых оболочек // Докл. АН. 2017. Т. 476. № 5. С. 512–517.
Poli R., Kennedy J., Blackwell T. Particle swarm optimization: an overview // Swarm Intel. 2007. V. 1. P. 33–57.
Kennedy J., Eberhart R. Particle swarm optimization // Proceedings of IEEE International Conference on Neural Networks. IV. 1995. P. 1942–1948.
Chiba K., Makino Y., Takatoya T. PSO/GA hybrid method and its application to supersonic-transport wing design // J. Comp. Sci. Tech. 2008. V. 2. № 1. P. 268–280.
Ardakani M.D., Khodadad M. Identification of thermal conductivity and the shape of an inclusion using the boubdary elements method and particle swarm optimization algorithm // Inverse Probl. Sci. Eng. 2009. V. 17. № 7. P. 855–870.
Mirzaei A., Shadrivov I.V., Miroshnichenko A.E., Kivshar Y.S. Optimization of cloaking in all dielectric multi-layer structures // IEEE Advanced Electromagnetic Materials in Microwaves and Optics. 2014. P. 208–210.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики




