Журнал вычислительной математики и математической физики, 2019, T. 59, № 2, стр. 235-246

Многометодная оптимизация управления в сложных прикладных задачах

А. И. Тятюшкин^*

ФГБУН Ин-т динамики систем и теории управления СО РАН
664033 Иркутск, ул. Лермонтова, 134, Россия

Поступила в редакцию 05.05.2018
После доработки 16.05.2018

DOI: 10.1134/S0044466919020145

Аннотация

Для получения численного решения краевой задачи с достаточно высокой точностью конструируется алгоритм, состоящий из итераций градиентного метода и итераций метода квазилинеаризации. Для нахождения “идеального” решения многокритериальной задачи оптимального управления предлагаются прямой и двойственный алгоритмы, которые обеспечивают эффективный поиск как коэффициентов свертки, так и оптимального управления. Эффективность предложенных многометодных алгоритмов показана на решении прикладных задач. Библ. 10. Фиг. 1.

Ключевые слова: многометодная оптимизация, оптимальное управление, краевая задача, многокритериальная задача, градиентный метод, принцип максимума, метод квазилинеаризации.

ВВЕДЕНИЕ

В процессе решения сложной задачи оптимального управления обычно последовательно реализуются различные алгоритмы, одни из которых имеют достаточно широкую область сходимости и, следовательно, допускают задание грубого начального приближения, а другие начинают с хорошего приближения и позволяют получать решение задачи с требуемой точностью. Так как большинство численных методов решения нелинейных задач сходится к управлениям, удовлетворяющим только необходимым условиям оптимальности, то такая многометодная технология оптимизации (см. [1]) дает возможность избежать попадания в локальный экстремум и повышает надежность расчета оптимального управления для нелинейной системы.

Многометодная технология решения задач оптимального управления заключается в том, что параллельно используется сразу несколько итерационных методов оптимизации для поиска решения одной и той же задачи. Основной проблемой применения многометодной технологии при численном решении задач оптимального управления является выбор метода для эффективного продолжения процесса оптимизации с того момента, когда ухудшилась сходимость текущего метода. Существующие программные средства для установления наиболее подходящего метода в основном ориентированы на последовательное применение методов и выполнение нескольких итераций каждым из них. Уровень интеллекта таких программ обычно оценивается по их возможностям осуществлять выбор метода без участия пользователя. Современные операционные системы позволяют обеспечить решение задачи путем организации параллельных вычислительных потоков для одновременного проведения расчетов несколькими методами. В каждом таком потоке можно реализовывать итерационный процесс одного из методов оптимизации и решение одной задачи вести несколькими методами одновременно. На многопроцессорных компьютерах для реализации каждого метода удобнее использовать отдельный процессор. После нахождения очередного приближения все методы оцениваются, например, по полученному приращению функционала, и из них выбирается наиболее эффективный метод для продолжения оптимизации, а полученное этим методом приближение передается остальным методам в качестве начального для выполнения следующей итерации. Начиная с этого приближения, всеми методами вновь выполняется одна или несколько итераций, и среди полученных приближений опять берется то, на котором достигнуто меньшее значение функционала.

Продолжая таким образом итерационный процесс до получения приближения, на котором с заданной точностью будет выполнен критерий оптимальности, найдем приближенное решение задачи. При этом решение будет найдено многометодным алгоритмом, состоящим из последовательности шагов разных методов, подключаемых к процессу оптимизации с целью ускорения его сходимости. Например, в случае параллельного использования трех методов (см. фигуру) лучшее приближение будет определяться по максимуму приращения функционала, полученного на данной итерации каждым из трех методов

${{u}_{{{{i}_{0}}}}} = \arg \mathop {\max }\limits_{i \in \left\{ {1,2,3} \right\}} \left( {I(u_{i}^{k}) - I(u_{i}^{{k - 1}})} \right).$

Затем это приближение передается всем трем методам для выполнения следующей итерации: $u_{i}^{{k + 1}} = {{u}_{{{{i}_{0}}}}}$, $i = 1,\,\,2,\,\,3$.

Фигура. Схема выполнения $k + 1$-й итерации многометодным алгоритмом для группы из трех методов: ${{M}_{1}}$, ${{M}_{2}}$, ${{M}_{3}}.$

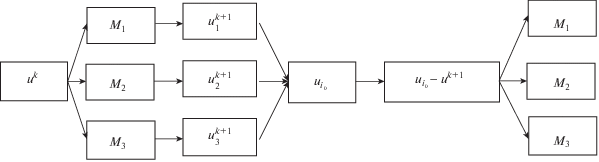
Заметим, что из одной и той же группы методов оптимизации при решении другой задачи может сгенерироваться совсем другой многометодный алгоритм, который будет более адекватно учитывать особенности новой задачи.

Следует также отметить, что выбор метода по приращению функционала будет работать правильно только тогда, когда всеми методами будет использоваться один и тот же способ аппроксимации управления и, кроме того, во всех методах будет обеспечиваться одинаковая точность интегрирования систем. В этом случае все методы оптимизации будут применяться к одной и той же полученной в результате дискретизации конечномерной задаче и значения параметров, по которым осуществляется выбор метода, будут давать более точную оценку эффективности каждого из методов.

Для поиска численного решения краевой задачи, возникающей после применения принципа максимума [2], в статье предлагается многометодная схема, которая состоит из итераций градиентного метода, приводящего решение в окрестность сходимости метода квазилинеаризации (см. [3]), и непосредственно итераций метода квазилинеаризации, обеспечивающего вычисление оптимального управления с заданной точностью.

Далее рассматривается многокритериальная задача оптимального управления и для поиска ее численного решения также предлагается многометодная схема, состоящая из итераций прямого и двойственного методов, обеспечивающая получение “идеального” управления.

Современные информационные технологии и многопроцессорная вычислительная техника позволяют создать программное обеспечение, реализующее многометодную технологию с параллельными вычислениями (см. [4]) для оптимизации сложных систем управления.

1. МНОГОМЕТОДНЫЙ АЛГОРИТМ ДЛЯ РЕШЕНИЯ ЗАДАЧИ ПЕРЕВОДА НЕЛИНЕЙНОГО ОБЪЕКТА

Одной из наиболее распространенных задач оптимального управления является задача перевода нелинейного объекта из одного состояния в другое по некоторому заданному критерию качества:

(1.1)

$\begin{gathered} I(u) = \int\limits_{{{t}_{0}}}^{{{t}_{1}}} {F(x,u,t)dt \to \min ,\quad } \dot {x} = f(x,u,t), \\ x({{t}_{0}}) = {{x}^{0}},\quad x({{t}_{1}}) = {{x}^{1}},\quad x(t) \in {{R}^{n}},\quad u(t) \in {{R}^{r}},\quad t \in [{{t}_{0}},{{t}_{1}}]. \\ \end{gathered} $

В виде (1.1) формулируются, например, задачи управления маневром и стабилизацией космического аппарата (см. [5]).

Для частного класса задач, допускающего явное выражение управления из условия H_u = 0, построим эффективный алгоритм метода квазилинеаризации [3], в котором хорошее начальное приближение отыскивается специальным градиентным методом. После применения принципа максимума будем иметь следующую краевую задачу:

(1.2)

$\begin{gathered} \dot {x} = X(x,\psi ,t),\quad \dot {\psi } = \Psi (x,\psi ,t), \\ x({{t}_{0}}) = {{x}^{0}},\quad x({{t}_{1}}) = {{x}^{1}}. \\ \end{gathered} $

Пусть известно достаточно хорошее начальное приближение, построенное, например, из физических или содержательных соображений. Тогда краевую задачу (1.2) можно решить методом квазилинеаризации, обеспечивающим высокую точность выполнения краевых условий. На итерациях этого метода рассматривается линеаризованная система

(1.3)

${{\dot {x}}^{{k + 1}}} = {{X}_{x}}({{x}^{k}},{{\psi }^{k}},t){{x}^{{k + 1}}} + {{X}_{\psi }}({{x}^{k}},{{\psi }^{k}},t){{\psi }^{{k + 1}}} + {{\rho }^{k}}(t),$

(1.4)

${{\dot {\psi }}^{{k + 1}}} = {{\Psi }_{x}}({{x}^{k}},{{\psi }^{k}},t){{x}^{{k + 1}}} + {{\Psi }_{\psi }}({{x}^{k}},{{\psi }^{k}},t){{\psi }^{{k + 1}}} + {{\eta }^{k}}(t),$

где k – номер итерации;

${{\rho }^{k}} = X({{x}^{k}},{{\psi }^{k}},t) - {{X}_{x}}({{x}^{k}},{{\psi }^{k}},t){{x}^{k}}(t) - {{X}_{\psi }}({{x}^{k}},{{\psi }^{k}},t){{\psi }^{k}}(t),$

${{\eta }^{k}} = \Psi ({{x}^{k}},{{\psi }^{k}},t) - {{\Psi }_{x}}({{x}^{k}},{{\psi }^{k}},t){{x}^{k}}(t) - {{\Psi }_{\psi }}({{x}^{k}},{{\psi }^{k}},t){{\psi }^{k}}(t).$

С помощью фундаментальной матрицы

$\Phi (t) = \left[ {\begin{array}{*{20}{c}} {{{\Phi }_{{11}}}(t)}&{{{\Phi }_{{12}}}(t)} \\ {{{\Phi }_{{21}}}(t)}&{{{\Phi }_{{22}}}(t)} \end{array}} \right],$

удовлетворяющей 2n-мерному уравнению

(1.5)

$\Phi = \left[ {\begin{array}{*{20}{c}} {{{X}_{x}}({{x}^{k}},{{\psi }^{k}},t)}&{{{X}_{\psi }}({{x}^{k}},{{\psi }^{k}},t)} \\ {{{\Psi }_{x}}({{x}^{k}},{{\psi }^{k}},t)}&{{{\Psi }_{\psi }}({{x}^{k}},{{\psi }^{k}},t)} \end{array}} \right]\Phi ,\quad \Phi ({{t}_{0}}) = E,$

решение системы (1.3), (1.4), исходящее из начальной точки (x^k ^+ 1(t₀), ψ^k ^+ 1(t₀)), записывается по формулам

(1.6)

$\begin{gathered} {{x}^{{k + 1}}}(t) = {{\Phi }_{{11}}}(t){{x}^{{k + 1}}}({{t}_{0}}) + {{\Phi }_{{12}}}(t){{\psi }^{{k + 1}}} + {{{\bar {x}}}^{{k + 1}}}(t), \hfill \\ {{\psi }^{{k + 1}}}(t) = {{\Phi }_{{22}}}(t){{x}^{{k + 1}}}({{t}_{0}}) + {{\Phi }_{{22}}}(t){{\psi }^{{k + 1}}} + {{{\bar {\psi }}}^{{k + 1}}}(t), \hfill \\ \end{gathered} $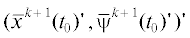

где

– частное решение системы (1.3), (1.4), соответствующее начальным условиям

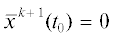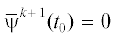Пусть решение (1.6) удовлетворяет краевому условию

${{\Phi }_{{11}}}({{t}_{1}}){{x}^{0}} + {{\Phi }_{{12}}}({{t}_{1}}){{\psi }^{{k + 1}}}({{t}_{0}}) + {{\bar {x}}^{{k + 1}}}({{t}_{1}}) = {{x}^{1}}.$

Тогда новое приближение для вектора начальных условий сопряженной системы ψ(t₀) найдем по формуле

(1.7)

${{\psi }^{{k + 1}}}({{t}_{0}}) = \Phi _{{12}}^{{ - 1}}({{t}_{1}})[{{x}^{1}} - {{\Phi }_{{11}}}({{t}_{1}}){{x}^{0}} - {{\bar {x}}^{{k + 1}}}({{t}_{1}})].$

Интегрируя систему (1.2) при начальных условиях x(t₀) = x⁰, ψ(t₀) = ψ^k ^+ 1(t₀), получаем точку x^k ^+ 1(t₁), которая удовлетворяет неравенству

$\left\| {{{x}^{{k + 1}}}({{t}_{1}}) - {{x}^{1}}} \right\| < \left\| {{{x}^{k}}({{t}_{1}}) - {{x}^{1}}} \right\|.$

Для получения первого приближения $\psi ({{t}_{0}}) = {{{\text{v}}}^{k}}$, достаточно близкого к искомому вектору ψ*(t₀), построим градиентную процедуру, не требующую хорошего начального приближения для сходимости итерационного процесса.

Введем функционал ${{I}_{1}}({\text{v}}) = \frac{1}{2}{{\left\| {x({{t}_{1}},{\text{v}}) - {{x}^{1}}} \right\|}^{2}}$, который является мерой уклонения решения системы (1.2) с начальными условиями $x({{t}_{0}}) = {{x}_{0}}$, $\psi ({{t}_{0}}) = {\text{v}}$ от заданной точки x¹, и поставим задачу поиска ${{{\text{v}}}^{*}} = \mathop {\arg \;\min }\limits_{{\text{v}} \in {{R}^{*}}} {{I}_{1}}({\text{v}})$. Поскольку теперь будет решаться задача со свободным правым концом, решение сопряженной системы ψ(t) должно удовлетворять условию трансверсальности

(1.8)

$\psi ({{t}_{1}}) = {{x}^{1}} - x({{t}_{1}},{\text{v}}).$

Построим функционал невязок

(1.9)

$I({\text{v}}) = {{I}_{1}}({\text{v}}) + \frac{1}{2}{{\left\| {\psi ({{t}_{1}}) + x(t,{\text{v}}) - {{x}^{1}}} \right\|}^{2}}$

и будем рассматривать задачу минимизации функционала (1.9) на решениях системы (1.2) с начальными условиями x(t₀) = x⁰, ψ(t₀) = v. Градиент функционала (1.9) по параметрам (v₁, …, v_n), определяющим начальные условия системы (1.2), вычисляется через решение системы, сопряженной к (1.2):

(1.10)

$\begin{gathered} \dot {\xi } = - X_{x}^{'}(x,\psi ,t)\xi - \Psi _{x}^{'}(x,\psi ,t)\zeta , \\ \dot {\zeta } = - X_{\psi }^{'}(x,\psi ,t)\xi - \Psi _{\psi }^{'}(x,\psi ,t)\zeta , \\ \xi ({{t}_{1}}) = 2({{x}^{1}} - x({{t}_{1}},{\text{v}}) - \psi ({{t}_{1}})), \\ \zeta ({{t}_{1}}) = {{x}^{1}} - x({{t}_{1}},{\text{v}}) - \psi ({{t}_{1}}), \\ \end{gathered} $

и равен $\nabla I({\text{v}}) = - \varsigma ({{t}_{0}})$.

Алгоритм 1

Для улучшения вектора v_k начальных условий сопряженной системы можно применить градиентную процедуру, состоящую из следующих операций:

Шаг 1. Интегрируется система (1.2) при x(t₀) = x⁰, ψ(t₀) = v^k, в узлах интегрирования запоминается решение x^k(t), ψ^k(t), t ∈ T.

Шаг 2. В обратном времени интегрируется система линейных дифференциальных уравнений (1.10), матрица коэффициентов которой вычисляется на решениях x^k(t) и ψ^k(t); при t = t₀ найдется градиент $\nabla I({\text{v}}) = - \varsigma ({{t}_{0}})$.

Шаг 3. С помощью процедуры одномерного поиска отыскивается параметр

${{\alpha }_{k}} = \mathop {\arg \min }\limits_{\alpha \geqslant 0} I({{{\text{v}}}^{k}} + \alpha \zeta ({{I}_{0}})).$

При этом с каждым значением α решается система (1.2) при x(t₀) = x⁰, ψ(t₀) = v^k + ας(t₀).

Шаг 4. Строится новое приближение v^k ^+ 1 = v^k + ας(t₀). Если I(v^k) – I(v^k ^+ 1) > ε, то при k = k + 1 повторяются операции ш. 1–3. В противном случае с ш. 5 выполняются операции метода квазилинеаризации.

Шаг 5. Решается матричное уравнение (1.5), и запоминается Φ(t₁).

Шаг 6. По формуле (1.7) находится вектор ψ^k ^+ 1(t₀).

Шаг 7. Выполняются операции на ш. 1 при ψ(t₀) = v^k = ψ^k ^+ 1(t₀), в результате находится x^k ^+ 1(t₁).

Шаг 8. Если выполняются неравенства $\left\| {{{x}^{{k + 1}}}({{t}_{1}}) - {{x}^{1}}} \right\| < \left\| {{{x}^{k}}({{t}_{1}}) - {{x}^{1}}} \right\|$ и $\left\| {{{x}^{{k + 1}}}({{t}_{1}}) - {{x}^{1}}} \right\| > \varepsilon $, то повторяются операции ш. 5–7.

Шаг 9. Если $\left\| {{{x}^{{k + 1}}}({{t}_{1}}) - {{x}^{1}}} \right\| < \left\| {{{x}^{k}}({{t}_{1}}) - {{x}^{1}}} \right\|$, то уменьшается шаг интегрирования, повышается точность одномерного поиска и вновь повторяются операции градиентной процедуры 1–4, а затем операции метода квазилинеаризации 5–7.

Шаг 10. Если $\left\| {{{x}^{{k + 1}}}({{t}_{1}}) - {{x}^{1}}} \right\| \leqslant \varepsilon $, т.е. точность выполнения краевых условий достигнута, то итерационный процесс прекращается.

Оптимальное управление вычисляется из условия H_u = 0 путем интегрирования системы (1.2) с найденными начальными условиями x(t₀) = x⁰, ψ(t₀) = ψ^k ^+ 1(t₀).

Трудоемкость выполнения операций ш. 1–3 оценивается трудоемкостью интегрирования 2n(2 + ν) скалярных уравнений, где ν – оценка сверху числа итераций одномерного поиска. Трудоемкость итерации метода квазилинеаризации эквивалентна интегрированию 2n + 4n² скалярных уравнений.

2. МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Пусть управляемый процесс описывается системой

(2.1)

$\dot {x} = f(x,u,t),\quad x({{t}_{0}}) = {{x}_{0}},\quad t \in T = [{{t}_{0}},{{t}_{1}}],$

где x(t) ∈ R ⁿ, u(t) ∈ R ^r; вектор-функция f(x, u, t) непрерывно дифференцируема по x и u и непрерывна по t, а управление стеснено ограничениями u(t) ∈ U, U – ограниченное замкнутое множество. На правых концах траекторий системы (2.1) определим непрерывно дифференцируемые выпуклые скалярные функции φ_j(x(t₁)), $j = \overline {1,m} $, которые будут играть роль критериев качества управления:

(2.2)

${{I}_{j}}(u) = {{\varphi }^{j}}(x({{t}_{1}})),\quad j = \overline {1,m} .$

Многоцелевое управление не может быть оптимальным по всем заданным критериям (2.2) одновременно, поэтому речь будет идти о поиске только эффективных (или слабо эффективных) решений [6].

2.1. Алгоритмы прямого поиска численного решения в многокритериальной задаче

Наиболее простой способ для нахождения таких решений состоит в решении последовательности однокритериальных задач с функционалом вида свертки

(2.3)

$I(\lambda ,u) = \sum\limits_{i = 1}^m {{{\lambda }_{i}}{{I}_{i}}(u)} \to \mathop {\min }\limits_{u \in U} $

при разных значениях λ = (λ₁, …, λ_m): λ_i ≥ 0, $\sum\nolimits_{i = 1}^m {{{\lambda }_{i}} = 1} $. Известно (см. [6]), что любое оптимальное решение однокритериальной задачи (2.1), (2.3) будет парето-оптимальным решением.

В соответствии с заданными функционалами (2.2) введем сопряженные системы

(2.4)

${{\dot {\psi }}_{j}} = - {{f}_{x}}(x,u,t){\kern 1pt} {\text{'}}{{\psi }_{j}}(t),\quad {{\psi }_{j}}({{t}_{1}}) = - \varphi _{x}^{j}(x({{t}_{1}})),\quad j = \overline {1,m} ,$

и с помощью их решений ψ_j = ψ_j(t) определим функции Гамильтона ${{H}^{j}}({{\psi }_{j}},x,u,t) = \psi _{j}^{'}(t)f(x,u,t)$, $j = \overline {1,m} $. Далее сформулируем принцип максимума для однокритериальной задачи (2.1), (2.3).

Пусть u*(t), x*(t), t ∈ T, – оптимальное управление и оптимальная траектория. Тогда существует вектор-функция ψ_λ = ψ_λ(t) – решение сопряженной системы

(2.5)

${{\dot {\psi }}_{\lambda }} = - f(x*,u*,t){\kern 1pt} '{\kern 1pt} {{\psi }_{\lambda }}(t),\quad {{\psi }_{\lambda }}({{t}_{1}}) = - \sum\limits_{j = 1}^m {{{\lambda }_{j}}\varphi _{x}^{j}(x{\kern 1pt} {\text{*}}({{t}_{1}}))} $

такая, что при каждом t ∈ T для функции ${{H}^{\lambda }}({{\psi }_{\lambda }},x,u,t) = \psi _{\lambda }^{'}(t)f(x,u,t)$ выполняется условие

(2.6)

${{H}^{\lambda }}({{\psi }_{\lambda }},x*,u*,t) = \mathop {\max }\limits_{u \in U} {{H}^{\lambda }}({{\psi }_{\lambda }},x*,u,t).$

Рассмотрим алгоритм поиска управления, удовлетворяющего принципу максимума (2.6) при некотором заданном λ.

Алгоритм 2

Предположим, что имеем некоторое заданное управление u^k(t) ∈ U, $t \in T$, как начальное приближение.

Шаг 1. Интегрируется уравнение (2.1) при u = u^k(t), в узлах интегрирования запоминается траектория x^k(t).

Шаг 2. В обратном времени интегрируется сопряженная система ${{\dot {\psi }}_{\lambda }} = - {{f}_{x}}({{x}^{k}},{{u}^{k}},t){\kern 1pt} '{\kern 1pt} {{\psi }_{\lambda }}(t)$, ${{\psi }_{\lambda }}({{t}_{1}}) = - \sum\nolimits_{j = 1}^m {{{\lambda }_{j}}\varphi _{x}^{j}({{x}^{k}}({{t}_{1}}))} $, при этом в каждом узле интегрирования вычисляются и запоминаются управление

${{\bar {u}}^{k}}(t) = \arg \mathop {\max }\limits_{u \in U} {{H}^{\lambda }}({{\psi }^{k}},{{x}^{k}},u,t),\quad t \in T,$

и скалярная функция

${{w}_{k}}({{\bar {u}}^{k}}(t),t) = {{H}^{\lambda }}({{\psi }^{k}},{{x}^{k}},{{\bar {u}}^{k}},t) - {{H}^{\lambda }}({{\psi }^{k}},{{x}^{k}},{{u}^{k}},t),\quad t \in T.$

Шаг 3. Находится точка τ_k: ${{w}_{k}}({{\bar {u}}^{k}}({{\tau }_{k}}),{{\tau }_{k}}) = \mathop {\max }\limits_{t \in T} {{w}_{k}}({{\bar {u}}^{k}}(t),t)$. Если ${{w}_{k}}({{\bar {u}}^{k}}({{\tau }_{k}}),{{\tau }_{k}}) = 0$, то u = u^k(t) удовлетворяет принципу максимума и итерационный процесс прекращается.

Шаг 4. Методом одномерной минимизации решается задача

$I(\lambda ,{{u}_{\varepsilon }}) \to \mathop {\min }\limits_{\varepsilon \in [0,1]} ,\quad {{u}_{\varepsilon }}(t) = \left\{ \begin{gathered} {{{\bar {u}}}^{k}}(t),\quad {\text{е с л и }}\quad {{w}_{k}}(t) \geqslant \varepsilon {{w}_{k}}({{\tau }_{k}}), \hfill \\ {{u}^{k}}(t),\quad {\text{е с л и }}\quad {{w}_{k}}(t) < \varepsilon {{w}_{k}}({{\tau }_{k}}), \hfill \\ \end{gathered} \right.$

где ${{w}_{k}}(t) = {{w}_{k}}({{\bar {u}}^{k}},t)$.

Шаг 5. При найденном оптимальном значении ε_k построим новое приближение для управления:

(2.7)

${{u}^{{k + 1}}}(t) = {{u}_{{{{\varepsilon }_{k}}}}}(t),$

которому соответствует наименьшее значение функционала на данной итерации.

Самыми простыми методами одномерной минимизации являются метод деления отрезка пополам и метод золотого сечения. Меньшее число пробных значений переменной требует метод парабол. Но в некоторых случаях необходимо применение методов поиска глобального минимума, которые требуют существенно большего числа пробных значений ε. При поиске ε_k можно использовать несколько потоков для одновременного интегрирования системы (2.1) с управлениями u_ε(t), t ∈ T, соответствующими разным значениям ε.

Шаг 6. При незначительном уменьшении функционала на ш. 4–5 (плохая сходимость) новое приближение для управления строится по формуле

(2.8)

${{u}^{{k + 1}}}(t) = {{u}^{k}}(t) + \alpha [{{\bar {u}}^{k}}(t) - {{u}^{k}}(t)],\quad \alpha \in [0,1],$

где для определения параметра α ∈ [0, 1] аналогично, как на ш. 4 для ε, применяется одномерный поиск. Для этого с выбранным α строится управление (2.8), затем с этим управлением интегрируется система (2.1), а в момент t = t₁ находится значение функционала. Меняя значение α, метод одномерной минимизации находит его оптимальное значение, при котором на данной итерации функционал I(λ, u^k ^+ 1) достигает наименьшего значения.

Шаг 7. Если на ш. 4–6 будет найдено новое приближения для управления, на котором достигается меньшее значение функционала, чем на предыдущей итерации, то выполняется новая итерация на ш. 1.

В противном случае итерационный процесс прекращается.

Как уже отмечалось, в силу структуры управлений, генерируемых итерационной формулой (2.7), погрешность численного интегрирования системы может стать причиной ухудшения сходимости еще до получения управления, удовлетворяющего принципу максимума. Тогда для продолжения процесса оптимизации необходимо применить аналог метода условного градиента (2.8), на итерациях которого конструируются управления не только с граничными, но и с внутренними относительно множества допустимых управлений значениями. Вычисления по формулам (2.7) и (2.8) проводятся параллельно с выбором такого u^k ^+ 1, которому соответствует меньшее значение функционала. Если в итерационной формуле (2.8) управление ${{\bar {u}}^{k}}(t)$ будет вычисляться из линеаризованного принципа максимума: ${{\bar {u}}^{k}}(t) = \arg \mathop {\max }\limits_{u \in U} {{H}_{u}}({{\psi }^{k}},{{x}^{k}},{{u}^{k}},t)'u(t)$, t ∈ T, то будем иметь итерации метода условного градиента. Для систем, линейных по управлению, ${{\bar {u}}^{k}}(t)$ будет совпадать с управлением, найденным из принципа максимума.

Итерационные процессы (2.7), (2.8) должны завершиться получением управления, для которого выполнится необходимое условие оптимальности ${{w}_{k}}({{\bar {u}}^{k}}({{\tau }_{k}}),{{\tau }_{k}}) = 0$. При этом будет найдено одно из парето-оптимальных решений, которое соответствует заданному вектору λ.

Поиск приближенного решения многокритериальной задачи, которое было бы приемлемым по нескольким критериям сразу, можно вести и среди парето-оптимальных решений, получаемых в результате применения описанного алгоритма 2 к последовательности однокритериальных задач (2.1), (2.3) при некоторых значениях вектора λ, заданных экспертами. При небольшом числе критериев перебор значений λ – достаточно простая процедура.

Другой подход к поиску решения многокритериальной задачи состоит в нахождении “идеального” управления, на котором достигается минимум функционала

(2.9)

$R(u) = \sum\limits_{i = 1}^m {{{{({{I}_{i}}(u) - I_{i}^{0})}}^{2}}} ,$

где значения $I_{i}^{0}$, $i = \overline {1,m} $, найдены путем решения однокритериальной задачи ${{I}_{i}}(u) \to \mathop {\min }\limits_{u \in U} $. Функционал (2.9) обеспечивает приближение, наиболее близкое к однокритериальным решениям.

Заметим, что до минимизации функционала (2.9) необходимо решить m однокритериальных задач оптимального управления для системы (2.1) c функционалами (2.2), а затем найти решение однокритериальной задачи с функционалом (2.9). Для решения многокритериальной задачи (2.1), (2.2), (2.9) можно использовать следующий алгоритм. Организовать m параллельных процессов для минимизации функционалов (2.2) на решениях системы (2.1) при допустимых управлениях из U. При этом для минимизации каждого из функционалов можно использовать алгоритм 2.

После удачного завершения процесса оптимизации получим наименьшие значения функционалов (2.2): $I_{i}^{0}$, $i = \overline {1,m} $. Далее применим алгоритм 2 для минимизации функционала (2.9). При этом сопряженная система будет иметь следующее конечное условие:

$\psi ({{t}_{1}}) = - 2\sum\limits_{j = 1}^m {({{\varphi }^{j}}(x({{t}_{1}})) - I_{j}^{0})\varphi _{x}^{j}(x({{t}_{1}}))} ,$

т.е. являться линейной комбинацией градиентов критериев (2.2), а в ш. 4–6 алгоритма 1 будет отыскиваться минимум функционала (2.9). Итерационные процессы (2.7), (2.8), реализованные в алгоритме 2, должны обеспечить получение приближенного решения многокритериальной задачи: оптимального управления и соответствующей ему траектории, на которых функционал (2.9) достигает минимума. Другими словами, полученное управление будет обеспечивать перевод системы (2.1) в точку, которая наиболее близка к точкам минимума критериев (2.2), и поэтому носит название идеального решения.

2.2. Двойственный метод для решения многокритериальной задачи

Изложенные выше способы решения многокритериальной задачи относятся к классу прямых методов. Рассмотрим теперь двойственный алгоритм, в основе которого лежит следующее

Утверждение. Задача минимизации функционала (2.3) является двойственной по отношению к задаче минимизации функционала (2.9).

Действительно, если в m-мерном пространстве критериев рассматривать вектор λ, $\left\| \lambda \right\| \leqslant 1$, и вектор y c координатами ${{y}_{j}} = {{\varphi }^{j}}(x({{t}_{1}})) - I_{j}^{o}$, j = 1, 2, …, m, то задачу (2.9) можно представить в виде ${{\left\| y \right\|}^{2}} \to \min $, что эквивалентно задаче $\left\| y \right\| \to \min $. По определению нормы имеем $\left\| y \right\| = \mathop {\max }\limits_{\left\| \lambda \right\| \leqslant 1} (\lambda ,y)$. Тогда $\min \left\| y \right\| = \min \mathop {\max }\limits_{\left\| \lambda \right\| \leqslant 1} (\lambda ,y)$. Так как функции φ^j(x) выпуклые, то и определяемое ими множество в пространстве критериев (на множестве достижимости) выпукло. Множество $\left\| \lambda \right\| \leqslant 1$, очевидно, также выпукло. Следовательно, операции min и max допускают перестановку: $\min \left\| y \right\| = \min \mathop {\max }\limits_{\left\| {\lambda \leqslant 1} \right\|} (\lambda ,y) = \mathop {\max }\limits_{\left\| {\lambda \leqslant 1} \right\|} \min (\lambda ,y)$. Таким образом, вместо минимизации функционала (2.9) можно решать задачу максимизации минимума функционала (2.3) на единичной сфере $\left\| \lambda \right\| \leqslant 1$. В результате получим λ*, при котором решение задачи (2.1), (2.2) будет обеспечивать минимум функции (2.9). Эффективный алгоритм нахождения единичного по норме вектора λ* рассматривается в [1] и носит название метода выпуклых оболочек. Здесь рассмотрим двойственный алгоритм 3, на внешних итерациях которого будет вестись максимизация по λ, а на внутренних итерациях – минимизация по u:

$\mathop {\max }\limits_{\left\| {\lambda \leqslant 1} \right\|} \mathop {\min }\limits_{u \in U} I(\lambda ,y) = \mathop {\max }\limits_{\left\| {\lambda \leqslant 1} \right\|} \mathop {\min }\limits_{x({{t}_{1}})} \sum\limits_{j = 1}^m {{{\lambda }_{j}}({{\varphi }^{j}}(x({{t}_{1}})) - I_{j}^{0})} .$

Алгоритм 3

Шаг 1. Задаем начальное приближение для коэффициентов свертки, например, λ_j = 1/m, $j = \overline {1,m} $.

Шаг 2. Применяя алгоритм 2 для минимизации функционала $I(\lambda ,u) = \sum\nolimits_{j = 1}^m {{{\lambda }_{j}}({{\varphi }^{j}}(x({{t}_{1}})) - I_{j}^{0})} $ по u при фиксированном векторе λ, найдем решение внутренней задачи. При этом на ш. 4–6 при поиске оптимальных значений параметров ε и α будет минимизироваться данный функционал

$I(\lambda ,u) = \sum\nolimits_{j = 1}^m {{{\lambda }_{j}}({{\varphi }^{j}}(x({{t}_{1}})) - I_{j}^{0}){\kern 1pt} } .$

Шаг 3. По окончании работы алгоритма 2 будет найдено управление, приводящее систему (2.1) в точку x(t₁), в которой для заданного λ функционал I(λ, u) будет минимальным, а полученные при этом значения φ_j(x(t₁)) – $I_{j}^{0}$ будут компонентами градиента функционала I(λ, u) по λ:

$I(\lambda ,u) = {{\varphi }^{j}}(x({{t}_{1}})) - I_{j}^{0},\;\;j = \overline {1,m} .$

Шаг 4. Применяя метод одномерного поиска для максимизации по α, найдем оптимальный шаг α вдоль градиента для изменения коэффициентов вектора λ с целью увеличения значения I(λ, u): $\lambda _{j}^{{k + 1}} = \lambda _{j}^{k} + \alpha ({{\varphi }^{j}}(x({{t}_{1}})) - I_{j}^{0})$, $j = \overline {1,m} $; затем полагаем $\lambda _{j}^{{k + 1}} = \lambda _{j}^{k}{\text{/}}\left\| \lambda \right\|$, $j = \overline {1,m} $. Заметим, что на практике из-за трудоемкости поиска шаг α иногда выбирают достаточно малым (необязательно оптимальным), лишь бы увеличить значение функционала.

Шаг 5. Если на ш. 4 достигнуто выполнение неравенства $I(\lambda _{{}}^{{k + 1}},u) > I(\lambda _{{}}^{k},u)$, то, полагая λ = λ^k ^+ 1, переходим на ш. 2 для продолжения процесса оптимизации. В противном случае итерационный процесс прекращается и найденное на последней итерации управление будет решением многокритериальной задачи в смысле минимума функционала (2.9).

3. ЧИСЛЕННОЕ РЕШЕНИЕ ПРИКЛАДНЫХ ЗАДАЧ

3.1. Оптимальное управление положением асимметричного космического аппарата

На основе предложенной многометодной технологии было найдено решение следующей нелинейной краевой задачи. Рассмотрим модель, описывающую вращательную динамику космического аппарата (КА), которая приведена в статье [5]:

$J(u) = \frac{1}{2}\int\limits_0^{100} {[u_{1}^{2}(t) + u_{2}^{2}(t) + u_{3}^{2}(t)]dt} \to \min ,$

${{\dot {\beta }}_{0}} = k( - {{\omega }_{1}}{{\beta }_{1}} - {{\omega }_{2}}{{\beta }_{2}} - {{\omega }_{3}}{{\beta }_{3}}),$

${{\dot {\beta }}_{1}} = k({{\omega }_{1}}{{\beta }_{0}} - {{\omega }_{2}}{{\beta }_{3}} + {{\omega }_{3}}{{\beta }_{2}}),$

${{\dot {\beta }}_{2}} = k({{\omega }_{1}}{{\beta }_{3}} + {{\omega }_{2}}{{\beta }_{0}} - {{\omega }_{3}}{{\beta }_{1}}),$

${{\dot {\beta }}_{3}} = k( - {{\omega }_{1}}{{\beta }_{2}} + {{\omega }_{2}}{{\beta }_{1}} + {{\omega }_{3}}{{\beta }_{0}}),\quad k = 0.5,$

${{\dot {\omega }}_{1}} = - {{\bar {I}}_{1}}{{\omega }_{2}}{{\omega }_{3}} + {{u}_{1}}{\text{/}}{{I}_{1}},$

${{\dot {\omega }}_{2}} = - {{\bar {I}}_{2}}{{\omega }_{1}}{{\omega }_{3}} + {{u}_{2}}{\text{/}}{{I}_{2}},$

${{\dot {\omega }}_{3}} = - {{\bar {I}}_{3}}{{\omega }_{1}}{{\omega }_{2}} + {{u}_{3}}{\text{/}}{{I}_{3}},$

где ${{\bar {I}}_{1}} = ({{I}_{3}} - {{I}_{2}}){\text{/}}{{I}_{1}}$, ${{\bar {I}}_{2}} = ({{I}_{1}} - {{I}_{3}}){\text{/}}{{I}_{2}}$, ${{\bar {I}}_{3}} = ({{I}_{2}} - {{I}_{1}}){\text{/}}{{I}_{3}}$, (I₁, I₂, I₃) – моменты инерции космического аппарата; (u₁, u₂, u₃) – компоненты управляющего вектора (вращающего момента); (β₀, β₁, β₂, β₃) – параметры Эйлера, (ω₁, ω₂, ω₃) – компоненты угловой скорости.

Вектор β удовлетворяет условию ${{\left\| {\beta (t)} \right\|}^{2}} = {\text{const}}$. Выбором начальных условий обеспечивается равенство $\left\| {\beta (t)} \right\| = 1$.

Требуется найти управление, обеспечивающее минимум функционалу J(u) и переводящее КА из заданного начального положения в заданное конечное состояние.

В [5] заданы следующие начальное и конечное состояния: x⁰ = (1, 0, 0, 0, 0.01, 0.005, 0.001), x¹ = (0.43047, 0.70106, 0.09230, 0.56098, 0, 0, 0), моменты инерции: I₁ = 10⁶, I₂ = 833333, I₃ = 916667, а начальное приближение для управления, с которого метод квазилинеаризации начинал сходиться к оптимальному, находилось аналитически из механических свойств системы.

Управление, на котором достигается максимум зависящей от u части функции Понтрягина, $Z(u) = {{\psi }_{5}}{{u}_{1}}{\text{/}}{{I}_{1}} + {{\psi }_{6}}{{u}_{2}}{\text{/}}{{I}_{2}} + {{\psi }_{7}}{{u}_{3}}{\text{/}}{{I}_{3}}$ – $u_{1}^{2} - u_{2}^{2} - u_{3}^{2}$, определяется по формулам: u₁ = ψ₅/(2I₁), u₂ = = ψ₆/(2I₂), u₃ = ψ₇/(2I₃).

Краевая задача (1.2) для данной системы имеет следующий вид:

${{\dot {x}}_{1}} = k( - {{x}_{5}}{{x}_{2}} - {{x}_{6}}{{x}_{3}} - {{x}_{7}}{{x}_{4}}),$

${{\dot {x}}_{2}} = k({{x}_{5}}{{x}_{1}} + {{x}_{7}}{{x}_{3}} - {{x}_{6}}{{x}_{4}}),$

${{\dot {x}}_{3}} = k({{x}_{6}}{{x}_{1}} - {{x}_{7}}{{x}_{2}} + {{x}_{5}}{{x}_{4}}),$

${{\dot {x}}_{4}} = k({{x}_{7}}{{x}_{1}} + {{x}_{6}}{{x}_{2}} - {{x}_{5}}{{x}_{3}}),$

${{\dot {x}}_{5}} = - 0.08333{{x}_{6}}{{x}_{7}} + {{\psi }_{5}}{\text{/}}(2I_{1}^{2}),$

${{\dot {x}}_{6}} = - 0.1{{x}_{5}}{{x}_{7}} + {{\psi }_{6}}{\text{/}}(2I_{2}^{2}),$

${{\dot {x}}_{7}} = 0.18182{{x}_{5}}{{x}_{6}} + {{\psi }_{7}}{\text{/}}(2I_{3}^{2}),$

${{\dot {\psi }}_{1}} = k({{\psi }_{2}}{{x}_{5}} + {{\psi }_{3}}{{x}_{6}} + {{\psi }_{4}}{{x}_{7}}),$

${{\dot {\psi }}_{2}} = k({{\psi }_{1}}{{x}_{5}} + {{\psi }_{3}}{{x}_{7}} - {{\psi }_{4}}{{x}_{6}}),$

${{\dot {\psi }}_{3}} = k({{\psi }_{1}}{{x}_{6}} - {{\psi }_{2}}{{x}_{7}} + {{\psi }_{4}}{{x}_{5}}),$

${{\dot {\psi }}_{4}} = k({{\psi }_{1}}{{x}_{7}} + {{\psi }_{2}}{{x}_{6}} - {{\psi }_{3}}{{x}_{5}}),$

${{\dot {\psi }}_{5}} = k({{\psi }_{1}}{{x}_{2}} - {{\psi }_{2}}{{x}_{1}} - {{\psi }_{3}}{{x}_{4}} + {{\psi }_{4}}{{x}_{3}}) + 0.1{{\psi }_{6}}{{x}_{7}} - 0.18182{{\psi }_{7}}{{x}_{6}},$

${{\dot {\psi }}_{6}} = k({{\psi }_{1}}{{x}_{3}} + {{\psi }_{2}}{{x}_{4}} - {{\psi }_{3}}{{x}_{1}} - {{\psi }_{4}}{{x}_{2}}) + 0.08333{{\psi }_{5}}{{x}_{7}} - 0.18182{{\psi }_{7}}{{x}_{5}},$

${{\dot {\psi }}_{7}} = k({{\psi }_{1}}{{x}_{4}} - {{\psi }_{2}}{{x}_{3}} + {{\psi }_{3}}{{x}_{2}} - {{\psi }_{4}}{{x}_{1}}) + 0.08333{{\psi }_{5}}{{x}_{6}} + 0.1{{\psi }_{6}}{{x}_{5}}.$

Краевые условия были заданы такими же, как и в [5]. Они приведены выше. Максимальное нарушение краевого условия на правом конце при нулевом управлении было равно 0.41622. Метод квазилинеаризации с этого управления не сходился. Градиентная процедура (алгоритм 1), начиная с ${{v}^{0}}$, соответствующего нулевому управлению, сократила невязку выполнения краевых условий на порядок, после чего с полученного ${{v}^{k}}$ метод квазилинеаризации стал сходиться и нарушение краевых условий уменьшилось до 10^–9. График полученного при этом управления практически совпадает с графиком управления, приведенного в [5].

Таким образом, многометодная схема в данной краевой задаче состоит из итераций двух методов: итераций градиентного метода, которые приводят в окрестность сходимости метода квазилинеаризации, и непосредственно итераций метода квазилинеаризации, которые обеспечивают вычисление оптимального управления с заданной точностью. Заметим, что ни одним из этих методов при его автономном использовании от начала и до конца невозможно было получить решение краевой задачи с удовлетворительной для практики точностью.

3.2. Оптимальное управление в задаче слежения за маневрирующей целью

Рассматривается прикладная задача управления маневром самолета при слежении за ним средствами наблюдения, например, РЛС. Необходимость применения нескольких критериев и многометодной технологии возникает, например, в задачах слежения за пилотируемой маневрирующей целью [7]. В силу особенности движения целей этого класса (самолет, корабль, подводная лодка), которая состоит в их способности к маневру – разворотам и быстрым изменениям скорости и высоты, модель оценивания движения в реальном времени при слежении за такой управляемой пилотируемой целью должна гарантировать необходимую точность слежения. Надежность расчета оптимального управления в этой сложной нелинейной модели обеспечивается применением арсенала эффективных математических методов для построения многометодных алгоритмов поиска численного решения [1].

3.2.1. Математическая модель задачи управления и слежения. Предположим, что сопровождаемая цель обладает хорошими маневренными свойствами и ее движение можно описать уравнением

(3.1)

$\dot {x} = Fx + Gw,\quad x(0) = M[x(0)],$

где x = x(t) – расширенный вектор состояния цели, включающий координаты формирующего фильтра, w = w(t) – случайный процесс в виде белого шума с корреляционной матрицей $M[w(t)w(t)'] = Q(t)\delta (t - \tau )$, F, G – матрицы, определяющие параметр фильтра, формирующего x(t). Информация о текущем положении цели (3.1) поступает от измерителя (РЛС): $z = Hx + \xi + v$, где H – матрица коэффициентов измерителя, ξ – случайный шум измерения с корреляционной матрицей $M[\xi (t)\xi (t)'] = R(t)\delta (t - \tau )$, $v = v(t)$ – помеха, создаваемая целью. Тогда структура фильтра, обеспечивающего минимум среднеквадратической ошибки $M[(x - y)(x - y)']$, где y – оценка вектора состояния x, имеет вид

(3.2)

$\dot {y} = Fy + K(z - Hy),\quad y(0) = M[x(0)],\quad K = PH{{R}^{{ - 1}}},$

(3.3)

$\dot {P} = FP - PH{\kern 1pt} '{\kern 1pt} {{R}^{{ - 1}}}HP + PF{\kern 1pt} {\text{'}} + GQG{\kern 1pt} ',\quad P(0) = M[x(0)x(0){\kern 1pt} '].$

В отличие от предполагаемой модели (3.1) реальное движение самолета описывается уравнением

(3.4)

${{x}_{g}} = {{F}_{g}}{{G}_{g}}u + \eta ,\quad {{x}_{g}}(0) = M[{{x}_{g}}(0)],$

где x_g ∈ X – действительный вектор состояния самолета, u ∈ V – вектор управления из заданного множества, η – формирующий белый шум модели.

Из уравнений (3.2)–(3.4) получим уравнение для ошибки фильтрации

(3.5)

$\varepsilon = {{x}_{g}} - y\,:\;\;\varepsilon = (F - KH)\varepsilon + Gu - K\text{v} + \Delta F{{x}_{g}} + \eta - K\xi ,$

где ΔF = F_g – F.

Используем соотношение $M{{\left\| \varepsilon \right\|}^{2}} = {{\left\| {\bar {\varepsilon }} \right\|}^{2}} + TrP(t)$, где $\bar {\varepsilon }$ – математическое ожидание ε(t), TrP(t) – след ковариационной матрицы ошибок фильтрации. Учитывая, что TrP(t) не зависит от η и ξ, достаточно потребовать достижения $\mathop {\max }\limits_{u,\text{v}} {{\left\| {\bar {\varepsilon }} \right\|}^{2}}$, где

(3.6)

$\dot {\bar {\varepsilon }} = (F - KH)\bar {\varepsilon } + Gu - K\text{v} + \Delta F{{x}_{g}}.$

3.2.2. Возможные постановки задач оптимального управления с различными критериями. Задачу синтеза оптимального противодействия процессу сопровождения движущейся цели можно сформулировать следующим образом [7]. Известны уравнения для ошибки фильтрации (3.5) и действительного движения самолета (3.4), заданы ограничения на траекторию: ${{x}_{{{{g}_{{\mathbf{H}}}}}}} \leqslant {{x}_{g}} \leqslant {{x}_{{{{g}_{{\mathbf{B}}}}}}}$, на управление: ${{u}_{{\min }}} \leqslant u \leqslant {{u}_{{\max }}}$ и на помеху: ${{v}_{{\min }}} \leqslant v \leqslant {{v}_{{\max }}}$. Требуется найти такие значения для управления u и параметра $v$, при которых математическое ожидание квадрата ошибки фильтрации ${{\left\| \varepsilon \right\|}^{2}}$ достигнет максимума за некоторое время T. Для описанной модели рассматривались следующие постановки задач оптимального управления.

1. Проверка управляемости системы, определяющая возможность перевода системы из начального состояния в некоторое заданное состояние за время T.

2. Задача оптимального быстродействия: вычисление управления, которое обеспечило бы достижение заданного уровня ошибки за минимально возможное время.

3. Нахождение управления, которое обеспечило бы достижение требуемого максимального уровня ошибки ε_max в конце заданного временного отрезка [0, T].

4. Вычисление управления, которое обеспечивало бы в каждой точке t временного отрезка [0, T] требуемое максимальное значение ошибки ε_max.

Для перечисленных задач наиболее естественным является выбор двух критериев: дальности ε₁ и скорости цели ε₂ и, следовательно, решать задачу с двумя критериями.

3.2.3. Численное решение. В качестве иллюстрации рассмотрим конкретную задачу оптимального управления самолетом и помехой из [7]:

$\begin{gathered} \dot {R} = V, \\ \dot {V} = a, \\ \dot {a} = - \alpha a + u, \\ \end{gathered} $

где R – дальность, V – скорость, a – ускорение цели, u – управление, α – предполагаемая интенсивность маневра.

Реальное движение самолета описывается уравнениями:

(3.7)

$\begin{gathered} \dot {R} = V, \\ \dot {V} = a, \\ \dot {a} = u. \\ \end{gathered} $

Перейдем к стандартной постановке задачи оптимального управления, объединив уравнения для ошибки слежения (3.6) движения (3.7) фильтра (3.3).

Совместная система уравнений (3.6), (3.7), (3.3) после введения вектора общих переменных

$z = ({{\varepsilon }_{1}},{{\varepsilon }_{2}},{{\varepsilon }_{3}},R,V,a,{{p}_{{11}}},{{p}_{{12}}},{{p}_{{13}}},{{p}_{{22}}},{{p}_{{23}}},{{p}_{{33}}})$

(в силу симметричности матрицы P остальные ее элементы не включены) будет иметь следующий вид:

${{\dot {z}}_{1}} = {{z}_{2}} - {{z}_{7}}({{z}_{1}} + \text{v}){\text{/}}r,$

${{\dot {z}}_{2}} = {{z}_{3}} - {{z}_{8}}({{z}_{1}} + \text{v}){\text{/}}r,$

${{\dot {z}}_{3}} = 0.1{{z}_{6}} - {{z}_{9}}({{z}_{1}} + \text{v}){\text{/}}r + u,$

${{\dot {z}}_{4}} = {{z}_{5}},$

${{\dot {z}}_{5}} = {{z}_{6}},$

${{\dot {z}}_{6}} = u,$

${{\dot {z}}_{7}} = 2{{z}_{8}} - z_{7}^{2}{\text{/}}r + 0.5\alpha ,$

${{\dot {z}}_{8}} = {{z}_{9}}{{z}_{{10}}} + {{z}_{7}}{{z}_{8}}{\text{/}}r + 0.12\alpha ,$

${{\dot {z}}_{9}} = {{z}_{{11}}} - {{z}_{7}}{{z}_{9}}{\text{/}}r + 0.166\alpha ,$

${{\dot {z}}_{{10}}} = 2{{z}_{{11}}} - z_{8}^{2}{\text{/}}r + 0.333\alpha ,$

${{\dot {z}}_{{11}}} = {{z}_{{12}}} - {{z}_{8}}{{z}_{9}}{\text{/}}r + 0.5\alpha ,$

${{\dot {z}}_{{12}}} = z_{9}^{2} + \alpha ,\quad t \in [0,\;10].$

Были заданы следующие начальные условия из [7]:

$z(0) = (0,\;0,\;0,\; - {\kern 1pt} 18.3,\;0.3,\;0,\;0.033489,\;0.033489,\;0,\;0.066978,\;0,\;0.00046).$

Искомыми являются управление u(t) и параметр $v$.

В качестве функционалов были выбраны ошибки измерения дальности и скорости цели: ${{I}_{1}}(u) = {{z}_{1}}(10)$, ${{I}_{2}}(u) = {{z}_{2}}(10)$, которые необходимо максимизировать.

Задано ограничение на управление: $\left| {u(t)} \right| \leqslant 0.0075$, $t \in [0,10]$ и на параметр: $\left| v \right| \leqslant 0.0015$. Значения других параметров были заданы следующими: r = 0.033489, α = 0.000092.

Решение найдено с помощью алгоритма 3 с применением методов из [1]. Оптимальные значения коэффициентов λ₁ и λ₂ примерно равны 0.5, т.е. критерии оказались равновесными.

Найденное оптимальное управление имеет релейную структуру, т.е. переключается с одной границы на другую (порядка десяти раз), при этом наблюдается рост ошибок сопровождения по дальности и по скорости, что согласуется с заданными критериями.

3.3. Нелинейная задача об оптимальном управлении электроприводом

В [8] нелинейная задача об оптимальном управлении электроприводом имеет вид

${{\dot {x}}_{1}} = {{x}_{2}},$

${{\dot {x}}_{2}} = u - x_{2}^{2},$

${{\dot {x}}_{3}} = {{u}^{2}},$

$T = [0,\;4.85],$

$x(0) = (0,\;0,\;0),$

$\left| {u \leqslant 1} \right|,$

${{\varphi }_{1}} = {{({{x}_{1}}(4.85) - 3.12)}^{2}},$

${{\varphi }_{2}} = x_{2}^{2}(4.85),$

${{\varphi }_{3}} = {{x}_{3}}(4.85).$

На полученном оптимальном управлении, которое оказалось внутренним относительно заданных ограничений, функционалы I₁(u) = φ₁ и I₂(u) = φ₂ достигли нулевых значений, а функционал I₃(u) = φ₃, стал равным 2.465441.

ЗАКЛЮЧЕНИЕ

В заключение отметим, что был решен целый ряд задач подобного типа (см., например, [9], [10]), которые различались видами функционалов, интервалами времени или другими параметрами. Заметим также, что компьютерная технология управления реальными процессами накладывает высокие требования к расчету законов управления в экстремальных ситуациях и для других технических объектов. Точный и надежный расчет оптимального управления необходим, например, при приведении электроэнергетической системы в рабочий режим при резких изменениях нагрузки. Таким образом, многометодная технология решения многокритериальных задач оптимального управления, реализованная в виде параллельных итерационных процессов оптимизации с выбором лучшего приближения, решает задачу с автоматическим применением разных методов оптимизации и тем самым существенно повышает эффективность поиска и надежность получения численного решения в прикладных задачах оптимального управления.

Список литературы

Тятюшкин А.И. Многометодная технология оптимизации управляемых систем. Новосибирск: Наука, 2006. 343 с.
Васильев О.В., Тятюшкин А.И. Об одном методе решения задач оптимального управления, основанном на принципе максимума // Ж. вычисл. матем. и мат. физ. 1981. Т. 21. № 6. С. 1376–1384.
Беллман Р., Калаба Р. Квазилинеаризация и нелинейные краевые задачи. М.: Мир, 1968.
Тятюшкин А.И. Параллельные вычисления в задачах оптимального управления // Сиб. журн. вычисл. матем. 2000. Т. 3. № 2. С. 181–190.
Junkins J.I., Turner J.D. Optimal continuous torque attitude maneuvers // AIAA / AAS Astrodynamics conf. Palo Alto, Calif., 1978.
Макаров И.М., Виноградская Т.М., Рубчинский А.А, Соколов В.Б. Теория выбора и принятия решений. М.: Физматлит, 1982. 328 с.
Зингер Р. Оценка характеристик оптимального фильтра для слежения за пилотируемой целью // Зарубежная радиоэлектроника. 1971. № 8. С. 40–56.
Петров Ю.П. Оптимальное управление электроприводом // Энергия. 1978. № 1. С. 49-50.
Тятюшкин А.И., Федунов Б.Е. Численное исследование свойств оптимального управления в одной задаче преследования // Изв. РАН, ТиСУ. 2005. № 3. С. 104–113.
Тятюшкин А.И., Федунов Б.Е. Возможности защиты от атакующей ракеты задней полусферы самолета вертикальным маневром // Изв. РАН, ТиСУ. 2006. № 1. С. 111–125.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал