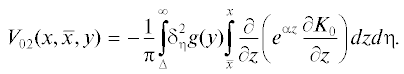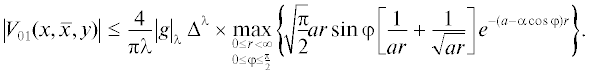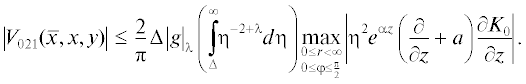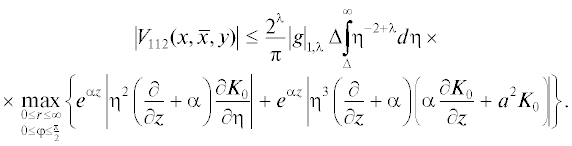Журнал вычислительной математики и математической физики, 2019, T. 59, № 2, стр. 264-276

1. ВВЕДЕНИЕ

Целью данной работы является получение ${{C}^{{2,\lambda }}}$-оценки решения заданного в полуплоскости однородного сингулярно возмущенного уравнения конвекции-диффузии с постоянными коэффициентами и направленной ортогонально от границы конвекцией через соответствующую норму правой части граничного условия Дирихле. Эта работа является продолжением исследований, начатых в [1], где рассматривалась та же задача, но для неоднородного уравнения с однородным граничным условием. Объединение этих результатов приводит к оценке полностью неоднородной задачи, что открывает короткий путь к получению оценок в ${{C}^{{k,\lambda }}}$, где $k > 2$. Более того, точность полученных оценок позволит их использовать для исследования уравнения с переменными коэффициентами, как это было сделано в [2] для одномерного случая (ср. с [3, гл. III]). Следует отметить, что ранее близкие оценки были получены в [4], но там оценивались коэффициенты Гёльдера только по направлению, задаваемому границей полуплоскости. Для получения этих оценок использовался аппарат преобразования Фурье по касательной переменной и соответствующая теорема о мультипликаторе. Эта красивая техника, к сожалению, не позволяет получить оценки коэффициентов Гёльдера по нормальному к границе направлению и тем самым не позволяет получить наш результат. С другой стороны, оценки из [4] не являются достаточными для исследования уравнения с переменными коэффициентами. Мы же для получения оценок используем аппарат функции Грина, который является более громоздким, однако позволяющим конструктивно получить оценки коэффициентов Гёльдера по любому направлению, т.е. с выписыванием при необходимости постоянных в этих оценках. Наша техника получения оценок предполагает раздельное оценивание коэффициентов Гёльдера по переменным $x$ и $y$. В связи с тем, что оценки по касательному направлению (у нас это направление $y$) уже получены в [4], мы в работе приводим доказательство оценок коэффициентов Гёльдера только по направлению $x$, а для оценок по $y$ формулируем результат и ссылаемся на [4].

Дальнейшее содержание работы таково. В разд. 2 дается постановка задачи и формулируется основной результат работы – теорема 1. В разд. 3 оцениваются коэффициенты Гёльдера по направлению $x$ самого решения и его первых производных. В разд. 4 оцениваются вторые производные.

На протяжении всей статьи для обозначения постоянных, которые не зависят от решения и малого параметра $\varepsilon $, будем использовать строчные буквы c с индексом или без. Одной и той же буквой часто будем обозначать различные постоянные.

2. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНОЙ РЕЗУЛЬТАТ

В правой полуплоскости $\mathbb{R}_{ + }^{2}$ плоскости $OXY$ ищется ограниченное решение задачи

Здесь $\Delta $ – оператор Лапласа, $\varepsilon \in (0,\;1]$ – малый параметр, $\alpha $ и $q$ – (постоянные, положительные) коэффициенты. Предполагается, что граничная функция $\mathcal{G}(Y)$ обладает некоторой (равномерной по $\varepsilon $) гладкостью. Требуется получить оценки коэффициентов Гёльдера решения $U(X,Y)$ и его производных.

Анализировать задачу (2.1), (2.2) удобнее в растянутых переменных

Пусть $U(X,Y) = U(\varepsilon x,\varepsilon y) = :u(x,y)$, а $\mathcal{G}(Y) = \mathcal{G}(\varepsilon y) = :g(y)$. В новых переменных задача (2.1), (2.2) примет вид При помощи функции Грина решение задачи (2.4), (2.5) представимо в виде где ${{K}_{0}}(z)$ есть функция Макдональда нулевого порядка, а

Чтобы сформулировать основной результат работы, введем некоторые обозначения. Будем через ${{C}^{{k,\lambda }}}$ обозначать пространство $k$ раз непрерывно дифференцируемых в $\mathbb{R}_{ + }^{2}$ функций, $k$-е производные которых удовлетворяют условию Гёльдера с показателем $\lambda $. Если какой-либо индекс $k$ или $\lambda $ будет равен нулю, то будем его опускать и писать просто ${{C}^{\lambda }}$, ${{C}^{k}}$ или $C$. Под полунормой $|\, \cdot \,|$ в пространстве ${{C}^{k}}$ будем понимать сумму максимумов модулей ее $k$-х производных, а в ${{C}^{{k,\lambda }}}$ – сумму коэффициентов Гёльдера этих производных, т.е.

Наконец, В процессе доказательств нам потребуются коэффициенты Гёльдера не по произвольному направлению, а по координатным. Будем их обозначать через ${{\left| f \right|}_{{C_{x}^{\lambda }}}}$ и ${{\left| f \right|}_{{C_{y}^{\lambda }}}}$. Оценки коэффициентов Гёльдера по произвольному направлению вытекают из них. Соответствующие нормы в одномерном случае описываются аналогично. Для краткости будем использовать в формулах также ${{\left| g \right|}_{0}}$, ${{\left| g \right|}_{\lambda }}$ вместо ${{\left| g \right|}_{C}}$ и ${{\left| g \right|}_{{{{C}^{\lambda }}}}}$ соответственно.

Теорема 1. Для решения $U(X,Y)$ задачи (1), (2) справедливы априорные оценки

Доказательству этой теоремы посвящены остальные разделы работы.

3. ОЦЕНКИ РЕШЕНИЯ И МЛАДШИХ ПРОИЗВОДНЫХ

Начнем со вспомогательного утверждения.

Лемма 3.1. Пусть положительные числа $a$ и $\alpha $ связаны соотношением (2.7), а $r > 0$, $0 \leqslant \varphi \leqslant \pi {\text{/}}2$. Тогда при $\delta \geqslant 0$, $\beta \geqslant 0$ справедлива оценка

Доказательство. Рассмотрим оцениваемую функцию $f(r,\varphi )$ как функцию, зависящую от $r$, считая $\varphi $ параметром. При $\beta = 0$ очевидно максимум достигается при $r = 0$, поэтому

При $\beta > 0$ функция $f(r,\varphi )$ неотрицательна, обращается в нуль при $r = 0$, экспоненциально убывает к нулю при $r \to \infty $ и поэтому имеет максимум по $r$ в некоторой точке $r{\text{*}}(\varphi )$. Этот максимум, зависящий от $\varphi $ как от параметра, есть При $\delta {\text{/}}2 \geqslant \beta $ отсюда, с учетом (2.7), непосредственно следует ограниченность $f(r,\varphi )$. При $\delta {\text{/}}2 \leqslant \beta $ исследование дополняется таким же рассмотрением зависимости найденной функции от $y = si{{n}^{2}}\tfrac{\varphi }{2}$. В результате имеем оценку С учетом (2.7) это завершает доказательство (3.1). Лемма доказана.

Полезной во многих случаях в дальнейшем будет следующая формула:

где ${{K}_{0}}$, ${{K}_{1}}$ – функции Макдональда нулевого и первого порядков соответственно, $a > 0$, $r = \sqrt {{{x}^{2}} + {{y}^{2}}} ,\quad sin\varphi = y{\text{/}}r.$

Перейдем к оценкам решения и его первых производных.

Лемма 3.2. Для решения $u(x,y)$ задачи (2.4), (2.5) справедлива оценка

Доказательство. Сначала несколько преобразуем представление (2.6) решения $u(x,y)$ задачи (2.4), (2.5), вычтя в подынтегральном выражении из функции $g(\eta )$ постоянное значение $g(y)$ и прибавив его снова. Получим

Здесь ${{K}_{0}} = {{K}_{0}}\left( {a\sqrt {{{x}^{2}} + {{{(\eta - y)}}^{2}}} } \right)$.

Последнее слагаемое теперь можно вычислить, учитывая четность по $(\eta - y)$ подынтегральной функции. После замены переменной интегрирования $\eta {\text{'}} = \eta - y$ и использования формулы ($\nu = 1$, $2\mu + 1 = 0$) последнее слагаемое в (3.4) принимает вид

После замены в (3.4) переменной $\eta {\kern 1pt} {\text{'}} = \eta - y$ при $\eta \geqslant y$ и $\eta {\kern 1pt} {\text{''}} = - \eta + y$ при $\eta \leqslant y$, опуская в дальнейшем штрихи у $\eta $, с учетом (3.5) и четности по $\eta $ функции $\partial {{K}_{0}}{\text{/}}\partial x$, приходим к представлению

где

Очевидно, что для оценки функции или ее производных в ${{C}^{\lambda }}$ достаточно оценить их величины в $C_{x}^{\lambda }$ и $C_{y}^{\lambda }$. Проведем оценки в $C_{x}^{\lambda }$. Пусть $\bar {x}$, $x$ – две различные точки положительной полуоси $Ox$. Для определенности будем полагать, что $\bar {x} < x$, так что $x - \bar {x} = \Delta > 0$. Оценим разность значений решения $u(x,y)$ из (3.6) в точках $x$ и $\bar {x}$

Начнем с оценки последнего слагаемого, Представив разность в квадратных скобках как интеграл по отрезку $[\bar {x},x]$ от производной функции ${{e}^{{ - (a - \alpha )z}}}$, из (3.9) получим Функция, стоящая под знаком ${\text{max}}$, неотрицательна, обращается в нуль при $z = 0$ и при $z \to \infty $. Поэтому она имеет максимум. Найдя его, получим оценку

Теперь рассмотрим оставшуюся часть (3.8), ${{V}_{0}}(x,\bar {x},y)$. Для ее оценки, следуя [3, гл. III], разобьем интервал интегрирования $[0,\infty )$ на два интервала: $[0,\Delta ]$ и $[\Delta ,\infty )$. Далее, в интеграле по $[\Delta ,\infty )$ разность выражений в квадратных скобках представим в виде интеграла по отрезку $[\bar {x},x]$ от соответствующей производной. Получим

где Оценим $\delta _{\eta }^{2}g(y)$ из (3.7) при $\eta \geqslant 0$Тогда из (3.12) будем иметь где $r = \sqrt {{{x}^{2}} + {{\eta }^{2}}} $, $\varphi = {\text{arctg}}\,\eta {\text{/}}x$. С учетом формулы (А.9) из работы [1], получим Используя теперь лемму 3.1 для каждого положительного слагаемого ($\delta = 1$, $\beta = 0$ в первом и $\delta = 1$, $\beta = 1{\text{/}}2$ во втором), придем к оценке Перейдем к рассмотрению ${{V}_{{02}}}(x,\bar {x},y)$ из (3.13). Заметим, что Сначала рассмотрим интеграл ${{V}_{{022}}}(x,\bar {x},y)$. Применив к интегралу по отрезку $[\bar {x},x]$ теорему о среднем и учтя (3.14), получим Для оценки максимума снова воспользуемся формулой (А9) из [1] и используем лемму 3.1 при ($\delta = 2$, $\beta = 1$) и ($\delta = 2$, $\beta = 3{\text{/}}2$). В результате имеем что вместе с (2.7) приводит к оценке

При оценке ${{V}_{{021}}}(x,\bar {x},y)$, поступая аналогично, получаем

Далее выполним интегрирование по $\eta $ и используем представление $\left( {\tfrac{\partial }{{\partial z}} + a} \right)\tfrac{{\partial {{K}_{0}}}}{{\partial z}}$ в полярных координатах формулой (3.2), а затем оценим величины $\left[ {{{K}_{1}}(r) - {{K}_{0}}(r)} \right]$, ${{K}_{1}}(r)$, ${{K}_{0}}(r)$ при помощи формул из [1, ф. (А.6), (А.9), (А.10)]. После применения к каждому из слагаемых вида ${{(sin\varphi )}^{\delta }}{{r}^{\beta }}{{e}^{{ - (a - \alpha cos\varphi )r}}}$ в полученном выражении леммы 3.1 при ($\delta = 2$, $\beta = 0$), ($\delta = 2,$, $\beta = 1{\text{/}}2$), ($\delta = 4$, $\beta = 3{\text{/}}2$) соответственно будем иметь Теперь, принимая во внимание (3.11)–(3.13) и собирая вместе оценки (3.10), (3.15), (3.16), (3.17), а также учитывая (2.7) и произвольность $x$ и $\bar {x}$, приходим к утверждению (3.3). Лемма доказана.

Лемма 3.3. Для производной $\partial u{\text{/}}\partial x$ решения задачи (2.4), (2.5) справедлива оценка

Доказательство. Используя представление (2.6) решения $u(x,y)$ задачи (2.4), (2.5), запишем выражение $\partial u{\text{/}}\partial x$ в виде

Проведем регуляризацию интеграла, для чего вычтем в подынтегральном выражении из $g(\eta )$ и прибавим к нему $S_{g}^{1}(\eta - y)$, где Теперь производную в (3.19) можно внести под знак интеграла, и, следовательно, представить $\partial u{\text{/}}\partial x$ в виде суммы где а ${{K}_{0}} = {{K}_{0}}(a\sqrt {{{x}^{2}} + {{{(\eta - y)}}^{2}}} )$.

Сделаем в интегралах (3.22) замену переменной $\eta {\text{'}} = \eta - y$. Заметим, что величина ${{I}_{{10}}}(x,y)$ с учетом (3.20) имеет вид

где ${{K}_{0}} = {{K}_{0}}\left( {a\sqrt {{{x}^{2}} + {{\eta }^{2}}} } \right)$ и легко может быть вычислена. Так как $\eta \tfrac{{\partial {{K}_{0}}}}{{\partial x}}$ – функция нечетная по $\eta $, то интеграл от нее равен нулю. Оставшийся в ${{I}_{{10}}}(x,y)$ интеграл уже был ранее вычислен в (3.5). Поэтому, выполнив необходимое дифференцирование, будем иметь

Теперь преобразуем ${{I}_{{11}}}(x,y)$. Для этого воспользуемся уравнением для ${{K}_{0}}\left( {a\sqrt {{{x}^{2}} + {{\eta }^{2}}} } \right)$: $ - \Delta {{K}_{0}} + {{a}^{2}}{{K}_{0}} = 0$. Тогда ${{I}_{{11}}}(x,y)$ примет вид

После интегрирования по частям в (3.24) слагаемого с производной по $\eta $ получим Так как функции $\left( {\partial {{K}_{0}}{\text{/}}\partial \eta } \right)$ и $\eta \left( {\alpha \partial {\text{/}}\partial x + {{a}^{2}}} \right){{K}_{0}}$ – нечетные по $\eta $, то интеграл от них равен нулю. Принимая это во внимание и учитывая (3.7), после замены переменной $\eta {\kern 1pt} {\text{'}} = - \eta $ в интеграле по отрицательной полуоси придем к представлению

Теперь можно переходить к оценке разности $\partial u{\text{/}}\partial x - \partial u{\text{/}}\partial{ \bar {x}}$. С учетом (3.21) имеем

Обозначим Тогда верно Оценим сначала ${{V}_{{10}}}(x,\bar {x},y)$. Как при оценке $\left| {{{V}_{{00}}}(x,\bar {x},y)} \right|$ (см. (3.9), (3.10), (3.23)), будем иметь

Теперь рассмотрим ${{V}_{{11}}}(x,\bar {x},y)$ (см. (3.25)). Снова, следуя [3, гл. III], представим интеграл по $\eta $ в виде суммы интегралов ${{V}_{{111}}}(x,\bar {x},y)$ и ${{V}_{{112}}}(x,\bar {x},y)$ по интервалам соответственно $[0,\Delta ]$ и $[\Delta ,\infty )$, затем в интеграле по интервалу $[\Delta ,\infty )$, как и при рассмотрении ${{\left| u \right|}_{{C_{x}^{\lambda }}}}$, представим разность входящих туда выражений, зависящих от $x$ и $\bar {x}$, в виде интеграла по отрезку $[\bar {x},x]$ от производной по соответствующей переменной. Получим

При рассмотрении интеграла в (3.27) учтем, что Будем иметь где $r = \sqrt {{{z}^{2}} + {{\eta }^{2}}} $, $\eta = rsin\varphi $.

При рассмотрении же интеграла в (3.28) (по $[\Delta ,\infty )$) заменим внутренний интеграл по теореме о среднем. Получим для ${{V}_{{112}}}(x,\bar {x},y)$ оценку

Дальнейший процесс доказательства схематично выглядит следующим образом. Выполним интегрирование по $\eta $ в (3.29), затем найдем максимумы входящих величин. Для этого оценим максимум модуля суммы суммой максимумов модулей отдельных выражений, предварительно преобразованных к удобному для исследования виду, перейдем в них от декартовых координат к полярным, а затем воспользуемся полученными в [1] представлениями и оценками этих выражений и применим лемму 3.1 к каждому слагаемому вида ${{(sin\varphi )}^{\delta }}{{r}^{\beta }}{{e}^{{ - (a - \alpha cos\varphi )r}}}$.

Более подробно. Воспользовавшись формулами из [1, ф. (А.3), (А.9)] и леммой 3.1 при ($\delta = 2$, $\beta = 0$), ($\delta = 2$, $\beta = 1{\text{/}}2$) в первом слагаемом из (3.29), а затем, после преобразования второго слагаемого из той же формулы к виду

воспользовавшись формулами из [1, ф. (В.5), (А.6)] и леммой 3.1 при ($\delta = 2$, $\beta = 1{\text{/}}2$), ($\delta = 4$, $\beta = 3{\text{/}}2$) в его первом слагаемом и формулами из [1, ф. (А.3), (Ф.9)] и леммой 3.1 при ($\delta = 2$, $\beta = 1$), ($\delta = 2$, $\beta = 3{\text{/}}2$) во втором слагаемом, после выполнения интегрирования по $\eta $ с учетом (2.7) придем к оценке

Аналогично поступаем и при оценке $\left| {{{V}_{{112}}}(x,\bar {x})} \right|$ из (3.30), т.е. очевидным образом преобразуем оцениваемое выражение к виду

а затем, воспользовавшись формулой из [1, ф. (В.7)] для представления преобразованного выражения в полярных координатах и оценками из [1, ф. (А.6), (А.9), (А.10)] производной $\partial {{K}_{0}}(r){\text{/}}\partial r$ и некоторых комбинаций производных, приходим к необходимости оценить величину в первом слагаемом. Во втором слагаемом после использования формул из [1, ф. (А.3), (А.9)] оказывается необходимым оценить величину В третьем слагаемом для представления в полярных координатах используем формулу из [1, ф. (В.6)], а для оценок необходимых комбинаций производных формулы из [1, ф. (А.7), (А.9), (А.10)], тогда становится необходимо оценить величину И, наконец, использование формул из [1, ф. (А.3), (А.9)] в четвертом слагаемом приводит к необходимости оценить величину Теперь применим лемму 3.1 к каждому отдельному слагаемому при соответствующих значениях $\delta $ и $\beta $ и выполним интегрирование по $\eta $. Тогда, принимая во внимание (2.7), получаем Объединяя (3.31) и (3.32), приходим к оценке Собирая вместе оценки (3.33), (3.26), с учетом (2.7) приходим к утверждаемой в лемме оценке (3.18). Лемма доказана.

Лемма 3.4. Для производной $\partial u{\text{/}}\partial y$ решения задачи (2.4), (2.5) справедлива оценка

Доказательство следует из оценки (3.3), если в последней заменить $g(y)$ на $g{\text{'}}(y)$, так как производная по $y$ совпадает с решением той же задачи (2.4), (2.5), но с правой частью $g{\text{'}}(y)$ граничного условия (2.5) вместо $g(y)$.

4. ОЦЕНКИ ВТОРЫХ ПРОИЗВОДНЫХ

Продолжим изучение задачи (2.4), (2.5). В этом разделе будут получены необходимые оценки вторых производных в $C_{x}^{\lambda }$.

Лемма 4.1. Для производной ${{\partial }^{2}}u{\text{/}}\partial {{x}^{2}}$ решения задачи (2.4), (2.5) справедлива оценка

Доказательство. Для того, чтобы выразить ${{\partial }^{2}}u{\text{/}}\partial {{x}^{2}}$, снова используем представление (2.6) решения $u(x,y)$ задачи (2.4), (2.5). Имеем

Так же, как и при доказательстве леммы 3.3, проведем регуляризацию интеграла, для чего вычтем в подынтегральном выражении из $g(\eta )$ и прибавим к нему величину $S_{g}^{2}(\eta - y)$, где Теперь производную можно внести под знак интеграла и записать в виде а ${{K}_{0}} = {{K}_{0}}\left( {a\sqrt {{{x}^{2}} + {{{(\eta - y)}}^{2}}} } \right)$.

Сделаем в (4.3) замену переменной интегрирования $\eta {\text{'}} = \eta - y$. Заметим, что с учетом (4.2) выражение ${{I}_{{20}}}(x,y)$ примет вид

где ${{K}_{0}} = {{K}_{0}}\left( {a\sqrt {{{x}^{2}} + {{\eta }^{2}}} } \right)$, и легко может быть вычислено. В силу нечетности функции $\eta \tfrac{{\partial {{K}_{0}}}}{{\partial x}}$ интеграл от нее равен нулю. Оставшийся в ${{I}_{{20}}}(x,y)$ интеграл уже был частично ранее вычислен в (3.5). Для вычисления последней его части, интеграла от ${{\eta }^{2}}\tfrac{{\partial {{K}_{0}}}}{{\partial x}}$, воспользуемся формулой из [5, ф. 6.596.3] при $\nu = 1$, $\mu = 1{\text{/}}2$. Получим Выполнив в ${{I}_{{20}}}(x,y)$ необходимое дифференцирование, с учетом (4.4) будем иметь Теперь преобразуем ${{I}_{{21}}}(x,y)$ (см. (4.3)). Для этого снова воспользуемся соотношением $\Delta {{K}_{0}} - {{a}^{2}}{{K}_{0}} = 0$. После двукратного интегрирования по частям в двух слагаемых, содержащих ${{\partial }^{2}}{{K}_{0}}{\text{/}}\partial {{\eta }^{2}}$, будем иметь Далее, сделаем замену переменной $\eta {\text{'}} = - \eta $ при $\eta < 0$. Так как ${{K}_{0}}$ и ее производные по $x$ как функции $\eta $ – четные, то, будучи умноженными на $\eta $, становятся нечетными. Поэтому интеграл от каждой из них равен нулю. Отсюда с учетом (3.7), получим следующее представление ${{I}_{{21}}}(x,y)$ из (4.6) где а ${{K}_{0}}(z,\eta ) = {{K}_{0}}\left( {a\sqrt {{{z}^{2}} + {{\eta }^{2}}} } \right)$.

Теперь можно переходить к оценке разности

где $x$, $\bar {x}$ – две произвольные точки оси $Ox$, и так же, как раньше, $0 < \bar {x} < x$, а разность $x - \bar {x} = \Delta $. Обозначим Тогда Оценим сначала ${{V}_{{20}}}(x,\bar {x},y)$. Как при оценке $\left| {{{V}_{{10}}}(x,\bar {x})} \right|$ из (3.26), с учетом (4.5), будем иметь

Рассмотрим теперь ${{V}_{{21}}}(x,\bar {x},y)$ (см. (4.7)). Снова, следуя [3, гл. III], представим интеграл по $\eta $ в виде суммы интегралов по интервалам $[0,\Delta ]$ и $[\Delta ,\infty )$, затем в интеграле по интервалу $[\Delta ,\infty )$, представим разность входящих туда выражений, зависящих от $x$ и $\bar {x}$, в виде интеграла по отрезку $[\bar {x},x]$ от производной по соответствующей переменной. Будем иметь

Дальше поступим так же, как в лемме 3.3 при рассмотрении ${{V}_{{11}}}(x,\bar {x},y)$ (см. (3.27), (3.28)), т.е. для ${{V}_{{211}}}(x,\bar {x},y)$ воспользуемся очевидной оценкой (см. (3.14)) а для ${{V}_{{212}}}(x,\bar {x},y)$ – также очевидной оценкой Получим Для вывода окончательных оценок осталось произвести интегрирование по $\eta $ и оценить максимумы соответствующих функций, являющихся коэффициентами при этих интегралах: Чтобы оценить эти коэффициенты, используем формулы, представляющие указанные выражения в полярных координатах, и оценки необходимых производных функции ${{K}_{0}}\left( {a\sqrt {({{z}^{2}} + {{\eta }^{2}}} } \right)$ или комбинаций этих производных, а затем применим к каждому выражению лемму 3.1 с соответствующими значениями параметров $\delta $ и $\beta $.

Точнее, при рассмотрении величин (1), (2) и (3) используем формулы из [1, ф. (А.9), (А.10)], содержащие оценки ${{K}_{0}}$ и ее производной в полярных координатах, что приводит к необходимости оценить выражения

Применение  леммы 3.1  при соответствующих значениях параметров $\delta $, $\beta $ доказывает ограниченность величин (1) и (2) постоянной, а выражение (3) оценивается величиной ${{(a - \alpha )}^{2}}\left[ {{{c}_{1}}{{\varepsilon }^{{ - 1/2}}} + {{c}_{2}}{{\varepsilon }^{{ - 1}}}} \right]$.

Рассматривая величину (4), используем формулу из [1, ф. (В.5)], выражающую оцениваемую функцию в полярных координатах, а затем применяем оценки из [1, ф. (А.6), (А.10)]. Это приводит нас к необходимости оценить величину

что и достигается применением леммы 3.1 при соответствующих значениях параметров $\delta $, $\beta $ и доказывает ограниченность величины (4) постоянной.

Для оценки величины (5), после очевидного преобразования $\alpha = a - (a - \alpha )$, используем формулу (3.2), выражающую оцениваемую величину в полярных координатах, а затем применяем оценки из [1, ф. (А.3), (А.9), (А.6), (А.10)]. В результате приходим к необходимости оценить выражение

Применение леммы 3.1 при соответствующих $\delta $, $\beta $ дает оценку $\left[ {{{c}_{3}} + {{c}_{4}}(a - \alpha ){{\varepsilon }^{{ - 1}}}} \right]$.

Аналогично поступаем при рассмотрении величины (6). Здесь мы также после очевидного преобразования $\alpha = a - (a - \alpha )$, использования формулы из [1, ф. (В.5)] для представления оцениваемой величины в полярных координатах и оценок из [1, ф. (А.6), (А.10)] сводим первоначальную оценку к оценке величины выражения

Снова применяем лемму 3.1 с необходимыми $\delta $, $\beta $, что дает оценку (6) величиной $\left[ {{{c}_{5}} + {{c}_{6}}(a - \alpha ){{\varepsilon }^{{ - 1/2}}}} \right]$.

Исследование величины (7) аналогично уже проведенному исследованию величины (5), что приводит к необходимости оценить выражение

Применяя снова лемму 1, имеем в этом случае оценку $\left[ {{{c}_{7}} + {{c}_{8}}{{{(a - \alpha )}}^{2}}{{\varepsilon }^{{ - 1/2}}} + {{c}_{9}}{{{(a - \alpha )}}^{3}}{{\varepsilon }^{{ - 1}}}} \right. + $ $ + \left. {\,{{c}_{{10}}}{{{(a - \alpha )}}^{3}}{{\varepsilon }^{{ - 3/2}}}} \right]$.

И, наконец, поступая аналогично при оценке выражения (8), т.е. в очередной раз заменяем $\alpha = a - (a - \alpha )$, используем формулы из [1, ф. (В.6), (В.5)], оценки из [1, ф. (А.7), (А.9), (А.10)] и применяем лемму 3.1 при соответствующих каждому слагаемому вида $si{{n}^{\delta }}\varphi {{r}^{\beta }}{{e}^{{ - (a - \alpha cos\varphi )r}}}$ значениях $\delta $, $\beta $, приходим к оценке выражения (8) величиной $\left[ {{{c}_{{11}}} + {{c}_{{12}}}(a - \alpha ){{\varepsilon }^{{ - 1/2}}}} \right]$.

Таким образом, после выполнения в (4.11) интегрирования по $\eta $, с учетом (2.7), получим

Принимая во внимание (4.8), (4.10) и объединяя оценки ${{V}_{{20}}}(x,\bar {x},y)$ из (4.9) и ${{V}_{{21}}}(x,\bar {x},y)$ из (4.12), приходим к утверждаемой в лемме оценке (4.1). Лемма доказана.

Лемма 4.2. Для производных ${{\partial }^{2}}u{\text{/}}\partial {{y}^{2}}$ и ${{\partial }^{2}}u{\text{/}}\partial x\partial y$ решения задачи (2.4), (2.5) справедливы оценки

Доказательство первой из этих оценок следует из оценки (3.18), если в последней заменить $g(y)$ на $g{\text{'}}(y)$, так как смешанная производная совпадает с производной по $x$ решения той же задачи (2.4), (2.5), но с правой частью $g{\text{'}}(y)$ граничного условия (2.5) вместо $g(y)$. Аналогично вторая оценка следует из (3.3) при замене в ней $g(y)$ на $g{\text{''}}(y)$.

5. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1

Суммируем оценки, полученные в разд. 1–4 (см. леммы 3.2–4.2).

Лемма 5.1. Для решения $U(X,Y)$ задачи (2.1), (2.2) справедливы оценки

Доказательство. Перепишем требующие доказательства неравенства (5.1) более подробно в нерастянутых переменных.

Имеем: при $k = 1$

при $k = 2$Для доказательства этих оценок используем результаты лемм 3.2–4.2 (см. формулы (3.3), (3.18), (3.34), (4.1), (4.13), (4.14)), а также интерполяционные неравенства (см., например, [2, лемма 1]) как для оценки самого решения и его производных в $C$, так и для функции $g(y)$: Из (5.2) и (5.3) для $g(y)$ следует, что Затем, учитывая очевидные неравенства после возвращения к исходным (нерастянутым переменным, см. (2.3)) $X = \varepsilon x$, $Y = \varepsilon y$, учитывая, что $0 < \varepsilon < 1$, и оценки (5.2)–(5.4), придем к утверждениям (5.1) леммы. Лемма доказана.

Замечание 1. Оценки решения $U(X,Y)$ задачи (2.1), (2.2) в $C_{y}^{{k,\lambda }}$ ($k = 0,\;1,\;2$) получаются аналогично оценкам в $C_{x}^{{k,\lambda }}$, но мы их использовать не будем.

Справедливость утверждений (2.8) теоремы 1 следует теперь из (5.1) и полученных в [4] оценок решения в $C_{y}^{{k,\lambda }}$ при $k = 0,\;1,\;2$. Тем самым теорема 1 полностью доказана.