Журнал вычислительной математики и математической физики, 2019, T. 59, № 2, стр. 325-333

О вычислении потенциала в многоатомных системах

О. А. Горкуша^1, *, В. Г. Заводинский^2, **

¹ ИПМатем ДВО РАН
680000 Хабаровск, ул. Дзержинского, 56, Россия

² Ин-т материаловедения ХНЦ ДВО РАН
680042 Хабаровск, ул. Тихоокеанская, 153, Россия

^* E-mail: 684bmts@rambler.ru
^** E-mail: vzavod@mail.ru

Поступила в редакцию 29.04.2018
После доработки 01.06.2018

DOI: 10.1134/S0044466919020066

Полный текст (PDF)

Аннотация

Предлагается численный метод нахождения потенциала многоатомной системы в прямом пространстве. Отличительная особенность метода состоит в разделении электронной плотности $\rho $ и потенциала $\varphi $ на две части: $\rho = {{\rho }_{0}} + \hat {\rho }$, $\varphi = {{\varphi }_{0}} + \hat {\varphi }$, где ${{\rho }_{0}}$ – сумма сферических атомных плотностей, а потенциал ${{\varphi }_{0}}$ порождается плотностью ${{\rho }_{0}}$. Потенциал $\hat {\varphi }$ находится путем решения уравнения Пуассона. Граничные условия получены путем разложения обратной величины расстояния между двумя точками в ряд по полиномам Лежандра. Для обеспечения точности метода расчетная область разбивается на многогранники Вороного и применяются асимптотические оценки итераций при замене характеристической функции гладкими приближениями. Для численного решения уравнения Пуассона использованы двухсеточный метод и Фурье-преобразование. Получена оценка точности метода $O({{h}^{{\gamma - 1}}})$, где $h$ – шаг сетки, $\gamma $ – фиксированное число, большее 1. Погрешность метода проанализирована на модельной двухатомной задаче. Библ. 19. Фиг. 2. Табл. 1.

Ключевые слова: уравнение Пуассона, электростатический потенциал, многогранники Вороного, мультипольное разложение, двухсеточный метод.

1. ВВЕДЕНИЕ

В задачах квантовой механики и квантовой химии часто возникает необходимость вычисления электростатического потенциала $\varphi (r)$, $r \in {{\mathbb{R}}^{3}}$, формируемого электронной плотностью $\rho (r)$ системы $m$ взаимодействующих атомов, расположенных в точках ${{R}_{1}},{{R}_{2}}, \ldots ,\;{{R}_{m}}$ (см. [1]–[3]). Формула, связывающая потенциал и плотность, выглядит весьма просто:

$\varphi (r) = \int\limits_\Omega {\frac{{\rho (r{\kern 1pt} {\text{'}})}}{{\left| {r - r{\kern 1pt} {\text{'}}} \right|}}} dr{\kern 1pt} {\text{',}}$

где $\Omega = \left\{ {r \in {{\mathbb{R}}^{3}}\,{\text{|}}\,\rho (r) \ne 0} \right\}$ – открытая, связная, ограниченная область с гладкой границей $(\partial \Omega \in {{C}^{{0,1}}})$.

Однако прямое численное интегрирование с неизбежностью обнажает почти неразрешимую проблему: для достижения разумной точности необходимо разбить интегрируемую область на достаточно малые элементарные ячейки, но время интегрирования при этом катастрофически растет. Проблема эта нетривиальна, и попыткам ее решения посвящено большое число работ, где предлагаются различные подходы, из которых наиболее разработанными являются метод быстрого Фурье-преобразования [4]–[7] и метод мультипольного разложения [8], [9]. Однако метод мультипольного разложения напрямую пригоден лишь для случаев, когда потенциал находится в точках, находящихся за пределами существования электронной плотности, а метод быстрого Фурье-преобразования (БПФ) обеспечивает хорошую точность лишь в обратном пространстве (пространстве волновых векторов). Для вычисления потенциала в прямом пространстве наиболее развит подход, опирающийся на решение уравнения Пуассона [10], [11], но его использование для многоатомных систем требует доработки с целью повышения точности. В нашей работе мы предлагаем комбинацию указанных подходов, а также некоторые другие разработки последних лет.

2. ОПИСАНИЕ ПОДХОДА

Прежде всего обратим внимание на тот факт, что в большинстве задач квантовой механики и квантовой химии расчеты ведутся итерационным способом, и на нулевой итерации электронная плотность многоатомной системы представляет собой сумму электронных плотностей невзаимодействующих (свободных) атомов или ионов. Поскольку электронные плотности свободных атомов (ионов) сферичны, то нулевая плотность системы ${{\rho }^{0}}(r)$ есть сумма сферических плотностей $\rho _{{{\text{sphere}}}}^{a}$, центрированных на атомах (ионах) с координатами ${{R}_{j}}:$

(1)

${{\rho }^{0}}(r) = \sum\limits_{j = 1}^m \,\rho _{{{\text{sphere}}}}^{a}\left( {\left| {r - {{R}_{j}}} \right|} \right).$

Сферические плотности заранее вычисляются с помощью подходящего квантово-механического метода, например, в рамках теории функционала плотности [2], и задаются в виде численных функций, зависящих от $R$ – расстояния до центра атома. Шаг величины $R$ обычно весьма мал, поэтому мы можем легко, быстро и достаточно точно вычислить электростатический потенциал отдельного свободного атома в сферических координатах:

$\varphi _{{{\text{sphere}}}}^{a}(R) = \frac{{2\pi }}{R}\int\limits_0^R {\rho _{{{\text{sphere}}}}^{a}} (r){{r}^{2}}dr + 2\pi \int\limits_R^\infty {\rho _{{{\text{sphere}}}}^{a}} (r)rdr,$

полагая, что $\rho _{{{\text{sphere}}}}^{a}(r) = 0$ при достаточно больших значениях $r.$ Зная потенциалы отдельных атомов в сферических координатах, мы можем с хорошей точностью найти начальный потенциал многоатомной системы в декартовых координатах, соответствующий начальной плотности (1):

(2)

${{\varphi }^{0}}(r) = \sum\limits_{j = 1}^m \,\varphi _{{{\text{sphere}}}}^{a}\left( {\left| {r - {{R}_{j}}} \right|} \right).$

В процессе итераций плотность системы изменяется. Обозначим это изменение через $\hat {\rho }(r)$ и в конкретных физических задачах, как правило, в области интегрирования, максимальное значение модуля плотности $\hat {\rho }(r)$ значительно меньше максимального значения плотности ${{\rho }^{0}}(r).$ То есть мы можем сказать, что для некоторого положительного числа $\hat {A}$ выполняется условие

(3)

$\mathop {max}\limits_{r \in \Omega } \left| {\hat {\rho }(r)} \right| < \hat {A}.$

Тогда текущую плотность $\rho (r)$ можно представить в виде суммы двух функций $\rho (r) = {{\rho }^{0}}(r) + \hat {\rho }(r)$, где ${{\rho }^{0}}(r)$ задается формулой (1), и потенциал, соответствующий плотности $\rho (r),$ приводится к виду

(4)

$\varphi (r) = {{\varphi }^{0}}(r) + \hat {\varphi }(r),\quad r \in \Omega $

с потенциалом ${{\varphi }^{0}}(r)$, определяемым формулой (2). Для нахождения $\hat {\varphi }(r)$ мы использовали уравнение Пуассона

(5)

$\Delta \hat {\varphi }(r) = - 4\pi \hat {\rho }(r),\quad r \in \Omega $

с граничными условиями

(6)

$\hat {\varphi }(r) = \int\limits_\Omega {\frac{{\hat {\rho }(r)}}{{\left| {r - r{\kern 1pt} {\text{'}}} \right|}}} dr{\kern 1pt} {\text{'}},\quad r \in \partial \Omega .$

3. ВЫЧИСЛЕНИЕ ГРАНИЧНЫХ ЗНАЧЕНИЙ ПОТЕНЦИАЛА

Рассмотрим интеграл (6). Разобьем расчетную область $\Omega $ на многогранники Вороного ${{\nu }^{{(j)}}}$

$\Omega = \bigcup\limits_{j = 1}^m \,{{\nu }^{{(j)}}},$

${{\nu }^{{(j)}}} = \left\{ {r \in \Omega \,|\,\left| {r - {{R}_{j}}} \right| = \mathop {min}\limits_{1 \leqslant k \leqslant m} \left| {r - {{R}_{k}}} \right|} \right\},$

центрированные на атомах, расположенных в точках ${{R}_{1}},\; \ldots ,\;{{R}_{m}}$ – аналогично тому, как задаются ячейки Вигнера–Зейтца в теории твердого тела (см. [12]–[14]).

Далее, с помощью характеристической функции области ${{\nu }^{{(j)}}}$

${{\chi }_{j}}(r) = \left\{ {\begin{array}{*{20}{l}} {1,}&{\;\;r \in {{\nu }^{{(j)}}};} \\ {0,}&{\;\;{\text{в }}\;{\text{п р о т и в н о м }}\;{\text{с л у ч а е }},} \end{array}} \right.$

представим плотность $\hat {\rho }(r)$ в виде суммы плотностей ${{\hat {\rho }}_{j}}(r) = \hat {\rho }(r) \cdot {{\chi }_{j}}(r)$. Тогда

(7)

$\begin{gathered} \hat {\varphi }(r) = \sum\limits_{j = 1}^m \,{{{\hat {\varphi }}}_{j}}(r), \\ {{{\hat {\varphi }}}_{j}}(r) = \int\limits_{{{\nu }^{{(j)}}}} {\frac{{\mathop {\hat {\rho }}\nolimits_j (r{\kern 1pt} {\text{'}})}}{{\left| {r - r{\kern 1pt} {\text{'}}} \right|}}} dr{\kern 1pt} {\text{'}}{\text{.}} \\ \end{gathered} $

Однако такой подход порождает серьезную проблему: плотность ${{\hat {\rho }}_{j}}(r)$ приобретает скачок на границе области ${{\nu }^{{(j)}}},$ что отрицательно влияет на сходимость и устойчивость численного метода. Один из способов решения этой проблемы – замена ступенчатой характеристической функции ее приближением, обладающим свойствами гладкости. В нашей работе мы использовали алгоритм построения такой функции, предложенный Becke [12].

Оценим точность этого подхода. Прежде всего заметим, что

${{\chi }_{j}}(r) = \prod\limits_{\begin{array}{*{20}{c}} {1 \leqslant i \leqslant m} \\ {i \ne j} \end{array}} \left( {1 - \Theta (\eta (r,i,j))} \right),$

где $\Theta $ – тета-функция Хевисайда, $\eta (r,i,j)$ – гиперболическая координата точки $r$ в конфокальной системе координат относительно фокусов в точках ${{R}_{i}}$ и ${{R}_{j}},$ по модулю не превышающая единицу:

$\eta (r,i,j) = \frac{{\left| {r - {{R}_{j}}} \right| - \left| {r - {{R}_{i}}} \right|}}{{\left| {{{R}_{i}} - {{R}_{j}}} \right|}}.$

Затем представим $\Theta (t)$ как предел последовательности ${{\left\{ {{{\Theta }_{k}}(t)} \right\}}_{{k > = 1}}}$ возрастающих функций, производные которых по переменной $t$ образуют $\delta $-образную последовательность. В работе [12] это представление выглядит следующим образом

${{\Theta }_{k}}(t) = \tfrac{{1 + {{s}_{k}}(t)}}{2},$

${{s}_{k}}(t) = \left\{ \begin{gathered} - 1,\quad t \leqslant - 1; \hfill \\ {{P}^{k}}(t),\quad \left| t \right| \leqslant 1,({{P}^{k}} = \underbrace {P \circ P \circ \ldots P}_{k\;{\text{р а з }}}); \hfill \\ 1,\quad t \geqslant 1. \hfill \\ \end{gathered} \right.$

Здесь $P(t)$ – полином, удовлетворяющий условиям $P( \pm 1) = \pm 1,$ ${{\left. {P{\kern 1pt} {\text{'}}(t)} \right|}_{{t = \pm 1}}} = 0$, позволяющим определить его степень и коэффициенты:

$P(t) = \frac{3}{2} \cdot t - \frac{1}{2} \cdot {{t}^{3}}.$

Полагая

${{\mathcal{P}}_{j}}(r;k) = \prod\limits_{\begin{array}{*{20}{c}} {1 \leqslant i \leqslant m} \\ {i \ne j} \end{array}} (1 - {{\Theta }_{k}}(\eta (r,i,j))),$

получим гладкое приближение характеристической функции ${{\tilde {\mathcal{P}}}_{j}}(r;k)$ в виде:

${{\tilde {\mathcal{P}}}_{j}}(r;k) = \frac{{{{\mathcal{P}}_{j}}(r;k)}}{{\sum\limits_{l = 1}^m {{{\mathcal{P}}_{l}}(r;k)} }}.$

Погрешность приближенного равенства ${{\chi }_{j}}(r) \approx {{\tilde {\mathcal{P}}}_{j}}(r;k)$ следует из оценки

$\Theta (t) = \left\{ \begin{gathered} {{\Theta }_{k}}(t),\quad t = \pm 1; \hfill \\ {{\Theta }_{k}}(t) + O({{a}^{{{{2}^{k}}}}}),\quad k \to \infty ,\quad \left| t \right| \in (0,1); \hfill \\ {{\Theta }_{k}}(t) - \frac{1}{2},\quad t = 0, \hfill \\ \end{gathered} \right.$

где $a$ – некоторое положительное число из интервала $(0,\;1)$. Тогда

${{\chi }_{j}}(r) = \left\{ \begin{gathered} {{{\tilde {\mathcal{P}}}}_{j}}(r;k),\quad r \in \left\{ {{{R}_{1}},\; \ldots ,\;{{R}_{m}}} \right\}; \hfill \\ {{{\tilde {\mathcal{P}}}}_{j}}(r;k) + \frac{{\mathcal{J}(r) - 1}}{{\mathcal{J}(r)}} + {{\varepsilon }_{1}}(a),\quad r \in \partial {{\nu }^{{(j)}}}; \hfill \\ {{{\tilde {\mathcal{P}}}}_{j}}(r;k) + {{\varepsilon }_{1}}(a),\quad {\text{в }}\;{\text{о с т а л ь н ы х }}\;{\text{с л у ч а я х }}. \hfill \\ \end{gathered} \right.$

Здесь величина $\mathcal{J}(r)$ равна числу областей, границы которых содержат точку $r$ – это либо $2,$ либо $3,$ причем $\mathcal{J}(r) = 3$ только в конечном числе точек, и

(8)

${{\varepsilon }_{1}}(a) = O({{a}^{{{{2}^{k}}}}}),\quad a \in (0,\;1),\quad k \to \infty .$

Используя полученные асимптотические формулы, приведем интеграл в (7) для вычисления ${{\hat {\varphi }}_{j}}(r)$ к виду

(9)

${{\hat {\varphi }}_{j}}(r) = \int\limits_{{{\nu }^{{(j)}}}} {\frac{{\hat {\rho }(r{\kern 1pt} {\text{'}}){{\chi }_{j}}(r{\kern 1pt} {\text{'}})}}{{\left| {r - r{\kern 1pt} {\text{'}}} \right|}}dr{\kern 1pt} {\text{'}}} = \int\limits_{{{\nu }^{{(j)}}}} {\frac{{\hat {\rho }(r{\kern 1pt} {\text{'}}){{{\tilde {\mathcal{P}}}}_{j}}(r{\text{'}};k)}}{{\left| {r - r{\kern 1pt} {\text{'}}} \right|}}} dr{\kern 1pt} {\text{'}} + \varphi _{j}^{'}(r) + {{\varepsilon }_{2}}(r),$

где

(10)

$\varphi _{j}^{'}(r) = \int\limits_{\partial {{\nu }^{{(j)}}}} {\frac{{\hat {\rho }(r{\kern 1pt} ')}}{{\left| {r - r{\kern 1pt} {\text{'}}{\kern 1pt} } \right|}} \cdot \frac{{\mathcal{J}(r{\kern 1pt} {\text{'}}) - 1}}{{\mathcal{J}(r{\kern 1pt} {\text{'}})}}dr{\text{'}}} {\text{,}}$

(11)

${{\varepsilon }_{2}}(r) = {{\varepsilon }_{1}}(a) \cdot \int\limits_{{{\nu }^{{(j)}}}\backslash {{O}_{\delta }}({{R}_{j}})} {\frac{{\hat {\rho }(r{\kern 1pt} {\text{'}})}}{{\left| {r - r{\kern 1pt} {\text{'}}{\kern 1pt} } \right|}}} dr{\kern 1pt} {\text{',}}$

и ${{O}_{\delta }}({{R}_{j}})$ – $\delta $-окрестность точки ${{R}_{j}}.$

Обозначим через $R({{\nu }^{{(j)}}})$ радиус минимальной сферы с центром в точке ${{R}_{j}},$ покрывающей область ${{\nu }^{{(j)}}}.$ Будем считать, что все точки, лежащие на границе $\partial \Omega ,$ расположены вне сферы. Тогда величину $\tfrac{1}{{\left| {r - r{\kern 1pt} {\text{'}}} \right|{\kern 1pt} }}$ можно представить в виде сходящегося ряда по системе многочленов Лежандра ${{P}_{l}}(cos\theta )$ [8], [9], [13], [15], [16]

$\frac{1}{{\left| {r - r{\kern 1pt} {\text{'}}{\kern 1pt} } \right|}} = \frac{1}{{\left| {r - {{R}_{j}}} \right|}}\sum\limits_{l = 0}^\infty \,{{t}^{l}}{{P}_{l}}(cos\theta ),\quad t = \frac{{\left| {r{\kern 1pt} {\text{'}} - {{R}_{j}}} \right|}}{{\left| {r - {{R}_{j}}} \right|}}$

с $\theta = \angle (\overrightarrow {r - {{R}_{j}}} ,\;\overrightarrow {r{\text{'}} - {{R}_{j}}} )$. Пользуясь оценкой

$\left| {\sum\limits_{l > L} \,{{t}^{l}}{{P}_{l}}(cos\theta )} \right| = O\left( {\frac{{{{t}^{L}}}}{{1 - t}}} \right),\quad L \to \infty ,$

запишем интеграл, стоящий в правой части соотношения (9), в виде

(12)

$\int\limits_{{{\nu }^{{(j)}}}} {\frac{{\hat {\rho }(r{\kern 1pt} {\text{'}}){{{\tilde {\mathcal{P}}}}_{j}}(r{\kern 1pt} {\text{'}};k)}}{{\left| {r - r{\kern 1pt} {\text{'}}{\kern 1pt} } \right|}}} dr{\kern 1pt} {\text{'}} = {{\tilde {\varphi }}_{j}}(r,k) + {{\varepsilon }_{3}}(r,j),$

где

(13)

${{\tilde {\varphi }}_{j}}(r,k) = \frac{1}{{\left| {r - {{R}_{j}}} \right|}}\int\limits_{{{\nu }^{{(j)}}}} {\hat {\rho }} (r{\kern 1pt} {\text{'}}{\kern 1pt} ){{\tilde {\mathcal{P}}}_{j}}(r{\text{'}};k) \cdot \sum\limits_{l = 0}^L {{\left( {\frac{{\left| {r{\kern 1pt} {\text{'}} - {{R}_{j}}} \right|}}{{\left| {r - {{R}_{j}}} \right|}}} \right)}^{l}}{{P}_{l}}(cos\theta )dr{\kern 1pt} {\text{',}}$

(14)

${{\varepsilon }_{3}}(r,j) = O\left( {\frac{{\hat {A}}}{{\left| {r - {{R}_{j}}} \right| - R({{\nu }^{{(j)}}})}} \cdot {{{\left( {\frac{{R({{\nu }^{{(j)}}})}}{{\left| {r - {{R}_{j}}} \right|}}} \right)}}^{L}}} \right),\quad L \to \infty .$

В последнем выражении константа $\hat {A}$ задается соотношением (3). Далее для оценки интегралов (10) и (11) воспользуемся асимптотическим неравенством

$\left| {\sum\limits_{l = 1}^\infty \,{{t}^{l}}{{P}_{l}}(cos\theta )} \right| \ll \frac{1}{{1 - t}},\quad {\text{п р и }}\quad t \in (0,\;1).$

Тогда

$\left| {\varphi _{j}^{'}(r)} \right| \leqslant \frac{{S(\partial {{\nu }^{{(j)}}})}}{{\left| {r - {{R}_{j}}} \right| - R({{\nu }^{{(j)}}})}} \cdot \mathop {max}\limits_{r{\text{'}} \in \partial {{\nu }^{{(j)}}}} \left| {\hat {\rho }(r{\kern 1pt} {\text{'}})} \right|,\quad {{\varepsilon }_{2}}(r) = {{\varepsilon }_{1}}(a),$

где $S$ – площадь границы области ${{\nu }^{{(j)}}}.$ Из последних двух оценок и формул (9), (12), (14) следует, что вклад в асимптотику интеграла ${{\hat {\varphi }}_{j}}(r)$ с главным членом (13) вносит сумма

(15)

${{\varepsilon }_{4}}(r,a,j) = {{\varepsilon }_{3}}(r,j) + {{\varepsilon }_{1}}(a),$

в которой оценки ${{\varepsilon }_{1}}(a),$ ${{\varepsilon }_{3}}(r,j)$ вычисляются по формулам (8) и (14). Подставляя полученное асимптотическое выражение для ${{\hat {\varphi }}_{j}}(r)$ в (7), приходим к равенству

(16)

$\hat {\varphi }(r) = \hat {\varphi }{\kern 1pt} '(r) + {{\varepsilon }_{4}}(r,a,j),$

где индекс $j$ обозначает ту область ${{\nu }^{{(j)}}},$ граница которой содержит точку $r$ и

(17)

$\hat {\varphi }{\kern 1pt} {\text{'}}(r) = \sum\limits_{j = 1}^m \,\tilde {\varphi }(r,k)$

с функцией $\tilde {\varphi }(r,k)$, заданной в (13).

4. ОЦЕНКА ЧИСЛЕННОГО РЕШЕНИЯ УРАВНЕНИЯ ПУАССОНА

Теперь перейдем непосредственно к решению уравнения Пуассона (5), (6). Учитывая (16), представим решение этой задачи в виде

(18)

$\hat {\varphi }(r) = u(r) + {{u}^{0}}(r),$

где $u$ – решение задачи (5) с граничным условием

(19)

${{\left. u \right|}_{{\partial \Omega }}} = \hat {\varphi }{\kern 1pt} {\text{',}}$

задаваемым соотношением (17), а ${{u}^{0}}$ – решение задачи Дирихле для уравнения Лапласа граничным условием ${{\left. {{{u}^{0}}} \right|}_{{\partial \Omega }}} = {{\varepsilon }_{4}}$. Так как решение ${{u}^{0}}$ достигает максимума на границе, то согласно (15)

(20)

$\begin{gathered} \left| {{{u}^{0}}(r)} \right| \ll {{\varepsilon }_{4}}(\hat {A}) + {{\varepsilon }_{1}}(a), \\ {{\varepsilon }_{4}}(\hat {A}) = O\left( {\mathop {max}\limits_{r \in \partial \Omega } \frac{{\hat {A}}}{{\left| {r - {{R}_{j}}} \right| - R({{\nu }^{{(j)}}})}} \cdot {{{\left( {\frac{{R({{\nu }^{{(j)}}})}}{{\left| {r - {{R}_{j}}} \right|}}} \right)}}^{L}}} \right),\quad L \to \infty . \\ \end{gathered} $

Для численного решения задачи (5), (19) мы использовали двухсеточный метод, описанный в работах [10], [13], [17].

Обозначим через ${{\Omega }^{h}}$ сетку с шагом $h$ на $\Omega ,$ через ${{\Gamma }^{h}}$ множество узлов $(ih,jh,kh),$ не принадлежащих ${{\Omega }^{h}},$ с условием

$\partial \Omega \subseteq \bigcup\limits_{(ih,jh,kh) \in {{\Gamma }^{h}}} \left\{ {(x,y,z) \in Cub{{e}_{h}}(ih,jh,kh)} \right\}$,

где $Cub{{e}_{h}}(x,y,z)$ – куб с длиной стороны, равной $h,$ и с центром в точке $(x,y,z),$ при этом хотя бы одна из вершин куба содержится в ${{\Omega }^{h}}.$ Объединение множеств ${{\Omega }^{h}}$ и ${{\Gamma }^{h}}$ обозначим через ${{\bar {\Omega }}^{h}}$. Поскольку граничные точки передают особенности формы границы $\partial \Omega ,$ то мы можем однородным способом конструировать разностную схему по всей области $\bar {\Omega }$.

Значение функции ${{u}^{h}}$ в точке $(ih,jh,kh)$ обозначим через $u_{{i,j,k}}^{h}.$ Задаче (5), (19) поставим в соответствие разностную задачу

${{({{L}^{h}}({{u}^{h}}))}_{{i,j,k}}} = - 4\pi \hat {\rho }(ih,jh,kh),\quad (ih,jh,kh) \in {{\Omega }^{h}},$

$u_{{i,j,k}}^{h} = \hat {\varphi }{\kern 1pt} {\text{'}}(ih,jh,kh),\quad (ih,jh,kh) \in {{\Gamma }^{h}},$

где

(21)

$\begin{gathered} {{({{L}^{h}}({{u}^{h}}))}_{{i,j,k}}} = \frac{{u_{{2i - 1,2j,2k}}^{{h/2}} - 2\tilde {u}_{{2i,2j,2k}}^{{h/2}} + u_{{2i + 1,2j,2k}}^{{h/2}}}}{{{{{(h{\text{/}}2)}}^{2}}}} + \frac{{u_{{2i,2j - 1,2k}}^{{h/2}} - 2\tilde {u}_{{2i,2j,2k}}^{{h/2}} + u_{{2i,2j + 1,2k}}^{{h/2}}}}{{{{{(h{\text{/}}2)}}^{2}}}} + \\ + \;\frac{{u_{{2i,2j,2k - 1}}^{{h/2}} - 2\tilde {u}_{{2i,2j,2k}}^{{h/2}} + u_{{2i,2j,2k + 1}}^{{h/2}}}}{{{{{(h{\text{/}}2)}}^{2}}}}, \\ \end{gathered} $

и величины $u_{{i,j,k}}^{{h/2}},$ $\tilde {u}_{{i,j,k}}^{{h/2}}$ – решения разностной задачи на предыдущей и текущей итерациях.

Известно, что разностная схема (21) сходится и погрешность относительно решения задачи (5), (19) имеет второй порядок аппроксимации. Учитывая представление решения $\tilde {\varphi }$ (18) и оценку (20), получаем погрешность приближенного решения относительно задачи (5), (6):

$\hat {\varphi }(r) = \tilde {u}_{{i,j,k}}^{h} + O({{h}^{2}}) + {{\varepsilon }_{1}}(h) + {{\varepsilon }_{4}}(\hat {A}),\quad r = (ih,jh,kh) \in {{\bar {\Omega }}^{h}}.$

Cогласно (20), ${{\varepsilon }_{4}}(\hat {A}) \ll \tfrac{{\hat {A}}}{h}$. Положив $\gamma = ln\hat {A}{\text{/}}lnh$ и используя (4), получаем асимптотическую формулу для $\varphi (r)$

(22)

$\varphi (r) = {{\varphi }^{0}}(r) + \tilde {u}_{{i,j,k}}^{h} + O\left( {max\left\{ {{{h}^{2}},{{h}^{{\gamma - 1}}}} \right\}} \right),\quad r = (ih,jh,kh) \in {{\bar {\Omega }}^{h}},$

в которой потенциал ${{\varphi }^{0}}(r)$ задается в (1).

5. ЧИСЛЕННАЯ СХЕМА РЕШЕНИЯ УРАВНЕНИЯ ПУАССОНА

Шаг итерационного процесса состоит из следующих этапов.

1. Производим одну итерацию на ${{\bar {\Omega }}^{{h/2}}}$, вычисляя $\tilde {u}_{{2i,2j,2k}}^{{h/2}}$ по формуле (21). Новое приближенное решение к решению на ${{\bar {\Omega }}^{h}}$ на этом этапе определяется формулой

$\tilde {u}_{{i,j,k}}^{h} = \tilde {u}_{{2i,2j,2k}}^{{h/2}}.$

2. Вычисляем параметр сходимости $\mu $ итерационного процесса по формуле

$\mu = \frac{{{{{\left\| {{{L}^{h}}({{{\tilde {u}}}^{h}}) - 4\pi \hat {\rho }} \right\|}}_{{{{{\bar {\Omega }}}^{h}}}}}}}{{{{{\left\| {{{L}^{h}}({{u}^{h}}) - 4\pi \hat {\rho }} \right\|}}_{{{{{\bar {\Omega }}}^{h}}}}}}},$

где оператор ${{L}^{h}}$ задается в (21), и $\left\| {\, \cdot \,} \right\|$ – дискретная норма в ${{\bar {\Omega }}^{h}}.$

3. Если $\mu $ близко к единице, то итерационный процесс завершен. Иначе мы интерполируем функцию $\tilde {u}_{{i,j,k}}^{h}$ c ${{\bar {\Omega }}^{h}}$ на ${{\bar {\Omega }}^{{h/2}}}$ при помощи оператора интерполяции, точного для многочленов второй степени. И переходим к первому пункту итерационного процесса.

Как и в каждой итерационной процедуре, важную роль играет выбор начальной функции. В нашем случае мы использовали в качестве начального приближения потенциал, вычисленный с помощью БПФ, а именно:

(23)

$\begin{gathered} u(r) = 4\pi \sum\limits_{{{m}_{x}},{{m}_{y}},{{m}_{z}}} \frac{{c({{m}_{x}},{{m}_{y}},{{m}_{z}})}}{{{{\lambda }^{2}} + {{{(2\pi h)}}^{2}} \cdot (m_{x}^{2} + m_{y}^{2} + m_{z}^{2})}}{{e}^{{i({{m}_{x}} \cdot x + {{m}_{y}} \cdot y + {{m}_{z}} \cdot z)}}}, \\ r = (x,y,z) \in \mathop {\overline {Cube(\Omega )} }\nolimits^h . \\ \end{gathered} $

Здесь $c({{m}_{x}},{{m}_{y}},{{m}_{z}})$ – коэффициенты Фурье функции $\hat {\rho }(r)$, $\lambda $ – некоторая константа, значительно меньшая единицы [18].

6. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

Как было сказано во Введении, Фурье-преобразование не дает возможности вычислить потенциал с достаточной точностью. В качестве иллюстрации на фиг. 1 приведены результаты расчета потенциала по формуле (23) при разных значениях параметра $\lambda $ для двухатомной модельной системы $(m = 2)$ с плотностью

(24)

$\rho (r) = \rho (r;\beta ,{{\alpha }_{1}},{{R}_{1}},\; \ldots ,\;{{\alpha }_{m}},{{R}_{m}}) = \sum\limits_{j = 1}^m \left( {{{\alpha }_{j}}{{{\left| {r - {{R}_{j}}} \right|}}^{2}}{{e}^{{ - \beta |r - {{R}_{j}}|}}}} \right),$

где $\beta = 2$ а.е.^–1, (а.е. = 0.0529 нм), множители ${{\alpha }_{1}}$, …, ${{\alpha }_{m}}$ задаются из условий нормировки.

Фиг. 1.

Зависимость вычисленного потенциала от полной плотности (в сравнении с аналитическим расчетом) от $\lambda .$ Сплошная линия – аналитический расчет, пунктир – расчет с использованием БПФ.

Формула (24) допускает возможность аналитического вычисления потенциала, а именно:

(25)

${{\varphi }_{{{\text{analitic}}}}}(r) = \frac{{4\pi }}{{{{\beta }^{4}}}}\sum\limits_{j = 1}^m \,{{\alpha }_{j}}\left( {\frac{{4!\left( {1 - {{e}^{{ - \beta {{r}_{j}}}}}} \right)}}{{{{r}_{j}}}} - {{e}^{{ - \beta {{r}_{j}}}}}\left( {{{\beta }^{2}}r_{j}^{2} + 6\beta {{r}_{j}} + 18} \right)} \right),\quad {{r}_{j}} = \left| {r - {{R}_{j}}} \right|.$

На фиг. 1 представлены для сравнения результаты аналитического вычисления потенциала. Мы видим, что можно подобрать такое значение $\lambda ,$ при котором потенциал, вычисленный с помошью Фурье-преобразования, будет очень близок к аналитическому потенциалу. Однако, как показывают практические расчеты (см. [19]), для вычислений потенциалов, соответствующих реальным атомам, оптимальные значения параметра $\lambda $ необходимо подбирать для каждого типа атомов, кроме того, результат Фурье-преобразования зависит от многих технических параметров (в том числе от размера ячейки, используемой для БПФ, от шага разбиения ячейки, и так далее), что делает применение Фурье-преобразования весьма затруднительным для реальных многоатомных систем.

Ключевым моментом предлагаемого метода является разделение полной плотности $\rho $ системы взаимодействующих атомов на начальную плотность ${{\rho }_{0}},$ состоящую из суммы сферических плотностей, центрированных на отдельных атомах и некой плотности $\hat {\rho }$, образующейся вследствие взаимодействия атомов в системе. Такой подход позволяет ограничить использование Фурье-преобразования лишь применением его для вычисления потенциала $\widehat \varphi $ от плотности $\hat {\rho }$, амплитуда которой, как правило, значительно меньше амплитуды плотности ${{\rho }_{0}}.$

Для численного эксперимента мы рассмотрели модельную двухатомную систему $(m = 2)$ с плотностью ${{\rho }_{0}},$ вычисляемую по формуле (24). Плотность $\widehat \rho $ представим в виде

$\begin{gathered} \hat {\rho }(r) = \rho (r; - \varepsilon ,{{R}_{1}}, - \varepsilon ,{{R}_{2}},2\varepsilon ,{{R}_{3}}) = \\ = \; - {\kern 1pt} \varepsilon {{\left| {r - {{R}_{1}}} \right|}^{2}}{{e}^{{ - \beta |r - {{R}_{1}}|}}} - \varepsilon {{\left| {r - {{R}_{2}}} \right|}^{2}}{{e}^{{ - \beta |r - {{R}_{2}}|}}} + 2\varepsilon {{\left| {r - {{R}_{3}}} \right|}^{2}}{{e}^{{ - \beta |r - {{R}_{3}}|}}}, \\ \end{gathered} $

где точка ${{R}_{3}}$ – середина отрезка $[{{R}_{1}},{{R}_{2}}],$ $\varepsilon $ – некоторое положительное число, определяющее амплитуду изменения плотности $\widehat \rho .$ Отметим, что

$\int\limits_\Omega {\hat {\rho }} (r)dr = 0,$

что соответствует сохранению заряда в системе.

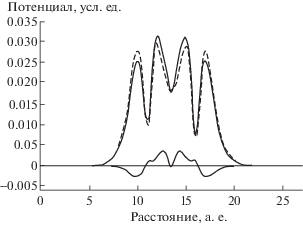
На фиг. 2 представлено соответствующее распределение плотности. Мы видим, что добавочная плотность $\widehat \rho $ имеет как положительные, так и отрицательные значения, что обеспечивает перетекание плотности из одних областей пространства в другие.

Фиг. 2.

Вид электронной плотности модельного димера вдоль прямой, проходящей через атомные центры. Точки – плотность ${{\rho }^{0}},$ составленная из сферических атомных функций невзаимодействующих атомов, нижняя сплошная кривая – межатомная плотность $\hat {\rho }$, образовавшаяся из-за взаимодействия атомов, верхняя сплошная кривая – суммарная плотность ${{\rho }^{0}} + \hat {\rho }$ атомной системы.

При таком подходе значения потенциалов, вычисленных разными методами, отличаются друг от друга весьма незначительно, и сравнение их в графическом виде малоинформативно. Поэтому мы вычислили среднее отклонение потенциалов от аналитического. В табл. 1 представлены результаты сравнения двух методов. Мы видим, что в данном случае погрешность вычисления потенциала с помощью БПФ весьма мала. Но ее можно еще более уменьшить с помощью метода, предлагаемого в данной работе, где Фурье-преобразование используется только в качестве нулевого приближения двухсеточного метода. Это позволяет почти на порядок уменьшить погрешность численного решения. Следует отметить, что при увеличении параметра $\lambda $ в $100$ раз величины погрешностей и того и другого метода изменяются не более, чем на 20%.

Таблица 1.

Абсолютные и относительные погрешности вычисления потенциала $\lambda = 0.005,$ $K = \frac{{max\hat {\rho }(r)}}{{max{{\rho }_{0}}(r)}}$

ε	K	Абсолютная погрешность		Относительная погрешность
ε	K	БПФ	Наш метод	БПФ	Наш метод
0.00500	0.0018	2.53791 × 10^–6	4.70817 × 10^–6	4.84735 × 10^–6	7.75075 × 10^–7
0.02480	0.0092	1.26257 × 10^–5	2.34225 × 10^–6	2.41153 × 10^–5	3.85499 × 10^–6
0.23512	0.0867	1.19498 × 10^–4	2.21687 × 10^–5	2.28298 × 10^–4	3.63969 × 10^–5
0.44380	0.1636	2.25581 × 10^–4	4.18484 × 10^–5	4.31078 × 10^–4	6.85429 × 10^–5

Представленный нами подход к нахождению потенциала был эффективно применен в работах по развитию нового безорбитального метода моделирования многоатомных систем (их содержание описано в книге [19]).

7. ВЫВОДЫ

1. Разбиение плотности на сумму неизменных сферических плотностей и добавочную плотность, изменяющуюся при взаимодействии атомов, резко увеличивает точность вычисления электростатического потенциала методом Фурье-преобразования.

2. Применение нашего метода позволяет уменьшить погрешность вычисления потенциала еще на порядок.

3. Теоретическая оценка погрешности метода позволяет контролировать параметры численного расчета – амплитуда добавочной плотности должна быть сравнима с величиной ${{h}^{\gamma }},$ с $\gamma \in (1,\;2)$.

Список литературы

Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивисткая теория. М.: Физматгиз, 1963.
Kohn W., Sham J.L. Self-consistent equations including exchange and correlation effects // Phys. Rev. 1965. V. 140. A1133.
Заводинский В. Компьютерное моделирование наночастиц и наносистем. М.: Физматлит, 2013.
Sköllermo G. A fourier method for the numerical solution of Poisson’s equation // Math. Comput. 1975. V. 29. P. 697.
Chun-Min Chang, Yihan Shao, Jing Kong. Ewald mesh method for quantum mechanical calculations // J. Chem. Phys. 2012. V. 136. 114112.
Бобров В.Б., Загородний А.Г., Тригер С.А. // Физ. низких температур. 2015. Т. 41. С. 1154.
Chelikowsky J.R., Troullier N., Saad Y. Finite-difference-pseudopotential method: Electronic structure calculations without a basis // Phys. Rev. Lett. 1994. V. 72. P. 1240.
Kleinman L., Bylander D.M. Efficacious form for model pseudopotentials // Phys. Rev. Lett. 1982. V. 48. P. 1425–1428.
Cheng H., Greebgard L., Rokhlin V. A fast adaptive multipole algorithm in three dimensions // J. Comput. Phys. 1999. V. 155. P. 468.
Mortensen J.J., Hansen L.B., Jacobsen K.W. Real-space grid implementation of the projector augmented wave method // Phys. Rev. B Condensed Matter. 2005. V. 71. 035109.
Chelikowsky J.R., Wu K., Troullier N., Saad Y. Higher-order finite-difference pseudopotential method: An application to diatomic molecules // Phys. Rev. B. 1994. V. 50. 11355.
Becke A.D. A multicenter numerical integration scheme for polyatomic molecules // J. Chem. Phys. 1988. V. 88. 2547.
Hiroshe Kikuji, Ono Tomoya, Fujimoto Yoshitaka, Tsukamoto Shigeru. First-Principles Calculations in Real-Space Formalism. London: Imperial College Press, 2005.
Okabe A., Boots B., Sugihara K., Chiv S.N., Kendall D.G. Spatial Tesselations: Concepts and Applications of Voronoi Diagrams. New York: Wiley, 2000.
Gonze X., Stumpf R., Scheffler M. Analysis of separable potentials // Phys. Rev. B. 1991. V. 44. 8503.
Troullier N., Martins J.L. Efficient pseudopotentials for plane-wave calculation // Phys. Rev. B. 1991. V. 43. 1993.
Brandt A. Multi-level adaptive solutions to boundary-value problems // Math. Comput. 1977. V. 31. P. 333.
Харрисон У. Электронная структура и свойства твердых тел. Т. 2 / Под ред. Ж.И. Алферова. М.: Мир, 1983.
Заводинский В. Квантовое моделирование многоатомных систем без волновых функций. Saarbrucken, Deutschland: LAP LAMBERT Academic Publishing, 2017.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал