1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 59, № 2, 2019

Журнал вычислительной математики и математической физики, 2019, T. 59, № 2, стр. 313-324

Решение уравнения растекания нефтяных разливов на поверхности моря характеристическим методом

Б. В. Архипов 1, *, Д. А. Шапочкин 1

1 ВЦ ФИЦ ИУ РАН
119991 Москва, ул. Вавилова, 40, Россия

* E-mail: arh12.bor12@yandex.ru

Поступила в редакцию 14.03.2018
После доработки 10.07.2018

Полный текст (PDF)

Аннотация

В работе рассматривается модель растекания нефтяного разлива на основе уравнения в частных производных, базирующаяся на рассмотрении баланса сил, действующих на осесимметричное пятно. Цель работы состоит в построении метода численного решения, способного правильно описать движение контактной границы разлива. Оригинальность предлагаемого подхода заключается в том, что в нем, с одной стороны, предлагаются граничные условия, специфические для каждой стадии Фэя, а с другой стороны, рассматривается способ численного решения уравнения растекания на основе метода характеристик. Показано, что получаемое численное решение согласуется с формулами Фэя. Библ. 23. Фиг. 4. Табл. 2.

Ключевые слова: математическое моделирование, нефтяной разлив, растекание, характеристический метод, граница разлива.

1. ВВЕДЕНИЕ

Проблемы, связанные с загрязнением окружающей среды в результате нефтяных разливов, привели к необходимости разработки математических моделей, описывающих процесс переноса и трансформации нефтяных разливов на поверхности моря. Эти модели выполняют важную роль при решении практических задач оценки воздействия на окружающую среду и ликвидации нефтяных разливов (см. [1]–[3]).

Сложность моделирования трансформации нефтяного разлива в окружающей среде заключается в многообразии процессов (воздействий), которым подвергается нефтяной объем, оказавшийся в естественных условиях. При исследовании данной проблемы, с одной стороны, необходимо одновременно учитывать процессы разной природы, описываемые зачастую в терминах различных областей знаний, а с другой стороны, возникают существенные трудности с количественным описанием некоторых из этих процессов, обусловленные отсутствием теорий, удовлетворительно описывающих происходящие явления (например, процессы растекания, диспергирования и эмульсификации) (см. [4]).

Реальное нефтяное пятно в процессе эволюции испытывает ряд превращений. В начальный период оно имеет довольно сложную форму, вытянутую по направлению ветра. В головной части пятна (толстый слик) сосредоточена большая часть массы нефти. В окружающем кольце (темная нефть) нефти существенно меньше. Остальная часть нефтяного пятна (тонкий слик) содержит не более доли процента от всей массы разлива и имеет толщину менее 1 мкм. В то же время площадь тонкого слика существенно превышает площадь остальной части (см. [4]). Со временем нефтяное пятно теряет сплошность и превращается сначала в набор полос, а затем отдельных пятен. Строго говоря, в настоящее время не существует модели, основанной на уравнениях гидродинамики, способной описать такие особенности, и поэтому в существующих моделях используются более или менее грубые подходы (параметризации), учитывающие лишь часть свойств, сопровождающих растекание.

Одни из первых результатов по количественному описанию растекания нефтяных разливов были получены в известных работах Фэя (см. [5], [6]). В этих работах было рассмотрено одномерное (плоско-параллельное) и осесимметричное растекание нефти по неподвижной водной поверхности. Было выделено три стадии процесса растекания (в зависимости от типа преобладающих сил, действующих на нефтяное пятно): инерционно-гравитационная, гравитационно-вязкая и поверхностно-вязкая. Для каждой из этих стадий была получена степенная зависимость радиуса пятна от времени (с различными показателями степени на различных стадиях) с коэффициентом пропорциональности, определяемым на основе экспериментальных данных.

Основными недостатками алгебраических формул Фэя и их аналогов (см. [4]), затрудняющими их практическое применение, являются разбиение процесса растекания на отдельные фазы (возникает необходимость в определении временных границ различных фаз). Кроме того, в этом подходе невозможно согласованно с растеканием учитывать влияние других процессов выветривания, приводящих к изменению массы разлива (испарение, эмульсификация, диспергирование и т.п.).

В ряде работ для описания процесса растекания нефтяных разливов используются обыкновенные дифференциальные уравнения (ОДУ), в определенном смысле обобщающие формулы Фэя (см. [7]–[11]). Данные ОДУ получаются при грубых допущениях о форме разлива (как правило, принимаемого в виде кругового цилиндра или конуса) и использовании приближенных формул для сил, влияющих на растекание (см. [11]). Моделирование растекания на основе ОДУ является несомненно более развитым подходом (в сравнении с использованием алгебраических формул), поскольку позволяет описывать весь процесс растекания в рамках одной общей постановки (без необходимости разбиения его на различные стадии), а также дает возможность относительно просто и естественно вводить в модель различные процессы выветривания, рассматривать одномерное или осесимметричное растекание, а также две постановки – непрерывное вытекание или залповый сброс.

Расширением модели на основе ОДУ являются модели, приводящие к уравнениям в частных производных (УрЧП) (см. [12]–[18]). Такие подходы позволяют учитывать некоторые дополнительные особенности, в том числе неправильную форму разлива, однако, они обычно требуют больших вычислительных затрат и достаточно трудны в реализации, в частности, в силу необходимости рассматривать контактную движущуюся границу, окаймляющую нефтяное пятно. При построении полноценных двумерных моделей движение контактной границы разлива описывается, как правило, достаточно грубо, на основе метода частиц с недостаточно обоснованными граничными условиями (см. [12]–[16]). Вопрос постановки граничных условий и точность этого метода для описания движения границы не исследованы. При использовании метода блуждающих частиц появляются дополнительные сложности согласования сплошности нефтяного разлива и дискретности используемого подхода.

В настоящей работе рассматривается уравнение растекания на основе УрЧП, подобного уравнению, приведенному в работах (см. [12], [13]), но в осесимметричном варианте. Цель работы состоит в построении метода численного решения, способного правильно описать движение границы разлива. Оригинальность предлагаемого подхода заключается в том, что в нем предлагается способ численного решения уравнения растекания на основе характеристического подхода. В результате реализации предложенного численного метода показано, что получаемое решение согласуется с аналитическими решениями и/или формулами Фэя на различных стадиях растекания, вытекающими из основного уравнения модели в результате уравнивания пар сил, в соответствии с подходом Фэя, преобладающих на каждой стадии процесса растекания.

2. ОБЩАЯ ПОСТАНОВКА, ЛАГРАНЖЕВЫ КООРДИНАТЫ, ПОЛУЧЕНИЕ АВТОМОДЕЛЬНЫХ РЕШЕНИЙ И ФОРМУЛЫ ФЭЯ

Рассмотрим растекание нефтяного разлива на поверхности моря на основе уравнений мелкой воды (см. [12]–[19]) в полярных координатах:

(1)
$\frac{{\partial rh}}{{\partial t}} + \frac{{\partial rhu}}{{\partial r}} = 0,$
(2)
$\frac{{\partial rhu}}{{\partial t}} + \frac{{\partial rh{{u}^{2}}}}{{\partial r}} = - \Delta ghr\frac{{\partial h}}{{\partial r}} - {{C}_{t}}r\frac{{2\sigma }}{{{{\rho }_{0}}{{h}_{m}}}}\frac{{\partial h}}{{\partial r}} - {{C}_{v}}\frac{{{{\rho }_{w}}}}{{{{\rho }_{0}}}}r\frac{{\nu _{w}^{{1/2}}}}{{{{R}^{{1/2}}}}}{{u}^{{3/2}}}.$

Обозначения основных величин приведены в табл. 1.

Таблица 1.  

Обозначения основных величин

Название Обозначение
Время t
Радиальная координата $r$
Радиальная компонента скорости u
Изменение толщины слоя нефти $h\left( r \right)$
Максимальная толщина слоя нефти ${{h}_{m}}$
Радиус нефтяного пятна R
Гравитационное ускорение g
Плотности нефти и воды ${{\rho }_{o}},\;{{\rho }_{w}}$
Кинематические вязкости нефти и воды ${{\nu }_{o}},\;{{\nu }_{w}}$
Динамические вязкости нефти и воды ${{\mu }_{o}},\;{{\mu }_{w}}$
Редуцированное гравитационное ускорение $\Delta g = \frac{{{{\rho }_{w}} - {{\rho }_{o}}}}{{{{\rho }_{w}}}}g$
Поверхностное натяжение на границах раздела вода–воздух, вода–нефть, нефть–воздух ${{\sigma }_{{wa}}},\;{{\sigma }_{{wo}}},\;{{\sigma }_{{oa}}}$
Коэффициент Харкинса $\sigma = {{\sigma }_{{wa}}} - {{\sigma }_{{wo}}} - {{\sigma }_{{oa}}}$
Напряжение трения ${{F}_{f}}$
Подбираемые константы ${{C}_{t}},\;{{C}_{\text{v}}}$

Граничные и начальные условия для системы (1), (2) рассмотрены ниже. Уравнение (2) выражает баланс четырех сил: 1 – силы инерции (левая часть), 2 – гравитационной силы (градиента давления, первое слагаемое справа), 3 – силы поверхностного натяжения, 4 – силы поверхностного трения слоя нефти о водную поверхность (см. [12], [13]). Отметим некоторые особенности используемого уравнения (2).

Во-первых, в гравитационный член (первое слагаемое в правой части уравнения) вместо полного гравитационного ускорения входит редуцированное ускорение $\Delta g = g\left( {{{\rho }_{w}} - {{\rho }_{0}}} \right){\text{/}}{{\rho }_{w}}$. Во-вторых, в правой части присутствует слагаемое, связанное с силой поверхностного натяжения. Для введения этой силы используется коэффициент Харкинса (см. [20], [21]) $\sigma = {{\sigma }_{{wa}}} - {{\sigma }_{{wo}}} - {{\sigma }_{{oa}}}$. В этом подходе для упрощения считаем, что сила поверхностного натяжения распространена по всему пятну и вызвана градиентом поверхностного натяжения (см. [12], [13]). В-третьих, оценку силы трения на нижней поверхности нефтяного слоя получаем на основе формулы Блазиуса для силы трения при обтекании плоской пластинки набегающим потоком со скоростью $u$ (см. [22]):

(3)
${{F}_{f}} \approx {{C}_{\tau }}{{\left( {\frac{{\rho _{w}^{2}{{\nu }_{w}}{{u}^{3}}}}{x}} \right)}^{{1/2}}},$
где $x$ – продольная координата, отсчитываемая от передней кромки пластинки. Ясно, что в настоящей модели нет претензии на подробное описание погранслоя в воде, его структуры и изменения по радиусу силы трения. Потому формула (3) используется для оценки этой силы, где расстояние, отсчитываемое от передней кромки пластинки, заменено линейным масштабом, равным радиусу разлива аналогично работе [12]. Отметим, что применимость такого подхода обосновывается тем фактом, что при его использовании автомодельные решения, выводимые ниже, дают правильный показатель степени в изменении радиуса, совпадающий с формулой Фэя. Сила трения записывается через параметры пограничного слоя, возникающего в воде, и в ее выражение входят плотность и вязкость воды, а не нефти.

Преобразуем задачу (1), (2) к безразмерной форме (см. [23]). Исходя из постановки, определяем набор определяющих (искомых и задаваемых) величин. Выбираем новые основные единицы, например, вместо кг, м, с (основные единицы в СИ) выбираем новые единицы объема ${{V}_{0}}\;[{{{\text{м }}}^{3}}]$ (начальный объем нефти), плотности ${{\rho }_{0}}\;[{\text{к г /}}{{{\text{м }}}^{3}}]$ (начальная плотность нефти), ускорения $\Delta g = g\left( {{{\rho }_{w}} - {{\rho }_{0}}} \right){\text{/}}{{\rho }_{w}}$ $[{\text{м /}}{{{\text{с }}}^{2}}]$. Выводим одночлены, связывающие масштабы производных единиц с масштабами исходных. Для значений масштабов основных независимых новых единиц выбираем специфические значения, связанные с числовыми значениями соответствующих определяющих параметров. Связь старых (размерных) и новых (безразмерных) значений имеет вид, показанный в табл. 2.

Таблица 2.  

Связь старых (размерных) и новых (безразмерных) значений

Название величины Связь “размерных” и “безразмерных” переменных
Длина $R = V_{0}^{{1/3}}\Re $
Время $t = \Delta {{g}^{{ - 1/2}}}V_{0}^{{1/6}}\tau $
Скорость $\dot {R} = V_{0}^{{1/6}}\Delta {{g}^{{1/2}}}\dot {\Re }$
Объем $V = V_{0}^{{}}\Upsilon $

Вводя безразмерные параметры

(4)
${{C}_{1}} = V_{0}^{{ - 1/2}}\Delta {{g}^{{ - 1/2}}}{{\nu }_{w}},\quad {{C}_{2}} = \rho _{0}^{{ - 1}}{{\rho }_{w}},\quad {{C}_{3}} = \rho _{0}^{{ - 1}}V_{0}^{{ - 2/3}}\Delta {{g}^{{ - 1}}}\sigma ,\quad {{C}_{4}} = {{C}_{v}}{{C}_{2}}C_{1}^{{1/2}},\quad {{C}_{5}} = {{C}_{t}}{{C}_{3}},$
получаем безразмерную постановку (для облегчения изложения будем обозначать все искомые функции в безразмерной постановке теми же переменными):

(5)
$\frac{{\partial rh}}{{\partial t}} + \frac{{\partial rhu}}{{\partial r}} = 0,$
(6)
$\frac{{\partial rhu}}{{\partial t}} + \frac{{\partial rh{{u}^{2}}}}{{\partial r}} = - rh\frac{{\partial h}}{{\partial r}} - {{C}_{5}}\frac{2}{{{{h}_{m}}}}r\frac{{\partial h}}{{\partial r}} - {{C}_{4}}\frac{r}{{{{R}^{{1/2}}}}}{{u}^{{3/2}}}.$

Лагранжевы координаты вводим путем замены независимых переменных следующего вида:

$\begin{gathered} t = t\left( {\xi ,\tau } \right) = \tau , \\ r = r\left( {\xi ,\tau } \right). \\ \end{gathered} $

Лагранжевы координаты отличаются от произвольных координат, изменяющихся со временем, тем свойством, что их скорость движения равна скорости частиц жидкости. Учитывая, что якобиан преобразования $J = \partial r{\text{/}}\partial \xi $, получаем постановку в лагранжевых координатах

(7)
$\frac{\partial }{{d\tau }}\left( {Jrh} \right) = 0,$
(8)
$\frac{\partial }{{d\tau }}\left( {Jrhu} \right) = - rh\frac{{\partial h}}{{\partial \xi }} - {{C}_{5}}\frac{2}{{{{h}_{m}}}}r\frac{{\partial h}}{{\partial \xi }} - {{C}_{4}}J\frac{r}{{{{R}^{{1/2}}}}}{{u}^{{3/2}}},$
(9)
$\frac{{\partial r}}{{\partial \tau }} = u.$

Для системы (7)–(9) необходимо сформулировать начальные и граничные условия. В качестве начальных условий необходимо задавать начальный радиус и распределение толщины нефтяного слоя и его скорости. Граничные условия формулируются ниже (36)–(38), (45).

Автомодельное решение (см. [12], [13], [17], [18], [23]) задачи (7)–(9) ищем в виде

(10)
$r = \xi {{\tau }^{\gamma }},\quad J = \frac{{\partial r}}{{\partial \xi }} = {{\tau }^{\gamma }},\quad R\left( \tau \right) = {{\xi }_{m}}{{\tau }^{\gamma }},\quad h = h\left( \xi \right){{\tau }^{\alpha }},\quad u\left( {\xi ,\tau } \right) = u\left( \xi \right){{\tau }^{\beta }} = \gamma \xi {{\tau }^{\beta }},$
где ${{\xi }_{m}}$ и $R\left( \tau \right)$ – граница разлива в лагранжевых и эйлеровых координатах соответственно. Из (9) следует $\frac{{\partial r}}{{\partial \tau }} = u\left( {\xi ,\tau } \right) = \gamma \xi {{\tau }^{{\gamma - 1}}}$, следовательно, $\beta = \gamma - 1$. Подставляя в (7) выражения для $r$, $J$ и $h$ из (10), получаем $\alpha + 2\gamma = 0$, т.е. $\alpha = - 2\gamma $. Суммируя, получаем выражения для основных искомых функций

(11)
$r = \xi {{\tau }^{\gamma }},\quad R\left( \tau \right) = {{\xi }_{m}}{{\tau }^{\gamma }},\quad J = \frac{{\partial r}}{{\partial \xi }} = {{\tau }^{\gamma }},\quad u\left( {\tau ,\xi } \right) = u\left( \xi \right){{\tau }^{{\gamma - 1}}},\quad u\left( \xi \right) = \gamma \xi ,\quad h\left( {\tau ,\xi } \right) = h\left( \xi \right){{\tau }^{{ - 2\gamma }}}.$

На инерционно-гравитационной стадии из (8) получаем $\frac{\partial }{{d\tau }}\left( {Jrhu} \right) = - rh\frac{{\partial h}}{{\partial \xi }}$. С учетом (7) это уравнение преобразуется к виду $J\frac{{\partial u}}{{d\tau }} = - \frac{{\partial h}}{{\partial \xi }}$. Подставляя в него (11), имеем ${{\tau }^{\gamma }}\gamma \xi \left( {\gamma - 1} \right){{\tau }^{{\gamma - 2}}} = $ $ = \; - {\kern 1pt} {{\tau }^{{ - 2\gamma }}}\frac{{\partial h\left( \xi \right)}}{{\partial \xi }}$. Приравнивая  сумму показателей нулю, получаем $\gamma = 0.5$. Для толщины слоя получаем уравнение $\gamma \xi \left( {\gamma - 1} \right) = - \frac{{\partial h\left( \xi \right)}}{{\partial \xi }}$, из которого находим $h\left( \xi \right) = {{h}_{m}} - 0.5\gamma \left( {\gamma - 1} \right){{\xi }^{2}}$. Величину ${{h}_{m}}$ (толщина в центре пятна) определяем из условия нормировки: $2\pi \int_0^{{{\xi }_{m}}} {h\left( \xi \right)\xi d\xi } = 1$. Это  условие вытекает из постоянства объема: $2\pi \int_0^{R(t)} {hrdr} = 1$. Из которого получаем

$2\pi \int\limits_0^{{{\xi }_{m}}} {h\left( \xi \right){{\tau }^{{ - 2\gamma }}}\xi {{\tau }^{\gamma }}d\xi {{\tau }^{\gamma }}} = 2\pi \int\limits_0^{{{\xi }_{m}}} {h\left( \xi \right)\xi d\xi } = 1.$

Т.е. постоянство объема выполняется, несмотря на изменяемость со временем $r\left( {\tau ,\xi } \right)$ и $h\left( {\tau ,\xi } \right)$. В результате на инерционно-гравитационной стадии выводим

(12)
$h = h\left( \xi \right){{\tau }^{{ - 1}}},\quad u\left( {\tau ,\xi } \right) = 0.5\xi {{\tau }^{{ - 0.5}}},\quad r = \xi {{\tau }^{{0.5}}},\quad J = \frac{{\partial r}}{{\partial \xi }} = {{\tau }^{{0.5}}},\quad R\left( \tau \right) = {{\xi }_{m}}{{\tau }^{{0.5}}}.$

На границе разлива для инерционно-гравитационной стадии получаем связь $h\left( {\tau ,{{\xi }_{m}}} \right)$ и $u\left( {\tau ,{{\xi }_{m}}} \right)$ в виде

$u\left( {\tau ,{{\xi }_{m}}} \right) = 0.5{{\xi }_{m}}{{\tau }^{{ - 0.5}}} = \frac{{0.5{{\xi }_{m}}}}{{{{{[h\left( {{{\xi }_{m}}} \right)]}}^{{1/2}}}}}{{[h\left( {{{\xi }_{m}}} \right){{\tau }^{{ - 1}}}]}^{{1/2}}} = \frac{{0.5{{\xi }_{m}}}}{{{{{[h\left( {{{\xi }_{m}}} \right)]}}^{{1/2}}}}}{{[h\left( {\tau ,{{\xi }_{m}}} \right)]}^{{1/2}}} = \sqrt {{{C}_{f}}h\left( {\tau ,{{\xi }_{m}}} \right)} ,$
т.е.

(13)
$\frac{{u\left( {\tau ,{{\xi }_{m}}} \right)}}{{\sqrt {{{C}_{f}}} }} = \sqrt {h\left( {\tau ,{{\xi }_{m}}} \right)} ,\quad {\text{г д е }}\quad {{C}_{f}} = \frac{{{{{\left( {0.5{{\xi }_{m}}} \right)}}^{2}}}}{{h\left( {{{\xi }_{m}}} \right)}}.$

На гравитационно-вязкой стадии из (8) следует

$0 = - rh\frac{{\partial h}}{{\partial \xi }} - {{C}_{4}}J\frac{r}{{{{R}^{{1/2}}}}}{{u}^{{3/2}}}.$

Подставляя в это уравнение (11), выводим

$0 = - \xi h\left( \xi \right)\frac{{\partial h\left( \xi \right)}}{{\partial \xi }} - {{C}_{4}}\frac{{\xi {{\tau }^{{6\gamma - 3/2}}}}}{{{{{\left( {{{\xi }_{m}}} \right)}}^{{1/2}}}}}{{\left( {\gamma \xi } \right)}^{{3/2}}}.$

Откуда $\gamma = 0.25$. Следовательно,

${{h}^{2}}\left( \xi \right) = h_{m}^{2} - {{C}_{4}}\frac{{{{{\left( \gamma \right)}}^{{3/2}}}}}{{{{{\left( {{{\xi }_{m}}} \right)}}^{{1/2}}}}}\left( {4{\text{/}}5} \right)\left( {{{\xi }^{{5/2}}}} \right).$

Величину ${{h}_{m}}$ определяем из условия нормировки. В результате на гравитационно-вязкой стадии получаем

(14)
$h = h\left( \xi \right){{\tau }^{{ - 0.5}}},\quad r = \xi {{\tau }^{{0.25}}},\quad R\left( \tau \right) = {{\xi }_{m}}{{\tau }^{{0.25}}},\quad u\left( {\tau ,\xi } \right) = u\left( \xi \right){{\tau }^{{ - 0.75}}} = \gamma \xi {{\tau }^{{ - 0.75}}}.$

Отсюда следует связь $h\left( {\tau ,{{\xi }_{m}}} \right)$ и $u\left( {\tau ,{{\xi }_{m}}} \right)$ на границе разлива на гравитационно-вязкой стадии

$u\left( {\tau ,{{\xi }_{m}}} \right) = 0.25{{\xi }_{m}}{{\tau }^{{ - 0.75}}} = \frac{{0.25{{\xi }_{m}}}}{{{{{[h\left( {{{\xi }_{m}}} \right)]}}^{{3/2}}}}}{{[h\left( {{{\xi }_{m}}} \right){{\tau }^{{ - 0.5}}}]}^{{3/2}}} = \frac{{0.25{{\xi }_{m}}}}{{{{{[h\left( {{{\xi }_{m}}} \right)]}}^{{3/2}}}}}{{[h\left( {\tau ,{{\xi }_{m}}} \right)]}^{{3/2}}} = {{[\sqrt {{{C}_{f}}h\left( {\tau ,{{\xi }_{m}}} \right)} ]}^{3}},$
т.е.

(15)
$\frac{{{{u}^{{1/3}}}\left( {\tau ,{{\xi }_{m}}} \right)}}{{\sqrt {{{C}_{f}}} }} = \sqrt {h\left( {\tau ,{{\xi }_{m}}} \right)} ,\quad {\text{г д е }}\quad {{C}_{f}} = \frac{{{{{\left( {0.25{{\xi }_{m}}} \right)}}^{{2/3}}}}}{{h\left( {{{\xi }_{m}}} \right)}}.$

Используя (11), на поверхностно-вязкой фазе из (8) получаем $0 = - {{C}_{5}}\frac{2}{{{{h}_{m}}}}\frac{{\partial h}}{{\partial \xi }} - \frac{{{{C}_{4}}J}}{{{{R}^{{1/2}}}}}{{u}^{{3/2}}}$ или $0 = - {{C}_{5}}\frac{2}{{{{h}_{m}}}}\frac{{\partial h\left( \xi \right)}}{{\partial \xi }} - \frac{{{{C}_{4}}{{\tau }^{\gamma }}}}{{{{{({{\xi }_{m}}{{\tau }^{\gamma }})}}^{{1.2}}}}}{{(\gamma \xi {{\tau }^{{\gamma - 1}}})}^{{3/2}}}$. Следовательно, $\gamma = 3{\text{/}}4$ и $h\left( \xi \right) = {{h}_{m}} - \frac{{{{C}_{4}}}}{{2{{C}_{5}}}}\frac{{{{h}_{m}}{{\gamma }^{{3/2}}}}}{{\xi _{m}^{{1/2}}}}\left( {2{\text{/}}5} \right){{\xi }^{{5/2}}}$. Из условия нормировки получаем ${{h}_{m}}$. В результате на поверхностно-вязкой стадии имеем

(16)
$r = \xi {{\tau }^{{3/4}}},\quad R\left( \tau \right) = {{\xi }_{m}}{{\tau }^{{3/4}}},\quad J = \frac{{\partial r}}{{\partial \xi }} = {{\tau }^{{3/4}}},\quad u\left( {\tau ,\xi } \right) = u\left( \xi \right){{\tau }^{{ - 1/4}}},\quad u\left( \xi \right) = \gamma \xi ,\quad h = h\left( \xi \right){{\tau }^{{ - 3/2}}}.$

Отсюда получаем связь $h\left( {\tau ,{{\xi }_{m}}} \right)$ и $u\left( {\tau ,{{\xi }_{m}}} \right)$ на границе для поверхностно-вязкой стадии

$u\left( {\tau ,{{\xi }_{m}}} \right) = 0.75{{\xi }_{m}}{{\tau }^{{ - 0.25}}} = \frac{{0.75{{\xi }_{m}}}}{{{{{[h\left( {{{\xi }_{m}}} \right)]}}^{{1/6}}}}}{{[h\left( {{{\xi }_{m}}} \right){{\tau }^{{ - 1.5}}}]}^{{1/6}}} = \frac{{0.75{{\xi }_{m}}}}{{{{{[h\left( {{{\xi }_{m}}} \right)]}}^{{1/6}}}}}{{[h\left( {\tau ,{{\xi }_{m}}} \right)]}^{{1/6}}} = {{[\sqrt {{{C}_{f}}h\left( {\tau ,{{\xi }_{m}}} \right)} ]}^{{1/3}}},$
т.е.

(17)
$\frac{{{{u}^{3}}\left( {\tau ,{{\xi }_{m}}} \right)}}{{\sqrt {{{C}_{f}}} }} = \sqrt {h\left( {\tau ,{{\xi }_{m}}} \right)} ,\quad {\text{г д е }}\quad {{C}_{f}} = \frac{{{{{\left( {0.75{{\xi }_{m}}} \right)}}^{6}}}}{{h\left( {{{\xi }_{m}}} \right)}}.$

Полученные условия (13), (15), (17) используются для численного решения соответствующих уравнений. Формулы Фэя [5], [6] для залпового сброса объема ${{V}_{0}}$ для разных стадий растекания имеют следующий вид. На инерционно-гравитационной стадии $R = {{k}_{{2i}}}\Delta {{g}^{{1/4}}}V_{0}^{{1/4}}{{t}^{{1/2}}}$, в безразмерном виде $\Re = {{k}_{{2i}}}{{\tau }^{{1/2}}}$. На гравитационно-вязкой стадии имеем $R = {{k}_{{2vf}}}V_{0}^{{1/3}}\Delta {{g}^{{1/6}}}{{({{\nu }_{w}})}^{{ - 1/12}}}{{t}^{{1/4}}}$ или $\Re = {{k}_{{2vf}}}C_{1}^{{ - 1/12}}{{\tau }^{{1/4}}}$. На поверхностно-вязкой получаем

$R = {{k}_{{2t}}}\left( {\frac{{{{\sigma }^{{1/2}}}}}{{\rho _{w}^{{1/2}}\nu _{w}^{{1/4}}}}} \right){{t}^{{3/4}}}$

или $\Re = {{k}_{{2t}}}C_{3}^{{1/2}}C_{1}^{{ - 1/4}}{{\tau }^{{3/4}}}$. Здесь коэффициенты ${{k}_{{2i}}} = 1.14$, ${{k}_{{2vf}}} = 1.45$, ${{k}_{{2t}}} = 2.3$ подобраны Фэем по экспериментальным данным.

3. ПОСТРОЕНИЕ ХАРАКТЕРИСТИЧЕСКОЙ ФОРМЫ И ЧИСЛЕННОЕ РЕШЕНИЕ

Придадим полученной системе характеристическую форму. Из (7)–(9) простыми преобразованиями получаем

(18)
$\frac{{\partial h}}{{d\tau }} + \frac{h}{J}\frac{{\partial u}}{{d\xi }} = - \frac{{hu}}{r},$
(19)
$\frac{{\partial u}}{{d\tau }} + \left( {1 + {{C}_{5}}\frac{2}{{h{{h}_{m}}}}} \right)\frac{1}{J}\frac{{\partial h}}{{\partial \xi }} = - \frac{{{{C}_{4}}}}{{h{{R}^{{1/2}}}}}{{u}^{{3/2}}},$
(20)
$\frac{{dr}}{{d\tau }} = u\left( {\xi ,\tau } \right).$

Введем $\alpha = {{\left( {1 + {{C}_{5}}\frac{2}{{h{{h}_{m}}}}} \right)}^{{ - 1/2}}}$ и представим (18), (19) в матричной форме:

(21)
$\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{{\partial h}}{{d\tau }}} \\ {\frac{{\partial u}}{{d\tau }}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0&{\frac{h}{J}} \\ {\frac{1}{{{{\alpha }^{2}}J}}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{{\partial h}}{{d\xi }}} \\ {\frac{{\partial u}}{{d\xi }}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - \frac{{hu}}{r}} \\ { - \frac{{{{C}_{4}}}}{{h{{R}^{{1/2}}}}}{{u}^{{3/2}}}} \end{array}} \right).$

Умножив (21) на вектор $\left( {l,m} \right)$, получим

(22)
$\left( {l,m} \right)\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{{\partial h}}{{d\tau }}} \\ {\frac{{\partial u}}{{d\tau }}} \end{array}} \right) + \left( {l,m} \right)\left( {\begin{array}{*{20}{c}} 0&{\frac{h}{J}} \\ {\frac{1}{{{{\alpha }^{2}}J}}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{{\partial h}}{{d\xi }}} \\ {\frac{{\partial u}}{{d\xi }}} \end{array}} \right) = \left( {l,m} \right)\left( {\begin{array}{*{20}{c}} { - \frac{{hu}}{r}} \\ { - \frac{{{{C}_{4}}}}{{h{{R}^{{1/2}}}}}{{u}^{{3/2}}}} \end{array}} \right).$

Определим собственные значения и векторы матрицы A:

(23)
$A = \left( {\begin{array}{*{20}{c}} 0&{\frac{h}{J}} \\ {\frac{1}{{{{\alpha }^{2}}J}}}&0 \end{array}} \right).$

Для нее получаем задачу на собственные значения

(24)
$\left( {l,m} \right)\left( {\begin{array}{*{20}{c}} 0&{\frac{h}{J}} \\ {\frac{1}{{{{\alpha }^{2}}J}}}&0 \end{array}} \right) = \lambda \left( {l,m} \right),$
откуда
$\left( {l \cdot 0 + m\frac{1}{{{{\alpha }^{2}}J}},\;l \cdot \frac{h}{J} + m \cdot 0} \right) = \lambda \left( {l,m} \right),$
или в виде линейной системы

(25а)
$l \cdot 0 + m\frac{1}{{{{\alpha }^{2}}J}} = \lambda l,$
(25б)
$l \cdot \frac{{\hat {h}}}{J} + m \cdot 0 = \lambda m.$

Из условия равенства нулю определителя этой системы

(26)
$D = \left\| {\begin{array}{*{20}{c}} { - \lambda }&{\frac{1}{{{{\alpha }^{2}}J}}} \\ {\frac{h}{J}}&{ - \lambda } \end{array}} \right\| = {{\lambda }^{2}} - \frac{h}{{{{\alpha }^{2}}{{J}^{2}}}} = 0$
получаем собственные значения,
(27)
$\lambda = \pm \frac{{\sqrt h }}{{\alpha J}},$
а из самой системы (25) находим собственные векторы матрицы A

(28)
$m = \pm \alpha \sqrt h l.$

Подставляя их в (22), получаем характеристическую форму

$\left( {{{l}_{1}}\frac{{\partial h}}{{d\tau }} + {{m}_{1}}\frac{{\partial u}}{{d\tau }}} \right) + {{\lambda }_{1}}\left( {{{l}_{1}}\frac{{\partial h}}{{d\xi }} + {{m}_{1}}\frac{{\partial u}}{{d\xi }}} \right) = \left( { - \frac{{hu}}{r}{{l}_{1}} - \frac{{{{C}_{4}}}}{{{{R}^{{1/2}}}}}{{u}^{{3/2}}}{{m}_{1}}} \right),$
$\left( {{{l}_{2}}\frac{{\partial h}}{{d\tau }} + {{m}_{2}}\frac{{\partial u}}{{d\tau }}} \right) + {{\lambda }_{2}}\left( {{{l}_{2}}\frac{{\partial h}}{{d\xi }} + {{m}_{2}}\frac{{\partial u}}{{d\xi }}} \right) = \left( { - \frac{{hu}}{r}{{l}_{2}} - \frac{{{{C}_{4}}}}{{{{R}^{{1/2}}}}}{{u}^{{3/2}}}{{m}_{2}}} \right).$

Переставляя слагаемые, получаем

(29а)
$\left( {\frac{{\partial h}}{{d\tau }} + {{\lambda }_{1}}\frac{{\partial h}}{{d\xi }}} \right) + \frac{{{{m}_{1}}}}{{{{l}_{1}}}}\left( {\frac{{\partial u}}{{d\tau }} + {{\lambda }_{1}}\frac{{\partial u}}{{d\xi }}} \right) = \left( { - \frac{{hu}}{r} - \frac{{{{C}_{4}}}}{{{{R}^{{1/2}}}}}{{u}^{{3/2}}}\frac{{{{m}_{1}}}}{{{{l}_{1}}}}} \right),$
(29б)
$\left( {\frac{{\partial h}}{{d\tau }} + {{\lambda }_{2}}\frac{{\partial h}}{{d\xi }}} \right) + \frac{{{{m}_{2}}}}{{{{l}_{2}}}}\left( {\frac{{\partial u}}{{d\tau }} + {{\lambda }_{2}}\frac{{\partial u}}{{d\xi }}} \right) = \left( { - \frac{{hu}}{r} - \frac{{{{C}_{4}}}}{{{{R}^{{1/2}}}}}{{u}^{{3/2}}}\frac{{{{m}_{2}}}}{{{{l}_{2}}}}} \right).$

Подставляя (28) и деля на $\sqrt h $, получаем систему в виде

(30)
$\left( {\frac{{\partial \sqrt h }}{{d\tau }} + \left| \lambda \right|\frac{{\partial \sqrt h }}{{d\xi }}} \right) + \frac{\alpha }{2}\left( {\frac{{\partial u}}{{d\tau }} + \left| \lambda \right|\frac{{\partial u}}{{d\xi }}} \right) = \left[ { - \frac{{\sqrt h u}}{{2\hat {r}}} - \frac{{{{C}_{4}}}}{{h{{R}^{{1/2}}}}}{{u}^{{3/2}}}\frac{\alpha }{2}} \right],$
(31)
$\left( {\frac{{\partial \sqrt h }}{{d\tau }} - \left| \lambda \right|\frac{{\partial \sqrt h }}{{d\xi }}} \right) - \frac{\alpha }{2}\left( {\frac{{\partial u}}{{d\tau }} - \left| \lambda \right|\frac{{\partial u}}{{d\xi }}} \right) = \left[ { - \frac{{\sqrt h u}}{{2r}} + \frac{{{{C}_{4}}}}{{h{{R}^{{1/2}}}}}{{u}^{{3/2}}}\frac{\alpha }{2}} \right],$
(32)
$\frac{{dr}}{{d\tau }} = u.$

Рассмотрим производную вдоль характеристики при $\frac{{d\xi \left( \tau \right)}}{{d\tau }} = \lambda $ и $y = \sqrt h $:

$\begin{gathered} \frac{{dF\left\{ {y\left[ {\tau ,\xi \left( \tau \right)} \right],u\left[ {\tau ,\xi \left( \tau \right)} \right]} \right\}}}{{d\tau }} = \frac{{\partial F}}{{\partial y}}\frac{{dy}}{{d\tau }} + \frac{{\partial F}}{{\partial u}}\frac{{du}}{{d\tau }} = \frac{{\partial F}}{{\partial y}}\left( {\frac{{\partial y}}{{\partial \tau }} + \frac{{\partial y}}{{\partial \xi }}\frac{{d\xi }}{{d\tau }}} \right) + \\ + \;\frac{{\partial F}}{{\partial u}}\left( {\frac{{\partial u}}{{\partial \tau }} + \frac{{\partial u}}{{\partial \xi }}\frac{{d\xi }}{{d\tau }}} \right) = \frac{{\partial F}}{{\partial y}}\left( {\frac{{\partial y}}{{\partial \tau }} + \lambda \frac{{\partial y}}{{\partial \xi }}} \right) + \frac{{\partial F}}{{\partial u}}\left( {\frac{{\partial u}}{{\partial \tau }} + \lambda \frac{{\partial u}}{{\partial \xi }}} \right). \\ \end{gathered} $

Из такого представления следует, что в левой части системы (30)–(32) стоят полные производные по характеристикам, так что ее можно переписать в виде

(33)
$\frac{{d{{F}_{1}}}}{{d\tau }} = \left( { - \frac{{\sqrt h u}}{{2r}} - {{C}_{4}}\frac{1}{{2h{{R}^{{1/2}}}}}{{u}^{{3/2}}}\alpha } \right)\quad {\text{п р и }}\quad \frac{{d\xi \left( \tau \right)}}{{d\tau }} = {{\lambda }_{1}},$
(34)
$\frac{{d{{F}_{2}}}}{{d\tau }} = \left( { - \frac{{\sqrt h u}}{{2r}} + {{C}_{4}}\frac{1}{{2h{{R}^{{1/2}}}}}{{u}^{{3/2}}}\alpha } \right)\quad {\text{п р и }}\quad \frac{{d\xi \left( \tau \right)}}{{d\tau }} = {{\lambda }_{2}},$
(35)
$\frac{{d{{F}_{3}}}}{{d\tau }} = u\quad {\text{п р и }}\quad \frac{{d\xi \left( \tau \right)}}{{d\tau }} = 0.$
Здесь ${{F}_{3}} = r$, $\frac{{\partial {{F}_{1}}}}{{\partial u}} = \frac{\alpha }{2}$, $\frac{{\partial {{F}_{2}}}}{{\partial u}} = - \frac{\alpha }{2}$, $\frac{{\partial {{F}_{1}}}}{{\partial y}} = 1$, $\frac{{\partial {{F}_{2}}}}{{\partial y}} = 1$. При $\alpha = {\text{const}}$ имеем ${{F}_{1}} = \sqrt h + \frac{{\alpha u}}{2}$, ${{F}_{2}} = \sqrt h - \frac{{\alpha u}}{2}$. Такое представление, с одной стороны, дает возможность определить $h,u$ из (30), (31) или (33), (34) и $r$ из (32) или (35), а с другой стороны, поскольку первые две характеристики идут слева и справа, подсказывает форму и количество граничных условий (ГУ). Для левой границы ГУ определяются из условия симметрии в виде $u = 0$, $\frac{{\partial \sqrt h }}{{\partial \xi }} = 0$. Последнее соотношение также вытекает из (19). Из (32) на левой границе определим $r = 0$. Особенная сложность заключается в задании ГУ для границы нефтяного разлива (для простоты – правой границы). Для определения двух из трех величин $u,\;\sqrt h ,\;r$ используем уравнения (30) и (32). Для определения 3-й величины необходимо дополнительное соотношение. В качестве таковых используем выражения (13), (15), (17), полученные из автомодельных решений. Из этих выражений вытекает, что при численном решении задачи (30)–(32) на отдельных стадиях Фэя (т.е. когда присутствуют только члены, соответствующие рассматриваемой стадии) необходимо задавать различные граничные условия. На гравитационно-инерционной стадии ГУ имеет вид (считаем, что ${{C}_{f}}$ – подбираемый параметр)
(36)
$\frac{u}{{\sqrt {{{C}_{f}}} }} = \sqrt h ,$
на гравитационно-вязкой стадии ГУ задаем в виде
(37)
$\frac{{{{u}^{{1/3}}}}}{{\sqrt {{{C}_{f}}} }} = \sqrt h ,$
для поверхностно-вязкой стадии определяем ГУ в виде

(38)
$\frac{{{{u}^{3}}}}{{\sqrt {{{C}_{f}}} }} = \sqrt h .$

ГУ в виде (36) применялось, например, в [17], [18], варианты (37), (38) рассматриваются впервые. Для решения задачи (30)–(32) построим сетку: ${{\xi }_{i}}{\text{ }}i = 0,1,2,\;...,\;N$. На этой сетке будем определять все искомые переменные: ${{h}_{i}},\;{{u}_{i}},\;{{r}_{i}},$ $i = 0,1,2,\;...,\;N$. Обратим внимание, что в левой части (30), (31) стоят производные от искомых функций $u,\sqrt h $ в виде операторов переноса, поэтому аппроксимируем уравнения (30), (31) по явной схеме с помощью направленных разностей. Введем аппроксимации

$\frac{{\partial F}}{{d\tau }} + \left| \lambda \right|\frac{{\partial F}}{{d\xi }} \approx \frac{{F_{i}^{{n + 1}} - F_{i}^{n}}}{{\Delta \tau }} + {{\left| \lambda \right|}_{L}}{{\left( {\frac{{\partial F}}{{d\xi }}} \right)}_{L}},$
$\frac{{\partial F}}{{d\tau }} - \left| \lambda \right|\frac{{\partial F}}{{d\xi }} \approx \frac{{F_{i}^{{n + 1}} - F_{i}^{n}}}{{\Delta \tau }} - {{\left| \lambda \right|}_{R}}{{\left( {\frac{{\partial F}}{{d\xi }}} \right)}_{R}},$
где

${{\left( {\frac{{\partial F}}{{d\xi }}} \right)}_{L}} \approx \frac{{F_{i}^{n} - F_{{i - 1}}^{n}}}{{\Delta \xi }},\quad {{\left( {\frac{{\partial F}}{{d\xi }}} \right)}_{R}} \approx \frac{{F_{{i + 1}}^{n} - F_{i}^{n}}}{{\Delta \xi }},$
${{\left| \lambda \right|}_{L}} = \frac{{\sqrt {{{h}_{i}}} }}{{{{\alpha }_{i}}{{J}_{L}}}},\quad {{\left| \lambda \right|}_{R}} = \frac{{\sqrt {{{h}_{i}}} }}{{{{\alpha }_{i}}{{J}_{R}}}},\quad {{J}_{L}} = \frac{{{{r}_{i}} - {{r}_{{i - 1}}}}}{{{{\xi }_{i}} - {{\xi }_{{i - 1}}}}},\quad {{J}_{R}} = \frac{{{{r}_{{i + 1}}} - {{r}_{i}}}}{{{{\xi }_{{i + 1}}} - {{\xi }_{i}}}}.$

Комбинируя полученные разностные уравнения, во внутренних узлах ${{\xi }_{i}},$ $i = 1,2,\;...,\;N - 1$, получаем

(39)
$2\frac{{\sqrt {{{h}^{{n + 1}}}} - \sqrt h }}{{\Delta \tau }} + \left[ {{{{\left| \lambda \right|}}_{L}}{{{\left( {\frac{{\partial \sqrt h }}{{d\xi }}} \right)}}_{L}} - {{{\left| \lambda \right|}}_{R}}{{{\left( {\frac{{\partial \sqrt h }}{{d\xi }}} \right)}}_{R}}} \right] + \frac{\alpha }{2}\left[ {{{{\left| \lambda \right|}}_{L}}{{{\left( {\frac{{\partial u}}{{d\xi }}} \right)}}_{L}} + {{{\left| \lambda \right|}}_{R}}{{{\left( {\frac{{\partial u}}{{d\xi }}} \right)}}_{R}}} \right] = - \frac{{\sqrt h u}}{r},$
(40)
$\alpha \frac{{{{u}^{{n + 1}}} - u}}{{\Delta \tau }} + \left[ {{{{\left| \lambda \right|}}_{L}}{{{\left( {\frac{{\partial \sqrt h }}{{d\xi }}} \right)}}_{L}} + {{{\left| \lambda \right|}}_{R}}{{{\left( {\frac{{\partial \sqrt h }}{{d\xi }}} \right)}}_{R}}} \right] + \frac{\alpha }{2}\left[ {{{{\left| \lambda \right|}}_{L}}{{{\left( {\frac{{\partial u}}{{d\xi }}} \right)}}_{L}} - {{{\left| \lambda \right|}}_{R}}{{{\left( {\frac{{\partial u}}{{d\xi }}} \right)}}_{R}}} \right] = - \frac{{{{C}_{4}}}}{{h{{R}^{{1/2}}}}}{{u}^{{3/2}}}\alpha .$

На правой границе в узле ${{\xi }_{N}}$ имеем

(41)
$\left( {\frac{{\sqrt {{{h}^{{n + 1}}}} - \sqrt h }}{{\Delta \tau }} + \left| \lambda \right|{{{\left( {\frac{{\partial \sqrt h }}{{d\xi }}} \right)}}_{L}}} \right) + \frac{\alpha }{2}\left( {\frac{{{{u}^{{n + 1}}} - u}}{{\Delta \tau }} + \left| \lambda \right|{{{\left( {\frac{{\partial u}}{{d\xi }}} \right)}}_{L}}} \right) = \left[ { - \frac{{\sqrt h u}}{{2r}} - F{{u}^{{n + 1}}}} \right],$
где $F = {{C}_{4}}\frac{1}{{h{{R}^{{1/2}}}}}{{u}^{{1/2}}}\frac{\alpha }{2}$. Дополнительно для каждой из стадий выбирается одно из ГУ (36)–(38). Тогда на гравитационно-инерционной фазе получаем
$\frac{{{{u}^{{n + 1}}}}}{{\sqrt {{{C}_{f}}} }} = \sqrt {{{h}^{{n + 1}}}} ,$
(42)
$\frac{{{{u}^{{n + 1}}}}}{{\sqrt {{{C}_{f}}} }} + \left( {\frac{\alpha }{2} + \Delta \tau F} \right){{u}^{{n + 1}}} = \sqrt h + \frac{\alpha }{2}u - \Delta \tau \frac{{\sqrt h u}}{{2r}} - \Delta \tau \left| \lambda \right|{{\left( {\frac{{\partial \sqrt h }}{{d\xi }}} \right)}_{L}} - \frac{\alpha }{2}\Delta \tau \left| \lambda \right|{{\left( {\frac{{\partial u}}{{d\xi }}} \right)}_{L}},$
на гравитационно-вязкой стадии
$\frac{{{{{({{u}^{{n + 1}}})}}^{{1/3}}}}}{{\sqrt {{{C}_{f}}} }} = \sqrt {{{h}^{{n + 1}}}} ,$
(43)
$\frac{{{{{({{u}^{{n + 1}}})}}^{{1/3}}}}}{{\sqrt {{{C}_{f}}} }} + \left( {\frac{\alpha }{2} + \Delta \tau F} \right){{u}^{{n + 1}}} = \sqrt h + \frac{\alpha }{2}u - \Delta \tau \frac{{\sqrt h u}}{{2r}} - \Delta \tau \left| \lambda \right|{{\left( {\frac{{\partial \sqrt h }}{{d\xi }}} \right)}_{L}} - \frac{\alpha }{2}\Delta \tau \left| \lambda \right|{{\left( {\frac{{\partial u}}{{d\xi }}} \right)}_{L}},$
на поверхностно-вязкой

$\frac{{{{{({{u}^{{n + 1}}})}}^{3}}}}{{\sqrt {{{C}_{f}}} }} = \sqrt {{{h}^{{n + 1}}}} ,$
(44)
$\frac{{{{{({{u}^{{n + 1}}})}}^{3}}}}{{\sqrt {{{C}_{f}}} }} + \left( {\frac{\alpha }{2} + \Delta \tau F} \right){{u}^{{n + 1}}} = \sqrt h + \frac{\alpha }{2}u - \Delta \tau \frac{{\sqrt h u}}{{2r}} - \Delta \tau \left| \lambda \right|{{\left( {\frac{{\partial \sqrt h }}{{d\xi }}} \right)}_{L}} - \frac{\alpha }{2}\Delta \tau \left| \lambda \right|{{\left( {\frac{{\partial u}}{{d\xi }}} \right)}_{L}}.$

Из этих соотношений определяем $u$ и $h$, а $r$ определяем из (32). На левой границе получаем ГУ в виде

(45)
$\frac{{\sqrt {h_{1}^{{n + 1}}} - \sqrt {h_{0}^{{n + 1}}} }}{{{{\xi }_{1}} - {{\xi }_{0}}}} = 0,\quad u = 0,\quad r = 0.$

На фиг. 1–4 приведено сравнение численного решения, полученного на основе УрЧП c параметрами ${{C}_{4}} = 2.7$, ${{C}_{5}} = 2.3$, ${{C}_{f}} = 1$ с решениями для радиуса разлива, полученными по формулам Фэя. На фиг. 1, 2 показаны численные решения для гравитационно-инерционной (без учета сил поверхностного натяжения и вязкости) и гравитационно-вязкой стадий (без учета силы поверхностного натяжения). На фиг. 3 приведено численное решение на поверхностно-вязкой стадии (без учета гравитационной силы). На фиг. 4 приведено численное решение полной задачи. Видно, что для автомодельных задач (стадий Фэя) решение совпадает с соответствующими фэевскими решениями после завершения начального периода адаптации (когда играет роль нестационарность).

Фиг. 1.

Сравнение численного решения, полученного на основе УрЧП без учета сил поверхностного натяжения и вязкости с решением для радиуса разлива, полученным по формуле Фэя на гравитационно-инерционной стадии (радиус и время в безразмерных координатах).

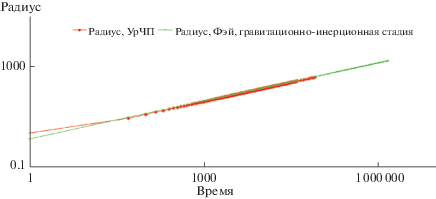
Фиг. 2.

Сравнение численного решения, полученного на основе УрЧП без учета силы поверхностного натяжения с решением для радиуса разлива, полученным по формуле Фэя на гравитационно-вязкой стадии (радиус и время в безразмерных координатах).

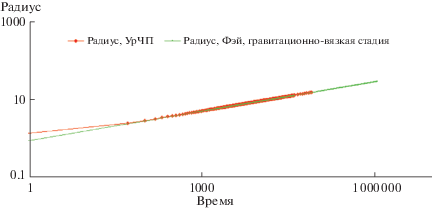
Фиг. 3.

Сравнение численного решения, полученного на основе УрЧП без учета силы гравитации с решением для радиуса разлива, полученным по формуле Фэя на поверхностно-вязкой стадии (радиус и время в безразмерных координатах).

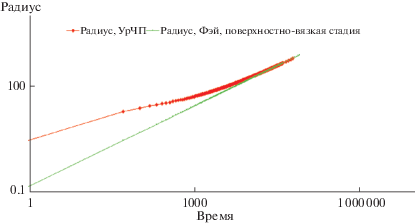
Фиг. 4.

Сравнение численного решения полной задачи, полученного на основе УрЧП с решениями для радиуса разлива, полученными по формулам Фэя на различных стадиях (радиус и время в безразмерных координатах).

Особая сложность возникает при решении полной задачи, поскольку для нее невозможно найти автомодельное решение и не известно ГУ. В этом случае задача решалась в едином алгоритме, с помощью переключения ГУ в определенные моменты времени. В начальный период при $\tau < 90$ (время в безразмерных переменных) ГУ бралось по формуле (36), в промежуточный период при $90 < \tau < 900$ по формуле (37), на завершающей стадии по (38). Видно (фиг. 4), что в начальный период численное решение наиболее близко к формуле Фэя на гравитационно-инерционной стадии, в промежуточное время видна близость к фэевскому решению на гравитационно-вязкой стадии, и на финальном этапе видна близость к фэевскому решению на поверхностно-вязкой стадии. При этом полученное решение несколько теряет гладкость при изменении ГУ. Это особенно заметно при переходе от гравитационно-вязкой к поверхностно-вязкой стадии.

4. ЗАКЛЮЧЕНИЕ

В работе рассматривается задача растекания нефтяного разлива по поверхности моря на основе осесимметричной постановки уравнений в частных производных. Исследован вопрос определения ГУ для рассматриваемой постановки. Показано, что на разных стадиях Фэя требуются специфические ГУ для достижения совпадения с формулами Фэя. Для гравитационно-инерционной стадии ГУ совпадают с применяемыми, например, в работах [17], [18], а на двух других стадиях предложены впервые. Построен метод численного решения на основе метода характеристик. Показано, что предложенный численный метод дает решение, согласованное с формулами Фэя на различных стадиях. Для решения полной задачи (в присутствии всех сил) предложен подход с переключением ГУ при переходе от одной стадии к другой.

Список литературы

  1. ASCE Task Committee on Modeling of Oil Spills. State-of-the-art review of modeling transport and fate of oil spills // J. Hydraulic Engng. 1996. V. 122. № 11. P. 594–610.

  2. Spaulding M.L. A State-of-the-art review of oil spill trajectory and fate modeling // Oil and Chem. Pollution. 1988. V. 4. P. 39–55.

  3. Reed M., Johansen O., Per Johan Brandvik, Per Daling, Lewis Alun, Fiocco R., Don Mackay, Prentki R. Oil spill modeling towards the close of the 20th century: Overview of the State of the Art // Spill Sci. & Technol. Bull. 1999. V. 5. № 1. P. 3–16.

  4. Lehr W.J. Review of modeling procedures for oil spill weathering behavior // Adv. Ecol. Sci. 2001. V. 9. P. 51–90.

  5. Fay J.A. The spread of oil slicks on a calm sea. Oil on the Sea. New York: Plenum Press, 1969. P. 53–63.

  6. Fay J.A. Physical processes in the spread of oil on a water surface // Proc. of the Joint Conference on Prevention and Control of Oil Spills. Washington, D.C.: American Petroleum Institute, 1971. P. 463–467.

  7. Scory S. Models used by the Belgian authorities in case of accidental spills at sea // Workshop on “Prediction of Short-Term Transport and Dispersion of Accidental Spills from Shipping and Off-Shore Industry”. Hague, Netherlands, 15–17 November. 1995. 5 p.

  8. Kuipers H.D. A simulation model for oil slicks at sea (SMOSS) // Department of Civil Engng, Delft University of Technology, North Sea Directorate, National Department of Public Works, Ministry of Transport and Public Works. Rijswijk. Delft. The Netherlands, 1981, 79 p.

  9. Kochergin I.E., Bogdanovsky A.A., Budaeva V.D., Makarov V.G., Mishukov V.F., Ovsienko S.N., Putov V.F., Reitsema L.A., Sciallabba J.W., Sergusheva O.O., Yarosh P.V. Modeling of oil spills for the shelf conditions of North-Eastern Sakhalin // Proc. 2nd Workshop on the Okhotsk Sea and Adjacent Areas, Canada, 1999a. P. 123–130.

  10. Antunes do Carmo1 J., Pinho J.L., Vieira J.P. Oil spills in coastal zones: Predicting Slick Transport and Weathering // Open Ocean Eng. J. 2010. V. 3. P. 129–142.

  11. Arkhipov B.V., Shapochkin D.A. Modeling of oil spill propagation in the sea // Math. modeling. 2018. V. 30. № 6. P. 39–59.

  12. Brovchenko I., Maderich V. Численный Лагранжев метод моделирования распространения поверхностных пятен нефти // Прикл. гидромехан. 2002. Т. 4. № 4. С. 23–31.

  13. Maderich V., Brovchenko I., Jung K. Oil Spreading in instantenious and continious spills on rotational Earth // Environ. Fluid Mech. 2012. P. 361–378.

  14. Ovsienko S., Zatsepa S., Ivchenko A. Study and Modelling of Behavior and Spreading of Oil in Cold Water and in Ice Conditions // Poac 99. Proc. 1999. V. 2. P. 848–857.

  15. Arkhipov B.V., Parkhomenko V.P., Solbakov V.V., Shapochkin D.A. Matematicheskoe modelirovanie rasprostraneniya neftianyh razlivov v morskoy srede. M.: VCRAN. 2001. 53 p.

  16. Arkhipov B., Koterov V., Solbakov V., Shapochkin D., Yurezanskaya Y. Numerical modeling of pollutant dispersion and oil spreading by the stochastic discrete particles method // Studies in Appl. Math. 2007. V. 120. № 1. P. 87–104.

  17. Hoult D.P. Oil spreading on the sea // Annual Rev. of Fluid Mech. 1972. V. 4. P. 341–368.

  18. Ungarish M. An introduction to gravity currents and intrusions. Haifa. Israel. CRC Press, A Chapman and Hall Book. 2009. 489 p.

  19. Friedrichs K.O. On the derivation of the shallow water theory // Commun. Pure and Appl. Math. 1948. V. 1. P. 81–85.

  20. Harkins W.D. The physical chemistry of surface films. New York: Reinhold, 1952. 163 p.

  21. Foda M., Cox R.G. The spreading of thin liquid films on a water-air interface // J. Fluid Mech. 1980. V. 101. № 1. P. 33–51.

  22. Loytsiansky L.G. Mechanics of fluid and gas. Second Revised Ed. Pergamon Press, 2014. 688 p.

  23. Sedov L.I. Similarity and dimensional methods in mechanics. 10-th ed., CRC Press, 1993. 493 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал