Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 534-546
Визуализация эффективной гиперповерхности и измерение эффекта масштаба в невыпуклых моделях анализа среды функционирования
В. Е. Кривоножко 1, 2, *, А. В. Лычев 1, **
1 МИСиС
119049 Москва, Ленинский пр-т, 4, Россия
2 МГУ, ВМК
119991 Москва, Ленинские горы, Россия
* E-mail: KrivonozhkoVE@mail.ru
** E-mail: Lychev@misis.ru
Поступила в редакцию 23.05.2018
Аннотация
В модели FDH (Free Disposal Hull) методологии анализа среды функционирования множество производственных возможностей является невыпуклым. В данной работе развивается алгоритм для построения сечений эффективной гиперповерхности (фронта) модели FDH. С практической точки зрения предлагаемый алгоритм необходим для визуализации и исследования эффективного фронта модели FDH. Основываясь на предлагаемом алгоритме, в работе развивается новая процедура для измерения эффекта масштаба модели FDH. По сравнению с существующими методами, предложенный подход не требует оценки эффективности производственных объектов в моделях с убывающим и возрастающим эффектом масштаба, что является достаточно сложной вычислительной задачей. Наши теоретические результаты подтверждаются вычислительными экспериментами с использованием реальных статистических данных из различных областей. Библ. 32. Фиг. 3. Табл. 1.
1. ВВЕДЕНИЕ
В научной литературе имеется большое количество работ, посвященных вычислению эффекта масштаба как характеристики эффективного фронта. Если эффективный фронт гладкий, то тип эффекта масштаба (постоянный, возрастающий или убывающий), наблюдаемый у эффективного производственного объекта, определяется масштабной эластичностью, измеряемой для данного объекта (см., например, [1]). Если эффективный фронт не гладкий, как в выпуклых моделях анализа среды функционирования, вышеупомянутый способ определения эффекта масштаба не применим. Примером такой модели является модель с переменным эффектом масштаба [2], для которой стандартное определение эластичности не определено для эффективных наблюдаемых объектов. Как было предложено в [3], эффект масштаба для эффективных объектов в подобных моделях может быть определен на основе понятия односторонних производных (эластичности). Математические основы такого подхода к определению масштабной эластичности могут быть найдены в работах [4]–[7].
(В работах [27]–[30] дается обзор последних результатов исследований по измерению эффекта масштаба. В статье [31] расширяется понятие эффекта масштаба на основе односторонней эластичности на модели с многогранными множествами производственных возможностей. В работе [23] развивается понятие эффекта масштаба на любые выпуклые модели.)
Модель FDH (Free Disposal Hull) была предложена в [8], в ней предположения выпуклости отброшены. Расширить понятия эффекта масштаба на модели FDH прямым способом нельзя в силу ступенчатой формы эффективного фронта в этой модели. Существующие методы для оценки эффекта масштаба в модели FDH можно разделить на две группы. Первая группа основывается на методах математического программирования, а вторая группа использует алгоритмы целенаправленного перебора.
В работах [9], [10] было введено понятие и предложен способ оценки эффекта масштаба для FDH модели с помощью расширения подходов, предложенных ранее в [11], [12]. Предложенные методы основываются на сравнении мер эффективности во входной модели FDH и связанных с ней моделей с постоянным, убывающим и возрастающим эффектом масштаба. Такая задача требует решения нелинейных смешанно-целочисленных моделей. В [13] было показано, что последняя модель может быть переформулирована как смешанно-целочисленная линейная модель, хотя размерность такой задачи увеличивается значительно. Очевидный недостаток этих подходов состоит в том, что они требуют больших вычислений.
В [14] развивается алгоритм на основе целенаправленного перебора для оценки эффекта масштаба в модели FDH. В [15] предлагается подход на основе линейного программирования для тех же целей. Однако, как заметил сам автор, предлагаемый подход не имеет каких-либо вычислительных преимуществ перед нелинейными методами, хотя линейный подход может быть легче с точки зрения практического применения.
В добавление к вычислительным сложностям при оценке эффекта масштаба в модели FDH, возникают также некоторые концептуальные проблемы. Как было показано в [16], [17], использование дополнительных моделей (с возрастающим и убывающим эффектом масштаба) для модели FDH дает глобальную оценку эффекта масштаба для эффективного объекта, которая отличается от общепринятой локальной оценки эффекта масштаба. Следует отметить, что без дополнительных или эвристических правил стандартные понятия локального эффекта масштаба в моделях FDH тривиальны и не представляют практического интереса. В самом деле, для любого эффективного объекта в модели FDH правосторонняя масштабная эластичность равняется нулю, а левосторонняя масштабная эластичность не определена (или формально может быть взята как бесконечность). Поэтому каждый эффективный объект в модели FDH проявляет убывающий эффект масштаба справа и возрастающий эффект масштаба слева. В статье [19] предлагается альтернативное определение локального эффекта масштаба в модели FDH, которое учитывает среднюю продуктивность объекта на луче в некоторой малой, но конечной, ε-окрестности производственного объекта, который оценивается. Итоговый эффект масштаба зависит от величины ε, выбранной аналитиком.
Согласно определению, данному в работах [16], [17], для произвольной модели анализа среды функционирования, включая модель FDH, тип глобального эффекта масштаба эффективного объекта зависит от расположения точки наибольшей продуктивности (most productive scale size – MPSS), определенной в [18]. Более того, глобальный эффект масштаба показывает: достигается ли наибольшая продуктивность конкретного объекта с помощью увеличения или уменьшения масштаба объекта или объект уже находится в точке наибольшей продуктивности.
Наша главная цель – развитие эффективного алгоритма для построения сечения эффективного фронта в моделях FDH с помощью различных двухмерных сечений. Как было отмечено в [19], существует сравнительно мало методов для визуализации фронта в FDH-моделях, наша статья вносит свой вклад в развитие данного направления.
Способность нашего подхода строить различные сечения моделей FDH имеет большое практическое значение. Например, сечение, которое показывает зависимость выходного вектора от пропорционального изменения входного вектора, может быть использовано для анализа и визуализации типов глобальных эффектов масштаба и расположения точки наибольшей продуктивности на фронте. Другие сечения в модели FDH могут быть использованы для анализа отклика отдельных входных или выходных показателей на изменение других входных или выходных показателей, связанных с граничными точками модели FDH. Они иллюстрируют зависимости между различными входными и выходными показателями.
Предлагаемый подход расширяет идеи метода, предложенного в [20] для построения сечений выпуклого фронта в моделях анализа среды функционирования – АСФ (на английском языке этот термин звучит как Data Envelopment Analysis – DEA) и обобщает оптимизационные алгоритмы, предложенные в [21], [22] для построения различных сечений в модели FDH.
Кроме визуализации эффективного фронта в модели FDH, в работе также показано, как можно эффективно оценить с помощью предложенного подхода глобальный эффект масштаба в модели FDH. В противоположность существующим методам, предлагаемый подход не требует оценки эффективности производственных объектов в дополнительных моделях, которые, как было отмечено выше, достаточно затратные с вычислительной точки зрения. Наши теоретические результаты подтверждаются вычислительными экспериментами с использованием реальных статистических данных из различных областей.
Статья организована следующим образом. В разд. 2 дается краткий обзор понятий глобального эффекта масштаба в модели FDH и методов их оценки, основанных на использовании вспомогательных моделей. В разд. 2 вводится также основной алгоритм для построения эффективного фронта в моделях FDH с помощью нескольких типов двухмерных плоскостей, имеющих практический интерес. В разд. 3 показывается, как предлагаемый подход может быть использован для оценки глобальных типов эффекта масштаба без оценки эффективности производственных объектов во вспомогательных моделях. В разд. 4 приводятся вычислительные эксперименты с предложенными алгоритмами. Разд. 5 содержит основные выводы.
2. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим множество $n$ наблюдаемых производственных объектов $({{X}_{j}},{{Y}_{j}})$, $j = 1,\; \ldots ,\;n$, где вектор выходных показателей ${{Y}_{j}} = ({{y}_{{1j}}},\; \ldots ,\;{{y}_{{rj}}}) \geqslant 0$ производится с помощью вектора входных показателей ${{X}_{j}} = ({{x}_{{1j}}},\; \ldots ,\;{{x}_{{mj}}}) \geqslant 0$. Предположим, что, по крайней мере, один входной показатель и один выходной показатель у каждого производственного объекта положительный. Модель FDH определяется следующим образом:
Рассмотрим также вспомогательные модели с постоянным (CRS), невозрастающим (NIRS) и неубывающим (NDRS) эффектом масштаба, сгенерированных с помощью множества ${{T}_{{{\text{FDH}}}}}$ соответственно. Они записываются следующим образом:
(1)
$\begin{gathered} {{T}_{{{\text{CRS}}}}} = \left\{ {(X,Y)\,\left| {\,(X,Y) = \delta (X{\kern 1pt} ',Y{\kern 1pt} '),} \right.} \right.\;\left. {(X{\kern 1pt} ',Y{\kern 1pt} ') \in {{T}_{{{\text{FDH}}}}},\;\delta \geqslant 0} \right\}, \\ {{T}_{{{\text{NIRS}}}}} = \left\{ {(X,Y)\,\left| {\,(X,Y) = \delta (X{\kern 1pt} ',Y{\kern 1pt} '),} \right.} \right.\left. {\;(X{\kern 1pt} ',Y{\kern 1pt} ') \in {{T}_{{{\text{FDH}}}}},\;0 \leqslant \delta \leqslant 1} \right\}, \\ {{T}_{{{\text{NDRS}}}}} = \left\{ {(X,Y)\,\left| {\,(X,Y) = \delta (X{\kern 1pt} ',Y{\kern 1pt} '),} \right.} \right.\;\left. {(X{\kern 1pt} ',Y{\kern 1pt} ') \in {{T}_{{{\text{FDH}}}}},\;\delta \geqslant 1} \right\}. \\ \end{gathered} $Методы вспомогательных моделей для оценки эффекта масштаба в модели FDH требуют оценки входной (или выходной) радиальной эффективности конкретного объекта $({{X}_{o}},{{Y}_{o}})$ в модели FDH и в зависимости от метода в некоторых из трех моделей (1). Без ограничения общности рассмотрим случай входной радиальной эффективности.
Входная радиальная эффективность $E_{{{\text{FDH}}}}^{i}({{X}_{o}},{{Y}_{o}})$ объекта $({{X}_{o}},{{Y}_{o}})$ в модели ${{T}_{{{\text{FDH}}}}}$ может быть оценена с помощью решения смешанно-целочисленной линейной задачи:
при ограничениях(2)
$\sum\limits_{j = 1}^n {{{X}_{j}}{{\lambda }_{j}}} \leqslant \theta {{X}_{o}},\quad \sum\limits_{j = 1}^n {{{Y}_{j}}{{\lambda }_{j}}} \geqslant {{Y}_{o}},\quad \sum\limits_{j = 1}^n {{{\lambda }_{j}}} = 1,\quad {{\lambda }_{j}} \in \{ 0,1\} ,\quad j = 1,\; \ldots ,\;n.$Оценка входной радиальной эффективности объекта $({{X}_{o}},{{Y}_{o}})$ в любой из трех вспомогательных моделей (1) требует больших вычислительных усилий. В [9] для этих целей была предложена общая формулировка смешанно-целочисленной нелинейной задачи:
при ограничениях(3)
$\sum\limits_{j = 1}^n {{{X}_{j}}{{\lambda }_{j}}} \leqslant \theta {{X}_{o}},\quad \sum\limits_{j = 1}^n {{{Y}_{j}}{{\lambda }_{j}}} \geqslant {{Y}_{o}},\quad {{\lambda }_{j}} = \delta {{w}_{j}},\quad {{w}_{j}} \in \{ 0,1\} ,\quad j = 1,\; \ldots ,\;n,\quad \delta \in \Gamma ,\quad \sum\limits_{j = 1}^n {{{w}_{j}}} = 1,$Обозначим через $E_{{{\text{CRS}}}}^{i}({{X}_{o}},{{Y}_{o}})$, $E_{{{\text{NIRS}}}}^{i}({{X}_{o}},{{Y}_{o}})$ и $E_{{{\text{NDRS}}}}^{i}({{X}_{o}},{{Y}_{o}})$ входные радиальные меры эффективности производственного объекта $({{X}_{o}},{{Y}_{o}})$ в соответствующей модели, эти меры эффективности равняются оптимальному значению ${{\theta }_{o}}$ в задаче (3) с соответствующим множеством $\Gamma $.
Пусть объект $({{X}_{o}},{{Y}_{o}})$ является (сильно) эффективным в модели FDH. По определению, производственный объект $({{X}_{o}},{{Y}_{o}})$ сильно эффективный, если не существует объекта $(X',Y') \in {{T}_{{{\text{FDH}}}}}$ такого, что $X' \leqslant {{X}_{o}}$, $Y' \geqslant {{Y}_{o}}$, и $({{X}_{o}},{{Y}_{o}}) \ne (X',Y')$. Предположение, что объект $({{X}_{o}},{{Y}_{o}})$ сильно эффективен, не является необходимым и сделано только для того, чтобы упростить изложение. Например, для того чтобы понятие (глобального) эффекта масштаба было корректно определено, достаточно предположить, что объект $({{X}_{o}},{{Y}_{o}})$ радиально эффективен по выходу в модели ${{T}_{{{\text{FDH}}}}}$. Для оценки эффекта масштаба, используя модели (2) и (3), необходимо предположить, что $({{X}_{o}},{{Y}_{o}})$ является радиально эффективным во входной и выходной модели [16, с. 243–244]. Очевидно, что это более слабое предположение, чем предположение сильной эффективности. В [16], [17] показывается, что при оценке и сравнении входной радиальной меры эффективности объекта $({{X}_{o}},{{Y}_{o}})$ во вспомогательных моделях с эффективностью в модели FDH можно определить: находится ли объект в точке наибольшей продуктивности, или он ближе к началу координат, или дальше от него, чем положение этой точки. Все это приводит к понятию глобального эффекта масштаба.
Рассмотрим теперь понятие глобального эффекта масштаба в случае FDH-модели. Начнем с определения, данного в [2].
Определение 1. Производственный объект $({{X}_{o}},{{Y}_{o}})$ находится в точке наибольшей продуктивности, если для всех объектов $(\varphi {{X}_{o}},\psi {\kern 1pt} {{Y}_{o}}) \in {{T}_{{{\text{FDH}}}}}$, где $\varphi $, $\psi > 0$, коэффициент $\psi {\text{/}}\varphi \leqslant 1$.
Проверка условия, находится ли объект $({{X}_{o}},{{Y}_{o}})$ в точке наибольшей продуктивности требует решения следующей задачи:
(4)
$\begin{gathered} M* = \max {\psi \mathord{\left/ {\vphantom {\psi \varphi }} \right. \kern-0em} \varphi }, \\ (\varphi {{X}_{o}},\psi {{Y}_{o}}) \in {{T}_{{{\text{FDH}}}}},\quad \varphi > 0,\quad \psi > 0. \\ \end{gathered} $Согласно определению 1, объект $({{X}_{o}},{{Y}_{o}})$ находится в точке наибольшей продуктивности тогда и только тогда, когда $M* = 1$.
Определение 2. Производственный объект $(\varphi {\text{*}}{{X}_{o}},\psi {\text{*}}{\kern 1pt} {{Y}_{o}}) \in {{T}_{{{\text{FDH}}}}}$ называется масштабным эталонным объектом (scale reference unit – SRU) для объекта $({{X}_{o}},{{Y}_{o}})$, если $\varphi = \varphi {\text{*}}$ и $\psi = \psi {\text{*}}$ являются оптимальным решением задачи (4), т.е., ${{\psi {\text{*}}} \mathord{\left/ {\vphantom {{\psi {\text{*}}} {\varphi {\text{*}}}}} \right. \kern-0em} {\varphi {\text{*}}}} = M{\text{*}}$.
Следует отметить, что объект $({{X}_{o}},{{Y}_{o}})$ может иметь несколько масштабных эталонных объектов.
Теорема 1 (см. [17]). Предположим, что объект $({{X}_{o}},{{Y}_{o}})$ является сильно эффективным в множестве ${{T}_{{{\text{FDH}}}}}$, но не находится в точке наибольшей продуктивности. Пусть объект $(\varphi {{X}_{o}},\psi {{Y}_{o}}) \in T$ будет для него масштабным эталонным объектом. Тогда либо переменные $\varphi $ и $\psi $ больше, чем 1, или обе они меньше, чем 1.
Согласно этой теореме, можно классифицировать все масштабные эталонные объекты для объекта $({{X}_{o}},{{Y}_{o}})$ на те, для которых $\varphi < 1$ и $\psi < 1$, и на те, для которых $\varphi > 1$ и $\psi > 1$.
Определение, приведенное ниже, позволяет разделить все эффективные объекты на четыре взаимоисключающих типа [16], [17].
Определение 3. Предположим, что объект $({{X}_{o}},{{Y}_{o}})$ является сильно эффективным в модели ${{T}_{{{\text{FDH}}}}}$. Тогда объект $({{X}_{o}},{{Y}_{o}})$ показывает:
1) глобальный постоянный эффект масштаба (G-CRS), если объект находится в состоянии наибольшей продуктивности,
2) глобальный убывающий эффект масштаба (G-DRS), если все его масштабные эталонные объекты меньше, чем объект $({{X}_{o}},{{Y}_{o}})$,
3) глобальный возрастающий эффект масштаба (G-IRS), если все его масштабные эталонные объекты больше, чем объект $({{X}_{o}},{{Y}_{o}})$,
4) глобальный квазипостоянный эффект масштаба (G-SCRS), если некоторые из его масштабных эталонных объектов меньше, а некоторые больше, чем объект $({{X}_{o}},{{Y}_{o}})$, но сам объект $({{X}_{o}},{{Y}_{o}})$ не находится в точке наибольшей продуктивности.
Интересно отметить, что определение, приведенное выше, применимо почти ко всем моделям T (см. [16]). Если модель T является выпуклой (т.е., если T есть модель с переменным эффектом масштаба), то первые три типа глобального эффекта масштаба совпадают с соответствующими стандартными типами локального эффекта масштаба, а квазипостоянный тип глобального эффекта масштаба не возможен [16], [23]. Если модель T является невыпуклой, то глобальная и локальная классификации эффекта масштаба в общем случае различны, при условии, что последняя определена корректно. В частности, объект может проявлять локальный убывающий эффект масштаба и глобальный возрастающий эффект масштаба в одно и то же время, что отражает разницу между локальным (маргинальным) улучшением продуктивности по сравнению с глобальным оптимумом продуктивности, достигаемым в точке наибольшей продуктивности. В [23] отмечено, что глобальный квазипостоянный тип эффекта масштаба представляет в основном теоретический интерес, и включен в рассмотрение для логической полноты классификации. В [17] показывается с помощью вычислительных экспериментов, что тип глобального квазипостоянного эффекта масштаба редко встречается в практических задачах.
Следующая теорема, которая вытекает из более общих результатов, доказанных в [16], дает нам практический инструмент для оценки глобального эффекта масштаба эффективного объекта в невыпуклых FDH-моделях. Он основан на анализе входной радиальной эффективности объекта $({{X}_{o}},{{Y}_{o}})$ в модели ${{T}_{{{\text{FDH}}}}}$ и связанных с ней дополнительных моделей с невозрастающим и неубывающим эффектом масштаба.
Теорема 2. Предположим, что объект $({{X}_{o}},{{Y}_{o}})$ сильно эффективен в модели ${{T}_{{{\text{FDH}}}}}$. Тогда он проявляет следующие свойства:
1) G-CRS тогда и только тогда, когда $E_{{{\text{NDRS}}}}^{i}({{X}_{o}},{{Y}_{o}}) = E_{{{\text{NIRS}}}}^{i}({{X}_{o}},{{Y}_{o}}) = E_{{{\text{FDH}}}}^{i}({{X}_{o}},{{Y}_{o}})$;
2) G-DRS тогда и только тогда, когда $E_{{{\text{NDRS}}}}^{i}({{X}_{o}},{{Y}_{o}}) < E_{{{\text{NIRS}}}}^{i}({{X}_{o}},{{Y}_{o}}) \leqslant E_{{{\text{FDH}}}}^{i}({{X}_{o}},{{Y}_{o}})$;
3) G-IRS тогда и только тогда, когда $E_{{{\text{NIRS}}}}^{i}({{X}_{o}},{{Y}_{o}}) < E_{{{\text{NDRS}}}}^{i}({{X}_{o}},{{Y}_{o}}) \leqslant E_{{{\text{FDH}}}}^{i}({{X}_{o}},{{Y}_{o}})$;
4) G-SCRS тогда и только тогда, когда $E_{{{\text{NDRS}}}}^{i}({{X}_{o}},{{Y}_{o}}) = E_{{{\text{NIRS}}}}^{i}({{X}_{o}},{{Y}_{o}}) < E_{{{\text{FDH}}}}^{i}({{X}_{o}},{{Y}_{o}})$.
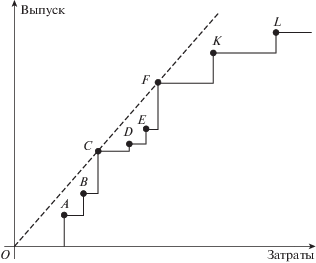
Пример 1. Рассмотрим модель FDH с одним входом и одним выходом, сгенерированную объектами A, B, C, D, E, F, K и L, и изображенную на фиг. 1. Все эти объекты сильно эффективны.
Из фиг. 1 видно, что объекты C и F находятся в точках наибольшей продуктивности и поэтому проявляют глобальный постоянный эффект масштаба. Это следует из того, что луч, идущий из начала координат и проходящий через точки C и F, имеет наибольший угол наклона среди всех лучей, проходящих через наблюдаемые объекты. Такой же факт следует из теоремы 2. Действительно, легко проверить, что входная радиальная эффективность объектов C и F в моделях ${{T}_{{{\text{NIRS}}}}}$ и ${{T}_{{{\text{NDRS}}}}}$ равняется 1. По утверждению 1 теоремы 2, оба объекта проявляют G-CRS.
Объекты A и B меньше, чем их масштабные эталонные объекты C и F. По определению 3, объекты A и B проявляют G-IRS. То же самое следует из теоремы 2, если принять во внимание, что входная радиальная эффективность этих объектов равна 1 в модели ${{T}_{{{\text{NDRS}}}}}$ и меньше чем 1 в модели ${{T}_{{{\text{NIRS}}}}}$.
Подобным образом объекты K и L больше, чем их масштабные эталонные объекты C и F, и поэтому оба объекта проявляют G-DRS. Это также следует из теоремы 2, потому что оба объекта эффективные в модели ${{T}_{{{\text{NIRS}}}}}$, но не эффективны во входной радиальной модели ${{T}_{{{\text{NDRS}}}}}$.
Наконец, объекты D и E проявляют G-SCRS. Это следует из определения 3, учитывая, что оба объекта D и E больше, чем их масштабный эталонный объект C, но меньше, чем их эталонный объект F. Ту же самую классификацию мы можем получить из теоремы 2, отмечая, что оба объекта D и E неэффективны во входных радиальных моделях ${{T}_{{{\text{NIRS}}}}}$ и ${{T}_{{{\text{NDRS}}}}}$.
Как было отмечено выше, оценка входной радиальной эффективности объекта $({{X}_{o}},{{Y}_{o}})$ в модели ${{T}_{{{\text{FDH}}}}}$ требует решения смешанной целочисленной линейной задачи. Однако оценка эффективности в дополнительных моделях NIRS и NDRS является более сложной задачей, которая требует решения смешанно-целочисленной нелинейной задачи. В [13] было показано, что последняя задача может быть переформулирована как смешанно-целочисленная линейная задача, но размер такой задачи значительно увеличивается.
Ниже мы представим два алгоритма. Первый алгоритм позволяет нам строить сечения эффективного фронта модели FDH с помощью двухмерных плоскостей специального вида, которые могут быть использованы для визуализации многомерного пространства. Второй алгоритм является расширением первого алгоритма, который позволяет определить тип глобального эффекта масштаба эффективного объекта $({{X}_{o}},{{Y}_{o}})$ без вычислений эффективности в дополнительных моделях.
3. АЛГОРИТМ ВИЗУАЛИЗАЦИИ ЭФФЕКТИВНОГО ФРОНТА
Рассмотрим любой объект $({{X}_{o}},{{Y}_{o}}) \in {{T}_{{{\text{FDH}}}}}$ и два ненулевых вектора (направления) ${{d}_{1}},{{d}_{2}} \in {{E}^{{m + r}}}$ таких, что вектор ${{d}_{1}}$ не параллелен вектору ${{d}_{2}}$. Определим двумерную плоскость в пространстве ${{E}^{{m + r}}}$ как
(5)
${\text{Pl}}({{X}_{o}},{{Y}_{o}},{{d}_{1}},{{d}_{2}}) = ({{X}_{o}},{{Y}_{o}}) + \alpha {\kern 1pt} {{d}_{1}} + \beta {\kern 1pt} {{d}_{2}},$Пусть ${\text{WEf}}{{{\text{f}}}_{P}}{{T}_{{{\text{FDH}}}}}$ обозначает слабо эффективный по Парето фронт модели ${{T}_{{{\text{FDH}}}}}$. Определим пересечение фронта с двумерной плоскостью (5) следующим образом:
Следуя работе [20] и придавая различные значения векторам ${{d}_{1}}$ и ${{d}_{2}}$, можно получить различные сечения слабо эффективного фронта ${\text{WEf}}{{{\text{f}}}_{P}}{{T}_{{{\text{FDH}}}}}$. Алгоритм, представленный ниже, позволяет выбирать направления ${{d}_{1}}$ и ${{d}_{2}}$ для следующих сценариев.
Сценарий 1. ${{d}_{1}} = ({{X}_{o}},0) \in {{E}^{{m + r}}}$, ${{d}_{2}} = (0,{{Y}_{o}}) \in {{E}^{{m + r}}}$. Введем переменные $\varphi = 1 + \alpha $ и $\psi = 1 + \beta $, отметим, что плоскость (5) состоит из всех точек, которые могут быть представлены в форме $(X,Y) = (\varphi {{X}_{o}},\psi {{Y}_{o}})$. Соответствующее сечение ${\text{Sec}}({{X}_{o}},{{Y}_{o}})$модели FDH может быть использовано для иллюстрации понятия масштабной эффективности и эффекта масштаба.
Сценарий 2. ${{d}_{1}} = ({{e}_{p}},0) \in {{E}^{{m + r}}},\;{{d}_{2}} = ({{e}_{s}},0) \in {{E}^{{m + r}}}$, где ${{e}_{p}}$ и ${{e}_{s}}$ – единичные векторы размерности m, чьи компоненты p и s соответственно равняются 1, остальные компоненты равняются нулю. При данном выборе направлений алгоритм построит входную изокванту по входным переменным p и s.
Сценарий 3. ${{d}_{1}} = (0,{{e}_{p}}) \in {{E}^{{m + r}}},\;{{d}_{2}} = (0,{{e}_{s}}) \in {{E}^{{m + r}}}$, где ${{e}_{p}}$ и ${{e}_{s}}$ являются единичными векторами размерности r, определенными таким же способом, как и в предыдущем пункте. Такой выбор направлений определяет выходную изокванту для выходных переменных p и s.
Сценарий 4. ${{d}_{1}} = ({{e}_{p}},0) \in {{E}^{{m + r}}},\;{{d}_{2}} = (0,{{e}_{s}}) \in {{E}^{{m + r}}}$, где ${{e}_{p}}$ и ${{e}_{s}}$ являются единичными векторами размерности m и r соответственно, определенными так же, как и в предыдущих пунктах. Данный выбор приведет к построению входной–выходной изокванты, определяемой входной переменной p и выходной переменной s.
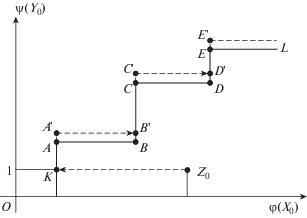
Представим теперь обобщенный алгоритм для построения сечений ${\text{Sec}}({{X}_{o}},{{Y}_{o}})$ в невыпуклой модели FDH, которые соответствуют различным направлениям ${{d}_{1}}$ и ${{d}_{2}}$, определенных выше. Работа алгоритма и доказательство теоремы 3, которая устанавливает его справедливость, иллюстрируются на фиг. 2. Роль малого параметра $\varepsilon $, который используется в алгоритме, объясняется далее.
Фиг. 2.
Кривая показывает сечение эффективного фронта в модели FDH, которая включает все объекты, которые могут быть записаны в виде $(X,Y) = (\varphi {{X}_{o}},\psi {{Y}_{o}})$, где $\varphi = 1 + \alpha $ и $\psi = 1 + \beta $, скалярные величины $\alpha $ и $\beta $ определяются в алгоритме 1.
Алгоритм 1
[ВХОД]: Объект ${{Z}_{o}} = ({{X}_{o}},{{Y}_{o}})$,
Векторы ${{d}_{1}}$, ${{d}_{2}}$,
Параметры ${{k}_{1}}$, ${{k}_{2}}$, $\varepsilon $.
[ВЫХОД]: Угловые точки ${{Z}_{l}}$, $l = 1,\; \ldots ,\;L$, сечения эффективного фронта модели FDH.
Параметрам ${{k}_{1}}$ и ${{k}_{2}}$ присваиваются следующие значения в зависимости от выбранного сценария:
а) ${{k}_{1}} = 1$ и ${{k}_{2}} = 1$ для сценариев 1 и 4;
б) ${{k}_{1}} = 1$ и ${{k}_{2}} = - 1$ для сценария 2;
в) ${{k}_{1}} = - 1$ и ${{k}_{2}} = 1$ для сценария 3.
Шаг 1. Решаем следующую оптимизационную задачу:
(6)
$\begin{gathered} \min {{k}_{1}}\alpha , \\ ({{Z}_{o}} + \alpha {{d}_{1}} + \beta {\kern 1pt} {{d}_{2}}) \in {{T}_{{{\text{FDH}}}}}, \\ \end{gathered} $Шаг 2. Находим две смежные угловые точки сечения эффективного фронта в модели FDH. Для этого решаем следующие две оптимизационные задачи.
Задача А:
(7)
$\begin{gathered} \max {{k}_{2}}\beta , \\ ({{Z}_{l}} + \beta {{d}_{2}}) \in {{T}_{{{\text{FDH}}}}}. \\ \end{gathered} $Определим ${{Z}_{{l + 1}}} = {{Z}_{l}} + \beta {\text{*}}{{d}_{2}}$, где $\beta {\text{*}}$ – оптимальное решение в задаче A, полагаем l = l + 1. Отметим, что, поскольку $\beta = 0$ – всегда допустимое значение в задаче (7) , мы получим $\beta * \geqslant 0$. Следовательно, задача (7) может быть эквивалентно решена либо с неотрицательной, либо со свободной переменной $\beta $.
Задача Б:
(8)
$\begin{gathered} \min {{k}_{1}}\alpha , \\ ({{Z}_{l}} + \alpha {{d}_{1}} + {{k}_{2}}\varepsilon {{d}_{2}}) \in {{T}_{{{\text{FDH}}}}}, \\ \end{gathered} $Если задача Б недопустима, переходим к шагу 3. В противном случае, определяем ${{Z}_{{l + 1}}} = {{Z}_{l}} + \alpha {\text{*}}{{d}_{1}}$, где $\alpha {\text{*}}$ является оптимальным решением задачи Б, полагаем $l = l + 1$. Переходим к началу шага 2.
Шаг 3. Останов. Точки ${{Z}_{l}}$, $l = 1,\; \ldots ,\;L$, сгенерированные алгоритмом, являются угловыми точками сечения слабо эффективного фронта модели FDH двухмерной плоскостью (5).
Теорема 3. Алгоритм 1 строит сечение ${\text{Sec}}({{X}_{o}},{{Y}_{o}})$ фронта в FDH модели за конечное число шагов.
Доказательство. Для конкретности, но без потери общности, рассмотрим сценарий 1. Пусть ${{d}_{1}} = ({{X}_{o}},0)$, ${{d}_{2}} = (0,{{Y}_{o}})$, ${{k}_{1}} = 1$ и ${{k}_{2}} = 1$. Заметим, что, согласно алгоритму, все сгенерированные им точки ${{Z}_{l}}$, $l = 1,\;...,\;L$, остаются на двухмерной плоскости (5), натянутой на векторы ${{d}_{1}}$ и ${{d}_{2}}$. Как показано на фиг. 2, шаг 1 идентифицирует крайнюю левую точку $K$ на сечении в модели FDH плоскостью (5), так как переменная $\alpha $ минимизируется и обе переменные $\alpha $ и $\beta $ являются свободными. На шаге 2 с помощью решения задачи А алгоритм находит угловую точку $A$ сечения модели FDH, которая максимизирует величину $\beta {\text{*}}$ при выходном векторе ${{Y}_{o}}$. Решая задачу Б, алгоритм сначала слегка выходит из допустимого множества модели FDH, что соответствует точке $A'$. Эта точка затем проецируется (вдоль горизонтальной оси) в допустимую область модели FDH, что дает в свою очередь допустимую точку $B'$. Удаляя избыточный выход $\varepsilon {{Y}_{o}}$ из точки $B'$, мы получаем угловую точку B. На этом заканчивается первая итерация. Вторая итерация проходит по той же схеме. За исключением того, что в качестве начальной точки используется точка B вместо точки K, и генерируются угловые точки C и D, последняя из которых становится начальной точкой следующей итерации. Алгоритм останавливается, когда он идентифицирует бесконечный горизонтальный луч $E'L$, в этом случае задача Б становится недопустимой.
В любом из четырех сценариев, сечение слабо эффективного фронта FDH-модели имеет конечное число угловых точек. (Например, на фиг. 2, алгоритм 1 генерирует 5 угловых точек в следующем порядке: A, B, C, D и E.) Поэтому описанный алгоритм останавливается после конечного числа итераций. На этом доказательство заканчивается.
Рассмотрим теперь выбор параметра $\varepsilon $ в алгоритме на примере сценария 1. Добавляя малую величину $\varepsilon > 0$ выходного вектора ${{Y}_{o}}$ к угловой точке ${{Z}_{l}}$, найденной при решении задачи А, мы получаем точку, которая лежит слегка выше допустимого множества модели FDH. (Это соответствует точкам $A'$, $C'$ и $E'$ на фиг. 2.) Решая задачу Б, мы либо найдем вертикальный отрезок модели FDH, где выходной вектор является допустимым, или (как в случае точки $E'$) определяем, что других угловых точек не существует.
Выбор величины $\varepsilon $ является важной частью алгоритма. С одной стороны, эта величина должна быть больше, чем величины малых допусков, используемых современными оптимизационными программами, например, больше чем ${{10}^{{ - 6}}}$. С другой стороны, величина $\varepsilon $ должна быть меньше чем точность данных, используемых в модели, например, мы можем взять $\varepsilon $ меньше чем ${{10}^{{ - 3}}}$ в большинстве приложений. В этом случае алгоритм не пропустит ни одной ступеньки FDH-фронта.
Роль параметра $\varepsilon $ в приведенном алгоритме подобна роли в подобных родственных алгоритмах для построения сечений в выпуклых DEA моделях. В последнем случае выбор $\varepsilon $ помогает избежать появления “ложных” вершин в производственной функции (см. [20]).
4. АЛГОРИТМ ДЛЯ ОЦЕНКИ ЭФФЕКТА МАСШТАБА
Реализация алгоритма 1 требует решения смешанных линейно-целочисленных задач (6)–(8), каждая из которых эквивалентна решению радиальной входной задачи по оценке эффективности для объекта $({{X}_{o}},{{Y}_{o}})$ в модели ${{T}_{{{\text{FDH}}}}}$ (2). Теперь покажем, что простые дополнительные вычисления, представленные ниже как алгоритм 2, могут быть использованы для определения типа глобального эффекта масштаба для любой угловой точки, сгенерированной алгоритмом 1. В частности, если начальный объект $({{X}_{o}},{{Y}_{o}})$ является сильно эффективным, этот объект сам является угловой точкой, и его глобальный эффект масштаба также определяется алгоритмом 2. Преимущества алгоритма 2 над другими методами, использующими дополнительные модели с возрастающим и убывающим эффектом масштаба, заключаются в том, что этот алгоритм не решает смешанно-целочисленные нелинейные задачи (3).
Рассмотрим множество угловых точек ${{Z}_{l}}$, $l \in \bar {L} = \{ 1,\; \ldots ,\;L\} $, сгенерированных алгоритмом 1. Каждая из этих точек эквивалентно определяется параметрами $({{\varphi }^{l}},{{\psi }^{l}}) = (1 + {{\alpha }^{l}},1 + {{\beta }^{l}})$, где ${{\alpha }^{l}}$ и ${{\beta }^{l}}$ являются оптимальными значениями в задачах А и Б. Следующий алгоритм находит индексное множество ${{\bar {L}}_{{\max }}}$ угловых точек, которые обладают наибольшей продуктивностью, а также наибольшую и наименьшую из них, которые мы обозначим через ${{l}_{1}}$ и ${{l}_{2}}$.
Алгоритм 2
[ВХОД]: Множество угловых точек $({{\varphi }^{l}},{{\psi }^{l}})$, $l \in \bar {L}$, сгенерированных алгоритмом 1.
[ВЫХОД]: Индексное множество ${{\bar {L}}_{{\max }}}$, индексы ${{l}_{1}}$ и ${{l}_{2}}$.
Шаг 1. Вычисляем индексное множество ${{\bar {L}}_{{\max }}} \subseteq \bar {L}$, определяемое следующим образом:
Шаг 2. Если индексное множество ${{\bar {L}}_{{\max }}}$ содержит единственный элемент $l{\text{*}}$, полагаем ${{l}_{1}} = {{l}_{2}} = l{\text{*}}$. В противном случае, пусть
Отметим, что для каждой угловой точки $({{\varphi }^{l}},{{\psi }^{l}})$, где $l \in {{\bar {L}}_{{\max }}}$, мы получим один и тот же коэффициент ${{{{\psi }^{{l*}}}} \mathord{\left/ {\vphantom {{{{\psi }^{{l*}}}} {{{\varphi }^{{l*}}}}}} \right. \kern-0em} {{{\varphi }^{{l*}}}}}$. Среди этих угловых точек ${{Z}_{{{{l}_{1}}}}}$ имеет наименьшее значение ${{\varphi }^{l}}$ и ${{Z}_{{{{l}_{2}}}}}$ имеет наибольшее значение ${{\varphi }^{l}}$.
Выход алгоритма 2 напрямую ведет к определению типа глобального эффекта масштаба для эффективной точки ${{Z}_{l}}$, $l \in \bar {L}$.
Теорема 4. Пусть производственный объект ${{Z}_{l}}$ является эффективным в модели ${{T}_{{{\text{FDH}}}}}$. Тогда он проявляет следующие свойства:
1) G-CRS, если $l \in {{\bar {L}}_{{\max }}}$;
2) G-IRS, если $l < {{l}_{1}}$;
3) G-DRS, если $l > {{l}_{2}}$;
4) G-SCRS, если ${{l}_{1}} < l < {{l}_{2}}$ и $l \notin {{\bar {L}}_{{\max }}}$.
Доказательство. На шаге 1 алгоритма 2 находится максимальный коэффициент ${{{{\psi }^{l}}} \mathord{\left/ {\vphantom {{{{\psi }^{l}}} {{{\varphi }^{l}}}}} \right. \kern-0em} {{{\varphi }^{l}}}}$ среди всех $l \in \bar {L}$. По определению 1, если $l \in {{\bar {L}}_{{\max }}}$, тогда объект ${{Z}_{l}}$ находится в точке наибольшей продуктивности и показывает глобальный постоянный эффект масштаба G-CRS. Если $l \in \bar {L}{\backslash }{{\bar {L}}_{{\max }}}$, то объект ${{Z}_{l}}$ не находится в точке наибольшей продуктивности, а множество ${{\bar {L}}_{{\max }}}$ является индексным множеством его масштабных эталонных объектов. В случаях 2 и 3 теоремы 4 все масштабные эталонные объекты больше и соответственно меньше, чем объект ${{Z}_{l}}$. В случае 4, по крайней мере, один эталонный объект больше, чем ${{Z}_{l}}$. Далее доказательство следует из определения 3.
Из вышеприведенной теоремы следует, что вместо использования методов оценки глобального эффекта масштаба, основанных на применении вспомогательных моделей с возрастающим и убывающим эффектом масштаба, можно использовать алгоритмы 1 и 2. Такой подход требует только решения смешанно-целочисленных линейных задач.
4. ВЫЧИСЛИТЕЛЬНЫЕ ЭКСПЕРИМЕНТЫ
Мы провели ряд вычислительных экспериментов для того, чтобы протестировать наши алгоритмы на реальных данных, взятых из различных областей. Эти эксперименты включают данные по российским банкам, рыболовным траулерам и шведским электрическим сетям. Исходные данные подробно описаны в работах [24], [25]. Все вычислительные эксперименты были проведены на персональном компьютере с процессором Intel Core i3 3.33ГГц с использованием оптимизатора LP-solve [26].
В таблице представлена основная информация об исходных данных и вычислительных экспериментах. В столбце “мера эффективности” показывается время вычислений по входной радиальной модели для всех производственных объектов из соответствующей базы данных с помощью решения смешанно-целочисленных линейных задач (2). Столбец “Сечения эффективного фронта” показывает время вычислений построения сечений модели FDH с помощью алгоритма 1 (сценарий 1) и оценки типа глобального эффекта масштаба алгоритмом 2.
Таблица.
Результаты вычислительных экспериментов
| Данные, годы | Число входных и выходных показателей | Число объектов | Время, с | |
|---|---|---|---|---|
| Мера эффективности | Сечения эффективного фронта | |||
| Российские банки, 2008 | 6 | 200 | 1.0 | 43.9 |
| Шведские электрораспределительные сетевые организации, 1987 | 8 | 163 | 0.9 | 43.4 |
| Рыболовные траулеры, 2003–2005 | 4 | 233 | 1.3 | 33.2 |
В таблице показано, что время вычислений всех сечений в модели FDH больше, чем время вычислений входной радиальной эффективности для всех производственных объектов. Однако это время не включает время вычислений мер эффективностей в модели с невозрастающим и неубывающим эффектом масштаба, которые необходимы для оценки эффекта масштаба в методах, описанных в [9], [17].
На фиг. 3а показано типичное сечение эффективного фронта в модели FDH, полученное в экспериментах по банкам для объекта 57. На фиг. 3б показана увеличенная часть того же графика в окрестности начала координат.
Фиг. 3.
Сечение эффективного фронта в модели FDH с использованием данных по банкам. Оно включает все производственные объекты модели, которые могут быть записаны в виде $(X,Y) = (\varphi {{X}_{o}},\psi {{Y}_{o}})$, где ${{X}_{o}}$ и ${{Y}_{o}}$ – входные и выходные векторы объекта 57.

Интересно отметить, что точки B и F лежат почти на одном и том же луче OF. Однако более точные расчеты показывают, что наклон луча OB равен 4.559 (тангенс угла наклона), в то время как наклон луча OF равняется 4.615. Поэтому объект F представляет собой объект с наибольшей продуктивностью среди всех объектов, изображенных на фигуре. Из этого следует, что все эффективные объекты, расположенные слева от F, включая объекты $A$, $B$, $C$, $D$ и $E$, проявляют глобальный возрастающий эффект масштаба. Подобным образом, можем сказать, что объект K проявляет глобальный убывающий эффект масштаба.
5. ЗАКЛЮЧЕНИЕ
В данной статье был представлен общий алгоритм, который строит различные двухмерные сечения эффективного фронта в невыпуклой модели FDH. Наши основные результаты связаны с построением сечений фронта, которые для данного объекта $({{X}_{o}},{{Y}_{o}})$ генерируют все объекты вида $(\varphi {{X}_{o}},\psi {{Y}_{o}})$, которые могут быть произведены в модели FDH. Предлагаемый подход может быть также применен к построению изоквант для двух входных или выходных показателей, или для одного входного и одного выходного показателя.
Наш подход может быть интересен, по крайней мере, с двух точек зрения. Во-первых, он может быть использован для визуализации многомерных множеств, которые включают невыпуклую модель FDH, помогают объяснить результаты оценки деятельности объектов, выявить лучшие (эффективные) объекты и т.д. Разработанный алгоритм может быть использован как отдельный модуль в дополнение к существующим инструментам оценки деятельности производственных объектов.
Во-вторых, предлагаемый подход ведет к альтернативному эффективному с вычислительной стороны методу обнаружения объектов с наибольшей продуктивностью и оценки глобального эффекта масштаба в невыпуклой модели FDH. Хорошо известно, что стандартные методы требуют для этой цели оценки входной или выходной радиальной эффективности производственного объекта в невыпуклой FDH-модели с невозрастающим и неубывающим эффектом масштаба. Для этого требуется решение либо частично целочисленных нелинейных задач оптимизации, или смешанных целочисленных линейных задач существенно большей размерности, и поэтому более затратной по времени, особенно для больших задач. В противоположность этому, наш подход требует решения только частично целочисленных задач существенно меньшего размера. Кроме того, производительность предлагаемого метода может быть существенно улучшена за счет применения алгоритмов целенаправленного перебора (см. [32]).
Мы протестировали наш подход на основе трех баз данных из реальных секторов. Вычислительные эксперименты подтверждают вычислительную эффективность и надежность разработанных алгоритмов.
Авторы выражают благодарность В.В. Подиновскому, чьи предложения привели к заметному улучшению статьи.
Список литературы
Førsund F.R., Hjalmarsson L. Calculating scale elasticity in DEA models // J. of the Operat. Research Soc. 2004. V. 55. № 10. P. 1023–1038.
Banker R.D., Charnes A., Cooper W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis // Management Sci. 1984. V. 30. № 9. P. 1078–1092.
Banker R.D., Thrall R.M. Estimation of returns to scale using data envelopment analysis // Europ. Journal of Operat. Research. 1992. V. 62. № 1. P. 74–84.
Hadjicostas P., Soteriou A.C. One-sided elasticities and technical efficiency in multi-output production: A theoretical framework // Europ. Journal of Operat. Research. 2006. V. 168. № 2. P. 425–449.
Chambers R.G., Färe R. A “calculus” for data envelopment analysis // J. of Productivity Analys. 2008. V. 30. № 3. P. 169–175.
Podinovski V.V., Førsund F.R., Krivonozhko V.E. A simple derivation of scale elasticity in data envelopment analysis // Europ. Journal of Operat. Research. 2009. V. 197. № 1. P. 149–153.
Podinovski V.V., Førsund F.R. Differential characteristics of efficient frontiers in data envelopment analysis // Operat. Research. 2010. V. 58. № 6. P. 1743–1754.
Deprins D., Simar L., Tulkens H. Measuring labor-efficiency in post offices / Eds. M. Marchand, P. Pestieau, H. Tulkens. The performance of public enterprises: concepts and measurements. Amsterdam: North-Holland, 1984. P. 243–267.
Kerstens K., Vanden Eeckaut P. Estimating returns to scale using non-parametric deterministic technologies: A new method based on goodness-of-fit // Europ. Journal of Operat. Research. 1999. V. 113. № 1. P. 206–214.
Briec W., Kerstens K., Leleu H., Vanden Eeckaut P. Returns to scale on nonparametric deterministic technologies: Simplifying goodness-of-fit methods using operations on technologies // J. of Productivity Analys. 2000. V. 14. № 3. P. 267–274.
Färe R., Grosskopf S., Lovell C.A.K. The structure of technical efficiency// Scandinavian Journal of Economics. 1983. V. 85. № 2. P. 181–190.
Färe R., Grosskopf S., Lovell C.A.K. The measurement of efficiency of production. Boston: Kluwer, 1985.
Podinovski V.V. On the linearisation of reference technologies for testing returns to scale in FDH models // Europ. Journal of Operat. Research. 2004. V. 152. № 3. P. 800–802.
Soleimani-damaneh M., Jahanshahloo G.R., Reshadi M. On the estimation of returns-to-scale in FDH models // Europ. Journal of Operat. Research. 2006. V. 174. № 2. P. 1055–1059.
Leleu H. A linear programming framework for free disposal hull technologies and cost functions: Primal and dual models // Europ. Journal of Operat. Research. 2006. V. 168. № 2. P. 340–344.
Podinovski V.V. Efficiency and returns to scale on the “no free lunch” assumption only // J. of Productivity Analys. 2004. V. 22. № 3. P. 227–257.
Podinovski V.V. Local and global returns to scale in performance measurement // J. of the Operat. Research Soc. 2004. V. 55. № 2. P. 170–178.
Banker R.D. Estimating most productive scale size using data envelopment analysis // Europ. Journal of Operat. Research. 1984. V. 17. № 1. P. 35–44.
Cesaroni G., Kerstens K., Van de Woestyne I. Global and local scale characteristics in convex and nonconvex nonparametric technologies: A first empirical exploration // Europ. Journal of Operat. Research. 2017. V. 259. № 2. P. 576–586.
Krivonozhko V.E., Utkin O.B., Volodin A.V., Sablin I.A., Patrin M. Constructions of economic functions and calculations of marginal rates in DEA using parametric optimization methods // J. of the Operat. Research Soc. 2004. V. 55. № 10. P. 1049–1058.
Кривоножко В.Е., Лычев А.В. Алгоритмы построения эффективного фронта для невыпуклых моделей на основе оптимизационных методов // Докл. АН. 2017. Т. 47. № 6. С. 625–629.
Krivonozhko V.E., Lychev A.V., Kalashnikov E.A. Constructions of input and output isoquants for nonconvex multidimensional models / (Eds) Yu.G. Evtushenko, M.Yu. Khachay, O.V. Khamisov, Yu.A. Kochetov, V.U. Malkova, M.A. Posypkin: Proc. of the OPTIMA-2017 Conference, Petrovac, Montenegro, October 2–7, 2017. P. 336–342.
Podinovski V.V. Returns to scale in convex production technologies // Europ. Journal of Operat. Research. 2017. V. 258. № 3. P. 970–982.
Førsund F.R., Hjalmarsson L., Krivonozhko V.E., Utkin O.B. Calculation of scale elasticities in DEA models: direct and indirect approaches // J. of Productivity Analys. 2007. V. 28. № 1–2. P. 45–56.
Krivonozhko V.E., Førsund F.R., Lychev A.V. A note on imposing strong complementary slackness conditions in DEA // Europ. Journal of Operat. Research. 2012. V. 220. № 3. P. 716–721.
Lp_solve reference guide. URL: http://lpsolve.sourceforge.net/5.5/. (дата обращения: 24.04.2018).
Banker R.D., Cooper W.W., Seiford L.M., Zhu J. Returns to scale in DEA / W.W. Cooper, L. Seiford, J. Zhu (Eds.), Handbook on data envelopment analysis (2nd ed.). New York: Springer Science + Busines Media, 2011. P. 41–70.
Zelenyuk V. A scale elasticity measure for directional distance function and its dual: Theory and DEA estimation // Europ. Journal of Operat. Research. 2013. V. 228. № 3. P. 592–600.
Sahoo B.K., Tone K. Scale elasticity in non-parametric DEA approach / (Ed) J. Zhu,d Data envelopment analysis: A handbook of models and methods. New York: Springer Science + Business Media, 2015. P. 269–290.
Кривоножко В.Е., Лычев А.В., Форсунд Ф.Р. Измерение эффекта масштаба в радиальных моделях методологии анализа среды функционирования // Ж. вычисл. матем. и матем. физ. 2017. Т. 57. № 1. С. 62–73.
Podinovski V.V., Chambers R.G., Atici K.B., Deineko I.D. Marginal values and returns to scale for nonparametric production frontiers // Operat.Research. 2016. V. 64. № 1. P. 236–250.
Кривоножко В.Е., Лычев А.В. Визуализация эффективного фронта для невыпуклых моделей на основе алгоритмов целенаправленного перебора // Докл. АН. 2017. Т. 477. № 1. С. 22–25.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики