Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 526-533

1. ВВЕДЕНИЕ

Квазигазодинамическая система уравнений (КГД) [1] обладает целым рядом достоинств, позволяющим успешно ее использовать для моделирования сложных газо- и гидродинамических течений. В первую очередь эти возможности раскрываются при расчетах на современных системах высокой и сверхвысокой производительности. Недостатком КГД системы является ее громоздкость, особенно наглядно выраженная в ее магнитогазодинамическом варианте (см. [2], [3]). Эта громоздкость выражается в большом количестве диссипативных членов, учет которых, впрочем, не вызывает сколько-нибудь принципиальных трудностей и связан лишь с большим объемом рутинной программистской работы.

В работе [4] предложен вариант упрощенной КГД системы. Его вывод опирается на две принципиальные особенности КГД системы – ее гиперболический характер и наличие диссипативного члена в правой части уравнения неразрывности. (Следует напомнить, что несмотря на эти особенности КГД система отличается от уравнений Навье–Стокса на члены второго порядка малости по числу Кнудсена [1].)

Для компактного варианта КГД и ее магнитогидродинамического аналога построение вычислительных алгоритмов может быть основано в значительной мере на копировании известных алгоритмов решения уравнений Навье–Стокса и диссипативных МГД уравнений. При этом естественно сохраняются преимущества, связанные с решением оригинальной КГД системы.

В данной работе обсуждаются алгоритмы решения компактной КГД системы и приводятся результаты расчета 3D течения вязкого теплопроводного газа на пространственной сетке, состоящей из 10⁷ узлов.

2. КОМПАКТНЫЕ КГД И МАГНИТОГАЗОДИНАМИЧЕСКИЕ КГД СИСТЕМЫ

Как уже отмечалось, характерной особенностью КГД системы является наличие диссипативного члена в уравнении неразрывности. Его появление напрямую связано с характерной особенностью КГД системы – гарантированным сглаживанием решения на расстоянии длины свободного пробега $l$ [5], [6].

Следует отметить, что уравнения Эйлера связаны с представлением функции распределения $f$ в виде локально-максвелловской ${{f}_{0}}$

где $\rho $ – плотность, ${{{\mathbf{u}}}_{i}}$ – макроскопическая скорость, $T$ – температура.

В свою очередь уравнения Навье–Стокса связаны с представлением функции распределения в виде двух членов разложения Чепмена–Энскога (см. [7]–[9])

где $\phi (\xi )$ – малая добавка порядка $O({\text{Kn}})$, зависящая от чиса Кнудсена.

Возможность представления вязких и теплопроводных членов с помощью только двух членов разложения, в отличие от громоздкого разложения Гильберта, связана с явным учетом физического факта, что вблизи равновесия функция распределения зависит от пространственных переменных и времени только посредством пяти газодинамических параметров $\rho $, ${\mathbf{u}}$ и $T$. В КГД системе дополнительно к зависимости от $\rho $, ${\mathbf{u}}$ и $T$ учитывается, что функция распределения ${{f}_{0}}$ слабо меняется на расстояниях длины свободного пробега $l$ (см. [1], [5]).

Диссипативный член в правой части уравнения неразрывности КГД может быть представлен в дивергентном виде:

где здесь $p$ – давление.

В свою очередь ${\mathbf{w}}$ имеет смысл дополнительной скорости, появление которой связано со сглаживанием решения на расстоянии $l$.

Для вывода компактной КГД системы воспользуемся тем феноменологическим приемом, который использовался при выводе уравнений механики сплошной среды. Следуя, например, [10] записываем эти уравнения в виде

где ${\mathbf{Q}}$ – интересующий газодинамический параметр, ${{{\mathbf{S}}}_{Q}}$ – поток, приводящий к изменению этого параметра.

При формировании ${{{\mathbf{S}}}_{Q}}$ наряду с используемыми для вывода уравнений газовой динамики макроскопической скорости ${\mathbf{v}}$, тензора молекулярной вязкости ${{P}_{{{\text{NS}}}}}$ и вектора теплового потока ${\mathbf{q}}$, учтем дополнительный импульс, связанный со скоростью ${\mathbf{w}}$ (2.4). Вместо $\partial {\mathbf{Q}}{\text{/}}\partial t$ в (2.5) изменение по времени $Q$ выразим в виде $\tfrac{{\partial {\mathbf{Q}}}}{{\partial t}} + \tfrac{\tau }{2}\tfrac{{{{\partial }^{2}}{\mathbf{Q}}}}{{\partial {{t}^{2}}}}$. Появление второй производной по времени, присущее КГД, связано с тем, что промежуток времени, на котором исследуется изменение параметра ${\mathbf{Q}}$, не может быть меньше (по порядку величины) характерного времени между столкновениями молекул, т.е. времени установления нового состояния равновесия.

С учетом этих факторов, выпишем компактной вариант КГД системы,

В качестве дополнительного обозначения в (2.6)–(2.8) используется $E$ – полная энергия, $E = \rho {{u}^{2}}{\text{/}}2 + \rho \varepsilon $, где $\varepsilon $ – внутренняя энергия.

Система (2.6)–(2.8) отличается от оригинальной КГД системы (см. [1], [4]), которая может быть предоставлена в виде

где тензор $P$ и вектор ${\mathbf{q}}{\text{*}}$ определяются следующими выражениями (см. [11]):

Аналогично системе (2.4), (2.6)–(2.8) компактный магнитогазодинамический вариант КГД примет вид

В системе (2.15)–(2.20) в дополнение к ранее введенным обозначениям используются следующие: ${\mathbf{B}}$ – вектор напряженности магнитного поля, ${{\nu }_{{\text{m}}}}$ – магнитная вязкость

здесь $\sigma $ – проводимость, $c$ – скорость света, ${{\tau }_{{\text{m}}}}$ – магнитное время

Выражение (22) для ${{\tau }_{{\text{m}}}}$ получено из следующих соображений. При получении квазигазодинамической  МГД  в правой  части  уравнения  магнитной индукции появляется ряд диссипативных членов (см. [3], [12]). Однако их анализ показывает, что вклад первого члена ${{\tau }_{{\text{m}}}}\left( {p + {{B}^{2}}{\text{/}}(8\pi )} \right)\left( {\partial {{B}_{i}}{\text{/}}\partial {{x}_{k}} - \partial {{B}_{k}}{\text{/}}\partial {{x}_{i}}} \right){\text{/}}(2\rho )$ основной. В свою очередь этот член по своей форме совпадает с ${{\nu }_{{\text{m}}}}\operatorname{rot} {\mathbf{B}}$. Обратим также внимание на то, что из (2.22) следует выражение для магнитной вязкости ${{\nu }_{{\text{m}}}}$:

которое по своей структуре совпадает с классическим выражением для молекулярной вязкости $\mu $,

Обсудим вопросы, связанные с построением вычислительных алгоритмов для компактной квазигазодинамической системы (2.4), (2.6)–(2.8) и ее магнитогазодинамического аналога (2.15)–(2.20).

3. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ

Обратим внимание на структуру компактной квазигазодинамической системы (2.4), (2.6)–(2.8). Ее отличие от уравнений Навье–Стокса заключается в появлении вторых производных по времени, умноженных на время $\tau $, и добавкой ${\mathbf{w}}$ к газодинамической скорости ${\mathbf{u}}$. Для решения этой системы предлагается использовать трехслойную явную схему, в которой неизвестные газодинамические параметеры на новом $j + 1$ слое по времени определяются по известным данным с $j$ и $j - 1$ слоя по времени. При этом пространственные производные аппроксимируются на центральном $j$ слое. Опишем более подробно эту схему.

Рассмотрение этой схемы проведем на примере гиперболического уравнения теплопроводности (см. [13]),

Здесь $F(t,{\mathbf{x}})$ – заданный источник тепла, $\tau {\text{*}}$ – коффециент, имеющий размерность времени.

Уравнение (3.1) может быть получено как частный случай уравнения энергии (2.12) в отсутствие газодинамичского движения. Однако в качестве коэффициента перед второй производной по времени здесь выбирается не время между столкновениями молекул $\tau $. Вместо него используется время $\tau {\text{*}}$, значение которого выбирается из следующих соображений. С одной стороны, его использование должно повышать устойчивость явной схемы, а с другой, член $\tau {\text{*}}{{\partial }^{2}}T{\text{/}}\partial {{t}^{2}}$ не должен вносить сколько-нибудь заметных изменений в решение классического уравнения теплопроводности. По сути дела должно выполнятся условие

В качестве такого значения $\tau {\text{*}}$ можно выбрать величину (см. [14], [15])

где $h{\text{*}}$ – характерный размер пространственной ячейки, $\text{v}{\text{*}}$ – характерное значение скорости.

Как показывает анализ трехслойной явной схемы для решения уравнения (3.1) с $\tau {\text{*}}$, определяемым с помощью выражения (3.3), она будет удовлетворять условию устойчивости (см. [14])

Это условие тоже достаточно жесткое, но все-таки более приемлемо, чем обычное условие устойчивости явной схемы для параболических уравнений

Особенно ярко преимущества трехслойной явной схемы с $\tau {\text{*}}$, определяемым выражением (3.3), проявляются на подробных пространственных сетках (см. [15]).

Рассмотрим, следуя [16], еще один вариант расчета уравнения (3.1) для простоты, полагая источник равным нулю. Перепишем (3.1) в виде

В начале определим пространственные потоки ${{\Phi }_{Q}}$. Затем из второго уравнения (3.7) получим где используя (3.8), окончательно получаем

Эта схема, сочетая в себе консервативный для вычисления ${{\Phi }_{Q}}$ подход и расчет по характеристикам, позволяет в практических вычислениях получить более мягкое ограничение для устойчивости, чем для трехслойной схемы. Однако асимптотически при $\tau {\text{*}}$, определяемое выражением (3.3), выполняется условие устойчивости (3.4).

Обратим внимание на то, что пространственные производные, входящие в систему (2.8)–(2.12) и ее магнитогазодинамического аналога (2.16)–(2.19), могут быть представлены в дивергентном виде, удобном для применения вычислительной процедуры, аналогичной (3.8)–(3.10).

Вернемся к трехслойной явной системе и обсудим аппроксимацию пространственных производных на среднем слое $t = {{t}^{j}}$. Структура уравнений (2.9)–(2.12) позволяет использовать уже разработанные методы решения уравнений Навье–Стокса. В самом деле величина ${\mathbf{w}}$ (2.10) выступает в качестве дополнения к газодинамической скорости ${\mathbf{u}}$. В свою очередь величина дополнительной скорости (2.10) определяется через пространственные производные уравнения Навье–Стокса. Следовательно, для нахождения ${\mathbf{w}}$ можно использовать ранее разработанные алгоритмы решения уравнений газовой динамики.

Аналогичные рассуждения об аппроксимации пространственных производных можно применить и для решения магнитогазодинамической системы (2.16)–(2.20).

4. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Составление тестовых расчетов с помощью компактной КГД системы, ее полного варианта и классических уравнений Навье–Стокса было проведено в [4]. Там же сравнивались аналогичные результаты для компактной магнитогазодинамической системы, расчетов, полученных с помощью полной квазигазодинамической МГД системы и расчетов с помощью классических МГД уравнений. В данной работе в качестве основы для решения использовалась компактная КГД система. Для ее решения использовалась простейшая трехслойная явная схема с $\tau {\text{*}}$ определяемым выражением (3.3). Эта схема хорошо адаптируется на архитектуру многопроцессорных, включая гибридные, вычислительных систем.

Приведем результаты расчетов сложной картины 3D течения вязкого газа на относительно небольших по размерности (10⁶–10⁷ узлов) пространственных сетках. В качестве примера рассматривалось дозвуковое и сверхзвуковое течение вязкого газа вблизи обратной ступеньки.

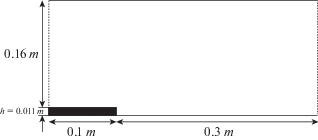
Схема расчетной области указана на фиг. 1. Специфической особенностью рассматриваемой конструкции является то, что ступенька имеет ограниченный размер $\Delta = 0.5h$ вдоль оси $z$.

Приведем исходные параметры рассматриваемых двух вариантов задачи. В первом варианте скорость набегающего потока в числах Маха (${\text{M}} = 1.25$) использовалась пространственная сетка ($200 \times 75 \times 100$). Соответственно число Рейнольдса, рассчитанное по высоте ступеньки $h$, равнялось ${\text{R}}{{{\text{e}}}_{h}} = 0.98 \times {{10}^{5}}$.

Во втором варианте (${\text{M}} = 0.75$, ${\text{R}}{{{\text{e}}}_{h}} = 0.59 \times {{10}^{5}}$) использовалась более подробная пространственная сетка ($600 \times 225 \times 100$). В обоих вариантах давление набегающего потока и его температура были одинаковы ($p = 1.5 \times {{10}^{4}}$ Па и температура $T = 170$ K).

Течения с такими высокими числами Рейнольдса характеризуются наличием интенсивной турбулентности. Для ее адекватного описания в прямом расчете, использующем дополнительные модели турбулентности, требуются более подробные пространственные сетки, состоящие из 10⁹–10¹⁰ расчетных узов. Их реализация вызывает потребность многократного увеличения используемых вычислительных ресурсов. Однако и данные расчеты на умеренных пространственных сетках с помощью рассматриваемой модели показывают ее возможности для моделирования сложных газодинамических течений.

На фиг. 2 показан профиль осредненного по времени давления за обратной ступенькой. Сразу же за ступенькой наблюдается характерный для этого типа течения провал давления.

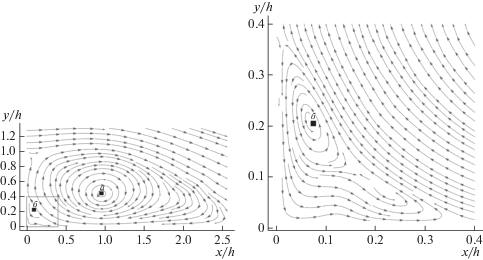
На фиг. 3 изображена картина поля скоростей. Обратим внимание на четкое разрешение основного вихря (маркер а на фиг. 3) и образование (маркер б на фиг. 3), которое можно интерпретировать как изображение более мелкого вихря.

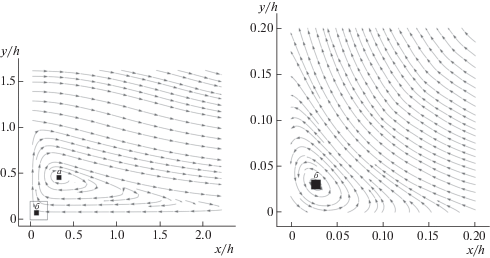
Продемонстрируем это также на примере расчета на более подробной пространственной сетке, состоящей из $1.35 \times {{10}^{7}}$ пространственных узлов и с меньшей скоростъю входного потока (${\text{M}} = 0.75$) и соответственно числа Рейнольдса, что приводит к эффекту еще большего увеличения расчетной сетки по сравнению с первым вариантом.

На фиг. 4 четко видны крупный вихрь (маркер а, фиг. 4) и более мелкий (маркер б, фиг. 4), т.е. на основе данной модели использование подробных сеток позволяет разрешать более тонкую структуру течения.

5. ЗАКЛЮЧЕНИЕ

Компактная квазигидродинамическая система является удобной и относительно простой моделью для расчета сложных газодинамических течений. Она так же как и исходная КГД модель допускает использование алгоритмов хорошо адаптируемых к архитектуре систем сверхвысокой производительности, ресурсы которых станут доступными в ближайшем будущем. Использование все более подробных пространственных сеток позволит описать детальную картину сложных газодинамических течений. Это позволяет надеяться, что компактная КГД система и построенные на ее основе вычислительные алгоритмы станут востребованным инструментарием для моделирования задач гидро и газовой динамики на вычислительных системах следующего десятилетия.