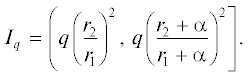Журнал вычислительной математики и математической физики, 2019, T. 59, № 4, стр. 716-728
Оптимизация числа и расположения кругов двух радиусов для k-покрытия ограниченного множества
Ш. И. Галиев 1, *, А. В. Хорьков 1, **
1 Казанский Национальный Исследовательский
Технический Университет им. А.Н. Туполева
420111 Казань, ул. К. Маркса, Россия
* E-mail: sh.galiev@mail.ru
** E-mail: alex22fcrk@yandex.ru
Поступила в редакцию 24.10.2017
После доработки 11.11.2018
Принята к публикации 14.11.2018
Аннотация
Предложен численный метод исследования k-покрытия выпуклого ограниченного замкнутого множества c непустой внутренностью кругами двух заданных радиусов. Представлен алгоритм нахождения приближенных значений чисел кругов и расположения их центров, для некоторых частных случаев найдены приближенные нижние границы плотностей k-покрытия заданной области. Рассмотрены также случаи, когда вводятся ограничения на расстояния между центрами покрывающих кругов и задачи с переменной (заданной) кратностью покрытия. Приведены численные расчеты, демонстрирующие результативность предложенных методов. Библ. 28. Фиг. 4. Табл. 2.
ВВЕДЕНИЕ
Задачи покрытия заданной области кругами одинаковых или разных радиусов важны для решения многих практических проблем, например, таких как расположение станций обслуживания, навигационных пунктов, сенсоров беспроводных сенсорных сетей для мониторинга заданной области, когда сенсоры могут иметь разные радиусы действия. Построение таких систем является задачей k-покрытия (k ≥ 1) заданной области кругами равных или разных радиусов.
В настоящее время существует много публикаций по покрытиям кругами одинакового радиуса, см. [1]–[11]. В этих работах рассматриваются разные методики определения расположений центров кругов, в частности, использование областей Вороного [1], [2], использование линейных и нелинейных математических моделей [2], [6]–[9], использование стержневых моделей [11] и многие другие методы, см., например, метод решения аналогичной задачи о p-медиане [12]. В публикациях по покрытиям кругами одинакового радиуса рассмотрены покрытия отдельных областей, например, квадрата, прямоугольника, треугольника, круга и некоторых других областей (см. [4]–[11]).
Имеются публикации, в которых рассматриваются k-покрытия (k ≥ 1), см., например, [13]–[19]. Задача k-покрытия кругами разных радиусов представлена в [20], где строится нелинейная модель задачи, которая затем преобразуется в линейную с большим числом переменных, вспомогательных переменных и ограничений. Некоторые результаты по определению числа кругов для k-покрытия некоторых заданных (выбранных) областей представлены в [19].
В настоящей статье предложен метод исследования k-покрытия произвольного выпуклого ограниченного замкнутого множества с непустой внутренностью кругами двух заданных радиусов. Представлен алгоритм нахождения приближенных значений чисел кругов и расположения их центров, для некоторых частных случаев найдены приближенные нижние границы плотностей k-покрытия заданной области. Рассмотрены случаи, когда вводятся ограничения на расстояния между центрами покрывающих кругов и задачи с переменной (заданной) кратностью покрытия. Приведены численные расчеты, демонстрирующие результативность предложенных методов.
1. ЗАДАЧА k-ПОКРЫТИЯ ОГРАНИЧЕННОГО МНОЖЕСТВА КРУГАМИ ДВУХ РАДИУСОВ
Пусть G – ограниченное выпуклое замкнутое множество с непустой внутренностью на плоскости P и имеются замкнутые круги заданных радиусов r1 и r2. Множество кругов указанных радиусов образует k-покрытие (k ≥ 1) области G, если каждая точка s из G принадлежит не менее чем k кругам.
Плотностью покрытия G считаем отношение суммарной площади покрывающих кругов к площади области G.
Пусть r1 > r2 и Δ > 0. С шагом Δx = Δy = Δ построим прямоугольную сетку на G. Совокупность линий, образующих сетку на G, порождает квадраты CΔ со стороной Δ. Если квадрат содержится целиком в G, то каждая его вершина является узлом сетки. Если квадрат $C_{\Delta }^{*}$ частично содержится в G, то каждую вершину $C_{\Delta }^{*}$, содержащуюся в G, точки входа границы G в $C_{\Delta }^{*}$ и точки выхода границы G из $C_{\Delta }^{*}$ считаем узлами сетки. Кроме того, на границе F области G ∩ $C_{\Delta }^{*}$ добавляем узловые точки, лежащие на F так, чтобы расстояние по кривой F между соседними узловыми точками было не больше Δ. Пусть TΔ состоит из всех указанных узлов сетки: TΔ = {t1, …, tn}, ti ∈ G, 1 ≤ i ≤ n. Если шаг построения сетки равен Δ/2, то TΔ/2 строится аналогично построению TΔ с добавлением всех точек TΔ к множеству построенных узлов для Δ/2, следовательно, TΔ ⊂ TΔ/2.
Вместо прямоугольной сетки на множестве G можно строить иную, например, косоугольную. Если G является равносторонним треугольником, то косоугольную сетку построим следующим образом. Выберем шаг Δ построения сетки так, что длина стороны треугольника делится нацело на Δ. Далее проведем линии, параллельные каждой стороне треугольника с шагом Δ (вдоль стороны треугольника). В результате линии, образующие сетку, порождают равносторонние треугольники CΔ со стороной Δ. Узлы этой сетки порождают множество TΔ.
В дальнейшем, если не оговорено иное, считаем, что построена прямоугольная сетка. Здесь и далее d(s, t) – евклидово расстояние между точками s и t.
Пусть заданы (выбраны) G, r1, r2, k (k ≥ 1), Δ и построено TΔ. Рассмотрим следующие задачи.
Задача 1. Найти k-покрытие области G кругами заданных радиусов r1 и r2 с центрами в G таким образом, чтобы минимизировать суммарную площадь покрывающих кругов и определить расположение их центров в G.
Задача 2. Найти k-покрытие области G кругами заданных радиусов r1 и r2 таким образом, чтобы минимизировать суммарную площадь покрывающих кругов и определить расположение их центров при условии, что центры кругов располагаются в точках построенного множества TΔ и в каждой точке из TΔ находится не более одного центра круга.
Задача 3. Найти k-покрытие множества TΔ кругами заданных радиусов r1 и r2 таким образом, чтобы минимизировать суммарную площадь покрывающих кругов и определить расположение их центров при условии, что центры покрывающих кругов могут располагаться только в точках множества TΔ и в каждой точке из TΔ находится не более одного центра круга.
Сначала рассмотрим задачу 3.
Легко видеть, что для разрешимости задача 3 достаточно выполнения следующего условия:
(1)
$\begin{gathered} {\text{д л я }}\;{\text{л ю б о й }}\;{\text{т о ч к и }}\;{{t}_{j}}\;{\text{и з }}\;{{T}_{\Delta }}\;{\text{с у щ е с т в у е т }}\;{\text{н е }}\;{\text{м е н е е }}\;k--{\text{ }}1\;{\text{р а з л и ч н ы х }}\;{\text{т о ч е к }}\;{{t}_{i}},\;{{t}_{i}} \ne {{t}_{j}}, \\ {\text{и з }}\;{{T}_{\Delta }}\;{\text{т а к и х }},\;{\text{ч т о }}\;{\text{р а с с т о я н и е }}\;{\text{о т }}\;{{t}_{j}}\;{\text{д о }}\;{\text{н и х }}\;{\text{н е }}\;{\text{п р е в о с х о д и т }}\;{{r}_{2}}. \\ \end{gathered} $Построим математическую модель задачи 3. Считаем, что выбрана величина Δ и построено (конечное) множество TΔ. Введем коэффициенты aij и ai, n + j, 1 ≤ i, j ≤ n:
(2)
${{a}_{{ij}}} = \left\{ \begin{gathered} 1,\quad {\text{е с л и }}\quad d({{t}_{i}},{{t}_{j}}) \leqslant {{r}_{1}}, \hfill \\ 0,\quad {\text{е с л и }}\quad d({{t}_{i}},{{t}_{j}}) > {{r}_{1}}, \hfill \\ \end{gathered} \right.\quad {{a}_{{i,n + j}}} = \left\{ \begin{gathered} 1,\quad {\text{е с л и }}\quad d({{t}_{i}},{{t}_{j}}) \leqslant {{r}_{2}}, \hfill \\ 0,\quad {\text{е с л и }}\quad d({{t}_{i}},{{t}_{j}}) > {{r}_{2}},\quad 1 \leqslant i,j \leqslant n. \hfill \\ \end{gathered} \right.\quad$zi – число центров кругов радиуса r1, расположенных в точке ${{t}_{i}}$, $1 \leqslant i \leqslant n;$
${{z}_{{n + j}}}$ – число центров кругов радиуса r2, расположенных в точке ${{t}_{j}}$, $1 \leqslant j \leqslant n$.
При рассмотрении задач k-покрытия 2 и 3 очевидно, что в любой точке из TΔ не может быть более одного центра круга радиуса r1 или r2. Следовательно, имеем ограничения:
кроме того, запишем ограничения: Если выполняются ограничения (1) и минимизируется сумма площадей покрывающих кругов, то условие (4) излишне.Минимизация суммарной площади кругов заданных радиусов, обеспечивающих требуемое покрытие области G, состоит в минимизации суммы S = $\pi r_{1}^{2}({{z}_{1}} + \ldots + {{z}_{n}})$ + $\pi r_{2}^{2}({{z}_{{n + 1}}} + \ldots + {{z}_{{2n}}})$. Минимизация S равносильна минимизации величины $({{z}_{1}} + \ldots + {{z}_{n}})$ + ${{\left( {\frac{{{{r}_{2}}}}{{{{r}_{1}}}}} \right)}^{2}}({{z}_{{n + 1}}} + \ldots + {{z}_{{2n}}})$. Построим задачу
(5)
$({{z}_{1}} + \ldots + {{z}_{n}}) + {{\left( {\frac{{{{r}_{2}}}}{{{{r}_{1}}}}} \right)}^{2}}({{z}_{{n + 1}}} + \ldots + {{z}_{{2n}}}) \to {\text{min}}.$(6)
$\begin{array}{*{20}{c}} {{{a}_{{11}}}{{z}_{1}} + {{a}_{{12}}}{{z}_{2}} + \ldots + {{a}_{{1,2n}}}{{z}_{{2n}}} \geqslant {{k}_{1}},} \\ \cdots \\ {{{a}_{{n1}}}{{z}_{1}} + {{a}_{{n2}}}{{z}_{2}} + \ldots + {{a}_{{n,2n}}}{{z}_{{2n}}} \geqslant {{k}_{n}},} \end{array}$Построенная задача (5)–(7) является задачей k-покрытия точек конечного множества TΔ, при которой суммарная площадь покрывающих кругов минимальна. В результате имеем задачу 0–1 линейного программирования (ЛП) размерности 2n. Известно, что общая задача вида (5)–(7) является NP трудной задачей, см. [21]–[24].
Приведенное условие (1) разрешимости задачи 3, т.е. задачи (5)–(7), трудно проверить. Построим легко проверяемые достаточные условия разрешимости этой задачи для кратности покрытия, не превышающей 10, когда рассматриваются конкретные множества G.
Рассмотрим случай, когда G является квадратом, обозначим его через Q. На Q с шагом Δx = = Δy = Δ построим прямоугольную сетку. Для упрощения положим, что длина стороны квадрата делится нацело на величину Δ. Рассмотрим покрытие Q кругами радиуса r1 и r2. Для точки s обозначим через R(s) замкнутый круг радиуса r2 с центром в точке s. Пусть s является вершиной квадрата Q, следовательно, s совпадает с некоторой точкой из TΔ (см. фиг. 1). Тогда при r2 = Δ множество Q ∩ R(s), очевидно, содержит 3 различные точки из TΔ, а при радиусе r2 = $\Delta \sqrt 2 $ множество Q ∩ R(s) содержит 4 различные точки из TΔ и т.д. Для любой другой точки s из TΔ (не являющейся вершиной квадрата) число различных точек из TΔ, содержащихся в Q ∩ R(s), будет не меньше, чем для случая, когда s – вершина квадрата. Таким образом, должны выполняться: если $1 \leqslant k \leqslant 3$, то ${\Delta } \leqslant {{r}_{2}}$, если $1 \leqslant k \leqslant 4$, то ${\Delta } \leqslant {{r}_{2}}{\text{/}}\sqrt 2 $, если $1 \leqslant k \leqslant 6$, то ${\Delta } \leqslant {{r}_{2}}{\text{/}}2$, если $1 \leqslant k \leqslant 9$, то ${\Delta } \leqslant {{r}_{2}}{\text{/}}2\sqrt 2 $, если $1 \leqslant k \leqslant 11$, то ${\Delta } \leqslant {{r}_{2}}{\text{/}}3$.
Пусть область G является равносторонним треугольником ${{G}_{t}}$, тогда построим на ${{G}_{t}}$ косоугольную сетку, как указано выше. Пусть s является вершиной треугольника ${{G}_{t}}$, следовательно, s совпадает с некоторой точкой из TΔ. Тогда при r2 = Δ множество ${{G}_{t}} \cap R(s)$ содержит 3 различные точки из TΔ, а при радиусе ${{r}_{2}} = \sqrt 3 {\Delta }$ множество ${{G}_{t}} \cap R(s)$ содержит 4 различные точки из TΔ и т.п. Для любой другой точки s из TΔ (не обязательно являющейся вершиной треугольника) число различных точек из TΔ, содержащихся в ${{G}_{t}} \cap R(s)$, будет не меньше, чем для случая, когда s – вершина треугольника. Таким образом, должны выполняться: если $1 \leqslant k \leqslant 3$, то ${\Delta } \leqslant {{r}_{2}}$, если $1 \leqslant k \leqslant 4$, то ${\Delta } \leqslant {{r}_{2}}{\text{/}}\sqrt 3 $, если $1 \leqslant k \leqslant 6$, то ${\Delta } \leqslant {{r}_{2}}{\text{/}}2$, если $1 \leqslant k \leqslant 8$, то ${\Delta } \leqslant 2{{r}_{2}}{\text{/}}3\sqrt 3 $ и если $1 \leqslant k \leqslant 10$, то ${\Delta } \leqslant {{r}_{2}}{\text{/}}3$.
В результате имеем соотношения между кратностью покрытия, шагом построения сетки, радиусом покрывающих кругов и областью G. При выполнении указанных достаточных соотношений будет выполняться условие (1), следовательно, будет разрешима задача 3.
Рассмотрим задачу 2.
Пусть выбрана величина шага Δ, построена прямоугольная сетка и множество TΔ. Решая задачу (5)–(7), (т.е. задачу 3), мы получим k-покрытие множества TΔ, при котором суммарная площадь кругов (покрывающих TΔ) минимальна. При покрытии множества TΔ кругами заданных радиусов r1 и r2 не гарантируется покрытие исходного множества G. Сетка с шагом Δ на множестве G порождает квадраты, диагональ которых равна $\Delta \sqrt 2 $. Если при решении задачи 3 уменьшить величины радиусов r1 и r2 на половину указанной диагонали и решить задачу (5)–(7), то круги исходных радиусов r1 и r2 для полученного расположения кругов гарантированно покроют все множество G. Таким образом, приближенное решение задачи 2 можно получить, решая задачу 3 для TΔ с уменьшенными на $\alpha = \Delta \sqrt 2 {\text{/}}2$ величинами радиусов кругов, полагая затем, что найденные круги имеют радиусы r1 и r2. При этом для разрешимости задачи 2 записываем те же достаточные условия, что и для разрешимости 3, заменив в них величину r2 на r2 – α. Таким образом, для разрешимости задач 2 и 3 можно проверять условия (1) либо получать достаточные условия, как сделано выше.
В дальнейшем для указания чисел покрывающих кругов используем запись m1/m2, которая означает, что имеется m1 кругов радиуса r1 и m2 кругов радиуса r2.
Многочисленные вычислительные эксперименты показывают, что чем меньше величина Δ – шаг построения сетки, тем ближе результаты к оптимальному покрытию. Так, например, при покрытии единичного квадрата Q кругами радиусов 0.55 и 0.2 для Δ, последовательно равных 0.1, 0.05, 0.025, 0.0125 и 0.01 плотность (однократного) покрытия Q равна соответственно: 2.654, 1.829, 1.760, 1.704 и 1.454. Указанные плотности покрытия получены для чисел кругов, равных соответственно: 2/6, 1/7, 0/14, 1/6 и 1/4.
Решение задачи 2 считаем приближенным решением задачи 1.
2. ЭВРИСТИЧЕСКИЙ АЛГОРИТМ
С уменьшением величины шага сетки мы получаем более точное решение исходной задачи 2 или 3. Однако при этом растет размерность задачи и решение ее за приемлемое время становится проблематичным. Так как рассматриваемая задача NP трудная, то используются различные эвристические процедуры. В данной работе предлагается эвристический алгоритм решения задачи (5)–(7) для больших значений n. Для n ≤ 2000 нам удается решать задачу без эвристик. Для больших значений n (в некоторых случаях до n ≤ 14 000) мы решаем задачу с использованием следующего эвристического алгоритма. Сначала введем часто используемое понятие релаксированной и ядерной задач.
Релаксация широко используется в различных работах (см., например, [25], [26]). Пусть мы имеем некоторую задачу 0–1 ЛП, в которой переменные zi, 1 ≤ i ≤ m принимают значения только из множества {0, 1}. Под релаксацией этой задачи понимается та же задача, но в которой указанные условия целочисленности заменены условиями: 0 ≤ zi ≤ 1, 1 ≤ i ≤ m. Хорошо известно, что решение релаксированной задачи ЛП менее затратное по времени, чем решение исходной целочисленной задачи.
Построим ядерную задачу. Пусть решена релаксированная задача ЛП и среди ее решений $z_{j}^{*}$, $1 \leqslant j \leqslant m$, имеются нецелочисленные значения. Из переменных zj, $1 \leqslant j \leqslant m$, выбираем, положим, l переменных zj по некоторому критерию, например, для которых $z_{j}^{*}$ не меньше, чем остальные $z_{i}^{*}$. Таким образом, ядерная задача будет иметь только l переменных, которые считаем целочисленными. Ограничения ядерной задачи получаются из ограничений исходной задачи с учетом только выделенных переменных. Ядерная задача строится так, чтобы ее размерность позволяла решить построенную ядерную (целочисленную) задачу точными методами без эвристик и случайных процедур за приемлемое время. Введем следующий алгоритм.
Алгоритм 1
Шаг 1. В задаче (5)–(7) ограничения ${{z}_{j}} \in \left\{ {0,1} \right\}$, $1 \leqslant j \leqslant 2n$, заменяем на $0 \leqslant {{z}_{j}} \leqslant 1$, ${\text{1}} \leqslant j \leqslant 2n$.
Шаг 2. Решаем полученную на ш. 1 релаксированную задачу ЛП. Пусть $z_{j}^{*}$, $1 \leqslant j \leqslant 2n$ – решения релаксированной задачи.
Шаг 3. Если все значения $z_{j}^{*}$, $1 \leqslant j \leqslant 2n$, целочисленные, то задача решена, иначе идем к ш. 4.
Шаг 4. Для построения ядерной задачи выбираем среди переменных zj, 1 ≤ j ≤ 2n, 4q переменные следующим образом (q – заранее выбранное число):
• среди переменных zj, 1 ≤ j ≤ n, выбираем q переменных, для которых $z_{j}^{*}$ не меньше остальных $z_{i}^{*}$, 1 ≤ i ≤ n. Пусть выбрали переменные ${{z}_{{\text{v}1}}}, \ldots ,{{z}_{{\text{v}q}}}$, из ${{z}_{1}}, \ldots ,{{z}_{n}}$;
• к выбранным переменным добавляем переменные ${{z}_{{\text{v}1 + n}}}, \ldots ,{{z}_{{\text{v}q + n}}}$ и считаем их тоже выбранными переменными;
• среди невыбранных переменных выбираем еще q, q > 0, переменных, для которых $z_{j}^{*}$, n + 1 ≤ ≤ j ≤ 2n, не меньше остальных $z_{i}^{*}$, n + 1 ≤ i ≤ 2n. Пусть выбрали переменные ${{z}_{{w1 + n}}}, \ldots ,{{z}_{{wq + n}}}$;
• к выбранным переменным добавляем переменные ${{z}_{{w1}}}, \ldots ,{{z}_{{wq}}}$.
Часть переменных для выбора может оказаться равной 0, тем не менее, эти переменные следует учитывать. Выбор индексов из такого множества нулевых значений осуществляем согласно равномерному закону распределения случайной величины. В результате получаем 4$q$ переменных:
Шаг 5. Выбранные 4q переменных считаем переменными ядерной задачи. Ограничения ядерной задачи получаем из ограничений исходной задачи с учетом только выбранных переменных. Считаем, что переменные ядерной задачи принимают значения 0 либо 1.
Шаг 6. Решаем ядерную задачу точными методами и полученные решения принимаем за решения исходной задачи.
При расчетах мы полагали, что q = 300.
В литературе предлагаются различные процедуры выбора переменных для ядерной задачи. Мы выбираем переменные, состоящие из 4 блоков (частей). Это обусловлено особенностями задачи и отнесением части переменных к кругам одного радиуса, а других переменных – к кругам второго радиуса. Построенный таким образом алгоритм оказался результативным.
Проверка приемлемости данного алгоритма в работе осуществлялась следующим образом. Практически каждый раз задача решалась данным алгоритмом и точным методом (когда наш компьютер позволял найти такое решение). Всегда, когда получалось точное решение и решение с помощью предложенного алгоритма, числа покрывающих кругов оказывались одинаковыми. На основе многочисленных экспериментов считаем данный алгоритм приемлемым. Также проверка решения осуществлялась построением различных новых сеток на G и построением программы, которая проверяла, осуществляется ли требуемое покрытие узлов построенных новых сеток. Для различных сеток в рассмотренных случаях всегда осуществлялось требуемое покрытие.
3. ОГРАНИЧЕНИЯ НА РАССТОЯНИЯ МЕЖДУ ЦЕНТРАМИ КРУГОВ
В ряде случаев важно, чтобы центры покрывающих кругов не совпадали. Например, при проектировании навигационных систем или сенсорных сетей в одной точке не должно располагаться более одного устройства.
Пусть задано, что расстояние между центрами кругов радиуса r1 не должно быть меньше заданного числа q1. Для каждой точки ti из $T = \left\{ {{{t}_{1}},{{t}_{2}},...,{{t}_{n}}} \right\}$ положим, что pi равно числу точек tj из T, j ≠ i, для которых $d({{t}_{i}},{{t}_{j}}) < {{q}_{1}}$. Введем коэффициенты:
(8)
$\begin{gathered} {{b}_{{11}}}{{z}_{1}} + {{b}_{{12}}}{{z}_{2}} + \ldots + {{b}_{{1n}}}{{z}_{n}} \leqslant {{p}_{1}}, \\ {{b}_{{21}}}{{z}_{1}} + {{b}_{{22}}}{{z}_{2}} + \ldots + {{b}_{{2n}}}{{z}_{n}} \leqslant {{p}_{2}}, \\ \ldots \\ {{b}_{{n1}}}{{z}_{1}} + {{b}_{{n2}}}{{z}_{2}} + ... + {{b}_{{nn}}}{{z}_{n}} \leqslant {{p}_{n}}. \\ \end{gathered} $Пусть задано, что расстояние между центрами кругов радиуса r2 не должно быть меньше заданного числа q2. Положим, что величины fi, cij определяются так же, как и величины pi, bij, 1 ≤ i, j ≤ n, но с использованием q2 вместо q1. Тогда условия, что расстояния между центрами кругов радиуса r2 должны быть не меньше заданного числа q2, запишутся в виде
(9)
$\begin{gathered} {{c}_{{11}}}{{z}_{{n + 1}}} + {{c}_{{12}}}{{z}_{{n + 2}}} + ... + {{c}_{{1n}}}{{z}_{{2n}}} \leqslant {{f}_{1}}, \\ {{c}_{{21}}}{{z}_{{n + 1}}} + {{c}_{{22}}}{{z}_{{n + 2}}} + ... + {{c}_{{2n}}}{{z}_{{2n}}} \leqslant {{f}_{2}}, \\ \ldots \\ {{c}_{{n1}}}{{z}_{{n + 1}}} + {{c}_{{n2}}}{{z}_{{n + 2}}} + ... + {{c}_{{nn}}}{{z}_{{2n}}} \leqslant {{f}_{n}}. \\ \end{gathered} $Далее, пусть задано, что расстояние между центрами кругов радиусов r1 и r2 не должно быть меньше заданного числа q3. Положим, что величины gi, eij, $1 \leqslant i,j \leqslant n$, определяются, как и величины pi, ${{b}_{{ij}}}$, ${\;}1 \leqslant i,j \leqslant n$, но с использованием q3 вместо q1. Также введем: ${{h}_{{i,n + i}}} = {{g}_{i}}$; ${{h}_{{ij}}} = 0$, ${\text{1}} \leqslant i \leqslant n$, $n + {\text{1}} \leqslant j \leqslant {\text{2}}n$, $j \ne i$. Тогда ограничения, что расстояние между центрами кругов радиусов r1 и r2 не меньше заданного числа q3 запишутся в виде (см. [27], [28])
(10)
$\begin{gathered} \left( {\begin{array}{*{20}{c}} {{{e}_{{11}}}}&{{{e}_{{12}}}}&{...}&{{{e}_{{1n}}}}&{{{h}_{{i,n + 1}}}}&0&{...}&0 \\ {{{e}_{{21}}}}&{{{e}_{{22}}}}& \ldots &{{{e}_{{2n}}}}&0&{{{h}_{{i,n + 2}}}}&{...}&0 \\ {}&\quad&\quad&\quad&\quad&\quad&\quad&\quad \\ {{{e}_{{n1}}}}&{{{e}_{{n2}}}}& \ldots &{{{e}_{{nn}}}}&0&0&{...}&{{{h}_{{i,n + n}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{z}_{1}}} \\ {{{z}_{2}}} \\ {...} \\ {{{z}_{{2n}}}} \end{array}} \right) \leqslant \left( {\begin{array}{*{20}{c}} {{{g}_{1}}} \\ {{{g}_{2}}} \\ {...} \\ {{{g}_{n}}} \end{array}} \right). \hfill \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \hfill \\ \end{gathered} $В случае когда q1 = q2 = q3 в ограничениях (9) и (10) полагаем, что: pi = fi = gi, 1 ≤ i ≤ n; ${{b}_{{ij}}} = {{c}_{{ij}}} = {{e}_{{ij}}}$, ${\text{1}} \leqslant i,j \leqslant n$. Указанные ограничения (8), (9) и (10) можно вводить либо все одновременно, либо те из них, которые необходимы для рассматриваемой задачи. В каждом из рассмотренных вариантов получаем задачу 0–1 ЛП.
При введении ограничений на расстояние между центрами кругов задача может оказаться неразрешимой. Например, для 3-покрытия равностороннего треугольника со стороной c, очевидно, нельзя требовать, чтобы расстояние между центрами кругов было более c, ибо тогда центры кругов будут вне треугольника. Считаем, что ограничения введены с учетом разрешимости задач.
4. НАХОЖДЕНИЕ НИЖНИХ ОЦЕНОК ПЛОТНОСТЕЙ ПОКРЫТИЙ ДЛЯ НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЕВ
Пусть задана область G, круги радиусов r1, r2, r1 > r2 и кратность покрытия k, 1 ≤ k ≤ 4. Среди всевозможных k-покрытий рассматриваем только те оптимальные (с минимальной суммарной площадью покрывающих кругов) покрытия, у которых минимальные расстояния между центрами кругов не меньше заданной величины λ, λ > 0. Считаем, что такие оптимальные покрытия существуют, либо должны быть найдены некоторым методом. Именно для таких покрытий отыскиваем нижнюю оценку плотности покрытия. Положим, что центры кругов радиусов r1 и r2 находятся в точках c1, …, cm, m > 1; C = $\{ {{c}_{1}}, \ldots ,{{c}_{m}}\} $, ${{c}_{i}} \in G$, $1 \leqslant i \leqslant m$, круги с центрами в C образуют требуемое оптимальное покрытие и выполняется условие
Выберем ${\Delta } \leqslant \lambda {\text{/}}3$ и построим множество ${{T}_{{\Delta }}} = \{ {{t}_{1}},{{t}_{2}}, \ldots ,{{t}_{n}}\} $, $\quad{{t}_{i}} \in G$, $1 \leqslant i \leqslant n$, $n \geqslant k$. Если точка ci из C совпадает с некоторой точкой tj из TΔ, то в силу (11) нет других точек из C \$\{ {{c}_{i}}\} $ совпадающих с tj. Если ci не совпадает с точкой из TΔ, то сдвинем ее к ближайшей tj из TΔ, в которой нет точки из C. Ближайшая к ci точка из TΔ находится на расстоянии, не превышающем $\alpha = {\Delta }\sqrt 2 {\text{/}}2$. Построим круг K с центром в tj и радиусом $3\Delta {\text{/}}2 - {\varepsilon }$, $0 < {\varepsilon } \leqslant 0.01\Delta $. Так как диаметр круга K меньше λ, то в $C{\backslash }\{ {{c}_{i}}\} $ нет других точек из C, которые можно переместить в tj сдвигом, не превышающим величину α. Таким образом, каждую точку из C можно сдвигом, не превышающим α, переместить в точку tj из TΔ, при этом в любую точку tj перемещается не более одной точки из C.
Кроме указанных сдвигов точек, увеличим радиусы покрывающих кругов на величину α. Совокупность кругов радиусов r1 и r2 с центрами в C образовали требуемое оптимальное покрытие G. Пусть при этом имеется $n_{1}^{0}$ кругов радиуса r1 и $n_{2}^{0}$ кругов радиуса r2. Тогда плотность оптимального покрытия равна ${{P}_{0}}({{r}_{1}},{{r}_{2}}) = (n_{1}^{0}r_{1}^{2} + n_{2}^{0}r_{2}^{2})\tau $, где $\tau = \pi {\text{/}}S(G)$ и S(G) – площадь множества G.
После смещения центров кругов в точки TΔ и увеличения их радиусов на α они образуют k-покрытие G, следовательно, и k-покрытие TΔ. Положим, что $P_{\alpha }^{\# } = (n_{1}^{0}{{({{r}_{1}} + \alpha )}^{2}} + n_{2}^{0}{{({{r}_{2}} + \alpha )}^{2}})\tau $. Решим задачу 3 k-покрытия TΔ кругами радиусов ${{r}_{1}} + \alpha $, ${{r}_{2}} + \alpha $. В результате получим n1 кругов радиуса r1 + α и n2 кругов радиуса r2 + α. Важно, что n1 и n2 найдены в отличие от неизвестных величин $n_{1}^{0}$ и $n_{2}^{0}$. Введем $P_{{\alpha ,{\text{о п т }}}}^{\# } = [{{n}_{1}}{{({{r}_{1}} + \alpha )}^{2}} + {{n}_{2}}{{({{r}_{2}} + \alpha )}^{2}}]\tau $. Очевидно, что $P_{\alpha }^{\# } - P_{{\alpha ,{\text{о п т }}}}^{\# } \geqslant 0$.
Пусть ${{m}_{1}} = n_{1}^{0} - {{n}_{1}}$, ${{m}_{2}} = n_{2}^{0} - {{n}_{2}}$. Тогда из $P_{\alpha }^{\# } - P_{{\alpha ,{\text{о п т }}}}^{\# } \geqslant 0$ получим
Введем новую величину $P_{*}^{\# }({{r}_{1}},{{r}_{2}}) = ({{n}_{1}}r_{1}^{2} + {{n}_{2}}r_{2}^{2})\tau $, где n1 и n2 найдены при решении задачи 3. Для краткости положим, что PN = $P_{*}^{\# }\left( {{{r}_{1}},{{r}_{2}}} \right)$. Теперь будем исследовать разность B = ${{P}_{0}}({{r}_{1}},{{r}_{2}}) - $ $ - \;P_{*}^{\# }({{r}_{1}},{{r}_{2}}) = ({{m}_{1}}r_{1}^{2} + {{m}_{2}}r_{2}^{2})\tau $ при различных возможных значениях m1 и m2.
а) Если m1 = m2 = 0, то $n_{1}^{0} = {{n}_{1}}$, $n_{2}^{0} = {{n}_{2}}$ и B = 0.
б) Если m1 = 0 либо m2 = 0, то из (12) получаем, что ${{m}_{2}} \geqslant 0$ либо ${{m}_{1}} \geqslant 0$ соответственно и $B \geqslant 0$, следовательно:
в) Рассмотрим случай m1 > 0, когда при решении задачи 3 число больших кругов уменьшается на некоторую величину p, p > 0. Число малых кругов изменяется на некоторую величину q, ${{n}_{2}} = n_{2}^{0} + q$ ($q \leqslant 0$ или q > 0). Тогда из (12) получаем $[p{{({{r}_{1}} + \alpha )}^{2}} - q{{({{r}_{2}} + \alpha )}^{2}}] \geqslant 0$. При этом $B = [pr_{1}^{2} - qr_{2}^{2}]\tau $. Если $q \leqslant 0$, то, очевидно, $B \geqslant 0$ и выполняется (13). Пусть q > 0, тогда $q \leqslant p{{\left( {\frac{{{{r}_{1}} + \alpha }}{{{{r}_{2}} + \alpha }}} \right)}^{2}}$. Если допустить, что при этом B < 0, то $pr_{1}^{2} - qr_{2}^{2} < 0$ и $q > p\frac{{r_{1}^{2}}}{{r_{2}^{2}}}$. Одновременно неравенства $q \leqslant p{{\left( {\frac{{{{r}_{1}} + \alpha }}{{{{r}_{2}} + \alpha }}} \right)}^{2}}$ и $q > p\frac{{r_{1}^{2}}}{{r_{2}^{2}}}$ не могут выполняться при любом $\alpha \geqslant 0$, тогда допущение B < 0 неверно, следовательно, $B \geqslant 0$ и выполняется (13).
г) Рассмотрим случай m1 < 0. Тогда при решении задачи 3 число больших кругов увеличилось на некоторое число p > 0. Если число малых кругов не изменилось, то m2 = 0 и из б) получим выполнение (13). Число кругов радиуса r1 и число кругов радиуса r2 не могут увеличиться одновременно. Пусть при увеличении числа больших кругов число малых кругов уменьшится на некоторую величину q > 0. Тогда из (12) получаем
(14)
$(n_{1}^{0} - (n_{1}^{0} + p)){{({{r}_{1}} + \alpha )}^{2}} + (n_{2}^{0} - (n_{2}^{0} - q)){{({{r}_{2}} + \alpha )}^{2}} = - p{{({{r}_{1}} + \alpha )}^{2}} + q{{({{r}_{2}} + \alpha )}^{2}} \geqslant 0.$(15)
$p > q{{\left( {\frac{{{{r}_{2}}}}{{{{r}_{1}}}}} \right)}^{2}}\quad {\text{и }}\quad p \leqslant q{{\left( {\frac{{{{r}_{2}} + \alpha }}{{{{r}_{1}} + \alpha }}} \right)}^{2}},$
В этом случае B < 0 и нижняя оценка для ${{P}_{0}}({{r}_{1}},{{r}_{2}})$ не найдена. Если указанные p и q не существуют, то допущение B < 0 неверно и выполняется (13).
Таким образом, в некоторых случаях нижняя оценка для ${{P}_{0}}({{r}_{1}},{{r}_{2}})$ не найдена (выполняются оба неравенства (15)). Если неравенства (15) не выполняются, то допущение, что B < 0 не имеет места и выполняется (13).
Рассмотрим частные случаи покрытия.
Пусть Q – единичный квадрат и требуется покрыть его кругами радиусов r1 = 0.55 и r2 = 0.30. Выберем α = 0.01 и ${\Delta } = 0.01\sqrt 2 $. Решив задачу 3, получим n1 = 0, n2 = 6. Тогда, очевидно, что ${{m}_{1}} \geqslant 0$. Для m1 = 0 согласно б) получаем (13), а при m1 > 0 из в) следует (13). В результате нижней оценкой P0(0.55, 0.30) является $P_{*}^{\# }(0.55,\quad0.30) = 1.696$.
Рассмотрим второй частный случай однократного покрытия Q кругами радиусов r1 = 0.55 и r2 = 0.25. Выбрав α = 0.04, ${\Delta } = 0.04\sqrt 2 $ и решив задачу 3, получим n1 = 0, n2 = 7. Тогда ${{m}_{1}} = n_{1}^{0}$, т.е. ${{m}_{1}} \geqslant 0$ далее, используя б) и в), получаем (13) и нижняя оценка для P0(0.55, 0.25) равна 1.374. Отметим, что полученные расположения 7 кругов радиуса 0.29 покрывают все множество TΔ, но не покрывают все Q. Выберем новые значения α = 0.01 и ${\Delta } = 0.01\sqrt 2 $. Решив задачу 3, получим n1 = 1, n2 = 4. Для возможных значений m1 = 0 или m1 > 0 выполняется (13), см. б) и в). Для возможного варианта m1 < 0 рассмотрим p и q, которые должны быть целыми числами больше нуля, см. г). Для q = 1 получим интервал I1 = (0.020661; 0.21556]. Можно убедиться, что I14 = (2.8924; 3.0178] содержит целое значение p = 3, а при q < 14 интервал Iq не содержит целых значений p. Величина p не должна превосходить n1, равного единице, следовательно, неравенства (15) не выполняются для приемлемых значений p и q, тогда выполняется (13) и нижней оценкой P0(0.55, 0.25) является $P_{*}^{\# }(0.55,0.25) = 1.735$. В результате, выбрав меньшие значения α и Δ, получим новую оценку плотности покрытия, равную 1.735, которая больше ранее полученной величины 1.374.
Рассмотрим третий частный случай. Требуется двукратно покрыть Q кругами радиусов r1 = 0.55 и r2 = 0.25. Положив α = 0.0125, ${\Delta } = 0.0125\sqrt 2 $ и решив задачу 3, получим n1 = 0, n2 = 16. Далее получаем, что нижняя оценка для плотности 2-покрытия равна 3.141. Если вместо указанных α = 0.0125 и ${\Delta } = 0.0125\sqrt 2 $ выбрать α = 0.01 и ${\Delta } = 0.01\sqrt 2 $, то, решив задачу 3, получим n1 = 1, n2 = 12. Далее, как и для второго частного случая, в частности, используя интервал I1 = (0.20661; 0.21556), убеждаемся, что выполняется (13) и нижняя оценка плотности 2-покрытия равна 3.306. Эта оценка больше, чем выше полученная величина 3.141, следовательно, уменьшая α и Δ, улучшаем оценку.
Аналогичные вычисления проводились для различных значений r1 и r2, укажем эти результаты в табл. 1. Задача 3 для получения нижних оценок плотности покрытий в данной работе решалась без привлечения эвристик. Как указано выше, нижняя оценка плотности покрытия в некоторых случаях может быть не найдена. В представленных численных расчетах такие случаи не выявлены.
Таблица 1.
Покрытие квадрата для заданных радиусов и кратностей покрытия
| Радиусы кругов r1/r2 | Кратность покрытия k | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| Приближенные нижние оценки (PN) плотностей покрытия и соответству-ющие им числа кругов | Полученные значения плотности покрытия и соответству-ющие им числа кругов | Приближенные нижние оценки (PN) плотностей покрытия и соответству-ющие им числа кругов | Полученные значения плотности покрытия и соответству-ющие им числа кругов | Приближенные нижние оценки (PN) плотностей покрытия и соответству-ющие им числа кругов | Полученные значения плотности покрытия и соответству-ющие им числа кругов | |
| 0.55/0.30 | 1.696 0/6 |
1.697 0/6 |
3.110 0/11 |
3.393 0/12 |
5.089 0/18 |
5.475 1/16 |
| 0.55/0.25 | 1.735 1/4 |
1.735 1/4 |
3.307 1/12 |
3.472 2/8 |
4.617 3/9 |
5.208 3/12 |
| 0.55/0.20 | 1.452 1/4 |
1.453 1/4 |
2.906 2/8 |
2.906 2/8 |
4.162 2/18 |
4.359 3/12 |
| 0.45/0.30 | 1.696 0/6 |
1.697 0/6 |
3.110 0/11 |
3/393 0/12 |
4.595 1/14 |
5.019 3/11 |
| 0.45/0.25 | 1.570 0/8 |
1.618 1/5 |
3.142 0/16 |
3.236 2/10 |
4.516 0/23 |
4.854 3/15 |
| 0.45/0.20 | 1.256 0/10 |
1.760 0/14 |
2.780 2/12 |
3.142 0/25 |
4.021 0/32 |
4.776 0/38 |
| 0.35/0.30 | 1.539 4/0 |
1.697 0/6 |
2.953 4/5 |
3.393 0/12 |
4.390 7/6 |
5.113 3/14 |
| 0.35/0.25 | 1.539 4/0 |
1.736 4/1 |
2.898 6/3 |
3.472 8/2 |
4.438 10/3 |
5.207 12/3 |
| 0.35/0.20 | 1.523 2/6 |
1.524 2/6 |
2.796 4/10 |
3.048 4/12 |
4.178 4/21 |
4.572 6/18 |
5. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
Рассмотрим покрытие единичного квадрата Q кругами заданных радиусов r1 и r2 таким образом, чтобы минимизировать суммарную площадь покрывающих кругов и определить расположение их центров при условии, что центры покрывающих кругов могут находиться только в точках множества TΔ. Для решения задач покрытия была разработана программа с использованием библиотеки CPLEX-12.6. Для заданных радиусов r1 и r2 программа строит релаксированную и ядерную задачи, решает построенные задачи и выдает результаты счета, в том числе и в графическом виде.
Результаты покрытия Q кругами радиусов r1 и r2 приведены в табл. 1, где указываются выбранные значения радиусов r1 и r2; кратность покрытия k; приближенные нижние оценки плотностей покрытия, т.е. величина PN = $P_{*}^{\# }({{r}_{1}},{{r}_{2}})$ и соответствующие значения чисел кругов радиусов r1 и r2; вычисленные значения плотности покрытия квадрата Q кругами радиусов r1 и r2 и соответствующие значения чисел кругов. Косая используется для разделения одной величины от другой. Все нижние оценки в табл. 1 записаны курсивом.
Из табл. 1 видно, что в некоторых случаях числа кругов, полученные для оценок плотностей, и вычисленные значения чисел кругов для k-покрытия совпадают, следовательно, результаты покрытий в этих случаях не улучшаемы.
Как уже отмечено, чем меньше величина Δ шага построения сетки, тем ближе результат к оптимальному значению. Для случая двукратного покрытия единичного квадрата Q кругами радиусов 0.55 и 0.25 были проведены расчеты нижней оценки плотности покрытия Q при различных значениях Δ: 0.04, 0.02 и 0.01. Для этих значений Δ нижняя оценка плотности покрытия равна 2.717, 3.078 и 3.306, соответственно при числах кругов 1/9, 2/6 и 1/12. Вычисленное значение плотности 2-покрытия квадрата Q кругами радиусов r1 и r2 для этого случая равно 3.472 при числах кругов 2/8. Следовательно, оптимальное значение плотности будет между числами 3.306 и 3.472.
Сравнительный анализ результатов проводился с использованием известных результатов по покрытиям единичного квадрата из работ [1], [2], [4], [8], [10], [11], [15], [18], [19].
При однократном покрытии кругами только одного из двух радиусов, плотность покрытия, как правило, минимальна, если выбрать наименьший из радиусов, то есть r2. Например, при радиусе r2 = 0.25 требуется 9 кругов для покрытия Q, которые дают плотность покрытия, равную 1.767. В данной работе получено, что использование кругов двух радиусов r1 = 0.55 и r2 = 0.25, или r1 = 0.45 и r2 = 0.20, или r1 = 0.35 и r2 = 0.25 позволяет уменьшить плотность покрытия (см. табл. 1). Также см. случай r1 = 0.35 и r2 = 0.20. Следовательно, использование кругов двух радиусов в ряде случаев уменьшает плотность покрытия.
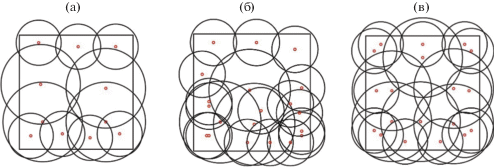
Покрытия квадрата для радиусов 0.35 и 0.20 при кратностях покрытия 1, 2 и 3 приведены на фиг. 2. Для кратности k = 1 приведен результат для случая, когда число кругов радиуса r1 фиксировано и равно 2.
Фиг. 2.
Покрытие квадрата кругами радиусов 0.35 и 0.20 при кратностях покрытия: (a) k = 1, m1 = 2; (б) k = 2 и (в) k = 3.

Рассмотрим покрытие, в котором нижняя половина квадрата Q (координаты y которых меньше или равны 0.5) покрывается с заданной кратностью k1, а верхняя часть Q покрывается с кратностью k2. Результаты для такого покрытия с переменной кратностью приведены в табл. 2, где приняты такие же обозначения, что и в табл. 1. На фиг. 3 приведены покрытия квадрата с переменной кратностью для радиусов кругов r1 = 0.35 и r2 = 0.20. На фиг. 3a кратность покрытия нижней половины квадрата равна k1 = 2, а верхней половины квадрата равна k2 = 1, на фиг. 3б k1 = 3, k2 = 1, на фиг. 3в k1 = 3, k2 = 2.
Таблица 2.
Покрытие квадрата с заданной переменной кратностью
| Радиусы кругов r1/r2 | Кратности покрытия k1 и k2 | |||||
|---|---|---|---|---|---|---|
| k1 = 2, k2 = 1 | k1 = 3, k2 = 1 | k1 = 3, k2 = 2 | ||||
| Числа кругов m1/m2 | Плотность покрытия | Числа кругов m1/m2 | Плотность покрытия | Числа кругов m1/m2 | Плотность покрытия | |
| 0.35/0.30 | 3/5 | 2.569 | 5/6 | 3.621 | 6/7 | 4.289 |
| 0.35/0.25 | 7/1 | 2.891 | 10/1 | 4.045 | 11/2 | 4.626 |
| 0.35/0.20 | 4/7 | 2.420 | 3/17 | 3.291 | 6/13 | 3.943 |
| 0.35/0.15 | 2/22 | 2.325 | 4/22 | 3.095 | 5/26 | 3.763 |
| 0.35/0.10 | 3/36 | 2.286 | 5/35 | 3.024 | 5/58 | 3.747 |
Фиг. 3.
Покрытие квадрата кругами радиусов 0.35 и 0.20 при кратностях покрытия: (a) k1 = 2, k2 = 1, (б) k1 = 3, k2 = 1 и (в) k1 = 3, k2 = 2.
Покрытия квадрата кругами радиусов r1 и r2 с ограничениями на расстояние между их центрами можно осуществлять при разных вариантах ограничений, например, когда расстояния между центрами кругов радиуса r1 не меньше величины a $({{d}_{{r1 - r1}}}({{c}_{i}},{{c}_{j}}) \geqslant a,\;i \ne j)$, либо заданы ограничения на расстояния между центрами кругов радиуса r2$({{d}_{{r2 - r2}}}({{c}_{i}},{{c}_{j}}) \geqslant a,\;i \ne j)$, либо заданы ограничения на расстояния между центрами кругов радиусов r1 и r2$({{d}_{{r1 - r2}}}({{c}_{i}},{{c}_{j}}) \geqslant a,\;i \ne j)$, либо заданы ограничения на расстояния между центрами любых кругов радиусов r1 и r2$({{d}_{{{\text{all}}}}}({{c}_{i}},{{c}_{j}}) \geqslant a,\;i \ne j)$.
На фиг. 4а–г приведены однократные покрытия квадрата кругами радиусов 0.35 и 0.20 с ограничениями на расстояния между центрами. На фигуре для каждого варианта покрытия указано ограничение между центрами кругов и полученные плотности покрытия. На фиг. 4а расстояние между центрами кругов радиуса r1 ограничено величиной 0.4, на фиг. 4б расстояние между центрами кругов радиуса r2 ограничено величиной 0.4, на фиг. 4в расстояние между центрами кругов радиусов r1 и r2 ограничено величиной 0.4, на фиг. 4г расстояние между любыми центрами покрывающих кругов ограничено величиной 0.4.
Фиг. 4.
Покрытия квадрата при наличии ограничений на расстояния между центрами покрывающих квадратов: (a) ${{d}_{{r1 - r1}}}({{c}_{i}},{{c}_{j}}) \geqslant 0.4$, p = 1.650, (б) ${{d}_{{r2 - r2}}}({{c}_{i}},{{c}_{j}}) \geqslant 0.4$, p = 1.791, (в) ${{d}_{{r1 - r2}}}({{c}_{i}},{{c}_{j}}) \geqslant 0.4$, p = 1.658, (г) ${{d}_{{{\text{all}}}}}({{c}_{i}},{{c}_{j}}) \geqslant 0.4$, p = 1.791, (д) ${{d}_{{r1 - r1}}}({{c}_{i}},{{c}_{j}}) \geqslant 0.4$, p = 3.550, (е) ${{d}_{{{\text{all}}}}}({{c}_{i}},{{c}_{j}}) \geqslant 0.2$, p = 3.320.

На фиг. 4д и 4е приведены полученные двукратные покрытия квадрата кругами радиусов 0.35 и 0.20, когда расстояние между центрами кругов радиусов r1 не меньше 0.4 (фиг. 4д) и когда расстояние между любыми центрами кругов не меньше 0.2 (фиг. 4е).
Расчеты проводились на компьютере Intel Core i7-3537U, 2.5GHz с оперативной памятью 6 Гб и установленной операционной системой Windows 10. Время счета каждого из приведенных результатов равнялось 1–3 мин. Полагая, что задачи покрытия для многих приложений решаются заранее, а не в режиме онлайн, считаем, что время решения приемлемо.
При исследовании построенных задач 0–1 ЛП можно использовать субградиентные и другие методы, см., например, работы [25], [26] и библиографию в них. Важно, что предложенный в данной работе подход является простым и результативным. Полученные численные результаты демонстрируют эффективность метода для различных вариантов задач k-покрытий.
ЗАКЛЮЧЕНИЕ
Предложен численный подход, позволяющий находить приближенное решение задачи k-покрытия кругами двух заданных радиусов ограниченных областей G. Метод позволяет находить покрытия частей области G с заданной кратностью для каждой части так, чтобы суммарная площадь покрывающих кругов была наименьшей. Рассмотрены варианты введения ограничений на расстояния между центрами покрывающих кругов. Для некоторых частных случаев покрытий найдены приближенные нижние границы плотностей k-покрытия заданной области. В каждом из указанных случаев задача покрытия сводится к задаче 0–1 ЛП. Для больших размерностей задач предлагается использовать релаксацию, затем построение и решение ядерных задач существенно меньшей размерности.
Данный метод, с построением сетки на G, можно распространить на случай покрытия в пространствах трех и более измерений. При решении задачи покрытия кругами одного радиуса мы получаем задачу 0–1 ЛП размерности n × n, где n – число узлов построенной на G сетки. При покрытии G шарами s разных (фиксированных) радиусов размерность задачи 0–1 ЛП будет равна (s × n) × n, не учитывая ограничения на расстояния между центрами шаров. Для решения таких задач требуются большие затраты машинного времени или иные методы решения задач 0–1 ЛП больших размерностей.
Авторы выражают искреннюю благодарность рецензенту за замечания и полезные рекомендации, позволившие значительно улучшить работу.
Список литературы
Брусов В.С., Пиявский С.А. Вычислительный алгоритм оптимального покрытия плоских областей // Ж. вычисл. матем. и матем. физ. 1971. Т. 11. № 2. С. 304–312.
Drezner Z. Facility location: A survey of applications and methods. NY: Springer, 1995. P. 571.
Erzin A., Astrakov S. // Min-density stripe covering and applications in sensor networks. Lect. Notes Comput. Sci., 6784, Berlin: Springer, 2011. P. 152–162.
Melissen J.B.M., Schuur P.C. Improved coverings of a square with six and eight equal circles // Electron. J. Combin. 1996. V. 3. № 32. P. 10 (electronic).
Melissen J.B.M. Loosest circle coverings of an equilateral triangle // Math. Mag. 1997. V. 70. P. 119–125.
Melissen J.B.M., Schuur P.C. Covering a rectangle with six and seven circles // Discrete Appl. Math. 2000. V. 99. P. 149–156.
Nurmella K.J. Conjecturally optimal coverings of an equilateral triangle with up to 36 equal circles // Exp. Math. 2000. V. 9. № 2. P. 241–250.
Nurmella K.J., Östergard P.R.J. Covering a square with up to 30 equal circles // Research report A62 Laboratory for Technology Helsinki University. 2000. http://www.tcs.hut.fi/Publications/reports.
Nurmela K.J. Covering a circle by congruent circular discs. Preprint, Department of Computer Sci. and Engng, Helsinky University of Technology. 1998.
Suzuki A., Drezner Z. The minimum number equitable radius location problems with continuous demand // European Journal of Operational Research. 2009. P. 17–30.
Tarnai T., Gaspar Z. Covering a Square by Equal Circles // Elemente der Math. 1995. V. 50. № 4. P. 167–170.
Ильев В.П., Ильева С.Д., Навроцкая А.А. Приближенное решение задачи о р-медиане на минимум // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 9. С. 1614–1621.
Fejes Tóth G. Multiple packing and covering of the plane with circles // Acta Math. Acad. Sci. Hungar. 1976. V. 27. № 1–2. P. 135–140.
Fejes Tóth G. Covering the plane with two kinds of circles // Discrete Comput. Geometry. 1995. V. 13. № 3. P. 445–457.
Ammari Y.M. Challenges and Opportunities of Connected k-Covered Wireless Sensor Networks. Berlin: Spinger, 2009. P. 342.
Астраков С.Н., Ерзин А.И., Залюбовский В.В. Сенсорные сети и покрытие плоскости кругами // Дискретный анализ и исследование операций. 2009. Т. 16. № 3. С. 3–19.
Kumar S., Lai T.H., Balogh J. On k-coverage in a mostly sleeping sensor network. In: Proc. ACM MobiCom. 2004. P. 144–158.
Галиев Ш.И., Карпова М.А. Оптимизация многократного покрытия ограниченного множества кругами // Ж. вычисл. матем. и матем. физ. 2010. Т. 50. № 7. С. 757–769.
Галиев Ш.И., Хорьков А.В. Многократные покрытия кругами равностороннего треугольника, квадрата и круга // Дискретный анализ и исследование операций. 2015. Т. 22. № 6. С. 5–28.
Krishnendu Chakrabarty, S Sitharama Iyengar, Hairong Qi, Eungchun Cho. Grid Coverage for Surveillance and Target Location in Distributed Sensor Networks // IEEE Transactions on Computers. V. 51. № 12. P. 1448–1458.
Garey M.R., Jonson D.S. Computers and Intractability: A Guide to the Theory of NP-completeness. 1979. W.H. Freeman. San Francisco.
Culberson J.C. Reckhow R/A. Covering polygons is hard // J. Algorithms. 1994. V. 17. P. 2–44.
Кузюрин Н.Н. О сложности построения асимптотически оптимальных покрытий и упаковок // Докл. РАН. 1998. Т. 363. № 1. С. 11–13.
Еремеев А.В., Заозерская Л.А., Колоколов А.А. Задача о покрытии множества: сложность, алгоритмы, экспериментальные исследования // Дискретный анализ и исследование операций. 2009. Т. 7. № 2. С. 22–46.
Bertsimas D., Vohra R. Rounding algorithms for covering problems // Math. Program. 1998. V. 80. P. 63–89.
Umetani S., Yagiura M. Relaxation heuristics for the set covering problem // J. the Operat. Research Soc. of Japan. 2007. V. 50. № 4. P. 350–375.
Galiev Sh.I., Lisafina M.S. Linear models for the approximate solution of the problem of packing equal circles into a given domain // European Journal of Operat. Research. 2013. V. 230. P. 505–514.
Галиев Ш.И., Лисафина М.С. Численные методы оптимизации упаковок равных ортогонально ориентированных эллипсов в прямоугольную область // Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 11. С. 1748–1762.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики