Журнал вычислительной математики и математической физики, 2019, T. 59, № 4, стр. 707-715

ВВЕДЕНИЕ

Податливые поверхности стали объектом довольно пристального внимания с ранних экспериментов [1], в которых было показано, что значительное затягивание процесса ламинарно-турбулентного перехода может быть достигнуто путем замены жесткой поверхности на деформируемую. Теоретическое изучение данного вопроса наталкивается на немалые трудности из-за сложности уравнений, описывающих взаимодействие течения с податливой поверхностью. Значительного упрощения можно добиться на базе концепции свободно взаимодействующего пограничного слоя (см. [2]–[4]), справедливой при высоких числах Рейнольдса. Эта концепция успешно применялась в ряде работ (см. [5] – для несжимаемого пограничного слоя, [6] и [7] – для пограничного слоя при трансзвуковых скоростях внешнего потока, [8] – для сверхзвукового пограничного слоя, [9] и [10] – для течения в плоском канале, [11] – для течения в круглой трубе), однако в большинстве из них учитывалась только упругость податливой поверхности и игнорировались ее продольное натяжение, изгибная жесткость и инерционность. В работах [8] и [11] был выявлен дестабилизирующий характер влияния инерционности податливой поверхности на течение в круглой трубе и сверхзвуковом пограничном слое соответственно. В данной работе изучается влияние инерционности податливой поверхности на течение в несжимаемом пограничном слое.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим обтекание податливой пластины равномерным потоком несжимаемой жидкости плотности $\rho _{\infty }^{*}$ и вязкости $\mu _{\infty }^{*}$ со скоростью $U_{\infty }^{*}$. Введем ортогональную систему координат, поместив ее начало на некотором расстоянии $L{\text{*}}$ от передней кромки и направив ось $х {\text{*}}$ вниз по потоку. Введем малый параметр $\varepsilon = {{R}^{{ - 1/8}}}$, считая число Рейнольдса $R = \rho _{\infty }^{*}U_{\infty }^{*}L{\text{*/}}\mu _{\infty }^{*}$ очень большим.

Пусть в течение вносится возмущение, вызванное локальной деформацией стенки. Будем считать, что характерные размеры двумерного возмущенного течения таковы, что оно описывается трехпалубной теорией свободного взаимодействия (см. [2]–[4]). Тогда в пределе $R \to \infty $ вся область течения распадается на три характерные подобласти: основную толщу пограничного слоя (где $y*\sim L{\text{*}}{{R}^{{ - 1/2}}}$), узкий пристеночный слой толщины $\Delta y*\sim L{\text{*}}{{R}^{{ - 5/8}}}$ и область потенциального внешнего потока (где $y*\sim L{\text{*}}{{R}^{{ - 3/8}}}$).

Согласно [2]–[4], течение в пристеночном слое подчиняется системе уравнений Прандтля для пограничного слоя:

где используются специальным образом обезразмеренные компоненты скорости $(u,v)$, давление $p$, координаты $(х ,\,у )$ и время t. Однако в отличие от классической постановки Прандтля давление является самоиндуцированным и подлежит определению наряду с прочими функциями течения.

Сращивание асимптотических разложений во всех трех областях приводит к так называемому условию свободного взаимодействия, которое для случая несжимаемого пограничного слоя на плоской пластине имеет вид (см. [2]–[4])

где функция $F(t,x)$, описывающая деформацию податливой стенки, связана следующим соотношением с давлением на стенке (см., например, [8]): где ${{p}_{0}}(t,x)$ – внешнее давление под пластиной, и все коэффициенты $K,{\kern 1pt} \,\alpha $, $\beta $ и $\gamma $ неотрицательны. Здесь $K$ характеризует упругость пластины, $\alpha $ и $\beta $ – ее продольное натяжение и изгибную жесткость, а $\gamma $ – инерционность.

Условие прилипания на стенке

завершает постановку граничных условий.

2. ДИСПЕРСИОННОЕ СООТНОШЕНИЕ

Изучим собственные малые колебания течения, линеаризовав систему (1.1)–(1.5) по малому параметру $\delta \to 0$ и положив внешнее давление ${{p}_{0}} = 0$:

Выделив в явном виде гармоническую зависимость получим систему обыкновенных дифференциальных уравнений, сводящуюся к уравнению Эйри (см., например, [12]). Из ее решения получаем дисперсионное соотношение связывающее комплексную частоту $\omega $ с волновым числом k собственных колебаний течения. Здесь ${\text{Ai}}(\zeta )$ – функция Эйри, экспоненциально затухающая в секторе $\left| {\arg \zeta } \right| < {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$.

В работе [13] исследовалось влияние только продольного натяжения и изгибной жесткости пластины на характер неустойчивости течения, из-за чего пластина считалась безынерционной ($\gamma = 0$). В настоящей статье мы будем исследовать влияние только инерционности пластины, так что положим $\alpha = \beta = 0$, чтобы избавиться от влияния продольного натяжения и изгибной жесткости пластины и упростить ситуацию. Тогда дисперсионное соотношение (2.2) принимает следующий вид (достаточно ограничиться диапазоном $k > 0$, поскольку легко видеть, что $\omega ( - k) = c.c.\omega (k)$, где c.c. означает операцию комплексного сопряжения):

Если предположить, что решение $\omega \to 0$ при $k \to 0$, то при $k = 0$ из диспресионного соотношения (2.3) получается уравнение $\Phi (\Omega ) = 0$, имеющее счетный набор корней ${{\Omega }_{n}}$, совпадающих с нулями функции $d{\text{Ai}}(\Omega ){\text{/}}d\zeta $. Именно такая ситуация встречалась ранее при изучении дисперсионного соотношения для случая жесткой пластины [12]. Таким образом, уравнение (2.3) имеет счетный набор корней ${{\Omega }_{n}}(k)$, начинающихся при $k = 0$ из нулей функции $d{\text{Ai}}(\Omega ){\text{/}}d\zeta $. При этом следует отметить, что первый корень будет неустойчив при всех $\gamma {\kern 1pt} $ и K, поскольку несложно получить его асимптотическое поведение

совпадающее в первых двух приближениях с таковым для случая жесткой пластины [12].

Однако это еще не все корни. Если предположить, что $\gamma {{\omega }^{2}} \to - K$ при $k \to 0$, то $\Omega \to \infty $, так что можно воспользоваться асимптотическим разложением $\Phi (\Omega ) = - \Omega + O({{\Omega }^{{ - 1/2}}})$ и получить еще два корня со следующими асимпотитками:

Физический смысл этих корней ясен: они связаны с собственными колебаниями податливой пластины при отсутствии пограничного слоя, когда ${{\omega }_{{ + , - }}} = \pm i\sqrt {K{\text{/}}\gamma } $.

Теперь рассмотрим другой предельный случай: $k \to \infty $. Если предположить, что правая часть $Q(k,\omega ) \to \infty $ при $k \to \infty $, то мы опять же возвращаемся к ситуации, ранее изученной для случая жесткой пластины [12]: тогда все корни ${{\Omega }_{n}}(k)$, начиная со второго, стремятся к нулям функции $\int_\Omega ^\infty {{\text{Ai}}(\zeta )d\zeta } $. Первый же корень ${{\Omega }_{1}}(k)$ является особенным: для него справедлива асимптотика ${{\Omega }_{1}}(k) \to {{(ik)}^{{1/3}}}k$ при $k \to \infty $. Что касается “новых” корней $\Omega {}_{{ + , - }}$, связанных с собственными колебаниями податливой пластины, то для нахождения их асимптотики следует опять же предположить, что $\gamma {{\omega }^{2}} \to - K$ (но уже при $k \to \infty $), после чего нетрудно получить

где константа ${{\Phi }_{0}} = - \,\Phi (0) > 0$. Таким образом, “минусовой” корень при больших $k$ всегда неустойчив: $\operatorname{Re} {{\omega }_{ - }}\sim \frac{{{{\Phi }_{0}}}}{4}\sqrt {\frac{3}{{\gamma K}}} {{k}^{{ - 1/3}}}$ при $k \to \infty $.

Исследуем теперь нейтральные колебания, у которых инкремент нарастания $\sigma = \operatorname{Re} \omega = 0.$ Это колебания вида $\omega = (0, - i{{\omega }_{*}})$, $k = {{k}_{*}}$, удовлетворяющие дисперсионному соотношению (2.3), так что для нахождения пары вещественных чисел $({{\omega }_{*}},{{k}_{*}})$ получается следующее уравнение:

Поскольку числа ${{\omega }_{*}}$ и ${{k}_{*}}$ вещественные, $\arg {{Q}_{*}}$ может равняться только $\pi {\text{/}}6$ или $ - \pi {\text{/}}6$. Можно показать, что при $\arg {{Q}_{*}} = - \pi {\text{/}}6$ уравнение (2.6) решений не имеет, тогда как при $\arg {{Q}_{*}} = \pi {\text{/}}6$ уравнение (2.6) аналогично уравнению, полученному при изучении нейтральных колебаний в пограничном слое на жесткой пластине [12]: Известно (см. [12]), что уравнение (2.8) имеет ровно одно решение ${{k}_{*}} = {{k}_{\infty }} = 1.005$, ${{\omega }_{*}} = {{\omega }_{\infty }} = 2.298$, и тогда из сравнения (2.7) с (2.8) немедленно получаем уравнение для нахождения ${{k}_{*}}$:

Расчеты показали, что уравнение (2.9) при всех $0 < \gamma < \infty $ имеет ровно 2 решения, причем несложно получить асимптотику этих решений в двух предельных случаях:

где ${{k}_{0}}$ является корнем уравнения $\frac{{k_{*}^{{4/3}}}}{{1 - {{k}_{*}}{\text{/}}K}} = k_{\infty }^{{4/3}}$ (оно получается из (2.9), если положить $\gamma = 0$).

Нетрудно видеть, что полученные нейтральные значения должны принадлежать первому ${{\omega }_{1}}$ и “минусовому” ${{\omega }_{ - }}$-корням дисперсионного соотношения (2.3), поскольку оба эти корня затухают ($\operatorname{Re} \omega < 0$) при малых k и становятся неустойчивыми ($\operatorname{Re} \omega > 0$) при достаточно больших k согласно асимптотикам (2.4) и (2.6). Как следствие, “плюсовой” корень ${{\omega }_{ + }}$, а также все “классические” корни ${{\omega }_{n}}$, начиная со второго, будут всегда устойчивы.

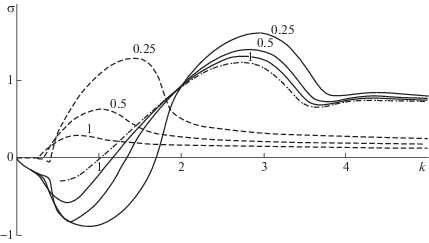
Перейдем теперь непосредственно к численным расчетам дисперсионного соотношения (2.3), представленным на фиг. 1 и фиг. 2 для $K = 1$. На них прослеживается зависимость инкремента нарастания возмущений $\sigma = \operatorname{Re} \omega $ от волнового числа k для ряда характерных значений параметра инерционности $\gamma $, указанных около соответствующих кривых. Сплошной линией проведены зависимости инкремента нарастания для “классического” первого корня ${{\omega }_{1}}$, а штриховой – для “минусового” ${{\omega }_{\_}}$. Штрихпунктирной линией отмечена зависимость $\operatorname{Re} {{\omega }_{1}}(k)$ для жесткой пластины, когда $\gamma \to \infty $ [12].

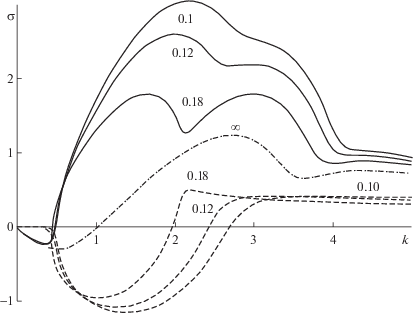
Прежде всего отметим, что при уменьшении параметра $\gamma $ от бесконечности (см. штрихпунктирную линию на фиг. 1) до $\gamma = 1$ характеристики первого корня (2.3) меняются весьма слабо: так, например, максимальный инкремент ${{\sigma }_{{\max }}} = \max \operatorname{Re} {{\omega }_{1}}\;(0 < k < \infty )$ увеличивается всего лишь на 6.5% (с ${{\sigma }_{{\max }}} = 1.24$ до 1.32), а характерное поведение кривой не меняется. Зато при этом начинает заявлять о себе “минусовой” корень, дорастая до величины при ${{\sigma }_{{\max }}} = 0.291$ при $\gamma = 1$. При дальнейшем уменьшении $\gamma $ с 1 до 0.25 этот корень испытывает бурный рост, быстро догоняя слабо растущий первый корень. И вот уже при $\gamma = 0.18$ (фиг. 2) локальные максимумы в распределении $\sigma $ сравниваются (достигая величины ${{\sigma }_{{\max }}} = 1.79$), но, что интересно, при этом первый локальный максимум, ранее принадлежавший корню ${{\omega }_{ - }}$, теперь захватывается корнем ${{\omega }_{1}}$ (такое странное, на первый взгляд, взаимодействие корней объясняется наличием точки ветвления корней уравнения (2.3) в комплексной плоскости k, подходящей близко к вещественной оси k при $\gamma \approx 0.2$; подробное исследование данного поведения выходит за рамки настоящей работы).

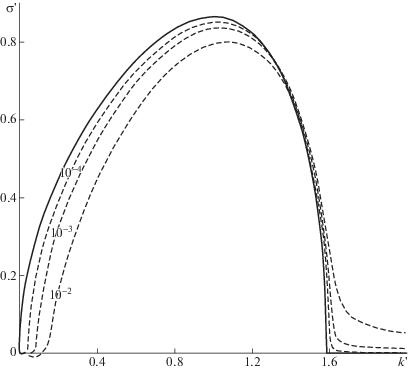
Если продолжать уменьшать $\gamma $, то при $\gamma = 0.12$ (см. фиг. 2) второй локальный максимум становится значительно меньше первого, и ведущая роль в формировании неустойчивости переходит к первому локальному максимуму (см. кривую для $\gamma = 0.1$ на фиг. 2), причем отвечающий ему инкремент нарастания ${{\sigma }_{{\max }}} = \max \operatorname{Re} {{\omega }_{1}}\;(0 < k < \infty )$ неограниченно возрастает при дальнейшем уменьшении $\gamma $. Чтобы понять характер этого неограниченного роста, перейдем к “штрихованным” переменным $k{\kern 1pt} ' = k{{\gamma }^{{1/3}}}$ и $\omega {\kern 1pt} ' = \omega {{\gamma }^{{2/3}}}$, тогда дисперсионное соотношение (2.3) примет следующий вид:

Считая $\Omega {\kern 1pt} '$ величиной порядка единицы, устремим $\gamma \to 0$. Тогда можно воспользоваться асимптотикой $\Phi (\Omega ) = - \Omega + O({{\Omega }^{{ - 1/2}}})$, благодаря чему дисперсионное соотношение (2.10) упрощается в первом приближении до и при дополнительном ограничении $\omega {\kern 1pt} {{'}^{2}} \gg K{{\gamma }^{{1/3}}}$ сводится к квадратному уравнению с корнями Нетрудно видеть, что корень $\omega _{ - }^{'}$ всегда устойчив, а $\omega _{ + }^{'}$ неустойчив в диапазоне $0 < k{\kern 1pt} ' < {{2}^{{2/3}}}$, причем $\sigma {\kern 1pt} ' = \operatorname{Re} \omega _{ + }^{'}$ достигает максимума $\frac{{\sqrt 3 }}{2}$ при $k{\kern 1pt} ' = 1$. Тогда, возвращаясь к исходным переменным, получаем оценку

Заметим, что асимптотическое решение (2.12) перестает быть пригодным только при малых $k{\kern 1pt} '$, точнее, при $k{\kern 1pt} '\sim K{{\gamma }^{{1/3}}}$, когда $\omega {\kern 1pt} {{'}^{2}}\sim K{{\gamma }^{{1/3}}}$ (то есть, не выполняется дополнительное ограничение, принятое выше). Такой асимптотический характер поведения неустойчивого корня подтверждается прямыми численными расчетами дисперсионного соотношения (2.3), приведенными на фиг. 3, где сплошная линия отвечает асимптотике $\sigma {\kern 1pt} ' = \operatorname{Re} \omega _{ + }^{'}$ из (2.10), а штриховые линии соответствуют неустойчивому корню (2.3) при $\gamma = {{10}^{{ - {\kern 1pt} 2}}}$, $\gamma = {{10}^{{ - {\kern 1pt} 3}}}$ и $\gamma = {{10}^{{ - {\kern 1pt} 4}}}$.

Разумеется, принятая модель течения развита в предположении, что все безразмерные величины имеют порядок единицы, в частности, $\gamma \sim 1$. Найденные асимптотические оценки при $\gamma \to 0$ лишь указывают на тенденции поведения характерных величин в указанном пределе, но могут послужить отправной точкой для построения другой асимптотической модели течения, что, однако, выходит за рамки данной работы.

3. ВОЛНОВОЙ ПАКЕТ

В целях дальнейшего анализа неустойчивости рассмотрим волновые пакеты, порождаемые импульсным воздействием внешнего давления на податливую пластину. Положим в (1.4) ${{p}_{0}}(t,x) = \delta {\kern 1pt} {{p}_{{00}}}(t,x)$, где ${{p}_{{00}}}(t,x)$ – заданная функция (ее вид выберем позже).

Считая возмущения малыми, линеаризуем задачу (1.1)–(1.5) по амплитудному параметру $\delta \to 0$ с помощью выражения (2.1), а затем разложим искомые функции (со “штрихом”) в интегралы Фурье–Лапласа. Например, разложение для функции p имеет вид

Тогда для образов искомых функций получается система дифференциальных уравнений (по $Y$), сводящаяся к решению уравнения Эйри. Окончательно имеем где

Считая импульсное воздействие точечным в пространстве и времени, положим ${{p}_{{00}}}(t,x) = \delta (х )\delta (t)$, где $\delta (x)$ – дельта-функция Дирака. Применяя теорему о вычетах к внутреннему интегралу в (3.1), получаем

где ${{\omega }_{n}}$, ${{\omega }_{ + }}$ и ${{\omega }_{ - }}$ – упомянутые выше корни дисперсионного соотношения (2.3). Пренебрегая вкладом всех затухающих корней, имеем где

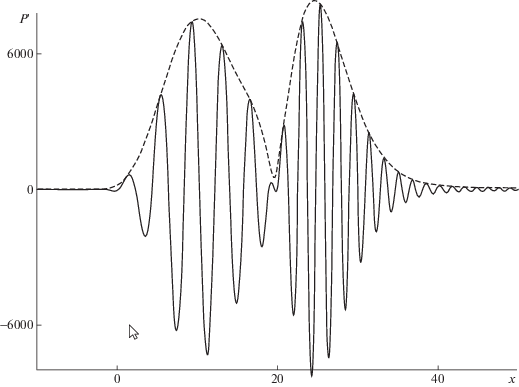
Был проведен ряд численных расчетов интеграла (3.3) с помощью метода трапеций с шагом $\Delta k = 0.0001$, что, как правило, обеспечивало 1%-ю точность вычислений. Результаты расчетов для $\gamma = 0.18$ представлены на фиг. 4 и фиг. 5 на моменты времени $t = 3$ и $t = 5$ соответственно (сплошной линией проведена функция $p{\kern 1pt} '(t,x)$, а штриховой – ее огибающая ${\text{|}}p_{c}^{'}(t,x){\text{|}}$). Значение $\gamma = 0.18$ интересно тем, что в этом случае инкремент нарастания $\sigma = \operatorname{Re} {{\omega }_{1}}(k)$ имеет два практически одинаковых максимума с ${{\sigma }_{{\max }}} \approx 1.79$ при ${{k}_{{1,\max }}} = {\text{1}}{\text{.65}}$ и ${{k}_{{1,\max }}} = {\text{2}}{\text{.98}}$, но группы волн из окрестности этих максимумов движутся с разной групповой скоростью $U = - \partial \operatorname{Im} {{\omega }_{1}}(k){\text{/}}\partial k$, а именно ${{U}_{1}} = - \partial \operatorname{Im} {{\omega }_{1}}({{k}_{{1,\max }}}){\text{/}}\partial k$ = 2.04, тогда как ${{U}_{2}} = - \partial \operatorname{Im} {{\omega }_{1}}({{k}_{{2,\max }}}){\text{/}}\partial k$ = 5.01. Из рисунков видно, что на момент $t = 3$ (фиг. 4) волновые пакеты только начинают отделяться друг от друга, и этот процесс разделения пакетов практически завершается к моменту $t = 5$ (фиг. 5).

ЗАКЛЮЧЕНИЕ

В рамках асимптотической теории свободного взаимодействия показано, что наличие инерционности пластины приводит к появлению двух дополнительных мод собственных колебаний, одна из которых всегда неустойчива, а вторая – устойчива. С уменьшением инерционности пластины возмущения становятся все более неустойчивыми, причем поначалу возмущения раздваиваются на два волновых пакета, а затем формируют единый пакет. Таким образом, инерционность пластины оказывает дестабилизирующее влияние на несжимаемый пограничный слой.