Журнал вычислительной математики и математической физики, 2019, T. 59, № 5, стр. 775-791
Вычисление оптимальных возмущений для систем с запаздыванием
Ю. М. Нечепуренко 1, М. Ю. Христиченко 2, *
1 ИВМ им. Г.И. Марчука РАН
119333 Москва, ул. Губкина, 8, Россия
2 ИПМ им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия
* E-mail: misha.hrist@gmail.com
Поступила в редакцию 25.05.2018
После доработки 28.11.2018
Принята к публикации 11.01.2019
Аннотация
Предлагаются и обосновываются новые быстрые алгоритмы вычисления максимальной амплификации нормы решения и оптимальных возмущений для систем с запаздыванием. Предложенные алгоритмы опробованы на системе четырех нелинейных дифференциальных уравнений с запаздывающим временем, представляющей собой модель экспериментальной инфекции, вызванной вирусами лимфоцитарного хориоменингита. Приводятся и обсуждаются результаты численных экспериментов. Библ. 12. Фиг. 8. Табл. 4.
1. ВВЕДЕНИЕ
Понятие оптимального возмущения стационарного состояния динамической системы без запаздывания, обеспечивающего максимально возможную амплификацию возмущения в заданной норме (увеличение нормы возмущения по сравнению с ее первоначальным значением), широко используют для описания механизма докритического ламинарно-турбулентного перехода в теории аэродинамической устойчивости, смотри, например, работы [1]–[3] и их библиографии. Для динамической системы с запаздыванием понятие оптимального возмущения стационарного состояния было впервые введено в работах [4]–[7]. На примере модели динамики лимфоцитарного хориоменингита у мышей, описанной в [8], было показано, что оптимальные возмущения позволяют, в частности, находить минимально достаточные терапии, позволяющие переводить организм из состояний с высокой вирусной нагрузкой в состояния с низкой вирусной нагрузкой. Для вычисления оптимальных возмущений был предложен и обоснован достаточно простой алгоритм, эффективный для систем с запаздыванием небольшой размерности и основанный на сведении исходной задачи к вычислению матричных произведений. При этом алгебраический размер матричных произведений был обратно пропорционален шагу сетки по времени, используемому для численного интегрирования исходной системы.
Для эффективного вычисления оптимальных возмущений в случае систем с запаздыванием большой размерности и/или требующих для численного интегрирования очень мелких шагов по времени необходимы алгоритмы, использующие в своей схеме только умножение матрицы на вектор. Такого типа алгоритмы были предложены недавно в работе [9] для систем обыкновенных дифференциальных уравнений без запаздывания. Данная работа посвящена обобщению этих алгоритмов на системы с запаздыванием.
Работа состоит из восьми разделов. В разд. 2 даются определения максимальной амплификации нормы решения и оптимальных возмущений, аналогичные данным в [7]. В разд. 3 изложена модификация простейшего алгоритма вычисления оптимального возмущения для введенного класса норм. В разд. 4 предложена дальнейшая модификация этого алгоритма с использованием метода Ланцоша, позволяющая эффективно вычислять оптимальные возмущения для задач большой размерности. В разд. 5 описан еще более эффективный алгоритм поиска оптимального возмущения, основанный на последовательной максимизации. В разд. 6 оцениваются вычислительные затраты алгоритмов, описанных в предыдущих разделах. В разд. 7 приводятся результаты численных экспериментов с предложенными алгоритмами на примере модели динамики заболевания, вызванного вирусами лимфоцитарного хориоменингита. Итог работы подводится в разд. 8.
2. ОПТИМАЛЬНЫЕ ВОЗМУЩЕНИЯ
Рассмотрим систему обыкновенных дифференциальных уравнений вида
где $0 < {{\tau }_{1}} < \; \ldots \; < {{\tau }_{p}}$, $U(t)$ является $n$-компонентным вектором переменных, а $F({{\xi }_{0}},{{\xi }_{1}},\; \ldots ,\;{{\xi }_{p}})$ – некоторое достаточно гладкое отображение. Будем предполагать, что решение задачи Коши для системы (2.1) существует и единственно для любого кусочно-непрерывного начального значения $U(t)$, $ - {{\tau }_{p}} \leqslant t \leqslant 0$.Нас будет интересовать поведение системы (2.1) вблизи устойчивого стационарного состояния $U(t) = \bar {U}$. Записывая решение вблизи стационарного состояния в виде $U(t) = \bar {U} + \varepsilon U{\kern 1pt} {\text{'}}(t) + O({{\varepsilon }^{2}})$, где $\varepsilon $ – малый по абсолютной величине параметр, подставляя это решение в (2.1) и требуя, чтобы полученные равенства выполнялись при всех сколь угодно малых значениях $\varepsilon $, для функции $U{\kern 1pt} {\text{'}}(t)$ получим систему линейных дифференциальных уравнений вида
(2.2)
$\frac{d}{{dt}}U{\kern 1pt} {\text{'}}(t) = {{L}_{0}}U{\kern 1pt} {\text{'}}(t) + \sum\limits_{j = 1}^p \,{{L}_{j}}U{\kern 1pt} {\text{'}}(t - {{\tau }_{j}}),$Для вектора переменных системы (2.2) введем в рассмотрение следующее семейство локальных норм в момент времени $t$:
(2.3)
${{\left\| {U{\kern 1pt} {\text{'}}{\kern 1pt} } \right\|}_{{D,\rho ,t}}} = \mathop {\left( {\int\limits_{t - {{\tau }_{p}}}^t \left( {\left\| {DU{\kern 1pt} {\text{'}}{\kern 1pt} (\xi )} \right\|_{2}^{2} + \rho \left\| {D\frac{{dU{\kern 1pt} {\text{'}}}}{{d\xi }}(\xi )} \right\|_{2}^{2}} \right)d\xi } \right)}\nolimits^{1/2} ,$Под оптимальным возмущением $U_{{{\text{opt}}}}^{'}(t)$ будем понимать решение системы (2.2), обеспечивающее максимальную амплификацию локальной нормы (2.3) возмущения по сравнению с ее первоначальным значением, то есть такое решение $U{\kern 1pt} {\text{'}}{\kern 1pt} (t)$, на котором достигается максимум величины
Оптимальное возмущение по определению является некоторым решением линейной системы (2.2) и, следовательно, полностью определяется своим значением в интервале $ - {{\tau }_{p}} \leqslant t \leqslant 0$. Поэтому при построении оптимального возмущения наряду с выбором нормы, в которой проводится оптимизация, принципиальным является вопрос о том, из какого пространства функций, заданных в интервале $ - {{\tau }_{p}} \leqslant t \leqslant 0$, мы берем начальные значения. Это пространство функций $[ - {{\tau }_{p}},0] \to {{\mathbb{R}}^{n}}$ мы далее будем обозначать через $\mathcal{Q}$. Для гарантированного существования максимума необходимо, чтобы $\mathcal{Q}$ было полным пространством в норме ${{\left\| {\, \cdot \,} \right\|}_{{D,\rho ,0}}}$. Для этого достаточно выбирать в качестве $\mathcal{Q}$ линейную оболочку какого-либо конечного набора кусочно-непрерывных базисных функций.
Найденное оптимальное возмущение используют для возмущения стационарного состояния исходной нелинейной системы (2.1), выбирая в качестве начального значения
при $ - {{\tau }_{p}} \leqslant t \leqslant 0$, где $\tilde {U}_{{{\text{opt}}}}^{'}(t)$ означает нормированное в ${{L}_{2}}$ норме оптимальное возмущение, а $\varepsilon $ – вещественный параметр. Варьируя абсолютную величину этого параметра, можно увеличивать или уменьшать начальное возмущение. В зависимости же от его знака, заданная компонента решения при $t > 0$ либо начинает нарастать, либо убывать.3. ПРОСТЕЙШИЙ АЛГОРИТМ ВЫЧИСЛЕНИЯ ОПТИМАЛЬНЫХ ВОЗМУЩЕНИЙ
Искать оптимальное возмущение удобнее в два этапа. Сначала вычисляем максимальную амплификацию
(3.1)
$\Gamma (t) = \mathop {max}\limits_{U{\kern 1pt} {\text{'}}} \frac{{{{{\left\| {U{\kern 1pt} {\text{'}}{\kern 1pt} } \right\|}}_{{D,\rho ,t}}}}}{{{{{\left\| {U{\kern 1pt} {\text{'}}{\kern 1pt} } \right\|}}_{{D,\rho ,0}}}}}$(3.2)
$U_{{{\text{opt}}}}^{'} \in arg\mathop {max}\limits_{U'} \frac{{{{{\left\| {U{\kern 1pt} {\text{'}}{\kern 1pt} } \right\|}}_{{D,\rho ,{{t}_{{{\text{opt}}}}}}}}}}{{{{{\left\| {U{\kern 1pt} {\text{'}}{\kern 1pt} } \right\|}}_{{D,\rho ,0}}}}}.$Если $D$, $\rho $ и $\mathcal{Q}$ фиксированы, то любое найденное оптимальное возмущение обеспечивает одну и ту же максимальную амплификацию локальной нормы решения. Обычно максимальная амплификация имеет только одну точку глобального максимума, а решение оптимизационной задачи (3.2) однозначно с точностью до ненулевой мультипликативной константы.
Оптимальные возмущения можно вычислять на основе любой разностной схемы, подходящей для решения задач Коши для систем обыкновенных дифференциальных уравнений с запаздывающим аргументом. Следуя работам [4]–[6], мы будем использовать неявную схему второго порядка BDF2 [10] на равномерной сетке
построенной в полуинтервале $( - {{\tau }_{p}},\infty )$ с шагом $\delta > 0$. При этом величины ${{m}_{j}} = \left[ {{{\tau }_{j}}{\text{/}}\delta } \right]$, где $[.]$ означает целую часть числа, будут дискретными аналогами задержек ${{\tau }_{j}}$. После дискретизации система (2.2) примет вид(3.3)
$\frac{{1.5{{U}_{k}} - 2{{U}_{{k - 1}}} + 0.5{{U}_{{k - 2}}}}}{\delta } = {{L}_{0}}{{U}_{k}} + \sum\limits_{j = 1}^p \,{{L}_{{{{\tau }_{j}}}}}{{U}_{{k - {{m}_{j}}}}},$Предполагая шаг $\delta $ достаточно малым, запишем уравнение (3.3) в виде
(3.4)
${{U}_{k}} = {{C}_{1}}{{U}_{{k - 1}}} + {{C}_{2}}{{U}_{{k - 2}}} + \sum\limits_{j = 1}^p \,{{C}_{{{{m}_{j}}}}}{{U}_{{k - {{m}_{j}}}}},$(3.6)
${{X}_{k}} = \left( {\begin{array}{*{20}{c}} {{{U}_{k}}} \\ \vdots \\ {{{U}_{{k - {{m}_{p}} + 1}}}} \end{array}} \right),\quad M = \left( {\begin{array}{*{20}{c}} {{{M}_{{11}}}}& \cdots &{{{M}_{{1{{m}_{p}}}}}} \\ \vdots &{}& \vdots \\ {{{M}_{{{{m}_{p}}1}}}}& \cdots &{{{M}_{{{{m}_{p}}{{m}_{p}}}}}} \end{array}} \right).$Чтобы ввести сеточный аналог максимальной амплификации (3.1), необходимо определить сеточный аналог нормы (2.3). Для численного интегрирования первого слагаемого под интегралом в (2.3) будем использовать формулу трапеций, а для интегрирования второго – формулу прямоугольников. При этом производную $dU{\kern 1pt} {\text{'}}{\kern 1pt} {\text{/}}d\xi $, входящую во второе слагаемое, будем аппроксимировать в точках ${{t}_{{k + 1/2}}}$ с помощью центральной разности:
В силу (3.5), (3.6), (3.7), сеточный аналог ${{\Gamma }_{k}}$ максимальной амплификации (3.1) нормы решения можно записать следующим образом:
Учитывая, что ${{X}_{0}} = Q\xi $, где $\xi $ – некоторый $nd$-компонентный вектор, имеем
Пусть $PG = \hat {Q}\hat {R}$ – QR-разложение, где $\hat {Q}$ – ортогональная прямоугольная матрица размера ${{m}_{p}} \times d$, а $\hat {R}$ – верхняя треугольная квадратная матрица порядка $d$. Вводя обозначения $\tilde {Q} = \hat {Q} \otimes I$, $\tilde {R} = \hat {R} \otimes D$, имеем $H{{X}_{0}} = \tilde {Q}\tilde {R}\xi = \tilde {Q}\widetilde \xi $, где $\tilde {\xi } = \tilde {R}\xi $. Следовательно,Для повышения эффективности вычисления ${{\Gamma }_{k}}$ вместо матрицы ${{H}^{{ - 1}}}\tilde {Q}$ будем использовать равную ей матрицу $Q{{\tilde {R}}^{{ - 1}}}$. Тогда для вычисления ${{\Gamma }_{k}}$ окончательно получим следующую формулу:
гдеТаким образом, вычисление ${{\Gamma }_{k}}$ сводится к формированию матрицы ${{Y}_{0}} = Q{{\tilde {R}}^{{ - 1}}}$ и вычислению матриц ${{Y}_{k}}$ по рекуррентной формуле ${{Y}_{k}} = M{{Y}_{{k - 1}}}$ с одновременным вычислением норм матриц $H{{Y}_{k}}$ для всех натуральных $k$, не превосходящих $N = \left[ {T{\text{/}}\delta } \right]$, где $T$ – произвольная априорная верхняя оценка ${{t}_{{{\text{opt}}}}}$. При этом, учитывая блочную структуру матрицы $M$, ее можно умножать на матрицу ${{Y}_{{k - 1}}}$ следующим образом:
Пусть ${{k}_{{{\text{opt}}}}}$ означает значение $k$, при котором достигается максимум ${{\Gamma }_{k}}$. Вычислив нормированный правый сингулярный вектор ${{\eta }^{{{\text{opt}}}}}$ матрицы ${{A}_{{{{k}_{{{\text{opt}}}}}}}}$, отвечающий ее максимальному сингулярному числу [11], начальное значение $X_{0}^{{{\text{opt}}}}$ сеточного аналога оптимального возмущения $X_{k}^{{{\text{opt}}}}$ можно найти по формуле $X_{0}^{{{\text{opt}}}} = Q{{\tilde {R}}^{{ - 1}}}{{\eta }^{{{\text{opt}}}}}$.
Отметим, что величина шага сетки по времени, необходимая для достаточно точного численного интегрирования системы уравнений (2.2), а значит и вычисления максимальной амплификации $\Gamma (t)$, значительно меньше, чем это требуется для последующего вычисления с приемлемой точностью максимума $\Gamma (t)$ и оптимального возмущения, на котором достигается этот максимум. Поэтому для сокращения вычислительных затрат простейшего алгоритма имеет смысл вычислять ${{\left\| {{{A}_{k}}} \right\|}_{2}}$ не для всех натуральных $k$, не превосходящих $N = \left[ {T{\text{/}}\delta } \right]$, а лишь для $k$ кратных $l$, где $l$ – некоторое заданное натуральное число.
Описанный алгоритм можно немного упростить, включив матрицу $D$ в матрицу $M$. Действительно, правая часть равенства (3.8) не изменится, если в матрицах $H$ и $\tilde {R}$ заменить матрицу $D$ единичной, а блоки ${{C}_{i}}$ матрицы $M$ заменить на $D{{C}_{i}}{{D}^{{ - 1}}}$. Мы будем считать, что такое предварительное преобразование матрицы $M$ выполнено и матрица $D$, фигурирующая в матрицах $H$ и $\tilde {R}$, – единичная.
4. МОДИФИКАЦИЯ ПРОСТЕЙШЕГО АЛГОРИТМА С ИСПОЛЬЗОВАНИЕМ МЕТОДА ЛАНЦОША
Учитывая, что $M$ и остальные матрицы, образующие ${{A}_{k}}$ в (3.8), являются разреженными матрицами большой размерности, для вычисления максимального сингулярного числа матрицы ${{A}_{k}}$ и отвечающего ему правого сингулярного вектора можно использовать метод Ланцоша [12], применяя его к матрице $A_{k}^{{\text{т }}}{{A}_{k}}$ для вычисления ее наибольшего собственного значения, корень из которого даст искомое сингулярное число, а собственный вектор матрицы $A_{k}^{{\text{т }}}{{A}_{k}}$, отвечающий ее максимальному собственному значению, – искомый сингулярный вектор. Формальная схема алгоритма приведена ниже.
Алгоритм 1
Вычисление максимального сингулярного числа матрицы $A_{k}^{{\text{т }}}{{A}_{k}}$ и отвечающего ему сингулярного вектора методом Ланцоша.
Input: матрицы $H$, $M$, $Q$, $\tilde {R}$ в разреженном формате, натуральное число $k$, начальный вектор $\text{v}$, минимальное допустимое относительное увеличение ${\text{tol}}$ приближенного сингулярного числа за один шаг, максимальное число шагов ${{r}_{{{\text{max}}}}}$ метода Ланцоша.
Output: приближенные значения наибольшего сингулярного числа $s$ и соответствующего правого сингулярного вектора $\text{v}$ матрицы ${{A}_{k}}$, определенной в (3.8).
if ${{r}_{{max}}} > 1$ then
while $r < {{r}_{{max}}}$ and ${{\beta }_{r}} > 0$ and ${{s}_{r}} \geqslant (1 + {\text{tol}}){{{\text{s}}}_{{{\text{r}} - 1}}}$ do
Сформировать $r \times r$ трехдиагональную матрицу ${{T}_{r}} = {\text{tridiag}}\left( {{{\beta }_{{i - 1}}},{{\alpha }_{i}},{{\beta }_{i}}} \right);$ ${{s}_{r}} = \sqrt {{{\lambda }_{{max}}}({{T}_{r}})} $
end while
Вычислить собственный вектор $y$, отвечающий максимальному собственному значению матрицы ${{T}_{r}}$.
end if
Выполнить один шаг степенного метода:
Метод Ланцоша строит последовательность векторов ${{q}_{1}},{{q}_{2}},\; \ldots ,\;{{q}_{r}}$, образующих ортонормированный базис в подпространстве Крылова
Для сокращения вычислительных затрат, в качестве начального вектора при $k > 1$ можно брать сингулярный вектор, найденный при предыдущем значении $k$. Кроме того, как и в случае простейшего алгоритма, имеет смысл вычислять ${{\left\| {{{A}_{k}}} \right\|}_{2}}$ не при всех натуральных $k$, не превосходящих $N = \left[ {T{\text{/}}\delta } \right]$, а лишь при $k$ кратных $l$, где $l$ – некоторое заданное натуральное число.
5. АЛГОРИТМ ПОСЛЕДОВАТЕЛЬНОЙ МАКСИМИЗАЦИИ
Алгоритм последовательной максимизации принципиально отличается от простейшего алгоритма и его модификации, описанной в предыдущем разделе, и состоит в следующем. Положим ${{k}_{1}} = \left[ {N{\text{/}}2} \right]$ и найдем максимальное сингулярное число матрицы ${{A}_{{{{k}_{1}}}}}$ и отвечающий ему нормированный правый сингулярный вектор $\eta $ с помощью метода Ланцоша, описанного выше. Вычислив последовательно нормы ${{\left\| {{{A}_{1}}\eta } \right\|}_{2}},\; \ldots ,\;{{\left\| {{{A}_{N}}\eta } \right\|}_{2}}$, положим
Алгоритм 2
Вычисление оптимального возмущения методом последовательной максимизации.
Input: матрицы $H$, $M$, $Q$, $\tilde {R}$ в разреженном формате, натуральное число $N$, параметры ${\text{tol}}$ и ${{r}_{{max}}}$ Алгоритма 1.
Output: приближенное значение сеточного аналога оптимального возмущения $X_{0}^{{{\text{opt}}}}$.
while ${{k}_{i}} \ne {{k}_{{i - 1}}}$ do
Найти максимальное сингулярное число матрицы ${{A}_{{{{k}_{i}}}}}$ и отвечающий ему нормированный правый сингулярный вектор $\eta $ с помощью алгоритма 1.
Вычислить нормы ${{\left\| {{{A}_{1}}\eta } \right\|}_{2}},\; \ldots ,\;{{\left\| {{{A}_{N}}\eta } \right\|}_{2}}$, и найти ${{k}_{{i + 1}}} = min\;arg\;ma{{x}_{{k \geqslant 1}}}{{\left\| {{{A}_{k}}\eta } \right\|}_{2}}$.
end while
Для сокращения вычислительных затрат в алгоритме последовательной максимизации можно вычислять нормы ${{\left\| {{{A}_{k}}\eta } \right\|}_{2}}$ не при всех $k$, а лишь при $k$, кратных $l$, где $l$ – некоторое заданное натуральное число, однако выигрыш от этого будет не столь значительным, как в двух предыдущих алгоритмах, поскольку в данном случае требуется вычислять нормы векторов, а не матриц.
6. ОЦЕНКА СЛОЖНОСТИ АЛГОРИТМОВ
Оценим главные члены числа арифметических операций и ячеек памяти, необходимые каждому из трех алгоритмов, описанных в предыдущих разделах. Под ячейкой памяти будем понимать 64-х битовое вещественное число с плавающей точкой. Учитывая, что основные вычислительные затраты простейшего алгоритма, его модификации, использующей метод Ланцоша, приходятся на вычисление максимальной амплификации, затраты на последующее вычисление оптимального возмущения мы для этих алгоритмов учитывать не будем.
В соответствии со сказанным в конце разд. 3, будем считать, что блоки матрицы $M$ преобразованы преобразованием подобия с матрицей $D$, а матрицу $D$ в матрицах $H$ и $\tilde {R}$ будем считать единичной порядка $n$. Поскольку матрица $P$ является верхним треугольным фактором разложения Холецкого симметричной положительно определенной трехдиагональной матрицы порядка ${{m}_{p}}$, количество ненулевых элементов в этой матрице есть $2{{m}_{p}} - 1$. Поэтому для хранения матрицы $P$ достаточно $2{{m}_{p}}$ ячеек памяти, а для умножения на вектор матрицы $H = P \otimes I$ без ее формирования – $3n{{m}_{p}}$ арифметических операций. Для хранения ненулевых и не единичных блоков матрицы $M$ достаточно $(p + 2){{n}^{2}}$ ячеек памяти, а для умножения этой матрицы на вектор – $2(p + 2){{n}^{2}}$ арифметических операций. Для хранения ${{m}_{p}} \times d$ матрицы $G$ достаточно ${{m}_{p}}d$ ячеек памяти, а для умножения матрицы $Q = G \otimes I$ на вектор без ее формирования – $2dn{{m}_{p}}$ арифметических операций. Наконец, поскольку $\hat {R}$ – верхняя треугольная квадратная матрица порядка $d$, для ее хранения требуется ${{d}^{2}}{\text{/}}2$ ячеек памяти, а для решения системы с этой матрицей достаточно ${{d}^{2}}$ арифметических операций. Поэтому для умножения матрицы ${{\tilde {R}}^{{ - 1}}} = {{\hat {R}}^{{ - 1}}} \otimes I$ на вектор без ее формирования достаточно $n{{d}^{2}}$ арифметических операций.
Таким образом, для умножения на вектор матриц $H$, $M$, $Q$ и ${{\tilde {R}}^{{ - 1}}}$ без их формирования достаточно соответственно $3n{{m}_{p}}$, $2(p + 2){{n}^{2}}$, $2n{{m}_{p}}d$ и $n{{d}^{2}}$ арифметических операций, а для хранения необходимой для этого информации об этих матрицах достаточно соответственно $2{{m}_{p}}$, $(p + 2){{n}^{2}}$, ${{m}_{p}}d$ и ${{d}^{2}}{\text{/}}2$ ячеек памяти.
Простейший алгоритм сначала формирует $n{{m}_{p}} \times nd$ матрицу ${{Y}_{0}} = Q{{\tilde {R}}^{{ - 1}}} = G{{\hat {R}}^{{ - 1}}} \otimes I$. Для этого достаточно ${{m}_{p}}{{d}^{2}}$ арифметических операций. Далее, на каждом $k$-ом шаге он вычисляет матрицу ${{Y}_{k}} = M{{Y}_{{k - 1}}}$, для чего достаточно $2(p + 2){{n}^{3}}d$ арифметических операций. Если $k$ кратно $l$, то на $k$-м шаге вычисляется матрица ${{A}_{k}} = H{{Y}_{k}}$, для чего достаточно $3{{n}^{2}}{{m}_{p}}d$ арифметических операций, и ее норма. Для вычисления последней с помощью R-SVD разложения [11] достаточно $2{{n}^{3}}{{m}_{p}}{{d}^{2}} + 2{{n}^{3}}{{d}^{3}}$ арифметических операций. Так как формирование матрицы $Q{{\tilde {R}}^{{ - 1}}}$ производится один раз и, следовательно, требует небольшого по сравнению с другими шагами числа операций, главный член суммарного числа арифметических операций простейшего алгоритма составляет
Здесь и далее предполагается, что $1 \ll d \ll {{m}_{p}}$, ${{m}_{p}} \ll N$, $p$ – небольшое натуральное число, $1 \leqslant n \ll {{m}_{p}}$.Для реализации простейшего алгоритма необходимо хранить текущую матрицу ${{Y}_{k}}$, которая является плотной и требует для хранения ${{n}^{2}}{{m}_{p}}d$ ячеек памяти. Это значительно больше числа ячеек памяти, необходимых для хранения информации о матрицах $H$ и $M$, необходимой для их умножения на вектор. Поэтому главный член числа ячеек памяти, необходимых для реализации простейшего алгоритма, – ${{n}^{2}}{{m}_{p}}d$.
Перейдем к оценке вычислительных затрат модификации простейшего алгоритма, использующей метод Ланцоша. Из выполненного выше анализа следует, что для умножения матрицы ${{A}_{k}}$ на вектор ${{q}_{r}}$ в главном члене достаточно $2n{{m}_{p}}d + 2k(p + 2){{n}^{2}}$ арифметических операций. Столько же арифметических операций достаточно и для умножения на вектор матрицы $A_{k}^{{\text{т }}}$. Остальные вычислительные затраты $r$-го шага метода Ланцоша пренебрежимо малы, кроме, может быть, вычисления максимального собственного значения симметричной трехдиагональной матрицы ${{T}_{r}}$, которое требует $O({{r}^{2}})$ арифметических операций c небольшой мультипликативной константой [11]. Однако, как показывает вычислительная практика, для нахождения максимального сингулярного числа матрицы ${{A}_{k}}$ и соответствующего ему правого сингулярного вектора в среднем достаточно не более полутора десятков шагов метода Ланцоша. Это число шагов плюс один шаг степенного метода мы будем обозначать через ${{r}_{{{\text{av}}}}}$. Поэтому главный член числа арифметических операций рассматриваемого алгоритма составляет
(6.2)
$2{{r}_{{{\text{av}}}}}\left( {2\frac{N}{l}n{{m}_{p}}d + \frac{{{{N}^{2}}}}{l}(p + 2){{n}^{2}}} \right).$Оценим теперь число арифметических операций, необходимое алгоритму последовательной максимизации. Каждая итерация этого алгоритма включает в себя нахождение максимального сингулярного числа и соответствующего ему правого сингулярного вектора матрицы ${{A}_{{{{k}_{i}}}}}$ с помощью метода Ланцоша, что, согласно полученным выше оценкам, можно выполнить за $4{{r}_{{{\text{av}}}}}(n{{m}_{p}}d + {{k}_{i}}(p + 2){{n}^{2}})$ арифметических операций. Также каждая итерация требует вычисления ${{\left\| {{{A}_{l}}\eta } \right\|}_{2}},{{\left\| {{{A}_{{2l}}}\eta } \right\|}_{2}}, \ldots ,{{\left\| {{{A}_{N}}\eta } \right\|}_{2}}$. Для этого, так как произведение $Q{{\tilde {R}}^{{ - 1}}}\eta $ вычисляется один раз, в главном члене достаточно $(2(p + 2){{n}^{2}} + 5n{{m}_{p}}{\text{/}}l)N$ арифметических операций. Следовательно, главный член числа арифметических операций алгоритма последовательной максимизации составляет
(6.3)
$q\left( {4{{r}_{{{\text{av}}}}}(n{{m}_{p}}d + (p + 2){{n}^{2}}{{k}_{{{\text{av}}}}}) + \left( {2(p + 2){{n}^{2}} + \frac{{5n{{m}_{p}}}}{l}} \right)N} \right).$Из выполненного анализа в частности следует, что с ростом числа уравнений $n$ число ячеек памяти, необходимых для реализации простейшего алгоритма, значительно больше, чем требуют два других алгоритма. Оценки числа операций (6.1), (6.2) и (6.3) позволяют заключить, что в этом случае простейший алгоритм проигрывает и по числу арифметических операций, так как с увеличением $n$ оно растет как ${{n}^{3}}$, а для модификации простейшего алгоритма и алгоритма последовательной максимизации – как ${{n}^{2}}$. Кроме того, при достаточно большом числе $d$ базисных функций число операций простейшего алгоритма так же значительно больше, чем у остальных алгоритмов, так как с увеличением $d$ оно растет как ${{d}^{2}}$, а для остальных алгоритмов – линейно. Наконец, поскольку ${{m}_{p}} \sim 1{\text{/}}\delta $ и $N \sim 1{\text{/}}\delta $, где $\delta $ – шаг сетки по времени, число операций каждого алгоритма пропорционально $1{\text{/}}{{\delta }^{2}}$. При этом константа пропорциональности простейшего алгоритма, его модификации, использующей метод Ланцоша, и алгоритма последовательной максимизации равна $2T{{n}^{3}}{{d}^{2}}{{\tau }_{p}}{\text{/}}l$, $2{{r}_{{{\text{av}}}}}(2Tn{{\tau }_{p}}d + {{T}^{2}}(p + 2){{n}^{2}}){\text{/}}l$ и $5Tn{{\tau }_{p}}{\text{/}}l$ соответственно. То есть она значительно меньше у алгоритма последовательной максимизации.
Таким образом, в случае систем с большим числом переменных и/или базисных функций и/или малых шагов по времени эффективнее модификация простейшего алгоритма, использующая метод Ланцоша, и еще более эффективен алгоритм последовательной максимизации.
7. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ
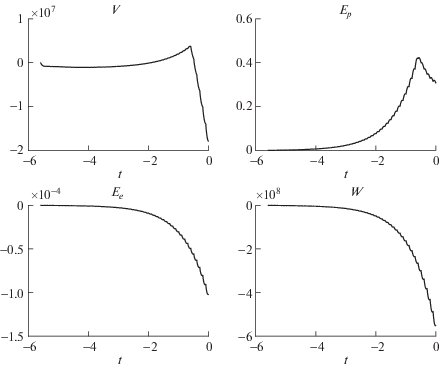
Проиллюстрируем работу простейшего алгоритма, его модификации, использующей метод Ланцоша, и алгоритма последовательной максимизации, которые далее для краткости будем называть соответственно алгоритмами I, II и III, на примере модели динамики инфекции, вызванной вирусами лимфоцитарного хориоменингита. Эта модель была сформулирована в работе [8] в виде системы нелинейных дифференциальных уравнений вида (2.1) с $p = 2$, ${{\tau }_{1}} = 0.6$, ${{\tau }_{2}} = 5.6$, и описывает динамику концентраций вирусных частиц $V$, клеток-прекурсоров ${{E}_{p}}$, клеток-эффекторов ${{E}_{e}}$ и кумулятивной вирусной нагрузки $W$. При значениях параметров, указанных в табл. 5 из [8], кроме $\beta = 0.102$ и ${{\alpha }_{{{{E}_{p}}}}} = 0.006$, данная модель имеет следующее устойчивое стационарное состояние: $V \approx 4.8 \times {{10}^{7}}$, ${{E}_{p}} \approx 1.0$, ${{E}_{e}} \approx 1.8 \times {{10}^{{ - 4}}}$, $W \approx 4.4 \times {{10}^{8}}$. В качестве базисных функций для вычисления оптимальных возмущений будем использовать следующие функции, качественно аппроксимирующие поведение препаратов в рамках однокамерных и двухкамерных фармакокинетических моделей:
(7.1)
$\phi (t,{{t}_{0}}) = \left\{ \begin{gathered} 0,\quad - {\kern 1pt} {{\tau }_{2}} \leqslant t < {{t}_{0}}, \hfill \\ exp\left\{ { - 3(t - {{t}_{0}})} \right\} - exp\left\{ { - 9(t - {{t}_{0}})} \right\},\quad {{t}_{0}} \leqslant t \leqslant 0. \hfill \\ \end{gathered} \right.$Для расчетов будем использовать равномерную сетку с шагом $\delta = 5 \times {{10}^{{ - 3}}}$. В качестве априорной верхней оценки ${{t}_{{{\text{opt}}}}}$ выберем $T = 30$. Таким образом, будем иметь $n = 4$, $p = 2$, $N = 6000$, ${{m}_{p}} = 1120$. Для каждой переменной будем использовать $d$ базисных функций вида (7.1) с узлами равномерной сетки в интервале $ - {{\tau }_{2}} < t < 0$ в качестве ${{t}_{0}}$. Расчеты будем проводить с $l = 1$ и 50. Для нахождения максимального сингулярного числа и отвечающего ему правого сингулярного вектора методом Ланцоша выберем $\operatorname{tol} = {\text{1}}{{{\text{0}}}^{{ - 9}}}$, а в качестве начального вектора «$\text{v}$ всегда будем выбирать случайный вектор.
Рассмотрим четыре тестовые задачи, которые в дальнейшем будем называть тестами 1–4. Между собой эти тесты отличаются значением параметра $d$, видом локальной нормы, в которой вычисляется оптимальное возмущение, и весами локальной нормы (диагональные элементы матрицы $D$). А именно, $d = 14$ в тесте $2$ и 56 во всех остальных тестах. В качестве локальной нормы, в тесте $4$ выбрана ${{L}_{2}}$-норма, а во всех остальных тестах – $W_{2}^{1}$. В тесте $3$ веса берутся единичными, а во всех остальных тестах они берутся равными величинам, обратным компонентам рассматриваемого стационарного состояния.
Для каждого из тестов с помощью алгоритмов I и II были рассчитаны максимальная амплификация, оптимальное возмущение и локальная норма оптимального возмущения. Максимальная амплификация для случая $l = 50$ изображена на фиг. 1а, 3а, 5а и 7а. Там же изображена локальная норма найденного оптимального возмущения, а компоненты его начального значения изображены на фиг. 2, 4, 6 и 8. Стоит отметить, что вид максимальной амплификации в случае тестов 1 и 2 (фиг. 1а и 3а соответственно) не является типичным. Более типичными являются максимальные амплификации, полученные для тестов 3 и 4 и изображенные на фиг. 5а и 7а соответственно.
Фиг. 1.
Максимальная амплификация (черная линия) для теста $1$ и локальная норма оптимального возмущения, полученные алгоритмами I и II (красная линия) (а) и локальные нормы приближений к оптимальному возмущению, найденных на итерациях алгоритма III: первой – зеленая, второй – синяя, третьей – красная линии (б).

Фиг. 3.
Максимальная амплификация (черная линия) для теста 2 и локальная норма оптимального возмущения, полученные алгоритмами I и II (красная линия) (а) и локальные нормы приближений к оптимальному возмущению, найденных на итерациях алгоритма III: первой – зеленая, второй – синяя линии (б).

Фиг. 5.
Максимальная амплификация (черная линия) для теста 3 и локальная норма оптимального возмущения, полученные алгоритмами I и II (красная линия) (а) и локальные нормы приближений к оптимальному возмущению, найденных на итерациях алгоритма III: первой – зеленая, второй – синяя (б).
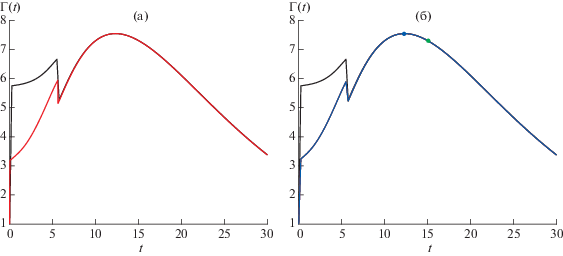
Фиг. 7.
Максимальная амплификация (черная линия) для теста 4 и локальная норма оптимального возмущения, полученные алгоритмами I и II (красная линия) (а) и локальные нормы приближений к оптимальному возмущению, найденных на итерациях алгоритма III: первой – зеленая, второй – синяя (б).

Фигуры 1б, 3б, 5б и 7б демонстрируют работу алгоритма III при $l = 50$. Крупные точки соответствуют моментам времени ${{k}_{1}}\delta $ (зеленая), ${{k}_{2}}\delta $ (синяя), ${{k}_{3}}\delta $ (красная), то есть первому, второму и третьему приближениям к ${{t}_{{{\text{opt}}}}}$.
В случае теста 1 все рассматриваемые алгоритмы дали одинаковые результаты ${{t}_{{{\text{opt}}}}} \approx 5.50$, $\Gamma ({{t}_{{{\text{opt}}}}}) \approx 12.5$ с точностью до 16 значащих десятичных цифр вне зависимости от значения $l$. В случае тестов 3 и 4 все алгоритмы с точностью до $16$ значащих десятичных цифр дали одинаковые результаты, но различные при $l = 1$ и $50$: ${{t}_{{{\text{opt}}}}} \approx 12.32$, $\Gamma ({{t}_{{{\text{opt}}}}}) \approx 7.5498$ при $l = 1$ и ${{t}_{{{\text{opt}}}}} \approx 12.25$, $\Gamma ({{t}_{{{\text{opt}}}}}) \approx 7.5496$ при $l = 50$ в случае теста 3, и ${{t}_{{{\text{opt}}}}} \approx 11.27$, $\Gamma ({{t}_{{{\text{opt}}}}}) \approx 39.7884$ при $l = 1$ и ${{t}_{{{\text{opt}}}}} \approx 11.25$, $\Gamma ({{t}_{{{\text{opt}}}}}) \approx 39.7883$ при $l = 50$ в случае теста 4.
В случае теста 2 алгоритмы I и II с точностью до $16$ значащих десятичных цифр дали одинаковые результаты ${{t}_{{{\text{opt}}}}} \approx 4.40$, $\Gamma ({{t}_{{{\text{opt}}}}}) \approx 4.817$ при $l = 1$ и ${{t}_{{{\text{opt}}}}} \approx 4.25$, $\Gamma ({{t}_{{{\text{opt}}}}}) \approx 4.815$ при $l = 50$. Алгоритм III остановился после $q = 2$ итераций. При этом были получены следующие результаты: ${{t}_{{{\text{opt}}}}} \approx 10.41$, $\Gamma ({{t}_{{{\text{opt}}}}}) \approx 2.26$ при $l = 1$ и ${{t}_{{{\text{opt}}}}} \approx 10.25$, $\Gamma ({{t}_{{{\text{opt}}}}}) \approx 2.25$ при $l = 50$. То есть в данном случае последовательная максимизация сходилась не к оптимальному возмущению, а к возмущению, на котором достигается локальный максимум.
В табл. 1 приведены среднее число шагов метода Ланцоша ${{r}_{{{\text{av}}}}}$ (оно оказалось одинаковым для алгоритмов II и III во всех тестах, кроме теста 4), число итераций $q$ алгоритма III и ${{k}_{{{\text{av}}}}}$. Подставляя эти величины и указанные ранее значения параметров расчета в формулы (6.1), (6.2), (6.3), получим приведенные в табл. 2 числа операций, необходимых каждому из рассматриваемых алгоритмов. Для двух первых алгоритмов учитывалось только число операций, необходимых для вычисления максимальной амплификации. В табл. 3 указаны времена работы всех трех алгоритмов в среде MATLAB на компьютере с 2-х ядерным процессором Intel Core i7 с частотой 2.4 GHz. Для двух первых алгоритмов учитывалось только время вычисления максимальной амплификации. Вычисление самого оптимального возмущения требовало еще $4.2$ и $0.3$ секунд соответственно. Алгоритм III для нахождения оптимального возмущения не требует дополнительных вычислений. Отношение числа операций, необходимых для реализации каждого алгоритма на время его работы, дает производительность, которая приведена в табл. 4.
Таблица 1.
Результаты работы алгоритмов II и III
| Тест 1 | Тест 2 | Тест 3 | Тест 4 | |||||
|---|---|---|---|---|---|---|---|---|
| $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | |
| ${{r}_{{{\text{av}}}}}$ | 6 | 6 | 6 | 6 | 5 | 5 | 6/5 | 6/5 |
| q | 4 | 3 | 2 | 2 | 3 | 2 | 4 | 2 |
| ${{k}_{{{\text{av}}}}}$ | 1845 | 2083 | 2541 | 2525 | 2642 | 2725 | 2444 | 2625 |
Таблица 2.
Число операций
| Алгоритм | Тест 1 | Тест 2 | Тест 3 | Тест 4 | ||||
|---|---|---|---|---|---|---|---|---|
| $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | |
| I | $2.7 \times {{10}^{{12}}}$ | $5.4 \times {{10}^{{10}}}$ | $1.7 \times {{10}^{{11}}}$ | $3.4 \times {{10}^{9}}$ | $2.7 \times {{10}^{{12}}}$ | $5.4 \times {{10}^{{10}}}$ | $2.7 \times {{10}^{{12}}}$ | $5.4 \times {{10}^{{10}}}$ |
| II | $6.4 \times {{10}^{{10}}}$ | $1.3 \times {{10}^{9}}$ | $3.7 \times {{10}^{{10}}}$ | $7.3 \times {{10}^{8}}$ | $5.3 \times {{10}^{{10}}}$ | $1.1 \times {{10}^{9}}$ | $6.4 \times {{10}^{{10}}}$ | $1.3 \times {{10}^{9}}$ |
| III | $5.8 \times {{10}^{8}}$ | $3.8 \times {{10}^{7}}$ | $2.8 \times {{10}^{8}}$ | $1.8 \times {{10}^{7}}$ | $4.3 \times {{10}^{8}}$ | $2.4 \times {{10}^{7}}$ | $2.5 \times {{10}^{8}}$ | $2.0 \times {{10}^{7}}$ |
Таблица 3.
Время работы (в секундах)
| Алгоритм | Тест 1 | Тест 2 | Тест 3 | Тест 4 | ||||
|---|---|---|---|---|---|---|---|---|
| $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | |
| I | 184.9 | 23.2 | 28.1 | 5.7 | 184.9 | 23.2 | 178.9 | 22.1 |
| II | 3155 | 63.2 | 3064 | 61.4 | 3154 | 63.2 | 3229 | 64.7 |
| III | 2.4 | 1.7 | 1.5 | 1.3 | 2.1 | 1.5 | 2.5 | 1.3 |
Таблица 4.
Производительность (число операций в секунду)
| Алгоритм | Тест 1 | Тест 2 | Тест 3 | Тест 4 | ||||
|---|---|---|---|---|---|---|---|---|
| $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | $l = 1$ | $l = 50$ | |
| I | $1.5 \times {{10}^{{10}}}$ | $2.3 \times {{10}^{9}}$ | $6.0 \times {{10}^{9}}$ | $6.0 \times {{10}^{8}}$ | $1.5 \times {{10}^{{10}}}$ | $2.3 \times {{10}^{9}}$ | $1.5 \times {{10}^{{10}}}$ | $2.4 \times {{10}^{9}}$ |
| II | $2.0 \times {{10}^{7}}$ | $2.1 \times {{10}^{7}}$ | $1.2 \times {{10}^{7}}$ | $1.2 \times {{10}^{7}}$ | $1.7 \times {{10}^{7}}$ | $1.7 \times {{10}^{7}}$ | $2.0 \times {{10}^{7}}$ | $2.0 \times {{10}^{7}}$ |
| III | $2.4 \times {{10}^{8}}$ | $2.2 \times {{10}^{7}}$ | $1.9 \times {{10}^{8}}$ | $1.4 \times {{10}^{7}}$ | $2.0 \times {{10}^{8}}$ | $1.6 \times {{10}^{7}}$ | $1.0 \times {{10}^{8}}$ | $1.5 \times {{10}^{7}}$ |
Из табл. $4$ видно, что производительность на алгоритме I при всех $l$ и на алгоритме III при $l = 1$ существенно выше производительности на алгоритме II при всех $l$ и на алгоритме III при $l = 50$. Это связано с тем, что некоторые стандартные функции среды MATLAB, реализующие матричные алгоритмы, особенно эффективно используют вычислительные возможности компьютера. На этих функциях достигается существенно более высокая производительность, чем на других стандартных функциях MATLAB и тем более на пользовательских реализациях тех же и других алгоритмов на языке среды MATLAB.
Поясним сказанное на примере теста 1. Вычисления алгоритма I при $l = 1$ можно разбить на три части: вычисление ${{Y}_{k}} = {{M}^{k}}{{Y}_{0}}$ при $0 \leqslant k \leqslant N$, вычисление матриц ${{A}_{k}} = H{{Y}_{k}}$ для всех найденных матриц ${{Y}_{k}}$, и вычисление вторых норм всех найденных матриц ${{A}_{k}}$. Для первой части достаточно $2 \times {{10}^{8}}$, для второй – $1.8 \times {{10}^{{10}}}$, для третьей – $2.7 \times {{10}^{{12}}}$ арифметических операций. Первая часть была реализована нами на языке MATLAB без существенного использования стандартных функций, во второй части использовалось стандартное умножение на разреженную матрицу в разреженном формате. В третьей части использовалась очень эффективная стандартная функция norm (время ее работы совпадает с временем вычисления сингулярных чисел с помощью стандартной функции svd на матрице того же размера). Первая часть потребовала $20.6$, вторая – $26$, третья – $158$ секунд. Таким образом, производительности на этих трех частях алгоритма I оказались существенно различными и составляли соответственно $9.7 \times {{10}^{6}}$, $6.9 \times {{10}^{8}}$ и $1.7 \times {{10}^{{10}}}$ операций в секунду. При $l = 50$ алгоритм I выполняет в 50 раз меньше умножений на матрицу $H$ и вычислений матричных норм по сравнению с числом умножений на матрицу $M$. Как следствие, производительность на нем уменьшается на порядок.
В алгоритме II число умножений на матрицу $H$ пренебрежимо мало по сравнению с числом умножений на матрицу $M$, а нормы матриц стандартными функциями вообще не вычисляются. Отсюда и сравнительно низкая производительность.
На алгоритме III более высокая производительность при $l = 1$, чем при $l = 50$, достигается благодаря большему вкладу в общее число операций вычисления ${{\left\| {{{A}_{l}}\eta } \right\|}_{2}},{{\left\| {{{A}_{{2l}}}\eta } \right\|}_{2}},\; \ldots ,\;{{\left\| {{{A}_{N}}\eta } \right\|}_{2}}$, для которого мы использовали стандартную функцию norm и стандартное умножение на разреженную матрицу.
8. ЗАКЛЮЧЕНИЕ
В данной работе алгоритмы, разработанные ранее для вычисления оптимальных возмущений стационарных состояний систем без запаздывания, были модифицированы для поиска оптимальных возмущений стационарных состояний систем с запаздыванием. Был выполнен сравнительный анализ вычислительных затрат этих алгоритмов. Их работа была проиллюстрирована на примере модели динамики заболевания, вызванной вирусами лимфоцитарного хориоменингита.
Алгоритмом, наиболее точно вычисляющим оптимальные возмущения, очевидно, является простейший алгоритм, поскольку в нем вычисление максимального сингулярного числа и отвечающего ему правого сингулярного вектора выполняются с машинной точностью. Однако для систем с достаточно большим количеством переменных он требует больше памяти и числа арифметических операций. Менее точной, но более эффективной является модификация этого алгоритма с использованием метода Ланцоша, хотя по времени работы наша реализация этой модификации в среде MATLAB в рассмотренных случаях уступает нашей реализации простейшего алгоритма в силу используемых в коде стандартных процедур умножения на разреженную матрицу и вычисления второй нормы матрицы, очень эффективно реализованных в среде MATLAB.
Наиболее эффективным алгоритмом вычисления оптимального возмущения оказался алгоритм последовательной максимизации. Он предпочтительнее с точки зрения объема требуемой памяти и количества операций, более того, время работы его реализации в среде MATLAB значительно меньше времен работы простейшего алгоритма и его модификации, использующей метод Ланцоша. Хотя алгоритм последовательной максимизации не гарантирует, вообще говоря, получения правильного результата во всех случаях, поскольку этот метод может сойтись к локальному максимуму, тем не менее его имеет смысл использовать при больших параметрических расчетах, выборочно контролируя результат с помощью одного из двух других алгоритмов.
Список литературы
Boiko A.V., Nechepurenko Y.M., Sadkane M. Fast computation of optimal disturbances for duct flows with a given accuracy // Ж. вычисл. матем. и матем. физ. 2010. Т. 50. № 11. С. 2017–2027.
Boiko A.V., Nechepurenko Y.M., Sadkane M. Computing the maximum amplification of the solution norm of differential-algebraic systems // Comput. Math. Model. 2012. V. 23. № 2. P. 216–227.
Nechepurenko Y.M., Sadkane M. A low-rank approximation for computing the matrix exponential norm // SIAM J. Matrix. Anal. Appl. 2011. V. 32. № 2. P. 349–363.
Бочаров Г.А., Нечепуренко Ю.М., Христиченко М.Ю., Гребенников Д.С. Оптимальные возмущения систем с запаздывающим аргументом для управления динамикой инфекционных заболеваний на основе многокомпонентных воздействий // Современная математика. Фундаментальные направления. 2017. Т. 63. № 3. С. 392–417.
Бочаров Г.А., Нечепуренко Ю.М., Христиченко М.Ю., Гребенников Д.С. Управление моделями вирусных инфекций с запаздывающими переменными на основе оптимальных возмущений // Препринты ИПМ им. Келдыша. 2017. № 52. 28 с.
Bocharov G.A., Nechepurenko Yu.M., Khristichenko M.Yu., Grebennikov D.S. Maximum response perturbation-based control of virus infection model with time-delays // Russian J. Num. Anal. Math. Model. 2017. V. 32. № 5. P. 275–291.
Бочаров Г.А., Нечепуренко Ю.М., Христиченко М.Ю., Гребенников Д.С. Оптимальные возмущения бистабильных систем с запаздыванием, моделирующих вирусные инфекции // Докл. АН. 2018. Т. 481. № 2. С. 123–126.
Bocharov G.A. Modelling the dynamics of LCMV infection in mice: conventional and exhaustive CTL responses // J. Theor. Biol. 1998. V. 192. № 3. P. 283–308.
Nechepurenko Y.M., Sadkane M. Computing humps of the matrix exponential // J. Comput. Appl. Math. 2017. V. 319. P. 87–96.
Hairier E., Norsett S., Wanner G. Solving ordinary differential equations. Berlin: Springer, 1987.
Golub G.H., Van Loan C.F. Matrix computations. London: Jhon Hopkins University press, 1989.
Parlett B.N. The symmetric eigenvalue problem. Berkeley: SIAM, 1998.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики