Журнал вычислительной математики и математической физики, 2019, T. 59, № 5, стр. 762-774

О нелинейной спектральной задаче для диэлектрического волновода c Керровской нелинейностью

А. Л. Делицын^1, *, Л. Л. Делицын^2, **

¹ Институт проблем передачи информации им. А.А. Харкевича
127051 Москва, Большой каретный пер., 19, стр. 1, Россия;
Национальный исследовательский университет “Высшая школа экономики”
125319 Москва, Кочновский проезд, 3, Россия;
Главный научно-исследовательский испытательный центр робототехники Министерства Обороны Российской Федерации
119001 Москва, ул. Серегина, 5, Россия

² Московский государственный университет им. М.В. Ломоносова
125009 Москва, ул. Моховая, 9, стр. 1, Россия;
Московский Государственный Институт Культуры
141406 Московская обл., г. Химки, ул. Библиотечная, 7, Россия

^* E-mail: delitsyn@mail.ru
^** E-mail: delitsin@gmail.com

Поступила в редакцию 29.08.2018
После доработки 29.08.2018
Принята к публикации 11.01.2019

DOI: 10.1134/S0044466919050065

Полный текст (PDF)

Аннотация

Рассмотрена зависимость постоянных распространения плоских слоистых диэлектрических волноводов с Керровской нелинейностью от частоты. Дано объяснение возможного отличия их поведения от линейного случая, связанного исключительно с фиксированием значения собственной функции на границе слоя. Получены явные формулы для вычисления “дисперсионных кривых”. Проанализировано их поведение при различных способах определения собственной функции нелинейной задачи. Библ. 12. Фиг. 4. Табл. 1.

Ключевые слова: нелинейная задача на собственные значения, Керровская нелинейность, плоские волноводы.

1. ВВЕДЕНИЕ

Исследования качественных свойств спектральных задач теории волноводов были посвящены главным образом задачам для линейной системы уравнений Максвелла. Эти задачи характеризуются линейной зависимостью вектора индукции электромагнитного поля от вектора напряженности ${\mathbf{D}} = \varepsilon ({\mathbf{r}}){\mathbf{E}}$. Одним из случаев распределения диэлектрической проницаемости, допускающим точное решение, является диэлектрический слой [1].

Несомненный интерес, как с математической точки зрения, так и в приложениях, представляют нелинейные проблемы. Значительное число работ связано с рассмотрением нелинейной задачи на собственные значения для волноводов с Керровской нелинейностью [2]–[8]. В этом случае предполагается зависимость вектора индукции от вектора напряженности вида

${\mathbf{D}} = \alpha {\mathbf{E}} + \beta {{\left| {\mathbf{E}} \right|}^{2}}{\mathbf{E}}.$

Особенностью этой нелинейной задачи является то, что система уравнений Максвелла

$\operatorname{rot} {\mathbf{E}} = - \frac{1}{c}\frac{{\partial {\mathbf{H}}}}{{\partial t}},\quad \operatorname{rot} {\mathbf{H}} = \frac{1}{c}\frac{{\partial {\mathbf{D}}}}{{\partial t}}$

допускает решения в виде

${\mathbf{E}} = {\mathbf{E}}({\mathbf{r}}){{e}^{{ - i\omega t}}},\quad {\mathbf{H}} = {\mathbf{H}}({\mathbf{r}}){{e}^{{ - i\omega t}}}$

как и в линейном случае.

Будем рассматривать далее волновод в виде диэлектрического слоя. Коэффициенты, описывающие связь индукции и напряженности электрического поля, задаются кусочно-постоянной функцией $\alpha $:

$\alpha = \left\{ {\begin{array}{*{20}{l}} {{{\varepsilon }_{1}},\quad x > h,} \\ {{{\varepsilon }_{2}},\quad - {\kern 1pt} h < x < h,} \\ {{{\varepsilon }_{3}},\quad x < - h,} \end{array}} \right.$

и $\beta $, отличной от нуля в слое, где она принимает положительное значение, которое будем также обозначать $\beta $:

$\beta = \left\{ {\begin{array}{*{20}{l}} {0,\quad x > h,} \\ {\beta ,\quad - {\kern 1pt} h < x < h,} \\ {0,\quad x < - h.} \end{array}} \right.$

Считаем, что

${{\varepsilon }_{i}} > 0,\quad i = 1,2,3,\quad {{\varepsilon }_{2}} > {{\varepsilon }_{1}},\quad {{\varepsilon }_{2}} > {{\varepsilon }_{3}},\quad \beta > 0.$

Как известно [5], в этом случае задача поиска решений вида

${\mathbf{E}} = {\mathbf{E}}(x,y){{e}^{{i\gamma z}}},\quad {\mathbf{H}} = {\mathbf{H}}(x,y){{e}^{{i\gamma z}}},$

${\mathbf{E}} = \{ 0,{{E}_{y}},0\} ,\quad {\mathbf{H}} = \{ {{H}_{x}},0,{{H}_{z}}\} $

системы уравнений Максвелла приводит в слое к скалярной задаче относительно ${{E}_{y}}$. Введем обозначение $u = {{E}_{y}}$. Большое количество работ [2]–[8] посвящено рассмотрению следующей нелинейной задачи на собственные значения, либо родственным задачам, относительно параметра ${{\gamma }^{2}}$.

Требуется найти решение нелинейного уравнения Дюффинга

(1)

$u{\text{''}} + ({{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}})u + {{k}^{2}}\beta {{u}^{3}} = 0\quad {\text{п р и }}\quad - {\kern 1pt} h < x < h,$

и линейных

(2)

$u{\text{''}} + ({{k}^{2}}{{\varepsilon }_{1}} - {{\gamma }^{2}})u = 0\quad {\text{п р и }}\quad x > h,$

(3)

$u{\text{''}} + ({{k}^{2}}{{\varepsilon }_{3}} - {{\gamma }^{2}})u = 0\quad {\text{п р и }}\quad x < - h.$

Условия сопряжения, выражающие соответствующие условия сопряжения для решений уравнений Максвелла, в точках разрыва диэлектрической проницаемости имеют вид

(4)

$u(h - 0) = u(h + 0),\quad u'(h - 0) = u'(h + 0),$

(5)

$u( - h - 0) = u( - h + 0),\quad u'( - h - 0) = u'( - h + 0).$

Кроме того, напомним, что мы рассматриваем лишь случай, когда диэлектрическая проницаемость внутреннего слоя выше, чем проницаемости окружающих его полупространств:

${{\varepsilon }_{1}} < {{\varepsilon }_{2}},\quad {{\varepsilon }_{3}} < {{\varepsilon }_{2}}.$

Поведение решения на бесконечности задается в виде требования $u \in {{L}_{2}}( - \infty ,\infty )$.

Если считать, что $\beta $ равняется нулю, то соответствующая задача становится хорошо изученной линейной спектральной задачей для волноводного слоя. Ее основным свойством является существование при любом $0 < k < \infty $, по крайней мере, одного собственного значения. Зависимости $\gamma (k)$ принято называть дисперсионными кривыми, поскольку величина $c\tfrac{k}{\gamma }$ равняется фазовой скорости, а $c\tfrac{{\partial k}}{{\partial \gamma }}$ – групповой скорости волны ($c$ – скорость света). Отметим также монотонный рост $\gamma (k)$.

В работе [6] рассмотрен общий несимметричный случай нелинейного слоя, граничащего с двумя полупространствами, заполненными линейными средами с разными диэлектрическими проницаемостями. Приведенные в [6] зависимости $\tfrac{\gamma }{k}$ от $k$ для нелинейного случая имеют принципиально иной характер, чем для линейного. По аналогии с линейным случаем мы будем называть эти зависимости “дисперсионными кривыми”. Даже первая кривая $\tfrac{\gamma }{k}$ определена только для конечного интервала $(0,{{k}_{{cr}}})$, где ${{k}_{{cr}}}$ – некоторое значение. После достижения этого значения кривая продолжает движение влево, а не вправо, как это имеет место в линейном случае.

Установленное поведение кривых не означает, тем не менее, наличия какого-либо нового типа волн. Мы покажем, что подобные кривые возникают, например, при заполнении нелинейной средой всего пространства и связаны исключительно со способом определения понятия собственного значения нелинейной задачи, принятого в [6]–[8]. В этих работах по сути собственная функция выделяется дополнительным условием $u(h) = A$ на границе диэлектрического слоя. Для нелинейной задачи собственные значения, соответствующие собственным функциям, не подчиненным дополнительным условиям, не являются изолированными точками. Собственные значения нелинейной задачи заполняют некоторые интервалы, которые соответствуют одной ветви собственного значения [9].

Далее мы докажем, что в симметричном случае собственное значение $\gamma (k)$ определено при всех $0 < k < \infty $. Если выделить ветвь собственных значений и собственных функций, фиксировав максимальное значение собственной функции, то зависимость $\gamma (k)$ будет качественно эквивалентна линейному случаю.

2. О ПОВЕДЕНИИ γ(k) В ЗАВИСИМОСТИ ОТ УСЛОВИЙ НА СОБСТВЕННУЮ ФУНКЦИЮ

Рассмотрим наиболее простую волноводную задачу на собственные значения, когда нелинейная среда заполняет все пространство. Требуется найти решения уравнения

(6)

$u{\text{''}} + {{k}^{2}}{{\varepsilon }_{2}}u + {{k}^{2}}\beta {{u}^{3}} = {{\gamma }^{2}}u,\quad - {\kern 1pt} \infty < x < \infty ,$

удовлетворяющие условию $u \in {{L}_{2}}( - \infty ,\infty )$. Рассмотрим задачу поиска четных решений уравнения (6). Будем искать на полуоси $(0,\infty )$ решение, удовлетворяющее при $x = 0$ условию

(7)

$u{\kern 1pt} '(0) = 0,$

допускающее четное продолжение на вещественную ось.

Решение из ${{L}_{2}}$ задачи (6), (7) хорошо известно [10]:

(8)

$u = \frac{a}{{coshak\sqrt {\tfrac{\beta }{2}} x}}.$

Это решение является частным случаем четного решения уравнения (6),

$u = a\operatorname{cn} (\mu x,\chi ) = a\operatorname{cn} \left( {\sqrt {{{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}}} x,\sqrt {\frac{{{{k}^{2}}\beta {{a}^{2}}}}{{2({{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}})}}} } \right),$

зависящего от параметра $a$, где $\operatorname{cn} (\mu x,\chi )$ – эллиптический косинус с модулем $\chi $.

Условие $u \in {{L}_{2}}(0,\infty )$ приводит к требованию, чтобы значение модуля эллиптического косинуса равнялось

$\chi = \sqrt {\frac{{{{k}^{2}}\beta {{a}^{2}}}}{{2({{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}})}}} = 1.$

Отсюда определяется собственное значение

(9)

${{\gamma }^{2}} = {{k}^{2}}{{\varepsilon }_{2}} + \frac{1}{2}{{k}^{2}}\beta {{a}^{2}}.$

Собственное значение ${{\gamma }^{2}}$ зависит от параметра $a$, определяющего максимальное значение или амплитуду собственной функции $u$. При фиксированном значении ${{k}^{2}}$ собственное значение ${{\gamma }^{2}}$ зависит от параметра $a$ и заполняет при его изменении от нуля до бесконечности $0 < a < \infty $ полуось ${{k}^{2}}{{\varepsilon }_{2}} < {{\gamma }^{2}} < \infty $. Если для выделения “дисперсионной кривой” фиксировать максимальное значение собственной функции $a$, то зависимость ${{\gamma }^{2}}$ от ${{k}^{2}}$ будет линейной.

Фиксируем теперь значение собственной функции $u$ в произвольной точке, например $x = 1$. Будем использовать дополнительное условие

(10)

$u(1) = 1.$

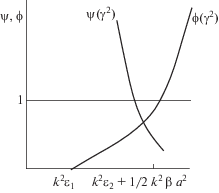
Несмотря на нелинейность задачи, указанный выбор не умаляет общности результата, который аналогично получается для любого другого значения $u(1)$. Рассмотрим зависимость собственного значения $\gamma $ от $k$. Условие (10) приводит к условию на $a$:

$\frac{a}{{cosh\left( {ak\sqrt {\tfrac{\beta }{2}} } \right)}} = 1$

или

(11)

$a = cosh\left( {ak\sqrt {\frac{\beta }{2}} } \right).$

Значение $a$ определяется из уравнения (11). Рассматривая графики двух функций $f(a) = a$ и $g(a) = cosh\left( {ak\sqrt {\tfrac{\beta }{2}} } \right)$, легко описать поведение решений уравнения (11) (см. фиг. 1). В п. 4 на фиг. 3, 4 будет приведено поведение “дисперсионных кривых” для слоя при различном способе определения собственных значений с помощью дополнительного требования на собственную функцию.

Фиг. 1.

Пересечение кривых $f(a) = a$ и $g(a) = cosh\left( {ak\sqrt {\tfrac{\beta }{2}} } \right)$.

Фиг. 2.

Пересечение кривых $\psi ({{\gamma }^{2}})$ и $\varphi ({{\gamma }^{2}})$.

Фиг. 3.

“Дисперсионные кривые” $k = k\left( {\tfrac{\gamma }{k}} \right)$ при фиксированных значениях $u(0) = a.$

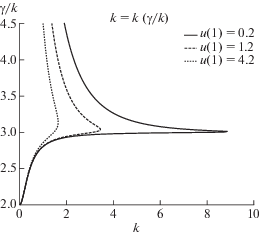
Фиг. 4.

“Дисперсионные кривые” $k = k\left( {\tfrac{\gamma }{k}} \right)$ при фиксированных значениях $u(1).$

Уравнение (11) имеет два решения при $k$, изменяющихся от нуля до некоторого критического значения, которое соответствует точке касания функции $coshak\sqrt {\tfrac{\beta }{2}} $ и прямой. При больших значениях $k$ уравнение решений не имеет. При подстановке $a$ в выражение собственного значения при малых значениях $k$ получается монотонно растущая ветвь “дисперсионной кривой”, которая после прохождения критического значения соответствует второму значению ветви, движущемуся влево, а не вправо. Подобная кривая соответствует кривым, полученным в работах [6]–[8]. Ее поведение связано с определением собственного значения. Приведем явную зависимость $k$ от $\tfrac{\gamma }{k}$. Из уравнения (11) вытекает

(12)

$k = \sqrt {\frac{2}{\beta }} \frac{{cos{{h}^{{ - 1}}}a}}{a},$

где $a$ зависит от $\tfrac{\gamma }{k}$:

(13)

$a = \sqrt {\frac{2}{\beta }\left( {\mathop {\left( {\frac{\gamma }{k}} \right)}\nolimits^2 - {{\varepsilon }_{2}}} \right)} .$

3. СУЩЕСТВОВАНИЕ СОБСТВЕННОГО ЗНАЧЕНИЯ НЕЛИНЕЙНОЙ ЗАДАЧИ

Обратимся к симметричному случаю задачи (1)–(5), когда ${{\varepsilon }_{1}} = {{\varepsilon }_{3}}$. Ограничиваясь поиском четных решений, рассматриваем задачу не на всей прямой $( - \infty ,\infty )$, а на полуоси $(0,\infty )$. Для краткости записи будем считать, что $h = 1$. В качестве краевых условий используем условие в нуле

(14)

$u'(0) = 0$

и условия сопряжения

(15)

$u(1 - 0) = u(1 + 0),$

(16)

$u{\kern 1pt} '(1 - 0) = u{\kern 1pt} '(1 + 0).$

Условия на бесконечности поставим в виде

(17)

$u \in {{L}_{2}}(0,\infty ).$

В работах [6]–[8] утверждается, что при фиксированном значении при $x = h$ собственной функции каждая “дисперсионная кривая” $\gamma (k)$ существует только на конечном отрезке $[0,{{k}_{{cr.}}}]$. Это утверждение может быть верным только при специальном определении собственной функции, использованном авторами указанных работ для несимметричной задачи. Оно связано с фактически накладываемым дополнительным условием на значение собственной функции при $x = h$, а не условием, например, на амплитуду собственной функции. При больших по значению ${{k}^{2}}$ определенная при помощи такого условия “дисперсионная кривая” перестает существовать. Докажем, что при фиксированной амплитуде cобственное значение ${{\gamma }^{2}}$ существует при всех ${{k}^{2}}$.

Утверждение 1. При условии, что

$\tfrac{{{{k}^{2}}\beta {{a}^{2}}}}{{2({{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}})}} < 1,$

любое решение уравнения (1), удовлетворяющее краевому условию (14), имеет вид

(18)

$u = a\operatorname{cn} (\mu x,\chi ) = a\operatorname{cn} \left( {\sqrt {{{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}}} x,\;\sqrt {\frac{{{{k}^{2}}\beta {{a}^{2}}}}{{2({{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}})}}} } \right),$

где ${\text{cn}}$ – эллиптический косинус, модуль $\chi $ которого равен

(19)

$\chi = \sqrt {\frac{{{{k}^{2}}\beta {{a}^{2}}}}{{2({{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}})}}} ,$

параметр –

$\mu = \sqrt {{{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}}} .$

Амплитуда $a$ определяется значением $u$ в нуле.

Проверка утверждения 1 осуществляется подстановкой функции $u$, определенной (18), в уравнение (1) $.$

Любое решение уравнения (2) в полупространстве, удовлетворяющее условию (17), имеет вид

(20)

$u = A{{e}^{{ - \sqrt {{{\gamma }^{2}} - {{k}^{2}}{{\varepsilon }_{1}}} x}}}\quad {\text{п р и }}\quad x > 1,$

где $A$ – произвольная константа.

Существование собственного значения сводится к поиску ${{\gamma }^{2}}$, для которого выполняются условия сопряжения в точке $x = 1$, что эквивалентно уравнению

(21)

$\frac{{u{\kern 1pt} '(1 - 0)}}{{u(1 - 0)}} = \frac{{u{\kern 1pt} '(1 + 0)}}{{u(1 + 0)}}$

при условии $u(1 - 0) \ne 0$.

Продифференцируем (18), (20) и подставим соответствующие выражения в (21). В результате справедливо

Утверждение 2. Дисперсионное уравнение имеет вид

(22)

$\frac{{\operatorname{sn} (\mu ,\chi )\operatorname{dn} (\mu ,\chi )}}{{\operatorname{cn} (\mu ,\chi )}} = \sqrt {\frac{{{{\gamma }^{2}} - {{k}^{2}}{{\varepsilon }_{1}}}}{{{{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}}}}} ,$

где $\operatorname{sn} (\mu ,\chi ),\;\operatorname{cn} (\mu ,\chi )$ – эллиптические синус и косинус, $\operatorname{dn} (\mu ,\chi )$ – эллиптическая функция, иногда называемая дельта амплитуды [11].

Утверждение 3. При любом положительном $k$ существует собственное значение ${{\gamma }^{2}}({{k}^{2}})$.

Рассмотрим уравнение

(23)

Обозначим

$\psi ({{\gamma }^{2}}) = \frac{{\operatorname{sn} (\mu ,\chi )\operatorname{dn} (\mu ,\chi )}}{{\operatorname{cn} (\mu ,\chi )}},$

$\phi ({{\gamma }^{2}}) = \sqrt {\frac{{{{\gamma }^{2}} - {{k}^{2}}{{\varepsilon }_{1}}}}{{{{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}}}}} .$

В этих обозначениях уравнение (23) имеет вид

(24)

$\psi ({{\gamma }^{2}}) = \phi ({{\gamma }^{2}}).$

Пусть

${{\gamma }^{2}} = \tfrac{1}{2}{{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}}.$

Тогда, поскольку $\chi ({{\gamma }^{2}}) = 1$, то левая часть уравнения (23) $\psi ({{\gamma }^{2}})$ равняется

$\frac{{\operatorname{sn} (\mu ,\chi )\operatorname{dn} (\mu ,\chi )}}{{\operatorname{cn} (\mu ,\chi )}} = \tanh \sqrt {\frac{\beta }{2}} ak < 1.$

Правая часть уравнения $\phi ({{\gamma }^{2}})$ принимает значение

$\sqrt {\frac{{\tfrac{1}{2}\beta {{a}^{2}} + ({{\varepsilon }_{2}} - {{\varepsilon }_{1}})}}{{\tfrac{1}{2}\beta {{a}^{2}}}}} > 1.$

Будем уменьшать ${{\gamma }^{2}}$ от ${{k}^{2}}{{\varepsilon }_{2}} + \tfrac{1}{2}{{k}^{2}}\beta {{a}^{2}}$ к меньшим значениям в направлении ${{k}^{2}}{{\varepsilon }_{1}}$ (см. фиг. 2).

Либо левая часть уравнения (23) – непрерывная функция $\psi $ от переменной ${{\gamma }^{2}}$ на отрезке $\left[ {{{k}^{2}}{{\varepsilon }_{1}},\;\tfrac{1}{2}{{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}}} \right]$, либо существует значение $\gamma _{0}^{2}$, принадлежащее $\left[ {{{k}^{2}}{{\varepsilon }_{1}},\;\tfrac{1}{2}{{k}^{2}}\beta {{a}^{2}} + {{k}^{2}}{{\varepsilon }_{2}}} \right]$, для которого левая часть $\psi ({{\gamma }^{2}})$ обращается в бесконечность. Учитывая, что аргументы эллиптических функций при этом увеличиваются, то, хотя их модуль $\chi $ уменьшается, значения эллиптических синусов и косинуса остаются положительными до тех пор, пока эллиптический косинус не обратится в нуль. В результате $\psi ({{\gamma }^{2}})$ – либо непрерывная положительная функция на отрезке $\left[ {{{k}^{2}}{{\varepsilon }_{1}},\;{{k}^{2}}{{\varepsilon }_{2}} + \tfrac{1}{2}{{k}^{2}}\beta {{a}^{2}}} \right]$, либо стремится к $ + \infty $ при стремлении ${{\gamma }^{2}}$ к $\gamma _{0}^{2}$ справа. В обоих случаях, в силу непрерывности $\phi ({{\gamma }^{2}})$, существует точка пересечения кривых $\phi ({{\gamma }^{2}})$ и $\psi ({{\gamma }^{2}})$. Следовательно, при любом положительном $k$ существует собственное значение ${{\gamma }^{2}}$. Заметим, что амплитуда $a$, от которой зависит собственное значение, может принимать произвольное ненулевое значение.

Заметим, что справедливо

Утверждение 4. Существует конечное значение параметра ${{k}^{2}}$, которому соответствует собственное значение ${{\gamma }^{2}} = {{k}^{2}}{{\varepsilon }_{2}}$.

При ${{\gamma }^{2}} = {{k}^{2}}{{\varepsilon }_{2}}$ дисперсионное уравнение принимает вид

(25)

$\frac{{{\text{sn}}\left( {{{k}^{2}}\beta {{a}^{2}},\tfrac{1}{2}} \right){\text{dn}}\left( {{{k}^{2}}\beta {{a}^{2}},\tfrac{1}{2}} \right)}}{{{\text{cn}}\left( {{{k}^{2}}\beta {{a}^{2}},\tfrac{1}{2}} \right)}} = \sqrt {\frac{{{{\varepsilon }_{2}} - {{\varepsilon }_{1}}}}{{\beta {{a}^{2}}}}} .$

При ${{k}^{2}} = 0$ левая часть уравнения (25) равняется нулю. При ${{k}^{2}} \to \tfrac{{K\left( {\tfrac{1}{2}} \right)}}{{\beta {{a}^{2}}}}$ левая часть стремится к бесконечности, здесь $K$ – полупериод эллиптических функций ($K$ – эллиптический интеграл I рода в форме Лежандра).

Таким образом, для нелинейной задачи значение ${{k}^{2}}{{\varepsilon }_{2}}$ достигается собственным значением ${{\gamma }^{2}}$ при некотором значении $k$, а верхней границей служит ${{k}^{2}}{{\varepsilon }_{2}} + \tfrac{1}{2}{{k}^{2}}\beta {{a}^{2}}$.

4. СПОСОБ ВЫЧИСЛЕНИЯ И СВОЙСТВА СЕМЕЙСТВА “ДИСПЕРСИОННЫХ КРИВЫХ”

4.1. Способ вычисления $k = k(\gamma {\text{/}}k)$ при помощи эллиптического интеграла

Обращая формулу (18), запишем при $x = h$

$k = \frac{1}{h}\sqrt {\frac{2}{\beta }} \frac{\chi }{a}\mathop {{\text{cn}}}\nolimits^{ - 1} \left( {\frac{{{{u}_{1}}}}{a},\chi } \right).$

Здесь и далее используются обозначения ${{u}_{1}} = u(h)$ и $a = u(0)$.

Функция $\mathop {{\text{cn}}}\nolimits^{ - 1} $, обратная к эллиптическому косинусу, выражается при помощи неполного эллиптического интеграла (см. [11, с. 21]). Таким образом, имеем

(26)

$k = \frac{1}{h}\sqrt {\frac{2}{\beta }} \frac{\chi }{a}\int\limits_{{{u}_{1}}/a}^1 {\frac{{dv}}{{\sqrt {(1 - {{v}^{2}})({{\chi }^{2}}{{v}^{2}} + 1 - {{\chi }^{2}})} }}{\kern 1pt} } .$

Отметим, что в выражение для $k$ входят ${{u}_{1}}$, $a$ и $\chi $, при этом эллиптический модуль $\chi $ зависит от $\gamma {\text{/}}k$ и от $a$. Следовательно, в данной нелинейной задаче функция $k = k(\gamma {\text{/}}k,a,{{u}_{1}})$ зависит от трех переменных (а также от $h$ и проницаемостей, которые в нашей задаче являются постоянными).

Чтобы удостовериться в справедливости (26), рассмотрим первый интеграл уравнения (1), который находится при помощи умножения обеих частей (1) на $u'$ и отыскания первообразной

$\frac{1}{2}{{(u')}^{2}} + ({{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}})\frac{{{{u}^{2}}}}{2} + {{k}^{2}}\beta \frac{{{{u}^{4}}}}{4} = C.$

Условие (14) равенства производной нулю в нуле ($u'(0) = 0$) позволяет найти константу интегрирования

$C = ({{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}})\frac{{{{a}^{2}}}}{2} + {{k}^{2}}\beta \frac{{{{a}^{4}}}}{4}.$

Подставим найденное значение константы в первый интеграл, тогда

(27)

${{(u')}^{2}} = ({{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}})({{a}^{2}} - {{u}^{2}}) + {{k}^{2}}\frac{\beta }{2}({{a}^{4}} - {{u}^{4}}) = ({{a}^{2}} - {{u}^{2}})\left( {{{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}} + {{k}^{2}}\frac{\beta }{2}({{a}^{2}} + {{u}^{2}})} \right).$

Используя обозначение $\chi $ для модуля эллиптического косинуса (19), получаем

(28)

${{(u')}^{2}} = \frac{\beta }{2}\frac{{{{k}^{2}}}}{{{{\chi }^{2}}}}({{a}^{2}} - {{u}^{2}})({{\chi }^{2}}{{u}^{2}} + (1 - {{\chi }^{2}}){{a}^{2}}).$

Возьмем квадратный корень из обеих частей, выбирая отрицательную ветвь. Получившееся автономное обыкновенное дифференциальное уравнение первого порядка решается в квадратурах, что и приводит, после замены переменной и пределов интегрирования, к формуле (26)

$kh = - \sqrt {\frac{2}{\beta }} \chi \int\limits_a^{{{u}_{1}}} {\,\frac{{du}}{{\sqrt {({{a}^{2}} - {{u}^{2}})({{\chi }^{2}}{{u}^{2}} + (1 - {{\chi }^{2}}){{a}^{2}})} }}} = \sqrt {\frac{2}{\beta }} \frac{\chi }{a}\int\limits_{{{u}_{1}}/a}^1 {\,\frac{{dv}}{{\sqrt {(1 - {{v}^{2}})({{\chi }^{2}}{{v}^{2}} + 1 - {{\chi }^{2}})} }}} \,.$

Интеграл, фигурирующий в правой части равенства, носит название неполного эллиптического интеграла первого рода [11]. Путем замены переменных $v = cos(t)$, ${{u}_{1}}{\text{/}}a = cos(\phi )$ и $m = {{\chi }^{2}}$, он приводится к виду, в котором может быть вычислен при помощи вызова функции $ellipkinc$ библиотеки SciPy языка Python или функции $ellipticF$ системы MATLAB

$ellipkinc(\phi ,m) = \int\limits_0^\phi {\frac{{dt}}{{\sqrt {1 - msi{{n}^{2}}(t)} }}} \,.$

Входными параметрами обеих функций являютcя $\phi = arccos({{u}_{1}}{\text{/}}a)$ и $m = {{\chi }^{2}}$.

4.2. Связь между значениями собственных функций, налагаемая граничными условиями

Чтобы вычислить $k$ по формуле (26), необходимо задать $\gamma {\text{/}}k$, ${{u}_{1}}$ и $a$. Покажем, что условия непрерывности собственной функции и ее производной на границе слоя позволяют выразить одну из переменных, ${{u}_{1}}$ или $a$, через другую и $\gamma {\text{/}}k$.

Как отмечено выше, в полупространстве решение имеет вид (20). Тогда справедливо равенство

${{(u')}^{2}} = ({{\gamma }^{2}} - {{k}^{2}}{{\varepsilon }_{1}}){{u}^{2}}.$

В разд. 3 с целью упрощения записи при доказательстве существования собственных значений мы использовали слой единичной толщины. Здесь и далее мы будем использовать произвольную толщину слоя $h$, чтобы получить формулы, непосредственно пригодные для численных экспериментов. Поэтому условия сопряжения, аналогичные (15) и (16), следует переписать в точке $x = h$ как

$u(h - 0) = u(h + 0)\quad {\text{и }}\quad u'(h - 0) = u'(h + 0).$

Поскольку мы ищем функцию, которая на границе слоя ($x = h$) непрерывна вместе с первой производной, приравняем правую часть этого равенства к правой части (27) и подставим вместо $u$ значение на границе ${{u}_{1}}$

$({{\gamma }^{2}} - {{k}^{2}}{{\varepsilon }_{1}})u_{1}^{2} = ({{a}^{2}} - u_{1}^{2})\left( {{{k}^{2}}{{\varepsilon }_{2}} - {{\gamma }^{2}} + {{k}^{2}}\frac{\beta }{2}({{a}^{2}} + u_{1}^{2})} \right).$

При помощи алгебраических преобразований получаем связь $\gamma {\text{/}}k$, ${{u}_{1}}$ и $a$ в виде

(29)

$\frac{\beta }{2}{{a}^{4}} + ({{\varepsilon }_{2}} - {{(\gamma {\text{/}}k)}^{2}}){{a}^{2}} - ({{\varepsilon }_{2}} - {{\varepsilon }_{1}})u_{1}^{2} - \frac{\beta }{2}u_{1}^{4} = 0.$

Формулу (29) можно рассматривать и как квадратное уравнение относительно $u_{1}^{2}$, и как квадратное уравнение относительно ${{a}^{2}}$. При первом подходе мы фиксируем какое-либо значение амплитуды собственной функции в нуле, $a$, и решаем (29) относительно $u_{1}^{2}$:

(30)

$u_{1}^{2} = \frac{{ - ({{\varepsilon }_{2}} - {{\varepsilon }_{1}}) + \sqrt {{{{({{\varepsilon }_{2}} - {{\varepsilon }_{1}})}}^{2}} + 2\beta {{a}^{2}}\left( {{{\varepsilon }_{2}} + \tfrac{1}{2}\beta {{a}^{2}} - {{{(\gamma {\text{/}}k)}}^{2}}} \right)} }}{\beta }.$

Теперь мы можем рассчитать кривую $k = k(\gamma {\text{/}}k)$ для выбранного параметра $a$ при помощи формулы (26) в любой интересующей нас точке $\gamma {\text{/}}k$. При этом амплитуда $a$ будет играть роль параметра семейства таких кривых, а значение на границе полупространства, ${{u}_{1}}$, – меняться вместе с $\gamma {\text{/}}k$.

При втором подходе в качества параметра семейства кривых закрепляется значение собственной функции на границе $u(x = h) = {{u}_{1}}$. Тогда решение квадратного уравнения (29) дает квадрат амплитуды

(31)

${{a}^{2}} = \frac{{{{{(\gamma {\text{/}}k)}}^{2}} - {{\varepsilon }_{2}} + \sqrt {\mathop {({{{(\gamma {\text{/}}k)}}^{2}} - {{\varepsilon }_{2}})}\nolimits^2 + 2\beta u_{1}^{2}\left( {{{\varepsilon }_{2}} + \tfrac{1}{2}\beta u_{1}^{2} - {{\varepsilon }_{1}}} \right)} }}{\beta }.$

Подстановка этой величины в (26) позволяет вычислить значения $k$ для любых интересующих нас значений $\gamma {\text{/}}k$ при постоянном значении собственной функции на границе слоя ${{u}_{1}}$. В данном случае именно граничное значение играет роль параметра семейства кривых. При этом амплитуда $a$ будет меняться в зависимости от $\gamma {\text{/}}k$.

Мы можем изучать функцию $k = k(\gamma {\text{/}}k)$ как однопараметрическое семейство кривых. В зависимости от того, что именно, $a$ или ${{u}_{1}}$ мы выберем в качестве параметра семейства кривых, “дисперсионные кривые” будут вести себя весьма различным образом.

В качестве параметров семейства “дисперсионных кривых” можно использовать и другие величины, на чем мы здесь не останавливаемся.

4.3. Алгоритм вычисления “дисперсионных кривых”

Представим алгоритм вычисления “дисперсионных кривых”, который позволяет вычислить явным образом $k$ как функцию от $\varepsilon {\kern 1pt} * = {{(\gamma {\text{/}}k)}^{2}}$. В дальнейшем при численных расчетах мы полагаем $h = 1$. В табл. 1 приведены два варианта алгоритма расчета $k$ для заданного $\varepsilon {\kern 1pt} *$. Первый вариант отвечает фиксированному в качестве параметра кривой $a$ и переменной величине ${{u}_{1}}$, а второй – фиксированному параметру ${{u}_{1}}$ и переменной величине $a$.

Таблица 1.

Два варианта алгоритма расчета $k$ для заданного $\varepsilon {\kern 1pt} *$

Шаг	Вариант 1	Вариант 2
Задать параметр кривой
1	$a = u(0) > 0$	${{u}_{1}} = u(h) > 0$
Задать аргумент $\varepsilon {\kern 1pt} * = {{(\gamma {\text{/}}k)}^{2}}$, удовлетворяющий условию
2	${{\varepsilon }_{1}} < \varepsilon {\kern 1pt} * < {{\varepsilon }_{2}} + \beta {{a}^{2}}{\text{/}}2$	$\varepsilon {\kern 1pt} * > {{\varepsilon }_{1}}$
3	Вычислить $u_{1}^{2}$ по формуле (30)	Вычислить ${{a}^{2}}$ по формуле (31)
4	Вычислить лежандров модуль по формуле (19)
5	Вычислить $k$ по формуле (26)
6	Вычислить собственное значение $\gamma = k\sqrt {\varepsilon {\kern 1pt} *} $

Результаты расчетов при $h = 1$ приведены на фиг. 3 и 4 .

Продемонстрируем далее, что в зависимости от выбора параметра семейства “дисперсионных кривых” поведение этих кривых может существенно отличаться.

Под “дисперсионной кривой” здесь подразумевается функция $k = k(\gamma {\text{/}}k)$ при фиксированном значении некоторого параметра, а под семейством таких кривых – совокупность таких функций для всех возможных значений параметра.

Так, если в качестве параметра семейства выбрать значение собственной функции в нуле $u(0) = a$, то функция $k(\gamma {\text{/}}k)$ определена лишь на интервале ${{\varepsilon }_{1}} < \gamma {\text{/}}k < {{\varepsilon }_{2}} + \beta {\text{/}}2{{a}^{2}}$ и неограниченно возрастает на нем, а если в качестве параметра взять значение на границе слоя ${{u}_{1}} = u(h)$, то функция $k(\gamma {\text{/}}k)$ определена и ограничена при всех $\gamma {\text{/}}k > 0$. В случае линейной задачи для изображения дисперсионных кривых обычно используется первый подход. Cопоставление результатов для линейного и нелинейного случая имеет смысл лишь при единообразном способе изображения кривых.

4.4. О монотонном росте кривой $k(\gamma {\text{/}}k)$ при постоянном $a$

Выберем в качестве параметра семейства “дисперсионных кривых” амплитуду собственной функции в нуле $a = u(0)$ и зафиксируем это значение. Таким образом, в этом разделе $a$ – константа. Для удобства введем переменную $\varepsilon {\kern 1pt} * = {{(\gamma {\text{/}}k)}^{2}}$, таким образом, $k = k(\sqrt {\varepsilon {\kern 1pt} *} )$.

Докажем, что при

(32)

${{\varepsilon }_{1}} < \varepsilon {\kern 1pt} * < {{\varepsilon }_{2}} + \beta {{a}^{2}}{\text{/}}2$

$k$ возрастает как функция $\gamma {\text{/}}k = \sqrt {\varepsilon {\kern 1pt} *} $. Это будет означать, что при выбранном способе параметризации семейства “дисперсионных кривых”, их поведение в нелинейном ($\beta \ne 0$) и линейном ($\beta = 0$) случаях не проявляет качественных отличий.

Воспользуемся выражением (26)

(33)

$k = \frac{1}{h}\sqrt {\frac{2}{\beta }} \frac{\chi }{a}\int\limits_{{{u}_{1}}/a}^1 {\frac{{dv}}{{\sqrt {(1 - {{v}^{2}})({{\chi }^{2}}{{v}^{2}} + 1 - {{\chi }^{2}})} }}} \,.$

Заметим, что от $\varepsilon {\kern 1pt} *$ в этом выражении зависят $\chi $ и ${{u}_{1}}$. Зависимость $\chi $ от $\varepsilon {\kern 1pt} *$ выявляется из (19) при замене ${{(\gamma {\text{/}}k)}^{2}} = \varepsilon $

(34)

${{\chi }^{2}} = \frac{1}{2}\frac{{\beta {{a}^{2}}}}{{{{\varepsilon }_{2}} + \beta {{a}^{2}} - \varepsilon {\kern 1pt} *}},$

а зависимость ${{u}_{1}}$ от $\varepsilon {\kern 1pt} *$ – из формулы (30) при аналогичной замене.

Из вида формул (33), (34) и (30) следует (в силу теоремы о дифференцируемости интеграла по параметру, см., например, [12, с. 66]), что $k$ дифференцируема по $\varepsilon {\kern 1pt} *$, и производная может быть найдена по правилу дифференцирования сложной функции

(35)

$\frac{{\partial k}}{{\partial \varepsilon {\kern 1pt} *}} = \frac{{\partial k}}{{\partial {{u}_{1}}}}\frac{{\partial {{u}_{1}}}}{{\partial \varepsilon {\kern 1pt} *}} + \frac{{\partial k}}{{\partial {{\chi }^{2}}}}\frac{{\partial {{\chi }^{2}}}}{{\partial \varepsilon {\kern 1pt} *}}.$

Таким образом, требуется доказать, что сумма (35) положительна на интервале (32). Возрастание $k$ по $\sqrt {\varepsilon {\kern 1pt} *} $ будет следовать из этого автоматически, поскольку

$\frac{{\partial k}}{{\partial \sqrt {\varepsilon {\kern 1pt} *} }} = 2\sqrt {\varepsilon {\kern 1pt} *} \frac{{\partial k}}{{\partial \varepsilon {\kern 1pt} *}}.$

Покажем, что положительны оба слагаемых (35). Начнем с первого из них. Дифференцируя интеграл, стоящий в (33), по нижнему пределу, получаем

$\frac{{\partial k}}{{\partial {{u}_{1}}}} = - \frac{1}{h}\sqrt {\frac{2}{\beta }} \frac{\chi }{{{{a}^{2}}}}\frac{1}{{\sqrt {\left( {1 - \tfrac{{u_{1}^{2}}}{{{{a}^{2}}}}} \right)\left( {{{\chi }^{2}}\tfrac{{u_{1}^{2}}}{{{{a}^{2}}}} + 1 - {{\chi }^{2}}} \right)} }} < 0.$

Далее, при помощи дифференцирования выражения (30) находим

$\frac{{\partial {{u}_{1}}}}{{\partial \varepsilon {\kern 1pt} *}} = - \frac{1}{{2{{u}_{1}}}}\frac{{{{a}^{2}}}}{{\beta u_{1}^{2} + {{\varepsilon }_{2}} - {{\varepsilon }_{1}}}} < 0.$

Таким образом, первое слагаемое суммы (35) положительно как произведение двух отрицательных сомножителей.

Рассмотрим теперь второе слагаемое. Разделим числитель и знаменатель подынтегрального выражения в (33) на $\chi $ и продифференцируем по квадрату этого параметра

$\frac{{\partial k}}{{\partial {{\chi }^{2}}}} = \frac{1}{2}\frac{1}{h}\frac{1}{{{{\chi }^{4}}}}\sqrt {\frac{2}{\beta }} \frac{1}{a}\int\limits_{{{u}_{1}}/a}^1 \,\frac{{dv}}{{\sqrt {1 - {{v}^{2}}} \mathop {\left( {\left( {{{v}^{2}} + \tfrac{1}{{{{\chi }^{2}}}} - 1} \right)} \right)}\nolimits^{3/2} }} > 0,$

поскольку из (32) и (34) следует, что $0 < \chi < 1$. (Неравенство является строгим, поскольку при условии (32) из формулы 30 следует ${{u}_{1}} < a$; следовательно, интеграл не обращается в ноль.)

Наконец, из (34) очевидно, что

$\frac{{\partial {{\chi }^{2}}}}{{\partial \varepsilon {\kern 1pt} *}} > 0.$

Таким образом, второе слагаемое суммы (35) тоже положительно, чем и завершается доказательство.

4.5. О неограниченности $k(\gamma {\text{/}}k)$ при фиксированном $a$ и $\gamma {\text{/}}k \to {{\varepsilon }_{2}} + \beta {{a}^{2}}$

Заметим сначала, что из (30) следует

$\mathop {lim}\limits_{\varepsilon * \to {{\varepsilon }_{2}} + \beta {{a}^{2}}/2} {{u}_{1}} = 0,$

а из (34) следует

$\mathop {lim}\limits_{\varepsilon * \to {{\varepsilon }_{2}} + \beta {{a}^{2}}/2} \chi = 1.$

Для $0 < {{v}^{2}} \leqslant 1$ имеем $1 - {{v}^{2}} \leqslant 1$, откуда следует

$\frac{1}{{\sqrt {(1 - {{v}^{2}})({{\chi }^{2}}{{v}^{2}} + 1 - {{\chi }^{2}})} }} \geqslant \frac{1}{{\sqrt {{{\chi }^{2}}{{v}^{2}} + 1 - {{\chi }^{2}}} }},$

а значит, для (33) верна оценка снизу

$k \geqslant \frac{1}{h}\sqrt {\frac{2}{\beta }} \frac{\chi }{a}\int\limits_{{{u}_{1}}/a}^1 \,\frac{{dv}}{{\sqrt {{{\chi }^{2}}{{v}^{2}} + 1 - {{\chi }^{2}}} }} = \frac{1}{h}\sqrt {\frac{2}{\beta }} \frac{1}{a}ln\left( {\frac{{\chi + 1}}{{\chi {{u}_{1}}{\text{/}}a + \sqrt {{{\chi }^{2}}{{{({{u}_{1}}{\text{/}}a)}}^{2}} + 1 - {{\chi }^{2}}} }}} \right).$

При ${{u}_{1}} \to 0$ и $\chi \to 1$ выражение справа неограниченно возрастает. Следовательно,

$\mathop {lim}\limits_{\varepsilon * \to {{\varepsilon }_{2}} + \beta {{a}^{2}}/2} k = + \infty .$

Итак, если в качестве параметра семейства взята амплитуда $a$, то “дисперсионные кривые” непрерывно возрастают на интервале (32), устремляясь к бесконечности на его правом конце.

4.6. Об ограниченности $k\left( {\tfrac{\gamma }{k}} \right)$ при фиксированном значении $u(h)$

Зафиксируем теперь в качестве параметра семейства “дисперсионных кривых” значение на границе $u(h) = {{u}_{1}}$. Амплитуда $a$ теперь становится переменной величиной, изменяясь вместе с $\varepsilon {\kern 1pt} *$ в соответствии с (31). Поскольку $v \leqslant 1$ и $\chi \leqslant 1$, а значит,

${{\chi }^{2}}{{v}^{2}} + \mathop \chi \nolimits^{'2} \geqslant {{v}^{2}},$

получим для (33) оценку сверху

$k \leqslant \frac{1}{h}\frac{\chi }{a}\sqrt {\frac{2}{\beta }} \int\limits_{{{u}_{1}}/a}^1 {\,\frac{{dv}}{{v\sqrt {1 - {{v}^{2}}} }}} = \frac{1}{h}\sqrt {\frac{2}{\beta }} \frac{\chi }{a}cos{{h}^{{ - 1}}}(a{\text{/}}{{u}_{1}}).$

Действительно, делая замену $w = 1{\text{/}}v$, имеем

$\int\limits_{{{u}_{1}}/a}^1 {\frac{{dv}}{{v\sqrt {1 - {{v}^{2}}} }}} = \int\limits_1^{a/{{u}_{1}}} {\frac{{dw}}{{\sqrt {{{w}^{2}} - 1} }}} = cos{{h}^{{ - 1}}}(a{\text{/}}{{u}_{1}}).$

Наконец, поскольку при $z > 0$

$cos{{h}^{{ - 1}}}z = ln(z + \sqrt {{{z}^{2}} - 1} ) \leqslant ln2z \leqslant \frac{{2z}}{e}$

с учетом $\chi \leqslant 1$, получаем оценку сверху

$k \leqslant \frac{1}{h}\sqrt {\frac{2}{\beta }} \frac{2}{e}\frac{1}{{{{u}_{1}}}},$

справедливую для всех ${{\varepsilon }^{*}}$. Таким образом, значения $k$ принадлежат ограниченному интервалу.

Установим теперь поведение $k$ при $\varepsilon {\kern 1pt} * \to \infty $. Подставляя (31) в (34), получаем

$\chi = \frac{{{{a}^{2}}}}{{\sqrt {{{a}^{4}} + \left( {2\tfrac{{{{\varepsilon }_{2}} - {{\varepsilon }_{1}}}}{\beta }u_{1}^{2} + u_{1}^{4}} \right)} }},$

откуда следует $\mathop {lim}\limits_{a \to \infty } \chi = 1$.

В результате имеем

$\mathop {lim}\limits_{a \to \infty } k \leqslant \frac{1}{h}\sqrt {\frac{2}{\beta }} \mathop {lim}\limits_{a \to \infty } \left[ {\frac{\chi }{a}cos{{h}^{{ - 1}}}\left( {\frac{a}{{{{u}_{1}}}}} \right)} \right] = 0.$

Функция $k(\varepsilon {\kern 1pt} *)$ стремится к нулю при $\varepsilon {\kern 1pt} * \to \infty $.

При $\varepsilon {\kern 1pt} * \to {{\varepsilon }_{1}}$ в силу (29) ${{u}_{1}} \to a$. Поэтому нижний предел интегрирования в интеграле (26), определяющем $k,$ стремится к $1$. В результате функция $k$ стремится к нулю при $\varepsilon {\kern 1pt} * \to {{\varepsilon }_{1}}$. Как следует из (33), $k$ непрерывна и положительна. Поскольку $k$ стремится к нулю при $\varepsilon {\kern 1pt} * \to \infty $ и $\varepsilon {\kern 1pt} * \to {{\varepsilon }_{1}}$ и является ограниченной величиной при $\varepsilon {\kern 1pt} * > {{\varepsilon }_{1}}$, то она достигает максимума внутри полубесконечного интервала [12].

Мы делаем вывод, что в случае, если в качестве параметра семейства “дисперсионных кривых” берется граничное значение $u(h)$, то свойства таких кривых не имеют аналогов в линейном случае. Это означает, что результаты сравнения кривых для нелинейных и линейных сред, вообще говоря, зависят от того, как параметризуется семейство кривых.

Список литературы

Маркузе Д. Оптические волноводы. М.: Мир, 1974.
Litvak A.G., Mironov V.A. Surface waves on the sepaation boundary between nonlinear media // Izv. VUZ Radiofiz. 1968. № 11. P. 1911–1912.
Fedyanin V.K., Mihalache D. P-Polarized Nonlinear Surface Polaritons in Layered Structures // Z. Phys. B – Condensed Matter 1982. V. 47. № 9. P. 167–173.
Елеонский В.М., Оганесьянц Л.Г., Силин В.П. Векторная структура электромагнитного поля в самосфокусированных волноводах // Успехи физ. наук. 1972. Т. 107. № 6. С. 516–518.
Michalache D., Bertolotty E.M., Sibilia C. Nonlinear wave propagation in planar structures. Progress in Optics XXVII. North. Holland: Elsevier. 1989.
Валовик Д.В. Распространение электромагнитных ТЕ-волн в нелинейной среде с насыщением // Радиотехн. и электроника. 2011. Т. 56. № 11. С. 1329–1335.
Валовик Д.В., Смирнов Ю.Г., Смолькин Е.Ю. Нелинейная задача сопряжения на собственные значения, описывающая распространение ТЕ-волн в двухслойных цилиндрических диэлектрических волноводах // Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 7. С. 1150–1161.
Валовик Д.В., Смолькин Е.Ю. Расчет постоянных распространения неоднородных нелинейных двухслойных круглых цилиндрических волноводов методом задачи Коши // Радиотехн. и электроника, 2013. Т. 58. № 8. С. 759–767.
Красносельский М.А. Топологические методы в теории нелинейных интегральных уравнений. М.: Гостехиздат, 1956.
Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Наука, 1979.
Сикорский Ю.С. Элементы теории эллиптических функций c приложениями к механике. М.: URSS. 2014.
Валле-Пуссен Ш.Ж. Курс анализа бесконечно малых. Т. 2. Москва–Ленинград: Гос. техиздат, 1933.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал