Журнал вычислительной математики и математической физики, 2019, T. 59, № 5, стр. 838-858

1. ФОРМУЛИРОВКА ЗАДАЧИ И ВВОДНЫЕ ЗАМЕЧАНИЯ

Пусть $\Sigma = \{ (x,y,z) \in {{\mathbb{R}}^{3}}:0 \leqslant x \leqslant h,\;(y,z) \in {{\mathbb{R}}^{2}}\} $ – слой, расположенный между двумя полупространствами в ${{\mathbb{R}}^{3}}$ (см. фиг. 1).

Рассмотрим распространение монохроматической ТЕ-волны $({\mathbf{E}},{\mathbf{H}}){{e}^{{ - i\omega }}}$ в слое $\Sigma $, где

компоненты полей (1.1) имеют вид здесь $\omega $ – круговая частота, $\gamma $ – неизвестный вещественный параметр (постоянная распространения).

Поля (1.1), (1.2) удовлетворяют уравнениям Максвелла

условию непрерывности касательных компонент поля на границах $x = 0$, $x = h$ и условию излучения на бесконечности: электромагнитное поле экспоненциально затухает при ${\text{|}}x{\text{|}} \to \infty $; при этом значение ${{\left. {{{e}_{y}}} \right|}_{{x = 0 - 0}}} = A \ne 0$ предполагается фиксированным (без потери общности $A > 0$).

Диэлектрическая проницаемость пространства имеет вид

где $a > 0$ – вещественный параметр, ${{\epsilon }_{s}},\;{{\epsilon }_{l}},\;{{\epsilon }_{c}}$ – положительные вещественные постоянные такие, что а $f\; \in {{C}^{1}}[0, + \infty )$ – монотонно возрастающая функция и $f(0) = 0$. Во всем пространстве $\mu = {{\mu }_{0}} > 0$ – магнитная проницаемость вакуума.

В сформулированной задаче искомыми являются значения параметра $\gamma $, которые отвечают распространяющимся в $\Sigma $ волнам (1.1), (1.2). Далее будет показано, что параметр $\gamma $ удовлетворяет некоторому (трансцендентному) уравнению, которое называется дисперсионным уравнением. Исследование этого уравнения позволяет получить результаты о разрешимости изучаемой задачи.

Условие (1.5) означает, что в линейном случае (при $a = 0$) среда в слое является оптически более плотной по сравнению со средами, заполняющими полупространства. Такое условие необходимо для существования распространяющихся волн вида (1.1), (1.2) в слое $\Sigma $ при $a = 0$ (см. разд. 3).

Зависимость от модуля поля в (1.4) отвечает эффектам самовоздействия в нелинейной оптике [1]–[3]. Функция $f$ наделена свойствами, которые позволяют применять развитую ниже теорию для изучения широкого круга нелинейностей, отвечающих средам с центром инверсии [1], [2]. Свойствам, наложенным на функцию $f$, в частности, удовлетворяют полиномы по четным степеням с положительными коэффициентами, степенная функция с произвольным положительным показателем степени, логарифмическая нелинейность, различные типы ограниченных нелинейностей [1]–[11].

Первая достаточно строгая постановка изучаемой здесь задачи, насколько нам известно, появилась в [12]. Результаты, накопившиеся к 1991 г. в этой области, подробно изложены в работе [4], где имеется обширная библиография, см. также [5], [6]. Отметим, что несмотря на относительную простоту уравнений (1.3) для функции $f({\text{|}}{\mathbf{E}}{{{\text{|}}}^{2}}) = {\text{|}}{\mathbf{E}}{{{\text{|}}}^{2}}$ для полей (1.1)–(1.2), существенный прогресс в такой задаче был достигнут сравнительно недавно, см. [7], [8], а также [9], посвященную изучению полиномиальной нелинейности.

В настоящей работе построен общий математический аппарат, позволяющий исследовать сформулированную выше задачу для широкого круга нелинейностей. Статья имеет следующую структуру. В разд. 2 физическая задача сведена к нелинейной задаче на собственные значения типа Штурма–Лиувилля на отрезке; в разд. 3 кратко изложены известные результаты о разрешимости линейной задачи; в разд. 4 получено и исследовано дисперсионное уравнение; в разд. 5 получены достаточные условия существования собственных значений; в разд. 6 получены дальнейшие результаты для нелинейности, имеющей степенной рост, логарифмической нелинейности и ограниченных нелинейностей; доказательства представлены в разд. 7.

2. НЕЛИНЕЙНАЯ ЗАДАЧА ТИПА ШТУРМА–ЛИУВИЛЛЯ

Подставив поля (1.1)–(1.2) в систему (1.3) и обозначив $(\, \cdot \,)' = \tfrac{d}{{dx}}$, получаем

Отсюда находим ${{\gamma }^{2}}{{e}_{y}} - e_{y}^{{''}} = {{\omega }^{2}}\mu \epsilon {{e}_{y}}$, при этом ${{h}_{x}} = - \tfrac{\gamma }{{\omega \mu }}{{e}_{y}}$, ${{h}_{z}} = - \tfrac{i}{{\omega \mu }}e_{y}^{'}$.

Обозначив $u: = {{e}_{y}}$, из найденного получаем

где $\varepsilon : = {{\omega }^{2}}\mu \epsilon $, $\alpha : = {{\omega }^{2}}\mu a$, а ${{\varepsilon }_{j}}: = {{\omega }^{2}}\mu {{\epsilon }_{j}}$ и $j \in \{ s,l,c\} $.

В полупространствах $x < 0$ и $x > h$ уравнение (2.1) линейное; с учетом условий на бесконечности решения этого уравнения имеют вид

где ${{k}_{s}} = \sqrt {{{\gamma }^{2}} - {{\varepsilon }_{s}}} > 0,$ ${{k}_{c}} = \sqrt {{{\gamma }^{2}} - {{\varepsilon }_{c}}} > 0$ и ${{\varepsilon }_{s}} \geqslant {{\varepsilon }_{c}}.$

Внутри слоя $\Sigma $ уравнение (2.1) принимает вид

где $u \equiv u(x;\gamma )$, $x \in [0,h]$; при этом $\gamma $ – вещественный спектральный параметр (без потери общности $\gamma > 0$), $\alpha > 0$ – постоянная, а $f \in {{C}^{1}}[0, + \infty )$ – монотонно возрастающая функция и $f(0) = 0$.

Известно, что касательные компоненты электромагнитного поля непрерывны на границе раздела сред [13], [14]. Здесь таковыми являются ${{e}_{y}}$ и ${{h}_{z}}$. Из непрерывности этих компонент следуют условия сопряжения:

где $\mathop {\left. {[u]{\kern 1pt} } \right|}\nolimits_{x = {{x}_{0}}} = li{{m}_{{x \to {{x}_{0}} - 0}}}u(x) - li{{m}_{{x \to {{x}_{0}} + 0}}}u(x)$.

Используя найденные для полупространств $x < 0$ и $x > h$ решения и условия сопряжения, получаем краевые условия

где величина является фиксированной (известной). Предполагаем, что

Поскольку уравнение (2.2) и условия (2.3) зависят от ${{\gamma }^{2}}$, то достаточно изучить случай $\gamma > 0$. Из условий ${{k}_{s}},{{k}_{c}} > 0$ и ${{\varepsilon }_{s}} \geqslant {{\varepsilon }_{c}}$ следует, что

Итак, задача о распространении волн сведена к нелинейной задаче на собственные значения типа Штурма–Лиувилля (2.2)–(2.6).

Введем необходимое

Определение 1. Число $\gamma = \hat {\gamma }$, удовлетворяющее условию (2.6), и такое, что при фиксированном значении $u(0) \ne 0$ (без потери общности $u(0) > 0$) существует функция $u \equiv u(x;\hat {\gamma })$, которая удовлетворяет уравнению (2.2) и условиям (2.3)–(2.5), будем называть собственным значением задачи (2.2)–(2.6), а функцию $u(x;\hat {\gamma })$, соответствующую собственному значению $\hat {\gamma }$, – собственной функцией задачи (2.2)–(2.6).

Задачу (2.2)–(2.6) назовем задачей $\mathcal{P}$, а ее собственные значения обозначим через $\hat {\gamma }$ и ${{\hat {\gamma }}_{i}}$; в последнем случае предполагается, что собственные значения упорядочены по возрастанию.

Замечание 1. Определение 1 является неклассическим аналогом известного определения характеристического числа линейной оператор-функции, нелинейно зависящей от спектрального параметра [15].

Подчеркнем, что всюду ниже, когда речь идет о собственных значениях, имеются в виду собственные значения, удовлетворяющие определению 1. Другими словами, приводимые ниже утверждения и теоремы не относятся к понятию собственного значения в общеупотребительном смысле.

Отметим, что многие задачи нелинейной теории волноводов остаются вне пределов досягаемости известных подходов нелинейного анализа [16–19]. Например, вариационные методы [16], [17] не подходят для исследования задачи $\mathcal{P}$, поскольку для их применения естественное дополнительное условие является условием типа $\left\| u \right\| = {\text{const}}$. Упомянем еще работу [20], в которой для решения (нелинейной) задачи теории волноводов применяется тем не менее теория из [16]. В [20] доказано существование бесконечного числа собственных значений при дополнительном условии $\left\| u \right\| = t$; при этом различным собственным значениям отвечают различные ${\text{const}}$. Из изложенного в работе [20] материала можно сделать вывод, что теория из [16] не применима в случае, если хотя бы одна из границ волновода открыта, а также если нелинейность не является степенной функцией.

3. ЛИНЕЙНАЯ ЗАДАЧА

Линейную задачу (при $\alpha = 0$) назовем задачей ${{\mathcal{P}}_{0}}$, а ее собственные значения обозначим $\tilde {\gamma }$ и ${{\tilde {\gamma }}_{i}}$; в последнем случае предполагается, что собственные значения упорядочены по возрастанию. Задача ${{\mathcal{P}}_{0}}$ является классической в электродинамике и хорошо изучена [13]. Можно показать, что справедливо

Утверждение 1. Существует постоянная ${{h}_{0}} > 0$ такая, что для любого $h > {{h}_{0}}$ задача ${{\mathcal{P}}_{0}}$ имеет конечное число (не менее одного) положительных и простых собственных значений ${{\tilde {\gamma }}_{i}} \in (\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$. Если ${{\varepsilon }_{s}} = {{\varepsilon }_{c}}$, то ${{h}_{0}} = 0$.

Собственные значения $\gamma = {{\tilde {\gamma }}_{i}}$ задачи ${{\mathcal{P}}_{0}}$ являются (однократными) корнями дисперсионного уравнения

где ${{k}_{l}} = \sqrt {{{\varepsilon }_{l}} - {{\gamma }^{2}}} > 0$ (см. [13]).

Замечание 2. Если ${{\varepsilon }_{l}} < {{\varepsilon }_{s}}$, то задача ${{\mathcal{P}}_{0}}$ не имеет решений.

4. ДИСПЕРСИОННОЕ УРАВНЕНИЕ

Условия

которые следуют из условий (2.3) и (2.4), составляют начальные данные задачи Коши для уравнения (2.2). Таким образом, изучение задачи $\mathcal{P}$ естественно начать с изучения вопроса о глобальной однозначной разрешимости указанной задачи Коши.

Умножая (2.2) на $u{\kern 1pt} '$, интегрируя и используя (4.1), получаем

где а $C = ({{\varepsilon }_{l}} - {{\varepsilon }_{s}}){{A}^{2}} + \alpha F({{A}^{2}}) > 0$ – постоянная.

Подставляя $x = h$ в (4.2), используя (2.3) и обозначая $B = u(h)$, получаем

Это уравнение имеет только два вещественных решения $B = \pm B'$.

Используя (4.2), можно показать, что задача Коши (2.2), (4.1) имеет единственное непрерывное решение $u \equiv u(x;\gamma )$, определенное при $x \in [0,h]$, если это решение не обращается в нуль на $(0,h)$. Если же $u \equiv u(x;\gamma )$ обращается в нуль в некоторых точках интервала $(0,h)$, то в таких точках надо продолжить функцию $u$, подклеивая к ней функцию $ - u$, сдвинутую на некоторую величину. Эта процедура будет реализована в доказательстве утверждения о разрешимости задачи Коши, сформулированного ниже.

Введем новые переменные:

Используя условия (2.3), находим

Значения $\eta (x)$ зависят в том числе от $\gamma $ и $\alpha $; для сокращения записи не будем явно указывать зависимость от этих параметров.

Используя (4.3), запишем уравнение (2.2) в виде системы

Первый интеграл системы (4.5) имеет вид где постоянная $C$ определена в (4.2).

Поскольку формула (4.6) неявно определяет функцию $\tau \equiv \tau (\eta ;\gamma )$, то второе уравнение системы (4.5) можно переписать в виде $\eta {\kern 1pt} ' = - w(\eta ;\gamma )$, где

Легко проверить, что $w(\eta ;\gamma ) > 0$ для всех $\gamma $, удовлетворяющих условию (2.6). Действительно, пусть $w$ в какой-то точке обращается в нуль. Из равенства $w = 0$ находим ${{\eta }^{2}} + {{\varepsilon }_{l}} - {{\gamma }^{2}} = - \alpha f(\tau )$. Подставляя найденное в (4.6), получаем

Поскольку $f$ монотонно возрастает, то $f{\kern 1pt} ' > 0$, и значит, $C < 0$. Но из (14) известно, что $C > 0$. Полученное противоречие показывает, что $w(\eta ;\gamma ) > 0$ при $\gamma > \sqrt {{{\varepsilon }_{s}}} $.

Итак, $\eta {\kern 1pt} ' = - w(\eta ;\gamma ) < 0$ и, следовательно, функция $\eta (x)$ монотонно убывает. Из второй формулы (4.3) следует, что $\eta $ непрерывна если и только если $u$ не обращается в нуль. Предположим, что $u(x)$ имеет $n \geqslant 0$ нулей ${{x}_{1}},\; \ldots ,\;{{x}_{n}} \in (0,h)$, тогда $\eta (x)$ имеет $n$ точек разрыва ${{x}_{1}},\; \ldots ,\;{{x}_{n}}$. Очевидно, что если $u\not { \equiv }0$, то $u{\kern 1pt} '({{x}_{i}}) \ne 0$ для всех $i = \overline {1,n} $. Действительно, если непостоянное решение $u$ уравнения (2.2) обращается в нуль вместе со своей производной $u{\kern 1pt} '$ в некоторой точке, то из классических результатов о (локальном) существовании и единственности решения задачи Коши для обыкновенного дифференциального уравнения следует, что $u \equiv 0$ [21]. Таким образом, все точки разрыва являются точками разрыва II рода.

Из монотонного убывания $\eta (x)$ и формул (4.4) следует, что

Теперь осталось проинтегрировать уравнение $\eta {\kern 1pt} ' = - w(\eta ;\gamma )$ на каждом из (полу) интервалов $[0,{{x}_{1}})$, $({{x}_{1}},{{x}_{2}})$, $...$, $({{x}_{n}},h]$ и использовать условия (4.8), чтобы получить

Утверждение 2. Задача Коши (2.2), (4.1) глобально и однозначно разрешима, а ее (классическое) решение $u \equiv u(x;\gamma )$ непрерывно зависит от точки $(x,\gamma ,\alpha ) \in [0,h] \times (\sqrt {{{\varepsilon }_{s}}} , + \infty ) \times (0, + \infty )$; при этом если решение $u \equiv u(x;\gamma )$ имеет $n \geqslant 0$ нулей при $x \in (0,h)$, то выполняется формула

где значение $\eta (h)$, вообще говоря, не фиксировано.

Дисперсионное уравнение задачи $\mathcal{P}$ получается из соотношения (4.9) при использовании второго из условий (4.4) и имеет вид

где $n = 0,1,\; \ldots $

Соотношение (4.10) является семейством (но не системой) уравнений при различных $n$. Функция $\Phi (\gamma ;n)$ не зависит от $h$.

Результатом, позволяющим перейти от изучения задачи $\mathcal{P}$ к изучению дисперсионного уравнения (4.10), является

Теорема 1 (об эквивалентности). Дисперсионное уравнение (4.10) эквивалентно задаче $\mathcal{P}$ в том смысле, что число $\hat {\gamma }( > {\kern 1pt} \sqrt {{{\varepsilon }_{s}}} )$ является собственным значением задачи $\mathcal{P}$, если и только если существует целое число $\hat {n} \geqslant 0$ такое, что $\gamma = \hat {\gamma }$ удовлетворяет уравнению $\Phi (\gamma ;\hat {n}) = h$; при этом собственная функция $u \equiv u(x;\hat {\gamma })$ имеет $\hat {n}$ (простых) нулей

где $i = \overline {1,\hat {n}} $.

В связи с теоремой 1 естественно ввести

Определение 2. Собственное значение $\hat {\gamma }$ задачи $\mathcal{P}$ имеет кратность $p$, если $\gamma = \hat {\gamma }$ является корнем кратности $p$ уравнения (4.10).

Вывод уравнения (4.10) основан на том, что функция $w(s;\gamma )$, определенная формулой (4.7), сохраняет знак. Сохранение знака обеспечивает необращение в нуль знаменателя подынтегрального выражения в (4.10), при условии, что знаменатель существует. Однако функция $\tau \equiv \tau (\eta ;\gamma )$, определенная формулой (4.6), может не существовать при некоторых $\gamma $, а значит, при таких $\gamma $ не существует и функция $w(s;\gamma )$. Обозначим через ${{\gamma }_{{max}}}$ такое наименьшее значение $\gamma > \sqrt {{{\varepsilon }_{s}}} $, при котором не существует (положительной) функции $\tau $. Если $\tau > 0$ существует для любого $\gamma > \sqrt {{{\varepsilon }_{s}}} $, то ${{\gamma }_{{max}}} = + \infty $. Будем использовать обозначение $\Gamma : = (\sqrt {{{\varepsilon }_{s}}} ,{{\gamma }_{{max}}})$.

Заметим, что рассуждения предыдущего абзаца не противоречат утверждению 2, поскольку когда речь идет об уравнении (4.10), то выполняются оба условия (4.4). В случае обсуждаемой задачи Коши выполняется лишь первое из этих условий, а решение этой задачи может не обращаться в нуль (подробности см. в доказательстве утверждений 2 и 4).

Итак, имеет место

Утверждение 3. Определенная формулой (4.10) функция $\Phi \equiv \Phi (\gamma ;n)$ для всякого целого $n \geqslant 0$ существует, непрерывна и положительна для всех $\gamma \in \Gamma $.

Из теоремы 1 и утверждения 3 вытекает

Следствие 1. Дисперсионное уравнение (4.10) эквивалентно (в смысле теоремы 1) задаче $\mathcal{P}$ для всех $\gamma \in \Gamma $.

Ниже получены оценки на ${{\gamma }_{{max}}}$, позволяющие точно определить множество $\Gamma $, на котором имеет место установленная в теореме 1 эквивалентность. А именно, справедливо

Утверждение 4. Если $f$ – неограниченная функция, то ${{\gamma }_{{max}}} = + \infty $; если же $f$ ограничена, то ${{\gamma }_{{max}}} = \sqrt {{{\varepsilon }_{l}} + \alpha {{f}_{{max}}}} $, где ${{f}_{{max}}} = li{{m}_{{\tau \to + \infty }}}f(\tau )$.

Определенный интерес представляет

Теорема 2 (о периодичности). Пусть $\gamma = \hat {\gamma }$ – собственное значение задачи $P$, а $u \equiv u(x;\hat {\gamma })$, где $x \in [0,h]$, отвечающая ему собственная функция. Если функция $u(x;\hat {\gamma })$ имеет более двух нулей при $x \in (0,h)$, то она периодическая с периодом $\Theta = 2\int_{ - \infty }^{ + \infty } \tfrac{{ds}}{{w(s;\hat {\gamma })}}$.

Замечание 3. Нахождение условий существования периодического решения нелинейного автономного уравнения, даже в том случае, когда не удается определить период, является задачей, привлекающей внимание исследователей [22], [23]. В задаче $\mathcal{P}$ не только найдены условия существования периодического решения, но и указана явная формула для периода (см. теорему 2).

Замечание 4. В линейном случае всякая собственная функция в слое $\Sigma $ имеет вид $u(x) = $ $ = {{C}_{1}}sin{{k}_{l}}x + {{C}_{2}}cos{{k}_{l}}x$, где ${{C}_{1}}$ и ${{C}_{2}}$ – постоянные, определяемые из условий (2.3). Поскольку такая функция $u$ не может быть периодической, если нигде не обращается в нуль, то в линейной задаче не существует знакопостоянных периодических решений. В нелинейном случае могут существовать знакопостоянные периодические решения, см. [8].

5. ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ

Пусть

где $k = 0,1,\; \ldots $, а функция $\Phi (\gamma ;k)$ определена в (4.10).

Поскольку $\Phi (\gamma ;k) > 0$, то $h_{{inf}}^{{(k)}}$ всегда существует и имеет конечное значение. Если существует $\gamma \in \Gamma $, в окрестности которого функция $\Phi (\gamma ;k)$ стремится к бесконечности, то считаем $h_{{sup}}^{{(k)}} = + \infty $. Заметим, что $h_{{sup}}^{{(k)}}$ может стремиться к бесконечности только если $\gamma \to {{\gamma }_{{max}}}$.

Достаточное условие существования по крайней мере одного собственного значения задачи $\mathcal{P}$ дает

Теорема 3. Пусть $h_{{inf}}^{{(p)}} < h_{{sup}}^{{(p)}}$ для некоторого $p = p{\kern 1pt} '$ и $h$ таково, что $h_{{inf}}^{{(p')}} < h < h_{{sup}}^{{(p')}}$, тогда задача $\mathcal{P}$ имеет по крайней мере одно решение.

Пусть $\Delta = [0, + \infty ) \subset \mathbb{R}$, а ${{B}_{\delta }}(x)$ – открытый шар радиуса $\delta $ с центром в точке $x$, где $\delta > 0$ – фиксированное число. Обозначим $R_{\Delta }^{\delta } = \bigcup\nolimits_{x \in \Delta } \,{{B}_{\delta }}(x)$ – (открытую) окрестность множества $\Delta $ на комплексной плоскости $C$. Тогда имеет место

Утверждение 5. Функция $\tau (\eta ;\gamma )$, неявно заданная формулой (18), существует, непрерывна и положительна для всех $(\eta ,\gamma ) \in \mathbb{R} \times \Gamma $. Если при этом $f \equiv f(z)$ является аналитической функцией $z$ при $z \in R_{\Delta }^{\delta } \subset \mathbb{C}$, то функция $\tau (\eta ;\gamma )$ аналитически зависит от $\gamma $ при $\gamma \in \Gamma $.

Из результатов следствия 1 и утверждения 5 вытекает

Теорема 4. Пусть $h_{{inf}}^{{(p)}} < h_{{sup}}^{{(p)}}$ для всех $\mathcal{P}$, функция $f(z)$ является аналитической функцией $z$ при $z \in R_{\Delta }^{\delta } \subset \mathbb{C}$ и $h$ таково, что для некоторого $p = p{\kern 1pt} '$ выполняется неравенство $h_{{inf}}^{{(p')}} < h < h_{{{\text{sup}}}}^{{(p')}}$, тогда множество собственных значений задачи $\mathcal{P}$ не пусто и является дискретным на $\Gamma $, то есть на каждом отрезке $\Gamma {\kern 1pt} ' \subset \Gamma $ содержится не более конечного числа (изолированных) собственных значений.

Величины $h_{{inf}}^{{(k)}}$ и $h_{{sup}}^{{(k)}}$ можно находить численно.

Пусть параметры задачи $\mathcal{P}$ таковы, что отвечающая ей (линейная) задача ${{\mathcal{P}}_{0}}$ имеет $k$ собственных значений. В этих условиях можно доказать существование собственных значений задачи $\mathcal{P}$, близких к решениям задачи ${{\mathcal{P}}_{0}}$, если постоянная $\alpha ( > {\kern 1pt} 0)$ достаточно мала.

Сначала сформулируем

Утверждение 6. Если $\sqrt {{{\varepsilon }_{s}}} < \gamma < \sqrt {{{\varepsilon }_{l}}} $, то $li{{m}_{{\alpha \to + 0}}}\Phi (\gamma ;n) = {{\Phi }_{0}}(\gamma ;n)$, где $n \geqslant 0$ – целое число, и имеет место уравнение

Используя утверждение 6, можно показать, что справедлива

Теорема 5. Пусть задача ${{\mathcal{P}}_{0}}$ имеет $k$ решений ${{\tilde {\gamma }}_{i}}$ $(i = \overline {1,k} )$, тогда найдется постоянная $\alpha {\kern 1pt} {\text{''}} > 0$ такая, что для любого $\alpha = \alpha {\kern 1pt} ' < \alpha {\kern 1pt} ''$ существует по крайней мере $k$ собственных значений ${{\hat {\gamma }}_{i}}$ $(i = \overline {1,k} )$ задачи $P$ и верно, что ${{\hat {\gamma }}_{i}} \in (\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$; при этом $li{{m}_{{\alpha {\kern 1pt} ' \to + 0}}}{{\hat {\gamma }}_{i}} = {{\tilde {\gamma }}_{i}}$ $(i = \overline {1,k} )$.

Доказательство теоремы 5 по существу представляет собой вариант метода возмущений и основано на использовании уравнений (4.10) и (5.1). Аналогичный результат может быть доказан с использованием принципиально иного подхода, основанного на полуобращении с помощью функции Грина линейной части дифференциального оператора, определенного уравнением (2.2), см., например, [24].

Вычислив интегралы в (5.1) и упростив, получаем уравнение

где $n = 0,1,\; \ldots $ . Взяв $tan$ от (5.2), получаем (3.1).

Дальнейшие результаты о собственных значениях задачи $\mathcal{P}$ получены в п. 6 при дополнительных условиях на функцию $f$ и без предположения о малости $\alpha $.

Замечание 5. Из теоремы 1 следует, что если $\gamma = \hat {\gamma }$ является решением уравнения $\Phi (\gamma ;\hat {n}) = h$, то собственная функция $u(x;\hat {\gamma })$ имеет $\hat {n}$ нулей. В задаче $\mathcal{P}$ могут существовать собственные функции, отвечающие различным собственным значениям, но имеющие одно и то же число нулей. В задаче ${{\mathcal{P}}_{0}}$ существует не более одной собственной функции с заданным числом нулей.

6. ПРИМЕРЫ И ПРИЛОЖЕНИЯ

Уравнение (4.10) можно записать в виде, более удобном для дальнейшего анализа. А именно, справедливо

Утверждение 7. Уравнение (4.10) эквивалентно уравнению

где $v(\tau ;\gamma ) = 2\sqrt \tau \sqrt {C - ({{\varepsilon }_{l}} - {{\gamma }^{2}})\tau - \alpha F(\tau )} $, $\gamma \in \Gamma $, $\tau = {{\tau }_{i}}$ есть (единственный) положительный корень уравненияа $\tau = {{\tau }_{ + }}$ есть (единственный) положительный корень уравненияпри этом ${{\tau }_{c}} \leqslant {{\tau }_{s}} < {{\tau }_{ + }}$, постоянная $C$ определена в (4.2).

Из утверждения 7 вытекает

Следствие 2. Пусть $T(\gamma ) = \int_{ - \infty }^{ + \infty } \tfrac{{ds}}{{w(s;\gamma )}}$, тогда справедлива формула

где $\tau = {{\tau }_{ + }}$ – (единственный) положительный корень уравнения (6.3).

Из формулы (4.10) и теоремы 3 следует неравенство

где $n = 0,1,\; \ldots $, $\gamma \in \Gamma $, а функция $T(\gamma )$ определена в следствии 2.

Неравенство (6.5) позволяет свести изучение разрешимости задачи $\mathcal{P}$ к изучению поведения $T(\gamma )$ при $\gamma \to {{\gamma }_{{max}}}$.

7. ДОКАЗАТЕЛЬСТВА

Доказательство утверждения 2. Если функция $f({{u}^{2}})$ является ограниченной при $u \in \mathbb{R}$, то известно, что задача Коши (2.2), (4.1) имеет единственное непрерывное решение $u \equiv u(x;\gamma )$, определенное при $x \in [0,h]$ [28].

Если функция $f$ является неограниченной, то из формулы (4.2) можно видеть, что для любого фиксированного значения $\gamma $ переменная $u$ может принимать значения из ограниченного подмножества $\mathbb{R}$. Отсюда следует, что и величина $u{\kern 1pt} '$ также принимает лишь ограниченные значения (при фиксированном значении $\gamma $).

Если искомое решение $u \equiv u(x;\gamma )$ имеет нули при $x \in (0,h)$, то можно провести процедуру продолжения, склеивая экземпляры функции $u$ противоположных знаков в ее нулях. Мы, по существу, воспользуемся этим методом, но в переменных (4.3), чтобы попутно получить формулу (4.9).

Итак, пусть $u$ имеет $n \geqslant 0$ нулей ${{x}_{1}},\; \ldots ,\;{{x}_{n}} \in (0,h)$, тогда $\eta (x)$ имеет $n$ точек разрыва ${{x}_{1}},\; \ldots ,\;{{x}_{n}}$; причем все точки разрыва являются точками разрыва второго рода.

Интегрируя уравнение $\eta {\kern 1pt} ' = - w(\eta ;\gamma )$ на каждом из (полу) интервалов $[0,{{x}_{1}})$, $({{x}_{1}},{{x}_{2}})$, $...$, $({{x}_{n}},h]$, получаем

Подставляя $x = 0$, $x = {{x}_{{i + 1}}} - 0$, $x = h$ в (первую, вторую и третью соответственно) строки (7.1), находим

С учетом найденных ${{c}_{i}}$ формулы (7.1) принимают вид

Подставляя $x = {{x}_{1}} - 0$, $x = {{x}_{i}} + 0$, $x = {{x}_{n}} + 0$ в (первую, вторую и третью соответственно) строки предыдущей формулы, получаем

Отсюда, принимая во внимание формулы (4.4) и (4.8), находим

Формулы (7.2) дают явные выражения для расстояний между нулями функции $u$, в частности, отсюда получается явная формула для $i$-го нуля ${{x}_{i}}$ функции $u$. Кроме того, из формул (7.2) следует сходимость всех рассматриваемых несобственных интегралов.

Далее, складывая все соотношения (7.2), получаем

Формула (4.9) тривиально следует из полученного соотношения.

Итак,  мы  доказали,  что  задача  Коши  (2.2), (4.1) глобально и однозначно разрешима при $x \in [0,h]$. Ее решение $u \equiv u(x;\gamma )$ непрерывно зависит от $x$ и параметров $\gamma ,\alpha $ при $(x,\gamma ,\alpha ) \in [0,h] \times (\sqrt {{{\varepsilon }_{s}}} , + \infty ) \times (0, + \infty )$. Этот результат следует из непрерывности правой части уравнения (2.2) и условий (2.3) по переменным $x,u$ и параметрам.

Рассмотрим решение $u \equiv u(x;\gamma )$ задачи Коши (2.2), (4.1). В случае если выполняются только условия (4.1), величина $\eta $ не обязательно изменяется от $ - \infty $ до $ + \infty $. Например, если $f$ ограничена и $\gamma > {{\gamma }_{{max}}}$, то решение $u$ в нуль не обращается, также не обращается в нуль и производная $u{\kern 1pt} '$ этого решения. Это приводит к тому, что переменная $\eta $ изменяется в области $(\delta ,{{k}_{s}})$, где $\delta \equiv \delta (\gamma )$.

Доказательство теоремы 1. Поскольку уравнение (4.10) является следствием задачи $\mathcal{P}$, то всякое собственное значение этой задачи является также и корнем этого уравнения. Докажем обратное. Пусть $\gamma = \hat {\gamma }$ – решение дисперсионного уравнения (4.10) при $n = \hat {n}$ и выполняются условия (4.1), где $\gamma = \hat {\gamma }$.

Рассмотрим задачу Коши для уравнения (2.2) с условиями (4.1). Существование единственного непрерывного решения $u \equiv u(x;\hat {\gamma })$, определенного при $x \in [0,h]$, следует из утверждения 2.

Используя найденное решение $u$ задачи Коши, построим функции $\tau = {{u}^{2}}$ и $\eta = u{\kern 1pt} {\text{'/}}u$. Ясно, что $\tau (0;\hat {\gamma }) = {{A}^{2}}$ и $\eta (0;\hat {\gamma }) = {{k}_{s}}$. Предположим, что $\eta (h;\hat {\gamma }) \ne - {{k}_{c}}$. Для определенности пусть $\eta (h;\hat {\gamma }) = - a < - {{k}_{c}}$.

При помощи $\tau $ и $\eta $ построим выражение

аналогичное (4.10). Полученное соотношение есть в точности Поскольку $\gamma = \hat {\gamma }$ является решением уравнения (4.10) при $n = \hat {n}$, то

Вычислив разность двух последних выражений, получаем

Поскольку $w(s;\gamma ) > 0$, то очевидно, что допущение $ - a < - {{k}_{c}}$ неверно. Также неверно и допущение $ - a > - {{k}_{c}}$. Стало быть $ - a = - {{k}_{c}}$.

По построению функция $u \equiv u(x;\hat {\gamma })$ удовлетворяет первому из условий (2.3). Выполнение условия $\eta (h) = - {{k}_{c}}$ означает, что $u$ удовлетворяет и второму из условий (2.3). Но тогда $u$ является собственной функцией, а $\gamma = \hat {\gamma }$ – собственным значением задачи $\mathcal{P}$. Таким образом, (спектральная) эквивалентность задачи $\mathcal{P}$ и уравнения (4.10) доказана.

Формулы (7.2) дают явные выражения для расстояний между нулями функции $u$, в частности, отсюда получается формула для $i$-го нуля ${{x}_{i}}$ функции $u$.

Доказательство утверждения 3. По определению множества $\Gamma $ функция $\tau \equiv \tau (\eta ;\gamma ) > 0$ существует при всех $\gamma \in \Gamma $ и непрерывно зависит от $(\eta ,\gamma ) \in \mathbb{R} \times \Gamma $. Поскольку функция $w(\eta ;\gamma ) > 0$ и непрерывно зависит от $\gamma \in \Gamma $, то отсюда следует результат утверждения.

Доказательство утверждения 4. Запишем первый интеграл (4.6) в виде ${{g}_{1}}(\tau ;\eta ,\gamma ) = {{g}_{2}}(\tau )$, где ${{g}_{1}}(\tau ;\eta ,\gamma ): = ({{\eta }^{2}} + {{\varepsilon }_{l}} - {{\gamma }^{2}})\tau $, а ${{g}_{2}}(\tau ): = C - \alpha F(\tau )$.

Функция ${{g}_{1}}$ – прямая, проходящая через точку $(0,0)$, с угловым коэффициентом $({{\eta }^{2}} + {{\varepsilon }_{l}} - {{\gamma }^{2}})$, принимающим значения от $ - \infty $ до $ + \infty $ при $\eta \in ( - \infty , + \infty )$ и $\gamma \in (\sqrt {{{\varepsilon }_{s}}} , + \infty )$; функция ${{g}_{2}}$ монотонно убывает до $ - \infty $, а своего максимального значения, равного $C > 0$, достигает при $\tau = 0$. Отсюда можно заключить, что если $f$ неограничена, то функция $\tau \equiv \tau (\eta ;\gamma ) > 0$, определенная неявно соотношением (4.6), существует для любых $\eta $ и $\gamma > \sqrt {{{\varepsilon }_{s}}} $. Это означает, что ${{\gamma }_{{max}}} = + \infty $.

Если $f$ ограничена, то функция ${{g}_{2}}$ при достаточно больших $\tau $ “почти” линейна по $\tau $. Ясно, что искомой функции $\tau (\eta ;\gamma )$ не существует, если ${{g}_{1}}$ и ${{g}_{2}}$ не пересекаются. Подстановка ${{f}_{{max}}} = ma{{x}_{{\tau \to \infty }}}f(\tau )$ вместо $f$ и ${{f}_{{max}}}\tau $ вместо $F$ при больших $\tau $ в уравнение ${{g}_{1}} = {{g}_{2}}$ дает $({{\eta }^{2}} + {{\varepsilon }_{l}} - {{\gamma }^{2}})\tau = C - \alpha {{f}_{{max}}}\tau $. Прямые, отвечающие левой и правой частям полученного соотношения, не пересекаются, как только их угловые коэффициенты совпадают. Приравнивая эти коэффициенты, находим ${{\gamma }^{2}} = {{\eta }^{2}} + {{\varepsilon }_{l}} + \alpha {{f}_{{max}}}$. Минимального положительного значения правая часть полученного соотношения достигает при $\eta = 0$. Таким образом, ${{\gamma }_{{max}}} = \sqrt {{{\varepsilon }_{l}} + \alpha {{f}_{{max}}}} $.

Как было отмечено при доказательстве утверждения 2, величина $\eta $ не обязательно изменяется от $ - \infty $ до $ + \infty $. А именно, если $f$ ограничена и $\gamma > {{\gamma }_{{max}}}$, то решение $u$ в нуль не обращается, также не обращается в нуль и производная $u{\kern 1pt} '$ этого решения. Это значит, что переменная $\eta $ изменяется в интервале $(\delta ,{{k}_{s}})$, где $\delta \equiv \delta (\gamma )$. Таким образом, уравнение ${{g}_{1}} = {{g}_{2}}$ всегда имеет решение.

Доказательство теоремы 2. Рассмотрим систему

эквивалентную уравнению (2.2). Пусть пара $(u(x),v(x))$ – решение системы (7.3) и $u(x)$ имеет три нуля ${{x}_{1}},{{x}_{2}},{{x}_{3}} \in (0,h)$, причем ${{x}_{1}} < {{x}_{2}} < {{x}_{3}}$. Из формул (7.2) ясно, что ${{x}_{2}} - {{x}_{1}} = {{x}_{3}} - {{x}_{2}} = \Theta {\text{/}}2$. Легко проверить, что если пара $(u(x),v(x))$ – решение, то и пара $( - u(\Theta + 2{{x}_{1}} - x),v(\Theta + 2{{x}_{1}} - x))$ – также решение.

Пусть

Используя систему (7.3) легко проверить, что функции $u(x)$ и $ - u(\Theta + 2{{x}_{1}} - x)$ в точке $x = {{x}_{2}}( = \,{{x}_{1}} + \Theta {\text{/}}2)$ склеены со вторым порядком гладкости.

Пусть теперь $k \geqslant 3$ и ${{x}_{1}},{{x}_{2}},\; \ldots ,\;{{x}_{k}} \in (0,h)$ – нули функции $u(x)$. Тогда для любой точки $x{\kern 1pt} * \in (0,h)$ существует целое число $q - 1$ такое, что $x{\kern 1pt} * = x{\kern 1pt} {\text{'}} + q\Theta $, где $x{\kern 1pt} ' \in [{{x}_{1}},{{x}_{3}}]$. Положим

Другими словами, $(\tilde {u}(x),\tilde {v}(x))$ – периодическое решение системы (7.3) с периодом $\Theta $. В силу классических результатов о (локальном) существовании и единственности решения обыкновенного дифференциального уравнения других решений нет [21].

Докажем этот результат иначе. Поскольку $u({{x}_{i}}) = 0$, то из (14) следует, что $(u({{x}_{1}}),v({{x}_{1}})) = (0, - \sqrt C )$. Анализируя поведение $u(x)$ и $u{\kern 1pt} '(x)$ в окрестностях точек $x = {{x}_{2}}$ и $x = {{x}_{3}}$ и используя (14), получаем

Таким образом, $(u({{x}_{1}}),v({{x}_{1}})) = (u({{x}_{3}}),v({{x}_{3}}))$. Решение автономной системы, обладающее таким свойством, является периодическим [21]. Единственность этого решения следует из тех же рассуждений, что были использованы выше.

Доказательство теоремы 3. Для всех $\gamma _{{max}}^{ * } \leqslant {{\gamma }_{{max}}}$, где $\gamma _{{max}}^{ * } > \sqrt {{{\varepsilon }_{s}}} $ – постоянная, интегралы в уравнении (6.1) сходятся, а значит, $h_{{inf}}^{{(p)}}$ и $h_{{sup}}^{{(p)}}$ существуют и имеют конечные значения.

В силу утверждения 3 функция $\Phi (\gamma ;k)$ является непрерывной функцией параметра $\gamma \in \Gamma $. Отсюда получаем, что для всякого $h_{{inf}}^{{(p)}} < h < h_{{sup}}^{{(p)}}$ существует по крайней мере одно решение уравнения (4.10), которое в силу теоремы 1 является собственным значением задачи $\mathcal{P}$.

Доказательство утверждения 5. Существование неотрицательной непрерывной функции $\tau \equiv \tau (\eta ;\gamma )$ для $(\eta ,\gamma ) \in \mathbb{R} \times \Gamma $ следует из утверждения 3. Остается доказать аналитичность этой функции по $\gamma $ при $\gamma \in \Gamma $. Функция $\tau \equiv \tau (s;\gamma )$ определена соотношением (4.6). Учитывая, что в окрестности каждой точки $(s{\kern 1pt} *,\gamma {\kern 1pt} *) \in \mathbb{R} \times \Gamma $ существует функция $\tau \equiv \tau (s*;\gamma *)$ и $f(z)$ аналитична по $z$ при $z \in R_{\Delta }^{\delta }$, то по теореме о неявной функции $\tau $ зависит аналитически от $\gamma $ [29].

Доказательство теоремы 4. Существование по крайней мере одного собственного значения для $h_{{inf}}^{{(p')}} < h < h_{{sup}}^{{(p')}}$ следует из теоремы 3.

Пусть $f(z)$ – аналитическая функция, тогда в силу утверждения 5 функция $\tau \equiv \tau (s;\gamma )$ аналитически зависит от $\gamma $ при $\gamma \in \Gamma $, но тогда и функция $\Phi (\gamma ,k)$ также является аналитической функцией параметра $\gamma $ при $\gamma \in \Gamma $. Поскольку неравенство $h_{{inf}}^{p} < h_{{sup}}^{p}$ справедливо для всех $\mathcal{P}$, то отсюда, в силу аналитичности функции $\Phi (\gamma ,k)$ по $\gamma $, следует, что $\Phi (\gamma ,k)$ не может оставаться постоянной на любом открытом множестве $\gamma \in \Gamma {\kern 1pt} '' \subset \Gamma $. Как известно, аналитическая функция на любом ограниченном подмножестве области аналитичности всякое свое значение принимает конечное число раз [29]. Отсюда следует, что на каждом отрезке $\Gamma {\kern 1pt} ' \subset \Gamma $ содержится не более конечного числа (изолированных) собственных значений задачи $\mathcal{P}$.

Доказательство утверждения 6. Пусть $\gamma \in [\sqrt {{{\varepsilon }_{s}}} + \delta ,\sqrt {{{\varepsilon }_{l}}} - \delta ]$, где $\delta > 0$ достаточно мало. Обозначим ${{w}_{0}}: = {{s}^{2}} + {{\varepsilon }_{l}} - {{\gamma }^{2}}$. В этом случае $1{\text{/}}w$ стремится к $1{\text{/}}{{w}_{0}}$ равномерно относительно $\gamma $ при $\alpha \to + 0$. Переходя к пределу $\alpha \to + 0$ в уравнении (4.10), получаем дисперсионное уравнение (5.1) линейной задачи, где можно положить $\gamma \in (\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$.

Доказательство теоремы 5. Рассмотрим уравнение (5.1) и предположим, что оно имеет $k$ решений ${{\tilde {\gamma }}_{i}}$ $(i = \overline {1,k} )$. Из утверждения 1 следует, что все решения ${{\tilde {\gamma }}_{i}} \in (\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$ и являются однократными корнями уравнения (5.1).

Обратимся к уравнению (4.10). Вычтем из обеих частей этого уравнения величину ${{\Phi }_{0}}(\gamma ;n)$, определенную в (5.1), получим

После приведения левой части к общему знаменателю, имеем Нули правой части полученного уравнения являются однократными собственными значениями ${{\tilde {\gamma }}_{i}}$ линейной задачи; при этом все собственные значения ${{\tilde {\gamma }}_{i}}$ лежат внутри интервала $(\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$. Отсюда следует, что существует отрезок $\Delta = [\sqrt {{{\varepsilon }_{s}}} + \delta ,\sqrt {{{\varepsilon }_{l}}} - \delta ]$, где $\delta > 0$ – достаточно мало, такой, что ${{\tilde {\gamma }}_{i}} \in \Delta $ при $i = \overline {1,k} $. Это значит, что найдутся отрезки ${{\Gamma }_{i}}$ такие, что ${{\tilde {\gamma }}_{i}} \in {{\Gamma }_{i}} \subset \Delta $ при $i = \overline {1,k} $ и на концах каждого из отрезков ${{\Gamma }_{i}}$ непрерывная функция $h - {{\Phi }_{0}}(\gamma ;n)$ принимает значения разных знаков.

При условии $\gamma \in \Delta $ выражение $({{s}^{2}} + {{\varepsilon }_{l}} - {{\gamma }^{2}})w(s;\gamma ) \geqslant {{\delta }^{2}} > 0$. Это значит, что интегралы в полученном выше уравнении не имеют особенностей. Поскольку при ограниченных $\gamma $ функция $\tau \equiv \tau (s;\gamma )$ ограничена, то ограничена и $f(\tau )$. Тогда ясно, что несобственные интегралы сходятся. Отсюда следует, что левая часть полученного уравнения может быть сделана как угодно малой, если достаточно мало $\alpha $. Принимая во внимание, что правая часть меняет знак при переходе через $\gamma = {{\tilde {\gamma }}_{i}}$, получаем, что найдется $\alpha '$ такое, что при $\alpha = \alpha {\kern 1pt} '$ в окрестности всякого $\gamma = {{\tilde {\gamma }}_{i}}$ уравнение (4.10) имеет по крайней мере один корень $\gamma = {{\hat {\gamma }}_{i}}$; при этом $\alpha {\kern 1pt} '$ можно выбрать так, что ${{\hat {\gamma }}_{i}} \in {{\Gamma }_{i}}$.

Доказательство утверждения 7. Поскольку и $\tau $, и $w$ зависят от ${{s}^{2}}$, то левую часть уравнения (4.10) можно записать в виде

Далее, выразив $\eta ( = \,s)$ из интеграла (4.6) и воспользовавшись этим явным выражением, можно в уравнении (4.10) перейти к интегралам по $d\tau $. Действительно, из (4.6) при $\eta = s$ получаем $2s\tau ds + ({{s}^{2}} + {{\varepsilon }_{l}} - {{\gamma }^{2}})d\tau + \alpha f(\tau )d\tau = 0$, а поскольку $s \geqslant 0$, то $s = + {{\tau }^{{ - 1/2}}}{{(C - ({{\varepsilon }_{l}} - {{\gamma }^{2}})\tau - \alpha F(\tau ))}^{{1/2}}}$. Отсюда находим

и тогда

Новые пределы интегрирования определяются из (4.6) следующим образом. Запишем (4.6) при $\eta = s$ в такой форме

Из монотонности $f$ следует, что $(C - \alpha F(\tau )){\kern 1pt} ' = - \alpha f(\tau ) < 0$ и $(C - \alpha F(\tau )){\kern 1pt} '' = - \alpha f{\kern 1pt} '(\tau ) < 0$. Поскольку $C > 0$, то, привлекая геометрические соображения, получаем, что изучаемое уравнение всегда имеет не более одного (однократного) положительного корня, а если ${{s}^{2}} + {{\varepsilon }_{l}} - {{\gamma }^{2}} > 0$, то такой корень необходимо существует. Отсюда следует, что $\tau = {{\tau }_{s}}$, $\tau = {{\tau }_{c}}$ и $\tau = {{\tau }_{ + }}$ есть (однократные) положительные корни уравнений (6.2) и (6.3) соответственно. Условие ${{\varepsilon }_{l}} > {{\varepsilon }_{s}} \geqslant {{\varepsilon }_{c}}$ влечет ${{\tau }_{c}} \leqslant {{\tau }_{s}} < {{\tau }_{ + }}$. Из геометрических соображений также следует, что $li{{m}_{{s \to + \infty }}}\tau (s) = 0$.

Используя полученные результаты, приходим к (6.1).

Доказательство утверждения 8. В силу теоремы 3 функция $\Phi (\gamma ;n)$ непрерывна по $\gamma $ при $\gamma \in \Gamma $, где в силу утверждения 4 значение ${{\gamma }_{{max}}} = + \infty $. Другими словами, функция $T(\gamma )$ непрерывна для всех $\gamma \in (\sqrt {{{\varepsilon }_{s}}} , + \infty )$.

Можно видеть, что функция $\tau \equiv \tau (\eta ;\gamma )$, определяемая (4.6), неограничена при $\gamma \to + \infty $. По этой причине формула (4.6) неудобна для дальнейшего анализа. “Нормируем” (4.6) так, чтобы избежать появления больших значений $\tau (\eta ;\gamma )$. Используя “нормированные” переменные $\tau = {{\gamma }^{{2/q}}}\bar {\tau }$ и $\eta = \gamma \bar {\eta }$, перепишем (4.6) в виде

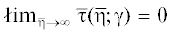где $\mathop {\bar {\varepsilon }}\nolimits_l = {{\varepsilon }_{l}}{{\gamma }^{{ - 2}}}$, $\bar {C} = C{{\gamma }^{{ - 2 - 2/q}}}$. Неявная функция $\bar {\tau } \equiv \bar {\tau }(\bar {\eta };\gamma )$, определяемая (7.4), положительна и ограничена для всех возможных значений $\gamma $. Заметим, что независимо от $\gamma $.

Используя следствие 2, получаем формулу

где $\tau = {{\bar {\tau }}_{ + }}$ – единственный положительный корень (7.4) при $\bar {\eta } = 0$. Отметим, что ${{\bar {\tau }}_{ + }} = {{\gamma }^{{ - 2/q}}}{{\tau }_{ + }}$.

Выражение под “большим” радикалом в (7.5) есть ни что иное, как левая часть (7.4) при $\bar {\eta } = 0$. Положив $\bar {\eta } = 0$, используя (6.7) и переходя к пределу при $\gamma \to \infty $ и $\bar {\eta } = 0$, получаем из (7.4) уравнение $\bar {\tau }\left( {1 - \tfrac{\alpha }{{q + 1}}\mathop {\bar {\tau }}\nolimits^q } \right) = 0$, которое имеет не менее двух вещественных корней: $\tau _{ - }^{0} = 0$ и $\tau _{ + }^{0} = {{\left( {\tfrac{{q + 1}}{\alpha }} \right)}^{{1/q}}}$. Отсюда следует, что уравнение (7.4) при $\bar {\eta } = 0$ и достаточно больших $\gamma $ имеет не менее двух вещественных корней, которые обозначим ${{\bar {\tau }}_{ - }}$ и ${{\bar {\tau }}_{ + }}$, где ${{\bar {\tau }}_{ + }} > 0$.

Можно показать, что $li{{m}_{{\gamma \to \infty }}}{{\bar {\tau }}_{ - }} = \tau _{ - }^{0}$ и $li{{m}_{{\gamma \to \infty }}}{{\bar {\tau }}_{ + }} = \tau _{ + }^{0}$. Однако корень ${{\tau }_{ - }}$ может быть отрицательным, в этом случае предполагаем, что ${{\tau }_{ - }}$ – наибольший из отрицательных корней. Поскольку $\tau = {{u}^{2}}$, то отрицательные значения $\tau $ отвечают чисто мнимым значениям $u$. Для использования отрицательных $\tau $, ниже мы продолжим выражение (7.4) в область $\bar {\tau } < 0$.

Найдем асимптотические выражения для ${{\bar {\tau }}_{ - }}$ и ${{\bar {\tau }}_{ + }}$ при больших $\gamma $. Величины $\tau _{ - }^{0}$ и $\tau _{ + }^{0}$ являются первыми приближениями к ${{\bar {\tau }}_{ - }}$ и ${{\bar {\tau }}_{ + }}$ соответственно. Используя (6.7), перепишем равенство (7.4) в виде ${{g}_{1}}(\bar {\tau };\bar {\eta },\gamma ) = {{g}_{2}}(\bar {\tau };\gamma )$, где ${{g}_{1}}(\bar {\tau };\bar {\eta },\gamma ): = (\mathop {\bar {\eta }}\nolimits^2 + {{\bar {\varepsilon }}_{l}} - 1)\bar {\tau }$, ${{g}_{2}}(\bar {\tau };\gamma ): = \bar {C} - \tfrac{\alpha }{{q + 1}}{\text{|}}\bar {\tau }{{{\text{|}}}^{q}}\bar {\tau } - {{\gamma }^{{ - 2 - 2/q}}}{{F}_{1}}({{\gamma }^{{2/q}}}\bar {\tau })$. Для продолжения ${{g}_{2}}$ в область отрицательных значений $\bar {\tau }$ использован знак модуля. Поскольку в уравнении (6.1) и интеграле (6.4) переменная интегрирования неотрицательна, то знак модуля не влияет на вычисления при $\bar {\tau } \geqslant 0$, но позволяет корректно использовать значение ${{\bar {\tau }}_{ - }}$. Имея в виду формулы (1.4), (4.2), ясно, что использованное продолжение является естественным.

Функция $\bar {\tau }(\bar {\eta };\gamma )$ для различных $\bar {\eta }$ представлена на фиг. 2а; на фиг. 2б показаны ${{\bar {\tau }}_{ - }} \equiv {{\bar {\tau }}_{ - }}(\gamma ) < 0$ и ${{\bar {\tau }}_{ + }} \equiv {{\bar {\tau }}_{ + }}(\gamma ) > 0$, которые являются решениями уравнения ${{g}_{1}} = {{g}_{2}}$ при $\bar {\eta } = 0$; фиг. 2в демонстрирует, что происходит при $\bar {\eta } = 0$ и $\gamma \to \infty $.

Используя (7.4) при $\bar {\eta } = 0$ и найденные приближения, получаем

где ${{r}_{ - }} > 2 + 2{\text{/}}q$, ${{r}_{ + }} > 0$ зависят от свойств ${{F}_{i}}$.

Ясно, что “большой” радикал в (7.5) обращается в нуль при $\bar {\tau } = {{\bar {\tau }}_{ - }}$ и $\bar {\tau } = {{\bar {\tau }}_{ + }}$; при этом $\mathop {\bar {\tau }}\nolimits_ - \to 0,$ когда $\gamma \to + \infty $. Другими словами, при $\gamma \to + \infty $ в (7.5) получаем логарифмическую особенность в окрестности точки $\bar {\tau } = 0$.

Выражение под “большим” радикалом в (7.5) можно записать в виде

где ${{f}_{0}}({{\bar {\tau }}_{ + }}) = 0$ и $li{{m}_{{\gamma \to + \infty }}}{{f}_{0}}(\bar {\tau }) = 1 - \tfrac{\alpha }{{q + 1}}{\text{|}}\bar {\tau }{{{\text{|}}}^{q}}$. Пусть $g(\bar {\tau }) = \tfrac{1}{{\sqrt {{{f}_{0}}(\bar {\tau })} }}$, тогда формулу (7.5) можно переписать в виде

Пусть ${{g}_{0}}(\bar {\tau }) = \tfrac{1}{{\sqrt {li{{m}_{{\gamma \to + \infty }}}{{f}_{0}}(\bar {\tau })} }}$. Тогда

Первое слагаемое в правой части (7.7) оценивается так где ${{r}_{1}} > 0$. Далее имеем Второе слагаемое в правой части (7.7) вычисляется точно и дает

Теперь, используя формулы для ${{\bar {\tau }}_{ - }}$ и ${{\bar {\tau }}_{ + }}$, находим

Используя (7.6), вычисляем

Объединяя результаты, получаем (6.8).

Доказательство теоремы 6. Из формулы (6.8) ясно, что $T(\gamma ) \to 0$ при $\gamma \to + \infty $. Отсюда с учетом неравенств (6.5) следует существование целого числа ${{n}_{0}} \geqslant 0$ такого, что уравнение (4.10) имеет по крайней мере одно решение для каждого $n = {{n}_{0}},\;{{n}_{0}} + 1,\; \ldots $ Таким образом, задача $\mathcal{P}$ имеет бесконечно много решений ${{\hat {\gamma }}_{i}}$, где $li{{m}_{{i \to \infty }}}{{\hat {\gamma }}_{i}} = + \infty $.

Из формулы (6.8) видно, что главный член асимптотического разложения не зависит от $\alpha $ и, следовательно, для любого $\alpha > 0$ существует бесконечное число собственных значений, которые не связаны с каким-либо решением линейной задачи.

Неравенство (6.9) следует из формул (6.5) и (6.8).

Умножая уравнение (2.2) на $u$ и интегрируя по $[0,h]$, получаем

Левая часть полученного выражения стремится к бесконечности при $\gamma \to + \infty $ и, следовательно, так же ведет себя и правая часть. Отсюда получаем, что $ma{{x}_{{x \in [0,h]}}}|u(x;{{\hat {\gamma }}_{i}})| \to \infty $ при ${{\hat {\gamma }}_{i}} \to + \infty $. Этот $max{\text{|}}u(x;\hat {\gamma }){\text{|}}$ можно оценить точнее. Действительно, если $u(x;\hat {\gamma })$ имеет более одного нуля внутри $(0,h)$, то найдется точка $x{\kern 1pt} * \in (0,h)$ такая, что $u{\kern 1pt} '(x{\kern 1pt} *) = 0$. Искомый $max$ равен $u(x{\kern 1pt} *)$. Положив $u{\kern 1pt} ' = 0$ в (4.2), получаем, в общем случае, трансцендентное уравнение, оценивая максимальный корень которого при условии, что $f$ удовлетворяет (6.6), находим $ma{{x}_{{x \in [0,h]}}}\left| {u(x;\hat {\gamma })} \right| = O({{\hat {\gamma }}^{{1/q}}})$.

Доказательство теоремы 7. Используя формулу (6.8) для задач $\mathcal{P}({{q}_{1}})$ и $\mathcal{P}({{q}_{2}})$, получаем ${{T}_{j}}(\gamma ) = 2(1 + q_{j}^{{ - 1}}){{\gamma }^{{ - 1}}}ln\gamma + O({{\gamma }^{{ - 1}}})$, где $j = 1,2$. Отсюда ясно, что если ${{q}_{1}} < {{q}_{2}}$, то ${{T}_{1}} > {{T}_{2}}$ для достаточно больших $\gamma $ и, следовательно, ${{\hat {\gamma }}_{{1,i}}} > {{\hat {\gamma }}_{{2,i}}}$.

Доказательство утверждения 9. Как следует из (4.2), первый интеграл уравнения (2.2) имеет вид

где $C = ({{\varepsilon }_{l}} - {{\varepsilon }_{s}}){{A}^{2}} + \alpha ((1 + {{A}^{2}})ln(1 + {{A}^{2}}) - {{A}^{2}}) > 0$.

Первый интеграл системы (4.5) принимает вид

где $C$ определена в (7.8); при этом $w(s;\gamma ) = {{s}^{2}} + {{\varepsilon }_{l}} - {{\gamma }^{2}} + \alpha ln(1 + \tau )$, а функция $\tau \equiv \tau (s;\gamma ) \geqslant 0$ определяется из (7.9) при $\eta = s$.

В силу утверждения 3 функция $\Phi (\gamma ;n)$ непрерывна по $\gamma $ при $\gamma \in \Gamma $. Для функции $ln(1 + \tau )$ справедливо утверждение 4, а значит, ${{\gamma }_{{max}}} = + \infty $. Тогда функция $T(\gamma )$ непрерывна для всех $\gamma \in (\sqrt {{{\varepsilon }_{s}}} , + \infty )$.

В соответствии со следствием 2 получаем

где ${{\tau }_{ + }}$ – положительный корень уравнения (7.9) при $\eta = 0$.

Для того чтобы найти оценку для ${{\tau }_{ + }}$, рассмотрим уравнения

Уравнение (7.11) имеет единственный положительный корень $\tau = {{\tau }_{{min}}}$. Легко видеть, что при больших $\tau $ и $\gamma $ справедливо неравенство ${{\tau }_{{min}}} < {{\tau }_{ + }}$. Решив уравнение (7.11), получаем

Обозначим $k_{l}^{2}: = {{\varepsilon }_{l}} - {{\gamma }^{2}}$. Оценим интеграл $T$. Для достаточного больших значений $\gamma $, при этом $k_{l}^{2} < 0$, получаем

Вычислив интеграл ${{T}_{{min}}}$, для достаточно больших $\gamma $ легко получить оценку которая вместе с неравенством $T \geqslant {{T}_{{min}}}$ дает (6.10).

Доказательство утверждения 10. Из утверждения 9 следует, что $li{{m}_{{\gamma \to \infty }}}T(\gamma ) = \infty $. Это и значит, что для всякого $h$ большего, чем некоторое ${{h}_{{min}}} > 0$, уравнение (4.10) имеет по крайней мере одно решение. Ясно, что

Поскольку ${{h}_{{min}}} \geqslant h{\kern 1pt} ' > 0$, где $h{\kern 1pt} '$ – некоторое положительное число, то отсюда получаем, что для всякого $h = h{\kern 1pt} {\text{*}}$ найдется целое $n = n{\kern 1pt} * \geqslant 0$ такое, что $n{\kern 1pt} {\text{*}}{{h}_{{min}}} > h{\kern 1pt} {\text{*}}$. Но тогда получаем, что для $h = h{\kern 1pt} {\text{*}}$ уравнение (4.10) не имеет решений при $n \geqslant n{\kern 1pt} {\text{*}}$.

Справедливость предельного перехода при $\alpha \to + 0$ обоснована в утверждении 6.

Доказательство утверждения 11. Оценивая функцию $1{\text{/}}w(s;\gamma )$, получаем

Используя эти неравенства, находим

Интегралы в левой и правой частях (7.2) элементарно вычисляются и дают

Из найденных формул следуют искомые оценки.

Неограниченность $\Phi (\gamma ;n)$ при $\gamma \to {{\gamma }_{{max}}}$ получаем из следующих рассуждений. Пусть $\delta {\kern 1pt} ' > 0$ – фиксированное достаточно малое число. Тогда уравнение (4.10) при любом целом $n \geqslant 0$ содержит слагаемое

Пусть ${{U}_{{{{\gamma }_{{max}}}}}}$ – достаточно малая полуокрестность (на вещественной оси $\mathbb{R}$) точки ${{\gamma }_{{max}}}$. Рассмотрим уравнение (4.6) при $s \in [0,\delta ]$ и таких $\gamma \in {{U}_{{{{\gamma }_{{max}}}}}}$, что решение $\tau \equiv \tau (s;\gamma )$ уравнения (4.6) существует. Из доказательства утверждения 4 следует, что при достаточно малом $\delta {\kern 1pt} '$ решение $\tau (s;\gamma )$ удовлетворяет неравенству $\tau (s;\gamma ) \leqslant {{\tau }_{ + }}$, где ${{\tau }_{ + }}$ достаточно большая постоянная. Отсюда следует, что $f(s) \leqslant f({{\tau }_{ + }})$, где $f({{\tau }_{ + }})$ тем меньше отличается от ${{f}_{{max}}}$, чем меньше $\delta {\kern 1pt} '$ и ${{U}_{{{{\gamma }_{{max}}}}}}$. Очевидно, имеют место оценки

Пусть $r(s): = \sqrt {{{\varepsilon }_{l}} - {{\gamma }^{2}} + \alpha f(s)} $. Вычисляя интеграл в левой части, получаем

Если ${{\gamma }^{2}} \to - \mathop {\delta {\kern 1pt} '}\nolimits^2 + {{\varepsilon }_{l}} + \alpha f({{\tau }_{ + }})$, то $\tfrac{{\delta {\kern 1pt} '}}{{r({{\tau }_{ + }})}} \to 1$ независимо от $\delta {\kern 1pt} '$. Но если $\delta {\kern 1pt} ' \to 0$, то $f({{\tau }_{ + }}) \to {{f}_{{max}}}$, а значит, $r({{\tau }_{ + }}) \to 0$. Отсюда следует, что левая часть полученного выше неравенства неограниченно возрастает при ${{\gamma }^{2}} \to {{\varepsilon }_{l}} + \alpha {{f}_{{max}}}$. Но тогда и $li{{m}_{{\gamma \to {{\gamma }_{{max}}}}}}\Phi (\gamma ;n) = + \infty $.