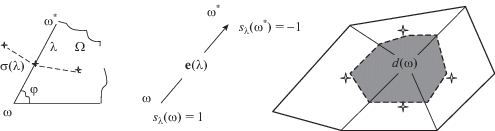Журнал вычислительной математики и математической физики, 2020, T. 60, № 1, стр. 122-131

1. ВВЕДЕНИЕ

Проблемы моделирования течений в среде, содержащей газогидратные включения, активно изучаются в связи с промышленным освоением северных и арктических регионов, шельфовых месторождений углеводородов и т.д. В соответствующих этим районам условиях поровое пространство среды, например, многолетнемерзлых грунтов в исходном состоянии, соответствующем низкой температуре и высокому давлению, полностью или частично заполнено так называемыми клатратными соединениями молекул газа и воды, находящимися в твердом состоянии [1]. Газогидратные отложения метастабильны и существуют в условиях, близких к границе их фазовой устойчивости. Повышение температуры либо понижение уровня давления, вызванное, например, техногенными причинами, приводит к разложению гидрата на газ и воду. Возможен и обратный процесс формирования гидратных отложений, например, при транспортировке газа в условиях низких температур. Названные явления необходимо учитывать при проектировании технологий в добывающей, транспортной, строительной и других хозяйственных отраслях, в оценках экологического характера и рисков техногенных катастроф [2].

Модель эволюции среды с газогидратными включениями “мультифизична”. Она описывает связанные гидродинамические, геомеханические и физико-химические процессы [1], [2]. Флюидодинамика свободных воды и газа в пористой среде при наличии в ней твердых гидратных включений обладает рядом особенностей [3], [4].

Согласно правилу фаз Гиббса, термодинамически равновесная система, в которой вещество находится в трехфазном состоянии (в нашем случае это газогидрат, свободные “жидкие” вода и газ), обладает только одной термодинамической степенью свободы. В этом случае температура диссоциации газогидрата и давление в среде связаны термобарической зависимостью ${{T}_{{{\text{dis}}}}} = f(P)$, а за основную термодинамическую переменную можно выбрать величину (например, внутренние энергии воды или газа), через которую удобно выразить температуру и давление. В дальнейшем это понадобится для описания равновесной флюидодинамики гидратосодержащей среды. Однако при наличии талой зоны (зоны полностью разложившегося гидрата) термодинамика среды описывается двумя независимыми параметрами, например, давлением и температурой – $P,\;T$. Наибольший практический интерес представляет именно совместная эволюция пространственно разделенных талых и гидратосодержащих зон. Следующим важным обстоятельством является то, что исходная система уравнений флюидодинамики, сформулированная в виде законов сохранения массы, импульса, и полной энергии среды, в терминах растепленности ${{S}_{\nu }}$ (доля свободного от гидрата порового пространства), влагонасыщенности ${{S}_{w}}$, давления $P$ и температуры $T$ обладает смешанными гиперболическими и параболическими свойствами. Непосредственное использование такой системы к расчету динамики гидратосодержащей среды, например, на основе аппроксимации системы флюидодинамических уравнений “в целом”, позволяет выполнять вычисления только при неоправданно малых значениях шага интегрирования по времени. Причина этого явления кроется в необходимости расчета динамики жидкости и, одновременно, межфазного тепло-массообмена.

В работах [5], [6] предложена численная методика решения задачи флюидодинамики гидратосодержащей среды, основанная на неполном расщеплении уравнений разностной схемы по физическим процессам. Разностное уравнение для поля давления (или уравнение пьезопроводности) решается в отдельном блоке алгоритма. При этом разностная производная по времени вместе с давлением включает и гидратонасыщенность. Практическое применение данной методики оказалось затруднительным ввиду физически неоправданного измельчения шага интегрирования по времени, чтобы избежать неустойчивости счета.

Сопоставление характерных времен моделируемых процессов в ряде экспериментов показывает, что характерное время разложения гидратов составляет 10²–10⁴ с, тогда как процесс разработки газогидратного месторождения длится годами (10⁶–10⁸ с). Поэтому адекватным описанием флюидодинамики гидратосодежащих сред (коллекторов, грунтов и т.д.) будут уравнения модели, основанной на балансовых соотношениях в предположении равновесности диссоциации газовых гидратов. Разностная схема, рассматриваемая в данной работе, построена для модели такого типа.

Целью настоящего исследования является построение семейства двухслойных полностью консервативных разностных схем (ПКРС, [7]) на разностных сетках нерегулярной структуры, часто называемых неструктурированными. Принцип полной консервативности важен для совместного моделирования трехфазной среды с процессами в талой зоне. В случае изменения термобарических условий и исчезновения гидратной фазы меняется как количество неизвестных, так и тип уравнений. Эти процессы могут проходить весьма интенсивно на малых пространственно-временных масштабах сравнительно с масштабами всей изучаемой гидратосодержащей области. Поэтому для получения физически адекватных решений, также как и в случае моделирования газодинамических быстропротекающих процессов [7], важно на уровне разностной схемы сохранить присущие исходной модели балансы для областей течения с существенно разными и переменными по времени свойствами. Построение ПКРС выполняется методом опорных операторов, который позволяет построить однородные аппроксимации входящих в исходные уравнения дифференциальных операторов [1], [2], сохраняющие присущие им свойства, например, самосопряженность, положительная определенность. Дискретизация по времени выполняется путем “взвешивания” с профилированными по пространству временными весами. Для разработки ПКРС флюидодинамики в гидратосодержащей среде предлагается так называемая свободно-объемная аппроксимация сеточных функций по времени. Это нелинейная аппроксимация, включающая зависимость от доли объема в порах, занятом фдюидами, и является простой в реализации.

В работах [8]–[10] предложена конечно-разностная модель двухкомпонентной флюидодинамики в пористой среде с гидратными включениями. Для решения системы разностных уравнений предложена схема расщепления на блок расчета переноса насыщенностей флюидов при известном поле скорости (подсистема уравнений, обладающая гиперболическими свойствами) и пьезопроводный блок (уравнение параболического типа).

В настоящей работе также рассматривается решение начально-краевой задачи посредством раздельного учета (расщепления) физических процессов. Поскольку уравнения рассматриваемой нами начально-краевой задачи выражают балансы массы компонент и внутренней энергии флюидов, гидрата и скелета пористой среды, мы рассматриваем вопрос о том, как построить алгоритм расщепления, не нарушающий эти балансы.

2. ПОСТАНОВКА ЗАДАЧИ

В пространственной области $O$ с границей $\partial O$ рассмотрим термодинамически равновесные двухкомпонентные (вода, метан) трехфазные уравнения флюидодинамики в среде с газогидратными включениями [11]:

Приняты обозначения: индексы $l = g,\;w,\;\nu ,\;s$ относятся к газу, воде, гидрату и скелету пористой среды. Здесь (2.1) – уравнение баланса массы воды, (2.2) – уравнение баланса массы метана, (2.3) – выражает закон Дарси, записанный для скорости движения свободной воды ${{{\mathbf{V}}}_{w}}$ в порах для двухкомпонентной несмешивающейся системы (вода, метан) с абсолютной проницаемостью $k = k({\mathbf{r}},\,{{S}_{\nu }},\,P)$ и относительной проницаемостью ${{k}_{{rw}}} = {{k}_{{rw}}}(\,{{S}_{w}})$, ${{\mu }_{w}}$ – вязкость воды. Уравнение (2.4) также выражает закон Дарси для скорости свободного метана ${{{\mathbf{V}}}_{g}}$ с относительной проницаемостью ${{k}_{{rg}}} = {{k}_{{rg}}}(\,{{S}_{w}})$ и вязкостью ${{\mu }_{g}}$. Наконец, (2.5) – уравнение баланса общей внутренней энергии системы, включающей энергии свободной воды, свободного метана, гидрата и скелета. Символом ${{\varepsilon }_{l}}$ обозначены внутренние энергии  единиц массы  компонент. Уравнение (2.6) определяет общий тепловой поток ${\mathbf{W}}$ в среде с коэффициентами теплопроводности ${{\lambda }_{l}}(P,T)$; $g{\mathbf{k}}$ – вектор ускорения силы тяжести, направленный вертикально вниз; P – давление; ${{S}_{w}}$ – водонасыщенность; ν – гидратонасыщенность; ${{S}_{\nu }} = 1 - \nu $ – растепленность (суммарная доля флюида в порах); ${{\rho }_{l}}(P,T)$ – плотности фаз; ${{\beta }_{w}}$ – массовая доля воды в гидрате; ${\mathbf{r}}$ – радиус-вектор; t – время; ${{q}_{w}}$, ${{q}_{g}}$ и ${{q}_{\varepsilon }}$ – плотности соответствующих источников, зависящие от параметров (t, ${\mathbf{r}}$, ${{S}_{w}}$, ${{S}_{\nu }}$, P, T).

По правилу фаз Гиббса равновесная трехфазная двухкомпонентная система обладает одной степенью свободы [11]. Следовательно, для газового гидрата, находящегося в равновесии с жидкой водой или льдом, зависимость (2.7) имеет однозначный характер.

Уравнениям исходной системы соответствуют интегральные (балансные) соотношения, которые в общем виде можно представить как

где $u,\;{\mathbf{X}}$ – некоторая скалярная величина (зависящая от температуры, давления, внутренней энергии, концентраций компонент потока и т.п.) и вектор, физически связанный с потоком этой величины.

Энтальпии единицы массы ${{i}_{l}} = {{\varepsilon }_{l}} + \frac{P}{{{{\rho }_{l}}}}$ гидрата, свободных воды и газа термодинамически согласованы в смысле следующего соотношения:

где $h$ – скрытая теплота фазового перехода единицы массы гидрата. Для удельных (на единицу массы) энтальпий фаз также справедливо [11], [12] с коэффициентами дросселирования Нижним индексом $p$ в (2.11) обозначена частная производная по температуре при постоянном давлении; ${{c}_{{pl}}}$ и ${{V}_{l}} = \frac{1}{{{{\rho }_{l}}}}$ – удельные теплоемкости при постоянном давлении и объемы фаз соответственно. Для газовой фазы с уравнением состояния коэффициент дросселирования можно записать в виде При неизотермическом течении неидеального газа с коэффициентом сверхсжимаемости ${{z}_{g}}$ коэффициент дросселирования ${{k}_{d}}_{g} \ne 0$ (эффект Джоуля–Томсона [12]).

Из уравнений (2.1), (2.2), (2.5) путем преобразований с исключением производных по времени от водонасыщенности ${{S}_{w}}$ и растепленности ${{S}_{\nu }}$ получается уравнение “пьезопроводности” [10]:

Здесь

В уравнения (2.14) входят удельные (на единицу массы) скачки при фазовом переходе объема и внутренней энергии соответственно:

Уравнение (2.14) описывает термодинамически равновесную “диссипативную” эволюцию жидкой, газовой и гидратной фаз. Его можно использовать для решения исходной системы по схеме итераций с раздельным учетом физических процессов, “отщепив” от решения уравнений (2.1)–(2.4), описывающих адвекцию параметров насыщенности среды (газом, водой). Отметим, что при фиксированных термодинамических параметрах среды уравнения (2.1)–(2.4) обладают свойствами уравнений гиперболического типа [10].

Введем новую величину – бароемкость гидратной системы ${{D}_{P}}$ соотношением:

и перепишем уравнение (2.14) в более компактной форме: В (2.15) ${{({\kern 1pt} \cdot {\kern 1pt} )}_{p}}$ означает производную по давлению с учетом зависимости (2.7). Используя (2.7), из (2.3), (2.4), (2.14) можно получить вместо (2.15) уравнения относительно внутренних энергий – ${{\varepsilon }_{w}}$ либо ${{\varepsilon }_{g}}$. При этом учитывается, что в нашем случае имеется единственный независимый термодинамический параметр.

3. АППРОКСИМАЦИИ НА СТРУКТУРНО-НЕРЕГУЛЯРНЫХ СЕТКАХ

Мы будем рассматривать аппроксимации на примере сеток нерегулярной структуры с правильным примыканием ячеек, в том смысле, что соседние ячейки примыкают только по инцидентным им элементам одинаковой размерности, т.е. по граням, ребрам, вершинам (узлам ячеек) соответственно. Конкретные построения аппроксимаций операций векторного анализа с выбором локальных базисных векторов, построением соответствующих базисных объемов ${{{V}_{\varphi }}}$ иллюстрируются на примере треугольно-четырехугольной сетки на плоскости. Описание конструкции разностных операторов носит общий характер и распространяется на трехмерные сетки из ячеек – тетраэдров, гексаэдров, призм и их сочетаний.

Будем считать, что область расчета O имеет кусочно-гладкую границу. Обозначим множество ячеек покрывающей ее нерегулярной сетки через ${\left( \Omega \right)}$, множество узлов через ${\left( \omega \right)}$, гранями ${\left( \sigma \right)}$ и ребрами ${\left( \lambda \right)}$. Ограничимся случаем, когда сетка состоит из треугольных и четырехугольных ячеек. Будем считать, что в трехмерном пространстве, арифметизированном декартовой системой координат, в направлении, ортогональном расчетной плоскости, мы в качестве расчетной области берем “слой” единичной толщины (решение задачи не зависит от этой координаты), и, таким образом, формально можем рассматривать разностные схемы в терминах “объемов ячеек, объемов приузловых доменов” и “площадей граней”. Будем считать, что множество ячеек покрывает всю расчетную область таким образом, что ячейки могут иметь общими элементами только инцидентные им узлы, ребра, грани. Введем также “сопряженную” сетку, состоящую из доменов, построенных около узлов ${\left( \omega \right)}$ исходной сетки. Эту сетку, множество доменов которой обозначим через ${d\left( \omega \right)}$, подчиним условию, что она полностью покрывает расчетную область, и назовем замкнутой сеткой приузловых доменов (см. пример на фиг. 1). Обозначим через ${\left( {\sigma (\lambda )} \right)}$ внутренние границы узловых доменов $d(\omega )$. К узлам разностной сетки отнесем векторные базисы, множество которых обозначим через ${\left( \varphi \right)}$ (см. фиг. 1).

Базисы ${(\varphi )}$ исходных (ковариантных) ортов ${\mathbf{e}}(\lambda )$ образованы ориентированными ребрами (см. фиг. 1). Под центрами ячеек $\Omega $ и ребер $\lambda $ будем понимать средние арифметические радиус-векторов инцидентных им узлов $\omega $. Линия, проведенная через центры двух смежных ячеек и центр соответствующего ребра, или через граничное ребро $\partial \lambda $ и примыкающую ячейку, составляет часть границы приузлового домена, площадь которой можно вычислить по формуле

Будем считать, что эта часть границы ориентирована по орту ${\mathbf{e}}(\lambda )$ (см. фиг. 1). Здесь ${\mathbf{e}}_{\varphi }^{'}(\lambda )$ – орты взаимных (контравариантных) базисов по отношению к исходным базисам ${\mathbf{e}}(\lambda )$. Базисный объем дается формулой ${{v}_{\varphi }} = \frac{1}{6}\left| {{\mathbf{e}}({{\lambda }_{1}}) \times {\mathbf{e}}({{\lambda }_{2}})} \right|$ для треугольной ячейки Ω, содержащей базис $\varphi $, и ${{v}_{\varphi }} = \frac{1}{4}\left| {{\mathbf{e}}({{\lambda }_{1}}) \times {\mathbf{e}}({{\lambda }_{2}})} \right|$ для четырехугольной ячейки, если ${{\lambda }_{1}}(\varphi )$ и ${{\lambda }_{2}}(\varphi )$ – ребра, образующие базис $\varphi $. Сумма $\sum\nolimits_{\varphi (\lambda )}^{} {\kern 1pt} $ вычисляется по всем базисам $\varphi $, в которые входит данное ребро $\lambda $, а базисы $\varphi (\lambda )$ здесь попарно входят в ячейки ${{\Omega }\left( {\lambda } \right)}$, примыкающие к ребру λ. Замкнутые вокруг узла $\omega $ ломаные линии ${{\mathbf{\sigma }}(\lambda (\omega ))}$ образуют узловые домены ${d(\omega )}$. Приведенное выражение для ${{\mathbf{\sigma }}\left( \lambda \right)}$ можно понимать как метрическую операцию на разностной сетке. Выбор способа вычисления площади приузлового домена подчиняется естественному условию нормировки Она определяет конструкцию сопряженной сетки.

Рассмотрим некоторое векторное поле X, заданное своими представлениями ${{{X}_{\varphi }}}$ в базисах ${\mathbf{e}}(\lambda )$, либо ${\mathbf{e}}_{\varphi }^{'}(\lambda )$. Разностный оператор дивергенции поля ${\mathbf{X}}$, действующий по правилу ${\text{DI}}{{{\text{N}}}_{w}}:\left( \varphi \right) \to \left( \omega \right)$, определим из теоремы Гаусса на ${d(\omega )}$, аппроксимируя соответствующие интегралы:

Здесь $\sum\nolimits_{\lambda (\omega )}^{} {\kern 1pt} $ – суммирование по всем ребрам $\lambda $, имеющим общий узел $\omega $.

Множители ${{{W}_{\varphi }}}(\lambda ) > 0$, задаваемые в базисах $(\varphi )$ на образующих их ребрах $\lambda (\varphi )$, связаны с монотонизацией сеточных решений в следующем смысле. В соответствии с анализом гиперболичности линеаризованной группы уравнений (2.1), (2.2) для насыщенностей при фиксированных давлении и температуре [10] аппроксимация абсолютной проницаемости $k({{S}_{\nu }})$ выбирается вниз по потоку. Относительные проницаемости ${{k}_{{rw}}}(\,{{S}_{w}})$ и ${{k}_{{rg}}}(\,1 - {{S}_{w}})$ берутся вверх по потоку. Это и учитывается при выборе множителей ${{{W}_{\varphi }}}(\lambda )$. Если индекс “$w$” в выражениях ${{\operatorname{DIN} }_{w}}X,$ ${{\tau }_{{wx}}}(\lambda ),$ ${\mathbf{e}}_{{w\varphi }}^{'}$ и ${{\operatorname{GRAD} }_{w}}u$, отсутствует, это означает, что ${{W}_{\varphi }}(\lambda ) = 1$ во всех базисах $(\varphi )$, т.е. отсутствие монотонизации решения в указанном выше смысле.

Обозначая через ${{(\;)}_{\Delta }}$ аппроксимацию соответствующих дифференциальных выражений, имеем

Данное тождество является “опорным” для согласования аппроксимаций операторов дивергенции и градиента.

Положим, что поле градиентов ${{\text{GRA}}{{{\text{D}}}_{w}}:\left( \omega \right) \to \left( \varphi \right)}$ задано своими представлениями в базисах $(\varphi )$

Полагая в базисах $(\varphi )$ в качестве ${{{{\mathbf{X}}}_{\varphi }}}$ векторное “потоковое” поле ${{{{\mathbf{X}}}_{{w\varphi }}} = {{K}_{\varphi }}{{{\operatorname{GRAD} }}_{w}}u}$, от которого зависят скорости флюидов по формулам (2.3), (2.4), согласно закону Дарси, получим самосопряженный неотрицательный оператор ${ - {{{\operatorname{DIN} }}_{w}}{{{\mathbf{X}}}_{w}}:{\text{(}}\omega {\text{)}} \to {\text{(}}\omega {\text{)}}}$ или ${ - {{{\operatorname{DIN} }}_{w}}K{{{\operatorname{GRAD} }}_{w}}:{\text{(}}\omega {\text{)}} \to {\text{(}}\omega {\text{)}}}$. Векторное поле “потоков” ${{{\mathbf{X}}}_{w}}$ представлено своими компонентами ${{{\mathbf{X}}}_{{w\varphi }}}$. Оно зависит от скалярной сеточной функции $u$, заданной в узлах $(\omega )$, и от сеточной функции – аналога симметричного положительно-определенного тензора проводимости $K$, задаваемого своими представлениями ${{K}_{\varphi }}$ в базисах $(\varphi )$. Можно показать, что оператор ${ - {{{\operatorname{DIN} }}_{w}}K{{{\operatorname{GRAD} }}_{w}}:{\text{(}}\omega {\text{)}} \to {\text{(}}\omega {\text{)}}}$ будет строго положительным в случае однородного граничного условия $u = 0$.

При ${{W}_{\varphi }}(\lambda ) \to 1$ оператор $ - {{\operatorname{DIN} }_{w}}K\operatorname{GRAD} $ становится близок к самосопряженному неотрицательному оператору $ - \operatorname{DIN} K\operatorname{GRAD} $, хотя является самосопряженным и неотрицательным только на ортогональной сетке $(\Omega )$).

Для сохранения свойств самосопряженности и знакоопределенности этого оператора на нерегулярных треугольно-четырехугольных сетках предлагаются два семейства аппроксимаций, определяемые следующими построениями.

1. Аппроксимации с неполной монотонизацией.

Выделим множество ячеек сетки $(\Omega {\kern 1pt} *)$ таких, что в них имеется хотя бы один неортогональный базис $\varphi {\kern 1pt} {\text{*}}$. При построении аппроксимации потоков на основе (2.3), (2.4), т.е. пропорционально градиенту давления, с помощью базисов $(\varphi (\Omega {\kern 1pt} *))$, определенных внутри ячеек $\Omega {\kern 1pt} {\text{*}}$, положим ${{W}_{\varphi }}(\lambda ) = 1$. Т.е. в этих ячейках монотонизация сеточного решения отсутствует. Для остальных ячеек, т.е. тех, которые содержат только ортогональные базисы, монотонизация выполняется. Тензорное поле проводимости ${{K}_{\varphi }}$ вычисляется по переменным растепленности ${{S}_{\nu }}$ и влагонасыщеннности ${{S}_{w}}$ непосредственно в узлах $\omega $, к которым относятся приузловые ячейки $(\Omega {\kern 1pt} *)$. В этом случае оператор ${{\operatorname{DIN} }_{w}}K\operatorname{GRAD} :(\omega ) \to (\omega )$будет самосопряженным и знакоопределенным.

2. Квазимонотонные схемы.

Обозначим через $(\varphi {\kern 1pt} *)$ множество неортогональных базисов сетки. Соответственно к множеству $(\varphi ){\text{/}}(\varphi {\kern 1pt} *)$ относятся ортогональные базисы. Для аппроксимации векторного поля ${\mathbf{X}} = K{\text{grad}}u$ введем ${{{\mathbf{X}}}_{{w\varphi }}} = {{K}_{\varphi }}\operatorname{GRAD} _{w}^{*}u$,

Соответствующий оператор ${{\operatorname{DIN} }_{w}}K\operatorname{GRAD} _{w}^{*}:(\omega ) \to (\omega )$ будет обладать свойствами самосопряженности и знакоопределенности.

При решении уравнения пьезопроводности в соответствующем блоке алгоритма расщепления применяемая монотонизация не нарушает свойство знакоопределенности квадратичных форм от градиентов термодинамических величин, определяющих, согласно закону Дарси, скорости отдельных флюидов.

4. АППРОКСИМАЦИЯ УРАВНЕНИЯ ПЬЕЗОПРОВОДНОСТИ ФЛЮИДОДИНАМИКИ В ПОРИСТОЙ СРЕДЕ С ГАЗОГИДРАТНЫМИ ВКЛЮЧЕНИЯМИ

Построения по методу опорных операторов выполним с помощью следующих сеточных функций. К сеточным узлам $(\omega )$ будем относить величины

К сеточным базисам $(\varphi )$ в соответствии с описанием в п. 3 отнесем векторные функции

Сеточные функции, представляющие материальные свойства веществ, отнесем к ячейкам $\Omega $

Эти свойства на внутренних границах среды могут меняться скачкообразно.

Для дальнейшего изложения отметим, что объемы $\overline {{{m}_{\omega }}} $ поровой доли в домене $d(\omega )$ и в его части $\overline {{{{(1 - m)}}_{\omega }}} $, занятой каркасом пористой среды, связаны соотношениями

Примем, что для интегрирования уравнений по времени используется равномерная сетка с шагом $\tau $. На временных слоях этой сетки $t$ и $\hat {t} = t + \tau $ определим разностные производные по времени ${{a}_{t}} = (\hat {a} - a){\text{/}}\tau $. Для узловых сеточных функций будем использовать интерполяции по времени вида ${\text{ }}{{a}^{{(\delta )}}} = \delta \hat {a} + (1 - \delta )a$, причем интерполяционный вес $\delta $ может быть переменным по множеству узлов $(\omega )$. Например, под величиной

будем понимать “свободно-объемный” весовой множитель, т.е. интерполяционный вес ${{\delta }_{\nu }}$ определяется долей порового объема, свободного для движения жидкости и газа. Выбранная аппроксимация позволяет производить преобразования разностных уравнений при их расщеплении по физическим процессам так, чтобы сохранить формы балансов соответственно уравнениям исходной системы. Другие интерполяции по времени будем обозначать как $[\;]\widetilde {}$. Они могут использоваться не только для узловых сеточных функций, но и других, отнесенных к ячейкам $(\Omega )$ или базисам $(\varphi )$.

Запишем теперь аппроксимацию уравнений (2.1), (2.2) и (2.5), обозначив индексом S в выражениях ${\text{DI}}{{{\text{N}}}_{s}}$ и ${\text{GRA}}{{{\text{D}}}_{s}}$ один из описанных видов монотонизации решения сеточных уравнений насыщенностей ${{S}_{w}}$ и ${{S}_{\nu }}$.

Разностные уравнения балансов массы водной и газовой компонент имеют вид

С помощью оператора ${\text{GRA}}{{{\text{D}}}_{s}}$ потоки воды $({{\rho }_{w}}{{{\mathbf{V}}}_{w}})\widetilde {}$ и газа $({{\rho }_{g}}{{{\mathbf{V}}}_{g}})\widetilde {}$ аппроксимируются в базисах $\varphi $ с учетом уравнений (2.3), (2.4), например, неявно по времени любым из стандартных способов [7], [10]:

Здесь под $\mathop {\left( {} \right)}\nolimits_{\underline \Delta \varphi }^\sim $ понимаются аппроксимации соответствующих выражений в сеточных базисах $(\varphi )$ с некоторой интерполяцией по времени.

При наличии термобарической зависимости вида (2.7) для сохранения свойства знакоопределенности квадратичных форм градиентов величин вида $\int {\varepsilon \operatorname{div} (\rho {\mathbf{V}})dV} $ (см. также (4.5) ниже) предпочтительно использовать закон Дарси в энергетической формулировке. Получим ее из следующих соображений.

С учетом термобарической зависимости (2.7) в зоне равновесия фаз гидрат–вода–газ можно написать

где $\varepsilon _{{wp}}^{'}$ и $\varepsilon _{{gp}}^{'}$ – полные производные от внутренней энергии по давлению с учетом (2.7).

Аппроксимацию следующих из закона Дарси уравнений (2.3), (2.4) в базисах $\varphi $ с учетом термобарического соотношения (2.7) представим в энергетической форме:

Таким образом, имеем

Уравнение баланса внутренней энергии, аппроксимирующее (2.5), имеет вид

Индекс up в выражении для энергии воды ${{(\varepsilon _{w}^{{({{\delta }_{\nu }})}})}_{{{\text{up}}}}}$ обозначает, что соответствующие величины берутся вверх (up wind) по потоку $({{\rho }_{w}}{{{\mathbf{V}}}_{w}})\widetilde {}$ в определенной ранее дивергенции ${{\operatorname{DIN} }_{s}}({{\rho }_{w}}{{{\mathbf{V}}}_{w}})\widetilde {}$. Аналогично индекс up понимается в выражении для энергии газа ${{(\varepsilon _{g}^{{({{\delta }_{\nu }})}})}_{{{\text{up}}}}}$.

Работа сил давления $[P({{{\mathbf{V}}}_{w}} + {{{\mathbf{V}}}_{g}})]\widetilde {}$ и полный поток тепла ${\mathbf{W}}\widetilde {}$ аппроксимируются в базисах $(\varphi )$ неявно по времени, также как потоки $({{\rho }_{w}}{{{\mathbf{V}}}_{w}})\widetilde {}$ и $({{\rho }_{g}}{{{\mathbf{V}}}_{g}})\widetilde {}$ [7], [10]:

В итоге проделанных построений получаем аппроксимацию уравнения пьезопроводности (2.14), разностно эквивалентную исходной системе уравнений балансов (4.1)–(4.3):

В выражение ${\text{DIG}}\widetilde {_{\varepsilon }}$ (4.5) в соответствующих комбинациях входит монотонная (вверх по потоку) аппроксимация для $\varepsilon _{w}^{{({{\delta }_{\nu }})}}$ и $\varepsilon _{g}^{{({{\delta }_{\nu }})}}$.

5. ЗАКЛЮЧЕНИЕ

Методами теории опорных операторов на сетках нерегулярной структуры построено семейство полностью консервативных разностных схем, аппроксимирующих уравнения двухкомпонентной флюидодинамики в пористой гидратосодержащей среде. Предложен итерационный алгоритм решения разностных уравнений путем последовательного учета (расщепления) физических процессов. С этой целью введена специальная “свободно-объемная” аппроксимация уравнения пьезопроводности в гидратосодержащей среде. По сравнению с ранее использованными в данной предметной области методиками предложенные алгоритмы свободны от жестких ограничений по устойчивости на шаг численного интегрирования уравнений флюидодинамики. Алгоритмы расщепления применяются для уравнений в форме, эквивалентной системе разностных “балансных” уравнений массы, импульса, полной внутренней энергии среды, содержащей флюиды, твердый газогидрат и скелет.

Специфика процессов переноса насыщенности в гидратосодержащей пористой среде учтена при выборе способа монотонизации сеточного решения. В рассматриваемой модели флюидодинамики монотонизация сеточного решения ${{W}_{\varphi }}(\lambda )$, выполняемая с учетом свойств гиперболичности системы (2.1), (2.2), согласно результатам анализа [10], обеспечивает корректный расчет растепленности гидрата ${{S}_{\nu }}$, а также влаго- и газонасыщенностей ${{S}_{w}}$ и ${{S}_{g}} = 1 - {{S}_{w}}$.

Предложенная методика позволяет сохранить свойства знакоопределенности и самосопряженности дифференциальных операторов второго порядка (типа ${\text{divgrad}}$). Как показывает численное решение некоторых прикладных задач (формирование депрессионных воронок, эволюция зон растепленности и др. [13]–[15]), вместе с монотонизацией решения это улучшает качество разностного описания неизотермической двухкомпонентной флюидодинамики в пористой гидратосодержащей среде.

Построение полностью консервативной разностной схемы описано для случая нерегулярных плоских сеток, составленных из трех- и четырехугольных ячеек. Однако метод построения имеет общих характер, и предлагаемые аппроксимации распространяются на случай трехмерных сеток, составленных из ячеек – тетраэдров, гексаэдров, призм и их сочетаний.