Журнал вычислительной математики и математической физики, 2020, T. 60, № 1, стр. 57-69

1. ВВЕДЕНИЕ

Существуют два типа особенностей решений ОДУ, известных как неподвижные и подвижные особенности. Неподвижные особенности обычно изучают с помощью метода нормальных форм, который позволяет (в простых случаях) описать поведение решений в окрестности неподвижной точки. Это описание, однако, является в основном качественным. Для получения конструктивного описания решения необходимо представить его в виде асимптотического разложения, что дает локальную параметризацию решения вблизи сингулярности (см. [1]). Ситуация, когда требуется конструктивное описание решения, т.е. предъявление формул, по которым решение может быть вычислено с достаточной точностью вблизи сингулярности, возникает, например, при решении сингулярных краевых задач (метод “погранслоя”). Для подвижных особенностей в неинтегрируемых системах ОДУ не существует методов конструктивного описания решения вблизи особенности без привлечения численных методов. Один из способов локализации и вычисления таких особенностей предложен в [2].

Однако в данной работе мы рассмотрим другой тип особых, или вырожденых, решений ОДУ, которые мы называем нелокальными особенностями (за неимением другого термина). Насколько нам известно, это понятие не встречается в литературе.

Основное отличие этих особенностей от двух упомянутых выше типов состоит в том, что они не являются (вообще говоря) особенностями фиксированного решения ОДУ, либо особенностью самих уравнений, но являются особенностями на некотором семействе решений. В данной статье мы ограничиваемся только семействами периодических решений ОДУ.

В многопараметрических задачах механики таких, например, как задачи небесной механики, довольно типична ситуация, когда существование особенности на семействе периодических решений очевидно. В то же время природа особенности и ее местоположение известны (ежели вообще) лишь приближенно.

Это случается, например, когда численный алгоритм дает отказ по каким-то причинам и семейство не может быть далее продолжено. Здесь проблема состоит в том, чтобы определить причину отказа алгоритма и предложить способ устранения препятствий для продолжения семейства.

Типичный пример – это потеря устойчивости решения на семействе, что может быть интерпретировано как некоторая топологическая особеность на семействе решений. Это также может быть пересечение семейства решений с другим аналогичным семейством, т.е. бифуркация на семействе. Но возможны и более причудливые ситуации.

Любой алгоритм, предназначенный для расчета решений на семействе в случае общего положения, даст отказ не только на вырожденном решении, но и в некоторой его окрестности.

Как оказалось, такого рода вырожденные решения можно вычислять с помощью уравнений в вариациях высокого порядка, причем с той же точностью, что и невырожденные решения.

Данный метод основан на конструировании некоторого специального характеристического многообразия, вложенного в конечномерное евклидово пространство таким образом, что многобразие может быть интерпретировано как график всех решений ОДУ при всех возможных значениях параметров. Тогда каждое решение ОДУ рассматривается либо как точка на многообразии, либо как функция, заданная на многообразии.

Поскольку локальными координатами введенного многобразия являются начальные данные решения и его параметры, то частные производные решения (любого порядка) по локальным координатам характеристического многообразия удовлетворяют уравнениям в вариациях, которые получаются рекурсивно формальным дифференцированием исходного уравнения по начальным данным решения и параметрам, входящим в уравнение.

Полученные уравнения в вариациях вместе с исходным уравнением (которое уместно обозначить как вариацию нулевого порядка) рассматриваются как дифференциальные тождества для частных производных решения, заданные на характеристическом многообразии.

Близкой аналогией к введенному понятию является понятие римановой поверхности (комплексного) решения ОДУ. Риманова поверхность решения может рассматриваться либо как график решения над комплексной плоскостью, либо как аналитическое многообразие, представляющее решение ОДУ (см. [2]).

Введем формальное определение характеристического многообразия.

Пусть имеется аналитическая система ОДУ, зависящая от конечного набора параметров аналитическим образом.

Рассмотрим вначале случай, когда параметры фиксированы. Тогда решение, которое мы обозначим $X(t)$, полностью определяется данными Коши, т.е. начальными значениями решения $X({{t}_{0}})$.

Поведение некоторого малого объема фазового пространства в окрестности точки $X({{t}_{0}})$ за время $0 < t = {{t}_{1}} - {{t}_{0}}$ описывается матрицей монодромии, компоненты которой выражаются с помощью решений классических уравнений в вариациях.

Утверждается, что полностью эквивалентное описание получается при рассмотрении следующего аналитического конечномерного многообразия

где начальное время ${{t}_{0}}$ фиксировано, а начальные данные $X({{t}_{0}})$ принадлежат некоторой ограниченной области.

Данное утверждение очевидно, если принять во внимание, что речь идет по сути о графике решения, в то время как матрица монодромии выступает в роли первой производной, вычисленной в точке ${{t}_{1}} = {{t}_{0}} + t$.

Таким образом, имеем аналитическое многообразие ${{\chi }_{t}}$, так как решения (по предположению) зависят от начальных данных аналитически. Размерность многообразия ${{\chi }_{t}}$, очевидно, совпадает с размерностью системы.

В общем случае к начальным данным, т.е. локальным координатам характеристического многообразия ${{\chi }_{t}}$, добавляются параметры системы, от которых зависит решение.

Точно так же как аналитическая функция полностью определяется значениями своих производных, заданных в одной точке, поведение решений аналитической системы ОДУ в окрестности точки ${{t}_{1}}$ полностью определяется набором значений частных производных решения по начальным данным и параметрам, т.е. по локальным координатам характеристического многообразия. А эти частные производные удовлетворяют формальным уравнениям в вариациях.

Таким образом, предлагаемый подход по сути использует методы дифференциальной геометрии и требует большого объема символьных преобразований. Однако эти вычисления легко программируются в современных системах компьютерной алгебры (CAS), а сами уравнения в вариациях вместе с исходными уравнениями образуют треугольную систему ОДУ, которая также генерируется автоматически.

Как мы увидим, данная интерпретация уравнений в вариациях позволяет выразить особенности на семействах решений в терминах геометрии характеристического многообразия и получить для них (особенностей) соответствующие уравнения. Мы проиллюстрируем этот подход на примере классической проблемы центр-фокус (см. разд. 2), а также на более сложном примере уравнения маятникового типа (см. разд. 3), которое описывает колебания и вращения спутника на эллиптической орбите, т.е. уравнения Белецкого.

2. ПРОБЛЕМА ЦЕНТРА-ФОКУСА

Рассмотрим полиномиальную систему ОДУ на плоскости, имеющую монодромную особую точку в начале координат. Предполагается, что система зависит от некоторого набора параметров или коэффициентов также полиномиальным образом.

Классическая проблема центра-фокуса состоит в определении набора условий на коэффициенты системы, при которых особая точка ноль является центром.

Эти условия называются условиями центра и часто оказываются алгебраическими, во всяком случае для того небольшого количества относительно простых задач, для которых проблему центра-фокуса удается решить.

До недавнего времени (см. [3]) проблема различения центра и фокуса была решена лишь для некоторых частных случаев полиномиальных систем, среди которых можно выделить системы с невырожденной линейной частью; системы, линейная часть которых является нильпотентной жордановой клеткой; и системы, укорочение которых однородно и невырождено. Все эти случаи можно классифицировать как системы с одним ребром диаграммы Ньютона.

Существующие методы исследования этих систем сводятся либо к построению нормальной формы, либо к отысканию формального первого интеграла. Условия центра, которые при этом получаются, неизбежно теряют часть информации об асимптотике отображения последования исходной системы.

Мы предлагаем метод вычисления фокусных величин, который полностью сохраняет эту информацию и позволяет вычислить необходимое количество условий центра в аналитическом виде или численно.

Рассмотрим более широкий класс полиномиальных систем ОДУ с одним ребром диаграммы Ньютона, чем указано выше. А именно, системы, которые с помощью перенормировки $x$, $y$ и $t$ приводятся к виду

где $j,m,n \in \mathbb{N}$; $m$ и $n$ взаимно просты; и многоточие обозначает мономы, которые попадают либо внутрь диаграммы Ньютона (случай первой категории согласно Ляпунову [4]), либо внутрь и на ребро диаграммы Ньютона, обращенное к началу координат (случай второй категории). Ляпунов рассмотрел системы (1) для случая $j = m = 1$ (см. [4]).

Заметим, что укорочение системы (1) первой категории – это гамильтонова система, имеющая центр в нуле. Интегральные кривые этой системы ${{x}^{{2jn}}}{\text{/}}n + {{y}^{{2jm}}}{\text{/}}m = {\text{const}}$ вытянуты вдоль одной из осей координат (если $m \ne n$) таким образом, что при стягивании фазовой кривой к началу координат отношение минимального и максимального диаметра фигуры, образованной фазовой кривой, стремится к нулю. Ясно, что обычная полярная замена координат в этом случае сингулярна.

Для системы (1) сделаем обобщенную полярную замену координат:

где $m$ и $n$ те же, что и в системе (1). Тогда система (1) принимает вид

Замена переменных, предложенная Ляпуновым для систем (1) с $j = m = 1$, использует введенные им специальные функции, что позволяет упростить некоторые формулы, но требует исследования интегралов от этих специальных функций. Ляпунов сводит эти интегралы к нескольким типам, которые требуют отдельного исследования [4, стр. 299].

Назовем степенью монома ${{x}^{k}}{{y}^{l}}$ ($k,l \in {{\mathbb{N}}_{0}}$) в первом уравнении системы (1) его квазиоднородную степень $(k - 1)m + ln$, а во втором уравнении системы (1) – его квазиоднородную степень $km + (l - 1)n$. Очевидно, в случае первой категории степень мономов системы (1) превосходит $2jmn - n - m$. Если же некоторые мономы системы (1) имеют степень $2jmn - n - m$, то они, очевидно, лежат на ребре диаграммы Ньютона системы (1), и это случай второй категории.

Определим функцию

где $r{\kern 1pt} '$ – это правая часть уравнения (3). Очевидно, этот предел существует в силу введенной нами обобщенной полярной замены (2).

Теорема 1. Если знаменатель функции $F(\varphi )$ не обращается в ноль для достаточно малых $\left| {\operatorname{Im} \varphi } \right|$, то особая точка ноль системы (1) монодромна.

Доказательство. Числитель и знаменатель функции $F(\varphi )$ суть тригонометрические полиномы с коэффициентами мономов степени $2jmn - n - m$ системы (1), причем знаменатель функции $F(\varphi )$, очевидно, удовлетворяет условию теоремы при достаточно малых коэффициентах мономов укороченной системы (1). Разложим правую часть уравнения (3) в ряд Тейлора по $r$. Каждый член этого разложения является дробью, знаменатель которой – это некоторая степень знаменателя функции $F(\varphi )$. Следовательно, правая часть уравнения (3) и функция $r(\varphi )$ аналитичны для достаточно малых $\left| r \right|$ и $\left| {\operatorname{Im} \varphi } \right|$, поэтому решение ОДУ (3) существует для $\varphi \in [0,2\pi ]$, т.е. особая точка монодромна. Q.E.D.

Например, для системы ($j = 1$, $m = 1$, $n = 2$) имеем

Знаменатель $co{{s}^{4}}\varphi + 2aco{{s}^{2}}\varphi sin\varphi + 2si{{n}^{2}}\varphi \ne 0$ при условии $\left| a \right| < \sqrt 2 $.

Заметим, что в единственном случае первой категории при $j = m = n = 1$ получим $F(\varphi ) = 0{\text{/}}(co{{s}^{2}}(\varphi ) + si{{n}^{2}}(\varphi )) \equiv 0$, что также считаем допустимым.

Пусть $r(0) = \rho $ является начальным значением радиус-вектора $r(\varphi )$, который опишет полный круг и при $\varphi = 2\pi $ примет значение $r(2\pi )$. Тогда, согласно разд. 1, характеристическое многообразие (кривая) $\chi $ для уравнения (3) имеет вид, представленный на фиг. 1.

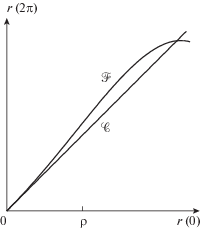
Введенный нами формализм сводит исследование проблемы центра-фокуса к исследованию поведения кривой $\chi $ в зависимости от коэффициентов системы.

Например, в классическом случае $j = m = n = 1$ имеем задачу о бифуркации Андронова–Хопфа.

Пусть вначале кривая $\chi = \mathcal{F}$ на фиг. 1 пересекает биссектрису в нуле трансверсально. Это соответствует случаю грубого фокуса.

При изменении параметра системы кривая $\mathcal{F}$ будет как-то извиваться, но главным образом поворачиваться относительно биссектрисы так, что при некотором значении параметра она будет касаться биссектрисы в нуле. Это в точности соответствует моменту, когда пара комплексно-сопряженных собственных значений линейной части системы пересекает мнимую ось (негрубый фокус).

Но уже в следующий момент, т.е. при ненулевой надкритичности, кривая $\mathcal{F}$ снова будет пересекать биссектрису в нуле трансверсально, но с другой стороны. При этом неизбежно образуется точка пересечения кривой $\mathcal{F}$ и биссектрисы, что соответствует предельному циклу.

Если приблизить локально кривую $\mathcal{F}$ куском окружности, то можно также получить известную качественную оценку роста величины предельного цикла как корня квадратного из надкритичности.

Таким образом, бифуркация Андронова–Хопфа, которая не считается элементарной и не преподается на курсах дифференциальных уравнений даже для студентов-математиков, под данным углом зрения выглядит довольно очевидной.

Что касается общего случая на фиг. 1, то расположение кривой $\chi $ по отношению к биссектрисе $\mathcal{C}$ позволяет судить об устойчивости или неустойчивости фокуса, а также о наличии предельных циклов и об их устойчивости в системе координат (2). Например, кривая $\mathcal{F}$ на фиг. 1 соответствует неустойчивому фокусу, а точка пересечения $\mathcal{F} \cap \mathcal{C}$ соответствует устойчивому предельному циклу уравнения (3).

Для исходной системы устойчивость и неустойчивость меняются местами, если обход особой точки ноль совершается по часовой стрелке.

Разумеется, пока что нам удалось провести лишь качественный анализ задачи, и проблема состоит в том, как транслировать полученные знания в вычислительные формулы. Мы применим для этого формальные уравнения в вариациях.

Алгоритм вычисления уравнений в вариациях произвольного порядка для уравнения $r{\kern 1pt} ' = f(r,\varphi )$ состоит в следующем.

Запишем это уравнение как уравнение в вариациях нулевого порядка, сделав в нем подстановку $r = {{r}_{0}}$, т.е. $r_{0}^{'} = f({{r}_{0}},\varphi )$, и пусть ${{r}_{0}}(\varphi )$ является решением этого уравнения с начальным значением $\rho = {{r}_{0}}(0) \ne 0$. Введем обозначение

Формальным дифференцированием находим уравнения в вариациях Начальные значения для решений уравнений в вариациях ${{r}_{k}}(\varphi )$ суть ${{r}_{1}}(0) = 1$ и ${{r}_{k}}(0) = 0$, $k = 2,3, \ldots $

Заметим, что величины ${{r}_{n}}(2\pi )$, $n = 1,2,3, \ldots $, суть производные к кривой $\mathcal{F}$ на фиг. 1 в точке $\rho = {{r}_{0}}(0) \ne 0$. Нам же нужны производные к кривой $\mathcal{F}$ в начале координат, так как набор этих производных полностью определяет аналитическую кривую $\mathcal{F}$ и дает ее асимптотическое (и, в данном случае, сходящееся) разложение.

Уравнения в вариациях на нулевом решении вычисляются следующим образом.

Сначала нужное количество уравнений в вариациях вычисляется в точке $\rho = r(0) \ne 0$, а затем $\rho $ устремляется к нулю, т.е. делается подстановка ${{r}_{0}}(\varphi ) = 0$.

Пример. Пусть имеем уравнение $r{\kern 1pt} ' = r{{f}_{1}}(\varphi ) + {{r}^{2}}{{f}_{2}}(\varphi ) + \ldots $. В силу замены (2) любая система (1) приводится к такому виду, причем ${{f}_{1}}(\varphi ) = F(\varphi )$, определенная в теореме 1. Тогда уравнения в вариациях имеют вид

Теорема 2. Пусть выполнено условие теоремы $1$. Особая точка ноль системы (1) является центром тогда и только тогда, когда все уравнения в вариациях на нулевом решении уравнения (3) имеют в качестве решений 2π-периодические функции, ограниченные на вещественной оси.

Доказательство. Согласно разд. 1, построим характеристическое многобразие уравнения (3) $\chi = \{ r(0),r(2\pi )\} $ для достаточно малых начальных значений $r(0)$.

Согласно теореме 1, множество $\chi $ является аналитической кривой, проходящей через начало координат. Это либо кривая $\mathcal{F}$ (фокус), либо кривая $\mathcal{C}$ (центр) (см. фиг. 1).

Очевидно, особая точка ноль системы (1) является центром тогда и только тогда, когда множество $\chi $ является биссектрисой первого квадранта плоскости ${{\mathbb{R}}^{2}}$.

Пусть ${{r}_{k}}(\varphi )$, $k = 1,2, \ldots $, суть решения уравнений в вариациях, и $\rho = {{r}_{0}}(0) \ne 0$ – это начальное значение решения уравнения (3).

Величины ${{r}_{k}}(2\pi )$, $k = 1,2, \ldots $, являются значениями производных к кривой $\chi $ в точке $\rho $ (см. фиг. 1).

Все решения уравнений в вариациях зависят аналитически от начального значения $\rho $ согласно теореме 1. Поэтому величины ${{r}_{k}}(2\pi )$, $k = 1,2, \ldots $, для уравнений в вариациях на нулевом решении уравнения (3) являются значениями производных к кривой $\chi $ в нуле.

Аналитическая кривая является биссектрисой первого квадранта плоскости ${{\mathbb{R}}^{2}}$ тогда и только тогда, когда имеет в нуле те же производные, т.е. ${{r}_{1}}(2\pi ) = 1$, ${{r}_{k}}(2\pi ) = 0$, $k = 2,3, \ldots $ . Эти величины совпадают с начальными значениями решений уравнений в вариациях, поэтому достаточность условия теоремы доказана.

Далее мы будем иметь дело с уравнениями в вариациях на нулевом решении.

Докажем необходимость. Первое уравнение в вариациях имеет вид

где $F(\varphi )$, определенная формулой (4), является $2\pi $-периодической функцией. Поэтому если ${{r}_{1}}(2\pi ) = 1$, то ${{r}_{1}}(\varphi )$ также $2\pi $-периодическая функция. Очевидно, получаем По индукции $k$-е уравнение в вариациях имеет вид где ${{G}_{k}}(\varphi )$ – это $2\pi $-периодическая функция, ограниченная на вещественной оси. Поэтому если ${{r}_{k}}(2\pi ) = 0$, то ${{r}_{k}}(\varphi )$ также $2\pi $-периодическая функция. Очевидно, имеем

На самом деле ${{G}_{k}}(\varphi )$ делится на $r_{1}^{2}(\varphi )$, что следует из формулы (8). Попутно доказано, что все уравнения в вариациях на нулевом решении интегрируются в квадратурах. Q.E.D.

Замечание. Для бесконечногладких систем не существует теоремы, аналогичной теореме 2. Для таких систем возможна ситуация, когда кривые $\mathcal{F}$ и $\mathcal{C}$ имеют бесконечный порядок касания в нуле, но не совпадают (например, для линейного осциллятора с экспоненциально малым трением). Возможна также ситуация центрофокуса, когда кривая $\mathcal{F}$ пересекает кривую $\mathcal{C}$ бесконечное число раз в любом интервале значений $0 < r(0) < \varepsilon \to 0$. Каждое такое пересечение соответствует, как было отмечено, предельному циклу.

Таким образом, величины ${{r}_{k}}(2\pi )$, $k = 1,2, \ldots $, являются фокусными для монодромной особой точки системы (1). Если ${{r}_{1}}(2\pi ) \ne 1$, то имеет место грубый фокус (первого порядка по определению), т.е. кривая $\mathcal{F}$ трансверсальна биссектрисе $\mathcal{C}$ в начале координат. Для случая первой категории фокус, очевидно, не может быть грубым. Если ${{r}_{1}}(2\pi ) = 1$, ${{r}_{l}}(2\pi ) = 0$, $l < k$, но ${{r}_{k}}(2\pi ) \ne 0$, тогда имеет место негрубый фокус (порядка $k$ по определению). Очевидно, порядок негрубого фокуса соответствует порядку касания кривых $\mathcal{F}$ и $\mathcal{C}$ в начале координат.

Обращаем внимание, что фокусные величины содержат больше информации, чем просто условия центра, так как они полностью характеризуют отображение последования вблизи нуля.

Как следует из теоремы 2, величины ${{r}_{k}}(2\pi )$, $k = 1,2, \ldots $, находятся из треугольной системы ОДУ, которая всегда интегрируется в явном виде. Например, для случая

все вычисления сводятся к операциям с тригонометрическими полиномами и легко программируются в CAS.

Более сложные случаи проблемы центр-фокус, а также вычисление предельных циклов любого вырождения, рассмотрены в [3].

3. ВЫРОЖДЕНИЯ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ УРАВНЕНИЯ БЕЛЕЦКОГО

С момента своего открытия [5] уравнение Белецкого использовалось как для целей космической навигации, так и для объяснения движения небесных тел.

В настояшее время это уравнение используется главным образом в качестве модельной задачи для тестирования различных алгоритмов вычисления вырожденных решений на семействах периодических решений (см. [6]).

Пусть центр масс спутника движется по эллиптической орбите и одна из его главных осей инерции нормальна к плоскости орбиты. Уравнение плоских движений спутника относительно его центра масс имеет вид

Здесь $\delta $ – удвоенный угол между радиус-вектором центра масс и одной из главных осей инерции спутника; $\mu $ – инерциальный параметр спутника; $e$ – эксцентриситет орбиты, по которой движется спутник; $\nu $ – истинная аномалия положения спутника на орбите.

Нелинейное дифференциальное уравнение второго порядка (9) маятникового типа имеет периодические коэффициенты и два параметра $e$ и $\mu $, лежащие в прямоугольнике $e < 1$, $\left| \mu \right| \leqslant 3$ (область физических значений параметров). Однако в качестве модельной задачи уравнение (9) рассматривалось для произвольных значений $e$ и $\mu $.

Уравнение (9) обладает рядом симметрий:

При $e < 1$ уравнение (9) регулярно. При $e = 1$ и $\nu = \pi $ оно сингулярно, ибо коэффициент при старшей производной обращается в ноль.

Мы рассмотрим лишь некоторые из вырождений на семействах симметричных (нечетных) $2\pi $-периодических решений уравнения (9) для демонстрации возможностей нашего метода.

Предложенная техника обобщается как для исследования несимметричных периодических решений разного периода, так и для периодических решений с различным числом вращения (см. [6], [7]).

Рассмотрим евклидово пространство с координатами $\Omega = \{ {{\omega }_{1}}, \ldots ,{{\omega }_{6}}\} $, которое мы назовем пространством симметрий. Согласно разд. 1 определим аналитическое многообразие $\chi $ всех возможных решений уравнения (9) как множество

где $\delta (\nu )$ – это решение уравнения (9) с начальными данными $\delta (0),\delta {\kern 1pt} '(0) \in ( - \infty ,\infty )$ при фиксированных параметрах $e \in ( - 1,1)$ и $\mu \in ( - \infty ,\infty )$.

Множество $\chi $, очевидно, является четырехмерным аналитическим многообразием, так как величины $\delta (\pi )$, $\delta {\kern 1pt} '(\pi )$ однозначно определяются по четырем предыдущим и зависят от них аналитически.

Многообразие $\chi $ инвариантно по отношению к линейным автоморфизмам пространства симметрий:

что следует из симметрий (10) уравнения (9).

Каждую точку многообразия $\chi $ мы отождествим с решением уравнения (9), которому она соответствует.

Величины $\delta (0),\;\delta {\kern 1pt} '(0),\;e,\;\mu $ являются локальными координатами на многообразии $\chi $. Они также, очевидно, являются глобальными координатами. Тот факт, что многообразие $\chi $ покрывается одной картой, не означает, что оно имеет простую структуру. Из результатов [8] следует, что многообразие $\chi $ устроено фрактально вблизи краев $e = \pm 1$.

Мы могли бы использовать значения $\delta (2\pi ),\;\delta {\kern 1pt} '(2\pi )$ в (11), но значения при $\nu = \pi $ более подходят для симметричных периодических решений. Эти решения имеют простую геометрическую интерпретацию.

Из определения $\chi $ немедленно получаем, что семейства симметричных периодических решений образуют двумерные подмногообразия, поскольку они задаются пересечением

Нетрудно показать, что и в общем случае все семейства периодических решений являются двупараметрическими.

Каждая точка многообразия $\chi $ соответствует единственному решению уравнения (9), а само уравнение является дифференциальным тождеством, заданным на многообразии. Поэтому мы можем дифференцировать это тождество по локальным координатам многобразия и получать таким образом уравнения в вариациях произвольного порядка и в любой комбинации начальных данных и параметров. Это делается следующим образом.

При фиксированном значении независимой переменной $\nu $, $\delta (\nu )$ является аналитической функцией, заданной на многообразии $\chi $, т.е. $\delta (\nu ) = \delta (\nu )(p)$, где $p = (\delta (0),\delta {\kern 1pt} '(0),e,\mu ) \in \chi $.

Пусть точка $p \in \chi $ фиксирована. Обозначим $\Delta = (\Delta \delta (0),\Delta \delta {\kern 1pt} '(0),\Delta e,\Delta \mu )$, тогда $\delta (\nu ) = \delta (\nu ,\Delta )$. Пусть $m = ({{m}_{1}},{{m}_{2}},{{m}_{3}},{{m}_{4}})$ обозначает мультииндекс. Пусть

По формуле Тейлора имеем А также, $\partial {{\delta }_{m}}(\nu ,p){\text{/}}\partial \nu = \delta _{m}^{'}(\nu ,p)$, в силу возможности менять порядок дифференцирования.

${{\delta }_{{0,0,0,0}}}(0,p) = \delta (0)$, $\delta _{{0,0,0,0}}^{'}(0,p) = \delta {\kern 1pt} '(0)$, ${{\delta }_{{1,0,0,0}}}(0,p) = \partial \delta (0){\text{/}}\partial \delta (0) = 1$ и $\delta _{{0,1,0,0}}^{'}(0,p) = \partial \delta {\kern 1pt} '(0){\text{/}}\partial \delta {\kern 1pt} '(0) = 1$. Для всех остальных значений мультииндекса $m$, ${{\delta }_{m}}(0,p) = \delta _{m}^{'}(0,p) = 0$.

Таким образом, все уравнения в вариациях получаются формальным дифференцированием исходного уравнения (9) по локальным координатам многообразия $\chi $, т.е. начальным значениям и параметрам.

В традиционных обозначениях вариации функции $\delta $ имеют вид

Чтобы уменьшить размер формул, обозначим $a = 1 + ecos\nu $, $b = 2esin\nu $, $c = cos\delta (\nu )$, $s = sin\delta (\nu )$ и опустим зависимость функций от $\nu $. Тогда

Эти уравнения могут понадобиться вплоть до определенного порядка в зависимости от вырожденности особенности, которую требуется разрешить. Все они легко вычисляются в какой-либо CAS.

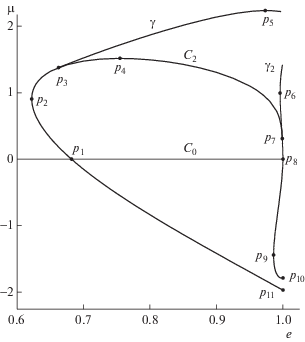
Обозначим семейства симметричных и несимметричных периодических решений $\mathcal{F}$ и $\mathcal{G}$ соответственно. Тогда имеем следующую картину с наиболее типичными вырождениями на этих семействах (см. фиг. 2).

Опишем некоторые особенности на семействах периодических решений, представленные на фиг. 2.

Точка ${{p}_{2}}$ дает пример чисто геометрической (или топологической) особенности на семействе решений, поскольку она проявляется только при численном продолжении решения по параметру $e$. Программа даст отказ вблизи точки ${{p}_{2}}$, т.е. придется продолжать семейство по другому параметру.

Точка ${{p}_{2}}$ задается уравнением (см. [6])

Таким образом, чтобы найти ${{p}_{2}}$, нужно использовать уравнение (15) вместе с уравнениями для периодического решения в случае общего положения.

Заметим, что точка ${{p}_{4}}$ полностью аналогична точке ${{p}_{2}}$, и чтобы ее найти, нужно лишь поменять параметр $\mu $ на $e$ в (15).

Как мы полагаем, это является одним из основных преимуществ нашего метода, так как один раз выведенные формулы пригодны не только для других параметров в той же задаче, но и во всех подобных уравнениях (т.е. с двумя параметрами и с аналогичными симметриями). Изменится только набор уравнений в вариациях.

Кривые ${{C}_{0}}$ и ${{C}_{2}}$ являются проекциями двух пересечений $\mathcal{F} \cap \mathcal{G}$, одно из которых (${{C}_{0}}$) соответствует интегрируемому случаю для $\mu = 0$, а другое (${{C}_{2}}$) соответствует случаю общего положения.

Обе кривые ${{C}_{0}}$ и ${{C}_{2}}$ задаются уравнением $y_{0}^{'}(\pi ) = 0$ (см. [6]), т.е.

что, на самом деле, является формулировкой теоремы об ответвлении несимметричных периодических решений от симметричных. Доказательство получается с помощью регулярной теории возмущений (см. [6]).

Здесь мы докажем другую теорему, которая интерпретирует понятие устойчивости периодических решений в терминах геометрии их многообразий.

Напомним, что устойчивость периодического решения в линейном приближении определяется следом ${\text{Tr}} = {{y}_{0}}(2\pi ) + y_{1}^{'}(2\pi )$ матрицы монодромии, т.е. периодическое решение неустойчиво, если $\left| {{\text{Tr}}} \right| > 2$. Для симметричных периодических решений след вычисляется по формуле

которая получается, если рассмотреть матрицу монодромии на интервале $\nu \in [ - \pi ,\pi ]$ и использовать симметрию решений. Таким образом, границы областей устойчивости, т.е. критические семейства симметричных периодических решений, являются вырождениями коразмерности 1.

Теорема 3. Пусть точка $p$ принадлежит многообразию $\mathcal{G}$. В случае общего положения параметр $\mu $ имеет условный экстремум на кривой ${{\mathcal{L}}_{e}} = \mathcal{G} \cap \{ e = e(p)\} $ в точке $p$ тогда и только тогда, когда ${\text{Tr}}(p) = 2$.

Доказательство. Параметризуем кривую ${{\mathcal{L}}_{e}}$ величиной $\phi = \delta (0)$ в окрестности точки $p$. В пространстве симметрий $\Omega $ имеются две гиперповерхности: $\{ \delta (0) = \delta (2\pi )\} $ и $\{ \delta {\kern 1pt} '(0) = \delta {\kern 1pt} '(2\pi )\} $, которым принадлежат многообразие $\mathcal{G}$ и его сечение гиперплоскостью $\{ e = e(p)\} $.

Продифференцируем уравнения этих гиперповерхностей по параметру $\phi $ вдоль кривой ${{\mathcal{L}}_{e}}$. Получаем уравнения

откуда находим (опуская $(2\pi )$) Определитель матрицы монодромии ${{y}_{0}}(\nu )y_{1}^{'}(\nu ) - y_{0}^{'}(\nu ){{y}_{1}}(\nu )$ является $2\pi $-периодической функцией по формуле Лиувилля, а коэффициент при $\partial \mu {\text{/}}\partial \phi $ в (18) не равен нулю в случае общего положения. Q.E.D.

Теорема 3 останется справедливой, если параметры $e$ и $\mu $ поменять местами, а также если параметризовать кривую ${{\mathcal{L}}_{e}}$ величиной $\delta {\kern 1pt} '(0)$ вместо $\delta (0)$.

Теорема 3 описывает складки на многообразии $\mathcal{G}$, где ребро складки дается формулой ${\text{Tr}} = 2$.

В качестве приложения рассмотрим кривую $\gamma $ на фиг. 2 (или фиг. 5 в [9]), которая является проекцией одной из таких складок на плоскость $\{ e,\mu \} $. Одно из вырождений коразмерности 2, где коэффициент при величине $\partial e{\text{/}}\partial \phi $ в формуле (18) при замене $\mu \to e$ обращается в ноль – это экстремальное значение параметра $\mu $ на кривой $\gamma $ (точка ${{p}_{5}}$ на фиг. 2), так как система (17) ($\mu \to e$) в точке ${{p}_{5}}$ необходимо вырождена. Согласно формуле (18) ($\mu \to e$), точка ${{p}_{5}}$ удовлетворяет системе уравнений

Вычисления дают для точки ${{p}_{5}}$:

Это вырождение означает, что кривые ${{\mathcal{L}}_{\mu }} = \mathcal{G} \cap \{ \mu = const\} $ являются замкнутыми вблизи точки ${{p}_{5}}$, и эти кривые стягиваются к точке ${{p}_{5}}$ при $\mu \to \mu ({{p}_{5}})$, т.е. ${{p}_{5}}$ – это эллиптическая точка на многообразии $\mathcal{G}$.

Существует еще одна проекция складки на многообразии $\mathcal{G}$ на плоскость $\{ e,\mu \} $, где ребро складки дается формулой ${\text{Tr}} = 2$. Это кривая ${{\gamma }_{2}}$ на фиг. 2. Она была пропущена в работе [9], хотя вывод о ее существовании можно сделать на основании анализа рисунков, приведенных в [9]. Точка ${{p}_{6}}$ на кривой ${{\gamma }_{2}}$ полностью аналогична точке ${{p}_{5}}$ на кривой $\gamma $. Если многообразие $\mathcal{G}$ рассекать гиперплоскостями $\{ e = {\text{const}}\} $, то, согласно теореме 3, точка ${{p}_{6}}$ будет соответствовать вырождению коразмерности 2, где коэффициент при величине $\partial \mu {\text{/}}\partial \phi $ обращается в ноль, т.е. она находится из системы уравнений

Вычисления дают для точки ${{p}_{6}}$:

Аналогичные вырождения встречаются на семействах периодических решений ограниченной задачи трех тел и играют ключевую роль для объяснения структуры распределения астероидов (см. [10], [11]).

Как было отмечено, кривая $\gamma $ (а также ${{\gamma }_{2}}$) является проекцией двух симметричных друг другу складок на семействе $\mathcal{G}$. Одна из складок, условно говоря, расположена выше фиг. 2, а другая соответственно ниже. Тогда точка ${{p}_{3}}$ – это место встречи этих двух складок на семействе симметричных периодических решений $\mathcal{F}$, которое расположено в плоскости рисунка, т.е. точка ${{p}_{3}}$ – вершина симметричной сборки.

Данная ситуация аналогична сборке, найденной В.И. Арнольдом в задаче о течении Пуазейля (см. [12]).

Точка ${{p}_{3}}$ задается уравнением (см. [6])

Вычисления дают для точки ${{p}_{3}}$:

Заметим, что для вычисления точки ${{p}_{3}}$ (как и для других особенностей на фиг. 2) мы не пользуемся интерполяцией, а вычисляем особенность как решение некоторой невырожденной системы краевых задач, которая соответствует данному вырождению.

Наконец, точка ${{p}_{1}}$ – это место, где пересекаются три двумерных многообразия периодических решений, т.е. это вырождение коразмерности 2. На изучение этой точки были потрачены значительные усилия.

Сначала она была вычислена с помощью метода усреднения (см. [13]), а затем по сути тем же методом усреднения, но с некоторыми модификациями (см. [14, стр. 233]), которые впоследствии получили название “приведение к нормальной форме в окрестности семейства”.

Этот подход повышает коразмерность вырождения, поскольку в качестве малого параметра приходится использовать величину $\sqrt {\left| \mu \right|} $, и приводит к чрезвычайно громозким вычислениям.

Наш метод дает относительно простые и легко выводимые формулы (см. [7]).

Мы отсылаем читателя к работам [6], [7], где приводится детальный вывод формул для вырождений, представленных на фиг. 2.

4. ЗАКЛЮЧЕНИЕ

Применение методов компьютерной алгебры в прикладных задачах является не только очевидно полезным, но в ряде случаев является совершенно необходимим. Приведем простой, но довольно типичный пример.

Рассмотрим семейство алгебраических кривых

которое можно также интерпретировать как некоторую трехмерную поверхность (с довольно сложным рельефом). При фиксированном $z$ кривая ${{F}_{z}}(x,y)$ является линией уровня этой поверхности.

Спрашивается, какие особые точки могут иметь кривые ${{F}_{z}}(x,y)$, и где они расположены.

Численные эксперименты показывают, что при $z < 0$ кривые ${{F}_{z}}(x,y)$ замкнуты и гомеоморфны окружности. Однако при $z \geqslant 0$ возможны “бифуркации”, т.е. самопересечения кривой ${{F}_{z}}(x,y)$.

Ясно, что такие точки будут гиперболическими, т.е. при $z$, близких к точке бифуркации $z = {{z}_{*}},$ кривые ${{F}_{z}}(x,y)$ будут иметь локальные экстремумы как по $x$, так и по $y$.

Для эллиптической точки (экстремум на самой поверхности) ситуация идентична.

Таким образом, чтобы найти все критические точки, надо решить систему уравнений

Прямое численное решение систем уравнений, подобных (20), является делом довольно бесперспективным, так как неизвестно не только число решений, но и их примерное расположение (т.е. начальные приближения для итерационного метода).

Полиномиальные системы типа (20) решаются либо с помощью вычисления базиса Гребнера, либо с помощью вычисления результантов, что явно не является упражнением для ручного счета.

В данном случае система (20) сводится к решению одного полиномиального уравнения 9-й степени.

Задачи, весьма схожие с только что изложенной, возникают в самых различных прикладных задачах, от задач небесной механики (см. [10], [11]), до задач в теории устойчивости механизмов (см. [15]).

Вот только роль алгебраических кривых в этих задачах могут играть семейства решений, а особые точки кривых становятся вырождениями на семействах.

Изложенный в этой статье способ локализации особенностей на семействах периодических решений ОДУ является аналогом и обобщением данного примера.

Аналитическая зависимость решений ОДУ от начальных данных и параметров позволяет рассматривать семейства решений как некие аналитические “кривые” или поверхности со своими особенностями, которые требуется локализовать.

Структура этих особенностей может быть довольно сложной, как показывают примеры, данные в разд. 2, 3. Поэтому одним дифференцированием, т.е. матрицей монодромии, редко удается обойтись.

Обобщением матрицы монодромии являются уравнения в вариациях произвольного порядка по начальным данным и параметрам.

Таким образом, для каждой особой точки на семействе решений удается предъявить невырожденную систему краевых задач, решение которой соответствует особенности.

В заключение заметим, что уравнения в вариациях высокого порядка используются в задачах механики крайне редко, а смешанные вариации (т.е. по начальным данным и параметрам) вообще никогда не использовались, насколько нам известно.

Мы полагаем, причиной этому послужило традиционное определение вариаций как мультилинейных дифференциальных операторов в некотором (вообще говоря) бесконечномерном функциональном пространстве, что не способствует привлечению методов компьютерной алгебры.