Журнал вычислительной математики и математической физики, 2020, T. 60, № 1, стр. 39-56

1.1. Структура работы

В разд. 2 напоминается теория нормальной формы автономной функции Гамильтона ${{\gamma }_{0}}(\xi ,\eta )$, изложенная в [2, гл. 1].

В разд. 3 теория нормальной формы периодического возмущения ${{\gamma }_{1}}(\xi ,\eta ,\mu ,\psi )$, описанная в [2, гл. 2], доводится до приведенной нормальной формы ${{\tilde {h}}_{1}}({\mathbf{\tilde {u}}},\tilde {v},\mu )$, введенной в [1]. При этом локальным семействам периодических решений системы (1.2) соответствуют локальные семейства неподвижных точек системы (1.4).

В разд. 4 излагается алгоритм вычисления локальных семейств неподвижных точек системы (1.4), основанный на степенной геометрии [3].

Затем в разд. 5 рассматривается пример параметрического резонанса с $n = 2$, в котором описываются вычисления локальных семейств периодических решений исходной системы.

В разд. 6 обсуждаются те части этих вычислений, в которых может быть полезна компьютерная алгебра.

Отметим, что понятия “нормальная форма системы Гамильтона” и “нормальная форма функции Гамильтона” взаимозаменяемы: в нормальной форме системы функция Гамильтона имеет нормальную форму и наоборот.

3.1. Постановка упрощенной задачи

В окрестности стационарного решения

рассматривается система Гамильтона с $n$ степенями свободы где $\gamma $ – степенной ряд по $\xi ,\;\eta ,\;\mu $ с $2\pi $-периодическими по $\psi $ коэффициентами с $s$ малыми параметрами $\mu = ({{\mu }_{1}}, \ldots ,{{\mu }_{s}})$. В нашем случае линейная по $\xi ,\;\eta $ часть этой системы при $\mu = 0$ является постоянной. Согласно ограничению 1 ее матрица имеет только простые элементарные делители с собственными значениями ${{\lambda }_{1}}, \ldots ,{{\lambda }_{n}}, - {{\lambda }_{1}}, \ldots , - {{\lambda }_{n}}$. Положим $\lambda = ({{\lambda }_{1}}, \ldots ,{{\lambda }_{n}})$.

3.2. Линейная нормализация

Сделаем линейное каноническое преобразование $\xi ,\nu \to {\mathbf{x}},{\mathbf{y}}$, которое приводит линейную часть системы (3.2) при $\mu = 0$ к линейной нормальной форме с гамильтонианом

где $\left\langle { \cdot , \cdot } \right\rangle $ – скалярное произведение, ${\mathbf{z}} = ({\mathbf{x}},{\mathbf{y}})$ и $G$ – диагональная матрица $G = \{ \lambda , - \lambda \} $. При этом функция Гамильтона $\gamma (\xi ,\eta ,\mu ,\psi )$ принимает вид $g({\mathbf{x}},{\mathbf{y}},\mu ,\psi )$.

3.3. Нелинейная нормализация

Существует нелинейное каноническое периодическое преобразование

которое переводит функцию Гамильтона $g({\mathbf{x}},{\mathbf{y}},\mu ,\psi )$ в ряд Пуассона (нормальную форму) где  ${\mathbf{u}} = ({{u}_{1}}, \ldots ,{{u}_{n}})$, ${\mathbf{p}} = ({{p}_{1}}, \ldots ,{{p}_{n}})$, ${{{\mathbf{u}}}^{{\mathbf{p}}}} = u_{1}^{{{{p}_{1}}}} \cdots u_{n}^{{{{p}_{n}}}}$, ${\mathbf{p}},{\mathbf{q}} \in {{\mathbb{Z}}^{n}}$, ${\mathbf{r}} \in {{\mathbb{Z}}^{s}}$, $m \in \mathbb{Z}$, ${\mathbf{p}},{\mathbf{q}},{\mathbf{r}}\; \geqslant \;0$,  и  в разложении (3.4) имеются только резонансные члены с

3.4. Приведенная нормальная форма

Затем замена

приводит периодическую нормальную форму (3.4) к постоянной функции Гамильтона где При $\mu = 0$ в $\tilde {h}$ отсутствует квадратичная часть по ${\mathbf{\tilde {u}}},{\mathbf{\tilde {v}}}$.

3.5. Понижение числа степеней свободы

Пусть $k$ – число линейно независимых решений ${\mathbf{p}} \in {{\mathbb{Z}}^{n}}$ системы уравнений

Тогда существует каноническая замена координат в результате которой приведенная нормальная форма гамильтониана (3.5) сводится к гамильтониану с $k + 1$ степенью свободы и $n - k - 1 + s$ параметрами. Эта замена описана в [2, гл. 1].

3.6. Вещественный случай

Если исходная система Гамильтона (3.2) была вещественной, то в приведенной нормальной форме (3.5) коэффициенты ${{\tilde {h}}_{{{\mathbf{pqr}}m}}}$ связаны соотношениями вещественности и комплексные координаты ${\mathbf{\tilde {u}}},\;{\mathbf{\tilde {v}}}$ переводятся в вещественные координаты ${\mathbf{\tilde {U}}},\;{\mathbf{\tilde {V}}}$ стандартной линейной заменой

с постоянной блочной матрицей $Q$, которая описана в [2, гл. 1].

Малые параметры $\mu $ и линейные автоморфизмы системы (3.2) сохраняются при нормализующем преобразовании (3.3).

3.7. Периодические решения

Даже если нормализующее преобразование (3.3) расходится в окрестности решения (3.1), то оно сходится на локальных семействах периодических решений (проходящих через решение (3.1)), которым в системе с приведенной нормальной формой функции Гамильтона (3.5) соответствуют локальные семейства неподвижных точек.

Они являются решениями ${\mathbf{\tilde {u}}},\;{\mathbf{\tilde {v}}},\;\mu $ системы $2n$ уравнений

При $\mu = 0$ разложение гамильтониана $\widetilde h$ начинается с членов третьей степени по ${\mathbf{\tilde {u}}},\;{\mathbf{\tilde {v}}}$, но при $\mu \ne 0$ – с членов первой степени.

4.1. Общее описание метода

Для вычисления семейств решений системы (3.7), проходящих через точку

надо найти все первые приближения системы (3.7) в окрестности точки (4.1). Для этого можно воспользоваться степенной геометрией [3]. Она предписывает для каждого из уравнений системы (3.7) вычислить границу выпуклой оболочки целочисленных показателей ${\mathbf{p}},{\mathbf{q}},{\mathbf{r}}\; \geqslant \;0$, удовлетворяющих системе (3.6) и присутствующих в этом уравнении (многогранник Ньютона), и с их помощью находить “укороченные системы” системы (3.7). Решения укороченных систем дают первые приближения для решений полной системы (3.7).

Но часть этих решений можно находить проще. А именно, выделять укороченные гамильтонианы $\hat {h}({\mathbf{\tilde {u}}},{\mathbf{\tilde {v}}},\mu )$ с помощью многогранника Ньютона самого гамильтониана $\hat {h}({\mathbf{\tilde {u}}},{\mathbf{\tilde {v}}},\mu )$. Затем из них отбираются те, для которых система уравнений

является укороченной системой для системы (3.7).

Для этих укороченных гамильтонианов $\hat {h}$ решения системы (4.2) являются первыми приближениями для решений полной системы (3.7). Вычисление укороченных гамильтонианов $\hat {h}$ основано на следующей конструкции.

4.2. Многогранник и нормальные конусы

Пусть в ${{\mathbb{R}}^{m}}$ задано несколько точек $\{ {{Q}_{1}}, \ldots ,{{Q}_{k}}\} = {\mathbf{S}}$. Здесь $Q = ({{q}_{1}}, \ldots ,{{q}_{m}})$. Их выпуклая оболочка

является многогранником. Его граница $\partial \Gamma $ состоит из вершин $\Gamma _{j}^{{(0)}}$, ребер $\Gamma _{j}^{{(1)}}$ и граней $\Gamma _{j}^{{(d)}}$ разных размерностей $d:1 < d\;\leqslant \;m - 1$. Если задан вещественный $m$-вектор $P = ({{p}_{1}}, \ldots ,{{p}_{m}})$, то максимум и минимум скалярного произведения $\left\langle {P,Q} \right\rangle = {{p}_{1}}{{q}_{1}} + \ldots + {{p}_{m}}{{q}_{m}}$ на ${\mathbf{S}}$ достигаются на точках ${{Q}_{i}}$, лежащих на границе $\partial \Gamma $. Каждой грани $\Gamma _{j}^{{(d)}}$ соответствует граничное подмножество ${\mathbf{S}}_{j}^{{(d)}} = {\mathbf{S}} \cap \Gamma _{j}^{{(d)}}$. Выделим для каждой грани $\Gamma _{j}^{{(d)}}$ (включая вершины $\Gamma _{j}^{{(0)}}$ и ребра $\Gamma _{j}^{{(1)}}$) то множество векторов $P$, для которых максимум $\left\langle {P,Q} \right\rangle $ достигается на точках ${{Q}_{i}} \in \Gamma _{j}^{{(d)}}$. Это будет ее нормальный конусПри этом вектор $P$ лежит в пространстве $\mathbb{R}_{*}^{m}$, двойственном пространству ${{\mathbb{R}}^{m}}$. Вообще, здесь мы находимся в ситуации аффинной геометрии.

Пусть все грани размерности $d + 1$, содержащие грань $\Gamma _{j}^{{(d)}}$ размерности $d$, суть $\Gamma _{1}^{{(d + 1)}}, \ldots ,\Gamma _{k}^{{(d + 1)}}$. Тогда нормальный конус ${\mathbf{U}}_{j}^{{(d)}}$ является выпуклой конической оболочкой нормальных конусов ${\mathbf{U}}_{1}^{{(d + 1)}}, \ldots ,{\mathbf{U}}_{k}^{{(d + 1)}}$. Поэтому вычисление нормальных конусов удобнее начинать с граней максимальной размерности.

Все векторы нормального конуса ${\mathbf{U}}_{j}^{{(d)}}$ ортогональны грани $\Gamma _{j}^{{(d)}}$. В силу однородности нормальных конусов достаточно рассмотреть их пересечения с двумя гиперплоскостями (скажем, $\sum {{{p}_{j}}} = \pm 1$) и отмечать на них пересечения ${\mathbf{U}}_{{j \pm }}^{{(d)}}\;\mathop = \limits^{{\text{def}}} \;{\mathbf{U}}_{j}^{{(d)}} \cap \left\{ {\sum {{{p}_{j}}} = \pm 1} \right\}$, которые назовем приведенными нормальными конусами. Имеются стандартные программы как для вычисления выпуклых оболочек, так и для вычисления их граней и их нормальных конусов [5], [6]. В частности, они имеются в системе Maple.

Пусть множество ${\mathbf{S}}$ лежит в линейном подпространстве $\mathcal{L} \subset {{\mathbb{R}}^{m}}$, нормальном векторам ${{L}_{1}}, \ldots ,{{L}_{l}}:\mathcal{L} = \left\{ {Q:\left\langle {Q,{{L}_{i}}} \right\rangle = 0,i = 1, \ldots ,l} \right\}$. Тогда всякий нормальный конус ${\mathbf{U}}_{j}^{{(d)}}$ равен прямому произведению линейного подпространства $\mathcal{M} = \left\{ {P = \sum\nolimits_{i = 1}^l {{{\beta }_{i}}{{L}_{i}}} } \right\}$, нормального к $\mathcal{L}$, и некоторого конуса $\mathop U\limits^* {\kern 1pt} _{j}^{{(d)}}$, лежащего в $\mathcal{L}$. Поэтому в этом случае удобно рассматривать концентрированные нормальные конусы

где ${{\mathcal{K}}_{ \pm }} = \{ P:\left\langle {P,E} \right\rangle = \pm 1\} ,\quad E = (1,1, \ldots ,1)$. Они определяются формулами (4.4) и

4.3. Укороченные многочлены и степенные ряды

Пусть задан многочлен (или степенной ряд)

где ${\mathbf{w}} = ({{w}_{1}}, \ldots ,{{w}_{m}})$, $Q = ({{q}_{1}}, \ldots ,{{q}_{m}}) \in {{\mathbb{Z}}^{m}}$, $Q\; \geqslant \;0$, ${{f}_{Q}}$ – постоянные коэффициенты. Ему соответствует носитель По множеству ${\mathbf{S}} = {\mathbf{S}}(f)$ строится его выпуклая оболочка $\Gamma (f) = \Gamma ({\mathbf{S}})$, которая называется многогранником Ньютона суммы (4.6). Каждой его грани $\Gamma _{j}^{{(d)}}$ соответствуют: укороченный многочлени нормальный конус ${\mathbf{U}}_{j}^{{(d)}}$ по (4.4).

4.4. Укороченные системы

Рассмотрим систему $2n$ “алгебраических” уравнений

от $m$ неизвестных ${\mathbf{w}} = ({{w}_{1}}, \ldots ,{{w}_{m}})$ с $m > 2n$, где ${{f}_{{iQ}}}$ – постоянные коэффициенты, $Q \in {{\mathbb{Z}}^{m}}$, $Q = ({{q}_{1}}, \ldots ,{{q}_{m}})\; \geqslant \;0$. Пусть точка ${\mathbf{w}} = 0$ является решением системы (4.8). Надо найти семейства решений системы (4.8), проходящие через эту точку. Если в точке ${{{\mathbf{w}}}^{0}}$ ранг матрицы то по теореме о неявной функции $2n$ координат ${{w}_{j}}$ можно разложить в степенные ряды по оставшимся координатам ${{w}_{j}}$. Если условие (4.9) не выполнено, то можно искать степенные разложения решений системы (4.8) по параметрам ${{\tau }_{1}}, \ldots ,{{\tau }_{l}} \to \infty $. Для вычисления первых членов этих разложений надо для каждого ${{f}_{i}}({\mathbf{w}})$ вычислить его носитель ${{{\mathbf{S}}}_{i}} = {\mathbf{S}}({{f}_{i}})$, его многогранник Ньютона ${{\Gamma }_{i}} = \Gamma ({{S}_{i}})$ по (4.3), все его грани $\Gamma _{{ik}}^{{(d)}}$ и их нормальные конусы ${\mathbf{U}}_{{ik}}^{{(d)}}$ по (4.4). Набор граней называется согласованным, если не пусто пересечение их нормальных конусов Тогда система укороченных уравнений является укороченной системой для системы (4.8). Решения этой системы являются первыми приближениями решений (4.10) полной системы (4.8), содержащими кривые вида где $m$-вектор $P = ({{p}_{1}}, \ldots ,{{p}_{m}})$ лежит в пересечении (4.11). Здесь параметр $\tau \to \infty $.

Отметим следующие свойства укороченных систем (4.12).

1. Каждая сумма $\hat {f}_{{i,{{k}_{i}}}}^{{({{d}_{i}})}}({\mathbf{w}})$ содержит хотя бы одно слагаемое ${{f}_{{iQ}}}{{{\mathbf{w}}}^{Q}}$.

2. Укороченные системы, у которых одна из сумм $\hat {f}_{{i{{k}_{i}}}}^{{({{d}_{i}})}}({\mathbf{w}})$ состоит только из одного слагаемого ${{f}_{{iQ}}}{{{\mathbf{w}}}^{Q}}$, не дают первых приближений решений.

3. Этот подход дает только решения, у которых все координаты ${{w}_{i}}$ отличны от тождественного нуля. Для отыскания решений с тождественно нулевыми координатами надо их занулить в исходной системе и в полученной системе строить многогранник Ньютона и т.д.

4. Нас интересуют только те укороченные системы (4.12), у которых нормальный конус (4.11) пересекается с конусом задачи $K = \{ P:P < 0\} $.

4.5. Укороченные системы, полученные из укороченной функции Гамильтона

Пусть $\tilde {h}({\mathbf{\tilde {u}}},{\mathbf{\tilde {v}}},\mu )$ – функция Гамильтона и $\hat {h}_{j}^{{(d)}}({\mathbf{\tilde {u}}},{\mathbf{\tilde {v}}},\mu )$ – ее укороченный многочлен (4.7).

Теорема 2. Система (4.2) с $\hat {h} = \hat {h}_{j}^{{(d)}}$ является укороченной системой системы (3.7), если каждая из частных производных в (4.2) содержит хотя бы одно слагаемое. При этом пересечение (4.11) совпадает с нормальным конусом ${\mathbf{U}}_{j}^{{(d)}}$ грани $\Gamma _{j}^{{(d)}}$ для $\Gamma = \Gamma (\tilde {h})$.

Согласно свойству 2 укороченные системы (4.2), где хотя бы одна из частных производных состоит из одного монома, не годятся. Согласно свойству 3 для тех решений укороченной системы (4.2), у которых хотя бы одна координата тождественно равна нулю, надо проверить их существование в системе с обнуленными соответствующими координатами.

4.6. Дальнейшие члены разложений

Для вычисления дальнейших членов разложений семейств неподвижных решений надо выделить особые точки на вычисленных семействах, т.е. те точки $\left( {{\mathbf{\tilde {u}}},{\mathbf{\tilde {v}}},\mu } \right)$, в которых ранг матрицы

Тогда в неособых точках, где этот ${\text{Rank}} = 2n$, можно применить соответствующее степенное преобразование [3] и теорему о неявной функции. Для анализа решений вблизи особой точки вычисленного семейства надо эту точку сдвинуть в начало координат и снова выделять укороченные системы, находить их решения и т.д.

Замечание 1. Вся изложенная выше теория справедлива и без ограничения 1. Но при нем вычисления упрощаются.

5.1. Постановка задачи

Пусть число степеней свободы $n = 2$, система (3.2) аналитически зависит от $s$ малых параметров $\mu = ({{\mu }_{1}}, \ldots ,{{\mu }_{s}})$, имеет линейный автоморфизм $\xi ,\eta \to - \xi , - \eta $, при $\mu = 0$ гамильтониан $\gamma $ не зависит от $\psi $ и собственные значения ${{\lambda }_{1}},\;{{\lambda }_{2}}$ линейной части системы суть $ \pm i,\; \pm \tfrac{i}{2}$.

Введем обозначения

Тогда в приведенной нормальной форме (3.5), опуская тильды, получаем

где ибо $\operatorname{Im} \lambda = \left( {1,\tfrac{\sigma }{2}} \right)$, $\operatorname{Re} \lambda = 0$. При $\mu = 0$ квадратичная часть ряда $h$ по ${{w}_{1}},\;{{w}_{2}},\;{{w}_{3}},\;{{w}_{4}}$ отсутствует. При этом в разложении (5.1) имеются только члены с четными степенями ${{q}_{1}} + {{q}_{2}} + {{q}_{3}} + {{q}_{4}}$, ибо нормальная форма сохраняет линейный автоморфизм ${{w}_{1}},\;{{w}_{2}},\;{{w}_{3}},\;{{w}_{4}} \to - {{w}_{1}},\; - {{w}_{2}},\; - {{w}_{3}},\; - {{w}_{4}}$.

5.2. Укорочения невозмущенного гамильтониана

Поскольку при $\mu = 0$ гамильтониан $\gamma $ не зависит от угловой переменной $\psi $, т.е. является гамильтонианом автономной системы вблизи неподвижной точки $\xi = \eta = 0$, то при $\mu = 0$ приведенная нормальная форма (5.1) содержит только члены, у которых

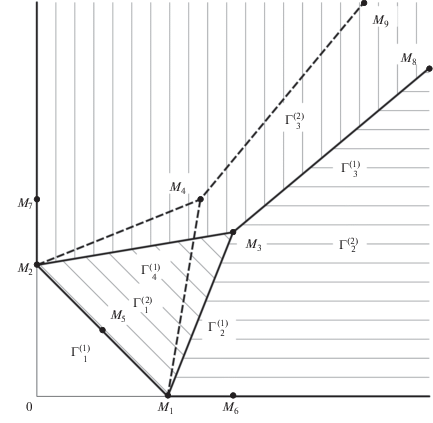
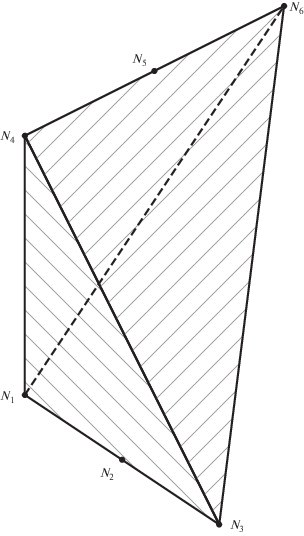
Ниже рассмотрим случай Это же верно и для приведенной нормальной формы (5.1). Ее часть содержит только члены, для которых выполнено (5.3); сумма ${{q}_{1}} + {{q}_{2}} + {{q}_{3}} + {{q}_{4}}\;\mathop = \limits^{{\text{def}}} \;r$ четна и $r\; \geqslant \;4$.

Предположим, что все члены в (5.5) с этими свойствами обладают ненулевыми коэффициентами ${{h}_{{{{q}_{1}}{{q}_{2}}{{q}_{3}}{{q}_{4}}}}}$. Тогда многогранник Ньютона ${\mathbf{N}} = \Gamma ({{h}_{0}})$ разложения (5.5) является трехмерным, имеет четыре вершины в точках $M = ({{q}_{1}},{{q}_{2}},{{q}_{3}},{{q}_{4}}):$ ${{M}_{1}} = (2,2,0,0)$, ${{M}_{2}} = (0,0,2,2)$, ${{M}_{3}} = (0,2,4,0)$, ${{M}_{4}} = (2,0,0,4)$;

9 ребер:

и 6 граней: Здесь квадратные скобки обозначают выпуклую оболочку, а фигурные – часть линейного многообразия, натянутого на указанные точки. Все остальные показатели $Q = ({{q}_{1}},{{q}_{2}},{{q}_{3}},{{q}_{4}})$ в разложении (5.5) являются положительными линейными комбинациями точек ${{M}_{1}}, \ldots ,{{M}_{4}}$. Многогранник Ньютона ${\mathbf{N}}$ показан на фиг. 1. Этот результат получен как выпуклая оболочка точек $M$, удовлетворяющих уравнению (5.3) с целыми ${{q}_{i}}\; \geqslant \;0$ и с суммой $r\;\leqslant \;12$ согласно п. 4.2.

Согласно п. 4.2 вычислим концентрированные нормальные конусы граней и ребер многогранника Ньютона ${\mathbf{N}}$. Здесь $l = 1$ и ${{L}_{1}} = (2, - 2,1, - 1)$ согласно (5.3) и (5.4). По формулам (4.4) и (4.5)

т.е. Аналогично находим

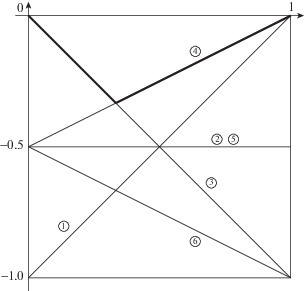
Расположение всех концентрированных нормальных конусов в координатах ${{p}_{1}},{{p}_{2}}$ показано на фиг. 2.

При этом

Наконец, если вершины ${{M}_{i}}$ обозначить через то получим

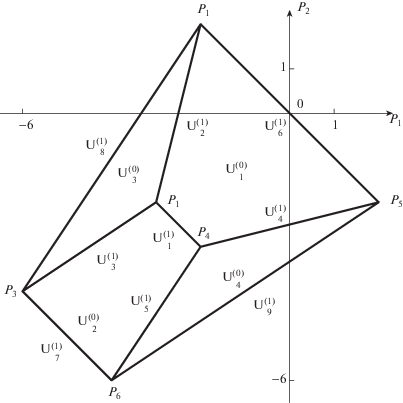
Теперь заметим, что у всех $Q = ({{q}_{1}},{{q}_{2}},{{q}_{3}},{{q}_{4}})$, лежащих на грани $\Gamma _{2}^{{(2)}}$, координата ${{q}_{4}} \equiv 0$, на грани $\Gamma _{3}^{{(2)}}$ координата ${{q}_{1}} \equiv 0$, на грани $\Gamma _{5}^{{(2)}}$ координата ${{q}_{3}} \equiv 0$, на грани $\Gamma _{6}^{{(2)}}$ координата ${{q}_{2}} \equiv 0$. Это означает, что укорочения ${{\hat {h}}_{0}}$ гамильтониана ${{h}_{0}}$ не содержат одну из координат. Следовательно, частная производная укороченного гамильтониана по этой координате тождественно равна нулю. По теореме 2 такой укороченный гамильтониан не дает укороченную систему. Кроме того, ${\mathbf{U}}_{2}^{{(2)}},\;{\mathbf{U}}_{3}^{{(2)}},\;{\mathbf{U}}_{5}^{{(2)}},\;{\mathbf{U}}_{6}^{{(2)}}$ не пересекаются с конусом задачи $K = \{ P < 0\} $. Остаются только грани $\Gamma _{1}^{{(2)}},\;\Gamma _{4}^{{(2)}}$ и ребро $\Gamma _{1}^{{(1)}}$. Все остальные ребра $\Gamma _{2}^{{(1)}}, \ldots ,\Gamma _{9}^{{(1)}}$ и все вершины $\Gamma _{1}^{{(0)}}, \ldots ,\Gamma _{4}^{{(0)}}$ лежат на гранях $\Gamma _{2}^{{(2)}},\;\Gamma _{3}^{{(2)}},\;\Gamma _{5}^{{(2)}},\;\Gamma _{6}^{{(2)}}$. Поэтому соответствующие им укороченные функции Гамильтона не дают укороченных систем.

Найдем пересечения нормальных конусов ${\mathbf{U}}_{1}^{{(2)}}$ и ${\mathbf{U}}_{4}^{{(2)}}$ с замыканием конуса задачи $\bar {K} = \{ P\;\leqslant \;0\} $. Нормальный конус ${\mathbf{U}}_{1}^{{(2)}}$ состоит из векторов $P = {{\alpha }_{1}}{{P}_{1}} + \omega {{L}_{1}}$, где ${{\alpha }_{1}} > 0$ и $\omega \in \mathbb{R}$. Поскольку ${{P}_{1}} = \left( { - \tfrac{3}{{10}}, - \tfrac{1}{5}, - \tfrac{3}{{20}}, - \tfrac{7}{{20}},} \right)$ и ${{L}_{1}} = (2, - 2,1, - 1)$, то условие $P\;\leqslant \;0$ означает выполнение 4-х неравенств:

Они эквивалентны неравенствам Поскольку ${{\alpha }_{1}}\; \geqslant \;0$, то $ - \tfrac{1}{{10}}{{\alpha }_{1}}\; \geqslant \; - \tfrac{7}{{20}}{{\alpha }_{1}}$, и неравенства (5.6) сводятся к Здесь 2 крайних положения:

$\omega = \tfrac{3}{{20}}{{\alpha }_{1}}$, ему соответствует ${{R}_{1}} = \left( {0, - \tfrac{1}{2},0, - \tfrac{1}{2}} \right)$, и

$ - \tfrac{1}{{10}}{{\alpha }_{1}} = \omega $, ему соответствует ${{R}_{2}} = \left( { - \tfrac{1}{2},0, - \tfrac{1}{4}, - \tfrac{1}{4}} \right)$.

Итак,

Аналогично вычисляем где ${{R}_{3}} = \left( { - \tfrac{1}{2},0, - \tfrac{1}{2},0} \right)$.

Поэтому здесь имеем три укороченных гамильтониана, дающих укороченные системы,

где $\alpha ,\;\beta ,\;\gamma ,\;\delta ,\;\varepsilon $ – постоянные, отличные от нуля.

5.3. Укорочения возмущенного гамильтониана

При ${{q}_{1}} + {{q}_{2}} + {{q}_{3}} + {{q}_{4}} = r = 2$ уравнение (5.2) имеет 6 решений $({{q}_{1}},{{q}_{2}},{{q}_{3}},{{q}_{4}})$:

Выпуклая оболочка этих шести точек является трехмерным тетраэдром, показанным на фиг. 3. Им соответствуют мономы

Все остальные допустимые решения уравнения (5.2) являются положительными линейными комбинациями указанных 6 решений (5.9). Более того, выпуклая оболочка решений уравнения (5.2) с $r = 2k$ является также трехмерным тетраэдром, подобным тетраэдру фиг. 3.

Точкам (5.9) в возмущении гамильтониана (5.1) соответствуют слагаемые

Предположим, что в приведенной нормальной форме (5.1) коэффициенты указанных 6 мономов (5.10) отличны от нуля. Вектор $ - E = - (1,1,1,1) \in {{\mathbb{Z}}^{4}}$ нормален ребру $\Gamma _{1}^{{(1)}}$ и набору точек (5.9), т.е.

Поэтому согласно разд. 4 сумма является укороченным гамильтонианом для (5.1).

Внешние нормали $R$ к грани $\Gamma _{1}^{{(2)}}$, лежащие в конусе задачи $R\;\leqslant \;0$, образуют сектор, натянутый на векторы ${{R}_{1}} = \left( {0, - \tfrac{1}{2},0, - \tfrac{1}{2}} \right)$ и ${{R}_{2}} = \left( { - \tfrac{1}{2},0, - \tfrac{1}{4}, - \tfrac{1}{4}} \right)$, т.е. $R = a{{R}_{1}} + b{{R}_{2}}$, где $a,b \in \mathbb{R}$ и $a,b\; \geqslant \;0$. Если ограничиться только такими векторами $R$, у которых $\left\langle {R,E} \right\rangle = - 1$, то $a + b = 1$. Следовательно,

и $a \in [0,1]$.

Вычислим скалярные произведения $\left\langle {R,{{N}_{i}}} \right\rangle $, где $R$ из (5.12) и ${{N}_{i}}$ из (5.8). Получим

Графики этих функций ${{f}_{i}}(a)$ на интервале $a \in [0,1]$ показаны на фиг. 4. При этом номера $i$ этих функций соответствуют ${{N}_{i}}$ в (5.13).

Из фиг. 4 видно, что наибольшие значения принимают ${{f}_{3}}(a)$ и ${{f}_{4}}(a)$. Следовательно, согласно разд. 4, грани $\Gamma _{1}^{{(2)}}$ соответствует укороченный гамильтониан

Аналогично находим, что грани $\Gamma _{4}^{{(2)}}$ соответствует укороченный гамильтониан Положим Теперь укороченные гамильтонианы (5.11), (5.14), (5.15) суть

5.4. Неподвижные точки, соответствующие первому укорочению ${{\hat {h}}_{1}}$

Для него система уравнений (4.2) при $\widehat h = {{\hat {h}}_{1}}$ есть

Умножая эти уравнения на ${{u}_{1}}$ (первое), ${{v}_{1}}$ (второе), ${{u}_{2}}$ (третье), ${{v}_{2}}$ (четвертое) и сравнивая полученные уравнения: первое со вторым и третье с четвертым, получаем равенства Из них следует, что Теперь система (5.18) сводится к двум уравнениям: Решения системы (5.18) описываются следующими уравнениями:

1) ${{u}_{1}}{{v}_{1}} = {{u}_{2}}{{v}_{2}} = 0$,

2) ${{u}_{1}}{{v}_{1}} = 0$, ${{u}_{2}}{{v}_{2}} = - \tfrac{1}{{2\gamma }}\left( {b{\kern 1pt} {\text{*}} + 2\omega \sqrt {a{\kern 1pt} {\text{*}}c{\kern 1pt} {\text{*}}} } \right)$, $\omega = \pm 1$,

3) ${{u}_{1}}{{v}_{1}} = - \tfrac{1}{{2\alpha }}\left( {B{\kern 1pt} {\text{*}} + 2\varkappa \sqrt {A{\kern 1pt} {\text{*}}C{\kern 1pt} {\text{*}}} } \right)$, ${{u}_{2}}{{v}_{2}} = 0$, $\varkappa = \pm 1$,

4) ${{u}_{1}}{{v}_{1}}\, = \,\left[ {\beta {\kern 1pt} \left( {b{\kern 1pt} {\text{*}}\, + \,2\omega \sqrt {a{\kern 1pt} {\text{*}}c{\kern 1pt} {\text{*}}} } \right)\, - \,2\gamma {\kern 1pt} \left( {B{\kern 1pt} {\text{*}}\, + \,2\varkappa \sqrt {A{\kern 1pt} {\text{*}}C{\kern 1pt} {\text{*}}} } \right)} \right]{\text{/}}\Delta $, ${{u}_{2}}{{v}_{2}}\, = \,\left[ {\beta {\kern 1pt} \left( {B{\kern 1pt} {\text{*}}\, + \,2\varkappa \sqrt {A{\kern 1pt} {\text{*}}C{\kern 1pt} {\text{*}}} } \right)\, - \,2\alpha {\kern 1pt} \left( {b{\kern 1pt} {\text{*}}\, + \,2\omega \sqrt {a{\kern 1pt} {\text{*}}c{\kern 1pt} {\text{*}}} } \right)} \right]{\text{/}}\Delta $,

где $\Delta = 4\alpha \gamma - {{\beta }^{2}}$, $\varkappa = \pm 1$, $\omega = \pm 1$. Всего 9 семейств решений.

По нашему предположению $\alpha ,\gamma \ne 0$, поэтому решения 2) и 3) существуют. При $\Delta = 0$ решений 4) нет, и только при дополнительном условии

имеются два семейства решений:

5) $2\alpha {{u}_{1}}{{v}_{1}} + \beta {{u}_{2}}{{v}_{2}} + B{\kern 1pt} {\text{*}} + 2\varkappa \sqrt {A{\kern 1pt} {\text{*}}C{\kern 1pt} {\text{*}}} = 0$, $\varkappa = \pm 1$ .

Решения 2) сохраняются в укороченной системе (5.18), если в ней положить ${{u}_{1}} = {{v}_{1}} = 0$. Поэтому согласно свойству 3 п. 4.4 они являются первыми приближениями семейств решений полной системы (3.7). Аналогично для решений 3).

Найдем особые точки на семействах решений 2). Согласно (4.12) для особых точек решения 2) выполнено либо уравнение на $\mu $:

либо уравнение на $u_{2}^{2},\;v_{2}^{2},\;\mu $: либо оба эти уравнения одновременно.

Переход от комплексных координат ${\mathbf{u}},\;{\mathbf{v}}$ к вещественным ${\mathbf{U}},\;{\mathbf{V}}$ дается преобразованием

Для исходного вещественного гамильтониана константы таковы: где черта сверху означает комплексное сопряжение. При этом и решения уравнений 1)–5) вещественны и имеют вид

5.5. Второе укорочение ${{\hat {h}}_{2}}$

Согласно (5.8), (5.14), (5.16), (5.17) имеем

Поэтому система (4.2) для $\widehat h = {{\hat {h}}_{2}}$ имеет вид Если ${{v}_{1}}$ и ${{u}_{2}} \ne 0$, то подсистема из первого и четвертого уравнений (5.21) имеет решение только при $\Delta = 4\alpha \gamma - {{\beta }^{2}} = 0$, и это решение есть В этом случае система (5.21) сводится к системе Решения последних трех уравнений суть при $C{\kern 1pt} {\text{*}} \ne 0$ и $a{\kern 1pt} {\text{*}} \ne 0$. Они образуют 8 семейств. При $s = 1$, $\tau = {{\mu }^{{ - 1}}}$ и $\tau \to \infty $ имеем на этом решении т.е. векторный порядок $P = \left( {{{p}_{1}}, - \tfrac{1}{4}, - \tfrac{1}{4},{{p}_{1}}} \right)$. Он должен лежать в конусе укорочения ${\mathbf{U}}_{1}^{{(2)}} \cap \bar {K}$, описанном в (5.7), т.е. Это возможно только при $a = \tfrac{1}{2}$, $b = 1$. Тогда ${{p}_{1}} = - \tfrac{1}{2}$. Следовательно, произвольное ${{v}_{2}}$ должно иметь порядок $\sqrt \mu $.

При этом согласно (5.19) вещественные части решения (5.23) выделяются условиями

5.6. Третье укорочение $\mathop {\hat {h}}\nolimits_3 $

Согласно (5.8), (5.15), (5.16), (5.17) имеем

Аналогично п. 5.5 получаем решение системы (4.2) при ${{u}_{1}}$ и ${{v}_{2}} \ne 0$ и $\Delta = 0$: Они образуют 8 семейств.

5.7. Общая ситуация

Итак, получены следующие 26 семейств неподвижных точек:

• семейства 2 и 3 из (5.20) при любых параметрах;

• семейства 4 из (5.20) при $\Delta \ne 0$;

• семейства 5 из (5.20), семейства (5.23) и (5.22) при $\Delta = 0$.

Но нет уверенности, что здесь найдены первые приближения всех локальных семейств неподвижных точек приведенной нормальной формы системы Гамильтона. Это требует еще поиска укороченных систем, которые не являются гамильтоновыми, в конусах ${\mathbf{U}}_{2}^{{(1)}}, \ldots ,{\mathbf{U}}_{9}^{{(1)}}$, ${\mathbf{U}}_{1}^{{(0)}}, \ldots ,{\mathbf{U}}_{4}^{{(0)}}$, и их дальнейшего анализа.

Рассмотренная здесь задача возникает при изучении движений спутника на слабо эллиптической орбите вблизи параметрического резонанса [7], там число $s$ малых параметров равно 3.