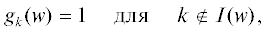Журнал вычислительной математики и математической физики, 2020, T. 60, № 2, стр. 338-348

1. ВВЕДЕНИЕ

Широкому классу сложных систем присуща сетевая структура связей, прежде всего, речь идет о многопользовательских распределенных системах. Математически разделяют одно- и многопродуктовые (МП-) сети. В первом случае потоки для различных пользователей системы смешиваются в сети. Во втором – они подчиняются совместным ограничениям, но не являются взаимозаменяемыми, т.е. для пользователя в стоковой вершине важен источник доставляемого к нему потока и наоборот. В предлагаемой статье рассмотрен в некотором смысле промежуточный случай – без указанного “наоборот”. Вводится понятие кластерной структуры связей, когда все потоки из одного источника неразличимы на ребрах графа сети (относятся к одному виду продукта). Математически это соответствует МП-сетям (поскольку разные источники порождают разные виды продукта), но позволяет несколько упростить анализ уязвимости системы. Содержательно подобные модели возникают в управляющих сетях [1], в том числе при управлении связью в условиях больших разрушений инфраструктурных систем [2]. Социальные сети несомненно имеют признаки МП-сетей, хотя при анализе их уязвимости это, как правило, не учитывают (см., например, работы [3]–[7]). То же можно сказать и об исследованиях робастности авиатранспортных сетей [8].

Построенная модель (сужающая круг рассматриваемых МП-сетей) приводит к новому классу повреждений, которые будут учитываться при анализе уязвимости сетевой системы. Идея использования минимального разреза в качестве показателя для оценки уязвимости сети (однопродуктовой) восходит к классической работе Фрэнка и Фриша [9]. В настоящей статье эта идея обобщается на кластерные разрезы, т.е. не просто разделяющие источник и сток, а отделяющие источник от всех его стоков. При этом уязвимость сети с нашей точки зрения характеризует не сама величина разреза, которая показывает лишь уязвимость данного кластера, а число кластеров, затрагиваемых изучаемым разрезом. Косвенно такой подход близок к идее, лежащей в основе показателя, задаваемого средним коэффициентом кластеринга [3], [7]. Однако, в отличие от имеющихся постановок с оценками снижения коэффициента кластеринга, которые приводят к NP-трудным задачам, решаемым приближенно и/или эвристическими методами, постановки, предлагаемые в данной работе, ориентированы на эффективные потоковые алгоритмы. Кроме того, если взять коэффициент кластеринга для конкретной вершины, то он отражает свойства ее собственного кластера, а учет влияния на другие вершины появляется лишь в результате осреднения. Тем самым не дается способа ранжирования вершин сети по отношению к определенному множеству повреждений, что составляет основную цель проводимого ниже исследования.

Работа состоит из трех частей. В первой вводятся основные понятия: в разд. 2 формально описан рассматриваемый новый класс сетевых систем – с кластерной структурой связей (К-сети), в разд. 3 задается представительный набор учитываемых повреждений сети, обобщающий на К-сети понятие минимального разреза [10] (но не сводящийся к минимальным вершинным разрезам). Во второй части (разд. 4) поставлена оригинальная задача ранжирования повреждений из заданного набора по трем критериям: прямого влияния на информационные кластеры, косвенного влияния и мощности разреза. Соответствующие характеристики эффективно вычисляются алгоритмами потокового программирования [11]. Для поиска недоминируемых [12] по этим критериям повреждений указан графический метод. В третьей части (разд. 5) для К-сетей развит подход, предложенный нами в [13] для анализа уязвимости МП-сетей. Проводится оценка подверженности кластеров повреждениям по двум показателям: прямого и косвенного ущерба. Прямой ущерб определяется долей тех повреждений (в данном наборе), при которых поток в кластере передать вообще невозможно. Косвенный ущерб характеризует долю разрушенных связей в кластере при повреждениях, затрагивающих его лишь частично. Подобный показатель ранее другими авторами не изучался, несмотря на его содержательную ценность. На качественном уровне (для модельного примера) последний показатель сравнивается со стандартно используемым коэффициентом кластеринга для графа сети.

2. СЕТЕВАЯ ПОТОКОВАЯ МОДЕЛЬ

Рассмотрим математическую запись модели передачи многопродуктового (МП-) потока в сети с многими источниками и стоками [14]. МП-сеть $\left\langle {V,R,P} \right\rangle $ задается множествами:

$V = \{ {{v}_{1}},...,{{v}_{n}}\} $ – вершин (узлов) сети;

$R = \{ {{r}_{1}},...,{{r}_{e}}\} \subset V \times V$ – ребер физического графа $G(d) = \left\langle {V,R} \right\rangle $ сети, с пропускной способностью, равной вектору $d$, компоненты которого ${{d}_{k}}$ ограничивают суммарные потоки по ребру ${{r}_{k}}$, $k = 1,2, \ldots ,e$; считается, что граф $G(d)$ без петель и сдвоенных ребер;

а также $P = \{ {{p}_{1}},...,{{p}_{m}}\} \subset V \times V$ – дуг графа тяготений, или логического графа сети, соответствующих тем парам несовпадающих вершин сети (далее – тяготеющим парам), между которыми передается поток определенного вида (продукта) с учетом направления передачи. В исследуемой далее модели (в отличие от общих МП-постановок [14]) будем полагать, что каждой вершине сопоставлен один и тот же вид продукта для всех выходящих из нее потоков, и называть этот набор логических дуг кластером данного вида продукта.

Для упрощения обозначений предположим, что все физические ребра неориентированные. При этом для определения потоков по ребрам графа $G(d)$ назовем прямым направление от вершины с меньшим номером к вершине с большим и каждое ребро ${{r}_{k}}$ физического графа сети будем представлять двумя ориентированными дугами с номерами $k$ и $k + e$ для прямого и обратного направлений соответственно. Для любой вершины ${{v}_{j}} \in V$ обозначим через $S({{v}_{j}})$ множество индексов выходящих из нее дуг:

а через $T({{v}_{j}})$ множество индексов входящих дуг: (В случае ориентированного ребра физического графа можно формально добавить в модель ограничение, зануляющее поток по дуге, направленной противоположно ориентации данного ребра.)

Для каждой $i$-й тяготеющей пары введем обозначение ${{p}_{i}} = ({{v}_{{{{s}_{i}}}}},{{v}_{{{{t}_{i}}}}})$, где вершина ${{v}_{{{{s}_{i}}}}}$ называется источником, а ${{v}_{{{{t}_{i}}}}}$ – стоком ${{s}_{i}}$-го вида продукта (в частности, информационного потока). Вершины источник и сток определяются согласно ориентации дуги логического графа сети. Обозначим через ${{P}_{j}} = \{ {{p}_{i}} \in P\,{\text{|}}\,{{v}_{{{{s}_{i}}}}} = {{v}_{j}}\} $ кластер тяготеющих пар с источником в вершине ${{v}_{j}}$ – $j$-го вида продукта (информационного потока), далее также называемый $j$-й кластер, $j = 1,2, \ldots ,n$.

Введем матричную переменную $x = \{ {{x}_{{jk}}}\} $ размерности $n \times 2e$. Элемент ${{x}_{{jk}}}$ обозначает количество продукта $j$-го вида ($j$-го информационного потока), проходящее за единицу времени по ребру ${{r}_{k}} \in R$ в прямом направлении для $k \leqslant e$ или по ребру ${{r}_{{k - e}}} \in R$ в обратном направлении, если $k > e$. Все ${{x}_{{jk}}} \geqslant 0$. Кроме неотрицательности, для возможных значений переменной $x$ должны выполняться условия сохранения потока каждого вида:

Значение $z_{j}^{i} \geqslant 0$ равно величине входного потока, который пропускается (за единицу времени) по сети от источника ${{v}_{j}}$ к стоку i-й тяготеющей пары при распределении потоков x_jk по физическим ребрам сети. Значение z_j равно полной величине j-го вида потока (в кластере P_j) и определяется как сумма значений $z_{j}^{i}$ по всем тяготеющим парам p_i, входящим в кластер P_j, Таким образом, зависимость МП-потока $z = ({{z}_{1}},...,{{z}_{n}})$ от x линейна.

Ограничения (2.1), (2.2) формально показывают отличие рассматриваемых сетей от стандартных МП-сетей и однопродуктовых сетей с многими источниками и стоками (многополюсных) [11]. (Во втором случае индексы $i$ и $j$ не используются, а $z$ является числом.) По содержанию понятия кластерных сетей предложим следующее пояснение.

На ребрах графа $G(d)$ МП-сети потоки разных кластеров не смешиваются, но подчиняются единым ограничениям. Каждому ребру ${{r}_{k}} \in R$ физического графа $G(d)$ МП-сети приписано число ${{d}_{k}}$, названное пропускной способностью ребра ${{r}_{k}}$ и измеряемое в условных единицах потоков, для передачи которых предназначена данная сеть. Тем самым, различные виды потоков должны измеряться в сопоставимых единицах. Как правило, речь идет об однотипных потоках, различающихся порождающими их вершинами и не являющихся взаимозаменяемыми (например, потоки рекламной продукции или энергоресурсов). В вершине-источнике может находиться определенный контент (или добываться ресурс), который считывают (получают, покупают) его потребители, находящиеся в вершинах-стоках данного вида продукта. Поток из одной вершины не подменяется для потребителя теми, которые приходят из других источников. Но потоки от одного источника к разным потребителям могут перемешиваться на ребрах физического графа сети (как вода в водопроводе) и идти различными путями в разные (во все) стоки для этого вида продукта. Каждый источник (точнее, стоящий за ним пользователь сети) стремится к передаче суммарного потока, сгенерированного или хранящегося в нем, в максимальном объеме. Подобные МП-сети, ограничения на потоки в которых подчиняются условиям (2.1), (2.2), будем называть кластерными и использовать для них термин К-сети.

Компоненты вектора $d = ({{d}_{1}},...,{{d}_{e}})$ известны, фиксированы и неотрицательны. В начальный момент они предполагаются строго положительными, но далее с помощью придания им нулевых значений удобно моделировать разрушение, т.е. исключение из графа сети, соответствующих ребер. Формально вектор $d$ задает следующие ограничения-неравенства на распределение потоков в сети:

Ограничения (2.3) линейны и совместно с ограничениями (2.1), (2.2) формируют многогранник возможных распределений потоков а также множество достижимых векторов МП-потока

При использовании МП-модели для анализа сетевых систем определяется МП-поток, т.е. вектор величин потоков, которые удается одновременно передать между заданными парами вершин логического графа сети. Обычно, всем дугам логического графа приписаны числа ${{f}_{i}}$ и исследуется возможность пропускать набор величин ${{f}_{i}}$ – потоков для тяготеющих пар ${{p}_{i}} \in P$. Поскольку структура связей в рассматриваемой модели определяется кластерами, то достаточно учитывать агрегированные величины

Далее еще упростим модель.

В данной работе ставится задача априорного ранжирования вершин К-сети по подверженности их кластеров влиянию структурных повреждений физического графа сети. Поэтому не будем вводить требований ${{F}_{j}}$ на передачу потока, рассуждая в терминах максимально достижимых величин. Тем самым, с точки зрения требований на передачу все вершины (и все кластеры) будем считать равноправными, а их возможности по передаче своего потока будут задаваться возможностями физического графа $G(d)$, лежащего в основе анализируемой К-сети. Понятно, что свойства распространения потоков из вершины зависят и от состава ее кластера, который различается для разных вершин. В простейшем случае полного графа тяготений имеется $m = n(n - 1)$ тяготеющих пар и в каждом однопродуктовом кластере ровно $n - 1$ тяготеющая пара по всем вершинам сети, кроме той, которая является источником потока для данного кластера. В общем случае, для определенности будем предполагать, что если $({{v}_{j}},{{v}_{i}}) \in {{P}_{j}}$, то и $({{v}_{i}},{{v}_{j}}) \in {{P}_{i}}$, т.е. логические связи являются обоюдными, а на число связей (величину отдельного кластера) накладывать ограничений не будем.

3. КЛАСТЕРНЫЕ СТРУКТУРНЫЕ ПОВРЕЖДЕНИЯ

Структурное повреждение сети определяется подмножеством ее физических ребер, пропускная способность которых полагается равной нулю. Для спецификации конкретного структурного повреждения введем идентификатор $w$ и каждое повреждение $w$ будем задавать списком индексов $I(w)$ исключаемых из $R$ (разрушенных) ребер. Обозначив через $d(w)$ вектор пропускной способности ребер после повреждения $w$, получим

Введем также параметр $\mu (w) = \left| {I(w)} \right|$ мощности повреждения $w$ как общего числа поврежденных ребер. Скажем, что структурное повреждение $w$ является кластерным, если при удалении набора ребер $\{ {{r}_{k}}\,{\text{|}}\,k \in I(w)\} $ максимально возможный поток хотя бы одного вида продукта оказывается равным нулю, т.е. в множестве (2.4) с $d = d(w)$ не найдется вектора со всеми положительными компонентами. Тем самым, кластерные структурные повреждения соответствуют разрезам [10], полностью отделяющим хотя бы одну вершину сети от стоков ее кластера. Ниже рассмотрим в определенном смысле минимальные такие повреждения (МК-повреждения).

Представим гипотетическую ситуацию, когда все ресурсы сети задействованы для передачи единственного вида потока из одной выделенной вершины ${{v}_{j}} \in V$, а из всех остальных потоки полагаются равными нулю. Указанный способ управления К-сетью будем называть монокластерным режимом (МК-режимом) передачи потока ${{z}_{j}}$. Максимальный поток, который можно передать из фиксированной вершины в МК-режиме, является решением стандартной, в данном случае однопродуктовой [11], задачи о максимальном потоке. Достаточно для источника ${{v}_{j}}$ кластера ${{P}_{j}}$ ввести в граф $G(d)$ дополнительный (фиктивный) сток – вершину ${{v}_{{ - j}}}$, который соединить со всеми стоками кластера дополнительными (фиктивными) ребрами неограниченной пропускной способности, и решить задачу на максимум потока из ${{v}_{j}}$ в ${{v}_{{ - j}}}$ для расширенного таким образом графа, который будем обозначать как ${{\overline G }_{j}}(d)$. Ее решение будет эквивалентно решению задачи поиска

Поток величины $z_{j}^{0}$ является максимальным для кластера ${{P}_{j}}$ в исходной МП-сети. Назовем его МК-потоком и предположим, что $z_{j}^{0} > 0$ $\forall {{v}_{j}} \in V$.

МК-потоку $z_{j}^{0}$ в указанной выше задаче с фиктивным стоком на графе ${{\bar {G}}_{j}}(d)$ сопоставлен, по крайней мере, один минимальный разрез [11] (далее – МК-разрез). Пусть $w = h(j)$ – соответствующее повреждение МП-сети. По теореме Форда-Фалкерсона суммарная пропускная способность ребер из множества $\{ {{r}_{k}} \in R\,{\text{|}}\,k \in I(h(j))\} $ равна МК-потоку $z_{j}^{0}$, а одновременное удаление из физического графа сети этого множества ребер отделяет от ее стоков вершину ${{v}_{j}}$ и обнуляет МК-поток $z_{j}^{0}$. Обозначим через $H(j) = \{ {{h}_{1}}(j),{{h}_{2}}(j), \ldots \} $ набор таких МК-разрезов, относящихся к $j$-му кластеру. Последовательно для каждой вершины ${{v}_{j}} \in V$ решим задачу (3.1), т.е. вычислим значения $z_{j}^{0}$ для $j = \overline {1,n} $, и сформируем множество

Разрезы из множества $H{\text{*}}$ назовем МК-повреждениями I рода.

Теперь в исходном физическом графе сети формально положим пропускную способность всех ребер равной единице и найдем поочередно для каждой вершины ${{v}_{j}} \in V$ максимальный поток $z_{j}^{*}$ из решения задачи типа (3.1), но для случая $d = {\mathbf{1}}$, где ${\mathbf{1}}$ есть $e$-мерный вектор из единиц. Получим

Значение $z_{j}^{*}$ равно минимально возможному числу ребер у разрезов, отделяющих вершину ${{v}_{j}}$ от всех ее стоков. Обозначим соответствующее МК-повреждение $w$ как $q(j)$, тогда $z_{j}^{*} = \mu (q(j)) = \left| {I(q(j))} \right|$, где $I(q(j))$ – список номеров ребер, образующих данный разрез, $\mu (q(j))$ – его мощность. С учетом неединственности введем $Q(j) = \{ {{q}_{1}}(j),{{q}_{2}}(j), \ldots \} $ – множество разрезов минимальной мощности для кластера ${{P}_{j}}$. После решения цепочки задач (3.2) построим $Q(j)$, $j = 1,2, \ldots ,n$, и составим из них множество При удалении из графа $G(d)$ всех ребер $\{ {{r}_{k}} \in R{\kern 1pt} {\text{|}}{\kern 1pt} k \in I(q(j))\} $ для такого разреза, где $q(j) \in Q{\text{*}}$, соответствующая вершина ${{v}_{j}} \in V$ оказывается отделена от всех ее стоков (или от ${{v}_{{ - j}}}$ в графах ${{\bar {G}}_{j}}(d)$ и ${{\bar {G}}_{j}}({\mathbf{1}})$), а максимальный поток $z_{j}^{0}$, как и $z_{j}^{*}$, становится равным нулю. Минимальные разрезы из $Q{\kern 1pt} {\text{*}}$ будем называть МК-повреждениями II рода.

МК-повреждение III рода возникает при удалении всех ребер, инцидентных какой-либо вершине $v \in V$. Введем по определению: $U{\text{*}} = \{ u(1), \ldots ,u(n)\} $ множество повреждений III рода, где $I(u(j)) = S({{v}_{j}}) \cup T({{v}_{j}})$ – список номеров $k$ ребер ${{r}_{k}} \in R$ инцидентных вершине ${{v}_{j}}$.

Рассмотрим объединение множеств $H{\kern 1pt} {\text{*}} \cup Q{\kern 1pt} {\text{*}} \cup U{\kern 1pt} {\text{*}}$ МК-повреждений I, II, III рода. В объединенном множестве могут содержаться разрезы с одинаковыми наборами ребер. Исключим из объединения $H{\kern 1pt} {\text{*}} \cup Q{\kern 1pt} {\text{*}} \cup U{\kern 1pt} {\text{*}}$ повторные разрезы, тогда оставшиеся сформируют множество МК-повреждений $W = \{ {{w}_{1}}, \ldots ,{{w}_{c}}\} $, для которого каждый элемент $I(w)$ состоит из уникального набора индексов, не совпадающего ни с однимдругим $I(w{\text{'}})$ при $w \ne w{\text{'}}$. Здесь и далее $c$ – результирующее число элементов в $W$.

Разрезы, попавшие в множество $W$, зависят не только от свойств графа $G(d)$, но и от структуры логических связей К-сети – наборов тяготеющих пар, составляющих ее потоковые кластеры. Например, если граф тяготений – полный, то $W = U{\text{*}}$ и эффективно вычисляется, а $c = n$. Подобная структура служит моделью и для задач с неизвестным графом тяготений, когда потенциально возможны любые логические связи. В общем случае МК-повреждения I и II рода тоже играют важную роль при исследовании уязвимости К-сетей. Так, если физический граф К-сети разделяется на две части ребром-мостом, а все ее логические связи проходят между частями (вершины кластеров имеют адресатами лишь пользователей на другой стороне), то указанное ребро-мост приобретет самостоятельное значение как отдельное повреждение, только войдя в $Q{\text{*}}$ или $H{\text{*}}$. На практике построение $W$ следует начинать с $U{\text{*}}$, затем искать , а потом добавлять разрезы из $Q{\kern 1pt} {\text{*}}$, в принципе, не обязательно все. Но чем представительнее множество $W$, тем значимее получаемые результаты.

4. АНАЛИЗ И ОЦЕНКИ ПОВРЕЖДЕНИЙ

Перейдем к анализу последствий для К-сети от удаления указанных конфигураций физических ребер (задаваемых МК-повреждениями из множества $W$). Возьмем произвольное МК-повреждение $w \in W$. На первом шаге вычислим общее число $N(w)$ кластеров ${{P}_{j}}$, для которых МК-поток окажется равным нулю после данного повреждения. Для этого найдем

для $j = \overline {1,n} $ и введем По построению $N(w) = \left| {{{V}^{0}}(w)} \right| \geqslant 1$, так как $w$ является МК-повреждением, т.е. отделяет хотя бы одну вершину от всех ее стоков. Рассмотрим множество ${{V}^{ + }}(w) = V{\backslash }{{V}^{0}}(w)$ вершин, не полностью лишенных возможности передачи своего потока МК-повреждением $w$. Если оно не пусто, то перейдем ко второму шагу.

На втором шаге проанализируем изменения величин МК-потоков для тех кластеров, по которым частично сохранился поток в поврежденной сети. Введем умозрительную характеристику $g(w)$ длины ребер графа $G(d)$ (не имеющую отношения к физической длине линий связи моделируемой сетевой системы), зависящую от $w$ следующим образом:

где $e$ – число ребер физического графа сети.

Для заданного вектора $g(w)$ найдем кратчайшие пути в графе $G(d)$ между всеми парами вершин ${{v}_{l}}$ и ${{v}_{j}}$ из ${{V}^{ + }}(w)$, обозначим их длины через ${{b}_{{jl}}}(w)$. Сформируем множество

где ${{b}_{{jl}}}(w)$ – длина кратчайшего пути соединения для ${{v}_{l}}$ и ${{v}_{j}}$ в графе $G(d)$ с длинами ребер $g(w)$ при МК-повреждении $w \in W$. На основе $B(w)$ построим т.е. множество тяготеющих пар, для которых длина кратчайшего пути соединения оказалась меньше $2e$ (существует возможность “обойти” разрушенные повреждением $w$ ребра). Заметим, что, если тяготеющая пара ${{p}_{i}} = ({{v}_{{{{s}_{i}}}}},{{v}_{{{{t}_{i}}}}}) \in {{P}^{ + }}(w)$, то и для противоположного направления ${{p}_{{i{\text{'}}}}} = ({{v}_{{{{t}_{i}}}}},{{v}_{{{{s}_{i}}}}}) \in {{P}^{ + }}(w)$. Поэтому множество ${{P}^{ + }}(w)$ тяготеющих пар, не разделенных повреждением $w$, состоит из четного числа элементов.

Введем ${{P}^{0}}(w) = P{\backslash }{{P}^{ + }}(w)$ – множество тяготеющих пар, разделяемых повреждением $w$. Тройка чисел $\left\langle {N(w),\left| {{{P}^{0}}(w)} \right|,e - \mu (w)} \right\rangle $ количественно характеризует каждое повреждение $w \in W$. Чем больше компоненты указанного вектора, тем опаснее для К-сети повреждение $w$. Худший вариант, если $w$ позволяет разрушить связи всех тяготеющих пар. Тогда $N(w) = n$, $\left| {{{P}^{0}}(w)} \right| = \left| P \right| = m$ , а затраченная мощность $\mu (w)$ минимальна для такого глобального нарушения связей, обозначим ее через ${{\mu }^{0}}$. Однако подобное $w$ не обязательно окажется МК-повреждением для некоторого кластера. Для дальнейшего будем считать, что $N(w) < n$ $\forall w \in W$, и рассматривать лишь $w$ с мощностью $\mu (w) < {{\mu }^{0}}$, ограничив $W$ только такими повреждениями любого рода. Отметим, что в данном случае $N(w) < n - 1$ $\forall w \in W$, поскольку единственная вершина не может остаться неотделенной.

С целью обеспечить независимость показателей ущерба сети будем вместо ${{P}^{0}}(w)$ использовать более узкое множество

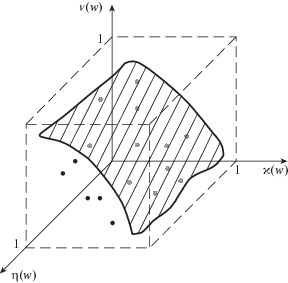
т.е. пар вершин, разделяемых МК-повреждением $w$, но не входящих в множество ${{V}^{0}}(w)$ источников кластеров, полностью изолируемых этим повреждением. Пусть $K(w) = \left| {{{P}^{ - }}(w)} \right|$. Теперь каждому повреждению $w$ можно сопоставить точку с координатами $\left\langle {N(w),K(w),e - \mu (w)} \right\rangle $ или в относительных величинах (для полного графа тяготений) В частности, точка $\left\langle {0.5,{\text{ }}0.6,{\text{ }}0.25} \right\rangle $ будет отвечать МК-повреждениям $w$, полностью разрушающим 50% кластеров, а оставшиеся уменьшающим на 60%, за счет вывода из строя 75% ребер графа $G(d)$. Например, при $n = 10$ после повреждения $w$ мощностью $9$ оказалось, что 5 вершин отделены от всех остальных, а у 5 других из 20 потенциально возможных между ними логических связей сохранились соединения лишь у 8 тяготеющих пар, т.е. у 4 пар вершин (с точностью до направления передачи). Исходный $G(d)$ и результирующий граф $G(d(w))$ приведены на фиг. 1. Граф тяготений для К-сети с фиг. 1 считаем полным.

Компонента $\nu $ вектора (4.3) показывает прямой ущерб передающей сети от МК-повреждения $w \in W$, т.е. сколько видов продукта или информационного потока не будет передано в К-сети (относительно исходного их числа $n$). Компонента $\varkappa $ характеризует средний (приведенный к количеству тяготеющих пар) косвенный ущерб кластерам. Значение $K(w)$ – суммарное по $j \in {{V}^{ + }}(w)$ число вершин ${{v}_{l}}$ (для тяготеющих пар из ${{v}_{j}}$ в ${{{v}}_{l}}$), которым не передается продукт $j$-го вида, тогда как некоторые другие виды передаются, $l \in {{V}^{ + }}(w)$. Если представить себе, что различные виды контента конкурируют за потребителя, то этот показатель будет не менее значим, чем показатель прямого ущерба (см. также далее в разд. 5 показатель косвенного ущерба ${{\varphi }_{j}}(W)$ для $j$-го кластера на классе МК-повреждений $W$). Последняя компонента в (4.3) $\eta $ – это доля оставшихся после повреждения ребер в графе сети $G(d(w))$.

Изобразим точки (4.3) на трехмерной картинке в соответствующих осях для всех МК-повреждений (см. фиг. 2). Те из них, которые находятся в окрестности границы Парето [12] полученного множества, описывают наиболее опасные для МП-сети МК-повреждения: достигаемые с минимальным числом повреждаемых в графе $G(d)$ ребер и/или приводящие к максимальному числу порушенных кластеров и/или разделяющие максимальное число тяготеющих пар в оставшихся кластерах, а также недоминируемые по всем трем критериям сразу. В частности, для К-сети с графом $G(d)$, показанным на фиг. 1 слева, получим, что соответствующее правому графу с фиг. 1 МК-повреждение является паретовским. Из остальных $w \in W = U{\text{*}}$ на границе парето находятся $u(7)$–$u(10)$. Действительно, для всех $j$, кроме $j = 6$, имеем $N(u(j)) = 1$ и $K(u(j)) = 0$, поскольку отделение одной такой ${{v}_{j}}$ не приводит к нарушению связи между всеми оставшимися. Следовательно, парето-оптимальной оказывается точка с минимальной мощностью $\mu (w) = 1$, которая отвечает указанным 4 вариантам МК-повреждений.

Найденные таким образом повреждения (вместе с величиной ${{\mu }^{0}}$) дают информативную характеристику способности физического графа МП-сети обеспечивать ее логические связи в условиях их кластерной структуры. При этом для вычисления значений введенных показателей применялись лишь высокоэффективные методы потокового программирования (решения задач на максимум потока или поиска кратчайшего пути) [15]. Для поиска недоминируемых точек имеет смысл сначала упорядочить $w \in W$ по возрастанию $\mu (w)$, а затем ранжировать повреждения одной мощности по двум другим критериям (аналогично [16]). Отметим, что в отличие от [16], [17] здесь не используются для оценки ущерба конкретные значения $z_{j}^{0}$ (3.1) максимальных потоков. Потому не важны и точные значения ${{d}_{k}}$ пропускной способности физических ребер сети, а только относительные величины (для определения множества $H{\text{*}}$). Фактически, с помощью ${{d}_{k}}$ моделируем число параллельных ребер в исходной сетевой системе (чтобы не противоречить математической модели МП-сети, параллельные ребра объединяются в одно с кратным увеличением пропускной способности). Так что действительно фиг. 2 характеризует именно структуру К-сети.

Замечание. Числовые значения для сети с фиг. 1, приводимые здесь и далее в разд. 5, не совпадают с рассчитанными нами в [13] (разд. 7) по двум причинам. Во-первых, в [13] речь шла о МП-сети (с полным графом тяготений), а здесь на том же графе анализируется К-сеть. Во-вторых, в [13] учитываемый набор повреждений содержит минимальные разрезы, а в настоящей работе содержит МК-разрезы. Кроме количественных, имеются еще и качественные расхождения, демонстрирующие специфику К-сетей. Например, в [13] к парето-оптимальным повреждениям, кроме указанных выше, были отнесены еще два минимальных разреза: из двух ребер $\{ ({{{v}}_{1}},{{{v}}_{6}}),({{{v}}_{2}},{{{v}}_{6}})\} $ и из трех ребер $\{ ({{{v}}_{3}},{{{v}}_{6}}),({{{v}}_{4}},{{{v}}_{6}}),({{{v}}_{5}},{{{v}}_{6}})\} $. Тем не менее в множество $W$ они не попали, не являясь кластерными разрезами (к которым относятся – для случая двух ребер – $\{ ({{{v}}_{1}},{{{v}}_{6}}),({{{v}}_{1}},{{{v}}_{2}})\} $ и $\{ ({{{v}}_{1}},{{{v}}_{2}}),({{{v}}_{2}},{{{v}}_{6}})\} $). Подобные варианты повреждений безусловно интересны с точки зрения косвенного ущерба, но для К-сети гипотетический “противник” (разрушающий сеть), который может удалением того же числа ребер разделить целый кластер, вряд ли воспользуется некластерными вариантами.

5. АНАЛИЗ СЕТИ

Построенные в разд. 4 характеристики ущерба от МК-повреждений также позволяют провести ранжирование информационных кластеров по их подверженности влиянию МК-повреждений – на всем классе $w \in W$. Для каждого МК-повреждения $w \in W$ по решению задач (4.1), (4.2) из разд. 4 определим для всех кластеров ${{P}_{j}}$ и тяготеющих пар в кластере, не разделенных повреждением $w$, следующие функции – индикаторы ущерба:

и $\forall {{{v}}_{j}} \in {{V}^{ + }}(w)$, ${{{v}}_{l}} \in {{V}^{ + }}(w)$Вычислим все значения индикаторных функций ${{\phi }_{j}}(w)$ и ${{\xi }_{{jl}}}(w)$ для $w \in W$.

Подсчитаем

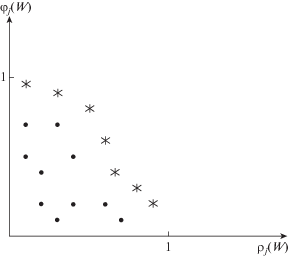
т.е. долю повреждений $w \in W$, при которых МК-поток (4.1) для $j$-го кластера окажется равным нулю. Введем ${{W}^{ + }}(j) = \{ w \in W\,{\text{|}}\,{{v}_{j}} \in {{V}^{ + }}(w)\} $ – множество таких МК-повреждений из $W$, что ${{z}_{j}}(w) > 0$, т.е. возможна передача потока в $j$-м кластере. Очевидно, ${{W}^{ + }}(j) \subseteq W{\backslash }\{ u(j),q(j),h(j)\} $. Определим т.е. среднюю по МК-повреждениям из ${{W}^{ + }}(j)$ долю тяготеющих пар в кластере ${{P}_{j}}$, для которых нарушается связь с источником $j$-го потока при сохранении связи с хотя бы одним источником потоков другого вида продукта. На основе значений ${{\rho }_{j}}(W)$ и ${{\varphi }_{j}}(W)$, найденных для всех кластеров, построим набор точек на плоскости с указанными координатами. Каждому ${{P}_{j}},j = \overline {1,n} $, поставим в соответствие точку (${{\rho }_{j}}(W)$, ${{\varphi }_{j}}(W)$) (см. фиг. 3). При одинаковых координатах точки могут совпадать.

Точки на фиг. 3, которые находятся “в относительной близости” от северо-восточной границы выпуклой оболочки построенного множества, соответствуют видам продуктов (информационных потоков), т.е. вершинам К-сети – источникам таких кластеров, которые наиболее уязвимы по отношению к МК-повреждениям $w \in W$ различного рода. Такие точки отмечены звездочкой на фиг. 3. При удалении из сети множеств ребер для МК-разрезов рассматриваемого класса потоки из отмеченных источников чаще (в большем числе случаев) оказываются равными нулю совсем или для большей доли стоков, не отделенных от иных источников – других видов продуктов. Укажем, что для исследуемой постановки свойства вершины как источника и как стока – получателя потока симметричны, т.е. если некоторый кластер более уязвим, то и на прием потока в порождающей его вершине МК-повреждения из $W$ оказывают большее влияние.

Найденные показатели фактически характеризуют свойства физического графа $G(d)$ К-сети (с данным кластерным составом): насколько его структура обусловливает уязвимость логических связей конкретной вершины. Это позволяет на практике ставить задачи построения новых физических ребер с целью укрепления положения логических связей. Понятно, что чем ближе граф $G(d)$ к полному, тем больше возможностей передачи МП-потока в сети (в том числе “обходными путями”), но добавление новых ребер всегда требует дополнительных затрат. Значит, важно заранее выявить наиболее подверженные влиянию МК-повреждений структуры. Наглядную основу для принятия решений в данном вопросе предоставляет фиг. 3. Притом не обязательно равноправно учитывать оба введенных показателя: из отмеченных точек в зависимости от содержания задачи анализа К-сети могут быть выбраны те, для которых хуже значение одного из критериев уязвимости (т.е. лексикографически оптимальные). Например, для сети с фиг. 1 (левый граф) выполнено: ${{\rho }_{j}}(W)$ = 0.1 $\forall j = \overline {1,6} $, ${{\varphi }_{j}}(W)$ = 0 $\forall j \ne \overline {1,5} $, ${{\rho }_{j}}(W)$ = 0.2 $\forall j = \overline {7,10} $, ${{\varphi }_{j}}(W)$ = 3/45 $\forall j = 1,2$, ${{\varphi }_{j}}(W)$ = 2/45 $\forall j = 3,4,5$, и видно, что наиболее уязвимыми оказываются вершины с номерами с 7-го по 10-й (по первому показателю) и 1, 2 (по второму).

Интересно сравнить данные оценки уязвимости для графа с фиг. 1 (схематично описывающего структуру сети управления) с аналогичными оценками для специально сконструированных графов с фиг. 1 из [3], задающих переход от симметричной регулярной структуры к случайной, между которыми находятся структуры социальных сетей “small-world”. В [3] замечено, что отражающий устойчивость связей в сети средний коэффициент кластеринга практически не отличается для small-world структур от исходного показателя для регулярной структуры и является довольно высоким. Аналогично, если вычислить характеристики ${{\rho }_{j}}(W)$ и ${{\varphi }_{j}}(W)$ для всех построенных в [3] графов сети при полном графе тяготений, то придем к минимальным значениям подверженности влиянию повреждений из $W$: ${{\rho }_{j}}(W)$ = 1/$n$, ${{\varphi }_{j}}(W)$ = 0 для всех ${{v}_{j}}$ (хотя можно представить себе случайные графы и с ненулевым значением ${{\varphi }_{j}}(W)$ для набора вершин ${{v}_{j}}$ степени 2, когда они соединены циклически). Таким образом, средний коэффициент кластеринга, основанный лишь на свойствах физического графа сети, рассматриваемой в [3] как однопродуктовик, дает агрегированное описание ее качеств неуязвимости, не противоречащее полученному в настоящей работе более тонкими методами.

Характеристики каждого отдельного повреждения из разд. 4 дают возможность построения и других показателей влияния МК-разрезов, например, использующих значения ущерба аналогично [17] или [13]. Рассмотрение в составе $W$ минимальных (в том или ином смысле) МК-повреждений делает полученные оценки более информативными в силу ожидаемости подобных повреждений. При этом в класс $W$ входят не только повреждения III рода, изучаемые в [7], [18], но и повреждения, предполагающие выход из строя ребер физического графа К-сети. Последнее становится важно в случае неполного графа тяготений. Отметим также показатель ${{\varphi }_{j}}(W)$, оценивающий уменьшение потока в кластере при сохранении вершины-источника (т.е. при косвенных повреждениях, возникших за счет разрушений, направленных против иных кластеров). Для поиска видов продукта, наиболее подверженных влиянию кластерных повреждений К-сети, значимы оба вида показателей: прямые и косвенные.

6. ЗАКЛЮЧЕНИЕ

В настоящей статье введен новый класс сетевых систем – К-сети, являющийся подклассом МП-сетей. Логический граф К-сети имеет кластерную структуру связей, когда один вид МП-потока передается из одной вершины сети по различным направлениям. Для К-сетей продолжены исследования работы [13] по построению агрегированных оценок уязвимости МП-сети путем применения эффективных методов потокового программирования. Предложены методы блиц-анализа конфигурации графа сети с целью априорного выявления подверженности возможных пользователей сети влиянию повреждений ее структуры. Специально не уточняются их заявки на передачу потока, чтобы провести наиболее общее рассмотрение.

С учетом объединения в кластеры тяготеющих пар принимаем во внимание не все виды структурных повреждений, а кластерные, т.е. разрушающие все логические связи хотя бы одной вершины, причем наиболее экономным и эффективным способом. В общем случае к ним относится не только стандартное удаление вершин [7], [18], но и удаление далеких от вершины ребер-мостов. Устойчивость кластера логических связей по отношению к множеству рассматриваемых повреждений, когда повреждение не нацелено прямо против вершины – источника кластера, предлагается считать показателем, обратным уязвимости. Рассмотрены две содержательно различающиеся характеристики уязвимости К-сетей и среди векторов их значений определяется граница Парето, выявляющая наиболее уязвимые вершины, передающие-получающие потоки в сети с кластерной структурой логических связей. В дальнейшем планируется учесть в постановке мощность потоковых кластеров, понимаемую как сумму (2.5) заявок на передачу продукта (информационного потока), образующего кластер.

Укажем, что данная работа выбивается из общего потока статей, посвященных выявлению критических вершин сети. В большинстве таких статей (см. литературу к [18]) ставятся задачи оптимизации: либо достигаемого разрушительного эффекта (возможно по нескольким критериям [19]), либо затрачиваемого ресурса, либо и того, и другого вместе [20], и исследуется их вычислительная сложность. Как правило, экстремальные задачи оказываются NP-трудными, тогда выделяются их подклассы (типы графов сети), допускающие использование полиномиальных схем, разрабатываются эвристические алгоритмы, предлагаются агрегированные оценки (например, тот же коэффициент кластеринга) и т.п. В [13] постановка оптимизационных задач на сетях имеет вспомогательный характер и рассматриваются лишь задачи, которые можно решить эффективными методами потокового программирования независимо от типа графа сети. При этом удается построить содержательные оценки уязвимости МП-сети по отношению к заданному классу в определенном смысле минимальных ее структурных повреждений. (При желании в число учитываемых повреждений сети можно включить и те, которые найдены в результате использования более сложной оптимизации, и уточнить оценки.) Распространению предложенной конструкции на К-сети посвящена и настоящая работа. Считаем, что такое распространение будет способствовать более глубокому изучению К-сетей, в том числе, с позиций анализа их уязвимости.