Журнал вычислительной математики и математической физики, 2020, T. 60, № 2, стр. 323-337

1. ВВЕДЕНИЕ

В связи с появлением рентгеновских лазеров [1], а также источников рентгеновских пико- и субпикосекундных импульсов, генерируемых лазерной плазмой [2], становится важным исследование особенностей взаимодействия импульсного рентгеновского излучения с веществом. Большой практический интерес представляет изучение возможностей нелинейного взаимодействия, приводящих к сокращению длительности и ширины рентгеновского импульса. Математические модели, описывающие такого рода процессы, оказываются, как правило, весьма сложными, поэтому особенно важное значение получает разработка достаточно точных и устойчивых вычислительных методов для расчетов по этим моделям.

Самофокусировку рентгеновского импульса при его прохождении через плазму вызывает действие пондеромоторных сил, вытесняющих свободные электроны плазмы из области высокой интенсивности импульса, в сочетании с отрицательной диэлектрической проницаемостью плазмы для рентгеновского излучения, так как его несущая частота больше плазменной [3]. В настоящей работе предлагается вычислительный метод исследования математической модели этого процесса для плоских импульсов. Приведены результаты численных экспериментов на ЭВМ. Показана возможность получения эффекта при реально достижимых интенсивностях импульсов и значениях параметров плазмы. На основе решений прямой задачи при различных значениях параметров предложен и описан метод решения обратных задач для определения исходных характеристик плазмы и импульса по параметрам выходного импульса рентгеновского излучения.

2. ФИЗИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ И МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Пусть на границу плазмы $\left( {z = 0} \right)$, находящейся в области $z > 0$, падает импульс рентгеновского излучения следующего вида:

где $A\left( {x,z,t} \right)$ – медленно меняющаяся амплитуда импульса, $i$ – мнимая единица, $\omega $ – несущая частота импульса, $\chi $ – волновой вектор, а его абсолютное значение ${\omega \mathord{\left/ {\vphantom {\omega с}} \right. \kern-0em} с}$ – волновое число или пространственная частота, с – скорость света.

Считая, что медленно меняющаяся амплитуда $A\left( {x,z,t} \right)$ удовлетворяет условиям

получаем для нее следующее уравнение [4]: где диэлектрическая проницаемость $\varepsilon $ определяется выражением здесь $n\,\left( {x,z,t} \right)$ – плотность свободных электронов, $e$ и $m$ – заряд и масса электрона, $\gamma $ – эффективная частота соударений.

Для простоты изложения здесь и далее мы полагаем, что постоянная диэлектрическая проницаемость, связанная с ионной компонентой плазмы, равна единице. Поэтому $c$ – это скорость света в плазме, а не в вакууме, так же как и $\chi $ – волновой вектор волны в плазме. Считая, что продольный пространственный размер импульса ${{L}_{p}} = c{{\tau }_{p}}$, где ${{\tau }_{p}}$ – длительность импульса, много больше поперечного размера: ${{L}_{p}} \gg d$, будем описывать движение электронов плазмы в одномерном квазигидродинамическом приближении. При малых длительностях рентгеновского импульса движением ионов плазмы можно пренебречь. В этом случае уравнения движения плазмы имеют вид [4]

где ${{n}_{0}}$ – равновесное значение плотности электронов, а ${{\varepsilon }_{0}}$ – низкочастотная диэлектрическая проницаемость, $V\left( {x,z,t} \right)$ – скорость свободных электронов плазмы, $E\left( {x,z,t} \right)$ – кулоновское поле.

При выводе (**) мы полагали, что электронная температура не меняется, а давление $P$ совпадает с давлением идеального газа электронов:

Последний член в правой части первого уравнения (**) есть пондеромоторная сила: где пондеромоторный потенциал $U\left( {x,z,t} \right)$ определяется выражением Система уравнений (*), (**) представляет собой замкнутую систему уравнений в частных производных гиперболического типа для четырех переменных $A\left( {x,z,t} \right)$, $n\,\left( {x,z,t} \right)$, $V\left( {x,z,t} \right)$ и $E\left( {x,z,t} \right)$.

Введем следующую нормировку координат и неизвестных функций:

где ${{\tau }_{p}}$– длительность падающего импульса, а $d$ – его поперечный размер; где В этом случае система уравнений (*), (**) примет вид (штрихи у безразмерных переменных здесь и далее будем опускать): Система уравнений (1) дополняется следующими начальными: и граничными условиями: где $A\left( {x,z,t} \right)$ – медленно меняющаяся амплитуда импульса, $n\left( {x,z,t} \right)$ – плотность свободных электронов плазмы, $E\left( {x,z,t} \right)$ – кулоновское поле, $V\left( {x,z,t} \right)$ – скорость свободных электронов плазмы, $\alpha ,\;\beta ,\;\gamma ,\;\delta ,\;v$ – обобщенные параметры системы, $i$ – мнимая единица.

Система уравнений (1), (2), (3) записана в безразмерных нормированных величинах. Штрихи над ними опущены для простоты записи. Обобщенные параметры модели $\alpha ,\;\beta ,\;\gamma ,\;\delta ,\;v$ имеют вид

где $\omega _{p}^{2} = \frac{{4\pi {{e}^{2}}{{n}_{0}}}}{m},$ ${{\omega }_{p}}$ – плазменная частота, $\omega $ – несущая частота импульса, ${{n}_{0}}$ – начальное значение концентрации свободных электронов, ${{\varepsilon }_{0}}$ – низкочастотная диэлектрическая проницаемость, $e$ – заряд электрона, $m$ – масса покоя электрона, $c$ – скорость света в вакууме, ${{I}_{0}}$ – максимальная интенсивность входного импульса.

3. РАЗНОСТНАЯ СХЕМА И ВЫЧИСЛИТЕЛЬНЫЙ МЕТОД РЕШЕНИЯ ПРЯМОЙ ЗАДАЧИ

Нелинейную систему (1) дифференциальных уравнений в частных производных с начальными и граничными условиями (2), (3) будем решать разностным методом, подробно описанном в работе [5]. Так как система (1) является квазилинейной относительно медленно меняющейся амплитуды $A\left( {x,z,t} \right)$, то применение предлагаемого разностного метода решения является обоснованным. Это было также подтверждено многочисленными вычислительными экспериментами при различных значениях параметров задачи и сравнением их результатов с результатами соответствующих физических экспериментов, что показало хорошее соответствие построенной математической модели самофокусировки плоских рентгеновских импульсов в плазме реальному процессу и высокую точность предлагаемого вычислительного метода решения. Итак, введем сетки

основную общую сетку и промежуточную общую сетку

Разностную схему будем строить в ограниченной по $x$ и $z$ области $x \in \left[ { - D;D} \right]$, $z \in \left[ {0;L} \right]$. Тогда пространственные шаги сеток ${{\omega }_{{h{{h}_{z}}\tau }}}$ и $\omega _{{h{{h}_{z}}\tau }}^{'}$ будут равны $h = 2D{\text{/}}N$, ${{h}_{2}} = L{\text{/}}{{N}_{z}}$.

Обозначим через $y_{i}^{j}$ значение в узле $({{x}_{i}},{{z}_{j}},{{t}_{{k + 1}}})$ сеточной функции $y$, определенной на ${{\omega }_{{h{{h}_{z}}\tau }}}$, а через $\hat {y}_{i}^{j}$ значение в узле $({{x}_{i}},{{z}_{j}},{{t}_{{k + 1}}})$. Заменяя в системе (1) производные ${{\partial y} \mathord{\left/ {\vphantom {{\partial y} {\partial t}}} \right. \kern-0em} {\partial t}}$ и ${{\partial y} \mathord{\left/ {\vphantom {{\partial y} {\partial z}}} \right. \kern-0em} {\partial z}}$ первой разностной производной, ${{{{\partial }^{2}}y} \mathord{\left/ {\vphantom {{{{\partial }^{2}}y} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}}$ второй разностной производной: $y_{{x\bar {x},i}}^{j} = \Lambda y_{i}^{j} = {{(y_{{i + 1}}^{j} - 2y_{i}^{j} + y_{{i - 1}}^{j})} \mathord{\left/ {\vphantom {{(y_{{i + 1}}^{j} - 2y_{i}^{j} + y_{{i - 1}}^{j})} {{{h}^{2}}}}} \right. \kern-0em} {{{h}^{2}}}}$, ${{\partial y} \mathord{\left/ {\vphantom {{\partial y} {\partial x}}} \right. \kern-0em} {\partial x}}$ центральной разностной производной: ${{y_{{{{x}^{0}},i}}^{j} = (y_{{i + 1}}^{j} - y_{{i - 1}}^{j})} \mathord{\left/ {\vphantom {{y_{{{{x}^{0}},i}}^{j} = (y_{{i + 1}}^{j} - y_{{i - 1}}^{j})} {\left( {2h} \right)}}} \right. \kern-0em} {\left( {2h} \right)}}$, и обозначая $\bar {y}_{i}^{j} = \sigma y_{{i + 1}}^{j} + \left( {1 - 2\sigma } \right)y_{i}^{j} + \sigma y_{{i - 1}}^{j}$, получаем двухслойную разностную схему с весами, аппроксимирующую систему (1) со вторым порядком по $h,\;{{h}_{z}},\;\tau $. Перейдем к более подробному описанию этой схемы, представляющей собой систему разностных уравнений, аппроксимирующих уравнения системы (1).

Первое уравнение системы (1) будем аппроксимировать со вторым порядком по $h,\;{{h}_{z}},\;\tau $, в точке $\left( {{{x}_{i}},{{z}_{{j - 1/2}}},{{t}_{{k + 1/2}}}} \right)$ следующим разностным уравнением:

Заметим, что в случае ${{h}_{z}} = \tau $ левая часть уравнения (4) существенно упрощается и имеет вид $(\hat {A}_{i}^{j} - A_{i}^{{j - 1}}){\text{/}}\tau $. Расчеты проводились как для ${{h}_{z}} \ne \tau $, так и для ${{h}_{z}} = \tau $.

Для разностной аппроксимации второго уравнения системы (1) используем основную и промежуточную сетки $\omega _{{{{{_{{h{{h}_{z}}}}}}_{\tau }}}}^{{}}$ и $\omega _{{{{{_{{h{{h}_{z}}}}}}_{\tau }}}}^{'}$. Сеточную функцию, соответствующую функции $V\left( {x,z,t} \right)$ и определенную на сетке $\omega _{{{{{_{{h{{h}_{z}}}}}}_{\tau }}}}^{{}}$, обозначим $V_{i}^{j}$ в узле $({{x}_{{i,}}}{{z}_{j}},{{t}_{k}})$ и $\hat {V}_{i}^{j}$ в узле $({{x}_{i}},{{z}_{j}},{{t}_{{k + 1}}})$, а на сетке $\omega _{{h{{h}_{z}}\tau }}^{'}$, соответственно, $V1_{i}^{j}$ и $\hat {V}1_{i}^{j}$ в узлах $({{x}_{i}},{{z}_{j}},t_{k}^{'})$ и $({{x}_{i}},{{z}_{j}},t_{{k + 1}}^{'})$. Тогда для сеточных функций $V_{i}^{j}$ и $V1_{i}^{j}$ получим следующие разностные уравнения:

Не трудно убедиться, что эти уравнения аппроксимируют второе уравнение системы (1) со вторым порядком по $h,\;{{h}_{z}},\;\tau $ в точках $({{x}_{i}},{{z}_{j}},t_{k}^{'})$ и $\left( {{{x}_{i}},{{z}_{j}},{{t}_{{k + 1}}}} \right)$.

В формулах (4)–(6) используются следующие обозначения:

Значения веса $\sigma $ брались в диапазоне $0 \leqslant \sigma \leqslant 1{\text{/}}2$. Например, интерполируя квадратично функцию $\overline {\hat {y}_{i}^{j}} $ по значениям функции $\hat {y}_{i}^{j}$ в узлах $\left( {i - 1,j,k} \right)$, $\left( {i,j,k} \right)$, $\left( {i + 1,j,k} \right)$, получаем значение веса схемы $\sigma = 1{\text{/}}6$.

Для третьего уравнения системы (1), используя аналогичные обозначения, получаем:

Для четвертого уравнения системы (1):

Таким образом, получили симметричную нелинейную разностную схему с весами, аппроксимирующую систему дифференциальных уравнений в частных производных (1) со вторым порядком по $h,\;{{h}_{z}},\;\tau $.

В силу плоскостной симметрии входного импульса $A\left( {x,0,t} \right)$, функции $A\left( {x,z,t} \right)$ и $n\left( {x,z,t} \right)$ являются четными по $x$, а функции $V\left( {x,z,t} \right)$ и $E\left( {x,z,t} \right)$ – нечетными. Поэтому в качестве левых граничных условий возьмем

Для функции $\hat {E}_{i}^{j}$ этого граничного условия достаточно. Остальные граничные условия будем задавать аналогично условиям (3) системы (1), заменяя $\infty $ на достаточно большое $D$ (где действие пондеромоторных сил мало) и аппроксимируя производные со вторым порядком по $h$.

Начальные условия на нулевом слое по $t$ $\left( {k = 0} \right)$ зададим точно, в соответствии с уравнениями (2):

Разностное уравнение (4) решалось методом комплексной прогонки по оси $x$. Определим условия устойчивости этого метода для нашей задачи. Для этого запишем (4) в виде: Достаточным условием устойчивости метода правой прогонки, если ${{y}_{0}} = {{y}_{1}}$ и ${{y}_{N}} = {{y}_{{N - 1}}}$ (равенство нулю производной на границах), как доказано в [6], [7], является неравенство $\left| {C{{p}_{i}}} \right| > \left| {A{{p}_{i}}} \right| + \left| {B{{p}_{i}}} \right|$. Вычислив модули комплексных чисел $A{{p}_{i}},\;B{{p}_{i}},\;C{{p}_{i}}$, возведя обе части неравенства в квадрат и проведя необходимые алгебраические преобразования, окончательно получим: По физическому смыслу задачи всегда $\hat {n}_{i}^{j} \geqslant 0$ (концентрация электронов), поэтому для выполнения полученного неравенства достаточно, чтобы было $\nu \left( {1 - 2\sigma } \right) \geqslant - 2\nu \sigma ,$ что равносильно $\nu \geqslant 0$. Так как параметр $\nu \geqslant 0$ по определению, то достаточное условие устойчивости выполнено, т.е. метод комплексной прогонки для данной задачи является устойчивым.

Предлагаемая разностная схема и приведенный ниже алгоритм вычислений по ней позволяют находить значения всех неизвестных функций на каждом слое по $t$ и по $z$ без итераций, сохраняя при этом второй порядок аппроксимации по $h,{{h}_{z}},\tau $ на решении нелинейной задачи (1)–(3). В самом деле, из уравнения (7) видим, что:

Функции $n_{i}^{j}$ и $V1_{i}^{j}$ известны из предыдущего слоя по времени, поэтому методом прогонки по $x$ находим $\hat {n}_{i}^{j}$ на следующем слое по $t$. Из уравнения (4) имеем: Так как $\hat {n}_{i}^{j},\;i = 0,1,...,N$, уже найдено, находим методом комплексной прогонки $\hat {A}_{i}^{j}$ на следующем слое по $t$ и $z$.

Далее из уравнения (8) находим $\hat {E}_{i}^{j}$ по $\hat {n}_{i}^{j}$:

Затем из (5) вычисляем $\hat {V}_{i}^{j}$: И, наконец, из (6) находим $\hat {V}1_{i}^{j}$:

Заметим, что разностные уравнения (5) и (6) записаны в предположении, что $\left( {\overline {\hat {n}_{i}^{j}} , + \overline {n_{i}^{j}} } \right) \ne 0$ для уравнения (5) и $\overline {\hat {n}_{i}^{j}} \ne 0$ для уравнения (6). Однако эти члены могут обращаться в нуль, так как они аппроксимируют значения концентрации свободных электронов плазмы, которые могут быть полностью вытеснены из области высокой интенсивности рентгеновского импульса. В связи с этим возникает особенность при вычислении $\hat {V}_{i}^{j}$ и $\hat {V}1_{i}^{j}$, которая разрешается следующим образом. Из второго и третьего уравнений системы (1) следует, что если в какой-либо точке $M = \left( {{{x}_{0}},{{z}_{0}},{{t}_{0}}} \right)$ концентрация электронов $n\left( M \right) = 0$, то $n_{x}^{'}\left( M \right) = 0$, и $n_{t}^{'}\left( M \right) = 0$, а скорость электронов $V\left( M \right)$ не определена. Поэтому естественно положить в этой точке $V\left( M \right) = 0$. Это же следует и из физических соображений. В алгоритме, прежде чем вычислять $\hat {V}_{i}^{j}$ из уравнения (5), проверяется на равенство нулю сумма $(\hat {n}_{i}^{j} + n_{i}^{j})$. Если она равна нулю, то полагаем $\hat {V}_{i}^{j} = 0$ и переходим к вычислению $\hat {V}_{{i + 1}}^{j}$. Аналогично поступаем при вычислении $\hat {V}1_{i}^{j}$ из (6), только в этом случае на равенство нулю проверяется $\hat {n}_{i}^{j}$. При этом необходимо, чтобы вес схемы $\sigma $ был отличен от нуля. В противном случае, начиная с того момента, как $\hat {n}_{i}^{j}$ и $\hat {V}1_{i}^{j}$ обратятся в нуль в некотором узле $\left( {{{i}_{0}},{{j}_{0}},{{k}_{0}}} \right)$ они останутся таковыми на всех последующих слоях по времени (т.е. для всех $k \geqslant {{k}_{0}}$), как это видно из уравнения (7) с учетом сказанного выше. Если же вес схемы изменяется в интервале $0 < \sigma < 1{\text{/}}2$, то эта проблема не возникает, и по мере прохождения импульса, как показали многочисленные вычислительные эксперименты при различных значениях параметров задачи, сеточная функция концентрации электронов $n_{i}^{j}$ постепенно принимает начальные значения $\left( {n\left( {x,z,0} \right) = 1} \right)$, как и должно быть с физической точки зрения. Дополнительные ограничения на вес схемы $0 < \sigma < 1{\text{/}}2$ следуют из условия $\overline {\hat {n}_{i}^{j}} > 0$, если $\hat {n}_{i}^{j} > 0$.

Таким образом, с помощью описанного алгоритма (9)–(13) можно найти все неизвестные функции на следующем слое по времени, не прибегая к итерационному процессу. Это позволяет в несколько раз увеличить скорость вычислений, сохраняя при этом второй порядок аппроксимации. Отметим, что переход к бегущей системе координат: $z{\kern 1pt} ' = t - z$, $t{\kern 1pt} ' = t$ в задаче (1)–(3) не позволяет пространственно локализовать решение, так как, избавляясь от производной по $z$ в первом уравнении, получаем сумму производных $\partial {\text{/}}\partial t{\kern 1pt} '\; + \partial {\text{/}}\partial z{\kern 1pt} '$ вместо $\partial {\text{/}}\partial t$ во втором и третьем уравнениях системы (1). Поэтому для проведения расчетов при больших значениях $z$ по мере продвижения импульса применялся циклический перенос начальных значений функций $V\left( {x,z,t} \right)$, $n\left( {x,z,t} \right)$, $E\left( {x,z,t} \right)$ непосредственно перед фронтом импульса и осуществлялась передача значений функции $A\left( {x,z,t} \right)$ с границы $z = L$ на границу $z = 0$. При этом для сохранения второго порядка аппроксимации полагалось $h = \tau $. Таким образом, можно на ограниченных пространственных сетках рассчитывать поведение интенсивности импульса на сколь угодно больших трассах.

4. РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ

С целью выяснения зависимости поведения решения задачи (1)–(3) от параметров $\left( {\alpha ,\beta ,\gamma ,\delta ,\nu } \right)$, определения их оптимальных с точки зрения фокусировки импульса значений, а также практической проверки целесообразности применения предложенного вычислительного метода для решения такого рода задач был проведен ряд численных экспериментов на ЭВМ. В результате была показана возможность самофокусировки рентгеновского импульса в плазме при реально достижимых значениях параметров, найдены условия наиболее яркого проявления эффекта. Сравнение полученных результатов с реальными физическими экспериментами показало высокую точность предлагаемой математической модели и метода решения соответствующей задачи.

Как было отмечено во введении, в данной работе рассматривались пикосекундные рентгеновские импульсы. В ходе многочисленных вычислительных экспериментов были рассмотрены различные значения обобщенных параметров задачи $\alpha ,\;\beta ,\;\gamma ,\;\delta ,\;v$. В абсолютных величинах длительность импульса ${{\tau }_{p}}$ выбиралась в диапазоне от 0,5 до 10 пикосекунд (${{10}^{{ - 12}}}$ секунды), линейная несущая частота рентгеновского импульса $\nu $ – в диапазоне от $5 \times {{10}^{{17}}}$ до $5 \times {{10}^{{19}}}$, что соответствует диапазону изменения циклической частоты $\omega = 2\pi \,\nu $ от $\pi \times {{10}^{{18}}}$ до $\pi \times {{10}^{{20}}}$. Таким образом, длительность импульса была больше времени одного колебания волны рентгеновского излучения приблизительно в 10 000–10 000 000 раз.

На фиг. 1a–e показана пространственная динамика интенсивности импульса $I(x,z,t)$ по мере его продвижения в плазме в различные моменты времени: $t = {{t}_{0}} = {\text{ }}2.0$ (фиг. 1a), максимальная интенсивность на входе в плазму $\max I\left( {x,~z,~{{t}_{0}}} \right) = {{I}_{0}} = 1.0)$, $t = {{t}_{1}} = 2.9$ (фиг. 1б), $t = {{t}_{2}} = 3.1~$ (фиг. 1в), $t = {{t}_{3}} = 3.4$ (фиг. 1г), $t = {{t}_{4}} = 3.85$ (фиг. 1д).

В данном примере в результате самофокусировки максимальная интенсивность импульса увеличилась более чем в десять раз. При этом брались следующие значения параметров задачи: $\alpha = {\text{1}}.0$, $\beta = {\text{1}}.0$, $\gamma = 0.{\text{25}}$, $\delta = 0.{\text{1}}$, $\nu = {\text{3}}00$.

Теоретические вопросы устойчивости и сходимости подобных разностных схем подробно исследованы, например, в классической книге [10]. Для практического подтверждения устойчивости и сходимости построенной разностной схемы было проведено около тысячи вычислительных экспериментов при различных шагах $h,\;{{h}_{z}},\;\tau $, размерах сеток по оси $x$ (параметр $D$) и значениях параметров задачи $h = \tau $. Шаги сеток $h,\;{{h}_{z}},\;\tau $ брались равными $0.05 \times k$, где $k \in \left\{ {1,2,3,4} \right\}$. Варьирование шагов показало, что в совпадающих узлах полученных сеток значения решения отличаются не более чем на 3.1%, а для $k = 1,2$ – не более, чем на 0.37%, что указывает на хорошую сходимость схемы.

Параметр $D$, отвечающий за размер сеток по оси $x$, выбирался на основе численных экспериментов так, чтобы перенос правых граничных условий из $x \to \infty $ в $x = D$ не сказывался на поведении решения. Рассматривались различные $D \in \left[ {2.5,\;4.0} \right]$. Была также исследована зависимость решения задачи (1)–(3) от обобщенных параметров $\alpha ,\;\beta ,\;\gamma ,\;\delta ,\;\nu $ (4).

Параметр $\alpha = {{{{V}_{0}}{{\tau }_{p}}} \mathord{\left/ {\vphantom {{{{V}_{0}}{{\tau }_{p}}} d}} \right. \kern-0em} d}$ определяет отношение длины, пробегаемой электроном за длительность импульса, к поперечному размеру рентгеновского пучка. Из физических соображений наилучшую самофокусировку следует ожидать при $\alpha \approx 1$, что и подтвердили численные эксперименты. Также выяснилось, что увеличение параметров $\beta $ и $\nu $, отвечающих за влияние кулоновских сил на динамику электронной компоненты плазмы и за величину начальной концентрации свободных электронов, ведет к разбиению рентгеновского импульса на несколько параллельных пучков вдоль оси $z$. Этот эффект становится более ярким с увеличением параметра $\gamma $, определяющего интенсивность входного импульса и влияние пондеромоторных сил. Подробное описание исследуемого физического процесса дано в работе [4].

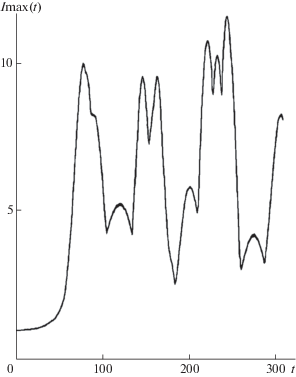
Приведем пример, экспериментально подтверждающий асимптотическую устойчивость используемой разностной схемы. Параметр $\delta $, определяющий дифракционное расплывание пучка, из физических соображений обратно пропорционален длине фокусировки, т.е. длине, на которой наступает максимальное сжатие пучка, после чего начинается режим насыщения, во время которого максимальная интенсивность импульса ${\text{Imax}}\left( t \right)$ циклически изменяется, как это видно из графиков на фиг. 2 и фиг. 3, полученных в результате вычислений.

Сравнение графиков на фиг. 2 и фиг. 3 показывает, что увеличение $\delta $ на порядок приводит к пропорциональному уменьшению длины фокусировки. Такое поведение решения свидетельствует также об асимптотической устойчивости построенной разностной схемы, так как все остальные параметры, кроме $\delta $, остаются неизменными, тогда как график на фиг. 3 рассчитывается в десять раз дольше, чем на фиг. 2, т.е. для его вычисления надо сделать в десять раз больше шагов по времени $t$ и глубине $z$. Небольшие отличия графиков на фиг. 2 и фиг. 3 связаны с тем, что чем больше параметр $\delta $, тем меньше длина фокусировки и тем менее плавно свободные электроны плазмы «отслеживают» изменения формы импульса.

С физической точки зрения, проведенные расчеты указывают на возможность использования самофокусировки импульсного рентгеновского излучения в плазме для повышения его интенсивности в широком диапазоне начальных значений параметров плазмы и импульса, а с математической – подтверждают надежность и целесообразность описанного в этой работе вычислительного метода для решения прямых задач такого типа и использования полученных результатов при различных значениях входных параметров для решения обратных задач, о чем будет рассказано в следующем разделе.

5. ПРИМЕНЕНИЕ МЕТОДА МНОЖЕСТВА ЭКВИВАЛЕНТНОСТИ ДЛЯ РЕШЕНИЯ ОБРАТНЫХ ЗАДАЧ ОПРЕДЕЛЕНИЯ НАЧАЛЬНЫХ ПАРАМЕТРОВ ПЛАЗМЫ И ИМПУЛЬСА ПО ХАРАКТЕРИСТИКАМ ПРОШЕДШЕГО ЧЕРЕЗ НЕЕ РЕНТГЕНОВСКОГО ИМПУЛЬСА

Решение такого рода обратных задач представляет особый интерес, поскольку позволяет дать ответы сразу на два важных вопроса.

1) Какими были начальные параметры плазмы, если рентгеновский импульс на выходе из нее имеет определенные (измеренные) характеристики?

2) Какими должны быть начальные параметры плазмы и импульса, чтобы рентгеновский импульс на выходе из нее имел желаемые характеристики?

Для решения этих задач будем применять метод множества эквивалентности [6]–[9] по одному или нескольким критериям. Для определения критериев могут быть использованы следующие характеристики выходного импульса.

1. Объемная форма импульса (по интенсивности) на выходе из плазмы в определенный момент времени.

2. Объемная форма импульса (по интенсивности) на выходе из плазмы в несколько различных моментов времени.

3. Динамика максимальной интенсивности импульса на выходе из плазмы за определенный промежуток времени.

Формально соответствующие критерии можно записать следующим образом:

Здесь используются следующие обозначения: $P = \left( {{{p}_{1}},{{p}_{2}},...,{{p}_{s}}} \right)$ – набор из $s$ интересующих нас исходных параметров плазмы и импульса. Например, это могут быть все пять обобщенных параметров (4) системы (1)–(3). Тогда $P = \left( {\alpha ,\beta ,\gamma ,\delta ,\nu } \right)$. Или в него могут входить, например, начальная концентрация свободных электронов плазмы ${{n}_{0}}$, низкочастотная диэлектрическая проницаемость плазмы ${{\varepsilon }_{0}}$ и несущая частота входного импульса $\omega $. В этом случае $P = \left( {{{n}_{0}},{{\varepsilon }_{0}},\omega } \right)$, а значения обобщенных параметров $\alpha ,\beta ,\gamma ,\delta ,\nu $ системы (1)–(3) будут вычислены в соответствии со значениями ${{n}_{0}},{{\varepsilon }_{0}},\omega $ по формулам (4); ${{P}^{0}} = (p_{1}^{0},p_{2}^{0},...,p_{s}^{0})$ – искомый набор из $s$ значений интересующих нас исходных параметров плазмы и импульса; $E$ – пространственная область определения (вычисления и измерения) функции интенсивности импульса $I\left( {P,x,z,{{t}_{n}}} \right)$ в момент времени $t = {{t}_{n}}$; $I\left( {P,x,z,{{t}_{n}}} \right)$ – вычисляемая в результате решения прямой задачи для каждого набора значений параметров $P$ функция интенсивности импульса в области $x,z \in E$ в момент времени $t = {{t}_{n}}$ (фиг. 1); ${{I}^{0}}({{P}^{0}},x,z,{{t}_{n}})$ – эталонная (измеренная или желаемая) функция интенсивности импульса для искомого набора значений параметров ${{P}^{0}}$ в области $x,z \in E$ в момент времени $t = {{t}_{n}}$; $T$ – промежуток времени, на котором определяется (измеряется) максимальная интенсивность рентгеновского импульса; ${\text{Imax}}\left( {P,t} \right)$ – вычисляемая в результате решения прямой задачи для каждого набора значений параметров $P$ функция максимальной интенсивности импульса в области $t \in T$ (фиг. 2, 3); $I{{\max }^{0}}({{P}^{0}},t)$ – эталонная (измеренная или желаемая) функция максимальной интенсивности импульса для искомого набора значений параметров ${{P}^{0}}$ в области $t \in T$.

Для решения обратной задачи определения начальных параметров плазмы необходимо минимизировать все эти $n + 1$ функционала. Другими словами – решить многокритериальную задачу минимизации по $n + 1$ критерию. Решать эту задачу будем методом множества эквивалентности [6]–[9]. Опишем поэтапно алгоритм применения этого метода для решения данной задачи.

Aлгоритм

Шаг. 1. По каждому из интересующих нас начальных параметров плазмы и импульса (на отрезке от минимально возможного значения этого параметра ${{a}_{i}}$ до максимально возможного значения ${{b}_{i}}$) вводим регулярную сетку

где ${{L}_{i}}$ – число точек сетки для $i$-го входного параметра, ${{h}_{i}}$ – соответствующий шаг этой сетки, $i = 1,...,s$.

И общую сетку в $s$-мерном пространстве всех рассматриваемых параметров

Шаг. 2. В каждом узле этой сетки решаем прямую задачу (1)–(3) описанным численным методом и вычисляем соответствующие значения $I\left( {P,x,z,{{t}_{n}}} \right)$.

Шаг. 3. Для каждого критерия ${{F}_{l}}$, $l = 1,...,n + 1$, решаем задачу минимизации и находим соответствующий набор начальных параметров ${{P}^{0}}$.

Шаг. 4. Для каждого из этих критериев определяем не только оптимальные решения, но и множество решений, близких к оптимальному (т.е. отличающихся от оптимального значения не более, чем на заданное число ${{R}_{l}} \geqslant 0$, $l = 1,...,n + 1$). Для каждого значения $l$ определяем множество ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, которое является множеством всех оптимальных и близких к оптимальному решений ${{P}^{0}} = (p_{1}^{0},p_{2}^{0},...,p_{s}^{0}) \in {{\Omega }_{l}}\left( {{{R}_{l}}} \right)$ по критерию ${{F}_{l}}$.

Шаг. 5. Находим множество, являющееся пересечением всех множеств ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$

Множество ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right)$ называется множеством эквивалентности с точки зрения всех критериев, так как все его элементы принадлежат одновременно всем множествам ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$ и являются оптимальными и близкими к оптимальным решениями по всем критериям. Любой набор начальных параметров, принадлежащий этому множеству, является решением задачи.

Обозначим число элементов множества ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right)$ через $r$, $r \geqslant 0$. Возможны два случая:

1) ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right) \ne \emptyset $, т.е. $r > 0$. В этом случае в качестве решения обратной задачи может быть взято любое ${{P}^{0}} = (p_{1}^{0},p_{2}^{0},...,p_{s}^{0}) \in {{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right)$, при этом оценка точности решения по каждому критерию ${{F}_{l}}$, $l = 1,...,n + 1$ будет определяться компонентами вектора $\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right)$.

2) ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right) = \emptyset $, т.е. $r = 0$. В этом случае надо изменить одно или несколько значений ${{R}_{l}}$, повторить расчеты по определению новых множеств ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$ и получить соответствующее им множество эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right)$.

Методы, определяющие множество эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right) \ne \emptyset $, являются методами регуляризации [11] для некорректных обратных задач в псевдометрическом пространстве критериев [8], [9] (даже при наличии неформализованных критериев), а каждое решение ${{P}^{0}} = (p_{1}^{0},p_{2}^{0},...,p_{s}^{0}) \in {{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right)$ – решением такой некорректной задачи.

В самом деле, наличие $n + 1$ формализованного критерия ${{F}_{l}}\left( P \right)$, $P \in D$, $l = 1,...,n + 1$, позволяет на множестве $D$ определить $n + 1$ функцию расстояния между двумя элементами $P{\kern 1pt} ' \in D$ и $P{\kern 1pt} '{\kern 1pt} ' \in D$:

Эти функции обладают следующими свойствами:

Введенные нами функции являются псевдометриками, а множество $D$ с такой метрикой называется псевдометрическим пространством. В отличие от метрического пространства, условие ${{R}_{l}}\left( {X,Y} \right) = 0$ может выполняться также и для некоторых $X \ne Y$.

Поэтому в нашем случае для любых $P{\kern 1pt} '$, $P{\text{''}} \in {{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{n + 1}}}} \right)$ будут выполняться условия устойчивости типа тихоновских условий для устойчивых задач [11]:

Таким образом, метод множества эквивалентности можно считать обобщением метода регуляризации для некорректных задач в многомерном псевдометрическом пространстве $D$ при наличии нескольких критериев. Это позволяет применять метод множества эквивалентности как для решения задач многокритериальной оптимизации [8], [9], так и для решения обратных задач математической физики, как показано в этой статье.

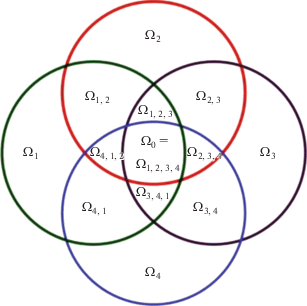
Описанный метод не имеет недостатка метода нахождения множества эффективных по Парето решений, поскольку при добавлении дополнительного критерия множество эквивалентности не растет, а наоборот сужается [8], [9] (фиг. 4). Поэтому при решении реальных задач из полученного этим методом множества эквивалентности экспертом могут выбираться решения, удовлетворяющие не только формализованным критериям, но и неформализованным, основанным на опыте и интуиции эксперта, при этом гарантированно не упуская наилучшее решение, которое при любом количестве критериев всегда будет находиться внутри найденного множества

Какое именно решение из множества эквивалентности выбрать – решает эксперт-исследователь, исходя из его опыта, неформализованных критериев и конкретных целей. Нередко бывает, что эксперт выбирает сразу несколько наборов начальных параметров из полученного множества эквивалентных решений. Например, чтобы проверить и сравнить возможность и удобство их реализации на практике. Важно отметить, что число критериев зависит от конкретных целей исследования процесса самофокусировки. Например, если цель заключается не в том, чтобы восстановить начальные параметры плазмы по измеренным характеристикам прошедшего через нее рентгеновского импульса, а только в том, чтобы определить такие значения начальных параметров плазмы и импульса, при которых импульс в результате процесса самофокусировки достигнет желаемой интенсивности, то достаточно найти множество решений, удовлетворяющее хотя бы одному из $n + 1$ критериев. В этом случае нет необходимости искать пересечение $n + 1$ множества эквивалентных решений для всех критериев. При этом остается возможность найти несколько разных наборов начальных параметров плазмы и импульса (решив обратную задачу по одному или нескольким критериям независимо друг от друга), при которых достигается желаемая интенсивность импульса после самофокусировки, и выбрать из них наиболее подходящие с точки зрения практического применения в различных конкретных условиях. Отметим также, что многочисленные вычислительные эксперименты показали, что для восстановления начальных параметров плазмы по измеренным характеристикам прошедшего через нее рентгеновского импульса вполне достаточно найти множество эквивалентности для трех-четырех критериев, то есть решить обратную задачу при $n = 2,\;3.$