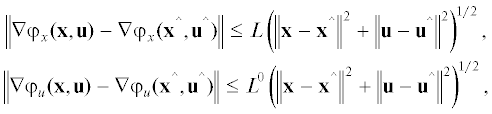Журнал вычислительной математики и математической физики, 2020, T. 60, № 2, стр. 221-233
Проекционный обобщенный двухточечный экстраградиентный квазиньютоновский метод решения седловых и других задач
В. Г. Малинов *
УлГУ
432000 Ульяновск, ул. Толстого, 42, Россия
* E-mail: vgmalinov@mail.ru
Поступила в редакцию 20.12.2018
После доработки 15.07.2019
Принята к публикации 17.10.2019
Аннотация
Исследуется указанный метод для решения седловых и других задач, когда седловые точки вычисляются для выпукло-вогнутой гладкой функции с липшицевыми частными градиентами на выпуклом замкнутом подмножестве евклидова пространства. Средствами выпуклого анализа доказана сходимость и получена оценка скорости сходимости метода, без предположения о сильной выпукло-вогнутости функции. Библ. 28.
1. ПОСТАНОВКА ЗАДАЧИ И ВВЕДЕНИЕ
1.1. На выпуклом замкнутом множестве $Q \times U \subset {{E}^{{n}}} \times {{E}^{{m}}}$ решаем задачу об отыскании седловой точки выпукло-вогнутой функции $\varphi ({\mathbf{x}},{\mathbf{u}})$, выпуклой по ${\mathbf{x}} \in Q \subset {{E}^{{n}}}$ и вогнутой по ${\mathbf{u}} \in U \subset {{E}^{{m}}}$, т.е. об отыскании точки $\left( {{\mathbf{x}}{\text{*}},{\mathbf{u}}{\text{*}}} \right) \in Q \times U$:
(1.1)
$\varphi \left( {{\mathbf{x}}{\text{*}},{\mathbf{u}}} \right) \leqslant \varphi \left( {{\mathbf{x}}{\text{*}},{\mathbf{u}}{\text{*}}} \right) \leqslant \varphi \left( {{\mathbf{x}},{\mathbf{u}}{\text{*}}} \right)\quad \forall {\mathbf{x}} \in Q,\quad {\mathbf{u}} \in U.$б) функция $\varphi ({\mathbf{x}},{\mathbf{u}})$ с овражными гиперповерхностями уровней определена в окрестности подмножества $W \subset Q \times U \subset {{E}^{{n + m}}}$, для всех фиксированных ${\mathbf{u}} \in U$ функция $g({\mathbf{x}}) = \varphi ({\mathbf{x}},{\mathbf{u}})$ выпукла на $Q \subset {{E}^{{n}}}$, а для каждого фиксированного ${\mathbf{x}} \in Q$ функция $h({\mathbf{u}}) = \varphi ({\mathbf{x}},{\mathbf{u}})$ вогнута на $U \subset {{E}^{{m}}}$; в) множество ${{W}_{*}} = {{Q}_{*}} \times U{\text{*}}$ седловых точек $\left( {{\mathbf{x}}{\text{*}},{\mathbf{u}}{\text{*}}} \right)$ функции $\varphi ({\mathbf{x}},{\mathbf{u}})$ на $W \subset {{E}^{{n + m}}}$ непустое; г) частные градиенты функции $\varphi ({\mathbf{x}},{\mathbf{u}})$ липшицевы на $Q \times U$,
где $L > 0$, ${{L}^{0}} > 0$ – константы Липшица. В терминах оператора проектирования седловая точка $\left( {{\mathbf{x}}{\text{*}},{\mathbf{u}}{\text{*}}} \right) \in {{W}_{*}}$ задачи (1.1) характеризуется равенствами [3](1.3)
${\mathbf{x}}{\text{*}} = {{P}_{Q}}\left[ {{\mathbf{x}}{\text{*}} - \tau \nabla {{\varphi }_{x}}\left( {{\mathbf{x}}{\text{*}},{\mathbf{u}}{\text{*}}} \right)} \right],\quad {\mathbf{u}}{\text{*}} = {{P}_{U}}\left[ {{\mathbf{u}}{\text{*}} + \tau \nabla {{\varphi }_{u}}\left( {{\mathbf{x}}{\text{*}},{\mathbf{u}}{\text{*}}} \right)} \right],\quad \tau > 0,$1.2. Различные классы экстремальных задач математической физики, оптимального управления, теории игр, математической экономики [1]–[7] приводят к решению задач вида (1.1)–(1.3). Например, вычисления оптимальных решений многих прямых и двойственных задач математического программирования могут быть сведены к отысканию седловых точек соответствующих функций Лагранжа или их модификаций [1]; задача выпуклого программирования (ЗВП)
Методов решения седловых задач (1.1) намного меньше, чем методов для задач оптимизации, это отмечено в [6] и других работах. Простейший из итеративных методов решения этой задачи – метод проекции градиента (МПГ) Эрроу–Гурвица ${{{\mathbf{x}}}^{{k + 1}}} = {{P}_{Q}}[{{{\mathbf{x}}}^{k}} - \tau \nabla {{f}_{x}}({{{\mathbf{x}}}^{k}},{{{\mathbf{u}}}^{k}})]$, ${{{\mathbf{u}}}^{{k + 1}}} = {{P}_{U}}[{{{\mathbf{u}}}^{k}} + \tau \nabla {{f}_{u}}({{{\mathbf{x}}}^{k}},{{{\mathbf{u}}}^{k}})]$, $\tau > 0$, $k \geqslant 0.$ Известно, для задачи минимизации $f({\mathbf{x}}) \to {\text{inf}}$, ${\mathbf{x}} \in Q \subset {{E}^{n}}$ на простом множестве $Q$ МПГ сходится, а для задач о точках равновесия сходимость МПГ доказана лишь при весьма ограничительных предположениях сильной выпукло-вогнутости, что не выполняется для многих нужных классов задач, например, функций Лагранжа задач минимизации при ограничениях, других седловых задач [1].
В работах [2] и [3] исследованы методы отыскания седловых точек модифицированной функции Лагранжа. В [4] предложены две модификации экстраградиентного метода (ЭГМ) с линейной скоростью сходимости решения седловой задачи для вогнуто-выпуклой функции $\varphi ({\mathbf{x}},{\mathbf{u}})$. Они требуют соответственно два и три вычисления градиента на каждую итерацию. Формулы лучшего из градиентов имеют вид
В [5] для решения задачи (1.1) предложен и обоснован, наряду с другими (в том числе и непрерывными), итерационный процесс
Рассматриваемые методы получили дальнейшее развитие в работе [6], где задачи вида (1.1) и многообразие других экстремальных задач и методы их решения обобщены к задачам и методам вычисления неподвижных точек экстремальных отображений.
В [7] предложены и исследованы два новых метода решения седловых и других задач, построенных на основе [8]. Один из них задан итерационными формулами
Поскольку методы переменной метрики (МПМ) не характеризуются уменьшением локальной скорости, целью нашей работы является построение для решения задач вида (1.1) проекционного МПМ, по скорости сходимости и точности превосходящего построенные на основе МПГ, и для случая такой задачи, что гиперповерхности уровней функции $\varphi ({\mathbf{x}},{\mathbf{u}})$ имеют овражный характер. Для решения такой задачи исследуем метод, объединяющий достоинства многоточечных (многошаговых) проекционных методов и МПМ.
2. ПРЕДЛАГАЕМЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ
2.1. Для решения задачи (1.1), на основе проекционного обобщенного двухшагового двухэтапного квазиньютоновского метода из работы [9], построим обобщенный двухточечный экстраградиентный квазиньютоновский метод:
(2.1)
$\begin{gathered} {{{\mathbf{z}}}^{k}} = {{P}_{Q}}[{{{\mathbf{x}}}^{k}} + {{\alpha }_{k}}{{{\mathbf{y}}}^{k}}],\quad {{{\mathbf{x}}}^{{k + 1}}} = {{P}_{Q}}[{{{\mathbf{z}}}^{k}} - {{\beta }_{k}}A_{k}^{{ - 1}}\nabla {{\varphi }_{x}}({{{\mathbf{z}}}^{k}},{{{\mathbf{u}}}^{k}})], \\ {{{\mathbf{w}}}^{k}} = {{P}_{U}}[{{{\mathbf{u}}}^{k}} + {{\alpha }_{k}}{{{\mathbf{v}}}^{k}}],\quad {{{\mathbf{u}}}^{{k + 1}}} = {{P}_{U}}[{{{\mathbf{w}}}^{k}} + {{\lambda }_{k}}{\mathbf{B}}_{k}^{{ - 1}}\nabla {{\varphi }_{u}}({{{\mathbf{x}}}^{{k + 1}}},{{{\mathbf{w}}}^{k}})],\quad k \geqslant 1, \\ \end{gathered} $(2.2)
$m{{\left\| {\mathbf{v}} \right\|}^{2}} \leqslant ({\mathbf{A}}({\mathbf{x}}){\mathbf{v}},{\mathbf{v}}) \leqslant M{{\left\| {\mathbf{v}} \right\|}^{2}},\quad 0 < m \leqslant M,\quad {\mathbf{v}},{\mathbf{x}} \in {{E}^{n}};$(2.3)
$m{{\left\| {\mathbf{v}} \right\|}^{2}} \leqslant ({\mathbf{B}}({\mathbf{u}}){\mathbf{v}},{\mathbf{v}}) \leqslant M{{\left\| {\mathbf{v}} \right\|}^{2}},\quad 0 < m \leqslant M,\quad {\mathbf{v}},{\mathbf{u}} \in {{E}^{m}}.$(2.4)
$\begin{gathered} {{\left\| {\mathbf{v}} \right\|}^{2}}{\text{/}}M \leqslant ({{{\mathbf{A}}}^{{ - 1}}}({\mathbf{x}}){\mathbf{v}},{\mathbf{v}}) \leqslant {{\left\| {\mathbf{v}} \right\|}^{2}}{\text{/}}m,\quad {\mathbf{v}},{\mathbf{x}} \in {{E}^{n}}; \hfill \\ {{\left\| {\mathbf{v}} \right\|}^{2}}{\text{/}}M \leqslant ({{{\mathbf{B}}}^{{ - 1}}}({\mathbf{u}}){\mathbf{v}},{\mathbf{v}}) \leqslant {{\left\| {\mathbf{v}} \right\|}^{2}}{\text{/}}m,\quad {\mathbf{v}},{\mathbf{u}} \in {{E}^{m}}. \hfill \\ \end{gathered} $Для метода (2.1) характеристики (1.3) седловой точки запишутся в виде
(2.5)
${\mathbf{x}}{\text{*}} = {{P}_{Q}}[{\mathbf{x}}{\text{*}} - \beta {{{\mathbf{A}}}^{{ - 1}}}({\mathbf{x}}{\text{*}})\nabla {{\varphi }_{x}}({\mathbf{x}}{\text{*}},{\mathbf{u}}{\text{*}})],\quad \beta > 0,$(2.6)
${\mathbf{u}}{\text{*}} = {{P}_{U}}[{\mathbf{u}}{\text{*}} + \lambda {{{\mathbf{B}}}^{{ - 1}}}({\mathbf{u}}{\text{*}})\nabla {{\varphi }_{u}}({\mathbf{x}}{\text{*}},{\mathbf{u}}{\text{*}})],\quad \lambda > 0.$Замечание 1. Отметим следующее: 1) везде в этой работе для простоты обозначено $\nabla {{\varphi }_{x}}$ – частный градиент по первому аргументу, а $\nabla {{\varphi }_{u}}$ – по второму; 2) поскольку в (2.1) операторы проекций в исходной метрике, критерии проекций по первой и второй переменным соответственно будут по первой метрике из (1.1) (см. [10, с. 189]):
(В новой метрике из п. 2.1 критериями проекций служат неравенства но здесь мы пользуемся (2.7), ибо в (2.1) проектирование в исходной метрике.)3. ВСПОМОГАТЕЛЬНЫЕ УТВЕРЖДЕНИЯ
Приведем неравенства, дополняющие необходимый для обоснования сходимости и оценки скорости сходимости методов математический аппарат.
3.1. Лемма 1. Если для (2.1) $\forall {{{\mathbf{u}}}^{k}} \in U \in {{E}^{m}}$ выпуклая функция $g({\mathbf{x}}) \in {{C}^{{1,1}}}(Q)$ такова, что
(3.1)
$(\nabla g({\mathbf{x}}{\text{*}}),{\mathbf{z}} - {\mathbf{x}}{\text{*}}) \geqslant 0,\quad {\mathbf{z}} \in Q.$Доказательство. Из (2.1) и критерия (2.7) проекции ${\mathbf{w}} = {{P}_{Q}}({\mathbf{v}})$, ${\mathbf{v}} \in {{E}^{n}}$, следует,
(3.2)
$\beta ({{{\mathbf{A}}}^{{ - 1}}}({\mathbf{v}})\nabla {{\varphi }_{x}}({\mathbf{v}},{{{\mathbf{u}}}^{k}}),{\mathbf{z}} - {\mathbf{v}}) = \beta (\nabla g({\mathbf{v}}),{\mathbf{z}} - {\mathbf{v}}) \geqslant 0,\quad \beta > 0.$3.2. Лемма 2. Если для (2.1) $\forall {{{\mathbf{x}}}^{k}} \in Q \subset {{E}^{n}}$ вогнутая функция $h\left( {\mathbf{u}} \right) \in {{C}^{{1,1}}}(U)$ такова, что
(3.3)
$(\nabla h\left( {{\mathbf{u}}{\text{*}}} \right),{\mathbf{u}}{\text{*}} - {\mathbf{w}}) \geqslant 0,\quad {\mathbf{w}} \in U.$Доказательство. Из (2.1) и критерия (2.7) проекции ${\mathbf{w}} = {{P}_{U}}({\mathbf{u}})$, ${\mathbf{u}} \in {{E}^{m}}$, имеем,
(3.4)
$ - \lambda ({{{\mathbf{B}}}^{{ - 1}}}({\mathbf{u}})\nabla {{\varphi }_{u}}({{{\mathbf{x}}}^{k}},{\mathbf{u}}),{\mathbf{w}} - {\mathbf{u}}) = \lambda \left( {\nabla h({\mathbf{u}}),{\mathbf{u}} - {\mathbf{w}})} \right) \geqslant 0,\quad \lambda > 0,\quad {\mathbf{w}} \in U.$3.3. Лемма 3. Для всякой тройки точек ${\mathbf{v}},{\mathbf{u}},{\mathbf{x}} \in {{E}^{n}}$ (или ${\mathbf{v}},{\mathbf{u}},{\mathbf{x}} \in {{E}^{m}}$)
(3.5a)
${{\left\| {{\mathbf{u}} - {\mathbf{v}}} \right\|}^{2}} \geqslant (\varepsilon - 1){{\left\| {{\mathbf{u}} - {\mathbf{x}}} \right\|}^{2}} - (1 - {{\varepsilon }^{{ - 1}}}){{\left\| {{\mathbf{v}} - {\mathbf{x}}} \right\|}^{2}},$Доказательство леммы 3 приведено в работе [7].
3.4.
Замечание 2. Верхняя и нижняя границы числа $\varepsilon > 0$ в (3.5а) зависят от соотношений длин сторон треугольника с вершинами ${\mathbf{v}},\;{\mathbf{u}},\;{\mathbf{x}}$; случай их расположения на одной прямой возможен. Пример не обременительных ограничений, при которых допустимы конкретные значения $\varepsilon > 0$ в доказательствах теорем:
(3.6)
$\left\| {0.5({\mathbf{v}} - {\mathbf{x}})} \right\| \leqslant \left\| {{\mathbf{u}} - {\mathbf{x}}} \right\| \leqslant \left\| {{\mathbf{u}} - {\mathbf{v}}} \right\|.$3.5. Лемма 4. Для всякой тройки точек ${\mathbf{u}},{\mathbf{v}},{\mathbf{w}} \in {{E}^{n}}$ (или ${\mathbf{u}},{\mathbf{v}},{\mathbf{w}} \in {{E}^{m}}$)
(3.7)
$\begin{gathered} (1 - \varepsilon ){{\left\| {{\mathbf{u}} - {\mathbf{v}}} \right\|}^{2}} + (1 - {{\varepsilon }^{{ - 1}}}){{\left\| {{\mathbf{w}} - {\mathbf{v}}} \right\|}^{2}} \leqslant {{\left\| {{\mathbf{u}} - {\mathbf{w}}} \right\|}^{2}} \leqslant \\ \leqslant \;(1 + \varepsilon ){{\left\| {{\mathbf{u}} - {\mathbf{v}}} \right\|}^{2}} + (1 + {{\varepsilon }^{{ - 1}}}){{\left\| {{\mathbf{v}} - {\mathbf{w}}} \right\|}^{2}},\quad \varepsilon > 0,\quad {\mathbf{u}},{\mathbf{v}},{\mathbf{w}} \in {{H}_{1}}. \\ \end{gathered} $Доказательство приведено в работе [7].
4. ОБОСНОВАНИЕ СХОДИМОСТИ МЕТОДА
Теорема 1. Пусть выполнены: предположения а)–г) из п. 1 о задаче (1.1) и функции $\varphi ({\mathbf{x}},{\mathbf{u}})$, неравенства (2.2)–(2.4), а параметры константы метода (2.1) таковы, что
(4.1)
$0 < \alpha < 1{\text{/}}4,\quad 0 < \beta < (3 - 8\alpha )m{\text{/}}(6L),\quad 0 < \lambda < 2m(3 - 8\alpha ){\text{/}}(3{{L}^{0}}) < 2m{\text{/}}{{L}^{0}}.$Тогда найдется седловая точка $\left( {{\mathbf{x}}{\text{*}},{\mathbf{u}}{\text{*}}} \right) \in {{Q}_{*}} \times U{\text{*}}$ функции $\varphi ({\mathbf{x}},{\mathbf{u}})$ такая, что процесс (2.1), (4.1) по норме пространства ${{E}^{n}} \times {{E}^{m}}$ к ней сходится, т.е. ${{{\mathbf{x}}}^{k}} \to {\mathbf{x}}{\text{*}} \in {{Q}_{*}}$, ${{{\mathbf{u}}}^{k}} \to {\mathbf{u}}{\text{*}} \in U{\text{*}}$ при $k \to \infty $ для всех $({{{\mathbf{x}}}^{0}},{{{\mathbf{u}}}^{0}}) \in {{E}^{{n + m}}}$.
Доказательство. Представим каждое уравнение из (2.1), пользуясь (2.7), в виде вариационного неравенства, тогда этот итерационный процесс запишется в виде
(4.2)
$({{{\mathbf{z}}}^{k}} - {{{\mathbf{x}}}^{k}} - {{\alpha }_{k}}{{{\mathbf{y}}}^{k}},{\mathbf{v}} - {{{\mathbf{z}}}^{k}}) \geqslant 0,\quad {\mathbf{v}} \in Q,$(4.3)
$({{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{z}}}^{k}} + {{\beta }_{k}}A_{k}^{{ - 1}}\nabla {{\varphi }_{x}}({{{\mathbf{z}}}^{k}},{{{\mathbf{u}}}^{k}}),{\mathbf{v}} - {{{\mathbf{x}}}^{{k + 1}}}) \geqslant 0,$(4.4)
$({{{\mathbf{w}}}^{k}} - {{{\mathbf{u}}}^{k}} - {{\alpha }_{k}}{{{\mathbf{v}}}^{k}},{\mathbf{u}} - {{{\mathbf{w}}}^{k}}) \geqslant 0,\quad {\mathbf{u}} \in U,$(4.5)
$({{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{w}}}^{k}} - {{\lambda }_{k}}{\mathbf{B}}_{k}^{{ - 1}}\nabla {{\varphi }_{u}}({{{\mathbf{x}}}^{{k + 1}}},{{{\mathbf{w}}}^{k}}),{\mathbf{u}} - {{{\mathbf{u}}}^{{k + 1}}}) \geqslant 0$Здесь сначала преобразуем первое и второе неравенства, пользуясь свойствами скалярного произведения, (2.1), неравенством Коши–Буняковского и нерасширяющим свойством оператора проектирования ([10, с. 190]). Положив ${\mathbf{v}} = {{{\mathbf{x}}}^{k}}$, из (4.2) имеем
(4.6)
$\begin{gathered} ({{{\mathbf{z}}}^{k}} - {{{\mathbf{x}}}^{k}} - \alpha {{{\mathbf{y}}}^{k}},{{{\mathbf{x}}}^{k}} - {{{\mathbf{z}}}^{k}}) \geqslant 0,\quad {\text{или}}\quad {{\left\| {{{{\mathbf{z}}}^{k}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} \leqslant \alpha ({{{\mathbf{y}}}^{k}},{{{\mathbf{z}}}^{k}} - {{{\mathbf{x}}}^{k}}) \leqslant \alpha \left\| {{{{\mathbf{y}}}^{k}}} \right\| \cdot \left\| {{{{\mathbf{z}}}^{k}} - {{{\mathbf{x}}}^{k}}} \right\| = \\ = \;\alpha \left\| {{{{\mathbf{y}}}^{k}}} \right\| \cdot \left\| {{{P}_{Q}}({{{\mathbf{x}}}^{k}} + \alpha {{{\mathbf{y}}}^{k}}) - {{P}_{Q}}({{{\mathbf{x}}}^{k}})} \right\| \leqslant {{\alpha }^{2}}{{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}}. \\ \end{gathered} $Положив ${\mathbf{v}} = {\mathbf{x}}{\text{*}}$, из (4.3) получим неравенство
(4.7)
$({{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{z}}}^{k}},{\mathbf{x}}{\text{*}} - {{{\mathbf{x}}}^{{k + 1}}}) + \beta (A_{k}^{{ - 1}}\nabla {{\varphi }_{x}}({{{\mathbf{z}}}^{k}},{{{\mathbf{u}}}^{k}}),{\mathbf{x}}{\text{*}} - {{{\mathbf{x}}}^{{k + 1}}}) \geqslant 0,$(4.8)
${{\left\| {{\mathbf{u}} - {\mathbf{w}}} \right\|}^{2}} = {{\left\| {{\mathbf{u}} - {\mathbf{v}}} \right\|}^{2}} + 2({\mathbf{u}} - {\mathbf{v}},{\mathbf{v}} - {\mathbf{w}}) + {{\left\| {{\mathbf{v}} - {\mathbf{w}}} \right\|}^{2}}\quad \forall {\mathbf{u}},{\mathbf{v}},{\mathbf{w}} \in {{E}^{n}},$(4.9)
${{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{z}}}^{k}}} \right\|}^{2}} - {{\left\| {{{{\mathbf{z}}}^{k}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} \leqslant 2\beta ({\mathbf{A}}_{k}^{{ - 1}}\nabla {{\varphi }_{x}}({{{\mathbf{z}}}^{k}},{{{\mathbf{u}}}^{k}}),{\mathbf{x}}{\text{*}} - {{{\mathbf{x}}}^{{k + 1}}}),\quad k \geqslant 1.$В (4.9) сначала преобразуем третье слагаемое в левой части с помощью нерасширяющего свойства оператора проектирования ([10, с. 190]):
(4.10)
$\begin{gathered} {{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{z}}}^{k}}} \right\|}^{2}} - (1 + \alpha ){{\left\| {{{{\mathbf{x}}}^{k}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} - ({{\alpha }^{2}} + \alpha ){{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}} + \\ \, + \alpha {{\left\| {{{{\mathbf{x}}}^{{k - 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} \leqslant 2\beta ({\mathbf{A}}_{k}^{{ - 1}}\nabla {{\varphi }_{x}}({{{\mathbf{z}}}^{k}},{{{\mathbf{u}}}^{k}}),{\mathbf{x}}{\text{*}} - {{{\mathbf{x}}}^{{k + 1}}}),\quad k \geqslant 1. \\ \end{gathered} $В (4.10) оценим скалярное произведение в правой части. Воспользуемся леммой 1 при $g({\mathbf{x}}) = f({\mathbf{x}})$ $\forall {\mathbf{x}} \in {{E}^{n}}$ , ${\mathbf{x}} = {{{\mathbf{z}}}^{k}}$. Представив скалярное произведение в виде суммы, прибавим к слагаемым правое неравенство (3.2), умноженное на два, соответственно при ${\mathbf{v}} = {\mathbf{x}}{\text{*}}$, ${\mathbf{z}} = {{{\mathbf{x}}}^{k}}$ и ${\mathbf{v}} = {{{\mathbf{x}}}^{k}}$, ${\mathbf{z}} = {{{\mathbf{x}}}^{{k + 1}}}$, затем преобразуем с учетом (1.2), (2.1), (2.2), (2.4), (2.5), (3.1), неравенства Коши–Буняковского, правого (3.7) при $\varepsilon = 2$
(4.11)
$\begin{gathered} (\nabla f({{{\mathbf{z}}}^{k}}) - \nabla f({\mathbf{v}}),{\mathbf{v}} - {{{\mathbf{x}}}^{{k + 1}}}) \leqslant K{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{z}}}^{k}}} \right\|}^{2}},\quad {\mathbf{v}},{{{\mathbf{x}}}^{{k + 1}}},{{{\mathbf{z}}}^{k}} \in Q\quad (K\;{\text{из}}\;{\text{леммы}}\;1): \\ 2\beta ({\mathbf{A}}_{k}^{{ - 1}}\nabla {{\varphi }_{x}}({{{\mathbf{z}}}^{k}},{{{\mathbf{u}}}^{k}}),{\mathbf{x}}{\text{*}} - {{{\mathbf{x}}}^{{k + 1}}}) = 2\beta (\nabla f({{{\mathbf{z}}}^{k}}),{\mathbf{x}}{\text{*}} - {{{\mathbf{x}}}^{{k + 1}}}) = 2\beta (\nabla f({{{\mathbf{z}}}^{k}}) - \nabla f({\mathbf{x}}{\text{*}}),{\mathbf{x}}{\text{*}} - {{{\mathbf{x}}}^{k}}) + \\ \, + 2\beta (\nabla f({{{\mathbf{z}}}^{k}}) - \nabla f({{{\mathbf{x}}}^{k}}),{{{\mathbf{x}}}^{k}} - {{{\mathbf{x}}}^{{k + 1}}}) \leqslant \tfrac{{L\beta }}{m}{{\left\| {{{{\mathbf{z}}}^{k}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} + \tfrac{{L\beta }}{m}{{\left\| {{{{\mathbf{z}}}^{k}} - {{{\mathbf{x}}}^{{k + 1}}}} \right\|}^{2}} \leqslant \tfrac{{4L\beta }}{m}{{\left\| {{{{\mathbf{z}}}^{k}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} + \\ \, + \tfrac{{3L\beta }}{{2m}}{{\left\| {{{{\mathbf{x}}}^{k}} - {{{\mathbf{x}}}^{{k + 1}}}} \right\|}^{2}} \leqslant \tfrac{{4L{{\alpha }^{2}}\beta }}{m}{{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}} + \tfrac{{3L\beta }}{{2m}}{{\left\| {{{{\mathbf{x}}}^{k}} - {{{\mathbf{x}}}^{{k + 1}}}} \right\|}^{2}}. \\ \end{gathered} $Второе слагаемое в левой части (4.10) оценим с помощью левого неравенства (3.7) при $\varepsilon = 1{\text{/}}4$, ${\mathbf{v}} = {{{\mathbf{z}}}^{k}}$, ${\mathbf{u}} = {{{\mathbf{x}}}^{{k + 1}}}$, ${\mathbf{w}} = {{{\mathbf{x}}}^{k}}$, затем учтем (4.6):
(4.12)
${{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{z}}}^{k}}} \right\|}^{2}} \geqslant \tfrac{3}{4}{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} - 3{{\left\| {{{{\mathbf{x}}}^{k}} - {{{\mathbf{z}}}^{k}}} \right\|}^{2}} \geqslant \tfrac{3}{4}{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} - 3{{\alpha }^{2}}{{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}}.$(4.13)
${{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{a}_{1}}{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} + \alpha {{\left\| {{{{\mathbf{x}}}^{{k - 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} \leqslant (1 + \alpha ){{\left\| {{\mathbf{x}}{\text{*}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} + {{a}_{2}}{{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}},\quad k \geqslant 1,$Теперь преобразуем (4.4) с помощью нерасширяющего свойства оператора проектирования ([10, с. 190]). При ${\mathbf{u}} = {{{\mathbf{u}}}^{k}}$ из (4.4) следует
(4.14)
$\begin{gathered} {{\left\| {{{{\mathbf{w}}}^{k}} - {{{\mathbf{u}}}^{k}}} \right\|}^{2}} \leqslant \alpha ({{{\mathbf{v}}}^{k}},{{{\mathbf{w}}}^{k}} - {{{\mathbf{u}}}^{k}}) \leqslant \alpha \left\| {{{{\mathbf{v}}}^{k}}} \right\| \cdot \left\| {{{{\mathbf{w}}}^{k}} - {{{\mathbf{u}}}^{k}}} \right\|, \\ \left\| {{{{\mathbf{w}}}^{k}} - {{{\mathbf{u}}}^{k}}} \right\| = \left\| {{{P}_{Q}}({{{\mathbf{u}}}^{k}} + \alpha {{{\mathbf{v}}}^{k}}) - {{P}_{Q}}({{{\mathbf{u}}}^{k}})} \right\| \leqslant \alpha \left\| {{{{\mathbf{v}}}^{k}}} \right\|, \\ {{\left\| {{{{\mathbf{w}}}^{k}} - {{{\mathbf{u}}}^{k}}} \right\|}^{2}} \leqslant {{\alpha }^{2}}{{\left\| {{{{\mathbf{v}}}^{k}}} \right\|}^{2}}. \\ \end{gathered} $Из (4.5) при ${\mathbf{u}} = {\mathbf{u}}{\text{*}}$ имеем
(4.15)
$({{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{w}}}^{k}}{\mathbf{,}}{{{\mathbf{u}}}^{{k + 1}}} - {\mathbf{u}}{\text{*}}) \leqslant \lambda ({\mathbf{B}}_{k}^{{ - 1}}\nabla {{\varphi }_{u}}({{{\mathbf{x}}}^{{k + 1}}},{{{\mathbf{w}}}^{k}}),{{{\mathbf{u}}}^{{k + 1}}} - {\mathbf{u}}{\text{*}}).$(4.16)
$\lambda (\nabla g({{{\mathbf{w}}}^{k}}),{{{\mathbf{u}}}^{{k + 1}}} - {\mathbf{u}}{\text{*}}) \leqslant \lambda \frac{R}{2}{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{w}}}^{k}}} \right\|}^{2}} = \frac{{{{L}^{0}}\lambda }}{{4m}}{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{w}}}^{k}}} \right\|}^{2}}.$В (4.15) первое скалярное произведение преобразуем с помощью тождества (4.8):
(4.17)
${{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + \left( {1 - \frac{{{{L}^{0}}\lambda }}{{2m}}} \right){{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{w}}}^{k}}} \right\|}^{2}} - {{\left\| {{{{\mathbf{w}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} \leqslant 0.$В (4.17) воспользуемся нерасширяющим свойством оператора проектирования:
(4.18)
${{\left\| {{{{\mathbf{w}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} \leqslant (1 + \alpha ){{\left\| {{{{\mathbf{u}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + (\alpha + {{\alpha }^{2}}){{\left\| {{{{\mathbf{v}}}^{k}}} \right\|}^{2}} - \alpha {{\left\| {{{{\mathbf{u}}}^{{k - 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}}.$(4.19)
${{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + {{a}_{5}}{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{u}}}^{k}}} \right\|}^{2}} + \alpha {{\left\| {{{{\mathbf{u}}}^{{k - 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} \leqslant (1 + \alpha ){{\left\| {{{{\mathbf{u}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + {{a}_{6}}{{\left\| {{{{\mathbf{v}}}^{k}}} \right\|}^{2}},\quad k \geqslant 1,$Сложив неравенства (4.13) и (4.19), получим
(4.20)
$\begin{gathered} {{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + {{a}_{1}}{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} + {{a}_{5}}{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{u}}}^{k}}} \right\|}^{2}} + \alpha {{\left\| {{{{\mathbf{x}}}^{{k - 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + \alpha {{\left\| {{{{\mathbf{u}}}^{{k - 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} \leqslant \\ \, \leqslant (1 + \alpha )\left( {{{{\left\| {{{{\mathbf{x}}}^{k}} - {\mathbf{x}}{\text{*}}} \right\|}}^{2}}} \right. + \left. {{{{\left\| {{{{\mathbf{u}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}}^{2}}} \right) + {{a}_{2}}{{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}} + {{a}_{6}}{{\left\| {{{{\mathbf{v}}}^{k}}} \right\|}^{2}},\quad k \geqslant 1. \\ \end{gathered} $Просуммируем (4.20) от $k = 1$ до $k = m$, $m \geqslant 1$, тогда
(4.21)
$\begin{gathered} \alpha {{\left\| {{{{\mathbf{x}}}^{0}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + \alpha {{\left\| {{{{\mathbf{u}}}^{0}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + {{\left\| {{{{\mathbf{x}}}^{{m + 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{a}_{1}}{{\left\| {{{{\mathbf{x}}}^{{m + 1}}} - {{{\mathbf{x}}}^{m}}} \right\|}^{2}} + {{\left\| {{{{\mathbf{u}}}^{{m + 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + {{a}_{5}}{{\left\| {{{{\mathbf{u}}}^{{m + 1}}} - {{{\mathbf{u}}}^{m}}} \right\|}^{2}} + \\ \, + \sum\limits_{k = 1}^{k = m - 1} {\left[ {({{a}_{1}} - {{a}_{2}}){{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}}^{2}} + ({{a}_{5}} - {{a}_{6}}){{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{u}}}^{k}}} \right\|}}^{2}}} \right]} \leqslant {{a}_{2}}{{\left\| {{{{\mathbf{x}}}^{1}} - {{{\mathbf{x}}}^{0}}} \right\|}^{2}} + {{a}_{6}}{{\left\| {{{{\mathbf{u}}}^{1}} - {{{\mathbf{u}}}^{0}}} \right\|}^{2}} + \\ \, + {{\left\| {{{{\mathbf{x}}}^{1}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{\left\| {{{{\mathbf{u}}}^{1}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + \alpha {{\left\| {{{{\mathbf{x}}}^{m}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + \alpha {{\left\| {{{{\mathbf{u}}}^{m}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}}, \\ \end{gathered} $(4.22)
$\begin{gathered} (1 - 2\alpha ){{\left\| {{{{\mathbf{x}}}^{{m + 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + (1 - 2\alpha ){{\left\| {{{{\mathbf{u}}}^{{m + 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + \sum\limits_{k = 1}^{k = m} {\left[ {({{a}_{1}} - 2\alpha ){{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}}^{2}} + ({{a}_{5}} - 2\alpha ){{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{u}}}^{k}}} \right\|}}^{2}}} \right]} \leqslant \\ \, \leqslant {{a}_{3}}{{\left\| {{{{\mathbf{x}}}^{0}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{a}_{7}}{{\left\| {{{{\mathbf{u}}}^{0}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + {{a}_{4}}{{\left\| {{{{\mathbf{x}}}^{1}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{a}_{8}}{{\left\| {{{{\mathbf{u}}}^{1}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}}, \\ \end{gathered} $Из (4.22) при $m \to \infty $ следует сходимость ряда
(4.23)
$\begin{gathered} \{ {{{\mathbf{x}}}^{{{{k}_{i}}}}};{{{\mathbf{u}}}^{{{{k}_{i}}}}}\} \to ({\mathbf{x}}{\text{*}};{\mathbf{u}}{\text{*}}),\quad {{k}_{i}} \to \infty \quad {\text{и}}\quad \left\| {{{{\mathbf{x}}}^{{{{k}_{i}}}}} - {\mathbf{x}}{\text{*}}} \right\| + \left\| {{{{\mathbf{u}}}^{{{{k}_{i}}}}} - {\mathbf{u}}{\text{*}}} \right\| \to 0,\quad {{k}_{i}} \to \infty , \\ \left\| {{{{\mathbf{x}}}^{{{{k}_{i}}}}} - {{{\mathbf{x}}}^{{{{k}_{i}} - 1}}}} \right\| + \left\| {{{{\mathbf{u}}}^{{{{k}_{i}}}}} - {{{\mathbf{u}}}^{{{{k}_{i}} - 1}}}} \right\| \to 0,\quad {{k}_{i}} \to \infty . \\ \end{gathered} $Тогда при $k \to \infty $ из второго и четвертого уравнений (2.1) следуют (2.5), (2.6), эквивалентные характеристике (1.3) седловой точки в терминах оператора проектирования; следовательно, $\left( {{\mathbf{x}}{\text{*}};{\mathbf{u}}{\text{*}}} \right)$ – седловая точка функции $\varphi ({\mathbf{x}},{\mathbf{u}})$, т.е. решение задачи (1.1).
Положим  ,
,  , выберем $\forall \varepsilon > 0$ и числа ${{k}_{{{{i}_{0}}}}} = r$ и $m > r$ так, чтобы выполнялись неравенства
, выберем $\forall \varepsilon > 0$ и числа ${{k}_{{{{i}_{0}}}}} = r$ и $m > r$ так, чтобы выполнялись неравенства
Просуммируем (4.20) от $k = m$ до $k = N$ при  ,
,  , $N > m > r$:
, $N > m > r$:
С учетом этих оценок и неравенств $1 - 2\alpha > 0$, $0 < {{a}_{1}} - 2\alpha < {{a}_{1}} - {{a}_{2}}$, $0 < {{a}_{5}} - 2\alpha < {{a}_{5}} - {{a}_{6}}$, верных при условиях (4.1), из (4.25) получим
Отсюда с учетом (4.23), (4.24), рассуждений и выкладок после (4.21), следует Из этого неравенства и предыдущих рассуждений следует, что вся последовательность $\{ {{{\mathbf{x}}}^{k}};{{{\mathbf{u}}}^{k}}\} $ из любой начальной точки сходится к седловой точке задачи (1.1), , $k \to \infty $, ибо пространство ${{E}^{{n + m}}}$ полное, неравенства (4.24) выполняются для седловой точки $\left( {{\mathbf{x}}{\text{*}};{\mathbf{u}}{\text{*}}} \right) \in {{Q}_{*}} \times U{\text{*}}$ и последовательность $\left\{ {{{{\left\| {{{{\mathbf{x}}}^{k}} - {\mathbf{x}}{\text{*}}} \right\|}}^{2}} + {{{\left\| {{{{\mathbf{u}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}}^{2}}} \right\}$ монотонна и ограничена.
, $k \to \infty $, ибо пространство ${{E}^{{n + m}}}$ полное, неравенства (4.24) выполняются для седловой точки $\left( {{\mathbf{x}}{\text{*}};{\mathbf{u}}{\text{*}}} \right) \in {{Q}_{*}} \times U{\text{*}}$ и последовательность $\left\{ {{{{\left\| {{{{\mathbf{x}}}^{k}} - {\mathbf{x}}{\text{*}}} \right\|}}^{2}} + {{{\left\| {{{{\mathbf{u}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}}^{2}}} \right\}$ монотонна и ограничена.
Теорема 1 доказана.
Следствие. Поскольку по теореме 1 (расстояние до точки минимума монотонно убывает) последовательность $\{ {{{\mathbf{x}}}^{k}};{{{\mathbf{u}}}^{k}}\} $ сходится монотонно, то имеют место неравенства
5. ОЦЕНКА СКОРОСТИ СХОДИМОСТИ МЕТОДА
Получим оценку скорости сходимости метода (2.1), (4.1) для выпукло-вогнутой функции.
Теорема 2. Пусть выполнены все условия теоремы 1, включая (4.1) и, кроме того:
1) выполнены неравенства (3.6); 2) параметры метода и функции таковы:
(5.1)
$\begin{gathered} 0 < \alpha < (\sqrt 3 - 1){\text{/}}4 \cong 0.18;\quad 0 < 16m\alpha + 48L\beta < 6m + 9{{L}^{0}}\lambda ; \\ 0 < \beta < (1 - 4\alpha - 8{{\alpha }^{2}})m{\text{/}}[2L(1 + 4{{\alpha }^{2}})],\quad 0 < \lambda < 2m(1 - 4\alpha - 8{{\alpha }^{2}}){\text{/}}[{{L}^{0}}(1 - 6{{\alpha }^{2}})]. \\ \end{gathered} $Тогда последовательность $\{ {{{\mathbf{x}}}^{k}};{{{\mathbf{u}}}^{k}}\} $ метода (2.1), (4.1) сходится к некоторой седловой точке $\left( {{\mathbf{x}}{\text{*}};{\mathbf{u}}{\text{*}}} \right) \in {{Q}_{*}} \times U{\text{*}}$ задачи (1.1) со скоростью геометрической прогрессии с оценкой
(5.2)
$\rho ({{{\mathbf{x}}}^{k}},{{{\mathbf{u}}}^{k}}) \leqslant {{q}^{k}}\rho ({{{\mathbf{x}}}^{0}},{{{\mathbf{u}}}^{0}}),\quad k \geqslant 1,$Доказательство. Заметим, что в условиях теоремы 4 неравенство (4.20) справедливо. Преобразуем его для получения оценки (5.2). Пятое и шестое слагаемые в (4.20) оценим с помощью левого неравенства (3.7); при ${\mathbf{u}} = {{{\mathbf{x}}}^{{k - 1}}}$, ${\mathbf{v}} = {\mathbf{x}}{\text{*}}$, ${\mathbf{w}} = {\mathbf{x}}{\text{*}}$, $\varepsilon = 2$ и ${\mathbf{u}} = {{{\mathbf{u}}}^{{k - 1}}}$, ${\mathbf{v}} = {{{\mathbf{u}}}^{k}}$, ${\mathbf{w}} = {\mathbf{u}}{\text{*}}$, $\varepsilon = 2$ соответственно получим два неравенства:
(5.3)
${{\left\| {{{{\mathbf{x}}}^{{k - 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} \geqslant - {{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}} + 0.5{{\left\| {{{{\mathbf{x}}}^{k}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}},\quad {{\left\| {{{{\mathbf{u}}}^{{k - 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} \geqslant - {{\left\| {{{{\mathbf{v}}}^{k}}} \right\|}^{2}} + 0.5{{\left\| {{{{\mathbf{u}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}}.$Аналогично для оценки частей третьего и четвертого слагаемых в левой части (4.20) из (3.5) при ${\mathbf{u}} = {{{\mathbf{x}}}^{{k + 1}}}$, ${\mathbf{x}} = {\mathbf{x}}{\text{*}}$, ${\mathbf{v}} = {{{\mathbf{x}}}^{k}}$, $\varepsilon = 4$ и ${\mathbf{u}} = {{{\mathbf{u}}}^{{k + 1}}}$, ${\mathbf{x}} = {\mathbf{u}}{\text{*}}$, ${\mathbf{v}} = {{{\mathbf{u}}}^{k}}$, $\varepsilon = 4$ соответственно получим два неравенства
(5.4)
$\begin{gathered} \frac{1}{3}{{a}_{1}}{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} \geqslant {{a}_{1}}{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} - \frac{3}{4}{{a}_{1}}{{\left\| {{{{\mathbf{x}}}^{k}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}}, \\ \frac{1}{3}{{a}_{5}}{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{u}}}^{k}}} \right\|}^{2}} \geqslant {{a}_{5}}{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} - \frac{3}{4}{{a}_{5}}{{\left\| {{{{\mathbf{u}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}}. \\ \end{gathered} $После подстановки оценок (5.3), (5.4) в (4.20), придем к неравенству
(5.5)
$\begin{gathered} (1 + {{a}_{1}}){{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + (1 + {{a}_{5}}){{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + 2{{a}_{1}}{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}}{\text{/}}3 + 2{{a}_{5}}{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{u}}}^{k}}} \right\|}^{2}}{\text{/}}3 \leqslant \\ \, \leqslant {{a}_{{23}}}{{\left\| {{{{\mathbf{x}}}^{k}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{b}_{{23}}}{{\left\| {{{{\mathbf{u}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} + {{a}_{{24}}}{{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}} + {{b}_{{24}}}{{\left\| {{{{\mathbf{v}}}^{k}}} \right\|}^{2}},\quad k \geqslant 1, \\ \end{gathered} $Далее покажем, что
(5.6)
${{a}_{{24}}}{{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}} - \frac{2}{3}{{a}_{1}}{{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}} \leqslant 0,\quad {{b}_{{24}}}{{\left\| {{{{\mathbf{v}}}^{k}}} \right\|}^{2}} - \frac{2}{3}{{a}_{5}}{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{u}}}^{k}}} \right\|}^{2}} \leqslant 0.$(5.7)
${{\left\| {{{{\mathbf{y}}}^{k}}} \right\|}^{2}} \geqslant {{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {{{\mathbf{x}}}^{k}}} \right\|}^{2}},\quad {{\left\| {{{{\mathbf{v}}}^{k}}} \right\|}^{2}} \geqslant {{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{u}}}^{k}}} \right\|}^{2}}.$В силу второго неравенства (5.7) и ${{b}_{{24}}} - 2{{a}_{5}}{\text{/}}3 \leqslant 0$ (при $0 < \alpha < \tfrac{{\sqrt 3 - 1}}{4} \cong 0.18$, $0 < \lambda < 2m(1 - 4\alpha - 8{{\alpha }^{2}}){\text{/}}[{{L}^{0}}(1 - 6{{\alpha }^{2}})]$), $\left( {{{b}_{{24}}} - 2{{a}_{5}}{\text{/}}3} \right)\left( {{{{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {{{\mathbf{u}}}^{k}}} \right\|}}^{2}} - {{{\left\| {{{{\mathbf{v}}}^{k}}} \right\|}}^{2}}} \right) \geqslant 0$, $2{{a}_{5}}{\text{/}}3 \geqslant {{b}_{{24}}} - 2{{a}_{5}}{\text{/}}3$, получим вторую оценку из (5.6):
Подставим оценки (5.6) в (5.5), тогда получим
(5.8)
$(1 + {{a}_{1}}){{\left\| {{{{\mathbf{x}}}^{{k + 1}}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + (1 + {{a}_{5}}){{\left\| {{{{\mathbf{u}}}^{{k + 1}}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}} \leqslant {{a}_{{23}}}{{\left\| {{{{\mathbf{x}}}^{k}} - {\mathbf{x}}{\text{*}}} \right\|}^{2}} + {{b}_{{23}}}{{\left\| {{{{\mathbf{u}}}^{k}} - {\mathbf{u}}{\text{*}}} \right\|}^{2}},\quad k \geqslant 1.$Учитывая, что ${{a}_{1}} < {{a}_{5}}$, ${{a}_{{23}}} < {{b}_{{23}}}$ при ${{L}^{0}}\lambda < 4L\beta $, в обозначении п. 1 из (5.8) получаем
(5.9)
$\rho ({{{\mathbf{x}}}^{{k + 1}}},{{{\mathbf{u}}}^{{k + 1}}}) \leqslant q\rho ({{{\mathbf{x}}}^{k}},{{{\mathbf{u}}}^{k}}) \leqslant ... \leqslant {{q}^{{k + 1}}}\rho ({{{\mathbf{x}}}^{0}},{{{\mathbf{u}}}^{0}}),$Теорема 2 доказана.
Замечание 3. Исследованный в данной статье проекционный экстраградиентный двухточечный метод (2.1) с переменной метрикой, для решения седловых задач, продолжает на итеративные проекционные методы идею использования операторов переменной метрики, впервые воплощенную в непрерывных проекционных методах минимизации [13].
Метод (2.1) обладает преимуществами, присущими двум классам методов решения оптимизационных задач: многоточечным методам и методам переменной метрики. Он является длинношаговым скоростным методом как многошаговые методы и не теряет скорость сходимости в окрестности седловой точки как квазиньютоновский метод. Нельзя переоценить и неравенство (3.5) в обосновании метода.
Замечание 4. Кратко рассмотрим другие методы по работам [14]–[28]. Прежде всего заметим, что задача (1.1) с помощью нормализованной функции вида $\Phi ({\mathbf{v}},{\mathbf{w}}) = \varphi ({\mathbf{z}},{\mathbf{u}}) - \varphi ({\mathbf{x}},{\mathbf{y}})$, где ${\mathbf{w}} = ({\mathbf{z}},{\mathbf{y}}),$ ${\mathbf{v}} = ({\mathbf{x}},{\mathbf{u}})$, преобразуется в задачу вычисления неподвижной точки экстремального включения
(7.1)
${\mathbf{v}}{\text{*}} = {\text{Arg}}\min \{ \Phi ({\mathbf{v}}{\text{*}},{\mathbf{w}})\,{\text{|}}\,{\mathbf{w}} \in \Omega \} ,\quad {\mathbf{v}} \in \Omega = Q \times U,$Кроме выше отмеченных, имеются работы, так или иначе связанные с использованием или построением методов решения седловых задач, для недифференцируемых и дифференцируемых функций. Из них неградиентные методы решения седловых задач рассматривались в работе [14]. В работе [15] описан субградиентный алгоритм для решения обобщенной равновесной задачи, частные случаи которой возникают в теории игр, при решении вариационных неравенств, в оптимизационных задачах. Метод решения негладких равновесных задач предложен в [23].
В работах [16], [17] предложены непрерывные проекционные экстраградиентные методы переменной метрики для решения задач равновесного программирования. Доказана сходимость методов. Идея построения непрерывных седловых и равновесных методов переменной метрики восходит к работе [13].
В работах [18]–[23] в целом предложены и исследованы итеративные методы решения задач, приводящих для своего решения к использованию имеющегося или к построению нового метода, для седловой задачи или вычисления неподвижной точки экстремального отображения. Из них в работах [18]–[20] предложены и исследованы двухточечные методы решения седловых задач. Оценки скорости сходимости методов получены в [19] и [20].
В работах [21]–[23] предложены методы типа проекции градиента для решения равновесных задач, из которых в [21] и [22] доказана сходимость методов.
В работах [24]–[28] предложены и исследованы методы решения задач оптимального управления (ЗОУ) сведением к задаче равновесного программирования, последняя решается с помощью экстраградиентных методов. Заслуживают внимания алгоритмы решения задач в них, идею одной из которых опишем для [24].
В работе [24] для ЗОУ со свободным правым концом на фиксированном промежутке времени записывается функция Лагранжа, седловая точка которой является решением исходной задачи. Седловая система неравенств для функции Лагранжа сводится к системе дифференциальных уравнений и одного вариационного неравенства. Последняя решается экстраградиентным методом на основе подхода из работы [21]. Доказана сходимость метода. Предложенный подход отличается тем, что на каждой итерации не решаются дифференциальные уравнения, а только вычисляются невязки.
Список литературы
Демьянов В.Ф., Певный А.Б. Численные методы разыскания седловых точек // Ж. вычисл. матем. и матем. физ. 1972. Т. 12. № 5. С. 1099–1127.
Антипин А.С. Об одном методе отыскания седловой точки модифицированной функции Лагранжа // Экономика и матем. методы. 1977. Т. 13. Вып. 3. С. 560–565.
Гольштейн Е.Г. О сходимости градиентного метода отыскания седловых точек модифицированной функции Лагранжа // Экономика и матем. методы. 1977. Т. 13. Вып. 2. С. 322–329.
Корпелевич Г.М. Экстраполяционные градиентные методы и их связь с модифицированными функциями Лагранжа // Экономика и матем. методы. 1983. Т. 19. Вып. 4. С. 694–703.
Антипин А.С. Градиентные и проксимальные управляемые процессы // Вопросы кибернетики. Анализ больших систем. М.: Научный совет по комплексной проблеме “Кибернетика” РАН, 1992. Вып. 178. С. 32–67.
Антипин А.С. Градиентный и экстраградиентный подходы в билинейном и равновесном программировании. М.: Изд-во ВЦ РАН, 2002.
Малинов В.Г. Проекционные обобщенные двухшаговые экстраградиентные методы для решения равновесных задач // Ж. cредневолжского матем. общества. 2012. Т. 14. № 2. С. 87–104.
Малинов В.Г. Четырехпараметрические двухшаговые проекционные методы минимизации // Ж. вычислит. матем. и матем. физики. 1996. Т. 36. № 12. С. 48–56.
Малинов В.Г. Проекционный двухшаговый МПМ и численное решение задачи оптимального управления // Ж. cредневолжского матем. общества. 2012. Т. 14. № 1. С. 83–91.
Васильев Ф.П. Численные методы решения экстремальных задач. М.: Наука, 1988.
Антипин А.С. Методы нелинейного программирования, основанные на прямой и двойственной модификации функции Лагранжа. М.: ВНИИ системных исследований, 1979.
Карманов В.Г. Математическое программирование. М.: Наука, 1986.
Антипин А.С., Васильев Ф.П. О непрерывном методе минимизации в пространствах с переменной метрикой // Известия вузов. Математика. 1995. № 12(403). С. 3–9.
Антипин А.С. О неградиентных методах оптимизации седловых функций // Вопросы кибернетики. № 136. Методы и алгоритмы анализа больших систем. М., 1987. С. 4–13.
Scheimberg S., Santos P.S.M. A subgradient method for an equilibrium problem // VI Moscow International Conference on Operations Research (ORM2010). Moscow, October 19–23, 2010. Proceedings / Eds. P.S. Krasnoschekov, A.A. Vasin – Moscow: MAKS Press, 2010. P. 209–211.
Антипин А.С., Будак Б.А., Васильев Ф.П. Непрерывный экстраградиентный метод первого порядка с переменной метрикой для решения задач равновесного программирования // Вестник МГУ. Сер. 15. Вычисл. матем. и кибернет. 2003. № 1. С. 37–40.
Будак Б.А. Непрерывный экстраградиентный метод второго порядка с переменной метрикой для решения задач равновесного программирования // Вестник МГУ. Сер. 15. Вычисл. матем. и кибернет. 2003. № 2. С. 27–32.
Меленьчук Н.В. Двухшаговый экстраградиентный метод для решения седловых задач // Омский научный вестник. Серия “Приборы, машины, технологии”. 2009. № 3 (83). С. 33–36.
Malinov V.G. Extragradient projection method for saddle-point problems // VI Moscow International Conference on Operations Research (ORM2010). Moscow, October 19–23, 2010. Proceedings / Eds. P.S. Krasnoschekov, A.A. Vasin. Moscow: MAKS Press, 2010. P. 207–209.
Малинов В.Г. Версии двух проекционных двухшаговых методов для решения седловых и других задач // VII Московская международная конференция по исследованию операций (ORM2013). Москва, 15–19 октября 2013 г. Труды. Том 2. С. 25–27.
Антипин А.С. Равновесное программирование: методы градиентного типа // Автоматика и телемехан. 1997. № 8. С. 1337–1347.
Antipin A.S. Iterative gradient projection type methods for computing fixed points of extremal mapping / In book: Parametric optimization and related topics IV. Verlag Peter Lang, 1997. P. 11–24.
Пинягина О.В. Метод решения негладких монотонных равновесных задач // VII Московская международная конференция по исследованию операций (ORM2013). Москва, 19–23 октября 2010 г. Труды. Москва: МАКС Пресс, 2010. С. 248–249.
Хорошилова Е.В., Антипин А.С. Экстраградиентный подход для решения задачи оптимального управления // VI Московская международная конференция (ORM2010). Москва, 19–23 октября 2010. Труды / Отв. ред. П.С. Краснощеков, А.А. Васин. М.: МАКС Пресс, 2010. С. 256–258.
Khoroshilova E.V. Extragradient-type method for optimal control problem with linear constraints and convex objective function // Optim. Lett. 2013. V. 7. № 6. P. 1193–2014.
Antipin A.S., Khoroshilova E.V. Optimal control with connected initial and terminal conditions // Proceedings of the Steklov Institute of Mathematics. 2015. V. 289. № 1. Suppl. P. 9–25.
Antipin A.S., Khoroshilova E.V. Saddle-point approach to solving problem of optimal control with fixed ends // J. Global Optim. 2016. V. 65. № 1. P. 3–17.
Khoroshilova E.V., Antipin A.S. Saddle-point method for solving terminal control problem with state constraints // IX Moscow International Conference on Operations Research (ORM2018). Moscow, October 22–27, 2018. Proceedings. In two volumes / Editor in-chief F. Ereshko. Moscow: MAKS Press, 2018. V. 2. P. 110–113.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики