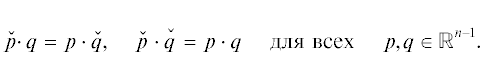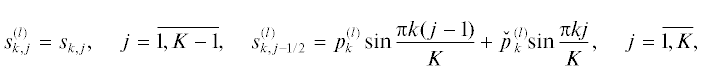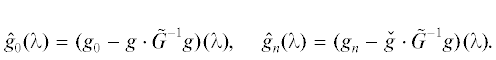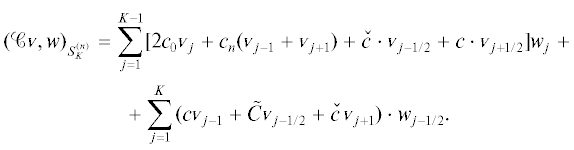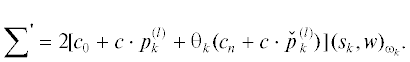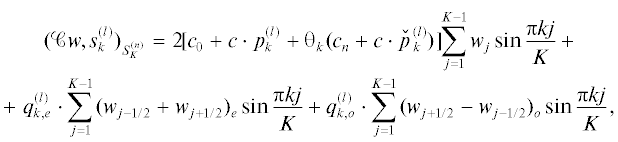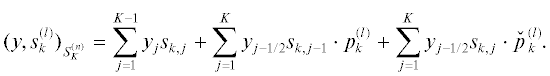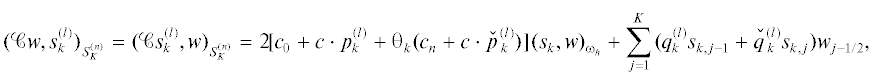Журнал вычислительной математики и математической физики, 2020, T. 60, № 2, стр. 234-252
Быстрые фурье-солверы для мкэ высокого порядка с тензорными произведениями для уравнения типа Пуассона
А. А. Злотник 1, *, И. А. Злотник 2, **
1 НИУ Высшая школа экономики
109028 Москва, Покровский б-р, 11, Россия
2 ЗАО РДК
115419 Москва, 2-й Верхний Михайловский пр., 9, стр. 2, Россия
* E-mail: azlotnik@hse.ru
** E-mail: ilya.zlotnik@gmail.com
Поступила в редакцию 22.08.2019
После доработки 22.08.2019
Принята к публикации 17.10.2019
Аннотация
Представлены прямые логарифмически оптимальные в теории и быстрые на практике алгоритмы реализации метода конечных элементов (МКЭ) на основе тензорных произведений 1D пространств МКЭ высокого порядка на многомерных прямоугольных параллелепипедах для решения уравнения типа Пуассона. Они основаны на хорошо известных фурье-подходах. Ключевыми новыми элементами являются детальное описание собственных пар 1D задач на собственные значения для МКЭ высокого порядка и быстрые прямой и обратный алгоритмы разложения по соответствующим собственным векторам, использующие одновременно несколько версий быстрого дискретного преобразования Фурье. Представлены результаты численных экспериментов в 2D и 3D случаях. Алгоритмы могут быть использованы для многочисленных приложений, в частности, для реализации методов конечных элементов высокого порядка с тензорными произведениями для различных эволюционных уравнений в частных производных, включая многомерные уравнение теплопроводности, волновое уравнение и уравнение Шрёдингера. Библ. 17. Фиг. 8. Табл. 6.
ВВЕДЕНИЕ
В работе представлены быстрые прямые алгоритмы реализации метода конечных элементов (МКЭ) на основе тензорных произведений 1D пространств МКЭ $n$-го порядка ($n \geqslant 2$) на прямоугольных параллелепипедах [1] для решения $N$-мерного уравнения типа Пуассона $ - \Delta u + \alpha u = f$ ($N \geqslant 2$) с краевыми условиями Дирихле. Алгоритмы основаны на хорошо известных Фурье-подходах (см., например, [2]–[5] и ссылки в них).
Ключевыми новыми элементами являются детальное описание собственных пар 1D задач на собственные значения для МКЭ высокого порядка и быстрые прямой и обратный алгоритмы разложения по соответствующим собственным векторам, использующие одновременно несколько версий БДПФ (быстрого дискретного преобразования Фурье), связанных не только с узлами сетки, но и с центрами элементов [6]. Это решает давно известную задачу (см., например, [5, c. 271]), и делает полные алгоритмы логарифмически оптимальными по отношению к числу элементов так же, как в случае полилинейных элементов ($n = 1$) или стандартных разностных схем. В краткой форме и в случае $N = 2$ алгоритмы представлены (без доказательств) в [7]. См. также методы другого типа для той же цели в [8], [9].
Отметим, что постоянная $\alpha $ может быть вещественной любого знака или даже комплексной, так что оператор $ - \Delta + \alpha $ может быть незнакоопределенным (в противоположность некоторым стандартным используемым итерационным методам).
Алгоритмы являются быстрыми с возрастанием количества элементов $K$ и на практике (причем более быстрыми, чем при стандартном теоретическом анализе, вследствие векторной обработки данных в обычных современных процессорах) и демонстрируют только слабое снижение эффективности с ростом $n$, начиная со стандартного случая $n = 1$. Для примера, в случае элементов 9-го порядка 2D МКЭ-система уравнений для $K = {{2}^{{20}}}$ элементов, содержащая почти $85 \times {{10}^{6}}$ неизвестных, и 3D МКЭ-система для $K = {{2}^{{18}}}$ элементов, содержащая более чем $190 \times {{10}^{6}}$ неизвестных, решаются за менее чем 2 и 15 мин соответственно на ординарном ноутбуке с использованием кода на Matlab R2016a, детали см. ниже.
Алгоритмы могут быть использованы для многочисленных других приложений, включая общие эллиптические уравнения 2-го порядка (для предобуславливания), для $N$-мерных уравнения теплопроводности, волнового уравнения, нестационарного уравнения Шрёдингера($\alpha $ может быть комплексным) и т.д., поскольку для их неявных дискретизаций по времени обычно получаются задачи рассматриваемого типа на верхнем слое по времени. В комбинации с другими методами они могут быть использованы для некоторых непрямоугольных областей и неравномерных сеток, в частности, с применением сеток, топологически эквивалентных равномерным прямоугольным [10]. Другие стандартные краевые условия также могут быть охвачены, см. краткое описание в [7]. Алгоритмы обладают высокой степенью параллелизуемости, так что они представляются полезными в научных вычислениях.
Подчеркнем также, что Фурье-структура алгоритмов является особенно ценной для решения некоторых задач волновой физики, в частности, использующих нелокальные граничные условия (см., например, [5], [11], [12]), откуда и возник наш собственный интерес.
Работа построена следующим образом. В разд. 1 даны формулировки стандартной 1D МКЭ-задачи на собственные значения и вспомогательных МКЭ-задач на собственные значения на эталонном элементе и внутри него. Основной разд. 2 посвящен описанию собственных значений и собственных векторов 1D МКЭ-задачи на собственные значения и быстрым прямому и обратному алгоритмам разложения по этим собственным векторам. Приложения к решению уравнения типа Пуассона в $N$-мерном прямоугольном параллелепипеде с краевым условием Дирихле описаны в разд. 3. Результаты численных экспериментов для $N = 2$ и 3 детально представлены в разд. 4; все они включают для сравнения известный случай $n = 1$.
1. ФОРМУЛИРОВКА 1D МКЭ ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
Сначала подробно рассмотрим МКЭ для простейшей 1D задачи на собственные значения для обыкновенного дифференциального уравнения (ОДУ)
Возьмем равномерную сетку $\mathop {\bar {\omega }}\nolimits_h $ с узлами ${{x}_{j}} = jh$, $j = \overline {0,K} $ (т.е. $0 \leqslant j \leqslant K$) и шагом $h = X{\text{/}}K$. Пусть $H_{h}^{{(n)}}[0,X]$ – МКЭ-пространство кусочно-полиномиальных функций $\varphi \in C[0,X]$ таких, что $\varphi (x) \in {{\mathcal{P}}_{n}}$ при $x \in [{{x}_{{j - 1}}},{{x}_{j}}]$, $j = \overline {1,K} $, с $\varphi (0) = \varphi (X) = 0$; здесь ${{\mathcal{P}}_{n}}$ – пространство многочленов степени не выше $n$, $n \geqslant 2$.
Пусть $S_{K}^{{(n)}}$ – пространство вектор-функций $w$ таких, что ${{w}_{j}} \in R$ при $j = \overline {0,K} $ с ${{w}_{0}} = {{w}_{K}} = 0$ и ${{w}_{{j - 1/2}}} \in {{\mathbb{R}}^{{n - 1}}}$, $j = \overline {1,K} $. Ясно, что $dimS_{K}^{{(n)}} = nK - 1$. Функция $\varphi \in H_{h}^{{(n)}}[0,X]$ однозначно определяется своими значениями в узлах сетки ${{\varphi }_{j}} = \varphi ({{x}_{j}})$, $j = \overline {0,K} $, с ${{\varphi }_{0}} = {{\varphi }_{K}} = 0$, и внутри элементов ${{\varphi }_{{j - 1/2}}} = \{ \varphi ({{x}_{{j - 1}}} + (l{\text{/}}n)h)\} _{{l = 1}}^{{n - 1}}$, $j = \overline {1,K} $, которые формируют элемент из $S_{K}^{{(n)}}$.
Воспользуемся следующей масштабированной операторной формой стандартной МКЭ-дискретизации задачи (1.1)
Здесь $\mathcal{A} = {{\mathcal{A}}^{{\text{T}}}} > 0$ и $\mathcal{C} = {{\mathcal{C}}^{{\text{T}}}} > 0$ – глобальные (масштабированные) операторы (матрицы) жесткости и масс, действующие в $S_{K}^{{(n)}}$ и вместе с $\lambda $ не зависящие от $h$; истинные приближенные собственные значения – это ${{\lambda }_{h}} = 4{{h}^{{ - 2}}}\lambda $.Пусть $A = \{ {{A}_{{kl}}}\} _{{k,l = 0}}^{n}$ и $C = \{ {{C}_{{kl}}}\} _{{k,l = 0}}^{n}$ – локальные матрицы жесткости и масс, связанные с эталонным элементом ${{\sigma }_{0}} = [ - 1,1]$, со следующими элементами
(1.3)
$A = \left( {\begin{array}{*{20}{c}} {{{a}_{0}}}&{{{a}^{{\text{T}}}}}&{{{a}_{n}}} \\ a&{\tilde {A}}&{\mathop a\limits^ {\kern 1pt} } \\ {{{a}_{n}}}&{\mathop a\limits^ {{{\kern 1pt} }^{{\text{T}}}}}&{{{a}_{0}}} \end{array}} \right),\quad C = \left( {\begin{array}{*{20}{c}} {{{c}_{0}}}&{{{c}^{{\text{T}}}}}&{{{c}_{n}}} \\ c&{\tilde {C}}&{\mathop c\limits^ {\kern 1pt} {\kern 1pt} } \\ {{{c}_{n}}}&{\mathop c\limits^ {{{\kern 1pt} }^{T}}}&{{{c}_{0}}} \end{array}} \right),\quad G(\lambda ) = \left( {\begin{array}{*{20}{c}} {{{g}_{0}}(\lambda )}&{{{g}^{{\text{T}}}}(\lambda )}&{{{g}_{n}}(\lambda )} \\ {g(\lambda )}&{\tilde {G}(\lambda )}&{\mathop g\limits^ {\kern 1pt} (\lambda )} \\ {{{g}_{n}}(\lambda )}&{\mathop g\limits^ {\kern 1pt} (\lambda )}&{{{g}_{0}}(\lambda )} \end{array}} \right).$Отметим, что ${{P}_{{ij}}} = {{\delta }_{{i(n - j)}}}$ и ${{P}^{{\text{T}}}} = {{P}^{{ - 1}}} = P$. Пусть $\mathbb{R}_{e}^{{n - 1}}$ и $\mathbb{R}_{o}^{{n - 1}}$ – подпространства четных и нечетных векторов в ${{\mathbb{R}}^{{n - 1}}}$, т.е. таких, что соответственно $Pp = p$ и $Pp = - p$. Разложение ${{\mathbb{R}}^{{n - 1}}} = \mathbb{R}_{e}^{{n - 1}} \oplus \mathbb{R}_{o}^{{n - 1}}$ (при $n \geqslant 3$) реализуется формулами
(1.4)
$p = {{p}_{e}} + {{p}_{o}},\quad {{p}_{e}}: = 0.5(p + \mathop p\limits^ ),\quad {{p}_{o}}: = 0.5(p - \mathop p\limits^ {\kern 1pt} ).$Теперь задачу (1.2) можно переписать в следующей явной форме
(1.6)
${{g}_{n}}(\lambda ){{v}_{{j - 1}}} + \mathop g\limits^ {\kern 1pt} (\lambda ) \cdot {{v}_{{j - 1/2}}} + 2{{g}_{0}}(\lambda ){{v}_{j}} + g(\lambda ) \cdot {{v}_{{j + 1/2}}} + {{g}_{n}}(\lambda ){{v}_{{j + 1}}} = 0,\quad j = \overline {1,K - 1} ,$(1.7)
$g(\lambda ){{v}_{{j - 1}}} + \tilde {G}(\lambda ){{v}_{{j - 1/2}}} + \mathop g\limits^ {\kern 1pt} (\lambda ){{v}_{j}} = 0,\quad j = \overline {1,K} ,$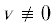 .
.
Рассмотрим также вспомогательные задачи на собственные значения на эталонном элементе ${{\sigma }_{0}}$ и внутри него
где ясно, что $A \geqslant 0$, $C > 0$ и $\tilde {A} = {{\tilde {A}}^{{\text{T}}}} > 0$, $\tilde {C} = {{\tilde {C}}^{{\text{T}}}} > 0$; см. некоторые их свойства в [11] (где была изучена задача, аналогичная (1.6), (1.7) на равномерной сетке на $[0,\infty )$ при $\lambda \in \mathbb{C}$). Обозначим через ${{S}_{n}}$ и ${{\tilde {S}}_{n}}$ их спектры. Пусть $\{ \lambda _{0}^{{(l)}},{{e}^{{(l)}}}\} _{{l = 1}}^{{n - 1}}$ – собственные пары задачи (1.9).Лемма 1.1. 1. Подпространства $\mathbb{R}_{e}^{{n - 1}}$ и $\mathbb{R}_{e}^{{n - 1}}$ инвариантны по отношению к $\tilde {A}$ и $\tilde {C}$. Поэтому каждый собственный вектор в $\{ {{e}^{{(l)}}}\} _{{l = 1}}^{{n - 1}}$ может быть выбран четным или нечетным. Также $\lambda _{0}^{{(l)}} > 0$, $l = \overline {1,n - 1} $.
2. Аналогичные свойства верны для задачи (1.8) за исключением наличия одного простого нулевого собственного значения.
Доказательство. Любая бисимметричная матрица $B$ порядка $n - 1$ коммутирует с $P$, т.е.
откуда следует основной результат п. 1. Свойство $\lambda _{0}^{{(l)}} > 0$, $l = \overline {1,n - 1} $, хорошо известно.Для п. 2 рассуждение аналогично с учетом того, что $A{{(1 \ldots 1)}^{{\text{T}}}} = 0$ (относительно простоты $\lambda = 0$ см. [11, утверждение 5]).
Прямым вычислением можно проверить, что все собственные значения в ${{S}_{n}}$ и ${{\tilde {S}}_{n}}$ являются простыми и ${{S}_{n}} \cap {{\tilde {S}}_{n}} = \not {0}$ по крайней мере при $1 \leqslant n \leqslant 9$, см. [11].
Для малых $n$ можно найти ${{S}_{n}}$ и ${{\tilde {S}}_{n}}$ аналитически (с помощью Mathematica), в частности, ${{\tilde {S}}_{2}} = \{ 2.5\} $, ${{\tilde {S}}_{3}} = \{ 2.5,10.5\} $, ${{\tilde {S}}_{4}} = \{ 14 \pm \sqrt {133} ,10.5\} $ и ${{\tilde {S}}_{5}} = \{ 14 \pm \sqrt {133} ,30 \pm 9\sqrt 5 \} $ (повторяемость собственных значений не случайна, см. [11]).
Выберем $\{ {{e}^{{(l)}}}\} _{{l = 1}}^{{n - 1}}$ как указано в лемме 1.1, с использованием масштабирования $\tilde {C}{{e}^{{(l)}}} \cdot {{e}^{{(l)}}} = 1$.
Лемма 1.2. Пусть $\tilde {G}(\lambda )p = - g(\lambda )$, где 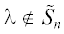 . Пусть векторы $a$ и $c$ разложены как
. Пусть векторы $a$ и $c$ разложены как
(1.11)
$a = \sum\limits_{l = 1}^{n - 1} \,{{a}^{{(l)}}}\tilde {C}{{e}^{{(l)}}},\quad c = \sum\limits_{l = 1}^{n - 1} \,{{c}^{{(l)}}}\tilde {C}{{e}^{{(l)}}},\quad {\text{с}}\quad {{a}^{{(l)}}} = a \cdot {{e}^{{(l)}}},\quad {{c}^{{(l)}}} = c \cdot {{e}^{{(l)}}}.$Доказательство. Для разложений $p = \sum\nolimits_{l = 1}^{n - 1} \,{{p}_{l}}{{e}^{{(l)}}}$ и (1.11) имеем
откуда легко следует результат.2. РЕШЕНИЕ 1D МКЭ-ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СООТВЕТСТВУЮЩИЕ АЛГОРИТМЫ, ОСНОВАННЫЕ НА БДПФ
Сделаем следующее
Предположение.
$(A)\;\;{\text{собственные}}\;{\text{значения}}\;{\text{в}}\;{{S}_{n}}\quad {\text{и}}\quad {{\tilde {S}}_{n}}\;{\text{простые}}\quad {\text{и}}\quad {{S}_{n}} \cap {{\tilde {S}}_{n}} = \not {0}.$
Напомним, что это верно по крайней мере при $2 \leqslant n \leqslant 9$ (ниже в разд. 4 это проверяется вплоть до $n = 21$).
Введем вспомогательное уравнение
(2.1)
$\widehat \gamma (\lambda ) \equiv - ({{g}_{0}} - g \cdot {{\tilde {G}}^{{ - 1}}}g)(\lambda ){\text{/}}({{g}_{n}} - \mathop g\limits^ {\kern 1pt} \; \cdot {{\tilde {G}}^{{ - 1}}}g)(\lambda ) = \theta ,$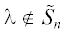 , с параметром $\theta $. Его решение эквивалентно нахождению корней многочлена степени не выше $n$, см. [11]. В частности, в силу леммы 1.2 это уравнение может быть переписано в виде
, с параметром $\theta $. Его решение эквивалентно нахождению корней многочлена степени не выше $n$, см. [11]. В частности, в силу леммы 1.2 это уравнение может быть переписано в виде
(2.2)
${{a}_{0}} - \lambda {{c}_{0}} + \sum\limits_{l = 1}^{n - 1} \,\frac{{{{{({{a}^{{(l)}}} - \lambda {{c}^{{(l)}}})}}^{2}}}}{{\lambda - \lambda _{0}^{{(l)}}}} = - \theta \left( {{{a}_{n}} - \lambda {{c}_{n}} + \sum\limits_{l = 1}^{n - 1} \,\frac{{(\mathop a\limits^ {{{\kern 1pt} }^{{(l)}}} - \lambda \mathop c\limits^ {{{\kern 1pt} }^{{(l)}}})({{a}^{{(l)}}} - \lambda {{c}^{{(l)}}})}}{{\lambda - \lambda _{0}^{{(l)}}}}} \right).$Введем простейшее скалярное произведение в $S_{K}^{{(n)}}$ и соответствующий квадрат $\mathcal{C}$-нормы
В следующей теореме описываются собственные значения и собственные векторы задачи (1.2).
Теорема 2.1. 1. Спектр задачи (1.2) состоит из ${{\tilde {S}}_{n}}$ и чисел $\{ \lambda _{k}^{{(l)}}\} _{{l = 1}}^{n}$, которые являются всеми $n$ (и всеми положительными вещественными) решениями уравнения (2.2) с $\theta = {{\theta }_{k}}: = cos\tfrac{{\pi k}}{K}$ при $k = \overline {1,K - 1} $. Числа $\{ \lambda _{k}^{{(l)}}\} _{{l = 1}}^{n}$ отличаются от $\{ \lambda _{0}^{{(l)}}\} _{{l = 1}}^{{n - 1}}$ и различны при фиксированном $k$.
2. Собственному значению $\lambda _{0}^{{(l)}}$ отвечает собственный вектор
(2.3)
$s_{{0,j}}^{{(l)}} = 0,\quad j = \overline {1,K - 1} ,\quad s_{{0,j - 1/2}}^{{(l)}} = {{( - P)}^{{j - 1}}}{{e}^{{(l)}}},\quad j = \overline {1,K} ,$3. Собственному значению $\lambda _{k}^{{(l)}}$ отвечает собственный вектор
где ${{s}_{{k,j}}}: = sin\tfrac{{\pi kj}}{K}$, а $p_{k}^{{(l)}} \in {{\mathbb{R}}^{{n - 1}}}$ служит решением невырожденной алгебраической системы уравнений $\tilde {G}(\lambda _{k}^{{(l)}})p_{k}^{{(l)}} = - g(\lambda _{k}^{{(l)}})$ при $k = \overline {1,K - 1} $, $l = \overline {1,n} $.4. Введенные собственные векторы являются $\mathcal{C}$-ортогональными, т.е.
для всех $k,\tilde {k} \in \overline {0,K - 1} $, $l \in \overline {1,n - {{\delta }_{{k0}}}} $, $\tilde {l} \in \overline {1,n - {{\delta }_{{\tilde {k}0}}}} $ таких, что $k \ne \tilde {k}$ и/или $l \ne \tilde {l}$.Как следствие, они образуют базис в $S_{K}^{{(n)}}$, т.е. любой $w \in S_{K}^{{(n)}}$ может быть однозначно разложен как
(2.6)
$w = \sum\limits_{l = 1}^{n - 1} \,{{w}_{{0l}}}s_{0}^{{(l)}} + \sum\limits_{k = 1}^{K - 1} \,\sum\limits_{l = 1}^n \,{{w}_{{kl}}}s_{k}^{{(l)}}.$Доказательство. Будем различать два случая.
1. Пусть сначала $\lambda \in {{\tilde {S}}_{n}}$ и $e$ удовлетворяет (1.9). Тогда для любого $j = \overline {1,K} $ с использованием уравнения (1.7) получим
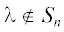 по предположению (A), то имеем $g(\lambda ) \cdot e \ne 0$ или $G(\lambda )\left( {\begin{array}{*{20}{c}} 0 \\ e \\ 0 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {g(\lambda ) \cdot e} \\ 0 \\ {\mathop g\limits^ (\lambda ) \cdot e} \end{array}} \right).$. В силу предположения (A) и леммы 1.1 $\lambda $ является простым в ${{\tilde {S}}_{n}}$ и $e$ четен или нечетен. Соответственно или $\mathop g\limits^ (\lambda ) \cdot e = g(\lambda ) \cdot e \ne 0$ и ${{{v}}_{j}} = - {{{v}}_{{j - 1}}}$, или $\mathop g\limits^ (\lambda ) \cdot e = - g(\lambda ) \cdot e \ne 0$ и ${{{v}}_{j}} = {{{v}}_{{j - 1}}}$. Поскольку ${{{v}}_{0}} = 0$, то в обоих случаях получим
Поэтому уравнение (1.7) сводится к $\tilde {G}{{{v}}_{{j - 1/2}}} = 0$, откуда следует, что ${{v}_{{j - 1/2}}} = {{c}_{{j - 1/2}}}e$.
по предположению (A), то имеем $g(\lambda ) \cdot e \ne 0$ или $G(\lambda )\left( {\begin{array}{*{20}{c}} 0 \\ e \\ 0 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {g(\lambda ) \cdot e} \\ 0 \\ {\mathop g\limits^ (\lambda ) \cdot e} \end{array}} \right).$. В силу предположения (A) и леммы 1.1 $\lambda $ является простым в ${{\tilde {S}}_{n}}$ и $e$ четен или нечетен. Соответственно или $\mathop g\limits^ (\lambda ) \cdot e = g(\lambda ) \cdot e \ne 0$ и ${{{v}}_{j}} = - {{{v}}_{{j - 1}}}$, или $\mathop g\limits^ (\lambda ) \cdot e = - g(\lambda ) \cdot e \ne 0$ и ${{{v}}_{j}} = {{{v}}_{{j - 1}}}$. Поскольку ${{{v}}_{0}} = 0$, то в обоих случаях получим
Поэтому уравнение (1.7) сводится к $\tilde {G}{{{v}}_{{j - 1/2}}} = 0$, откуда следует, что ${{v}_{{j - 1/2}}} = {{c}_{{j - 1/2}}}e$.
Теперь уравнение (1.6) сводится к
2. Пусть теперь 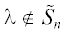 . Тогда из уравнения (1.7) получим
. Тогда из уравнения (1.7) получим
(2.8)
${{{v}}_{{j - 1/2}}} = - {{G}^{{ - 1}}}(\lambda )[{{{v}}_{{j - 1}}}g(\lambda ) + {{{v}}_{j}}\mathop g\limits^ (\lambda )],\quad j = \overline {1,K} .$(2.9)
${{\hat {g}}_{n}}(\lambda ){{{v}}_{{j - 1}}} + 2{{\hat {g}}_{0}}(\lambda ){{{v}}_{j}} + {{\hat {g}}_{n}}(\lambda ){{{v}}_{{j + 1}}} = 0,\quad j = \overline {1,K - 1} ,$Непосредственно проверяются следующие равенства
Если $\mathop {\hat {g}}\nolimits_n (\lambda ) = 0$ и $\mathop {\hat {g}}\nolimits_0 (\lambda ) \ne 0$, то уравнение (2.9) вместе с (2.8) приводит к ${v} = 0$, поэтому такое $\lambda $ не удовлетворяет (1.2).
Значит, $\mathop {\hat {g}}\nolimits_n (\lambda ) \ne 0$ и уравнение (2.9) упрощается до
(2.10)
${{{v}}_{{j - 1}}} - 2\hat {\gamma }(\lambda ){{{v}}_{j}} + {{{v}}_{{j + 1}}} = 0,\quad j = \overline {1,K - 1} ,$(2.11)
$2\sum\limits_{k = 1}^{K - 1} \,{{\tilde {v}}_{k}}({{\theta }_{k}} - \hat {\gamma }(\lambda )){{s}_{{k,j}}} = 0,\quad j = \overline {1,K - 1} .$(2.12)
$\hat {\gamma }(\lambda ) = {{\theta }_{k}}\quad {\text{для}}\;{\text{некоторого}}\quad k = \overline {1,K - 1} .$Отметим, что ${\mathbf{\tilde {v}}} = 0$ эквивалентно ${v} = 0$ в $S_{K}^{{(n)}}$ (с учетом формулы (2.8)). Поэтому $\lambda $ удовлетворяет (2.12); более того, ${{\tilde {v}}_{j}} = {{\delta }_{{kj}}}$ и, как следствие, ${{{v}}_{j}} = {{s}_{{k,j}}}$, $j = \overline {0,K} $, а также
Общее количество собственных значений 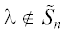 (с учетом возможной кратности) равно $dimS_{K}^{{(n)}} - (n - 1) = n(K - 1)$. Максимальное количество корней алгебраических уравнений (2.12) при всех $k$ то же самое, поэтому каждое уравнение (2.12) должно иметь ровно $n$ различных корней (при фиксированном $k$ записанный вектор $v$ определяется значением $\lambda $ однозначно).
(с учетом возможной кратности) равно $dimS_{K}^{{(n)}} - (n - 1) = n(K - 1)$. Максимальное количество корней алгебраических уравнений (2.12) при всех $k$ то же самое, поэтому каждое уравнение (2.12) должно иметь ровно $n$ различных корней (при фиксированном $k$ записанный вектор $v$ определяется значением $\lambda $ однозначно).
3. Свойство (2.5) заведомо выполняется для собственных векторов $s_{k}^{{(l)}}$ и $s_{{\tilde {k}}}^{{(\tilde {l})}}$, отвечающих различным собственным значениям задачи (1.2), в частности, при $k = 0$ и $\tilde {k} \ne 0$, или $k = \tilde {k}$ и $l \ne \tilde {l}$.
Оставшийся случай будет рассмотрен ниже в следствии 2.1 связанной с этим леммы 2.1.
Отметим, что: 1) векторы $s_{0}^{{(l)}}$ используются только для описания алгоритма, и только векторы ${{e}^{{(l)}}}$ применяются в его реализации; 2) $s_{{k,j}}^{{(l)}}$ не зависят от $l$; 3) векторы $p_{k}^{{(l)}}$ не зависят от $j$ и могут быть также вычислены в силу леммы 1.2.
Лемма 2.1. Пусть $w \in S_{K}^{{(n)}}$ и ${{w}_{{j - 1/2}}} = q{{w}_{{j - 1}}} + \mathop q\limits^ {{w}_{j}}$, $j = \overline {1,K} $, для некоторого $q \in {{\mathbb{R}}^{{n - 1}}}$. Тогда
при $k = \overline {1,K - 1} $, $l = \overline {1,n} $, где ${{({{s}_{k}},w)}_{{{{\omega }_{h}}}}}: = \sum\nolimits_{j = 1}^{K - 1} \,{{s}_{{k,j}}}{{w}_{j}}$.Доказательство. 1. Вспомнив обозначение (1.3), для любых $v,w \in S_{K}^{{(n)}}$, имеем
2. Согласно формулам (2.15) и (2.3) при четном ${{e}^{{(l)}}}$ получим
При нечетном ${{e}^{{(l)}}}$ аналогично получим
3. Формула (2.15) вместе с (2.4) и (2.5) влекут равенство
В силу формулы
сначала выводим Затем с использованием формул (2.5) и (2.10) получимСледствие 2.1. Верно свойство ортогональности (2.5) из теоремы 2.1, п. 4.
Доказательство. Остается рассмотреть случай $k,\tilde {k} \in \overline {1,K - 1} $ и $k \ne \tilde {k}$. Поскольку тогда ${{({{s}_{k}},{{s}_{{\tilde {k}}}})}_{{{{\omega }_{h}}}}} = 0$, то результат следует из (2.14).
Вычисление $w \in S_{K}^{{(n)}}$ по коэффициентам ${{w}_{{kl}}}$ разложения (2.6) назовем обратным ${{F}_{n}}$-преобразованием, а вычисление коэффициентов ${{w}_{{kl}}}$ по $w \in S_{K}^{{(n)}}$ – прямым ${{F}_{n}}$-преобразованием. Рассмотрим также связанное с этим разложение $y \in S_{K}^{{(n)}}$ вида
(2.20)
$y = \sum\limits_{l = 1}^{n - 1} \,{{\tilde {y}}_{{0l}}}\mathcal{C}s_{0}^{{(l)}} + \sum\limits_{k = 1}^{K - 1} \,\sum\limits_{l = 1}^n \,{{\tilde {y}}_{{kl}}}\mathcal{C}s_{k}^{{(l)}}$Опишем их быструю БДПФ-реализацию.
Теорема 2.2. 1. Обратное ${{F}_{n}}$-преобразование может быть реализовано в соответствии со следующими формулами
(2.21)
${{w}_{j}} = \sum\limits_{k = 1}^{K - 1} \,\left( {\sum\limits_{l = 1}^n \,{{w}_{{kl}}}} \right)sin\frac{{\pi kj}}{K},\quad j = \overline {1,K - 1} ,$(2.22)
$\begin{gathered} {{w}_{{j - 1/2}}} = {{( - P)}^{{j - 1}}}\sum\limits_{l = 1}^{n - 1} \,{{w}_{{0l}}}{{e}^{{(l)}}} + 2\sum\limits_{k = 1}^{K - 1} \,{{d}_{{k,e}}}cos\frac{{\pi k}}{{2K}}sin\frac{{\pi k(j - 1{\text{/}}2)}}{K} - \\ \, - 2\sum\limits_{k = 1}^{K - 1} \,{{d}_{{k,o}}}sin\frac{{\pi k}}{{2K}}cos\frac{{\pi k(j - 1{\text{/}}2)}}{K},\quad j = \overline {1,K} , \\ \end{gathered} $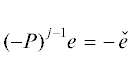 при четном $j$ для любого $e \in {{\mathbb{R}}^{{n - 1}}}$.
при четном $j$ для любого $e \in {{\mathbb{R}}^{{n - 1}}}$.
Набор $\{ {{w}_{j}}\} _{{j = 1}}^{{K - 1}}$ можно вычислить с помощью стандартного обратного БДПФ по синусам. Набор $\{ {{w}_{{j - 1/2}}}\} _{{j = 1}}^{K}$ можно вычислить с помощью $n - 1$ модифицированного обратного БДПФ, связанного с центрами элементов, в количестве $[n{\text{/}}2]$ по синусам и $[(n - 1){\text{/}}2]$ по косинусам с использованием продолжений ${{d}_{{K,e}}}: = 0$ и ${{d}_{{0,o}}}: = 0$, см. алгоритмы DST-I, DST-III и DCT-III в [6].
2. Прямое $F{{C}_{n}}$-преобразование можно реализовать на основе стандартной формулы
(2.23)
${{\tilde {y}}_{{kl}}} = {{(y,s_{k}^{{(l)}})}_{{S_{K}^{{(n)}}}}}{\text{/}}\left\| {s_{k}^{{(l)}}} \right\|_{C}^{2}.$(2.24)
${{(y,s_{0}^{{(l)}})}_{{S_{K}^{{(n)}}}}} = \left( {\sum\limits_{j = 1}^K \,{{{( - P)}}^{{j - 1}}}{{y}_{{j - 1/2}}}} \right){{e}^{{(l)}}},\quad \left\| {s_{0}^{{(l)}}} \right\|_{C}^{2} = K.$Во-вторых, при $k = \overline {1,K - 1} $, $l = \overline {1,n} $ верны следующие формулы:
(2.25)
${{(y,s_{k}^{{(l)}})}_{{S_{K}^{{(n)}}}}} = \sum\limits_{j = 1}^{K - 1} \,{{y}_{j}}sin\frac{{\pi kj}}{K} + p_{{k,e}}^{{(l)}} \cdot \sum\limits_{j = 1}^{K - 1} \,{{({{y}_{{j - 1/2}}} + {{y}_{{j + 1/2}}})}_{e}}sin\frac{{\pi kj}}{K} + p_{{k,o}}^{{(l)}} \cdot \sum\limits_{j = 1}^{K - 1} \,{{({{y}_{{j + 1/2}}} - {{y}_{{j - 1/2}}})}_{o}}sin\frac{{\pi kj}}{K},$(2.26)
$\left\| {s_{k}^{{(l)}}} \right\|_{C}^{2} = K\{ {{c}_{0}} + (\tilde {C}p_{k}^{{(l)}} + 2c) \cdot p_{k}^{{(l)}} + {{\theta }_{k}}[{{c}_{n}} + (\tilde {C}p_{k}^{{(l)}} + 2c) \cdot \mathop p\nolimits_k^{(l)} ]\} .$3. Аналогично п. 2, прямое ${{F}_{n}}$-преобразование можно реализовать на основе стандартной формулы
(2.27)
${{w}_{{kl}}} = {{(\mathcal{C}w,s_{k}^{{(l)}})}_{{S_{K}^{{(n)}}}}}{\text{/}}\left\| {s_{k}^{{(l)}}} \right\|_{C}^{2}.$(2.28)
${{(\mathcal{C}w,s_{0}^{{(l)}})}_{{S_{K}^{{(n)}}}}} = \left( {\tilde {C}\sum\limits_{j = 1}^K \,{{{( - P)}}^{{j - 1}}}{{w}_{{j - 1/2}}}} \right){{e}^{{(l)}}}.$При $k = \overline {1,K - 1} $, $l = \overline {1,n} $ применима формула (2.25) с $y: = \mathcal{C}w$. С другой стороны, верна также следующая формула
где $q_{{k,e}}^{{(l)}}$ и $q_{{k,o}}^{{(l)}}$ – соответственно четная и нечетная компоненты вектора $q_{k}^{{(l)}}: = \tilde {C}p_{k}^{{(l)}} + c$. Снова все эти коэффициенты можно вычислить с помощью $n$ стандартных прямых БДПФ по синусам.Доказательство. 1. Пусть коэффициенты ${{w}_{{kl}}}$ разложения (2.6) известны. В соответствии с первыми из формул (2.3) и (2.4) значения $w$ для целых индексов в (2.6) сводятся к (2.21).
Чтобы вычислить $w$ для полуцелых индексов, преобразуем вторую сумму в (2.6). В силу разложения (1.4) перепишем вторую формулу (2.4) в виде
2. Теперь рассмотрим вычисление коэффициентов в разложении (2.20) при заданном $y \in {{S}_{K}}$. В силу свойства ортогональности (2.5), они сначала могут быть выражены в виде (2.23) при $k = 0$, $l = \overline {1,n - 1} $ и $k = \overline {1,K - 1} $, $l = \overline {1,n} $.
Формулы (2.15) и (2.3) влекут равенства
В силу формул (2.3) для числителя формулы (2.23) при $k = 0$ можно записать
В силу формул (2.4) для того же числителя при $k = \overline {1,K - 1} $ получим
Поэтому сдвинув на 1 индекс во второй из этих сумм, применив тождество ${{a}_{1}}{{b}_{1}} + {{a}_{2}}{{b}_{2}} = $ $ = 0.5({{a}_{1}} + {{a}_{2}})({{b}_{1}} + {{b}_{2}}) + $ $0.5({{a}_{1}} - {{a}_{2}})({{b}_{1}} - {{b}_{2}})$ и вспомнив разложение (1.4), выведем3. Благодаря свойству ортогональности (2.5) справедлива формула (2.27).
В силу формул (2.3), (2.15), а также ${{\tilde {C}}^{{\text{T}}}} = \tilde {C}$ и $P = {{P}^{{\text{T}}}}$ для ее числителя при $k = 0$ можно записать
В силу формул (2.16), (2.18) для того же числителя при $k = \overline {1,K - 1} $ получим
где $q_{k}^{{(l)}} = \tilde {C}p_{k}^{{(l)}} + c$. Преобразовав последнюю сумму таким же образом, как второе и третье слагаемые в (2.30), установим (2.29).3. ПРИЛОЖЕНИЯ К ОБОБЩЕННОМУ УРАВНЕНИЮ ПУАССОНА
Для начала обратимся к простой 1D краевой задаче для ОДУ
где $\alpha \ne - {{(\pi i{\text{/}}X)}^{2}}$, $i \in \mathbb{N}$. Ее МКЭ-дискретизация имеет операторную форму где ${{f}^{h}} \in S_{K}^{{(n)}}$ – это МКЭ-усреднение $f$. Ее решение можно записать в виде(3.3)
$v = \sum\limits_{k = 0}^K \,\sum\limits_{l = 1}^{n - {{\delta }_{{k0}}}} \,\frac{{\tilde {f}_{{kl}}^{h}}}{{4{{h}^{{ - 2}}}\lambda _{k}^{{(l)}} + \alpha }}s_{k}^{{(l)}}$Теперь рассмотрим детально решение $N$-мерной ($N \geqslant 2$) краевой задачи
(3.4)
$ - \Delta u + \alpha u = f\quad {\text{в}}\quad \Omega = (0,{{X}_{1}}) \times \ldots \times (0,{{X}_{N}}),\quad {{\left. u \right|}_{{\partial \Omega }}} = 0,$Введем пространство $H_{{{{h}_{1}}}}^{{({{n}_{1}})}}[0,{{X}_{1}}] \otimes \ldots \otimes H_{{{{h}_{N}}}}^{{({{n}_{N}})}}[0,{{X}_{N}}]$ кусочно-полиномиальных функций в $\bar {\Omega }$, где ${{h}_{i}} = {{X}_{i}}{\text{/}}{{K}_{i}}$ и ${{n}_{i}} \geqslant 2$, $i = \overline {1,N} $. Пусть ${\mathbf{K}} = ({{K}_{1}}, \ldots ,{{K}_{N}})$ и ${\mathbf{n}} = ({{n}_{1}}, \ldots ,{{n}_{N}})$.
Введем также пространство вектор-функций $S_{{\mathbf{K}}}^{{({\mathbf{n}})}} = S_{{{{K}_{1}}}}^{{({{n}_{1}})}} \otimes \ldots \otimes S_{{{{K}_{N}}}}^{{({{n}_{N}})}}$. Например, при $N = 2$, эти функции являются числами для индексов $({{j}_{1}},{{j}_{2}})$, ${{j}_{1}} = \overline {0,{{K}_{1}}} $, ${{j}_{2}} = \overline {0,{{K}_{2}}} $ и векторами из ${{\mathbb{R}}^{{{{n}_{1}} - 1}}}$, ${{\mathbb{R}}^{{{{n}_{2}} - 1}}}$ и ${{\mathbb{R}}^{{({{n}_{1}} - 1) \times ({{n}_{2}} - 1)}}}$ соответственно для индексов
МКЭ-дискретизация задачи (3.4) может быть записана в следующей операторной форме
(3.5)
$(4h_{1}^{{ - 2}}{{\mathcal{A}}_{1}}{{\mathcal{C}}_{2}} \ldots {{\mathcal{C}}_{N}} + \ldots + 4h_{N}^{{ - 2}}{{\mathcal{A}}_{N}}{{\mathcal{C}}_{1}} \ldots {{\mathcal{C}}_{{N - 1}}}){v} + \alpha {{\mathcal{C}}_{1}} \ldots {{\mathcal{C}}_{N}}{v} = {{f}^{h}},\quad {v} \in S_{{\mathbf{K}}}^{{({\mathbf{n}})}},$Напомним, что случай неоднородных краевых условий Дирихле $u(x) = b(x)$ на $\partial \Omega $ в (3.4) мог бы быть легко охвачен сведением к (3.5) с модифицированным вектором ${{f}^{h}}$, зависящим от аппроксимации ${{b}^{h}}$ для $b$.
Чтобы вычислить ее решение, ${{F}_{n}}$-преобразования из теоремы 2.2 могут быть применены двояко.
(a) Рассмотрим кратное разложение ${{f}^{h}} \in S_{{\mathbf{K}}}^{{({\mathbf{n}})}}$ типа (2.20)
(3.6)
${{f}^{h}} = \sum\limits_{i = 1}^N \,\sum\limits_{{{k}_{i}} = 0}^{{{K}_{i}} - 1} \,\sum\limits_{{{l}_{i}} = 1}^{{{n}_{i}} - {{\delta }_{{{{k}_{i}}0}}}} \tilde {f}_{{{{k}_{1}}{{l}_{1}}, \ldots ,{{k}_{N}}{{l}_{N}}}}^{h}{{\mathcal{C}}_{1}}s_{{1,{{k}_{1}}}}^{{({{l}_{1}})}} \ldots {{\mathcal{C}}_{N}}s_{{N,{{k}_{N}}}}^{{({{l}_{N}})}}.$(3.7)
$v = \sum\limits_{i = 1}^N \,\sum\limits_{{{k}_{i}} = 0}^{{{K}_{i}} - 1} \,\sum\limits_{{{l}_{i}} = 1}^{{{n}_{i}} - {{\delta }_{{{{k}_{i}}0}}}} \,\frac{{\tilde {f}_{{{{k}_{1}}{{l}_{1}}, \ldots ,{{k}_{N}}{{l}_{N}}}}^{h}}}{{4h_{1}^{{ - 2}}\lambda _{{1,{{k}_{1}}}}^{{({{l}_{1}})}} + \ldots + 4h_{N}^{{ - 2}}\lambda _{{N,{{k}_{N}}}}^{{({{l}_{N}})}} + \alpha }}s_{{1,{{k}_{1}}}}^{{({{l}_{1}})}} \ldots s_{{N,{{k}_{N}}}}^{{({{l}_{N}})}}.$Алгоритм (a) состоит из двух достаточно стандартных шагов:
(1) нахождение коэффициентов разложения (3.6) для ${{f}^{h}}$ (посредством прямых $F{{C}_{n}}$-преобразований по ${{x}_{1}}$,…, ${{x}_{N}}$);
(2) нахождение $v$ по коэффициентам его разложения (3.7) (посредством обратных ${{F}_{n}}$-преобразований по ${{x}_{1}}$,…, ${{x}_{N}}$).
(б) Рассмотрим разложение ${{f}^{h}}$ типа (2.20) по ${{x}_{2}}$,…, ${{x}_{N}}$, т.е.
(3.8)
${{f}^{h}} = \sum\limits_{i = 2}^N \,\sum\limits_{{{k}_{i}} = 0}^{{{K}_{i}} - 1} \,\sum\limits_{{{l}_{i}} = 1}^{{{n}_{i}} - {{\delta }_{{{{k}_{i}}0}}}} \,\tilde {f}_{{{{k}_{1}}{{l}_{1}}, \ldots ,{{k}_{N}}{{l}_{N}}}}^{h}{{\mathcal{C}}_{2}}s_{{2,{{k}_{2}}}}^{{({{l}_{2}})}} \ldots {{\mathcal{C}}_{N}}s_{{N,{{k}_{N}}}}^{{({{l}_{N}})}},$(3.9)
$v = \sum\limits_{i = 2}^N \,\sum\limits_{{{k}_{i}} = 0}^{{{K}_{i}} - 1} \,\sum\limits_{{{l}_{i}} = 1}^{{{n}_{i}} - {{\delta }_{{{{k}_{i}}0}}}} \,{{v}_{{{{k}_{2}}{{l}_{2}}, \ldots ,{{k}_{N}}{{l}_{N}}}}}s_{{2,{{k}_{2}}}}^{{({{l}_{2}})}} \ldots s_{{N,{{k}_{N}}}}^{{({{l}_{N}})}},$(3.10)
$[4h_{1}^{{ - 2}}{{\mathcal{A}}_{1}} + (4h_{2}^{{ - 2}}\lambda _{{{{k}_{2}}}}^{{({{l}_{2}})}} + \ldots + 4h_{N}^{{ - 2}}\lambda _{{{{k}_{N}}}}^{{({{l}_{N}})}} + \alpha ){{\mathcal{C}}_{1}}]{{v}_{{{{k}_{2}}{{l}_{2}}, \ldots ,{{k}_{N}}{{l}_{N}}}}} = \tilde {f}_{{{{k}_{2}}{{l}_{2}}, \ldots ,{{k}_{N}}{{l}_{N}}}}^{h}.$Алгоритм (б) состоит из трех достаточно стандартных шагов:
(1) нахождение коэффициентов разложения (3.8) для ${{f}^{h}}$ (посредством прямых $F{{C}_{n}}$-преобразований по ${{x}_{2}}$, …, ${{x}_{N}}$);
(2) решение набора независимых 1D задач (3.10) для коэффициентов разложения $v$;
(3) нахождение $v$ по коэффициентам его разложения (3.9) (посредством обратных ${{F}_{n}}$-преобразований по ${{x}_{2}}$, …, ${{x}_{N}}$).
Реализация алгоритмов (a) и (б) требует соответственно $O({{K}_{1}} \ldots {{K}_{N}}lo{{g}_{2}}({{K}_{1}} \ldots {{K}_{N}}))$ и $O({{K}_{1}} \ldots {{K}_{N}}lo{{g}_{2}}({{K}_{2}} \ldots {{K}_{N}}))$ арифметических действий. Здесь не анализируется зависимость от ${\mathbf{n}}$, но она умеренная согласно численным экспериментам в следующем разделе.
Важно, что они могут быть применены для решения разнообразных эволюционных уравнений в частных производных (УрЧП) таких, как уравнение теплопроводности, волновое уравнение или уравнение Шрёдингера, поскольку для их неявных по времени дискретизаций обычно получаются задачи типа (3.5) на верхнем слое по времени.
Кроме того, алгоритм (б) непосредственно обобщается на случаи более общих уравнений, чем в (3.4), с коэффициентами зависящими от ${{x}_{1}}$ (что существенно, в частности, в полярных или цилиндрических координатах), различных краевых условий при ${{x}_{1}} = 0,{{X}_{1}}$ и неравномерной сетки по ${{x}_{1}}$ [3]. Он может быть также применен для сведения 3D задач в цилиндрической области к набору независимых 2D задач в основании цилиндра.
4. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ
1. Сначала проверим, что собственные значения каждой из задач (1.8) и (1.9) хорошо разделены. Определим их спектральные щели как
Фиг. 1.
Числа ${{\delta }_{n}}$ и ${{\tilde {\delta }}_{n}}$, связанные с минимальной спектральной щелью в задачах на собственные значения (1.8) и (1.9) (слева), а также cond $\tilde {A}$ и cond $\tilde {C}$ (справа) для задачи (1.9), в зависимости от $n$.

Представим также спектральные числа обусловленности $\tilde {A}$ и $\tilde {C}$ на фиг. 1 (справа) и обратим внимание на их быстрый рост с возрастанием $n$ (к сожалению).
Отметим, что все вычисления были выполнены на ординарном ноутбуке ASUS-U36S с Intel Core i3-2350M CPU 2.3 GHz, 8 Gb, Win 10 x64. Для реализации алгоритмов были разработаны коды на Matlab R2016a, и подчеркнем, что при этом были применены несколько базовых и продвинутых методов векторизации кодов [13], чтобы заметно ускорить их выполнение.
В случае 1D задачи для ОДУ (3.2) при $\alpha = 1$ дадим числа обусловленности глобальной матрицы МКЭ $4{{h}^{{ - 2}}}\mathcal{A} + \alpha \mathcal{C}$ при $\alpha = 1$ и ее локальной версии в зависимости от $K = 2,4,...,1024$ при $n = \overline {1,9} $ на фиг. 2 для последующих ссылок. Отметим их быстрый рост с возрастанием $K$.
Фиг. 2.
Числа обусловленности локальных (слева) и глобальных (справа) матриц в 1D задаче (3.2) при $\alpha = 1$ в зависимости от $K = 2,4,...,1024$ для $n = \overline {1,9} $.
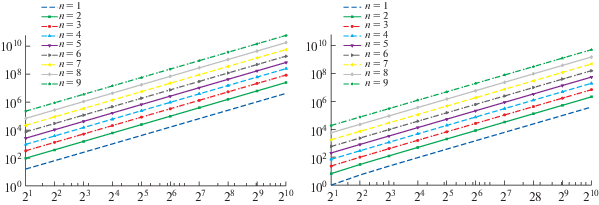
Далее проанализируем время выполнения ${{F}_{n}}$-преобразований в зависимости от выбора $K$ с его возрастанием до весьма высоких значений ${{2}^{{20}}}$. Рассмотрим три способа выбора $K$: степени двойки ($K = {{2}^{p}}$), простые числа и составные числа (не степени двойки). Простые и составные значения $K$ выбираются случайным образом между двумя последовательными степенями двойки, и сравнение выполняется в стиле [14]. Используются внешние функции comp_dst для DST-I и DST-III и comp_dct для DCT-III из Large Time-Frequency Analysis Toolbox [15], основанном на библиотеке FFTW [16], которая также используется в Matlab-функции fft для БДПФ.
Времена выполнения для DST-I и DST-III, а также наших прямого и обратного ${{F}_{n}}$-преобразований в случае $n = 5$ (для определенности) даны соответственно на фиг. 3 и 4. Время выполнения для нахождения пар $\{ \lambda _{k}^{{(l)}},p_{k}^{{(l)}}\} $ не принимается во внимание, поскольку оно становится пренебрежимо малым при многократном применении преобразований при фиксированном $K$, как это требуется ниже. Для наших преобразований времена выполнения соответственно выше (чем для DST-I и DST-III) из-за кратного использования БДПФ и некоторых дополнительных вычислений. Обратное ${{F}_{n}}$-преобразование требует меньше времени, чем прямое. Кроме того, наилучшие результаты получаются в основном для $K = {{2}^{p}}$, хотя это не так для DST-I (к счастью, оно применяется в оптимальном случае $K = {{2}^{p}} - 1$). Для двух других выборов $K$ времена выполнения похуже, но близки, и разница между всеми ними меньше, чем в случае как DST-I, так и DST-III. Эти результаты положительного плана. Отметим, что данные на фиг. 4 могут быть аппроксимированы линейными функциями при ${{2}^{5}} \leqslant K \leqslant {{2}^{{10}}}$ и ${{2}^{{10}}} \leqslant K \leqslant {{2}^{{20}}}$, но с довольно плоским наклоном в первом случае и заметно более крутым во втором.
Фиг. 3.
Времена выполнения (в секундах) для DST-I (слева) и DST-III (справа) для нескольких способов выбора $K$ между ${{2}^{5}}$ и ${{2}^{{20}}}$.
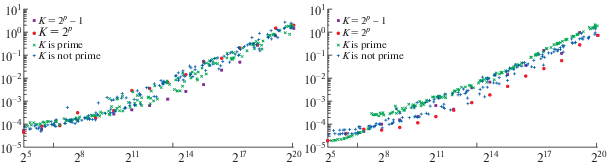
Фиг. 4.
Времена выполнения (в секундах) для прямого (слева) и обратного (справа) ${{F}_{n}}$-преобразований, $n = 5$, для нескольких способов выбора $K$ между ${{2}^{5}}$ и ${{2}^{{20}}}$.
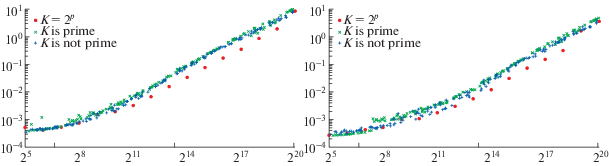
Замечание 4.1. Последнее явление объясняется продвинутой архитектурой современных процессоров, включая кэш-память, потоковые SIMD-расширения, продвинутые векторные расширения набора команд и т.д., а также применением указанных выше реализаций БДПФ высокого качества.
2. Наши основные вычислительные результаты относятся к решению задачи (3.4) как для $N = 2$, так и $N = 3$, при $\alpha = 1$ и ${{X}_{i}} = 1$. Возьмем для простоты ${{K}_{i}} = K$ и ${{n}_{i}} = n$. Для вычисления ${{f}^{h}}$ применим кратные квадратурные формулы Гаусса с $n + 1$ узлами по ${{x}_{i}}$. Собственные пары ${\text{\{ }}\lambda _{k}^{{(l)}},p_{k}^{{(l)}}{\text{\} }}$ 1D задач вычисляются с четверной точностью (с использованием Mathematica) для повышения устойчивости по отношению к ошибкам округления. Отметим, что система (3.5) содержит ${{(Kn - 1)}^{N}}$ неизвестных. Для сравнения включим в анализ простейший и известный случай $n = 1$, реализованный в коде единым образом.
Рассмотрим сначала 2D случай ($N = 2$) и возьмем гладкое точное решение $u(x): = sin(2\pi {{x}_{1}})sin(3\pi {{x}_{2}})\cosh (\sqrt 2 {{x}_{1}} - {{x}_{2}})$. Вычислим МКЭ-решение для различных значений $n$ и $K$ для того, чтобы изучить поведение его (абсолютной) погрешности, см. фиг. 5 и табл. 1 (где значения ${{R}_{C}}$ меньше 3 опущены). Поведение погрешности в равномерной сеточной норме для алгоритма (a) стандартно: скорость убывания ${{R}_{C}}$ в основном пропорциональна ${{(n + 1)}^{2}}$, за исключением случая $n = 2$, когда она выше и аналогична $n = 3$ (такое исключение ранее уже отмечалось в [17]). Любопытно, что при $n = 9$ и минимальном $K = 2$ погрешность уже меньше, чем при $n = 1$ и максимальном $K = 1024$. Разумеется, погрешность не может быть лучше, чем уровень ошибок округления, который достигается тем быстрее, чем выше $5 \leqslant n \leqslant 9$. Наблюдается почти полное отсутствие влияния ошибок округления.
Фиг. 5.
2D случай. Погрешности в равномерной сеточной норме для алгоритмов (a) и (б) в зависимости от $K = 2,4,...,1024$ при $n = \overline {1,9} $.
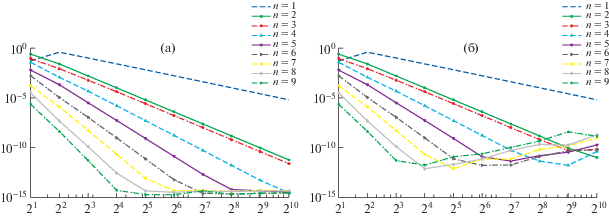
Таблица 1.
2D случай. Погрешности в равномерной сеточной норме и их отношения ${{R}_{C}}$ в зависимости от $K = 2,4, \ldots ,1024$ и $n = \overline {1,9} $ для алгоритма (a)
| K | n = 1 | RC | n = 2 | RC | n = 3 | RC | n = 4 | RC | n = 5 | RC |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 5.1 × 10–2 | – | 2.4 × 10–1 | – | 8.7 × 10–2 | – | 3.7 × 10–2 | – | 6.1 × 10–3 | – |
| 4 | 3.8 × 10–1 | – | 2.5 × 10–2 | 9.6 | 8.4 × 10–3 | 10.3 | 1.2 × 10–3 | 32.2 | 2.1 × 10–4 | 29.3 |
| 8 | 1.0 × 10–1 | 3.8 | 1.6 × 10–3 | 16.1 | 5.9 × 10–4 | 14.2 | 4.7 × 10–5 | 24.5 | 3.3 × 10–6 | 63.8 |
| 16 | 2.6 × 10–2 | 3.9 | 1.0 × 10–4 | 15.7 | 4.1 × 10–5 | 14.6 | 1.6 × 10–6 | 29.3 | 5.4 × 10–8 | 60.8 |
| 32 | 6.6 × 10–3 | 3.9 | 6.2 × 10–6 | 16.1 | 2.6 × 10–6 | 15.6 | 5.2 × 10–8 | 31.1 | 8.5 × 10–10 | 63.2 |
| 64 | 1.6 × 10–3 | 4.0 | 3.9 × 10–7 | 15.9 | 1.6 × 10–7 | 15.9 | 1.7 × 10–9 | 30.6 | 1.3 × 10–11 | 64.0 |
| 128 | 4.1 × 10–4 | 4.0 | 2.4 × 10–8 | 16.0 | 1.0 × 10–8 | 16.0 | 5.4 × 10–11 | 31.4 | 2.1 × 10–13 | 63.1 |
| 256 | 1.0 × 10–4 | 4.0 | 1.5 × 10–9 | 16.0 | 6.4 × 10–10 | 16.0 | 1.7 × 10–12 | 31.7 | 6.4 × 10–15 | 32.8 |
| 512 | 2.6 × 10–5 | 4.0 | 9.6 × 10–11 | 16.0 | 4.0 × 10–11 | 16.0 | 5.4 × 10–14 | 31.7 | 4.7 × 10–15 | – |
| 1024 | 6.4 × 10–6 | 4.0 | 6.0 × 10–12 | 16.0 | 2.5 × 10–12 | 16.0 | 2.9 × 10–15 | 18.6 | 3.6 × 10–15 | – |
| K | n = 6 | RC | n = 7 | RC | n = 8 | RC | n = 9 | RC |
|---|---|---|---|---|---|---|---|---|
| 2 | 1.6 × 10–3 | – | 1.6 × 10–4 | – | 3.2 × 10–5 | – | 2.3 × 10–6 | – |
| 4 | 1.1 × 10–5 | 148.2 | 1.3 × 10–6 | 129.3 | 4.8 × 10–8 | 657.8 | 4.3 × 10–9 | 521.5 |
| 8 | 1.1 × 10–7 | 98.0 | 5.5 × 10–9 | 229.1 | 1.3 × 10–10 | 373.8 | 5.3 × 10–12 | 817.1 |
| 16 | 9.6 × 10–10 | 117.1 | 2.2 × 10–11 | 254.6 | 2.8 × 10–13 | 459.0 | 5.2 × 10–15 | 1019.3 |
| 32 | 7.6 × 10–12 | 125.6 | 8.8 × 10–14 | 245.2 | 4.7 × 10–15 | 60.4 | 2.0 × 10–15 | – |
| 64 | 6.1 × 10–14 | 125.5 | 4.7 × 10–15 | 18.8 | 3.3 × 10–15 | – | 2.0 × 10–15 | – |
| 128 | 2.7 × 10–15 | 22.8 | 5.3 × 10–15 | – | 4.4 × 10–15 | – | 4.4 × 10–15 | – |
| 256 | 2.2 × 10–15 | – | 4.2 × 10–15 | – | 4.0 × 10–15 | – | 2.2 × 10–15 | – |
| 512 | 2.7 × 10–15 | – | 5.3 × 10–15 | – | 4.4 × 10–15 | – | 2.7 × 10–15 | – |
| 1024 | 3.1 × 10–15 | – | 4.9 × 10–15 | – | 4.4 × 10–15 | – | 2.7 × 10–15 | – |
Для алгоритма (б) ситуация аналогична, но только до уровня погрешности $ \sim $${{10}^{{ - 11}}}$. Как только это значение достигается при фиксированном $3 \leqslant n \leqslant 9$, далее наблюдается рост погрешности с возрастанием $K$, что означает ощутимое влияние ошибок округления. Оно происходит из-за соответствующего роста чисел обусловленности в системе (3.10) с возрастанием $K$ или $n$, см. выше фиг. 2. Как следствие, алгоритм (a) предпочтительнее (б), если требуется очень высокая точность. Отметим, что при использовании только двойной точности вычислений уровень наилучшей погрешности становится $ \sim {\kern 1pt} {{10}^{{ - 12}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 13}}}$ и результаты остаются устойчивыми для алгоритма (a), но они практически не меняются для алгоритма (б). Поэтому двойная точность всех вычислений возможна, если указанная точность достаточна (что имеет место в большинстве приложений). Отметим, что устойчивость метода должен повысить переход в разделе 1 от лагранжева базиса к ортогональным многочленам.
Проанализируем также времена выполнения обоих алгоритмов (с использованием кратного запуска кода и медианного времени их выполнения), см. фиг. 6 и табл. 2 и 3 для одних и тех же $K$ и $n$. Очевидно, что они не зависят от указанного выше специального выбора $u$. Время выполнения для вычисления пар $\{ \lambda _{k}^{{(l)}},p_{k}^{{(l)}}\} $ во внимание не принимается, поскольку рассматривается случай, когда они вычисляются заранее и хранятся (напомним, что они не зависят от данных задачи для УрЧП (3.4)). Обратим внимание на слабо сверхлинейную зависимость времен от $K$ и их слабый монотонный рост по $n$. Отметим, что все отношения последовательных времен исполнения в обеих таблицах даже меньше, чем нижняя граница 4 для соответствующих теоретических отношений (отношения меньше 1 опущены); см. в этой связи замечание 4.1. Вопреки теоретическим ожиданиям почти все отношения для алгоритма (a) меньше, чем для (б). Отношения растут с возрастанием $K$ и $n$, и для алгоритма (б) их наибольшее значение уже близко к 4. При максимальных $K = 1024$ и $n = 9$, система (3.5) содержит почти $85 \times {{10}^{6}}$ неизвестных, но требуется только менее 2 мин для ее решения, что является отличным результатом.
Фиг. 6.
2D случай. Времена выполнения (в секундах) для алгоритмов (a) и (б) в зависимости от $K = 8,16,...,1024$ при $n = \overline {1,9} $.

Таблица 2.
2D случай. Отношения времен выполнения для алгоритма (a) в зависимости от $K = 8,16, \ldots ,1024$ при $n = \overline {1,9} $
| K | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 |
|---|---|---|---|---|---|---|---|---|---|
| 8 | – | – | – | 1.46 | 1.6 | 1.97 | 2 | 2.02 | 2.01 |
| 16 | 1.15 | 1.55 | 1.8 | 2.07 | 2.1 | 2.1 | 2.13 | 2.14 | 2.15 |
| 32 | 1.74 | 2.24 | 2.31 | 2.35 | 2.35 | 2.35 | 2.37 | 2.42 | 2.49 |
| 64 | 1.99 | 2.29 | 2.37 | 2.38 | 2.41 | 2.45 | 2.55 | 2.57 | 2.81 |
| 128 | 2.37 | 2.44 | 2.51 | 2.57 | 2.62 | 2.69 | 3.24 | 3.19 | 3.1 |
| 256 | 2.46 | 2.49 | 2.46 | 2.53 | 3.07 | 3.08 | 2.9 | 3.08 | 3.05 |
| 512 | 2.49 | 2.66 | 2.66 | 3.33 | 3.02 | 3.15 | 2.99 | 3.08 | 3.11 |
| 1024 | 2.52 | 2.69 | 3.33 | 3.04 | 3.07 | 3.13 | 3.14 | 3.22 | 3.34 |
Таблица 3.
2D случай. Отношения времен выполнения для алгоритма (б) в зависимости от $K = 8,16, \ldots ,1024$ при $n = \overline {1,9} $
| K | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 |
|---|---|---|---|---|---|---|---|---|---|
| 8 | – | – | – | 1.17 | 1.28 | 1.97 | 1.99 | 1.99 | 2.01 |
| 16 | – | 1.39 | 1.64 | 2.02 | 2.09 | 2.08 | 2.13 | 2.2 | 2.22 |
| 32 | 2.04 | 1.84 | 2.17 | 2.38 | 2.47 | 2.54 | 2.49 | 2.53 | 2.61 |
| 64 | 1.57 | 2.26 | 2.42 | 2.42 | 2.44 | 2.52 | 2.67 | 2.74 | 2.88 |
| 128 | 2.34 | 2.49 | 2.52 | 2.67 | 2.77 | 2.85 | 3.21 | 3.21 | 3.27 |
| 256 | 2.5 | 2.6 | 2.64 | 2.8 | 3.13 | 3.27 | 3.25 | 3.34 | 3.44 |
| 512 | 2.58 | 2.76 | 2.91 | 3.31 | 3.37 | 3.29 | 3.31 | 3.4 | 3.43 |
| 1024 | 2.68 | 2.98 | 3.36 | 3.36 | 3.33 | 3.53 | 3.58 | 3.84 | 3.94 |
В заключение рассмотрим наиболее интересный 3D случай ($N = 3$) и возьмем точное решение $u(x): = sin(2\pi {{x}_{1}})sin(3\pi {{x}_{2}})sin(4\pi {{x}_{3}})cosh(\sqrt 2 {{x}_{1}} - {{x}_{2}} + {{x}_{3}}{\text{/}}\sqrt 3 )$. Опять вычислим МКЭ-решение для различных значений $K = 2,4, \ldots ,64$ и $n = \overline {1,9} $ и изучим поведение погрешности, см. фиг. 7 и табл. 4 (где значения ${{R}_{C}}$ меньше 3 опущены). Здесь можно сделать в основном те же самые выводы, что и в 2D случае. Отметим, что более плохие свойства устойчивости алгоритма (б) проявляются только при высоких $n = 8,9$, поскольку берется намного меньшее максимальное значение $K$.
Фиг. 7.
3D случай. Погрешности в равномерной сеточной норме для алгоритмов (a) и (б) в зависимости от $K = 2,4,...,64$ при $n = \overline {1,9} $.
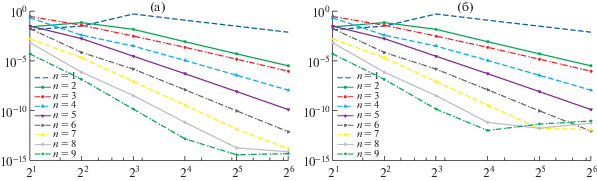
Таблица 4.
3D случай. Погрешности в равномерной сеточной норме и их отношения ${{R}_{C}}$ в зависимости от $K = 2,4, \ldots ,64$ и $n = \overline {1,9} $ для алгоритма (a)
| K | n = 1 | RC | n = 2 | RC | n = 3 | RC | n = 4 | RC | n = 5 | RC |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1.3 × 10–2 | – | 2.6 × 10–2 | – | 2.8 × 10–1 | – | 2.1 × 10–1 | – | 3.1 × 10–2 | – |
| 4 | 3.1 × 10–2 | – | 6.9 × 10–2 | – | 3.7 × 10–2 | 7.6 | 3.8 × 10–3 | 54.6 | 1.7 × 10–3 | 18.5 |
| 8 | 5.0 × 10–1 | – | 1.5 × 10–2 | 4.7 | 3.1 × 10–3 | 12.2 | 3.0 × 10–4 | 12.5 | 2.9 × 10–5 | 57.8 |
| 16 | 1.2 × 10–1 | 4.2 | 8.4 × 10–4 | 17.4 | 2.3 × 10–4 | 13.4 | 1.1 × 10–5 | 27.7 | 5.1 × 10–7 | 56.8 |
| 32 | 3.0 × 10–2 | 4.0 | 5.1 × 10–5 | 16.4 | 1.5 × 10–5 | 15.5 | 3.6 × 10–7 | 30.6 | 8.3 × 10–9 | 62.0 |
| 64 | 7.5 × 10–3 | 4.0 | 3.2 × 10–6 | 16.0 | 9.2 × 10–7 | 16.0 | 1.2 × 10–8 | 31.1 | 1.3 × 10–10 | 64.0 |
| K | n = 6 | RC | n = 7 | RC | n = 8 | RC | n = 9 | RC |
|---|---|---|---|---|---|---|---|---|
| 2 | 1.7 × 10–2 | – | 1.6 × 10–3 | – | 6.6 × 10–4 | – | 5.0 × 10–5 | – |
| 4 | 7.0 × 10–5 | 245.2 | 2.1 × 10–5 | 77.3 | 7.2 × 10–7 | 909.9 | 1.4 × 10–7 | 355.4 |
| 8 | 1.5 × 10–6 | 46.9 | 8.4 × 10–8 | 248.1 | 3.3 × 10–9 | 221.1 | 1.4 × 10–10 | 961.4 |
| 16 | 1.3 × 10–8 | 119.5 | 3.6 × 10–10 | 230.7 | 6.7 × 10–12 | 486.8 | 1.5 × 10–13 | 957.3 |
| 32 | 9.7 × 10–11 | 128.9 | 1.4 × 10–12 | 254.2 | 1.9 × 10–14 | 360.8 | 3.8 × 10–15 | 40.1 |
| 64 | 7.8 × 10–13 | 124.9 | 1.5 × 10–14 | 94.6 | 7.5 × 10–15 | – | 4.9 × 10–15 | – |
Времена выполнения в 3D случае представлены на фиг. 8 и в табл. 5 и 6. Опять естественны выводы, аналогичные сделанным в 2D случае. Все отношения в обеих таблицах заметно ниже, чем нижняя граница 8 для соответствующих теоретических отношений. Важно, что для максимальных $K = 64$ и $n = 9$ система (3.5) содержит более, чем $190 \times {{10}^{6}}$ неизвестных, но требуется только менее 15 мин для ее решения, что является хорошим результатом (результат менее быстрый, чем в 2D случае, из-за неэффективной Matlab-реализации вложенных циклов).
Фиг. 8.
3D случай. Времена выполнения (в секундах) для алгоритмов (a) и (б) в зависимости от $K = 2,4,...,64$ при $n = \overline {1,9} $.

Таблица 5.
3D случай. Отношения времен выполнения для алгоритма (a) в зависимости от $K = 4,8, \ldots ,64$ при $n = \overline {1,9} $
| K | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 |
|---|---|---|---|---|---|---|---|---|---|
| 4 | 1.68 | 2.05 | 2.34 | 4.51 | 4.35 | 4.62 | 4.58 | 4.52 | 4.49 |
| 8 | 1.15 | 2.6 | 3.82 | 4.23 | 4.23 | 4.25 | 4.22 | 4.29 | 4.24 |
| 16 | 4.21 | 4.47 | 4.31 | 4.22 | 4.29 | 4.27 | 4.29 | 4.3 | 4.31 |
| 32 | 4.85 | 4.79 | 4.8 | 4.89 | 4.78 | 4.84 | 4.83 | 4.86 | 5.03 |
| 64 | 4.32 | 4.46 | 4.78 | 4.77 | 4.88 | 4.93 | 5.05 | 5.16 | 5.52 |
Таблица 6.
3D случай. Отношения времен выполнения для алгоритма (б) в зависимости от $K = 4,8, \ldots ,64$ при $n = \overline {1,9} $
| K | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 |
|---|---|---|---|---|---|---|---|---|---|
| 4 | – | 1.9 | 2.09 | 4.24 | 4.32 | 4.51 | 4.47 | 4.51 | 4.41 |
| 8 | – | 2.29 | 3.6 | 4.19 | 4.25 | 4.23 | 4.23 | 4.26 | 4.25 |
| 16 | 3.65 | 4.28 | 4.29 | 4.3 | 4.32 | 4.35 | 4.36 | 4.44 | 4.46 |
| 32 | 4.89 | 4.75 | 4.78 | 4.81 | 4.81 | 4.96 | 4.94 | 5 | 5.22 |
| 64 | 4.43 | 4.68 | 4.87 | 4.89 | 5.01 | 5.08 | 5.31 | 5.47 | 5.71 |
Список литературы
Сьярле Ф. Метод конечных элементов для эллиптических задач. М.: Мир, 1980.
Swarztrauber P.N. The methods of cyclic reduction, Fourier analysis and the FACR algorithm for the discrete solution of Poisson’s equation on a rectangle // SIAM Review. 1977. V. 19. № 3. P. 490–501.
Самарский А.А., Николаев Е.В. Методы решения сеточных уравнений. М.: Наука, 1978.
Kwan Y.-Y., Shen J. An efficient direct parallel spectral-element solver for separable elliptic problems // J. Comput. Phys. 2007. V. 225. P. 1721–1735.
Bialecki B., Fairweather G., Karageorghis A. Matrix decomposition algorithms for elliptic boundary value problems: a survey // Numer. Algor. 2011. V. 56. P. 253–295.
Britanak V., Rao K.R., Yip P. Discrete cosine and sine transforms: general properties, fast algorithms and integer approximations. Oxford: Academic Press – Elsevier, 2007.
Злотник А.А., Злотник И.А. Быстрый прямой алгоритм реализации метода конечных элементов высокого порядка на прямоугольниках для краевых задач для уравнения Пуассона // Докл. АН. 2017. Т. 473. № 3. С. 131–137.
Кузнецов Ю.А. Вычислительные методы в подпространствах // В сб.: Вычислительные процессы и системы. Вып. 2. Под ред. Г.И. Марчука. М.: Наука, 1985. С. 265–350.
Du K., Fairweather G., Sun W. Matrix decomposition algorithms for arbitrary order ${{C}^{0}}$ tensor product finite element systems // J. Comput. Appl. Math. 2015. V. 275. P. 162–182.
Дьяконов Е.Г. Минимизация вычислительной работы. Асимптотически оптимальные алгоритмы для эллиптических задач. М.: Наука, 1989.
Zlotnik A., Zlotnik I. Finite element method with discrete transparent boundary conditions for the time-dependent 1D Schrödinger equation // Kinetic Relat. Models. 2012. V. 5. № 3. P. 639–667.
Ducomet B., Zlotnik A., Zlotnik I. The splitting in potential Crank-Nicolson scheme with discrete transparent boundary conditions for the Schrödinger equation on a semi-infinite strip // ESAIM: Math. Model. Numer. Anal. 2014. V. 48. № 6. P. 1681–1699.
Altman Y.M. Accelerating MATLAB Performance: 1001 Tips to Speed up MATLAB Programs. New York: Chapman and Hall/CRC, 2014.
Eddins S. Timing the FFT, http://blogs.mathworks.com/steve/2014/04/07/timing-the-fft/
Průša Z., Søndergaard P.L., Holighaus N., Wiesmeyr C., Balazs P. The large time-frequency analysis toolbox 2.0. Sound, music, and motion // Lecture Notes in Computer Science. V. 2014. P. 419–442.
Frigo M., Johnson S.G. The design and implementation of FFTW3 // Proc. IEEE. 2005. V. 93. P. 216–231.
Du K., Fairweather G., Nguyen Q.N., Sun W. Matrix decomposition algorithms for the C 0-quadratic finite element Galerkin method // BIT Numer. Math. 2009. V. 49. P. 509–526.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики