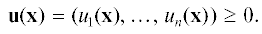Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 520-533
Проблема идентификации модели замещения производственных факторов
Е. Г. Молчанов *
Московский физико-технический институт
141701 Долгопрудный, Институтский пер., 9, Россия
* E-mail: molchanov.eg@mipt.ru
Поступила в редакцию 05.08.2019
После доработки 05.08.2019
Принята к публикации 18.11.2019
Аннотация
Исследована обобщенная модель Хаутеккера–Йохансена, позволяющая провести идентификацию замещения производственных факторов на основе публикуемой российской статистики. Исследованы комбинаторные структуры, связанные с задачей об оценке эластичности замещения производственных факторов на микроуровне. На языке комбинаторных структур – ромбических тайлингов – сформулированы и доказаны необходимое и достаточное условия разрешимости проблемы моментов, возникающей в задаче об оценке эластичности замещения производственных факторов на микроуровне. Проведена идентификация обобщенной модели Хаутеккера–Йохансена по данным российской статистики. Сопоставлены оценки импорта производственных факторов, полученные на основе гипотезы Леонтьева о постоянстве удельных затрат и вычисленные с помощью обобщенной модели Хаутеккера–Йохансена. Библ. 16. Фиг. 1. Табл. 1.
1. ВВЕДЕНИЕ
Традиционные способы обработки экономической статистики и моделирования производственной системы основаны на гипотезе о постоянстве пропорций потребляемых товаров и производственных факторов. В число таких подходов входят классические показатели и модели, такие как индекс Ласпейреса и модель межотраслевого баланса В.В. Леонтьева. В послевоенное тридцатилетие XX века в мировой экономике наблюдался экстенсивный восстановительный рост. В этот период в экономике появились оптимальные пропорции потребляемых товаров и производственных факторов, что хорошо описывается с помощью теорем Моришимы о магистрали в моделях экстенсивного экономического роста. Гипотеза о постоянстве пропорций потребляемых товаров и производственных факторов была оправданна, а собираемую статистику было принято анализировать с помощью модели Леонтьева. Такая обработка ведется и по сей день. Однако с последней четверти XX века эти пропорции стали меняться и зависеть от текущей конъюнктуры. Это происходило как вследствие открытия границ и появления большого выбора товаров, что привело к экономической нестабильности и разнообразию, так и из-за процесса глобализации, когда стандартизация и конкуренция привели к тому, что на внутренних рынках развивающихся стран отечественные товары стали конкурировать с импортными аналогами. Из-за изменения пропорций появились проблемы с идентификацией общепринятых моделей. Перечисленные эффекты должны найти отображение в обработке экономической статистики.
2. ОБОБЩЕННАЯ МОДЕЛЬ ХАУТЕККЕРА–ЙОХАНСЕНА
Будем описывать функционирование отрасли с помощью обобщенной модели Хаутеккера–Йохансена (см. [1]), в которой предполагается, что отрасль выпускает однородную продукцию и использует несколько производственных факторов текущего пользования (ПФТП).
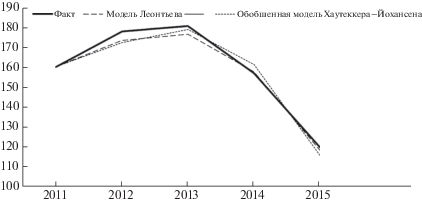
В данной модели производство распределено по технологиям, задающимся вектором ${\mathbf{x}} = ({{x}_{1}},\; \ldots ,\;{{x}_{n}})$ удельного потребления отечественных и импортных производственных факторов на выпуск единицы продукции, при этом возможно замещение производственных факторов на микроуровне: технологии с параметрами ${\mathbf{x}} = ({{x}_{1}},\; \ldots ,\;{{x}_{n}})$ и единичной мощностью соответствует производственная функция $min\left( {1,f\left( {\tfrac{{{{u}_{1}}}}{{{{x}_{1}}}},\; \ldots ,\;\tfrac{{{{u}_{n}}}}{{{{x}_{n}}}}} \right)} \right)$, где ${\mathbf{u}} = ({{u}_{1}},\; \ldots ,\;{{u}_{n}})$ – вектор затрат ПФТП. В качестве примера функции, описывающей замещение производственных факторов, будем использовать функцию с постоянной эластичностью замещения (CES-функцию), имеющую вид
(1)
$f({{\nu }_{1}},\; \ldots ,\;{{\nu }_{n}}) = {{(\nu _{1}^{{ - \varepsilon }} + \; \ldots \; + \nu _{n}^{{ - \varepsilon }})}^{{ - \tfrac{1}{\varepsilon }}}} = {{\nu }_{1}}{{ \oplus }_{\varepsilon }}\; \ldots \;{{ \oplus }_{\varepsilon }}{{\nu }_{n}},\quad где\quad \varepsilon \geqslant - 1.$Если $\varepsilon = - 1$, то $f({{\nu }_{1}},\; \ldots ,\;{{\nu }_{n}}) = {{\nu }_{1}} + \; \ldots \; + {{\nu }_{n}}$ и описывает полностью взаимозаменяемые производственные факторы. В этом случае обобщенная модель Хаутеккера–Йохансена перейдет в “стандартную” модель Хаутеккера–Йохансена, описанную, например, в [3], [4].
Рассмотрим задачу об оптимальном распределении ресурсов с целью максимизации суммарного выпуска отрасли:
(2)
$\int\limits_{R_{ + }^{n}} {min} \left( {1,f\left( {\frac{{{{u}_{1}}({\mathbf{x}})}}{{{{x}_{1}}}},\; \ldots ,\;\frac{{{{u}_{n}}({\mathbf{x}})}}{{{{x}_{n}}}}} \right)} \right)\mu (d{\mathbf{x}}) \to \mathop {max}\limits_{u({\mathbf{x}})} ,$(3)
$\int\limits_{R_{ + }^{n}} {{{u}_{j}}} ({\mathbf{x}})\mu (d{\mathbf{x}}) \leqslant {{l}_{j}},\quad j = 1, \ldots ,n,$Пусть ${\mathbf{p}} \circ {\mathbf{x}} = ({{p}_{1}}{{x}_{1}},\; \ldots \;,{{p}_{n}}{{x}_{n}})$. Тогда себестоимость производства единицы продукции по технологии ${\mathbf{x}}$ при ценах ${\mathbf{p}}$ равна $h({\mathbf{p}} \circ {\mathbf{x}})$.
Предложение 2.1 (см. [7]). Справедливы следующие утверждения.
• Если ${\mathbf{l}} \geqslant 0$, то задача (2)–(4) имеет решение в классе вектор-функций ${\mathbf{u}}({\mathbf{x}})$ с интегрируемыми по мере $\mu ( \cdot )$ компонентами.
• Для того, чтобы вектор-функция ${\mathbf{u}}({\mathbf{x}})$, удовлетворяющая (3), (4), была решением задачи (2)–(4), необходимо, а при ${\mathbf{l}} > 0$ достаточно, чтобы существовали такие одновременно не равные нулю числа ${{p}_{0}} \geqslant 0$, ${\mathbf{p}} = ({{p}_{1}},\; \ldots \;,{{p}_{n}}) \geqslant 0$, что
• ${\mathbf{u}}({\mathbf{x}}) = 0$ для почти всех по мере $\mu ( \cdot )$ ${\mathbf{x}} \in R_{ + }^{n}$, таких, что ${{p}_{0}} < h({\mathbf{p}} \circ {\mathbf{x}})$.
• $f({\mathbf{u}}({\mathbf{x}})) = 1$ для почти всех по мере $\mu ( \cdot )$ ${\mathbf{x}} \in R_{ + }^{n}$, таких, что ${{p}_{0}} > h({\mathbf{p}} \circ {\mathbf{x}})$.
Здесь и далее под выражениями вида ${\mathbf{l}} \geqslant 0$ подразумевается, что все компоненты указанного вектора неотрицательны. Интерпретируя множители Лагранжа ${{p}_{0}}$, ${\mathbf{p}} = ({{p}_{1}},\; \ldots ,\;{{p}_{n}})$ как цены на выпускаемую продукцию и ПФТП соответственно, получаем, что оптимальный механизм распределения ресурсов эквивалентен рыночному механизму, при котором технологии, приносящие прибыль при ценах ${{p}_{0}} \geqslant 0,{\text{ }}{\mathbf{p}} = ({{p}_{1}},\; \ldots ,\;{{p}_{n}}) \geqslant 0$, загружаются на полную мощность, а убыточные технологии не используются. При этом цены устанавливаются из условия равновесия спроса и предложения на рынке ПФТП.
2.1. Проблема моментов в задаче оценки эластичности замещения производственных факторов на микроуровне
Рассмотрим вопрос об идентификации обобщенной модели Хаутеккера–Йохансена в современных российских условиях. Исследование случая двух производственных факторов ($n = 2$), импортного и отечественного, особенно интересно в связи с тем, что в условиях глобализации мировой экономики на внутреннем рынке России отечественная продукция отраслей обрабатывающей промышленности конкурирует с импортом. В периоды, когда Центральный Банк РФ поддерживает стабильный курс рубля, импорт вытесняет с рынка отечественные товары из-за более высоких темпов инфляции в России, чем в развитых капиталистических странах, продукция которых импортируется в Россию. Когда происходит ослабление курса рубля из-за очередного экономического кризиса, происходит обратный процесс замещения импорта. В течение последних десятилетий эти периоды чередовались и способствовали процессам стандартизации. В результате производство адаптировалось к рыночным условиям за счет взаимозаменяемости производственных факторов на микроуровне, которую и нужно оценить.
В связи с этим, начиная с этого момента, будем считать, что производственных факторов $n = 2$.
В российской статистике доступны помесячные временные ряды объемов производства и цен на выпускаемую продукцию и производственные факторы. Также в статистике доступны таблицы национальных счетов – таблицы “ресурсов товаров и услуг” и таблицы “использования товаров и услуг”. Эти таблицы публикуются за каждый год и с существенной задержкой. С помощью этих таблиц можно выяснить потребление отраслью производственных факторов. Однако замещение производственных факторов происходит в быстром времени, гораздо меньше года. В связи с этим годичные данные потребления производственных факторов не годятся для восстановления технологической структуры производства $\mu (d{\mathbf{x}})$, но их можно использовать для проверки идентификации такой структуры.
Таким образом, единственными показателями, которые можно использовать для идентификации технологической структуры отрасли, являются помесячные временные ряды объемов производства и цен на выпускаемую продукцию и производственные факторы.
Обозначим через $y(t) > 0$ выпуск отрасли в период времени $t$, через ${{p}_{0}}(t)$ “– цену на выпускаемую продукцию в период времени $t$, через ${\mathbf{p}}(t) > 0$ – вектор цен на используемые отраслью ПФТП в период времени $t$. Так как согласно предложению 1 ${\mathbf{u}}({\mathbf{x}}) = 0$, если ${{p}_{0}} < h({\mathbf{p}} \circ {\mathbf{x}})$, и $f({\mathbf{u}}({\mathbf{x}})) = 1$, если ${{p}_{0}} > h({\mathbf{p}} \circ {\mathbf{x}})$, мы можем считать, что
Предложение 2.2. Для того, чтобы наблюдаемые временные ряды $\{ y(t),\;{{p}_{0}}(t),\;{\mathbf{p}}(t)\,|\,t = 1,\; \ldots ,\;T\} $ были согласованы с функцией себестоимости $h({\mathbf{p}} \circ {\mathbf{x}})$, нужно, чтобы была разрешима проблема моментов
(5)
$\int\limits_{R_{ + }^{n}} \theta ({{p}_{0}}(t) - h({\mathbf{p}}(t) \circ {\mathbf{x}}))\mu (d{\mathbf{x}}) = y(t),\quad t = 1,\; \ldots ,\;T,$Предложение 2.2 непосредственно следует из Предложения 2.1.
Важным случаем производственной функции, описывающей замещение производственных факторов, является функция с постоянной эластичностью замещения (CES-функция), заданная формулой (1). Отметим, что преобразование Янга, задающее функцию себестоимости $h({\mathbf{p}}(t) \circ {\mathbf{x}}),$ также приведет к CES-функции вида
Исследование проблемы моментов (5) приводит к дискретным постановкам обратных задач в моделях замещения производственных факторов и изучению их комбинаторных свойств.
2.2. Исследование проблемы моментов, возникающей в задаче оценки эластичности замещения производственных факторов на микроуровне
Обозначим через ${\mathbf{y}} = \left( {y(1),y(2),\; \ldots ,\;y(T)} \right)$ вектор, компонентами которого являются правые части уравнений (5), т.е. выпуски в различные периоды времени.
Неотрицательный ортант $\mathbb{R}_{ + }^{2}$ разбивается кривыми $\{ {\mathbf{x}}\,|\,{{p}_{0}}(t) = h({\mathbf{p}}(t) \circ {\mathbf{x}})\} $ на области. В силу положительной однородности функций себестоимости $h({\mathbf{p}}(t) \circ {\mathbf{x}})$ разбиение можно однозначно задать векторами
Обозначим через ${{\Lambda }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $ множество областей этого разбиения, а через $L$ – число элементов в множестве ${{\Lambda }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $. Сопоставим области $G \in {{\Lambda }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $ вектор $Z(G)$, компоненты которого вычисляются по формулеПредложение 2.3 (см. [6]). Для того, чтобы проблема моментов (5) была разрешима в классе неотрицательных мер $\mu (d{\mathbf{x}})$, необходимо и достаточно, чтобы $y = (y(1),\; \ldots ,\;y(T)) \in {{\Gamma }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $.
Для эффективного использования предложения 2.3 в проблеме идентификации обобщенной модели Хаутеккера–Йохансена нужно исследовать свойства многогранного конуса ${{\Gamma }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $, а также сопряженного к нему конуса, ребрами которого являются нормали к граням конуса ${{\Gamma }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $. Отметим (см. [1]), что нормали к граням конуса ${{\Gamma }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $ можно выбрать так, чтобы их компоненты были целочисленными.
Таким образом, для проверки принадлежности вектора $y$ к конусу ${{\Gamma }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $ необходимо конечное число раз исследовать условия вида ${\mathbf{yn}} \geqslant 0$, где ${\mathbf{n}}$ – целочисленные векторы нормалей к фасетам конуса ${{\Gamma }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $.
2.3. Комбинаторные свойства разбиения $\mathbb{R}_{ + }^{2}$ прямыми
В [1] описана замена переменных, которая получает разбиение положительного ортанта $\mathbb{R}_{ + }^{2}$ прямыми, эквивалентное разбиению $\mathbb{R}_{ + }^{2}$ CES-кривыми $\{ {\mathbf{x}}\,|\,{{p}_{0}}(t) = h({\mathbf{p}}(t) \circ {\mathbf{x}}) = ({{p}_{1}}{{x}_{1}}){{ \oplus }_{\rho }}({{p}_{1}}{{x}_{1}})\} $. В новых переменных задача определения эластичности замещения производственных факторов на микроуровне из диапазона $\rho \in [ - 1,0) \cup (0, + \infty )$ формулируется следующим образом: найти значения параметра $\rho \in [ - 1,0) \cup (0, + \infty )$, при которых разрешима проблема моментов
(6)
$\int\limits_{R_{ + }^{n}} \theta (1 - {{\tilde {p}}_{1}}(t,\rho ){{z}_{1}} - {{\tilde {p}}_{2}}(t,\rho ){{z}_{2}})\tilde {\mu }(d{\mathbf{x}}) = y(t),\quad t = 1,\; \ldots ,\;T,$Обозначим через ${{S}_{\rho }}(T)$ множество всех возможных конических оболочек $\left\{ {Z(G)\,|\,Z \in {{\Lambda }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} } \right\}$ при различных $\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $ при фиксированном $T$ и $\rho $. Конус ${{\Gamma }_{h}}\{ {\mathbf{\hat {p}}}(t)\,|\,t = 1,\; \ldots ,\;T\} $ будем считать зависящим от $\rho $ и обозначать через $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $, а области разбиения неотрицательного ортанта $R_{ + }^{2}$ “– через $\Lambda \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $.
Дополнительно перенумеруем временной ряд $t = 1,\; \ldots ,\;T$ так, чтобы $\mathop {\tilde {p}}\nolimits_1 (1,\rho ) < \mathop {\tilde {p}}\nolimits_1 (2,\rho ) < \; \ldots \; < \mathop {\tilde {p}}\nolimits_1 (T,\rho )$ $\mathop {\tilde {p}}\nolimits_1 (1,\rho ) < \mathop {\tilde {p}}\nolimits_1 (2,\rho ) < \; \ldots \; < \mathop {\tilde {p}}\nolimits_1 (T,\rho )$. При изменении параметра $\rho $ внутри промежутка $[ - 1,0)$ или $(0, + \infty )$ данные неравенства нарушаться не будут. После перенумерования временного ряда рассмотрим порядок, задаваемый величинами $\{ \mathop {\tilde {p}}\nolimits_2 (t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $. Пусть данный порядок описывается элементом симметрической группы $\sigma \{ \mathop {\tilde {p}}\nolimits_2 (t,\rho )\,|\,t = 1,\; \ldots ,\;T\} \in {{S}_{T}}$. Данный порядок также не изменяется при изменении параметра $\rho $ внутри промежутка $[ - 1,0)$ или $(0, + \infty )$.
Опишем разложение порядка $\sigma \{ \mathop {\tilde {p}}\nolimits_2 (t,\rho )\,|\,t = 1,\; \ldots ,\;T\} \in {{S}_{T}}$ на транспозиции следующим образом. Рассмотрим в $R_{ + }^{2}$ семейство лучей
(7)
$\left\{ {{{z}_{2}} = {{z}_{1}}\alpha \left| {\alpha \in \left( {0;\frac{\pi }{2}} \right),\;{{z}_{1}} > 0} \right.} \right\}$(8)
$\{ \mathop {\tilde {p}}\nolimits_1 \left( {t,\rho } \right){{z}_{1}} + \mathop {\tilde {p}}\nolimits_2 \left( {t,\rho } \right){{z}_{2}} = 1\,|\,t = 1,\; \ldots ,\;T\} .$Выпишем порядок $\pi \left( \alpha \right) = \left( {{{\pi }_{1}}\left( \alpha \right),\; \ldots ,\;{{\pi }_{T}}\left( \alpha \right)} \right) \in {{S}_{T}}$ пересечения луча семейства (7) при фиксированном $\alpha $ прямыми семейства (8). Здесь первая компонента $\pi \left( \alpha \right)$ будет соответствовать индексу кривой, соответствующей самой дальней от начала координат точке пересечения, а последняя компонента – самой ближней. При увеличении $\alpha $ в промежутке $\left( {0,\tfrac{\pi }{2}} \right)$ данный порядок будет меняться при каждом прохождении лучом семейства (7) точки пересечения пары прямых семейства (8). Опишем такое изменение символом ${{\sigma }_{t}}$, где $t = 1,\; \ldots ,\;T - 1$, который будет означать элементарную транспозицию в текущем порядке ${{\pi }_{t}}(\alpha )$ и ${{\pi }_{{t + 1}}}(\alpha )$ элементов. Выпишем при увеличении $\alpha $ в промежутке $\left( {0,\tfrac{\pi }{2}} \right)$ все символы, соответствующие транспозициям, в строку и получим слово. Обозначим это слово как $W\{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $. Заметим, что это слово однозначно определяет множество спектральных векторов разбиения и порождаемый им конус $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $. Действительно, если выписывать все символы, соответствующие транспозициям, при увеличении угла $\alpha $ в промежутке $(0,\alpha *)$, $\alpha * < \tfrac{\pi }{2}$, то вместо слова $W\{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $ может быть начальное подслово (т.е. подслово, содержащее самый левый символ исходного слова). Однако это подслово задает порядок $\pi (\alpha *)$, а этот полученный порядок $\pi (\alpha *)$ однозначно устанавливает спектры областей, через которые проходит луч $\left\{ {{{z}_{2}} = {{z}_{1}}\alpha {\text{*}},\;{{z}_{1}} > 0} \right\}$. Спектры этих областей имеют вид
Слова $W\{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $ являются представлением симметрической группы ${{S}_{T}}$ и удовлетворяют соотношениям Мура–Кокстера:
(9б)
${{\sigma }_{{{{t}_{1}}}}}{{\sigma }_{{{{t}_{2}}}}} = {{\sigma }_{{{{t}_{2}}}}}{{\sigma }_{{{{t}_{1}}}}},\quad если\quad \left| {{{t}_{1}} - {{t}_{2}}} \right| > 1;$(9в)
${{\sigma }_{t}}{{\sigma }_{{t + 1}}}{{\sigma }_{t}} = {{\sigma }_{{t + 1}}}{{\sigma }_{t}}{{\sigma }_{{t + 1}}}.$Описание симметрической группы с помощью таких соотношений изучено в работе Ласку–Шютценберже [8].
Операция (9а) изменяет конус $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $, однако является невозможной, поскольку предполагает пересечение пары прямых семейства (8) более одного раза.
Операция (9б) не меняет конус $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $, а следовательно, и разрешимость проблемы моментов.
Операция (9в) изменяет конус $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $ и соответствует проходу на одной прямой семейства (8) через точку пересечения пары других прямых при изменении параметра $\rho $.
В [1] показано, что если два разложения на транспозиции ${{W}_{1}}$, ${{W}_{2}}$ преобразуют порядок $i{{d}_{T}} = (1,\; \ldots ,\;T)$ в один и тот же порядок $\sigma \{ \mathop {{\mathbf{\tilde {p}}}}\nolimits_2 (t,\rho )\,|\,t = 1,\; \ldots ,\;T\} \in {{S}_{T}}$, то их можно получить друг из друга с помощью применения конечного числа соотношений Мура–Кокстера (9б) и (9в).
2.4. Ромбические тайлинги, соответствующие разбиению
Изменения конуса, происходящие при проходе одной прямой семейства (8) через точку пересечения пары других прямых при изменении параметра $\rho $, соответствующие операции (12C), удобно представлять в терминах деформаций ромбических тайлингов. Понятие ромбических тайлингов изучается, например, в [8].
Построим ромбический тайлинг, соответствующий разбиению $\Lambda \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $, следующим образом:
• Задание $T$ векторов
Зафиксируем $T$ векторов на плоскости, например,
• Вершины ромбического тайлинга
Сопоставим каждой области $G$ разбиения $\Lambda \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $ вершину ромбического тайлинга $\nu (G) = \sum\nolimits_{\{ j|{{z}_{j}}(G) = 1\} } {\mathop \xi \nolimits_j } $.
• Змейки ромбического тайлинга
Для каждого луча (7) в соответствии с порядком $\pi (\alpha ) = ({{\pi }_{1}}(\alpha ),\; \ldots ,\;{{\pi }_{T}}(\alpha ))$ соединим отрезками пары вершин ромбического тайлинга, $\sum\nolimits_{j = {{\pi }_{1}}(\alpha )}^{{{\pi }_{k}}(\alpha )} {\mathop {\mathbf{\xi }}\nolimits_j } $ и $\sum\nolimits_{j = {{\pi }_{{k + 1}}}(\alpha )}^{{{\pi }_{T}}(\alpha )} {\mathop {\mathbf{\xi }}\nolimits_j } $, где $k = 1,\; \ldots ,\;T - 1$. Кроме того, соединим ${{\xi }_{{{{\pi }_{T}}(\alpha )}}}$ с началом координат 0. Полученная в результате ломаная кривая называется змейкой.
• Ромбы ромбического тайлинга
Если угол наклона луча $\alpha $ изменяется в диапазоне, в котором лучи не проходят через точки пересечения двух прямых семейства (8), то соответствующая им змейка остается без изменений. Если же луч проходит через точку пересечения кривых $\{ \mathop {{\mathbf{\tilde {p}}}}\nolimits_1 ({{\pi }_{j}}(\alpha ),\rho ){{z}_{1}} + \mathop {{\mathbf{\tilde {p}}}}\nolimits_2 ({{i}_{j}}(\alpha ),\rho ){{z}_{2}} = 1\} $, $\{ \mathop {{\mathbf{\tilde {p}}}}\nolimits_1 ({{\pi }_{{j + 1}}}(\alpha ),\rho ){{z}_{1}} + {{{\mathbf{\tilde {p}}}}_{2}}({{\pi }_{{j + 1}}}(\alpha ),\rho ){{z}_{2}} = 1\} $, то к змейке, соответствующей порядку $(\alpha - 0)$, добавляется вершина
Совокупность змеек и ромбов, соответствующих элементарным транспозициям, образует ромбический тайлинг. Границами этого ромбического тайлинга являются две змейки, соответствующие порядкам $i{{d}_{T}} = (1,\; \ldots ,\;T) \in {{S}_{T}}$ и $\sigma \{ \mathop {{\mathbf{\tilde {p}}}}\nolimits_2 (t,\rho )\,|\,t = 1,\; \ldots ,\;T\} \in {{S}_{T}}$.
Отметим, что векторы ромбического тайлинга, равные $\mathop {\mathbf{\xi }}\nolimits_i $, будут соответствовать парам областей, которые разрезает $i$-я прямая семейства (8). Таким образом, можно считать, что прямая семейства (8) соответствует множеству равных векторов ромбического тайлинга.
В терминах ромбических тайлингов можно сформулировать необходимое и достаточное условия разрешимости проблемы моментов в терминах ромбических тайлингов (см. [1]).
Достаточное условие разрешимости проблемы моментов (6). Пусть порядок $\lambda $ такой, что $y(\lambda (j)) > y(\lambda (j + 1))$, $j = 1,\; \ldots ,\;T - 1$. Если змейка, соответствующая порядку $\lambda $, содержится в ромбическом тайлинге, построенном по разбиению $\Lambda \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $, то проблема моментов (6) разрешима.
Необходимое условие разрешимости проблемы моментов (6). Пусть порядок $\lambda $ такой, что $y(\lambda (j)) > y(\lambda (j + 1))$, $j = 1,\; \ldots ,\;T - 1$. Если змейка, соответствующая порядку $\lambda $, выходит за границы ромбического тайлинга, построенного по разбиению $\Lambda \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $, то проблема моментов (6) неразрешима.
2.5. Деформации разбиений $R_{ + }^{2}$ при изменении коэффициента эластичности факторов на микроуровне
Если при изменении параметра $\rho $ сохраняются спектры областей разбиения ортанта $R_{ + }^{2}$ линиями (8), то конус $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $ и соответствующий ему ромбический тайлинг не изменятся. Поэтому разрешимость проблемы моментов может изменяться, если одна из линий (8) при изменении параметра $\rho $ проходит через точку пересечения двух других линий этого семейства. Для того, чтобы три линии:
(10)
$\begin{gathered} {{{\tilde {p}}}_{1}}{{({{t}_{1}})}^{{ - \rho }}}x_{1}^{{ - \rho }} + {{{\tilde {p}}}_{2}}{{({{t}_{1}})}^{{ - \rho }}}x_{2}^{{ - \rho }} = 1, \\ {{{\tilde {p}}}_{1}}{{({{t}_{2}})}^{{ - \rho }}}x_{1}^{{ - \rho }} + {{{\tilde {p}}}_{2}}{{({{t}_{2}})}^{{ - \rho }}}x_{2}^{{ - \rho }} = 1, \\ {{{\tilde {p}}}_{1}}{{({{t}_{3}})}^{{ - \rho }}}x_{1}^{{ - \rho }} + {{{\tilde {p}}}_{2}}{{({{t}_{3}})}^{{ - \rho }}}x_{2}^{{ - \rho }} = 1 \\ \end{gathered} $(11)
$\left| {\begin{array}{*{20}{c}} 1&1&1 \\ {{{{\tilde {p}}}_{1}}{{{({{t}_{1}})}}^{{ - \rho }}}}&{{{{\tilde {p}}}_{1}}{{{({{t}_{2}})}}^{{ - \rho }}}}&{{{{\tilde {p}}}_{1}}{{{({{t}_{3}})}}^{{ - \rho }}}} \\ {{{{\tilde {p}}}_{2}}{{{({{t}_{1}})}}^{{ - \rho }}}}&{{{{\tilde {p}}}_{2}}{{{({{t}_{2}})}}^{{ - \rho }}}}&{{{{\tilde {p}}}_{2}}{{{({{t}_{3}})}}^{{ - \rho }}}} \end{array}} \right| = 0.$Будем считать, что $\forall \;{{t}_{1}},{{t}_{2}}:1 \leqslant {{t}_{1}} < {{t}_{2}} \leqslant T$ верно ${{\tilde {p}}_{1}}({{t}_{1}}) \ne {{\tilde {p}}_{1}}({{t}_{2}})$, ${{\tilde {p}}_{2}}({{t}_{1}}) \ne {{\tilde {p}}_{2}}({{t}_{2}})$ в связи с ранее принятым предположением о том, что прямые (11) являются прямыми общего положения.
В [2] показано, что для любых $1 \leqslant {{t}_{1}} < {{t}_{2}} < {{t}_{3}} \leqslant T$ существует не более одного значения параметра $\rho $, удовлетворяющего уравнению (8).
2.6. Численный метод оценки эластичности замещения производственных факторов на микроуровне
Отметим все значения параметра $\rho $, соответствующие пересечению троек линий (10) в одной точке, на числовой оси. Данные значения разобьют $\left[ { - 1,0} \right) \cup \left( {0, + \infty } \right)$ на конечное число промежутков, в каждом из которых конус $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $ будет постоянным. Согласно предложению 2.3, разрешимость проблемы моментов (6) внутри каждого промежутка также будет неизменна.
Алгоритм нахождения параметра “Эластичность замещения производственных факторов на микроуровне”, согласованного со статистикой $\{ y(t),{{p}_{0}}(t),{{p}_{1}}(t),{{p}_{2}}(t)\} $
Шаг 1. Для каждой тройки $1 \leqslant {{t}_{1}} < {{t}_{2}} < {{t}_{3}} \leqslant T$ найти значение параметра $\rho $, соответствующее пересечению трех линий (10) в одной точке, и выделить значения $\rho $, принадлежащие $\left[ { - 1,0} \right) \cup \left( {0, + \infty } \right)$.
Шаг 2. Упорядочить найденные $\rho $ по возрастанию:
Шаг 3. Для каждого промежутка $({{\rho }_{i}},{{\rho }_{{i + 1}}})$, $0 \leqslant i \leqslant K - 1$, при каком-то произвольном значении $\rho $ из данного промежутка:
(а) для каждой пары прямых семейства (8) найти угол наклона $\alpha $, соответствующий их точке пересечения, в случае, если этот угол принадлежит промежутку $\left( {0,\tfrac{\pi }{2}} \right)$;
(б) упорядочить эти углы по возрастанию:
(в) для $\alpha * = ({{\alpha }_{0}};{{\alpha }_{1}})$, $\pi (\alpha *) = i{{d}_{T}}$ выписать спектры областей, через которые проходит луч (7);
(г) найти конус $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $. Для этого для каждого промежутка $({{\alpha }_{j}},{{\alpha }_{{j + 1}}})$, $1 \leqslant j \leqslant L - T - 1,$ при каком-то произвольном значении $\alpha {\text{*}}$ из данного промежутка;
(i) упорядочить точки пересечения луча (7) с прямыми (8) при $\alpha = \alpha {\text{*}}$ и выписать порядок $\pi (\alpha *)$;
(ii) выписать спектры областей, которые пересекает луч (7) при $\alpha = \alpha {\text{*}}$;
(iii) сравнить выписанные спектры со спектрами, выписанными на предыдущем шаге $(\alpha * \in ({{\alpha }_{{j - 1}}},{{\alpha }_{j}}))$ и исключить повторения;
(д) проверить принадлежность вектора ${\mathbf{y}}$ конусу $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1, \ldots ,\;T\} $. Данная проверка является задачей линейного программирования.
Отметим, что в части 3.г.iii) алгоритма после исключения повторений будет добавлена ровно одна область, спектр которой определяется однозначно из информации о спектрах, выписанных на предыдущем шаге $(\alpha * \in ({{\alpha }_{{j - 1}}},{{\alpha }_{j}}))$ и номеров пары прямых семейства (8), пересекающихся в точке, лежащей на луче вида (7) с углом наклона ${{\alpha }_{i}}$. Пусть известно, что эти прямые имеют номера ${{\pi }_{t}}(\alpha *)$ и ${{\pi }_{{t + 1}}}(\alpha *)$, $\alpha * \in ({{\alpha }_{{j - 1}}},{{\alpha }_{j}})$. Тогда спектр $Z(G)$ добавляемой области $G$ имеет вид
(12)
$\begin{array}{*{20}{c}} {{{Z}_{i}}(G) = 1,\quad если\quad i = {{p}_{1}}(\alpha *),\; \ldots ,\;{{p}_{{t - 1}}}(\alpha *),{{p}_{{t + 1}}}(\alpha *),} \\ {{{Z}_{i}}(G) = 0,\quad иначе.} \end{array}$В связи с этим вместо выполнения частей 3.г.ii) и 3.г.iii) возможно запоминать информацию о текущем порядке $\pi (\alpha )$, а при проходе из области $({{\alpha }_{{j - 1}}},{{\alpha }_{j}})$ в область $({{\alpha }_{j}},{{\alpha }_{{j + 1}}})$ этот порядок менять и добавлять область, спектр которой равен (12).
Сложность работы алгоритма зависит от двух величин – максимальной из длин переменных $(p_{0}^{t},p_{1}^{t},p_{2}^{t},{{y}^{t}})$, $t = 1,\; \ldots ,\;T$ и количества периодов времени $T$, причем главный вклад в сложность предложенного алгоритма вносит именно количество периодов времени $T$.
Теорема 2.1. Алгоритм нахождения параметра “Эластичность замещения производственных факторов на микроуровне” полиномиален по величине $T$.
Доказательство. Воспользуемся нумерацией структуры вышеприведенного алгоритма. Шаг 1 относится к нахождению значений параметра $\rho $, соответствующих пересечении трех линий (10) в одной точке. Этот шаг имеет какую-то фиксированную сложность, зависящую от заданной допустимой точности нахождения параметра $\rho $, применяется не более, чем $C_{T}^{3} < {{T}^{3}}$ раз (так как максимальное число пересечений равняется максимальному числу различных троек линий) и является полиномиальной по $T$.
Шаг 2 относится к упорядочиванию найденных в части 1 значений $\rho $ по возрастанию и имеет сложность не более, чем $O({{({{T}^{3}})}^{2}}) = O({{T}^{6}})$.
Шаг 3 применяется не более, чем ${{T}^{3}}$ раз и состоит из:
• Нахождения конуса $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $, упорядочивание не более, чем ${{T}^{2}}$ точек пересечения пар прямых семейства (8) – не более, чем $O({{({{T}^{2}})}^{2}}) = O({{T}^{4}})$.
• Для каждого $\alpha {\text{*}}$ (применяется не более, чем ${{T}^{2}}$ раз) сортировке $T$ точек пересечения и нахождение спектров – не более, чем ${{T}^{2}} \times O({{T}^{2}}) = O({{T}^{4}})$.
• Решения задачи линейного программирования.
Задача принадлежности вектора ${\mathbf{y}}$ конусу $\Gamma \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $ является задачей линейного программирования, состоящей из $T$ уравнений, каждое из которых содержит не более, чем ${{T}^{2}}$ переменных (количество переменных равно количеству областей и не превышает $C_{T}^{2}$), являющихся нулями или единицами. Таким образом, длина входа в битах, необходимая для задания этой задачи, не превосходит $O({{T}^{3}})$. Согласно методу эллипсоидов (см. [10]), задача линейного программирования является полиномиальной и сложность ее решения не превосходит $O({{T}^{4}} \times L)$, где $L$ – полная длина входа, т.е. сложность данной задачи не превосходит $O({{T}^{7}})$.
Таким образом, общая алгоритмическая сложность не превосходит $O({\mathbf{max}}\{ {{T}^{6}};{{T}^{4}};{{T}^{3}} \times {{T}^{7}}\} ) = O({{T}^{{10}}})$ $O({\mathbf{max}}\{ {{T}^{6}};{{T}^{4}};{{T}^{3}} \times {{T}^{7}}\} ) = O({{T}^{{10}}})$, и указанный алгоритм полиномиален по $T$.
Замечание. Отметим, что если проблема моментов (5) разрешима, то существует дискретное распределение мощностей по технологиям $(x_{1}^{k},x_{2}^{k},{{z}^{k}})$, где ${{z}^{k}}$ – суммарная мощность технологий, локализованных в точках $(x_{1}^{k},x_{2}^{k})$.
Действительно, если проблема моментов (6) разрешима, можно построить распределение мощностей по технологиям следующим образом: для каждой области $G \in \Lambda \{ {\mathbf{\tilde {p}}}(t,\rho )\,|\,t = 1,\; \ldots ,\;T\} $ выбрать круг ${{B}_{G}}({{{\mathbf{x}}}_{G}},{{r}_{G}}) = \left\{ {{\mathbf{x}} \in {{\mathbb{R}}^{2}}\left| {\left\| {{\mathbf{x}} - {{{\mathbf{x}}}_{G}}} \right\| < {{r}_{G}}} \right.} \right\} \in G$ и предположить, что
В этом случае неотрицательная абсолютно непрерывная мера с плотностью $f({\mathbf{x}})$ является решением проблемы моментов (6). Если устремить радиусы кругов ${{B}_{G}}({{{\mathbf{x}}}_{G}},{{r}_{G}})$ к нулю, то мы можем считать распределение мощностей по технологиям, согласованное с проблемой моментов (6), дискретным.
Очевидно, что возможное допустимое распределение мощностей по технологиям не единственно. Однако построение на основании реальной статистики хоть какого-либо распределения мощностей по технологиям, согласованного с проблемой моментов (6), позволит проанализировать функционирование отрасли. Для этого после построения распределения мощностей по технологиям необходимо построить функцию предложения каждой отрасли
С другой стороны, с учетом наличия некоторых интегральных годовых величин возможно построить оптимизационную задачу выбора распределения мощностей по технологиям, наилучшим образом соответствующего этим интегральным величинам.
3. ОЦЕНКА ИМПОРТОВЫТЕСНЕНИЯ С ПОМОЩЬЮ ОБОБЩЕННОЙ МОДЕЛИ ХАУТЕККЕРА–ЙОХАНСЕНА
3.1. Построение статистики индексов цен производственных факторов
В п. 2.6 описан алгоритм нахождения эластичности замещения производственных факторов на микроуровне. Входными данными для этого алгоритма служат временные ряды индексов выпусков, цен на выпускаемую отраслью продукцию и цен на импортные и отечественные производственные факторы $y(t)$, $p_{0}^{t}$, $p_{1}^{t}$, $p_{2}^{t}$, где $t = 1,\; \ldots ,\;T$ – периоды времени (кварталы). В этом п. будем считать, что индекс 1 в формулах будет отвечать за импортный, а индекс 2 – за отечественный производственный фактор.
Данные индексов выпусков и индексов цен на выпускаемую продукцию $y(t)$, $p_{0}^{t}$ доступны в статистике Росстата [13], [14]. В связи с тем, что волатильность цен в мировой экономике намного меньше, чем в российской экономике, будем считать цены на импортные факторы постоянными, индексировать их по статистике общемировой инфляции [15] и переводить в рубли по среднемесячному курсу ЦБ РФ доллара, евро или бивалютной корзины [16] (в зависимости от основного источника импорта производственных факторов в каждой из исследуемых отраслей).
Проведем агрегирование отраслей в зависимости от импортно-экспортных отношений [11]:
• 1 комплекс отраслей – экспортно-ориентированные отрасли (например, нефтегазовая отрасль, металлургия, минеральные удобрения);
• 2 комплекс отраслей – “эффективные” или “рыночные” инфраструктурные отрасли (например, электроэнергия, связь);
• 3 комплекс отраслей – отрасли обрабатывающей промышленности, конкурирующие с импортом (например, машиностроение, пищевая промышленность, химическое производство);
• 4 комплекс отраслей – “нерыночные” отрасли сферы услуг (например, ЖКХ, образование, здравоохранение).
Множества индексов матрицы Леонтьева размера $59 \times 59$, соответствующих 1–4 комплексам отраслей, будем обозначать через ${{K}_{1}}$, ${{K}_{2}}$, ${{K}_{3}}$ и ${{K}_{4}}$.
Статистика индексов цен на отечественные производственные факторы напрямую недоступна. В связи с тем, что основной вклад в изменение кривых нулевой себестоимости
(13)
${{({{p}_{1}}{{(t)}^{{ - \rho }}}x_{1}^{{ - \rho }} + {{p}_{2}}{{(t)}^{{ - \rho }}}x_{2}^{{ - \rho }})}^{{ - 1/\rho }}} = {{p}_{0}},\quad t = 1, \ldots ,\;T,$(14)
$\mathop {\left( {{{{\left( {\left( {\sum\limits_{j \in {{K}_{3}}} {{{a}_{{ij}}}} {{P}_{j}}(t)} \right){{x}_{1}}} \right)}}^{{ - \rho }}} + {{{({{p}_{2}}(t){{x}_{2}})}}^{{ - \rho }}}} \right)}\nolimits^{ - 1/\rho } = {{p}_{0}}(t) - \sum\limits_{j \in {{K}_{1}},{{K}_{2}},{{K}_{4}}} {{{a}_{{ij}}}} {{P}_{j}}(t).$3.2. Эластичность замещения производственных факторов
Используя алгоритм, описанный в п. 2.6, и модификации кривых нулевой себестоимости (14), проведем для некоторых отраслей российской экономики идентификацию величины $\rho $, согласованную со статистическими временными рядами индексов выпусков, цен на ПФТП и цен на выпускаемую продукцию. Величина $\rho = - 1$ соответствует линейной функции себестоимости, т.е. отсутствию замещения производственных факторов в модели Леонтьева. В результате идентификации все области $\rho $, согласованные с временными рядами, лежат в промежутке $\rho \in [ - 1,0)$, что соответствует неполному замещению производственных факторов.
Отметим, что для каждой отрасли ответом на вопрос “Какая эластичность производственных факторов согласована со статистическими данными?” является некоторый отрезок $[a,b] \subset [ - 1,0)$, из которого для дальнейшей идентификации распределения мощностей по технологиям необходимо выбрать одно конкретное значение.
Согласно замечанию из п. 2.6, возможны идентификация технологической структуры производства и построение функции спроса на импортный и отечественный производственные факторы. Для выбора конкретного значения эластичности замещения из отрезка и “лучшего” распределения мощностей по технологиям воспользуемся матрицами Леонтьева импорта и отечественной продукции. Согласно этим матрицам, возможно провести идентификацию годовой величины использования импорта производственных факторов и использования отечественных производственных факторов за 2011–2015 гг.
Пусть кривые нулевой себестоимости $\{ p_{0}^{t}(\rho ) = p_{1}^{t}(\rho ){{x}_{1}} + p_{2}^{t}(\rho ){{x}_{2}}\} $ разбивают положительный ортант $R_{ + }^{2}$ на $K$ областей ${{G}^{1}},\; \ldots ,\;{{G}^{K}}$. Обозначим через $(x_{1}^{k},x_{2}^{k})$ технологию, в которой можно сгруппировать всю суммарную мощность области ${{G}^{k}}$, $k \in (1,\; \ldots ,\;K)$:
Отметим, что $(x_{1}^{k},x_{2}^{k}) \in {{G}_{k}}$. Величина импорта производственных факторов будет равняться
(15)
$d_{1}^{t} = \sum\limits_k {x_{1}^{k}} {\kern 1pt} \theta (p_{0}^{t}(\rho ) - p_{1}^{t}(\rho )x_{1}^{k} - p_{2}^{t}(\rho )x_{2}^{k}){\kern 1pt} {{z}^{k}},\quad t = 1,\; \ldots ,\;T,$(16)
$d_{2}^{t} = \sum\limits_k {x_{2}^{k}} {\kern 1pt} \theta (p_{0}^{t}(\rho ) - p_{1}^{t}(\rho )x_{1}^{k} - p_{2}^{t}(\rho )x_{2}^{k}){\kern 1pt} {{z}^{k}},\quad t = 1,\; \ldots ,\;T.$(17)
$\sum\limits_{\tau = 2011,\; \ldots ,\;2015} {{{{\left( {f_{1}^{\tau } - \sum\limits_{t \in \tau } {d_{1}^{t}} } \right)}}^{2}}} + \sum\limits_{\tau = 2011,\; \ldots ,\;2015} {{{{\left( {f_{2}^{\tau } - \sum\limits_{t \in \tau } {d_{2}^{t}} } \right)}}^{2}}} \to \mathop {min}\limits_{x_{1}^{k},x_{2}^{k},{{z}^{k}},k \in (1,\; \ldots ,\;K)} ;$(18)
$d_{i}^{t} = \sum\limits_{k = 1}^K {x_{i}^{k}} {\kern 1pt} \theta (p_{0}^{t}(\rho ) - p_{1}^{t}(\rho )x_{1}^{k} - p_{2}^{t}(\rho )x_{2}^{k}){\kern 1pt} {{z}^{k}},\quad t = 1,\; \ldots ,\;T,\quad i = 1,2;$(19)
$\sum\limits_{k = 1}^K \theta (p_{0}^{t}(\rho ) - p_{1}^{t}(\rho )x_{1}^{k} - p_{2}^{t}(\rho )x_{2}^{k}){\kern 1pt} {{z}^{k}} = {{y}^{t}},\quad t = 1,\; \ldots ,\;T;$Эта задача не является задачей выпуклого программирования, так как ограничение (18) не является ни выпуклой, ни вогнутой функцией. Поэтому для решения задачи (17)–(20) при больших размерностях (порядка 200) необходимо применять различные эвристические соображения. Одним из таких соображений является исключение из задачи (17)–(20) переменных ${{z}^{k}}$, $k = 1,\; \ldots ,\;K$, соответствующих суммарным величинам мощностей каждой области ${{G}_{k}}$, $k = 1,\; \ldots ,\;K$. Для этого в задаче ((17), (18), (20)) зафиксируем значения переменных ${{z}^{k}}$, $k = 1,\; \ldots ,\;K$, так, чтобы они удовлетворяли условию (19). Чтобы подобрать такие значения, при формулировке задачи о принадлежности вектора конусу в виде задачи линейного программирования необходимо взять произвольную линейную целевую функцию. Фиксация ${{z}^{k}}$, $k = 1,\; \ldots ,\;K$, не позволит найти точное решение задачи (17)–(20), однако, тем не менее, позволит найти распределение мощностей по технологиям $x_{1}^{k}$, $x_{2}^{k}$, ${{z}^{k}}$, $k = 1,\; \ldots ,\;K$, которое, как будет показано в дальнейшем, описывает импорт производственных факторов с приемлемой точностью.
Выбор величин ($x_{1}^{k}$, $x_{2}^{k}$) можно осуществить, решив следующую задачу:
(21)
$\sum\limits_{\tau = 2011,\; \ldots ,\;2015} {{{{\left( {f_{1}^{\tau } - \sum\limits_{t \in \tau } {d_{1}^{t}} } \right)}}^{2}}} + \sum\limits_{\tau = 2011,\; \ldots ,\;2015} {{{{\left( {f_{2}^{\tau } - \sum\limits_{t \in \tau } {d_{2}^{t}} } \right)}}^{2}}} \to \mathop {min}\limits_{x_{1}^{k},x_{2}^{k},\,k \in (1,\; \ldots ,\;K)} ;$(22)
$d_{i}^{t} = \sum\limits_{k = 1}^K {x_{i}^{k}} {\kern 1pt} \theta (p_{0}^{t}(\rho ) - p_{1}^{t}(\rho )x_{1}^{k} - p_{2}^{t}(\rho )x_{2}^{k}){\kern 1pt} {{z}^{k}},\quad t = 1,\; \ldots ,\;T,\quad i = 1,2;$Эта задача является переформулировкой задачи (17)–(20) в случае, если величины ${{z}^{k}}$ считать фиксированными. Ограничения (22) и (23) являются линейными, а целевая функция (21) – суммой нескольких квадратов линейных функций. Таким образом, задача (21)–(23) является задачей выпуклого квадратичного программирования и может быть решена за полиномиальное время по длине ее входа (см. [12]).
Для выбора эластичности замещения производственных факторов на микроуровне задача (21)–(23) была численно решена для некоторого количества различных значений $\rho $ (порядка 10), равномерно распределенных на интервале допустимых значений. Значения $\rho $, соответствующие минимальной из величин (21), были отражены в табл. 1.
Таблица 1.
Величина $\rho $
| Отрасль | $\rho $ | $\delta (\rho )$ |
|---|---|---|
| Продукция и услуги сельского хозяйства и охоты | –0.451 | 0.221 |
| Продукция лесоводства, лесозаготовок и связанные с этим услуги | –0.760 | 0.046 |
| Рыба и прочая продукция рыболовства и рыбоводства; услуги, связанные с рыболовством и рыбоводством | –0.872 | 0.114 |
| Продукты пищевые и напитки, табак | –0.956 | 0.173 |
| Текстиль, одежда, меха, кожа и изделия из кожи | –0.764 | 0.219 |
| Древесина и изделия из дерева; Целлюлоза, бумага и изделия из бумаги; Продукция печатная | –0.827 | 0.315 |
| Вещества химические, продукты химические и волокна химические; Изделия резиновые и полимерные | –0.728 | 0.094 |
| Металлы | –0.834 | 0.341 |
| Готовые металлические изделия, кроме машин и оборудования | –0.926 | 0.062 |
| Машины и оборудование, не включенные в другие группировки (кроме оружия и боеприпасов) | –0.787 | 0.251 |
| Электрические машины и электрооборудование; Компоненты электронные, аппаратура для радио, телевидения и связи | –0.613 | 0.513 |
| Изделия медицинские; Приборы и инструменты для измерения, контроля, испытаний, навигации, управления; приборы оптические, кино-фотооборудование; Аппаратура, часы | –0.571 | 0.139 |
| Автотранспортные средства, прицепы и полуприцепы; Прочие транспортные средства | –0.891 | 0.406 |
3.3. Сравнительный анализ импортовытеснения
Так как для решения проблемы моментов (6) необходимо знание временных рядов цен на выпускаемую отраслью продукцию, были проидентифицированы все отрасли, кроме отраслей сферы услуг. Для отрасли услуг был использован индекс потребительских цен в сфере услуг, так как Росстатом публикуется только статистика цен на какие-либо конкретные услуги, а агрегированной статистики цен для классов ОКВЭД не публикуется.
Для сравнения полученных при идентификации данных для начала сопоставим величины фактического импорта производственных факторов и результаты идентификации величины импорта производственных факторов, основанные на применении традиционной технологии.
Сравним анализ потребления импортных производственных факторов, полученных с использованием симметричных таблиц импорта, с анализом по формуле (15). Для этого номинируем все выпуски и потребления в “натуральной величине”. В качестве натуральной величины возьмем текущие цены и выпуски, номинированные на величину курса корзины валют ЦБ РФ (0.55 доллара + 0.45 евро). Дополнительно данный курс умножим на величину общемировой инфляции по отношению к декабрю 2011 г.
На фиг. 1 жирная линия отвечает за фактическое потребление производственных факторов (единица изменения “– млн. валютных корзин ЦБ РФ). Штриховая линия отвечает за потребление импорта, найденного с помощью модели Леонтьева, если считать матрицу Леонтьева 2011 г. фиксированной. Пунктирная линия соответствует импорту производственных факторов, полученному при идентификации с помощью формулы (26).
Из графика видно, что импорт производственных факторов в натуральных величинах к 2015 г. упал на треть по сравнению с 2011 г. Причина этого – девальвация национальной валюты. Замена расчета импорта производственных факторов по постоянной матрице Леонтьева на расчет согласно обобщенной модели Хаутеккера–Йохансена улучшает приближение линии к фактическому описанию импорта. Тем не менее в 2015 г. расчет с использованием обобщенной модели Хаутеккера–Йохансена показывает более существенное уменьшение импорта по сравнению с фактическим.
Анализируя график, можно прийти к следующему выводу: идентификацию технологической структуры производства с помощью обобщенной модели Хаутеккера–Йохансена можно считать приемлемой. В рыночной экономике общедоступной информацией, на основе которой агенты принимают решения, являются цены (“невидимая рука” рынка А. Смита в интерпретации Л. Вальраса). Поэтому исследуются механизмы их формирования и прогнозирования. Результаты исследования доступны в оперативном режиме и могут служить информационным обеспечением технологии оценки импорта производственных факторов на основе обобщенной модели Хаутеккера–Йохансена. Альтернативная технология, основанная на матрице Леонтьева, требует информацию о выпусках, которая обычно известна с задержками.
Список литературы
Agaltsov A., Molchanov E., Shananin A. Inverse problems in models of resource distribution // J. of Geometric Analysis. 2018. V. 28. I. 1. P. 726–765.
Молчанов Е.Г. О модификациях ромбических тайлингов, возникающих в обратной задаче о распределении ресурсов // Тр. МФТИ. 2013. Т. 5. № 4. С. 87–95.
Houthakker H.S. The Pareto distribution and the Cobb-Douglas production function in activity analysis // Rev. Econ. Studies. 1955–1956. V. 23 (1). № 60. P. 27–31.
Johansen L. Production functions. Amsterdam-London: North Holland Co., 1972.
Данилов В.И., Карзанов А.В., Кошевой Г.А. Системы разделенных множеств и их геометрические модели // Успехи матем. наук. 2010. Т. 65. № 4 (394). С. 67–152.
Шананин А.А. Двойственность для задач обобщенного программирования и вариационные принципы в моделях экономического равновесия // Докл. АН. 1999. Т. 366. № 4. С. 462–464.
Шананин А.А. Обобщенная модель чистой отрасли производства // Матем. моделирование. 1997. Т. 9. № 9. С. 117–127.
Lascoux A., Schützenberger M.P. Le monoïde plaxique // Non-commutative Structures in Algebra and Geometric Combinatorics (Naples, 1978). Rome, CNR. 1981. P. 129–156 (Quad. Ric. Sci. V. 109).
Leclerc B., Zelevinsky A. Quasicommuting families of quantum Plücker coordinates // Amer. Math. Soc. Trans. 1998. Ser. 2. № 181. P. 85–108.
Хачиян Л.Г. Полиномиальные алгоритмы в линейном программировании // Ж. вычисл. матем. и матем. физ. 1980. Т. 20. В. 1. С. 51–68.
Обросова Н.К., Шананин А.А. Описание функционирования обрабатывающего сектора в макромодели Российской экономики // Тр. ИСА РАН. 2018. Т. 68. № 2. С. 63–67.
Козлов М.К., Тарасов С.П., Хачиян Л.Г. Полиномиальная разрешимость выпуклого квадратичного программирования // Ж. вычисл. матем. и матем. физ. 1980. Т. 20. В. 5. С. 1319–1323.
Федеральная служба государственной статистики. Национальные счета. URL: http://www.gks.ru/wps/wcm/connect/rosstat main/rosstat/ru/statistics/accounts/, 01.07.2018 г.
Федеральная служба государственной статистики. Цены. URL: http://www.gks.ru/wps/wcm/connect/rosstat main/rosstat/ru/statistics/tariffs/
URL: https://data.worldbank.org/, 01.07.2018 г.
База данных по курсам валют. URL: http://www.cbr.ru/currency base/, 01.07.2018 г.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики