Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 503-519

О применении закона сохранения энергии в модели холодной плазмы

А. А. Фролов^1, *, Е. В. Чижонков^2, **

¹ Физ. ин-т им. П.Н. Лебедева РАН
119991 Москва, Ленинский пр-т, 53, Россия

² МГУ им. М.В. Ломоносова
119899 Москва, Ленинские горы, Россия

^* E-mail: frolovaa@lebedev.ru
^** E-mail: chizhonk@mech.math.msu.su

Поступила в редакцию 20.08.2019
После доработки 20.08.2019
Принята к публикации 18.11.2019

DOI: 10.31857/S0044466920030096

Полный текст (PDF)

Аннотация

Для двухжидкостной гидродинамической модели холодной плазмы выведены дифференциальные соотношения, характеризующие закон сохранения энергии. При этом отдельно рассмотрен случай, когда движением более тяжелых ионов, по сравнению с электронами, можно пренебречь, а также ситуации с учетом или пренебрежением релятивистского фактора в динамике электронов. Для задачи о свободных плазменных колебаниях, инициированных коротким мощным лазерным импульсом, приведены результаты численных экспериментов по анализу выполнения закона сохранения энергии во всех различных вышеуказанных ситуациях. Основной результат заключается в том, что стандартное теоретическое исследование аппроксимации и устойчивости вместе с экспериментальным наблюдением за сохранением энергии существенно повышает достоверность вычислений. Библ. 16. Фиг. 10.

Ключевые слова: закон сохранения энергии, численное моделирование, плазменные колебания, эффект опрокидывания, конечноразностная схема, порядок точности.

ВВЕДЕНИЕ

Двухжидкостная гидродинамическая модель холодной плазмы хорошо известна и достаточно подробно описана в учебниках и монографиях по физике плазмы [1]–[4]. В настоящее время внимание к этой модели обусловлено, в первую очередь, задачами, связанными с распространением сверхмощных лазерных импульсов в плазме [5], [6]. В силу нелинейности рассматриваемых уравнений, в качестве рабочего инструмента исследований на первом плане находятся численные методы, хотя трудности их обоснования, связанные со сходимостью приближенных решений к точным, представляются весьма серьезными. Главной причиной этого являются качественные свойства дифференциальных уравнений модели холодной плазмы. В частности, речь идет об эффекте опрокидывания плазменных колебаний, который известен достаточно давно [7]. В терминах уравнений с частными производными гиперболического типа эффект опрокидывания имеет название “градиентная катастрофа”, т.е. когда из сколь угодно гладких начальных данных или правых частей формируется ограниченное разрывное решение, имеющее неограниченные пространственные производные. В такой ситуации для обоснования численного алгоритма стандартных аргументов (оценки аппроксимации для гладкого решения и доказательство устойчивости методом замороженных коэффициентов), вообще говоря, недостаточно. Кроме того, дополнительную сложность представляет принципиальное отсутствие, в силу теоремы Гаусса, даже постановки классической задачи Римана (задачи Коши с кусочно постоянными начальными данными), что позволяет снимать остроту проблемы в традиционных гиперболических постановках [8]. Вышесказанное приводит к необходимости поиска новых аргументов в пользу приближенных методов, используемых при расчетах в модели холодной плазмы.

В настоящей работе для оценки качества применяемого численного метода предлагается использовать закон сохранения энергии. Так как двухжидкостная гидродинамическая модель холодной плазмы является замкнутой, то сам закон сохранения является следствием дифференциальных уравнений и не может порождать новых физических выводов о свойствах системы. Зато контроль за его выполнением позволяет не только отбраковывать заведомо непригодные алгоритмы, но и экспериментально устанавливать порядок точности (сходимости) приближенного решения, так как простейшим следствием закона является априорная оценка для некоторой комбинации основных функций, представляющих решение дифференциальной задачи.

Статья организована следующим образом. В разд. 1 для двухжидкостной гидродинамической модели холодной плазмы выводятся дифференциальные соотношения, характеризующие закон сохранения энергии. При этом отдельно рассмотрен случай, когда движением более тяжелых ионов, по сравнению с электронами, можно пренебречь, а также ситуации с учетом или пренебрежением релятивистского фактора в динамике электронов. Второй раздел посвящен постановке задачи о свободных плазменных колебаниях, инициированных коротким мощным лазерным импульсом, которые по прошествии нескольких периодов завершаются эффектом опрокидывания. В третьем разделе приведены результаты численных экспериментов по анализу выполнения закона сохранения энергии во всех различных вышеуказанных ситуациях. При этом сам численный алгоритм не приводится; дается только краткое описание его свойств, в силу громоздкости и наличия доступных публикаций с подробным изложением формул [9], [10]. В заключении статьи систематизированы результаты проведенных исследований.

1. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ

1.1. Основные уравнения

Определим плазму как смесь холодных, идеальных, релятивистской электронной и нерелятивистской ионной жидкостей, тогда система описывающих ее гидродинамических уравнений совместно с уравнениями Максвелла в векторной форме будет иметь вид

(1)

$\frac{{\partial {{n}_{e}}}}{{\partial t}} + \operatorname{div} ({{n}_{e}}{{{\mathbf{v}}}_{e}}) = 0,$

(2)

$\frac{{\partial {{{\mathbf{p}}}_{e}}}}{{\partial t}} + \left( {{{{\mathbf{v}}}_{e}} \cdot \nabla } \right){{{\mathbf{p}}}_{e}} = e\left( {{\mathbf{E}} + \frac{1}{c}\left[ {{{{\mathbf{v}}}_{e}} \times {\mathbf{B}}} \right]} \right),$

(3)

$\gamma = \sqrt {1 + \frac{{{{{\left| {{{{\mathbf{p}}}_{e}}} \right|}}^{2}}}}{{m_{e}^{2}{{c}^{2}}}}} ,$

(4)

${{{\mathbf{v}}}_{e}} = \frac{{{{{\mathbf{p}}}_{e}}}}{{{{m}_{e}}\gamma }},$

(5)

$\frac{{\partial {{n}_{i}}}}{{\partial t}} + \operatorname{div} ({{n}_{i}}{{{\mathbf{v}}}_{i}}) = 0,$

(6)

$\frac{{\partial {{{\mathbf{v}}}_{i}}}}{{\partial t}} + \left( {{{{\mathbf{v}}}_{i}} \cdot \nabla } \right){{{\mathbf{v}}}_{i}} = \frac{{{{e}_{i}}}}{{{{m}_{i}}}}\left( {{\mathbf{E}} + \frac{1}{c}\left[ {{{{\mathbf{v}}}_{i}} \times {\mathbf{B}}} \right]} \right),$

(7)

$\frac{1}{c}\frac{{\partial {\mathbf{E}}}}{{\partial t}} = - \frac{{4\pi }}{c}\left( {e{{n}_{e}}{{{\mathbf{v}}}_{e}} + {{e}_{i}}{{n}_{i}}{{{\mathbf{v}}}_{i}}} \right) + \operatorname{rot} {\mathbf{B}},$

(8)

$\frac{1}{c}\frac{{\partial {\mathbf{B}}}}{{\partial t}} = - \operatorname{rot} {\mathbf{E}},\quad \operatorname{div} {\mathbf{B}} = 0,$

где $e$, ${{e}_{i}}$, ${{m}_{e}}$, ${{m}_{i}}$ – заряды и массы электронов и ионов соответственно (здесь заряд электрона имеет отрицательный знак: $e < 0$); $c$ – скорость света; ${{n}_{e}}$, ${{{\mathbf{p}}}_{e}}$, ${{{\mathbf{v}}}_{e}}$ – концентрация, импульс и скорость электронов; ${{n}_{i}}$, ${{{\mathbf{v}}}_{i}}$ – концентрация и скорость ионов; $\gamma $ – лоренцевский фактор; ${\mathbf{E}}$, ${\mathbf{B}}$ – векторы электрического и магнитного полей.

Система уравнений (1)–(8) является одной из простейших моделей бесстолкновительной плазмы, для которой справедливо так называемое квазигидродинамическое описание, приведенное выше и называемое в литературе просто гидродинамическим. Это приближение часто называют уравнениями двухжидкостной гидродинамики “холодной” плазмы; оно хорошо известно и достаточно подробно описано в учебниках и монографиях по физике плазмы (см., например, [1]–[4]).

1.2. Соотношение для энергии электромагнитного поля

Введем обозначение для полного электрического тока ${\mathbf{j}} = {{{\mathbf{j}}}_{e}} + {{{\mathbf{j}}}_{i}} \equiv e{{n}_{e}}{{{\mathbf{v}}}_{e}} + {{e}_{i}}{{n}_{i}}{{{\mathbf{v}}}_{i}}$. Умножим первое уравнение (8) скалярно на вектор $c{\mathbf{B}}$, а уравнение (7) – на вектор $c{\mathbf{E}}$, в результате получим

$\frac{\partial }{{\partial t}}\frac{{{{{\left| {\mathbf{B}} \right|}}^{2}}}}{2} + c({\mathbf{B}},\operatorname{rot} {\mathbf{E}}) = 0,\quad \frac{\partial }{{\partial t}}\frac{{{{{\left| {\mathbf{E}} \right|}}^{2}}}}{2} - c({\mathbf{E}},\operatorname{rot} {\mathbf{B}}) + 4\pi ({\mathbf{j}},{\mathbf{E}}) = 0,$

где, как и ранее, для вектор-функции ${\mathbf{F}}({\mathbf{x}},t)$ использовано обозначение квадрата евклидовой длины

${{\left| {\mathbf{F}} \right|}^{2}} = \sum\limits_{i = 1}^3 {{{{\left| {{{F}_{i}}({\mathbf{x}},t)} \right|}}^{2}}} ,$

а выражение $({\mathbf{F}},{\mathbf{G}})$ имеет смысл обычного скалярного произведения вектор-функций ${\mathbf{F}}({\mathbf{x}},t)$ и ${\mathbf{G}}({\mathbf{x}},t)$

$({\mathbf{F}},{\mathbf{G}}) = \sum\limits_{i = 1}^3 {{{F}_{i}}} ({\mathbf{x}},t){{G}_{i}}({\mathbf{x}},t).$

Складывая полученные выражения и учитывая известное равенство

$({\mathbf{F}},\operatorname{rot} {\mathbf{G}}) - ({\mathbf{G}},\operatorname{rot} {\mathbf{F}}) = \operatorname{div} [{\mathbf{G}} \times {\mathbf{F}}],$

после деления на нормировочный множитель $4\pi $ будем иметь соотношение для энергии электромагнитного поля [11]:

(9)

$\frac{\partial }{{\partial t}}\frac{{{{{\left| {\mathbf{E}} \right|}}^{2}} + {{{\left| {\mathbf{B}} \right|}}^{2}}}}{{8\pi }} + \frac{c}{{4\pi }}\operatorname{div} [{\mathbf{E}} \times {\mathbf{B}}] = - ({\mathbf{j}},{\mathbf{E}}),$

которое означает, что изменение плотности энергии электромагнитного поля во времени связано с ее переносом, а также передачей энергии частицам плазмы.

1.3. Модель неподвижных ионов

Примем допущение, что ионы, в силу многократного превышения электронов по массе, считаются неподвижными. Тогда ${\mathbf{j}} = {{{\mathbf{j}}}_{e}}$ и уравнения (5), (6) исключаются из рассмотрения. Будем выводить отдельно законы сохранения энергии при больших и малых скоростях электронов относительно скорости света.

1.3.1. Нерелятивистский случай. Для вывода закона сохранения энергии в нерелятивистском случае вместо соотношения (3) будем считать, что $\gamma \equiv 1$, что приводит к равенству ${{{\mathbf{p}}}_{e}} = {{m}_{e}}{{{\mathbf{v}}}_{e}}$. Исключим из уравнения (2) импульс ${{{\mathbf{p}}}_{e}}$, а затем умножим его скалярно на вектор ${{n}_{e}}{{{\mathbf{v}}}_{e}}$, в результате получим

(10)

${{m}_{e}}{{n}_{e}}\left( {{{{\mathbf{v}}}_{e}},\frac{{\partial {{{\mathbf{v}}}_{e}}}}{{\partial t}}} \right) + {{m}_{e}}{{n}_{e}}\left( {{{{\mathbf{v}}}_{e}},\left( {{{{\mathbf{v}}}_{e}} \cdot \nabla } \right){{{\mathbf{v}}}_{e}}} \right) = e{{n}_{e}}({{{\mathbf{v}}}_{e}},{\mathbf{E}}).$

Умножим уравнение (1) почленно на функцию $\frac{{{{m}_{e}}{{{\left| {{{{\mathbf{v}}}_{e}}} \right|}}^{2}}}}{2}$ и результат сложим с (10), будем иметь уравнение для плотности энергии электронов

(11)

$\frac{\partial }{{\partial t}}\left\{ {{{n}_{e}}\frac{{{{m}_{e}}{{{\left| {{{{\mathbf{v}}}_{e}}} \right|}}^{2}}}}{2}} \right\} + {\text{div}}\left\{ {{{n}_{e}}\frac{{{{m}_{e}}{{{\left| {{{{\mathbf{v}}}_{e}}} \right|}}^{2}}}}{2}{{{\mathbf{v}}}_{e}}} \right\} = ({{{\mathbf{j}}}_{e}},{\mathbf{E}}).$

Дифференциальная форма записи закона сохранения полной энергии электромагнитного поля и электронов плазмы в нерелятивистском случае следует из сложения равенств (9) и (11):

(12)

$\frac{\partial }{{\partial t}}\left\{ {\frac{{{{{\left| {\mathbf{E}} \right|}}^{2}} + {{{\left| {\mathbf{B}} \right|}}^{2}}}}{{8\pi }} + {{n}_{e}}\frac{{{{m}_{e}}{{{\left| {{{{\mathbf{v}}}_{e}}} \right|}}^{2}}}}{2}} \right\} + {\text{div}}\left\{ {\frac{c}{{4\pi }}[{\mathbf{E}} \times {\mathbf{B}}] + {{n}_{e}}\frac{{{{m}_{e}}{{{\left| {{{{\mathbf{v}}}_{e}}} \right|}}^{2}}}}{2}{{{\mathbf{v}}}_{e}}} \right\} = 0.$

1.3.2. Релятивистский случай. Умножим уравнение (2) скалярно на вектор ${{n}_{e}}{{{\mathbf{v}}}_{e}}$, будем иметь

(13)

${{n}_{e}}\left( {{{{\mathbf{v}}}_{e}},\frac{{\partial {{{\mathbf{p}}}_{e}}}}{{\partial t}}} \right) + {{n}_{e}}\left( {{{{\mathbf{v}}}_{e}},\left( {{{{\mathbf{v}}}_{e}} \cdot \nabla } \right){{{\mathbf{p}}}_{e}}} \right) = ({{{\mathbf{j}}}_{e}},{\mathbf{E}}).$

Преобразуем левую часть полученного равенства. Сначала отметим, что справедливо

(14)

$\left( {{{{\mathbf{v}}}_{e}},\frac{{\partial {{{\mathbf{p}}}_{e}}}}{{\partial t}}} \right) = {{m}_{e}}{{c}^{2}}\frac{{\partial \gamma }}{{\partial t}},\quad {\text{где}}\quad \gamma = \sqrt {1 + \frac{{{{{\left| {{{{\mathbf{p}}}_{e}}} \right|}}^{2}}}}{{m_{e}^{2}{{c}^{2}}}}} ,$

затем для преобразования выражения $\left( {{{{\mathbf{v}}}_{e}},\left( {{{{\mathbf{v}}}_{e}} \cdot \nabla } \right){{{\mathbf{p}}}_{e}}} \right)$ используем равенство

(15)

$\left( {{{{\mathbf{v}}}_{e}} \cdot \nabla } \right){{{\mathbf{p}}}_{e}} = {{m}_{e}}{{c}^{2}}\nabla \gamma - [{{{\mathbf{v}}}_{e}} \times \operatorname{rot} {{{\mathbf{p}}}_{e}}],$

которое устанавливается непосредственной проверкой. В результате соотношение (13) преобразуется к виду

(16)

${{n}_{e}}{{m}_{e}}{{c}^{2}}\frac{{\partial \gamma }}{{\partial t}} + {{m}_{e}}{{c}^{2}}\left( {{{n}_{e}}{{{\mathbf{v}}}_{e}},\nabla \gamma } \right) = ({{{\mathbf{j}}}_{e}},{\mathbf{E}}).$

Умножим уравнение (1) почленно на ${{m}_{e}}{{c}^{2}}\gamma $

${{m}_{e}}{{c}^{2}}\gamma \frac{{\partial {{n}_{e}}}}{{\partial t}} + {{m}_{e}}{{c}^{2}}\gamma \operatorname{div} ({{n}_{e}}{{{\mathbf{v}}}_{e}}) = 0$

и результат сложим с (16), получим

(17)

$\frac{\partial }{{\partial t}}\left\{ {{{m}_{e}}{{c}^{2}}{{n}_{e}}\gamma } \right\} + \operatorname{div} \left\{ {{{m}_{e}}{{c}^{2}}{{n}_{e}}\gamma {{{\mathbf{v}}}_{e}}} \right\} = ({{{\mathbf{j}}}_{e}},{\mathbf{E}}).$

Дифференциальная форма записи закона сохранения энергии в релятивистском случае следует из сложения равенств (9) и (17):

(18)

$\frac{\partial }{{\partial t}}\left\{ {\frac{{{{{\left| {\mathbf{E}} \right|}}^{2}} + {{{\left| {\mathbf{B}} \right|}}^{2}}}}{{8\pi }} + {{m}_{e}}{{c}^{2}}{{n}_{e}}\gamma } \right\} + {\text{div}}\left\{ {\frac{c}{{4\pi }}[{\mathbf{E}} \times {\mathbf{B}}] + {{m}_{e}}{{c}^{2}}{{n}_{e}}\gamma {{{\mathbf{v}}}_{e}}} \right\} = 0.$

Однако такая форма не обеспечивает переход к нерелятивистскому пределу при малых скоростях, т.е. когда ${{\left| {{{{\mathbf{v}}}_{e}}} \right|}^{2}}{\text{/}}{{c}^{2}} \ll 1$. Поэтому вместо полной энергии одной частицы $\varepsilon = {{m}_{e}}{{c}^{2}}\gamma $, которая включает энергию покоя ${{\varepsilon }_{0}} = {{m}_{e}}{{c}^{2}}$, следует использовать ее кинетическую энергию ${{\varepsilon }_{k}} = \varepsilon - {{\varepsilon }_{0}} = {{m}_{e}}{{c}^{2}}(\gamma - 1)$. При малых скоростях это выражение переходит в известную нерелятивистскую формулу ${{\varepsilon }_{k}} = {{m}_{e}}{{\left| {{{{\mathbf{v}}}_{e}}} \right|}^{2}}{\text{/}}2$.

Для получения описанной модификации умножим уравнение (1) почленно на ${{m}_{e}}{{c}^{2}}$ и вычтем его из (18), в результате будем иметь искомую форму закона сохранения энергии:

(19)

$\frac{\partial }{{\partial t}}\left\{ {\frac{{{{{\left| {\mathbf{E}} \right|}}^{2}} + {{{\left| {\mathbf{B}} \right|}}^{2}}}}{{8\pi }} + {{m}_{e}}{{c}^{2}}{{n}_{e}}(\gamma - 1)} \right\} + {\text{div}}\left\{ {\frac{c}{{4\pi }}[{\mathbf{E}} \times {\mathbf{B}}] + {{m}_{e}}{{c}^{2}}{{n}_{e}}(\gamma - 1){{{\mathbf{v}}}_{e}}} \right\} = 0.$

1.4. Учет движения ионов

Напомним, что в этом случае полный ток равен сумме токов электронов и ионов ${\mathbf{j}} = {{{\mathbf{j}}}_{e}} + {{{\mathbf{j}}}_{i}}$, поэтому с уравнениями (5), (6) следует предварительно выполнить действия, как в п. 1.3.1.

Умножим уравнения (6) скалярно на вектор ${{m}_{i}}{{n}_{i}}{{{\mathbf{v}}}_{i}}$, в результате получим

(20)

${{m}_{i}}{{n}_{i}}\left( {{{{\mathbf{v}}}_{i}},\frac{{\partial {{{\mathbf{v}}}_{i}}}}{{\partial t}}} \right) + {{m}_{i}}{{n}_{i}}\left( {{{{\mathbf{v}}}_{i}},\left( {{{{\mathbf{v}}}_{i}} \cdot \nabla } \right){{{\mathbf{v}}}_{i}}} \right) = {{e}_{i}}{{n}_{i}}({{{\mathbf{v}}}_{i}},{\mathbf{E}}).$

Умножив уравнение (5) почленно на функцию $\frac{{{{m}_{i}}{{{\left| {{{{\mathbf{v}}}_{i}}} \right|}}^{2}}}}{2}$ и результат сложив с (20), получим

(21)

$\frac{\partial }{{\partial t}}\left\{ {{{n}_{i}}\frac{{{{m}_{i}}{{{\left| {{{{\mathbf{v}}}_{i}}} \right|}}^{2}}}}{2}} \right\} + {\text{div}}\left\{ {{{n}_{i}}\frac{{{{m}_{i}}{{{\left| {{{{\mathbf{v}}}_{i}}} \right|}}^{2}}}}{2}{{{\mathbf{v}}}_{i}}} \right\} = ({{{\mathbf{j}}}_{i}},{\mathbf{E}}).$

Закон сохранения энергии в релятивистском случае с учетом динамики ионов следует из сложения равенств (9), (17) и (21):

(22)

$\frac{\partial }{{\partial t}}\left\{ {\frac{{{{{\left| {\mathbf{E}} \right|}}^{2}} + {{{\left| {\mathbf{B}} \right|}}^{2}}}}{{8\pi }} + {{m}_{e}}{{c}^{2}}{{n}_{e}}\gamma + {{n}_{i}}\frac{{{{m}_{i}}{{{\left| {{{{\mathbf{v}}}_{i}}} \right|}}^{2}}}}{2}} \right\} + {\text{div}}\left\{ {\frac{c}{{4\pi }}[{\mathbf{E}} \times {\mathbf{B}}] + {{m}_{e}}{{c}^{2}}{{n}_{e}}\gamma {{{\mathbf{v}}}_{e}} + {{n}_{i}}\frac{{{{m}_{i}}{{{\left| {{{{\mathbf{v}}}_{i}}} \right|}}^{2}}}}{2}{{{\mathbf{v}}}_{i}}} \right\} = 0.$

Для реализации перехода к нерелятивистскому пределу при малых скоростях, т.е. когда ${{\left| {{{{\mathbf{v}}}_{e}}} \right|}^{2}}{\text{/}}{{c}^{2}} \ll 1$, следует, как в п. 1.3.2, вместо полной энергии одной частицы $\varepsilon = {{m}_{e}}{{c}^{2}}\gamma $ использовать только кинетическую энергию. В результате модифицированный закон сохранения энергии примет вид

(23)

$\frac{\partial }{{\partial t}}\left\{ {\frac{{{{{\left| {\mathbf{E}} \right|}}^{2}} + {{{\left| {\mathbf{B}} \right|}}^{2}}}}{{8\pi }} + {{m}_{e}}{{c}^{2}}{{n}_{e}}(\gamma - 1) + {{n}_{i}}\frac{{{{m}_{i}}{{{\left| {{{{\mathbf{v}}}_{i}}} \right|}}^{2}}}}{2}} \right\} + {\text{div}}\left\{ {\frac{c}{{4\pi }}[{\mathbf{E}} \times {\mathbf{B}}] + {{m}_{e}}{{c}^{2}}{{n}_{e}}(\gamma - 1){{{\mathbf{v}}}_{e}} + {{n}_{i}}\frac{{{{m}_{i}}{{{\left| {{{{\mathbf{v}}}_{i}}} \right|}}^{2}}}}{2}{{{\mathbf{v}}}_{i}}} \right\} = 0.$

2. ПОСТАНОВКА ЗАДАЧИ О ПЛАЗМЕННЫХ КОЛЕБАНИЯХ

Сформулируем для основной системы уравнений (1)–(8) задачу о свободных плазменных колебаний, порождаемых коротким мощным лазерным импульсом. Предварительное изучение плазменных явлений, как правило, начинают с математической модели, в которой ионы считают неподвижными. Такой подход основан на том, что массы электрона и протона отличаются более чем на три порядка (отношение масс примерно равно 1836), что делает динамику ионов малозаметной, особенно на фоне высокоскоростных перемещений электронов. Однако когда рассматриваемые процессы продолжаются достаточно долго во времени (например, многопериодные плазменные колебания), влияние даже малых величин может привести к качественному изменению объектов наблюдения – функций, характеризующих гидродинамические макропараметры электронов и ионов (плотность, скорость и импульс), а также электрическое и магнитное поле.

С целью проведения анализа влияния динамики ионов на одномерные плоские плазменные колебания основную систему (1)–(8) можно существенно упростить. Примем допущения, что решение определяется только $x$-компонентами вектор-функций ${{{\mathbf{p}}}_{e}}$,${{{\mathbf{v}}}_{e}}$, ${{{\mathbf{v}}}_{i}}$ и ${\mathbf{E}}$, обозначим их как ${{p}_{e}}$, ${{v}_{e}}$, ${{v}_{i}}$ и ${{E}_{x}}$ соответственно, и что зависимость в указанных функциях от переменных $y$ и $z$ отсутствует, т.е. $\partial {\text{/}}\partial y = \partial {\text{/}}\partial z = 0.$

Тогда из системы (1)–(8) имеем

(24)

$\begin{array}{*{20}{c}} {\frac{{\partial {{n}_{e}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {{{n}_{e}}{{v}_{e}}} \right) = 0,\quad \frac{{\partial {{p}_{e}}}}{{\partial t}} = e{{E}_{x}} - {{m}_{e}}{{c}^{2}}\frac{{\partial \gamma }}{{\partial x}},\quad \gamma = \sqrt {1 + \frac{{p_{e}^{2}}}{{m_{e}^{2}{{c}^{2}}}}} ,} \\ {{{v}_{e}} = \frac{{{{p}_{e}}}}{{{{m}_{e}}\gamma }},\quad \frac{{\partial {{n}_{i}}}}{{\partial t}} + \frac{\partial }{{\partial x}}({{n}_{i}}{{v}_{i}}) = 0,\quad \frac{{\partial {{v}_{i}}}}{{\partial t}} + {{v}_{i}}\frac{{\partial {{v}_{i}}}}{{\partial x}} = \frac{{{{e}_{i}}}}{{{{m}_{i}}}}{{E}_{x}},} \\ {\frac{{\partial {{E}_{x}}}}{{\partial t}} = - 4\pi (e{{n}_{e}}{{v}_{e}} + {{e}_{i}}{{n}_{i}}{{v}_{i}}).} \end{array}$

Пусть ${{n}_{{e0}}}$ и ${{n}_{{i0}}}$ – значения невозмущенной электронной и ионной плотности (концентрации) в нейтральной плазме соответственно, так что ${{e}_{i}}{{n}_{{i0}}} + e{{n}_{{e0}}} = 0$. Определим ${{\omega }_{p}} = \mathop {\left( {4\pi {{e}^{2}}{{n}_{{e0}}}{\text{/}}{{m}_{e}}} \right)}\nolimits^{1/2} $ – плазменную частоту, ${{k}_{p}} = {{\omega }_{p}}{\text{/}}c$, и введем безразмерные величины

$\begin{array}{*{20}{c}} {\rho = {{k}_{p}}x,\quad \theta = {{\omega }_{p}}t,\quad {{N}_{e}} = \frac{{{{n}_{e}}}}{{{{n}_{{e0}}}}},\quad {{V}_{e}} = \frac{{{{v}_{e}}}}{c},\quad {{P}_{e}} = \frac{{{{p}_{e}}}}{{{{m}_{e}}c}},} \\ {{{N}_{i}} = \frac{{{{n}_{i}}}}{{{{n}_{{i0}}}}},\quad {{V}_{i}} = \frac{{{{v}_{i}}}}{c},\quad E = - \frac{{e{{E}_{x}}}}{{{{m}_{e}}c{{\omega }_{p}}}},\quad \delta = - \frac{{{{m}_{e}}}}{{{{m}_{i}}}}\frac{{{{e}_{i}}}}{e} > 0.} \end{array}$

В новых переменных система (24) примет вид

(25)

$\begin{array}{*{20}{c}} {\frac{{\partial {{N}_{e}}}}{{\partial \theta }} + \frac{\partial }{{\partial \rho }}\left( {{{N}_{e}}{{V}_{e}}} \right) = 0,\quad \frac{{\partial {{N}_{i}}}}{{\partial \theta }} + \frac{\partial }{{\partial \rho }}({{N}_{i}}{{V}_{i}}) = 0,\quad \frac{{\partial E}}{{\partial \theta }} = {{N}_{e}}{{V}_{e}} - {{N}_{i}}{{V}_{i}},} \\ {\gamma = \sqrt {1 + P_{e}^{2}} ,\quad {{V}_{e}} = \frac{{{{P}_{e}}}}{\gamma },\quad \frac{{\partial {{P}_{e}}}}{{\partial \theta }} + E + \frac{{\partial \gamma }}{{\partial \rho }} = 0,\quad \frac{{\partial {{V}_{i}}}}{{\partial \theta }} + {{V}_{i}}\frac{{\partial {{V}_{i}}}}{{\partial \rho }} = \delta E.} \end{array}$

Из первых трех уравнений (25) следует

$\frac{\partial }{{\partial \theta }}\left( {{{N}_{e}} - {{N}_{i}} + \frac{{\partial E}}{{\partial \rho }}} \right) = 0.$

Это соотношение справедливо как при отсутствии плазменных колебаний (${{N}_{e}} \equiv {{N}_{i}} \equiv 1$, $E \equiv 0$), так и при их наличии, поэтому отсюда имеем более простое выражение для электронной плотности:

(26)

${{N}_{e}}(\rho ,\theta ) = {{N}_{i}}(\rho ,\theta ) - \frac{{\partial E(\rho ,\theta )}}{{\partial \rho }}.$

Исключая из системы (25) плотность ${{N}_{e}}$, приходим к уравнениям, описывающим свободные плоские одномерные колебательные движения электронов и ионов в холодной идеальной плазме:

(27)

$\begin{array}{*{20}{c}} {\frac{{\partial {{P}_{e}}}}{{\partial \theta }} + E + \frac{{\partial \gamma }}{{\partial \rho }} = 0,\quad \gamma = \sqrt {1 + P_{e}^{2}} ,\quad {{V}_{e}} = \frac{{{{P}_{e}}}}{\gamma },} \\ {\frac{{\partial {{V}_{i}}}}{{\partial \theta }} - \delta E + {{V}_{i}}\frac{{\partial {{V}_{i}}}}{{\partial \rho }} = 0,\quad \frac{{\partial {{N}_{i}}}}{{\partial \theta }} + {{N}_{i}}\frac{{\partial {{V}_{i}}}}{{\partial \rho }} + {{V}_{i}}\frac{{\partial {{N}_{i}}}}{{\partial \rho }} = 0,} \\ {\frac{{\partial E}}{{\partial \theta }} - {{N}_{i}}({{V}_{e}} - {{V}_{i}}) + {{V}_{e}}\frac{{\partial E}}{{\partial \rho }} = 0.} \end{array}$

Отметим, что, кроме искомых переменных, в систему (27) входит малый параметр $\delta $, по сути характеризующий отношение масс электрона и протона ($\delta \approx 1{\text{/}}1836$).

Обсудим начальные и краевые условия для системы уравнений (27). Снабдим рассматриваемую систему на прямой $\rho \in ( - \infty ,\infty )$ начальными условиями следующего вида:

(28)

$\begin{array}{*{20}{c}} {{{E}_{0}}(\rho ) = \mathop {\left( {\frac{{{{a}_{ * }}}}{{{{\rho }_{ * }}}}} \right)}\nolimits^2 \rho exp\left\{ { - 2\frac{{{{\rho }^{2}}}}{{\rho _{ * }^{2}}}} \right\},} \\ {{{P}_{{{{e}_{0}}}}}(\rho ) = 0,\quad {{V}_{{{{i}_{0}}}}}(\rho ) = 0,\quad {{N}_{{{{i}_{0}}}}}(\rho ) = 1 + \frac{\delta }{{1 + \delta }}\frac{{\partial {{E}_{0}}(\rho )}}{{\partial \rho }},} \end{array}$

где параметры ${{\rho }_{ * }}$ и ${{a}_{ * }}$ характеризуют масштаб области локализации и максимальную величину ${{E}_{{max}}} = a_{ * }^{2}{\text{/}}({{\rho }_{ * }}2\sqrt {\text{e}} ) \approx 0.3a_{ * }^{2}{\text{/}}{{\rho }_{ * }}$ электрического поля (28) соответственно. Вид возмущения электрического поля ${{E}_{0}}(\rho )$ выбран из соображений, что подобные колебания могут возбуждаться в разреженной плазме (${{\omega }_{l}} \gg {{\omega }_{p}}$) лазерным импульсом с частотой ${{\omega }_{l}}$ при его фокусировке в линию (этого можно добиться при использовании цилиндрической линзы).

Если электрическое поле лазерного излучения имеет гауссово распределение по пространственным координатам и времени

(29)

${{E}_{L}}(\rho ,z,t) = {{E}_{{0L}}}exp\left\{ { - \frac{{{{\rho }^{2}}}}{{\rho _{ * }^{2}}} - \frac{{\omega _{p}^{2}}}{{\tau _{ * }^{2}}}\mathop {\left( {t - \frac{z}{c}} \right)}\nolimits^2 } \right\}cos\left[ {{{\omega }_{l}}\left( {t - \frac{z}{c}} \right)} \right],$

где ${{\tau }_{ * }} = {{\omega }_{p}}{{\tau }_{p}}$, ${{\rho }_{ * }} = {{k}_{p}}{{R}_{p}}$ – безразмерные значения длительности ${{\tau }_{p}}$ и радиуса фокального пятна ${{R}_{p}}$ лазерного импульса, то в некоторой точке $z,$ удаленной от заднего фронта импульса на расстояние, превышающее длину плазменной волны (${{k}_{p}}\left| z \right| \gg 1$), справедливо следующее соотношение, связывающее величину ${{a}_{ * }}$ с параметрами лазерного импульса [12]:

(30)

$a_{ * }^{2} = a_{0}^{2}{{\tau }_{ * }}\sqrt {\pi {\text{/}}2} exp( - \tau _{ * }^{2}{\text{/}}8),$

где ${{a}_{0}} = e{{E}_{{0L}}}{\text{/}}(m{{\omega }_{l}}c)$ – нормированная амплитуда лазерного поля. В условиях оптимального возбуждения кильватерной волны (${{\tau }_{ * }} = 2$), когда ее амплитуда максимальна, соотношение (30) принимает вид $a_{ * }^{2} = a_{0}^{2}\sqrt {2\pi {\text{/e}}} \approx 1.52a_{0}^{2}$.

В целях численного моделирования плазменных колебаний расчетную область необходимо ограничить; определим ее как отрезок $[ - d,d]$, на концах которого следует задать искусственные граничные условия. Обсуждению их построения посвящен разд. 3.6 в [10], здесь же мы ограничимся “обрезанием” бесконечной области с помощью однородных граничных условий I рода:

(31)

${{P}_{{{{e}_{0}}}}}( \pm d,\theta ) = {{V}_{{{{i}_{0}}}}}( \pm d,\theta ) = {{E}_{0}}( \pm d,\theta ) = 0,\quad {{N}_{{{{i}_{0}}}}}( \pm d,\theta ) = 1.$

Конечно, параметр $d$ следует выбирать достаточно большим. В силу экспоненциального затухания функции ${{E}_{0}}(\rho )$, достаточно положить $d = 4.5{{\rho }_{ * }}$. В этом случае имеем $ex{{p}^{2}}{\text{\{ }} - {{d}^{2}}{\text{/}}\rho _{ * }^{2}{\text{\} }} \approx 2.5768 \times {{10}^{{ - 18}}}$. Это означает, что при вычислениях с двойной точностью величина скачка начальной функции ${{E}_{0}}$ в точках $\rho = \pm d$ соизмерима с машинной точностью, т.е. с обычной погрешностью округления данных. Другими словами, при численном моделировании колебаний эффект обрезания начальных условий заметен совершенно не будет, что полностью соответствует понятию “искусственной границы”.

Такой подход является практически весьма удобным и потому наиболее часто используемым, однако его главный недостаток – чрезмерное увеличение расчетной области. Наблюдаемый эффект опрокидывания колебаний, как правило, реализуется в окрестности начала координаты $\rho $ на расстоянии менее $0.1{{\rho }_{ * }}$, поэтому более 90% вычислений являются своеобразной “платой” за использование “грубых” граничных условий. В данном случае оптимизация вычислений не является целью работы, следовательно, самый простой вариант граничных условий вполне подходит для проверки выполнения закона сохранения энергии.

Суммируя все вышесказанное, определим следующую начально-краевую задачу: найти в полуполосе ${\text{\{ }}(\rho ,\theta ):\theta > 0,\; - d < \rho < d{\text{\} }}$ решение уравнений (27), удовлетворяющее начальным (28) и граничным (31) условиям.

Напомним, что в эйлеровых переменных, с которыми мы имеем дело, принципиально важной для наблюдения за процессом опрокидывания колебаний является функция электронной плотности ${{N}_{e}}(\rho ,\theta )$, определяемая соотношением (26).

3. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

3.1. Краткое описание вычислительного алгоритма

Учитывая наличие малого параметра $\delta $, проведем масштабирование уравнений (27). Сделаем сначала замену искомых переменных

(32)

${{V}_{i}}(\rho ,\theta ) = \delta W(\rho ,\theta ),\quad {{N}_{i}}(\rho ,\theta ) = 1 + \delta K(\rho ,\theta ),$

а затем поделим уравнения для новых функций $W$ и $K$ на величину $\delta $. Заметим, что теперь индекс “$e$”, относящийся к функциям, характеризующим динамику электронов, становится малоинформативным и его можно опустить без потери смысла. После указанных изменений система (27) примет вид

(33)

$\begin{array}{*{20}{c}} {\frac{{\partial P}}{{\partial \theta }} + E + \frac{{\partial \gamma }}{{\partial \rho }} = 0,\quad \gamma = \sqrt {1 + {{P}^{2}}} ,\quad V = \frac{P}{\gamma },} \\ {\frac{{\partial W}}{{\partial \theta }} - E + \delta W\frac{{\partial W}}{{\partial \rho }} = 0,\quad \frac{{\partial K}}{{\partial \theta }} + (1 + \delta K)\frac{{\partial W}}{{\partial \rho }} + \delta W\frac{{\partial K}}{{\partial \rho }} = 0,} \\ {\frac{{\partial E}}{{\partial \theta }} - (1 + \delta K)(V - \delta W) + V\frac{{\partial E}}{{\partial \rho }} = 0.} \end{array}$

Начальные и краевые условия при масштабировании изменятся только у функции $K(\rho ,\theta )$, описывающей возмущение концентрации ионов:

(34)

$K(\rho ,\theta = 0) = \frac{1}{{1 + \delta }}\frac{{\partial {{E}_{0}}(\rho )}}{{\partial \rho }},\quad \left| \rho \right| < d;\quad K( \pm d,\theta ) = 0,\theta \geqslant 0.$

Таким образом, разностную схему определим для нахождения приближенного решения уравнений (33) с начальными и краевыми условиями (28), (31), (34).

Обратим внимание, что в системе (33) представлено взаимодействие двух физических процессов: нелинейные колебания в фиксированной точке пространства и их пространственно-временной перенос. Отнесем к описанию процесса нелинейных колебаний уравнения

(35)

$\begin{array}{*{20}{c}} {\frac{{\partial{ \tilde {P}}}}{{\partial \theta }} + \tilde {E} = 0,\quad \tilde {V} = \frac{{\tilde {P}}}{{\sqrt {1 + {{{\tilde {P}}}^{2}}} }},\quad \frac{{\partial{ \tilde {W}}}}{{\partial \theta }} - \tilde {E} = 0,} \\ {\frac{{\partial{ \tilde {K}}}}{{\partial \theta }} + (1 + \delta \tilde {K})\frac{{\partial{ \tilde {W}}}}{{\partial \rho }} = 0,\quad \frac{{\partial{ \tilde {E}}}}{{\partial \theta }} - (1 + \delta \tilde {K})(\tilde {V} - \delta \tilde {W}) = 0,} \end{array}$

а к их переносу в пространстве и времени уравнения

(36)

$\begin{array}{*{20}{c}} {\frac{{\partial{ \bar {P}}}}{{\partial \theta }} + \frac{{\partial{ \bar {\gamma }}}}{{\partial \rho }} = 0,\quad \bar {\gamma } = \sqrt {1 + {{{\bar {P}}}^{2}}} ,\quad \bar {V} = \frac{{\bar {P}}}{{\bar {\gamma }}},} \\ {\frac{{\partial{ \bar {E}}}}{{\partial \theta }} + \bar {V}\frac{{\partial{ \bar {E}}}}{{\partial \rho }} = 0,\quad \frac{{\partial{ \bar {W}}}}{{\partial \theta }} + \delta \frac{\partial }{{\partial \rho }}\left( {\frac{{{{{\bar {W}}}^{2}}}}{2}} \right) = 0,\quad \frac{{\partial{ \bar {K}}}}{{\partial \theta }} + \delta \bar {W}\frac{{\partial{ \bar {K}}}}{{\partial \rho }} = 0.} \end{array}$

В качестве основы для дискретизаций по времени обеих систем используется обычная схема с перешагиванием [13], а для уравнений переноса – схема Лакса–Вендроффа (“тренога”) [14]. Пусть $\tau $ – шаг по времени, тогда будем относить к “целым” моментам времени ${{\theta }_{j}} = j\tau $ ($j \geqslant 0$ – целое) величины $E$, $\tilde {E}$, $\bar {E}$, $\tilde {K}$, $\bar {K}$, к “полуцелым” ${{\theta }_{{j \pm 1/2}}}$ – $P$, $\tilde {P}$, $\bar {P}$, $\tilde {W}$, $\bar {W}$, а также зависимые от импульса $P$ величины $\gamma $ и $V$. Для дискретизации по пространству используется сетка с постоянным шагом $h$ так, что ${{\rho }_{m}} = mh$, $\left| m \right| \leqslant M$, $Mh = d$. Как уже говорилось выше, расчетные формулы численного алгоритма в работе не приводятся, в силу их громоздкости и наличия доступных публикаций с подробным изложением [9], [10].

Сделаем замечания об используемой схеме. Для каждой из вспомогательных задач (35), (36) при достаточной гладкости решения имеется аппроксимация порядка $O({{\tau }^{2}} + {{h}^{2}})$, что для суммарной схемы расщепления приводит к порядку $O(\tau + {{h}^{2}})$ [15]. Кроме того, схема для (35) безусловно устойчива, а для схемы, аппроксимирующей (36), справедливо условие устойчивости вида $\tau = O(h)$, полученное на основе спектрального признака и принципа замороженных коэффициентов [14]. Суммируя вышесказанное, ожидаем от приближенного решения сходимость порядка $O(\tau + {{h}^{2}})$ при выполнении условия устойчивости $\tau = O(h)$.

3.2. Расчеты по нерелятивистской модели

Будем считать ионы неподвижными, т.е. положим $\delta = 0$. Это дает из (32): ${{V}_{i}}(\rho ,\theta ) \equiv 0,$ ${{N}_{i}}(\rho ,\theta ) \equiv 1,$ а также существенное упрощение остальных уравнений в системе (27). Кроме того, будем предполагать скорость электронов малой по сравнению со скоростью света, и определим с этой целью параметры в начальных условиях (28) как ${{a}_{ * }} = 0.414$, ${{\rho }_{ * }} = 0.6$. Параметр $d$, характеризующий искусственную границу, положим $d = 4.5{{\rho }_{ * }}$. Вычисления проведем на последовательности вложенных сеток: $\tau = h \in {\text{\{ }}1{\text{/}}1600,\;1{\text{/}}3200,\;1{\text{/}}6400{\text{\} }}$.

Сначала обсудим эксперимент с аналитическим решением. Для данной постановки можно выписать формулы для аналитического решения на оси симметрии области (при $\rho = 0$), так называемое аксиальное решение [10]. При указанных параметрах оно существует неограниченно по времени; для наименее гладкой из всех функций – функции электронной плотности – формула имеет вид

$N(\rho = 0,\theta ) = \frac{{1 - \alpha }}{{1 - \alpha (1 - cos\theta )}},\quad \alpha = \mathop {\left( {\frac{{{{a}_{ * }}}}{{{{\rho }_{ * }}}}} \right)}\nolimits^2 .$

Лего видеть, что электронная плотность является $2\pi $-периодической по времени и колеблется в диапазоне [0.52, 10.96] (границы указаны с двумя верными знаками после десятичной точки).

На фиг. 1 представлена динамика относительной погрешности плотности электронов в центре области в течение примерно 20 периодов при $\tau = h = 1{\text{/}}6400$. Из графика видно, что верхняя огибающая колеблющейся погрешности представляет собой линейную по времени функцию, причем верхняя граница относительной погрешности не превышает 3%. График погрешности, полученный при расчете на сетке с удвоенными шагами $\tau = h = 1{\text{/}}3200$, имеет точно такой же вид, однако его верхняя граница соответствует примерно 7%, что вполне соответствует сходимости первого порядка по $\tau $. Следует отметить, что условие устойчивости носит асимптотический характер, т.е. справедливо только для достаточно малых параметров дискретизации по времени и пространству. Это подтверждается расчетом на еще более грубой сетке – $\tau = h = 1{\text{/}}1600$, когда линейный рост погрешности продолжается всего примерно 10 периодов, а затем разностное решение теряет устойчивость, что приводит к экспоненциальному росту относительной погрешности и к не соответствующим физическому смыслу отрицательным значениям дискретного аналога электронной плотности. Уточним, что если безразмерное время окончания счета не превышает $20\pi $, то сеточные параметры $\tau = h \approx 1{\text{/}}1500$ уже вполне пригодны для адекватного представления искомого решения.

Фиг. 1.

Динамика относительной погрешности плотности электронов в центре области $N(\rho = 0,\theta )$ (нерелятивистский случай).

Проведенные вычисления позволяют сформулировать гипотезу о первом порядке точности используемой разностной схемы, однако, представленные аргументы не достаточно убедительны. Дело в том, что явные формулы для аналитического решения (даже на одной прямой $\rho = 0$) являются настоящей экзотикой, т.е. не следует рассчитывать на существование их аналогов для других постановок. Кроме того, влияние второго параметра дискретизации $h$ при таком подходе отследить невозможно. Поэтому предложим другой подход для оценки качества используемой схемы, основанный на законе сохранения энергии.

В используемых безразмерных переменных нерелятивистский закон сохранения (12) имеет вид

(37)

$\frac{\partial }{{\partial \theta }}\{ {{E}^{2}} + N{{V}^{2}}\} + \frac{\partial }{{\partial \rho }}\{ N{{V}^{3}}\} = 0.$

После интегрирования (37) по отрезку $[ - d,d]$ получим сохранение во времени величины

$E{{n}^{d}}(\theta ) = \int\limits_{ - d}^d {[{{E}^{2}}(\rho ,\theta ) + N(\rho ,\theta ){{V}^{2}}(\rho ,\theta )]{\kern 1pt} d\rho } \equiv {\text{const}}.$

Полезной для дальнейших расчетов является формула, использующая ${{E}_{0}}(\rho )$ из (28):

(38)

$E{{n}^{\infty }}(0) = \int\limits_{ - \infty }^\infty {E_{0}^{2}} (\rho )d\rho = \frac{{a_{ * }^{4}}}{{{{\rho }_{ * }}}}\frac{{\sqrt \pi }}{{16}}.$

На фиг. 2 представлена динамика относительной погрешности энергии в течение примерно 20 периодов при $\tau = h = 1{\text{/}}6400$. Отметим, что относительная погрешность величины $E{{n}^{d}}(0)$, связанная с введением искусственной границы здесь достаточно мала: не превышает $6 \times {{10}^{{ - 14}}}$, поэтому на фигуре представлена нормировка на величину $E{{n}^{\infty }}(0)$. Из графика видно, что не только верхняя огибающая колеблющейся погрешности, но и нижняя огибающая асимптотически, начиная примерно с 8 периода, представляют собой линейные по времени функции, причем верхняя граница относительной погрешности не превышает 0.025%. График погрешности, полученный при расчете на сетке с удвоенными шагами $\tau = h = 1{\text{/}}3200$, имеет точно такой же вид, однако его верхняя граница примерно равна 0.05%, что полностью соответствует сходимости первого порядка по $\tau $. Как уже отмечалось выше, вследствие асимптотического характера условия устойчивости на более грубой сетке при $\tau = h = 1{\text{/}}1600$ график при удвоении значения верхней границы сохраняет свою форму примерно 10 периодов, а затем разностным решением теряется устойчивость.

Фиг. 2.

Динамика относительной погрешности энергии $E{{n}^{d}}(\theta )$ (нерелятивистский случай).

На основании проведенных расчетов можно сделать следующие выводы:

1) численный анализ нерелятивистских колебаний, проведенный с помощью используемой схемы, можно считать достоверным;

2) контроль за соблюдением закона сохранения энергии позволяет отследить не только порядок сходимости разностного решения к решению дифференциальной задачи, но и качественные свойства разностной схемы, например, свойственный ей линейный рост погрешности во времени;

3) необходимость частных аналитических решений для проверки точности расчетов отпадает: стандартное теоретическое исследование аппроксимации и устойчивости вместе с экспериментальным наблюдением за сохранением энергии существенно повышает достоверность вычислений.

3.3. Расчеты по релятивистской модели при неподвижных ионах

Будем, как и выше считать ионы неподвижными, т.е. положим $\delta = 0$, однако, будем предполагать скорость электронов сравнимой со скоростью света, поэтому определим с этой целью параметры в начальных условиях (28) как ${{a}_{ * }} = 2.07$, ${{\rho }_{ * }} = 3.0$. Параметр $d$, характеризующий искусственную границу выберем, как и ранее, $d = 4.5{{\rho }_{ * }}$. Вычисления проведем на вложенных сетках $\tau = h \in {\text{\{ }}1{\text{/}}1500,\;1{\text{/}}3000{\text{\} }}$.

В используемых безразмерных переменных релятивистский закон сохранения (19) при неподвижных ионах имеет вид

(39)

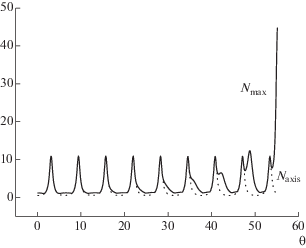
$\frac{\partial }{{\partial \theta }}\left\{ {\frac{{{{E}^{2}}}}{2} + N(\gamma - 1)} \right\} + \frac{\partial }{{\partial \rho }}\{ NV(\gamma - 1)\} = 0,$

где

$\gamma = \sqrt {1 + {{P}^{2}}} ,\quad P = \gamma V.$

После интегрирования (39) по отрезку $[ - d,d]$ получим сохранение во времени величины

$En{{r}^{d}}(\theta ) = \int\limits_{ - d}^d {\left[ {\frac{{{{E}^{2}}(\rho ,\theta )}}{2} + N(\rho ,\theta )(\gamma (\rho ,\theta ) - 1)} \right]} d\rho \equiv {\text{const}}.$

При вычислении $En{{r}^{\infty }}(0)$ потребуется формула (38).

В динамике релятивистских электронных колебаний наблюдаются две тенденции. Первая из них заключается в том, что внеосевые колебания несколько опережают по фазе колебания плотности на оси симметрии (при $\rho = 0$) и от периода к периоду этот фазовый сдвиг увеличивается. Вторая тенденция более наглядна: с течением времени происходит постепенное формирование абсолютного максимума плотности, расположенного вне оси и сравнимого по величине с осевыми. Хорошей иллюстрацией этим утверждениям является фиг. 3. На нем пунктиром изображено для электронной плотности изменение во времени в начале координат, а сплошной линией – динамика максимального по области значения. Сначала колебания носят регулярный характер, т.е. глобальные по области максимумы и минимумы плотности сменяют друг друга через половину периода и располагаются в начале координат. После седьмого регулярного (центрального) максимума в момент времени $\theta \approx 42.2$ возникает новая структура – внеосевой максимум электронной плотности, при этом регулярные колебания продолжают наблюдаться в окрестности начала координат. Внеосевой максимум, в свою очередь, в момент времени $\theta \approx 48.8$ становится больше осевого и на следующем периоде – в $\theta \approx 55.1$ – на его месте возникает сингулярность электронной плотности.

Фиг. 3.

Динамика электронной плотности при покоящихся ионах (релятивистский случай): ${{N}_{{{\text{max}}}}}$ – максимум по области (сплошная линия), ${{N}_{{{\text{axis}}}}}$ – значение при $\rho = 0$ (пунктирная линия).

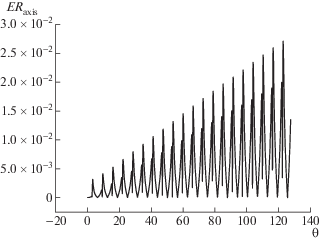
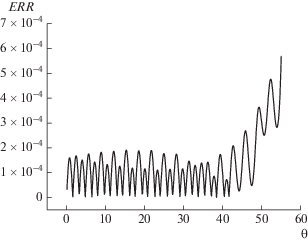
Сопоставим этому процессу фиг. 4, на котором представлена динамика относительной погрешности энергии вплоть до момента опрокидывания при $\tau = h = 1{\text{/}}3000$. Отметим, что относительная погрешность величины $En{{r}^{d}}(0)$, связанная с введением искусственной границы, здесь достаточно мала: не превышает $8 \times {{10}^{{ - 14}}}$, поэтому на фигуре представлена нормировка на величину $En{{r}^{\infty }}(0)$. Из графика видно, что верхняя граница относительной погрешности не превышает $0.06\% $, причем до формирования внеосевого максимума электронной плотности погрешность по времени не растет и ограничена величиной 0.02%. Это означает, что рост погрешности напрямую связан с ухудшением гладкости решения, что имеет место на завершающих периодах колебаний. Отметим, что график погрешности, полученный при расчете на сетке с удвоенными шагами $\tau = h = 1{\text{/}}1500$, имеет точно такой же вид, однако его верхняя граница примерно равна 0.11%, что полностью соответствует сходимости первого порядка по $\tau $.

Фиг. 4.

Динамика относительной погрешности энергии при покоящихся ионах $En{{r}^{d}}(\theta )$ (релятивистский случай).

Расчеты на более подробных сетках не производились, в силу численных результатов предыдущего раздела, а также на основании сравнения с расчетами в лагранжевых переменных [10], [16].

В данном варианте аналитические решения для проверки точности схемы не применялись, так как на прямой $\rho = 0$ они совпадают с аксиальными решениями нерелятивистских уравнений. Поэтому анализ погрешности для функции электронной плотности из предыдущего раздела вполне применим к обсуждаемым здесь экспериментам. В результате на основании проведенных расчетов можно сделать аналогичные выводы о достоверности численного анализа релятивистских колебаний, о пользе контроля за соблюдением закона сохранения энергии, а также, что стандартное теоретическое исследование аппроксимации и устойчивости вместе с экспериментальным наблюдением за сохранением энергии существенно повышает достоверность вычислений.

3.4. Расчеты по релятивистской модели при подвижных ионах

Обсудим результаты численного решения уравнений (33) с начальными и краевыми условиями (28), (31), (34) при $\delta = 1{\text{/}}2000$, т.е. при учете влияния движения ионов на процесс плоских релятивистских колебаний электронов.

Рассмотрим сначала результаты численных экспериментов при значениях ${{a}_{ * }} = 3.25$, ${{\rho }_{ * }} = 5$, $d = 4.5{{\rho }_{ * }}$, $\tau = h = 1{\text{/}}3000$, которые представлены на фиг. 5–7 .

Фиг. 5.

Динамика электронной плотности при подвижных ионах и внеосевом опрокидывании: ${{N}_{{{\text{max}}}}}$ – максимум по области (сплошная линия), ${{N}_{{{\text{axis}}}}}$ – значение при $\rho = 0$ (пунктирная линия).

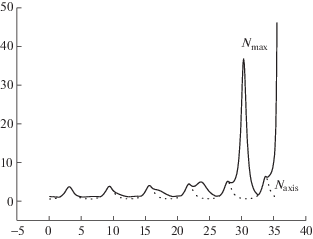
Фиг. 6.

Пространственные распределения электрического поля $E$ и скорости электронов $V$ в момент внеосевого опрокидывания при подвижных ионах: $E$ – сплошная линия, $V$ – пунктирная линия.

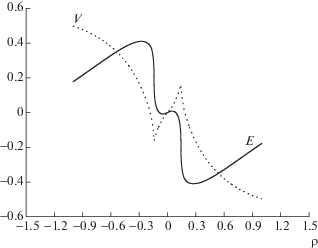
Фиг. 7.

Динамика относительной погрешности энергии при подвижных ионах $Enr{{i}^{d}}(\theta )$ и внеосевом опрокидывании.

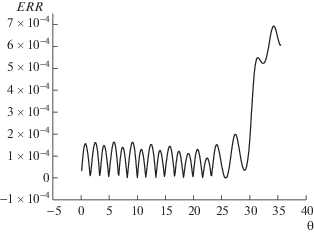
На фиг. 5 изображена зависимость от времени максимального значения электронной плотности в области $[ - d,d]$ и значения электронной плотности при $\rho = 0$. Легко заметить, что на начальных периодах колебаний максимальные значения плотности сосредоточены на оси симметрии, затем (на четвертом периоде) формируется локальный внеосевой максимум, рост которого в дальнейшем приводит к опрокидыванию колебаний. Амплитуды осевых колебаний при этом также растут, но значительно медленнее.

На фиг. 6 приведены зависимости от пространственной координаты функций электрического поля и скорости электронов в момент опрокидывания. Здесь наглядно прослеживается, что сингулярность плотности определяется производной сформировавшейся локально-ступенчатой функции $E(\rho )$ и располагается вне оси. Следует отметить, что скорость электронов в окрестности точки сингулярности непрерывна, но имеет скачок производной.

Графики, показанные на фиг. 5 и 6, являются типичными для внеосевого опрокидывания, независимо от учета динамики ионов, учета релятивизма и пространственной симметрии [10]. Однако в рассматриваемом случае ионы подвижны, их пространственное распределение отличается от константы, но причина опрокидывания в описанных расчетах – “самостоятельные” релятивистские электронные колебания, как и в предыдущем разделе.

В используемых безразмерных переменных релятивистский закон сохранения (23) при подвижных ионах имеет вид

(40)

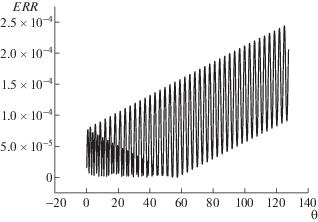
$\frac{\partial }{{\partial \theta }}\left\{ {\frac{{{{E}^{2}}}}{2} + {{N}_{e}}(\gamma - 1) + \frac{1}{\delta }\frac{{{{N}_{i}}V_{i}^{2}}}{2}} \right\} + \frac{\partial }{{\partial \rho }}\left\{ {{{N}_{e}}{{V}_{e}}(\gamma - 1) + \frac{1}{\delta }\frac{{{{N}_{i}}V_{i}^{3}}}{2}} \right\} = 0.$

С целью избежать путаницы здесь восстановлены индексы $e$ и $i$ так, как они используются в (25). После интегрирования (40) по отрезку $[ - d,d]$ получим сохранение во времени величины

$Enr{{i}^{d}}(\theta ) = \int\limits_{ - d}^d {\left[ {\frac{{{{E}^{2}}(\rho ,\theta )}}{2} + {{N}_{e}}(\rho ,\theta )(\gamma (\rho ,\theta ) - 1) + \frac{1}{\delta }\frac{{{{N}_{i}}(\rho ,\theta )V_{i}^{2}(\rho ,\theta )}}{2}} \right]} d\rho \equiv {\text{const}}.$

Наличие малого параметра $\delta $ в знаменателе не порождает особенности, так как при масштабировании системы (27) учитывается, что ${{V}_{i}}(\rho ,\theta ) = \delta W(\rho ,\theta )$. При вычислении $Enr{{i}^{\infty }}(0)$ здесь, как и ранее, потребуется формула (38).

Сопоставим обсуждаемому процессу фиг. 7, на котором представлена динамика относительной погрешности энергии вплоть до момента опрокидывания при $\tau = h = 1{\text{/}}3000$. Отметим, что относительная погрешность величины $Enr{{i}^{d}}(0)$, связанная с введением искусственной границы, здесь достаточно мала: не превышает $2 \times {{10}^{{ - 13}}}$, поэтому на рисунке представлена нормировка на величину $Enr{{i}^{\infty }}(0)$. Из графика видно, что верхняя граница относительной погрешности не превышает 0.07%, причем до формирования внеосевого максимума электронной плотности погрешность по времени не растет и ограничена величиной 0.02%. Это означает, что рост погрешности напрямую связан с ухудшением гладкости решения, что имеет место на завершающих периодах колебаний. Отметим, что график погрешности, полученный при расчете на сетке с удвоенными шагами $\tau = h = 1{\text{/}}1500$, имеет точно такой же вид, однако его верхняя граница примерно равна 0.12%, что полностью соответствует сходимости первого порядка по $\tau $. В целом расчет обсуждаемого варианта имеет близкое сходство с эффектом опрокидывания электронных колебаний при неподвижных ионах.

Познакомимся теперь с результатами численных экспериментов при значениях ${{a}_{ * }} = 2.07$, ${{\rho }_{ * }} = 3$, $\tau = h = 1{\text{/}}3000$, которые представлены на фиг. 8–10 .

Фиг. 8.

Динамика электронной плотности при подвижных ионах и осевом опрокидывании: ${{N}_{{{\text{max}}}}}$ – максимум по области (сплошная линия), ${{N}_{{{\text{axis}}}}}$ – значение при $\rho = 0$ (пунктирная линия).

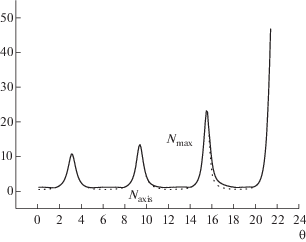
Фиг. 9.

Пространственные распределения электрического поля $E$ и скорости электронов $V$ в момент осевого опрокидывания при подвижных ионах: $E$ – сплошная линия, $V$ – пунктирная линия.

Фиг. 10.

Динамика относительной погрешности энергии при подвижных ионах $Enr{{i}^{d}}(\theta )$ и осевом опрокидывании.

На фиг. 8 изображена зависимость от времени максимального значения электронной плотности в области $[ - d,d]$ и значения электронной плотности при $\rho = 0$. Представленные на нем функции принципиально отличаются от функций на фиг. 5. Здесь максимальные значения электронной плотности монотонно возрастают от периода к периоду и располагаются строго на оси симметрии. Никаких внеосевых максимумов у функции электронной плотности не наблюдается вплоть до опрокидывания.

На фиг. 9 приведены зависимости от пространственной координаты функций электрического поля и скорости электронов при осевом опрокидывании. Так же как и на фиг. 6, наблюдаем, что сингулярность электронной плотности определяется производной сформировавшейся локально-ступенчатой функции $E(\rho )$, однако скачок в ее значениях здесь располагается при $\rho = 0$. Обратим внимание на пространственную зависимость скорости электронов при осевом опрокидывании: она, как и электрическое поле, подобна ступенчатой, т.е. разрывной функции. Такая структура качественно отличается от функции скорости, представленной на фиг. 6. Вышесказанное означает, что здесь мы имеем дело с совершенно другим типом опрокидывания колебаний. Параметры ${{a}_{ * }}$ и ${{\rho }_{ * }}$ совпадают с параметрами при расчете релятивистских колебаний с неподвижными ионами и должны гарантировать существование ограниченного аксиального решения [10] в течение всего наблюдаемого времени. Однако учет динамики ионов приводит к увеличению градиента электрического поля на оси симметрии области, что, в свою очередь, нарушает указанные условия существования, и гарантированно приводит к осевому опрокидыванию.

Сопоставим обсуждаемому процессу фиг. 10, на котором представлена динамика относительной погрешности энергии вплоть до момента опрокидывания при $\tau = h = 1{\text{/}}3000$. Отметим, что относительная погрешность величины $Enr{{i}^{d}}(0)$, связанная с введением искусственной границы, здесь достаточно мала: не превышает $2 \times {{10}^{{ - 13}}}$, поэтому на фигуре представлена нормировка на величину $Enr{{i}^{\infty }}(0)$. Из графика видно, что верхняя граница относительной погрешности не превышает 0.02%, причем вплоть до опрокидывания погрешность по времени не растет и ограничена указанной величиной. В данном случае гладкость решения (электрического поля) ухудшается постепенно, поэтому резких скачков погрешности не наблюдается. Отметим, что график погрешности, полученный при расчете на сетке с удвоенными шагами $\tau = h = 1{\text{/}}1500$, имеет точно такой же вид, однако его верхняя граница примерно равна 0.04%, что полностью соответствует сходимости первого порядка по $\tau $.

Обратим внимание, что графики относительной погрешности энергии на фиг. 7 и 10 замечательно согласуются с графиками максимальной по области электронной плотности (фиг. 5 и 7 ) и скорости электронов (фиг. 6 и 8 ). Как уже отмечалось выше, наиболее чувствительной к параметрам варианта является функция электронной плотности, которая опять же дает максимальный вклад в величину относительной погрешности энергии. При расчете внеосевого опрокидывания в $\theta \approx 31$ наблюдается примерно четырехкратный скачок максимального значения электронной плотности. Соответствующее увеличение погрешности энергии также имеет место, так как значение скорости и импульса электронов в этой точке пространства значимо отлично от нуля. С другой стороны, при расчете осевого опрокидывания при росте максимального значения электронной плотности соответствующего роста погрешности энергии не наблюдается, что связано с нулевым значением скорости и импульса электронов на оси симметрии области. Вышесказанное означает, что вычислительные потери энергии при осевом опрокидывании существенно меньше, чем при внеосевом.

В результате выводы, которые можно сделать на основании описанных в настоящем разделе расчетов, полностью совпадают с выводами из предыдущих разделов.

ЗАКЛЮЧЕНИЕ

В работе для двухжидкостной гидродинамической модели холодной плазмы выведены дифференциальные соотношения, характеризующие закон сохранения энергии. При этом отдельно рассмотрен случай, когда движением более тяжелых ионов, по сравнению с электронами, можно пренебречь, а также – ситуации с учетом или пренебрежением релятивистского фактора в динамике электронов. Для сформулированной задачи о свободных плазменных колебаниях, инициированных коротким мощным лазерным импульсом, приведены результаты численных экспериментов по анализу выполнения закона сохранения энергии во всех различных вышеуказанных ситуациях. На основании проведенных расчетов можно сделать выводы о достоверности численного анализа плазменных колебаний во всех рассмотренных случаях, о пользе контроля за соблюдением закона сохранения энергии, а также, что стандартное теоретическое исследование аппроксимации и устойчивости вместе с экспериментальным наблюдением за сохранением энергии существенно повышает достоверность вычислений.

Отдельно из результатов работы следует вывод о необходимости построения схем более высокого порядка точности по времени, чем первый, для моделирования долгопериодных плазменных колебаний, что особенно важно при учете динамики ионов. В противном случае ограничение на устойчивость может потребовать применения настолько малых параметров дискретизации, что даже в пространственно одномерном случае будут затребованы огромные вычислительные ресурсы.

Наконец, отметим, что основное применение выведенных законов сохранения энергии направлено на их использование в многомерных расчетах, где практически отсутствуют аргументы в пользу достоверности вычислений.

Список литературы

Александров А.Ф., Богданкевич Л.С., Рухадзе А.А. Основы электродинамики плазмы. М.: Высш. школа, 1978. С. 55–60.
Гинзбург В.Л., Рухадзе А.А. Волны в магнитоактивной плазме. М.: Наука, 1975. С. 46–51.
Силин В.П. Введение в кинетическую теорию газов. М.: Наука, 1971. С. 119.
Силин В.П., Рухадзе А.А. Электромагнитные свойства плазмы и плазмоподобных сред. Изд. 2-е испр. М.: Книжный дом “ЛИБРОКОМ”, 2012. С. 104–110.
Esarey E., Schroeder C.B., Leemans W.P. Physics of laser-driven plasma-based electron accelerators // Rev. Mod. Phys. 2009. V. 81. P. 1229.
Bulanov S.V., Esirkepov T.Zh., Hayashi Y. et al. On some theoretical problems of laser wake-field accelerators // J. Plasma Phys. 2016. V. 82. № 3. P. 905820308.
Dawson J.M. Nonlinear electron oscillations in a cold plazma // Phys. Review. 1959. V. 113. № 2. P. 383.
Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений, 2-е изд., испр. и доп. М.: Физматлит, 2012. С. 46–100.
Фролов А.А., Чижонков Е.В. Влияние динамики ионов на опрокидывание плоских электронных колебаний // Матем. моделирование. 2015. Т. 27. № 12. С. 3.
Чижонков Е.В. Математические аспекты моделирования колебаний и кильватерных волн в плазме. М.: Физматлит, 2018. С. 32–131.
Бекефи Дж. Радиационные процессы в плазме. М.: Мир, 1971. С. 24.
Горбунов Л.М., Фролов А.А., Чижонков Е.В., Андреев Н.Е. Опрокидывание нелинейных цилиндрических колебаний плазмы // Физ. плазмы. 2010. V. 36. № 4. С. 375.
Hockney R.W., Eastwood J.W. Computer simulation using particles. New York: McGraw-Hill Inc., 1981. P. 222–281.
Андерсон Д., Таннехил Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. Т. 1. М.: Мир, 1990. С. 179–189.
Годунов С.К., Рябенький В.С. Разностные схемы. Введение в теорию. М.: Наука, 1973. С. 284–289.
Фролов А.А., Чижонков Е.В. О релятивистском опрокидывании электронных колебаний в плазменном слое // Вычисл. методы и программ. 2014. Т. 15. С. 537.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал