Журнал вычислительной математики и математической физики, 2020, T. 60, № 4, стр. 639-651
Исследование энтропийных свойств линеаризованной редакции метода Годунова
С. К. Годунов 1, В. В. Денисенко 2, Д. В. Ключинский 3, С. В. Фортова 2, *, В. В. Шепелев 2
1 Институт математики СО РАН
630090 Новосибирск, пр-т Акад. Коптюга, 4, Россия
2 Учреждение Российской академии наук
Институт автоматизации проектирования РАН
123056 Москва, ул. 2-я Брестская, 19/18, Россия
3 Новосибирский государственный университет
630090 Новосибирск, ул. Пирогова, 1, Россия
* E-mail: sfortova@mail.ru
Поступила в редакцию 14.11.2019
После доработки 14.11.2019
Принята к публикации 16.12.2019
Аннотация
Представлены идеи по формулировке обобщенного решения для гиперболической системы уравнений газовой динамики в одномерной постановке. Важным аспектом работы является исследование схемы относительно выполнения закона неубывания энтропии, который должен выполняться на обобщенном решении и является обязательным с точки зрения физики. Понятие обобщенного решения формулируется в конечно-разностной постановке с помощью простейшей линеаризованной редакции классической схемы Годунова. Экспериментально показано, что данный вариант схемы обладает свойством гарантированного неубывания энтропии, позволяющим моделировать ее рост на ударных волнах без каких-либо поправок и дополнительных условий. Библ. 8. Фиг. 20. Табл. 4.
1. ВВЕДЕНИЕ
Данная работа является завершающей частью исследований коллективом авторов разрывных решений уравнений газовой динамики в одномерной постановке. В ходе исследований выработалась линеаризованная редакция классической схемы Годунова [1].
Работа по данной тематике была начата в 2015 г. Тогда С.К. Годуновым совместно с И.М. Куликовым была опубликована работа [2], где была предложена линеаризованная схема типа Годунова в лагранжевых координатах. Уже в то время речь впервые зашла об обеспечении схемой свойства неубывания энтропии при расчете разрывных решений. Однако на тот момент высказывались лишь предположения, а конкретные расчеты, подтверждающие это свойство, проведены не были.
В 2016 г. работа продолжилась уже в эйлеровых координатах. Линеаризация схемы состоит на рассмотрении римановых инвариантов рассматриваемой системы уравнений, с помощью которых рассчитывались давление, скорость и плотность на границе расчетных ячеек. В частности, плотность высчитывалась исходя из постоянства энтропии в расчетной ячейке согласно уравнению состояния $p = \sigma \left( S \right){{\rho }^{\gamma }}$. Этот вариант оказался крайне нестабилен на некотором типе задач, и поэтому было предложено от него отказаться. Однако расчеты, описывающее поведение и формирование стационарной структуры ударной волны, все равно были проведены и описаны в статье [3]. Тогда же было показано влияние числа Куранта на структуру ударных волн.
Новый вариант схемы (см. [4]) сформировался год спустя. Плотность на границе расчетной ячейки было решено интерполировать из середины ячейки согласно формулам, приведенным в статье. Однако текущая формулировка об интерполяции была получена лишь при изучении данной статьи во время прочтения книг [5]–[7], а также статьи [8]. В предыдущей же статье [4] были приведены лишь формулы для расчетов. На предложенном варианте схемы была проведена серия вычислительных экспериментов с распадами разрыва. В то же время было замечено, что в каждой расчетной ячейке выполняется закон неубывания энтропии по правилу
Однако расчеты показали, что присутствуют зоны, где это свойство не выполняется, хоть это и не противоречит слабой сходимости решений, так как эти зоны уменьшаются при измельчении расчетной сетки.
В данной работе мы предлагаем новое правило расчета неубывания энтропии. Оно в точности совпадает с законом
(1.2)
$\frac{{\partial \rho S}}{{\partial t}} + \frac{{\partial \left( {\rho uS} \right)}}{{\partial x}} \geqslant 0,$В данной статье мы в новой формулировке объясняем причину выбора формул для расчета плотности на границе, что было довольно неясно описано в предыдущей статье [4]. Обратим ваше внимание, что данная статья лишь уточнение предыдущих результатов.
В работе приведены результаты численных расчетов задач о распаде разрыва в разных конфигурациях, а также задачи о столкновении волны разрежения и ударной волны. Стоит отметить, что данный тип задач предполагает наличие граничных условий продолжения (boundary outflow conditions).
2. ОДНОМЕРНЫЕ УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ
Для формулировки обобщенного решения приведем систему уравнений газовой динамики в одномерном случае
(2.1)
$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho u)}}{{\partial x}} = 0, \\ ~\frac{{\partial (\rho u)}}{{\partial t}} + \frac{{\partial (p + \rho {{u}^{2}})}}{{\partial x}} = 0, \\ \frac{{\partial \left( {\rho \frac{{{{u}^{2}}}}{2} + \rho E} \right)}}{{\partial t}} + \frac{{\partial \left[ {u\left( {\rho \frac{{{{u}^{2}}}}{2} + \rho E + p} \right)} \right]}}{{\partial x}} = 0. \\ \end{gathered} $Однако в природе существуют не только непрерывные решения. В газовой динамике возможны ударные волны, на которых все величины газа изменяются скачком. Поэтому для построения обобщенного решения необходимо рассмотреть возможность разрывного решения. В данной работе такие решения мы будем моделировать численно. Отметим один удивительный факт, который наблюдается при рассмотрении приближенных решений с очень мелкими сетками. Оказывается, что графики величин $u$, $p$, $\rho $ (скорость газа, давление, плотность), полученные на мелкой сетке, по существу совпадают с решениями задач о распадах разрывов. Теория таких “распадов” была построена в 1924 г. Кочиным. Однако разрывы в давлении (ударные волны) при этом оказываются распределенными на небольшое число разностных ячеек, покрывающих “зоны”, попавшие в эти волны. Ширина этих “зон” при измельчении сетки стремится к нулю.
Надо также отметить совсем нетривиальный характер распределений плотности $\rho $ внутри волн разрежения и “слабую сходимость” этих распределений к пределам при измельчении сетки. Для того, чтобы в этих явлениях разобраться, нам пришлось изучить поведение энтропии $\sigma = p{\text{/}}{{\rho }^{\gamma }}$ внутри получаемых в расчетах распределений и характер сходимости энтропии при измельчении шага сетки.
Оказалось, что в используемой разностной модели осуществляется хорошо известный закон неубывания энтропии, но без введения явных диссипативных членов, а просто за счет предложенной разностной схемы. В следующем разделе мы опишем конечно-разностную схему, которая будет основана на вышеизложенных принципах. Для энтропийной переменной будем требовать выполнение закона ее неубывания на разрывном решении
(2.2)
$\frac{{\partial \rho \sigma }}{{\partial t}} + \frac{{\partial \left( {\rho u\sigma } \right)}}{{\partial x}} \geqslant 0.$Вычислительные эксперименты показывают, что данная постановка верна для определенного класса задач, рассчитанных с помощью линеаризованной схемы Годунова [4]. В следующей главе мы повторим ее основные идеи и опишем новые модификации.
Следует заметить, что в данной работе обобщенным решением разностных уравнений газовой динамики будем называть некоторые предельные решения, к которым при измельчении разностной сетки будут стремиться решения, полученные по линеаризованной разностной модели Годунова, и для которых выполняется закон неубывания энтропии (2.2) во всех расчетных ячейках и при любом моменте времени.
3. ЛИНЕАРИЗОВАННАЯ МОДЕЛЬ ГОДУНОВА
Линеаризованная разностная модель Годунова, которая сформировалась в последние несколько лет, была подробно описана в статье [4]. Основное отличие от классической схемы Годунова состоит в том, что на каждом временном слое $t = {{t}^{n}} = {\text{const}}$ на границах расчетных ячеек
вычисляются линейные распады разрыва вместо нелинейных. Решение этих задач для давления и плотности приведено ниже:(3.1)
$\begin{gathered} P_{j}^{{n + 1/2}} = \frac{{\frac{{p_{{j - 1/2}}^{n}}}{{\rho _{{j - 1/2}}^{n}c_{{j - 1/2}}^{n}}} + \frac{{p_{{j + 1/2}}^{n}}}{{\rho _{{j + 1/2}}^{n}c_{{j + 1/2}}^{n}}} + u_{{j - 1/2}}^{n} - u_{{j + 1/2}}^{n}}}{{\frac{1}{{\rho _{{j - 1/2}}^{n}c_{{j - 1/2}}^{n}}} + \frac{1}{{\rho _{{j + 1/2}}^{n}c_{{j + 1/2}}^{n}}}}}, \\ U_{j}^{{n + 1/2}} = \frac{{\rho _{{j - 1/2}}^{n}c_{{j - 1/2}}^{n}u_{{j - 1/2}}^{n} + \rho _{{j + 1/2}}^{n}c_{{j + 1/2}}^{n}u_{{j + 1/2}}^{n} + p_{{j - 1/2}}^{n} - p_{{j + 1/2}}^{n}}}{{\rho _{{j - 1/2}}^{n}c_{{j - 1/2}}^{n} + \rho _{{j + 1/2}}^{n}c_{{j + 1/2}}^{n}}}. \\ \end{gathered} $(3.2)
$u_{{j \pm \frac{1}{2}}}^{n} \pm \frac{{p_{{j \pm 1/2}}^{n}}}{{\rho _{{j \pm 1/2}}^{n}c_{{j \pm 1/2}}^{n}}} = U_{j}^{{n + 1/2}} \pm \frac{{P_{j}^{{n + 1/2}}}}{{\rho _{{j \pm 1/2}}^{n}c_{{j \pm 1/2}}^{n}}},$Значения плотности $R_{j}^{{n + 1/2}}$ в граничной точке ${{x}_{j}}$ определим формулами
(3.3)
$R_{j}^{{n + 1/2}} = \left\{ {\begin{array}{*{20}{c}} {\rho _{{j - 1/2}}^{n}\left( {1 - \frac{{U_{j}^{{n + 1/2}} - u_{{j - 1/2}}^{n}}}{{c_{{j - 1/2}}^{n}}}} \right),\quad {\text{если}}\quad U_{j}^{{n + 1/2}} \geqslant 0,} \\ {\rho _{{j + 1/2}}^{n}\left( {1 - \frac{{u_{{j + 1/2}}^{n} - U_{j}^{{n + 1/2}}}}{{c_{{j + 1/2}}^{n}}}} \right),\quad {\text{если}}\quad U_{j}^{{n + 1/2}} < 0.} \end{array}} \right.$Приведем небольшое обоснование выбранных формул, которое сформировалось в последнее время. Здесь числитель дроби $(U_{j}^{{n + 1/2}} - u_{{j - 1/2}}^{n}){\text{/}}c_{{j - 1/2}}^{n}$ показывает величину отклонения значения скорости в ячейке по отношению к только что рассчитанной скорости на границе. Эта величина делится на скорость звука в рассматриваемой ячейке. Стоит отметить, что скорость звука можно выбирать по-разному, например, как $c_{j}^{n} = c_{{j - 1/2}}^{n} + c_{{j + 1/2}}^{n}$. Далее разность полученной безразмерной величины и единицы умножатся на плотность $\rho _{{j - 1/2}}^{n}$ для получения значения плотности $R_{j}^{{n + 1/2}}$ на границе. Данный процесс можно описать как интерполяцию плотности в ячейке на границу. По знаку $U_{j}^{{n + 1/2}}$ определяем, из какой ячейки (левой или правой) должна происходить интерполяция плотности на границу.
После расчета на всех границах давления, скорости и плотности мы можем применить ко всем расчетным ячейкам конечно-разностные аналоги законов сохранения и пересчитать необходимые величины на слое ${{t}^{{n + 1}}} = {{t}^{n}} + {{\tau }^{{n + 1/2}}}$. Правила определения шага по времени ${{\tau }^{{n + 1/2}}}$ было описано в предыдущей статье [4].
Отметим, что после определения всех величин мы можем численно проверить закон неубывания энтропии в каждой расчетной ячейке
(3.4)
$\frac{{(\rho \sigma )_{{j - 1/2}}^{{n + 1}} - (\rho \sigma )_{{j - 1/2}}^{n}}}{{{{\tau }^{{n + 1/2}}}}} + \frac{1}{{x_{j}^{n} - x_{{j - 1}}^{n}}}(RU\sigma _{j}^{{n + 1/2}} - RU\sigma _{{j - 1}}^{{n + 1/2}}).$При измельчении расчетной сетки функции $\rho _{{j + 1/2}}^{n} = \rho ({{x}_{{j + 1/2}}},{{t}^{n}}),$ $u_{{j + 1/2}}^{n} = u({{x}_{{j + 1/2}}},{{t}^{n}})$, $p_{{j + 1/2}}^{n} = p({{x}_{{j + 1/2}}},{{t}^{n}})$ и $\sigma _{{j + 1/2}}^{n} = \sigma ({{x}_{{j + 1/2}}},{{t}^{n}})$, удовлетворяющие численным законам сохранения и закону неубывания энтропии для всех величин $j$ и $n$, будут стремиться к некоторому предельному решению, которое и будем называть обобщенным решением уравнений газовой динамики.
4. ВЫЧИСЛИТЕЛЬНЫЕ ЭКСПЕРИМЕНТЫ
Были проведены расчеты на трех конфигурациях задачи Римана о распаде произвольного разрыва (с одной волной разрежения и ударной волной, с двумя волнами разрежения и двумя ударными волнами), а также на задаче, где волна разрежения догоняет и пересекает ударную волну с уменьшением амплитуды последней. Предполагается, что расчетная область бесконечна, и мы следим лишь за фиксированным отрезком $a \leqslant x \leqslant b$, где $a = 0$, $b = 1$. Точки разрыва будут находиться внутри области. Время расчета обозначим через $T$. Разрывные (кусочно-постоянные) начальные условия определяют соответствующую конфигурацию распада.
4.1. Распад разрыва с волной разрежения и ударной волной
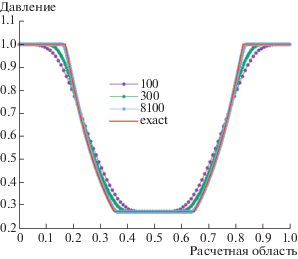
Разрыв задается в точке ${{x}_{0}} = 0.5$, время расчета $T = 0.5$. Исследуем конфигурацию с волной разрежения и ударной волной. Разрывные (кусочно-постоянные) начальные условия представлены в табл. 1.
Таблица 1
| Параметр/Величина | $x < {{x}_{0}}$ | $x > {{x}_{0}}$ | Контактный разрыв (решение) |
|---|---|---|---|
| Давление | 2.00 | 1.00 | 1.4017 |
| Плотность | 2.00 | 1.00 | 1.5512/1.2712 |
| Скорость | 0.00 | 0.00 | 0.2928 |
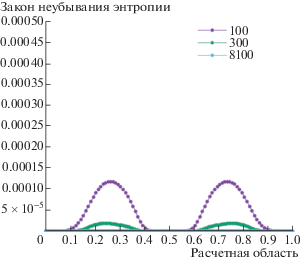
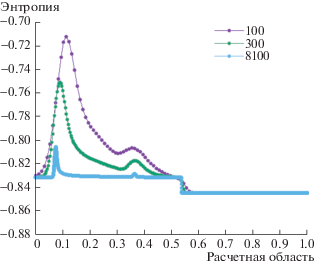
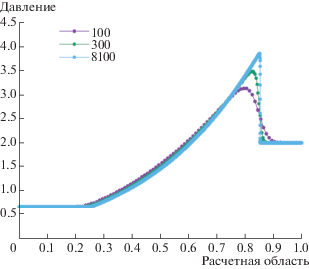
На графиках приведены сеточные решения для шагов по пространству $h = 1.0{\text{/}}N$, где $N$ бралось 100, 300 и 8100. Легко заметить сходимость сеточных решений к некоторому виду, который мы назвали “обобщенным решением” (фиг. 1 и фиг. 2). Выполнение закона неубывания энтропии представлено на фиг. 4. В зонах ударной волны энтропия повышается для всех значений сетки, на контактном разрыве и волне разрежения при очень мелком шаге энтропия сохраняется. Ширина зон повышения энтропии убывает при измельчении сетки, что также соответствует введенному понятию обобщенного решения.
4.2. Распад разрыва с двумя волнами разрежения
Разрыв задается в точке ${{x}_{0}} = 0.5$, время расчета $T = 0.2$. Точные разрывные (кусочно-постоянные) начальные условия для моделирования текущей конфигурации приведены в табл. 2.
Таблица 2
| Параметр/Величина | $x < {{x}_{0}}$ | $x > {{x}_{0}}$ | Контактный разрыв (решение) |
|---|---|---|---|
| Давление | 1.00 | 1.00 | 0.27 |
| Плотность | 1.00 | 1.00 | 0.34 |
| Скорость | –1.00 | 1.00 | 0.00 |
На графиках приведены сеточные решения для шагов по пространству $h = 1.0{\text{/}}N$, где $N$ бралось 100, 300 и 8100. Конфигурация с двумя волнами разрежения показывает, что в обе стороны от разрыва распространяются зоны непрерывного решения. Энтропия в этих зонах на предельном решении должна сохраняться, что и наблюдается (фиг. 8). Максимальное значение энтропии наблюдается в точке разрыва, а в зонах волн разрежения оно близко к нулю на мелкой сетке (фиг. 7). Обратим внимание на разностный эффект в точке разрыва ${{x}_{0}} = 0.5$ в виде “хвостика” на графике плотности (фиг. 6). Видно, что ширина этой погрешности уменьшается с измельчением сетки, хотя однозначно будет влиять на точность решения в этой зоне.
4.3. Распад разрыва с двумя ударными волнами
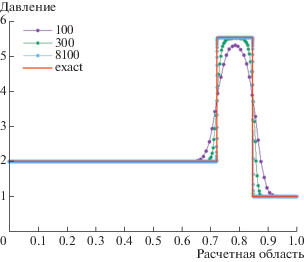
Последняя конфигурация задачи Римана о распаде произвольного разрыва включает в себя образование двух ударных волн, которые распространяются вправо. Разрыв задается в точке ${{x}_{0}} = 0.5$, время расчета $T = 0.1$. Начальные данные представлены в табл. 3.
Таблица 3
| Параметр/Величина | $x < {{x}_{0}}$ | $x > {{x}_{0}}$ | Контактный разрыв |
|---|---|---|---|
| Давление | 2.00 | 1.00 | 5.55 |
| Плотность | 3.00 | 2.00 | 6.035/5.939 |
| Скорость | 4.00 | 2.00 | 3.228 |
Численное решение показано на фиг. 9–12. При 100 точках сетки амплитуда волны немного меньше, чем при 900 и 8100 точках сетки в выбранный момент времени. Это показывает, что при не очень большом числе точек волне требуется немного больше времени, чтобы выйти на нужную амплитуду. Энтропия возрастает на обеих ударных волнах, причем на первой значительно больше. Ширина зоны возрастания также уменьшается при измельчении сетки, как и в предыдущих конфигурациях распадов разрывов.
4.4. Задача о столкновении волны разрежения с ударной волной
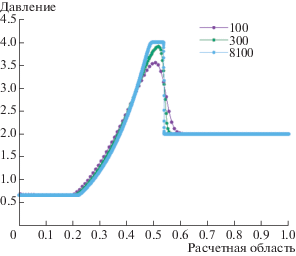
В этой задаче рассмотрим два вырожденных распада разрыва, которые со временем столкнутся в некоторой точке. У этой задачи нет аналитического решения. Начальные данные приведены в табл. 4. Волна разрежения образуется в точке ${{x}_{0}}$, а ударная волна в точке ${{x}_{1}}$. Обе волны будут распространяться вправо. Время расчета $T = 0.6$.
Таблица 4
| Параметр/Величина | $x < {{x}_{0}}$ | ${{x}_{0}} < x < {{x}_{1}}$ | $x > {{x}_{1}}$ |
|---|---|---|---|
| Давление | 0.67099 | 4 | 2 |
| Плотность | 1.36205 | 4.875 | 3 |
| Скорость | –0.7 | 0.50637 | 0 |
На графиках (фиг. 13–16) показан момент до столкновения. Видно, что 100 точек сетки не хватает, чтобы правильно описать зону между волной разрежения и ударной волной. Значение энтропии заметно выше на волне разрежения, чем на ударной волне (фиг. 15), однако энтропия все равно в зоне непрерывного решения остается постоянной в отличие от зоны разрывного решения (при использовании сетки размерностью 8100 узлов) (фиг. 16). На графиках (фиг. 17–20) приведен момент времени после столкновения ударной волны и волны разрежения. Видно, что амплитуда ударной волны уменьшилась (фиг. 17, 18) и со временем она будет продолжать уменьшаться. Максимальное значение прироста энтропии также уменьшилось (фиг. 20).
5. ЗАКЛЮЧЕНИЕ
В работе рассмотрены примеры построения обобщенного решения для одномерных уравнений газовой динамики в конечно-разностной постановке. Приведена простейшая линеаризованная модель типа Годунова для численного решения уравнений газовой динамики со свойством неубывания энтропии. Численные расчеты подтвердили высказанные гипотезы и предположения.
Важно отметить, что описанная линеаризованная модель не является идеальным инструментом для расчета сложных газодинамических течений, поэтому требуется дальнейшее улучшение схемы для достижения поставленных целей.
Ведется работа по расширению описанной модели на двумерный и трехмерный случай.
Список литературы
Годунов С.К. Разностный метод численного расчета разрывных решений уравнений гидродинамики // Матем. сборник. 1959. № 47. Вып. 3. С. 271–306.
Годунов С.К., Куликов И.М. Расчет разрывных решений уравнений гидродинамики с гарантией неубывания энтропии // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. № 6. С. 1008–1021.
Godunov S.K., Klyuchinskiy D.V., Safronov A.V., Fortova S.V., Shepelev V.V. Experimental study of numerical methods for the solution of gas dynamics problems with shock waves, IOP Conf. Series: Journal of Physics: Conf. Series 946 (2018) 012048.
Годунов С.К., Ключинский Д.В., Фортова С.В., Шепелев В.В. Экспериментальные исследования разностных моделей газовой динамики с ударными волнами // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 8. С. 5–19.
Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. Численное решение многомерных задач газовой динамики. М.: Наука, 1976. С. 100–110.
Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001.
Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. Berlin: Springer. Second Edition, June 1999.
Сафронов А.В. Разностный метод для уравнений газодинамики из соотношений на разрывах // Матем. моделирование. 2008. Т. 20. № 2. С. 76–84.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики