Журнал вычислительной математики и математической физики, 2020, T. 60, № 4, стр. 663-675

1. ВВЕДЕНИЕ

Численный метод, предложенный С.К. Годуновым, получил широкое распространение и стал за последние несколько десятилетий одним из основных методов решения систем гиперболических уравнений. На его основе были созданы мощные вычислительные технологии для решения прикладных и фундаментальных задач, связанных с расчетами сложных течений сжимаемой жидкости, в том числе: задач прикладной аэродинамики, взрывных процессов, термоядерного синтеза и многих других.

В основе метода Годунова лежит точное решение задачи Римана, более известной в газодинамике как задача о распаде произвольного разрыва. Фактически, это задача о взаимодействии двух сжимаемых однородных потоков, которая в силу автомодельности допускает точное аналитическое решение. Если в какой-то момент времени аппроксимировать на расчетной сетке газодинамические параметры кусочно-постоянным распределением, то последующая эволюция этого распределения на конечном малом интервале времени будет определяться точно с помощью решения задачи Римана. Это позволяет определить кусочно-постоянную аппроксимацию на новом временном слое. Применяя процедуру последовательно, можно получить численное решение на любом конечном интервале времени.

Численный метод, построенный на основе такого рассмотрения, суть стандартный метод конечного объема, где поток на грани счетной ячейки рассчитывается на точном решении соответствующей задачи Римана. Первоначально метод был разработан для модели одномерных течений газа [1], [2] и затем обобщен на многомерный случай [3], [4]. Отличительной чертой метода является то, что он в большей мере основывается на физических принципах аппроксимации, а не на математических, как большинство других численных методов. Именно по этой причине он получил широкое распространение во всем мире, и в настоящее время мы имеем уже устоявшийся термин в области вычислительной гидродинамики – методы годуновского типа.

Стандартный метод Годунова имеет первый порядок точности по времени и пространству на гладких решениях. Его обобщение на более высокие порядки состоит в замене кусочно-постоянных аппроксимаций на аппроксимации более высокого порядка точности (например, кусочно-линейные или кусочно-квадратичные). Это было предложено сначала в работе [5] и впоследствии активно развивалось в работах [6]–[9] и многих других авторов.

Основная трудность такого обобщения состоит в том, что задача Римана в этом случае теряет автомодельность и не допускает более простых аналитических решений. Новосибирской школой под руководством В.М. Тешукова была проведена большая серия исследований решений уравнений Эйлера, включая решения неавтомодельной задачи Римана [10].

Задача Римана с неконстантными начальными данными называется в литературе обобщенной задачей Римана (ОЗР) вслед за работой [11]. В ней ОЗР с линейными начальными данными рассматривается для одномерных уравнений в лагранжевых переменных и выводится аналитическое решение для производных по времени в начальный момент t = 0 вдоль контактного разрыва.

В работе [12] ОЗР исследуется в эйлеровых переменных, и решение строится в малой окрестности точки начального разрыва в плоскости (x, t). Точное аналитическое решение получается в первом приближении по параметру $\theta = \sqrt {{{x}^{2}} + {{t}^{2}}} $, когда $\theta \to 0$. Если мы рассмотрим ОЗР с линейным начальным распределением $q = {{q}^{ \pm }} + \left| x \right|{{S}^{ \pm }}$, где верхний индекс “+” или “–” берется для $x > 0$ или $x < 0$ соответственно, то решение ОЗР запишется в следующем виде:

где $\lambda = x{\text{/}}t$, ${{Q}^{0}}(\lambda ,{{q}^{ \pm }})$ обозначает стандартное автомодельное решение задачи Римана, ${{Q}^{1}}(\lambda ,{{q}^{ \pm }},{{S}^{ \pm }})$ представляет собой решение с точностью до $O({{\theta }^{2}})$. Последнее зависит от автомодельного решения ${{Q}^{0}}$ и может быть выписано аналитически в явном виде [12]. В частном случае, когда начальные данные ОЗР представляют собой линейное непрерывное распределение газодинамических параметров, ${{q}^{ + }} = {{q}^{ - }} = {{q}_{0}}$, ${{S}^{ + }} = - {{S}^{ - }} = {{S}_{0}}$, решение задачи с точностью до членов порядка $O({{\theta }^{2}})$ имеет вид где стандартно $u,{\text{ }}p,{\text{ }}s$ обозначают скорость, давление и энтропию соответственно, заглавные буквы – производную, $a = a(\rho ,e){\text{ }}$ – скорость звука, $с = a\rho $. Формулы (2) фактически описывают изменение линейного распределения газодинамических параметров на малом интервале времени с точностью до квадратичных членов по временной переменной.

Полученное решение ОЗР в свете подхода С.К. Годунова естественно использовать для обобщения метода на второй порядок точности аппроксимации. Для одномерных уравнений Эйлера это было сделано в работе [13]. В этой работе дискретное решение представляется двумя сеточными функциями $\{ q_{i}^{n}\} $ и $\{ S_{i}^{n}\} $, задаваемыми на ячейках расчетной сетки, которые аппроксимируют средние по ячейке значения параметров и их производные так, что в каждый момент времени решение в ячейке определяется линейным профилем $q_{i}^{n}(x) = q_{i}^{n} + S_{i}^{n}(x - {{x}_{i}})$. Имея решение ОЗР вида (1), можно предложить следующее естественное расширение второго порядка метода Годунова:

где $\Delta _{i}^{{ + ( - )}}( \cdot ) = {{( \cdot )}_{{i + 1(i)}}} - {{( \cdot )}_{{i(i - 1)}}}$ – односторонние конечные разности, ${{\Delta }_{i}}( \cdot ) = {{( \cdot )}_{{i + 1/2}}} - {{( \cdot )}_{{i - 1/2}}}$ – центральная разность.

Правая часть в уравнениях (3) вычисляется на решениях ОЗР:

с начальными данными вида ${{q}^{{ + ( - )}}} = q_{{i + 1(i)}}^{n} + S_{{i + 1(i)}}^{n}({{x}_{{i + 1/2}}} - {{x}_{{i + 1(i)}}})$ и ${{S}^{{ + ( - )}}} = + ( - )S_{{i + 1(i)}}^{n}$.

Разностная схема (3)–(4) является прямым продолжением второго порядка схемы Годунова. На гладких решениях она имеет второй порядок точности по времени и пространству и устойчива при стандартном курантовском условии на шаг по времени [13]. Ее реализация требует точного решения задачи Римана на гранях счетных ячеек и дополнительно вычислений решения ОЗР, которое зависит от возникающей волновой конфигурации. Приближенные римановские решатели, такие как двухволновое симметричное решение Русанова, HLL, HLLC, Roe [14], имеют целью упростить вычислительную работу и сделать алгоритм более однородным, что становится особенно важным при программной реализации, ориентированной на современные вычислительные системы с многоядерной архитектурой и специальными ускорителями. В этом свете представляется интересным рассмотреть вопрос о том, как модифицируются эти приближенные решения задачи Римана, когда начальные данные аппроксимируются кусочно-линейными распределениями.

2. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ ОЗР

Рассмотрим наиболее простое приближение задачи Римана – двухволновое симметричное решение, предложенное В.В. Русановым [15]. Это решение строится на предположении, что возмущенная область, образующаяся в результате распада произвольного разрыва, ограничена симметрично расположенными характеристиками, $ - \zeta \leqslant \lambda \leqslant \zeta $, где $\zeta $ – спектральный радиус матрицы Якоби $A = \partial f{\text{/}}\partial q$ потокового вектора по вектору консервативных переменных. При этом параметры возмущенной зоны – потоковый вектор $F{\text{*}}$ и $Q{\kern 1pt} {\text{*}}$ – определяются из условия, что слабая форма определяющих уравнений $\oint_\gamma {fdt - qdx} = 0$ выполняется на любом замкнутом контуре $\gamma $ [16]. Это приводит к следующим выражениям для параметров возмущенной зоны:

Пусть теперь начальные данные определяются кусочно-линейными распределениями, ${{q}^{ \pm }}(x) = {{q}^{ \pm }} + {{S}^{ \pm }}x$, соответственно слева (знак “–”) и справа (знак “+”) от точки начального разрыва $х = 0$. Определим вектор примитивных переменных $z = \{ u,p,s\} $. Тогда эволюция во времени начального линейного профиля вне возмущенной области будет определяться в соответствии с формулами (2) и может быть записана в следующем виде:

где функции ${{Z}^{ \pm }}(\lambda ,{{z}^{ \pm }})$ следуют из (2),

Таким образом, можно определить, как меняется со временем решение ОЗР на ограничивающих возмущенную зону характеристиках $\lambda = \pm \zeta $:

Вводя якобианы перехода от потоковых и консервативных переменных к примитивным,

можно также получить решение ОЗР на ограничивающих характеристиках в потоковых и консервативных переменных,

Параметры возмущенной зоны аппроксимируются средним потоковым вектором и средним консервативным вектором, которые теперь являются функциями времени, $F{\text{*}} = F{\text{*}}(t)$ и $Q{\kern 1pt} {\text{*}} = Q{\kern 1pt} {\text{*}}(t)$. Интегрирование слабой формы уравнений по контуру возмущенной области в плоскости (x, t) приводит к следующим выражениям для этих функций:

где

Формулы (10) имеют естественную, вполне понятную интерпретацию. Если определить значения решения ОЗР на крайних характеристиках возмущенной зоны на момент времени $t{\text{/}}2$ в соответствии с (9),

то (10) примут вид стандартных формул (5) русановского потока, но относительно величин (9),

Аналогичным рассмотрением можно доказать и более общее утверждение. Любое приближенное решение задачи Римана, основанное на многоволновой структуре возмущенной области и кусочно-постоянной аппроксимации, без изменений переносится на случай линейного распределения начальных данных. Необходимо только при определении волновой структуры использовать значения ${{q}^{ \pm }}$ слева и справа от точки начального разрыва, а при определении параметров в возмущенной области пользоваться значениями ${{\tilde {q}}^{ \pm }}$ на ограничивающих характеристиках на момент времени $t{\text{/}}2$. Например, метод HLL, который является обобщением метода Русанова, для линейных начальных данных ${{q}^{ \pm }}(x) = {{q}^{ \pm }} + {{S}^{ \pm }}x$ запишется в виде

где ${{\zeta }^{ \pm }} = {{\zeta }^{ \pm }}({{q}^{ - }},{{q}^{ + }})$ – скорости ограничивающих характеристик в методе HLL [14], а величины с волной вычисляются по формулам (12).

Такой подход можно обобщить на приближенный римановский решатель HLLC [14], где включается контактный разрыв внутри возмущенной зоны – $\zeta {\text{*}}$. При этом интегрирование закона сохранения по контуру, ограничиваемому характеристиками ${{\zeta }^{ - }}$, ${{\zeta }^{ + }}$ и прямой $t = {{t}^{{n + 1}}}$ на плоскости x – t, приводит к

где $\zeta {\text{*}}$ обозначает скорость контактного разрыва, $Q{\kern 1pt} {{{\text{*}}}^{ - }},\;Q{\kern 1pt} {{{\text{*}}}^{ + }}$ обозначает осредненное решение слева и справа контактного разрыва соответственно.

Используя соотношение Ренкина–Гюгонио вдоль разрывов ${{\zeta }^{ - }}$ и ${{\zeta }^{ + }}$, получаем

где $\Phi {\kern 1pt} {{{\text{*}}}^{ - }},\;\Phi {\kern 1pt} {{{\text{*}}}^{ + }}$ – численные потоки, соответствующие $Q{\kern 1pt} {{{\text{*}}}^{ - }},\;Q{\kern 1pt} {{{\text{*}}}^{ + }}$.

Используя уравнения (15) и (16) и соотношение $p{{{\text{*}}}^{ - }}(Q{\kern 1pt} {{{\text{*}}}^{ - }}) = p{{{\text{*}}}^{ + }}(Q{\kern 1pt} {{{\text{*}}}^{ + }})$, можно получить следующее определение для $\zeta {\text{*}}$:

где примитивные переменные плотности, скорости и давления определяются через соответствующие векторы консервативных переменных,

После несложных алгебраических манипуляций получим

После  определения $Q{\kern 1pt} {{{\text{*}}}^{ \pm }}$ (18) численные потоки $\Phi {\kern 1pt} {{{\text{*}}}^{ - }},\Phi {\kern 1pt} {{{\text{*}}}^{ + }}$ легко вычисляются по уравнениям (15)–(16).

3. ГИБРИДНАЯ ЯВНО-НЕЯВНАЯ СХЕМА ГОДУНОВА

Явная схема Годунова, построенная на вышерассмотренных точных или приближенных решениях ОЗР, имеет второй порядок точности по времени и пространству на гладких решениях и сходится к решению, если шаг по времени ограничен условием Куранта–Фридрихса–Леви. При этом шаг по времени оказывается пропорциональным минимальному размеру пространственной дискретизации расчетной области, что может приводить к значительному увеличению вычислительной работы в задачах, требующих разрешения сильно различающихся по пространственным масштабам структур. Это, в первую очередь, задачи с узкими переходными зонами (пограничные слои, ударные волны, контактные зоны, сдвиговые течения), где параметры течения резко меняются на очень малых расстояниях. Для разрешения этих особенностей требуются сетки с соответствующим локальным пространственным разрешением, которое может оказаться на несколько порядков меньше среднего по задаче сеточного размера. Таким образом, мы приходим к сильно неоднородным сеткам (в английской литературе “stiff grids”).

В большинстве задач существование мелких пространственных масштабов вовсе не означает наличие таковых во временных масштабах. Характерное время нестационарного процесса может быть и не связано с мелкомасштабными пространственными структурами, как, например, нестационарный – течения с пограничными слоями при больших числах Рейнольдса. Поэтому численное решение таких задач по явной схеме Годунова с очень мелким шагом по времени, диктуемым не физическим процессом, а исключительно условием устойчивости разностной схемы, является неэффективным в вычислительном плане. Оно может требовать выполнения очень большого числа шагов по времени, которое в ряде практических задач может оказаться неприемлемым даже для современных суперкомпьютерных систем с точки зрения практической реализации.

Решить дилемму сильно неоднородной пространственной сетки и физически обусловленного шага интегрирования по времени можно, рассмотрев вариант явно-неявной схемы. Неявность вносит излишнюю численную вязкость, которая стабилизирует разностную схему и снимает необходимость ограничения шага по времени из-за устойчивости. Этим фактом можно воспользоваться и попробовать разработать гибридную схему Годунова, которая работала бы как явная стандартная схема в области нормальной сетки, и плавно переходила на неявную компоненту в зонах сгущения сетки.

Идея гибридной явно-неявной схемы не нова. Один из возможных вариантов гибридизации был предложен в работе [17] и получил название в литературе схема CCG (по первым буквам фамилий авторов – Collinz, Collela, Glaz). Схема строилась на основе выполнения принципа убывания мах-нормы численного решения при любом шаге по времени. Было показано, что CCG схема обеспечивает выполнение этого условия для линейных уравнений. Однако формальный перенос схемы на нелинейные уравнения оказался неудачным. Простые эксперименты с уравнением Бюргерса обнаружили нарушение принципа убывания мах-нормы и возникновения нефизичных выбросов в численных решениях в окрестности ударной волны [18]. Для устранения этого артефакта фактически требуется уменьшение временного шага почти до курантовских значений.

В работе [18] был предложен достаточно простой общий принцип построения гибридных явно-неявных схем на основе имеющихся явных схем второго порядка точности. Он позволяет строить гибридные схемы, которые удовлетворяют следующим условиям: 1) переключение между явной и неявной компонентами моделируется локальной гладкой функцией, 2) в чисто явной моде схема имеет второй порядок точности по времени и пространству на гладких решениях и 3) свойство убывания мах-нормы численного решения выполняется при любом значении шага по времени.

Этот принцип имеет наглядную интерпретацию, в соответствии с которой рассматриваемая гибридная схема может быть представлена как явная схема, которая в качестве начальных данных использует не значения с предыдущего временного слоя, а с некоторого промежуточного. Интегрирование в ячейке при этом выполняется не для полного временного шага, а только для части, соответствующей промежуточному слою.

Промежуточный временной слой определяется скалярной величиной $\omega $, $0 \leqslant \omega \leqslant 1$, надлежащим образом определяемой в каждой счетной ячейке. С помощью этого параметра определяется промежуточное интерполированное значение вектора состояния, $q_{i}^{\omega } = q_{i}^{n} + (1 - {{\omega }_{i}}){{\Delta }^{n}}{{q}_{i}}$, где ${{\Delta }^{n}}( \cdot ) = {{( \cdot )}^{{n + 1}}} - {{( \cdot )}^{n}}$. Пусть теперь имеется некоторая явная схема второго порядка, которая записывается в операторном виде как

где ${{L}_{2}}$ является дискретным оператором перехода на шаге $\Delta t$, обеспечивающим второй порядок по времени и пространству. Тогда гибридная явно-неявная схема будет записываться следующим образом:

Гибридная схема трансформируется в чисто явную компоненту, когда параметр гибридизации в каждой счетной ячейке равен 1, и, напротив, в чисто неявную компоненту, когда он принимает значения, равные нулю. Наша цель выбрать этот параметр по возможности как можно ближе к 1, но при условии, чтобы свойство убывания мах-норм решения оставалось выполненным. Схему (20) можно переписать в эквивалентном виде:

Нетрудно заметить, что гибридная схема в форме (16) в точности совпадает с явной схемой (19) , где интегрирование по времени выполняется в каждой ячейке с промежуточного слоя. Таким образом, мы сможем выполнить условия убывания мах-норм, если потребуем устойчивость (21) как явной схемы, т.е. ${{\omega }_{i}}\Delta \leqslant \Delta x{\text{/}}r({{q}^{{{{\omega }_{i}}}}})$, где $r$ обозначает максимальную характеристическую скорость. Этот факт позволяет нам легко выписать выражение для определения оптимальных значений параметра гибридизации:

Штрафом за такую гибридизацию будет система нелинейных уравнений (20) и (22), которую необходимо решать на каждом временном слое. Один из методов решения этой задачи – метод псевдо-времени, когда неизвестный вектор ${{q}^{{n + 1}}}$ ищется как стационарное решение следующей задачи:

где $\tau $ – параметр псевдо-времени, и опущен индекс ячейки i.

Стационарное решение (23) получается применением стандартной одношаговой неявной схемы интегрирования по псевдо-времени $\tau $ и решением системы дискретных уравнений методом Ньютона. Для решения получающейся в результате линеаризации линейной системы алгебраических уравнений можно использовать любой итерационный метод. В настоящей работе мы применяем достаточно эффективный и легко реализуемый безматричный метод приближенной факторизации LU-SGS, предложенный в работе [19], [20].

Линейная система получается в результате линеаризации невязки $R({{q}^{{n + 1}}})$. Для того, чтобы выполнить эту процедуру, необходимо линеаризовать функцию годуновского численного потока, т.е. решение задачи Римана ${{Q}^{R}}({{q}^{ - }},{{q}^{ + }})$ относительно начальных данных. Эта линеаризация может быть выполнена аналитически с использованием решения вариационной задачи Римана (ВЗР), к рассмотрению которой мы переходим в следующем разделе.

4. ВАРИАЦИОННАЯ ЗАДАЧА РИМАНА

Математически ВЗР формулируется как задача о нахождении первой вариации решения автомодельной задачи Римана по отношению к малым вариациям начальных данных. С точки зрения газодинамики она описывает в линейном приближении взаимодействие двух однородных полей малых возмущений на фоне течения, возникающего при распаде начального разрыва. Другими словами, решение ВЗР дает фактически результатное поле, образующееся при взаимодействии однородных полей возмущений.

При решении дискретных уравнений гибридной явно-неявной схемы Годунова и связанной с ним линеаризацией годуновского численного потока необходимо определить вариацию точного решения задачи Римана, вызванную малым изменением в начальных данных. Эта вариация выражается в виде линейной формы относительно векторов вариации начальных данных слева и справа от начального разрыва через соответствующие вариационные матрицы. Таким образом, это рассмотрение приводит нас к необходимости решения ВЗР.

Рассмотрим стандартную автомодельную задачу Римана с константными начальными данными ${{q}^{ \pm }}$ и ее решение ${{Q}^{0}}(\lambda ,{{q}^{ \pm }})$. Задача, которую необходимо решить, это – как изменится решение ${{Q}^{0}}(\lambda ,{{q}^{ \pm }})$, если начальным данным придать малые изменения: ${{q}^{ \pm }} \to {{q}^{ \pm }} + \delta {{q}^{ \pm }}$.

Первая вариация решения ${{Q}^{0}}(\lambda ,{{q}^{ \pm }})$ определяется через лево- и правосторонние вариационные матрицы,

где вариационные матрицы ${{M}^{ \pm }}$ определяются в виде

Таким образом, решение ВЗР состоит в нахождении вариационных матриц при произвольных начальных данных.

Вариационные матрицы в зависимости от автомодельного параметра $\lambda $ являются кусочно-аналитическими матричными функциями. Их области аналитичности совпадают с соответствующими областями автомодельного решения ${{Q}^{0}}(\lambda ,{{q}^{ \pm }})$ и определяются структурой, возникающей в результате распада разрыва волновой конфигурацией. Матрицы являются константами по $\lambda $ в подобластях однородного течения, т.е. в невозмущенных областях левее и правее крайних волн возмущенной области, где они просто нулевые или единичные, и в контактных зонах, примыкающих к контактному разрыву. В области волны разрежения матрицы переменные, ${{M}^{ \pm }} = \mu _{{^{{RW}}}}^{ \pm }(\lambda )$. Эти матрицы, а также матрицы контактных зон могут быть найдены аналитически в явном виде [21].

Компактная форма записи решения ВЗР получается, если ввести понятие собственной и сопряженной величин. Величина называется собственной или сопряженной в зависимости от значения автомодельного параметра $\lambda $. Если, например, значение $\lambda $ таково, что оно соответствует положению слева от контактного разрыва, то всем величинам, относящимся к областям слева от контактного разрыва, приписывается атрибутика “собственный”, а величинам, относящимся к правосторонним областям, – “сопряженный”. И, наоборот, для $\lambda $ правее контактного разрыва правосторонние величины являются собственными, а левосторонние – сопряженными. Тогда, вводя верхний индекс “звездочка” для обозначения сопряженных величин, решение ВЗР запишется в следующем виде:

с собственными и сопряженными вариационными матрицами, равными

Общие выражения для матриц и для произвольного уравнения состояния, а также для частного случая двучленного уравнения состояния можно найти в работе [21].

Теперь вернемся к решению дискретных уравнений гибридной явно-неявной схемы (23) . Ньютоновские итерации по псевдовремени приводят к следующей линейной системе алгебраических уравнений относительно итерационного приращения вектора состояния:

где индекс s обозначает итерацию по псевдовремени. При составлении матрицы $\partial R{\text{/}}\partial {{q}^{{n + 1}}}$ рассмотрим два способа. Один будет основан на точной линеаризации годуновского потока с помощью вариационных матриц ВЗР, рассмотренных выше,

Другой будет приближенный, основанный на двухволновом симметричном приближении Русанова, который приводит к широко используемому в литературе методу приближенной линеаризации невязки вида

Полученные в результате схемы будем называть точной схемой (EL scheme) и приближенной схемой (AL scheme). Применим эти схемы к расчету двух типовых задач – невязкое обтекание профиля трансзвуковым потоком воздуха и вязкий пограничный слой на плоской пластине (задача Блазиуса). В первой задаче рассматривается профиль Жуковского под углом атаки 5° к набегающему потоку с числом Маха 0.85. Расчеты проводились на С-образной сетке из 128 ячеек по поверхности профиля и 100 ячеек между профилем и внешней границей, отстоящей от поверхности тела на расстоянии 15 его хорд. Вторая задача решалась при следующих параметрах: число Маха набегающего потока ${{{\text{M}}}_{\infty }} = 0.17$ и число Рейнольдса по длине пластины $\operatorname{Re} = 2.3 \times {{10}^{5}}$. Сетка сгущалась к поверхности пластины так, чтобы обеспечить условие ${{y}^{ + }} = 1$ в пристеночной ячейке.

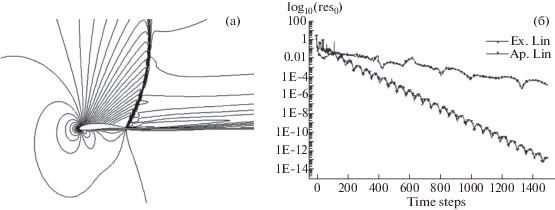
Расчеты проводились по схемам EL и AL . Очевидно, что левая часть (28) не влияет на решение, поэтому обе схемы приводят к одинаковому численному результату. Он показан на фиг. 1а и фиг. 2а соответственно для задач 1 и 2.

Сходимость невязки в этих задачах представлена соответственно на фиг. 1б и фиг. 2б. Сравниваются результаты, полученные при расчетах по схеме с точной линеаризацией (EL-схема) и приближенной линеаризацией (AL-схема). Из этих графиков видно, что EL-схема обеспечивает гораздо более быструю сходимость, чем AL-схема. Для достижения одинакового уровня сходимости в EL-схеме требуется число шагов почти на порядок меньше, чем в AL-схеме. Для второй задачи этот эффект оказывается еще больше. Фактически сходимость AL-схемы получается примерно такой же, как сходимость явной схемы, которая также приведена на рисунке для сравнения.

5. ПРИЛОЖЕНИЕ МЕТОДА ГОДУНОВА К АКУСТИЧЕСКИМ ЗАДАЧАМ

Как отмечалось выше, ВЗР фактически описывает взаимодействие малых возмущений на фоне неоднородного течения. Поэтому ее можно рассматривать как аналог стандартной задачи Римана для линеаризованных уравнений Эйлера и использовать для обобщения метода Годунова на класс задач акустики, т.е. задач распространения малых возмущений на фоне некоторого переменного течения.

Вывод метода Годунова для линеаризованных уравнений Эйлера мы начнем с рассмотрения полных уравнений, дискретизированных на некоторой пространственной сетке методом конечного объема:

где ${{q}_{i}}$ – вектор осредненных по ячейке консервативных переменных, ${{F}_{\sigma }}$ – локально-одномерный невязкий поток в нормальном направлении, ${{T}_{\sigma }}$ – матрица перехода к локальному ортонормированному базису, связанному с гранью ячейки.

В уравнении (25) вектор параметров течения расщепляется на два, представляющих базовые поток и поле малых возмущений, которые мы будем обозначать соответственно верхней чертой и “крышкой”, ${{q}_{i}} = {{\bar {q}}_{i}} + \varepsilon {{\hat {q}}_{i}}$, $\varepsilon = 1$. Потоковые члены тогда могут быть разложены на три составляющие: ${{F}_{\sigma }} = {{\bar {F}}_{\sigma }} + {{\hat {F}}_{\sigma }} + {{\tilde {F}}_{\sigma }}$, которые соответствуют базовому потоку порядка $O(1)$, линейному акустическому потоку, включающему члены порядка $O(\varepsilon )$, и нелинейным членам порядка $O({{\varepsilon }^{2}})$ и выше. Последние отмечены верхней волнистой чертой.

При этом делаются следующие предположения. Первое – базовое течение удовлетворяет исходной системе дискретизированных уравнений, и поэтому члены порядка $O(1)$ исключаются. Второе – вклад нелинейных потоков ${{\tilde {F}}_{\sigma }}$, которые, главным образом, определяют процессы генерации звука потоком, моделируется подходящим источником акустических возмущений. Он обычно строится на основе экспериментальных данных или $S$ данных прямого численного моделирования уравнений Навье–Стокса (или, при определенных ограничениях, LES-уравнений). Ниже мы предполагаем, что источники звука заданы.

Тогда уравнения линейной модели, описывающей распространение малых возмущений по заданному, вообще говоря, непостоянному базовому полю течения принимают следующий вид:

Основным моментом в рассматриваемом подходе является аппроксимация акустического потока ${{\hat {F}}_{\sigma }}$, который зависит как от параметров базового течения вблизи ребра, так и от величин малых возмущений. Мы решаем эту задачу годуновским подходом, рассматривая акустический поток как результат взаимодействия полей малых возмущений в прилегающих к ребру ячейках. Тогда искомый поток вычисляется через решение вариационной задачи Римана как

где $\hat {Q}_{\sigma }^{R}$ есть, по сути, решение ВЗР, которое выписывается через вариационные матрицы Здесь верхний индекс $\sigma $ указывает, что соответствующие значения берутся в центре грани. Для получения этих значений мы используем кусочно-линейное восполнение для примитивных (неконсервативных) переменных на основе вектора градиента, который вычисляется по значениям в соседних ячейках методом наименьших квадратов.

Таким образом, с учетом (33) система (32) является системой дифференциальных уравнений, которая интегрируется численно 3-х слойной схемой Рунге–Кутта, требующей минимального хранения данных и обеспечивающей при этом третий порядок аппроксимации:

Здесь $\Delta t$ – шаг по времени, который выбирается в соответствии со стандартным условием устойчивости, обеспечивающим значение числа Куранта меньше 1, а ${{R}_{i}}( \cdot )$ обозначает правую часть системы уравнений.

Верификация метода проводится на задаче о прохождении звуковой волны через фронт ударной волны. Основное течение соответствует течению перед и за фронтом стационарной плоской ударной волны. Плоская монохроматическая звуковая волна $q = {{q}_{0}}\exp [i(kx - \omega t)]$ падает нормально на поверхность ударной волны со стороны набегающего потока. Это моделируется заданием соответствующих возмущений на левой границе расчетной области (основное течение происходит слева направо).

Результаты расчетов приведены на фиг. 3. Слева показано распределение звукового давления вдоль направления основного течения для случая ударной волны с числом Маха ${{{\text{M}}}_{{sh}}} = 1.5$. Видно, что прохождение волны рассчитывается в предложенном подходе без какого-либо эффекта “численного отражения” на фронте ударной волны – форма волны перед скачком в точности совпадает с той, которая генерируется на входной границе. При переходе через скачок волна усиливается по амплитуде примерно в 2 раза. Также меняется ее длина волны в силу допплеровского эффекта. Отметим, что как в падающей волне, так и в проходящей отсутствует эффект численного затухания. Амплитуды этих волн практически не меняются по мере распространения вниз по потоку, хотя расчетная сетка, используемая в расчете, была относительно крупной – 20 и 15 ячеек на одну волну, соответственно в падающем и проходящем звуке.

При переходе через скачок амплитуда звуковой волны увеличивается. Как видно из приведенных результатов, это увеличение, по крайней мере, качественно, правильно улавливается предложенным методом, без искусственных “всплесков” или “провалов” в распределениях вблизи фронта волны. Количественно точность расчетов иллюстрируется фиг. 3б, где сравниваются расчетные и теоретические данные по коэффициенту усиления (отношение амплитуд волн, проходящей к падающей) для ударных волн различной интенсивности. Видно, что расчетные значения хорошо ложатся на теоретическую кривую во всем диапазоне от волн слабой интенсивности до сильных скачков.

6. ЗАКЛЮЧЕНИЕ

В работе рассмотрены обобщенная и вариационная постановки задачи Римана для системы уравнений газовой динамики. В первой постановке начальные данные имеют в общем случае неконстантное распределение слева и справа от точки начального разрыва. Во второй постановке исследуется первая вариация автомодельной задачи Римана при малых изменениях в начальных данных. С использованием решения обобщенной задачи Римана построены аналоги приближенных методов HLL и HLLC для случая линейного распределения начальных данных, которые могут быть обобщены и на произвольное нелинейное распределение. Полученные теоретические результаты позволили развить идеи метода Годунова и построить явно-неявный аналог метода, не требующий ограничения на шаг по времени и переходящий в чисто явной компоненте в схему Годунова второго порядка точности. Кроме этого, предложена схема Годунова для решения линеаризованных уравнений Эйлера, описывающих распространение малых возмущений на фоне непостоянного базового течения при наличии ударных волн и контактных разрывов.