Журнал вычислительной математики и математической физики, 2020, T. 60, № 5, стр. 917-932

ВВЕДЕНИЕ

Трехмерные задачи дифракции (трансмиссии) акустических волн на однородных локальных включениях встречаются в таких важных областях, как радиофизика, дефектоскопия, оптика, акустика океана и атмосферы, геофизика. Такие задачи решаются в основном численно, так как их аналитические решения могут быть найдены лишь в исключительных случаях.

При помощи методов теории потенциала упомянутые задачи могут быть сформулированы в интегральной форме. Изначально они сводились либо к системам двух слабо сингулярных граничных интегральных уравнений Фредгольма II рода с двумя неизвестными функциями (плотностями) [1], либо к смешанным системам, содержащим уравнения Фредгольма I и II рода [2]–[4]. Позже в работах [5], [6] были получены и исследованы эквивалентные этим задачам интегральные уравнения Фредгольма I и II рода с одной неизвестной плотностью. Такие уравнения удобны для численного исследования и получаемые в результате их дискретизации задачи менее требовательны к ресурсам компьютера по сравнению с другими эквивалентными формулировками.

В настоящей работе для численного решения задачи дифракции используется эквивалентное ей слабо сингулярное граничное интегральное уравнение Фредгольма I рода с одной неизвестной функцией [7]–[10]. Для построения дискретного аналога этого уравнения применяется специальный метод осреднения ядер слабо сингулярных интегральных операторов [11], [12]. Суть его заключается в следующем. Неизвестная плотность отыскивается в виде линейной комбинации гладких финитных функций, образующих разбиение единицы на поверхности включения. При дискретизации интегрального уравнения поверхностные интегралы приближаются выражениями, содержащими объемные интегралы. Это позволяет рассчитывать коэффициенты систем линейных алгебраических уравнений (СЛАУ), аппроксимирующих интегральные уравнения, по весьма простым формулам. Впервые такой подход был применен в [11] для численного решения интегральных уравнений, эквивалентных трехмерным задачам Дирихле для уравнения Лапласа. Позже он использовался в работах [7], [12]–[14].

Матрицы получаемых СЛАУ являются плотными. Прямые методы позволяют решать эти СЛАУ за $O({{n}^{3}})$ операций, где $n$ – порядок матрицы. В настоящей работе для их численного решения используется обобщенный метод минимальной невязки (GMRES) [15]. Как было установлено ранее [7], сложность GMRES в данном случае имеет оценку $O(m{{n}^{2}})$, где $m$ – количество итераций, которое значительно меньше $n$ и зависит от него весьма слабо. После того, как приближенное решение интегрального уравнения найдено, искомое приближенное решение задачи дифракции при помощи интегральных представлений восстанавливается в любой точке пространства.

На этапе решения СЛАУ при помощи GMRES большую часть времени занимают матрично-векторные умножения. Для снижения затрат времени в таких случаях предлагается использовать один из быстрых методов приближенного матрично-векторного умножения (см. обзор в [16]), т.е. таких методов, сложность которых составляет $o({{n}^{2}})$ при $n \to \infty $. В настоящей работе для этого применяется мозаично-скелетонный метод [14], [17], [18]. Его основная идея заключается в аппроксимации больших блоков плотных матриц матрицами малого ранга. В результате матрица СЛАУ полностью не вычисляется и не сохраняется, а в процедуре матрично-векторного умножения используется ее малоранговое приближение. Для реализации метода можно использовать ранее созданные алгоритмы и программы численного решения задач дифракции. В этом случае в них необходимо добавить только процедуры построения и хранения приближенной матрицы и изменить модуль матрично-векторного умножения, а метод дискретизации и процедура вычисления элементов исходной матрицы остаются прежними. Преимуществом метода также является возможность экономичного хранения приближенной матрицы, снижающего требования к памяти компьютера.

Ниже излагается численный метод решения трехмерной задачи дифракции, сформулированной в виде слабо сингулярного граничного интегрального уравнения Фредгольма I рода с одной неизвестной функцией. Описываются применение мозаично-скелетонного метода к численному решению такого уравнения и технология OpenMP для организации параллельных вычислений. Приводятся результаты численных экспериментов, которые позволяют судить об эффективности применяемого подхода.

1. ИСХОДНАЯ ЗАДАЧА И ЭКВИВАЛЕНТНОЕ ЕЙ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ

Рассмотрим трехмерное евклидово пространство ${{\mathbb{R}}^{3}}$ с ортогональной системой координат $o{{x}_{1}}{{x}_{2}}{{x}_{3}}$, заполненное однородной изотропной средой с плотностью ${{\rho }_{e}}$, скоростью распространения акустических колебаний ${{c}_{e}}$ и коэффициентом поглощения ${{\gamma }_{e}}$, в котором имеется ограниченное произвольной замкнутой поверхностью $\Gamma $ однородное изотропное включение с плотностью ${{\rho }_{i}}$, скоростью звука ${{c}_{i}}$ и коэффициентом поглощения ${{\gamma }_{i}}$. Области ${{\mathbb{R}}^{3}}$, занятые включением и вмещающей средой, обозначим через ${{\Omega }_{i}}$ и ${{\Omega }_{e}}$ (${{\Omega }_{e}} = {{\mathbb{R}}^{3}}{\backslash }{{\bar {\Omega }}_{i}}$) соответственно.

Пусть в области ${{\Omega }_{e}}$ имеются гармонические источники звука, возбуждающие во вмещающей среде исходное волновое поле давлений ${{u}_{0}}$. Звуковые волны распространяются в пространстве и, достигая включения, рассеиваются на нем. В результате в области ${{\Omega }_{e}}$ возникают отраженные волны, а в области ${{\Omega }_{i}}$ появляются проходящие волны. Поэтому комплексную амплитуду полного поля давлений $u$ можно представить в виде:

где ${{u}_{i}}$, ${{u}_{e}}$ – комплексные амплитуды поля давлений проходящего и отраженного волновых полей.

Сформулируем исходную задачу.

Задача 1. Найти в ограниченной области ${{\Omega }_{i}}$ трехмерного евклидова пространства ${{\mathbb{R}}^{3}}$ и в неограниченной области ${{\Omega }_{e}} = {{\mathbb{R}}^{3}}{\backslash }{{\Omega }_{i}}$, разделенных замкнутой поверхностью $\Gamma \in {{C}^{{r + \beta }}}$, $r + \beta > 1$, комплекснозначные функции ${{u}_{{i(e)}}} \in {{H}^{1}}({{\Omega }_{{i(e)}}},\Delta )$, удовлетворяющие интегральным тождествам

условиям сопряжения на границе раздела сред из ${{\Omega }_{i}}$ и ${{\Omega }_{e}}$а также условию излучения на бесконечности для ${{u}_{e}}$если на границе включения $\Gamma $ заданы функции ${{f}_{0}} \in {{H}^{{1/2}}}(\Gamma )$ и ${{f}_{1}} \in {{H}^{{ - 1/2}}}(\Gamma )$.

Здесь ${v}{\kern 1pt} {\text{*}}$ – комплексно сопряженная к ${v}$ функция, $\mathop {\left\langle { \cdot , \cdot } \right\rangle }\nolimits_\Gamma $ – отношение двойственности на ${{H}^{{1/2}}}(\Gamma ) \times {{H}^{{ - 1/2}}}(\Gamma )$, обобщающее скалярное произведение в ${{H}^{0}}(\Gamma )$, ${{u}^{ \pm }} \equiv {{\gamma }^{ \pm }}u$, ${{\gamma }^{ - }}:{{H}^{1}}({{\Omega }_{i}}) \to {{H}^{{1/2}}}(\Gamma )$, ${{\gamma }^{ + }}:{{H}^{1}}({{\Omega }_{e}}) \to {{H}^{{1/2}}}(\Gamma )$ – операторы следов, ${{N}^{ - }}:{{H}^{1}}({{\Omega }_{i}},\Delta ) \to {{H}^{{ - 1/2}}}(\Gamma )$, ${{N}^{ + }}:{{H}^{1}}({{\Omega }_{e}},\Delta ) \to {{H}^{{ - 1/2}}}(\Gamma )$ – операторы нормальных производных [19], ${{f}_{0}} = u_{0}^{ + }$, ${{f}_{1}} = {{N}^{ + }}{{u}_{0}}$,

$\omega $ – круговая частота колебаний, ${{c}_{{i(e)}}} > 0$, ${{\rho }_{{i(e)}}} > 0$, ${{\gamma }_{{i(e)}}} \geqslant 0$. Определения используемых здесь и далее функциональных пространств имеются в работе [19].

Замечание 1. Если ${\text{Im}}({{k}_{e}}) = 0$, то ${{u}_{e}} \in H_{{{\text{loc}}}}^{1}({{\Omega }_{e}},\Delta )$.

В работах [7], [8] доказана

Теорема 1. Задача 1 имеет не более одного решения.

Введем обозначения

Решение задачи 1 будем искать в виде потенциалов

где $q \in {{H}^{{ - 1/2}}}(\Gamma )$ – неизвестная плотность, ${{f}_{0}} \in {{H}^{{1/2}}}(\Gamma )$, ${{f}_{1}} \in {{H}^{{ - 1/2}}}(\Gamma )$, ${{p}_{{ei}}} = {{p}_{e}}{\text{/}}{{p}_{i}}$.

Ядрами этих интегральных операторов являются фундаментальные решения уравнений Гельмгольца и их нормальные производные. Поэтому, как показано в работе [8], они удовлетворяют тождествам (1) и условию излучения на бесконечности (3). Кроме того, выполнение для них первого из условий сопряжения (2) автоматически влечет за собой выполнение второго условия сопряжения. Подставляя потенциалы (5) в первое условие сопряжения, получаем слабо сингулярное интегральное уравнение Фредгольма I рода для определения неизвестной плотности $q$:

где

Для гладких функций уравнение (6) может быть записано в следующем виде [8]:

Справедлива [7]

Теорема 2. Пусть ${{f}_{0}} \in {{H}^{{1/2}}}(\Gamma )$, ${{f}_{1}} \in {{H}^{{ - 1/2}}}(\Gamma )$, ${{\gamma }_{e}} > 0$ или $\omega $ не является собственной частотой задачи

Тогда уравнение (6) корректно разрешимо в классе плотностей $q \in {{H}^{{ - 1/2}}}(\Gamma )$, и формулы (5) дают решение задачи 1.

2. ЧИСЛЕННЫЙ МЕТОД

Применяемый метод численного решения приведен в работе [9] и представляет собой развитие методики, предложенной и впервые апробированной в работе [11]. Кратко опишем общую схему его реализации. Построим покрытие поверхности $\Gamma $ системой ${\text{\{ }}{{\Gamma }_{m}}{\text{\} }}_{{m = 1}}^{M}$ окрестностей узловых точек $x_{m}^{'} \in \Gamma $, лежащих внутри сфер радиусов ${{h}_{m}}$ с центрами в $x_{m}^{'}$, и обозначим через $\left\{ {{{\varphi }_{m}}} \right\}$ подчиненное ему разбиение единицы. В качестве ${{\varphi }_{m}}$ будем использовать функции

где $x \in \Gamma $, ${{r}_{m}} = \left| {x - x_{m}^{'}} \right|$, ${{\varphi }_{m}} \in {{C}^{1}}(\Gamma )$ при $\Gamma \in {{C}^{{r + \beta }}}$, $r + \beta > 1$.

Приближенное решение уравнения (6) будем искать на сетке ${\text{\{ }}{{x}_{m}}{\text{\} }}$,

узлами которой являются центры тяжестей функций ${{\varphi }_{m}}$. Будем предполагать, что для всех $m = 1,2,\; \ldots ,\;M$ выполняются неравенства где $h$, $h{\text{'}}$ – положительные числа, зависящие от $M$, ${{q}_{0}}$ не зависит от $M$.

Вместо заданной на $\Gamma $ неизвестной функции $q$ будем искать обобщенную функцию $q{{\delta }_{\Gamma }}$, действующую по правилу

Приближать эту функцию будем выражением где ${{q}_{n}}$ – неизвестные коэффициенты,

В работе [9] показано, что для любых функций $\eta \in {{H}^{1}}({{\mathbb{R}}^{3}})$ и $q \in {{H}^{1}}(\Gamma )$ справедливо равенство

Приближение плотности потенциала простого слоя объемной плотностью позволяет получать простые формулы для аппроксимации интегрального оператора ${{A}_{{i(e)}}}$ из (4). Теоретическое обоснование изложенного подхода имеется в работе [11].

Интегральные операторы из (4) на $\Gamma $ аппроксимируются выражениями [7], [12]

${{n}_{{ml}}}$ – компоненты единичного вектора внешней нормали к поверхности $\Gamma $ в точке ${{x}_{m}}$.

Оператор в левой части уравнения (6) аппроксимируем композициями операторов (8)–(10):

а правую часть уравнения (6) – по формуле Решая полученную СЛАУ, находим приближенное решение интегрального уравнения в точках дискретизации. После этого приближенное решение исходной задачи дифракции с помощью интегральных представлений может быть найдено в любой точке пространства.

При решении СЛАУ с помощью GMRES на каждой итерации необходимо выполнить матрично-векторное умножение вида (11). Остановимся на этом подробнее. Для произвольного вектора с компонентами ${{p}_{n}}$ справедливо тождество:

Матрично-векторное умножение по формуле из левой части тождества предварительно требует $2{{M}^{3}} + {{M}^{2}}$ операций умножения для вычисления элементов ${{C}^{{mn}}}$, а затем ${{M}^{2}}$ умножений на каждой итерации. Правая часть этого тождества позволяет находить данное матрично-векторное произведение без вычисления элементов ${{C}^{{mn}}}$ и требует $4{{M}^{2}} + M$ операций умножения на итерацию. Поскольку количество итераций существенно мало по сравнению с порядком СЛАУ (см. результаты вычислительных экспериментов), использование правой части тождества значительно снижает вычислительную сложность решения задачи.

Дальнейшее уменьшение вычислительной сложности матрично-векторного умножения и, как следствие, всей задачи связано с использованием мозаично-скелетонного метода.

3. МОЗАИЧНО-СКЕЛЕТОННЫЙ МЕТОД

Введем определения, необходимые для описания мозаично-скелетонного метода [16]. Пусть ${{A}_{k}}$ – блок матрицы ${{A}^{{n \times m}}}$, а $\Pi ({{A}_{k}})$ – матрица размера $n \times m$, полученная из ${{A}_{k}}$ путем дополнения до $A$ нулями.

Определение 1. Конечное множество блоков ${\text{\{ }}{{A}_{k}}{\text{\} }}$ будем называть покрытием $A$, если

и мозаичным разбиением $A$, если, дополнительно, $\bigcap\nolimits_k^{} {{{A}_{k}}} = \emptyset $.

Определение 2. Мозаичным рангом матрицы $A \in {{\mathbb{C}}^{{n \times m}}}$, соответствующим некоторому покрытию, называется число

где сумма берется по всем блокам покрытия ${{A}_{k}} \in {{\mathbb{C}}^{{{{n}_{k}} \times {{m}_{k}}}}}$, и $\operatorname{mem} {{A}_{k}} = {\text{min\{ }}{{n}_{k}}{{m}_{k}},({{n}_{k}} + {{m}_{k}})\operatorname{rank} {{A}_{k}}{\text{\} }}$.

Мозаичный ранг определяет затраты памяти на хранение мозаичного разбиения матрицы $A$, а также вычислительную сложность матрично-векторного умножения.

Важным показателем эффективности данного метода является фактор сжатия $I$ [16]. Он определяется следующей формулой:

где $\operatorname{mem} {{A}_{p}}$ – объем памяти, необходимый для хранения матрицы в малоранговом формате, $\operatorname{mem} A$ – объем памяти для хранения исходной матрицы.

Определение 3. Будем называть скелетоном матрицу вида $u{v}{\kern 1pt} {\text{*}}$, где $u$ и ${v}$ – вектор-столбцы, ${v}{\kern 1pt} {\text{*}}$ обозначает вектор-строку, эрмитово-сопряженную к вектору ${v}$.

Из определения 3 следует, что $\operatorname{rank} (u{v}{\kern 1pt} *) = 1$.

Мозаично-скелетонный метод состоит из трех этапов: построение дерева кластеров, создание списка блоков и нахождение малоранговой аппроксимации. Для первого этапа входными данными является сетка, на которой проведена дискретизация. Совокупность всех точек сетки называется кластером нулевого уровня (или корнем дерева). На каждом шаге исходный кластер разбивается на несколько непересекающихся подкластеров. Так продолжается, пока уровень дерева не достигнет заданного. В качестве кластера нулевого уровня можно взять куб и погрузить туда область, на границе которой строится сетка. При переходе к следующему уровню дерева каждое ребро текущего кластера делится пополам, в результате чего получается 8 подкубов. Тогда все точки, принадлежащие исходному кубу, распределятся по 8 подкубам, образовав 8 подкластеров (возможно, некоторые из них будут пустыми). При достижении максимального уровня $k$, количество кластеров станет равным ${{8}^{k}}$.

Следующий этап – создание списка блоков. Два любых кластера определяют блок в матрице. Если точки кластеров геометрически удалены друг от друга, то блок попадает в “дальнюю” зону и для него будет построено приближение, а иначе – в “ближнюю”, тогда элементы блоков будут вычисляться по формулам (11).

На последнем этапе блоки “дальней” зоны приближаются матрицами малого ранга. Такие матрицы можно искать разными способами [17], [18]. В настоящей работе для этого используется алгоритм неполной крестовой аппроксимации, он является заключительным этапом мозаично-скелетонного метода [20].

Алгоритм

Приближение матрицы $A$ размера $n \times m$ матрицей ${{A}^{{(r)}}}$, являющейся суммой $r$ скелетонов.

Шаг 1. Пусть $p$ – номер вычисляемого скелетона. На этом шаге полагаем $p = 1$ и выбираем произвольный номер ${{j}_{p}}$ столбца матрицы $A$.

Шаг 2. В столбце с номером ${{j}_{p}}$ вычисляем все элементы матрицы $A$, далее из них вычитаем элементы всех полученных ранее скелетонов в этих позициях. В полученном столбце ${{u}_{p}}$ находим максимальный по модулю элемент. Пусть он расположен в строке с номером ${{i}_{p}}$.

Шаг 3. Вычисляем строку матрицы $A$ с номером ${{i}_{p}}$ и из нее также вычитаем элементы всех уже найденных скелетонов в соответствующих позициях. В полученной строке ${v}_{p}^{ * }$ находим наибольший по модулю элемент, причем элемент из столбца с номером ${{j}_{p}}$ повторно выбрать нельзя. Номер столбца, в котором находится этот максимальный элемент, обозначим через ${{j}_{{p + 1}}}$.

Шаг 4. По кресту с центром $({{i}_{p}},{{j}_{p}})$ строим скелетон так, чтобы коэффициенты матрицы

совпадали с коэффициентами исходной матрицы на позициях $p$ вычисленных столбцов ${{j}_{1}},\; \ldots ,\;{{j}_{p}}$ и $p$ вычисленных строк ${{i}_{1}},\; \ldots ,\;{{i}_{p}}$.

Шаг 5. Проверяем критерий остановки. Если он выполняется, то вычисления прекращаются. Если не выполняется, то устанавливаем $p: = p + 1$ и повторяем алгоритм с шага 2.

Аппроксимация (15) считается достаточно точной, если выполняется неравенство (критерий остановки)

где $\varepsilon $ – относительная погрешность аппроксимации, ${{\left\| {\, \cdot \,} \right\|}_{F}}$ – норма Фробениуса [21].

Для проверки этого критерия нужно вычислить $nm$ элементов матрицы $A$, что слишком трудоемко. Объем вычислений можно сократить, используя оценку сверху величины ${{\left\| {A - {{A}^{{(p)}}}} \right\|}_{F}}$, полученную в [20],

При этом критерий остановки принимает вид

Норму матрицы ${{A}^{{(p)}}}$ будем вычислять по рекуррентной формуле. Для ее вывода воспользуемся определением нормы Фробениуса $\left\| A \right\|_{F}^{2} = \operatorname{Tr} (A{\text{*}}A)$, где $A{\text{*}}$ – матрица, эрмитово-сопряженная к матрице $A$, $\operatorname{Tr} (A) = \sum\nolimits_{i = 1}^l {{{A}_{{ii}}}} $ – след матрицы $A$ [21]. Используя формулу (15), линейность следа и его инвариантность относительно циклической перестановки матриц [21], имеем

Последнее выражение можно переписать в виде

При использовании рекуррентной формулы (18) на $p$-м шаге требуется выполнить $O(p(m + n))$ операций умножения. Если в правой части (17) воспользоваться оценкой сверху для скалярных произведений, можно получить более предпочтительную с вычислительной точки зрения формулу

Она требует всего $O(m + n)$ операций на каждом шаге, однако при ее использовании критерий остановки становится не вполне корректным, так как в правую часть неравенства (16) вместо нормы ${{\left\| {{{A}^{{(p)}}}} \right\|}_{F}}$ подставляется ее оценка сверху. Вычислительные эксперименты, проведенные в широком диапазоне волновых чисел, показали, что использование формулы (19) не слишком ухудшает оценку точности малоранговой аппроксимации по сравнению с формулой (18), но позволяет уменьшить затраты времени на работу быстрого метода.

4. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

Для выполнения расчетов были использованы вычислительные ресурсы ЦКП “Центр данных ДВО РАН” [22]. Программа для численного решения задач дифракции написана на языке Фортран 90 и представляет собой консольное приложение, предназначенное для работы на многопроцессорных вычислительных системах. В качестве компилятора выступает Intel Fortran Compiler, также используются библиотека Intel Math Kernel Library (Intel MKL) и реализация стандарта OpenMP для данного компилятора.

Программное обеспечение состоит из 21 модуля, три из которых реализуют этапы мозаично-скелетонного метода. Распараллеливанию подвергались наиболее трудоемкие части программы – алгоритмы построения малоранговой аппроксимации в мозаично-скелетонном методе и матрично-векторного умножения в GMRES. В [20] даны рекомендации по реализации метода для платформ с распределенной памятью. В данной работе при помощи технологии OpenMP был реализован параллельный вариант для систем с общей памятью. В таком случае нет необходимости пересылать большие объемы данных между OpenMP потоками.

Сначала каждый поток получает блок и в зависимости от его зоны либо строит для него малоранговое приближение, либо вычисляет все элементы блока. Далее на этапе матрично-векторного умножения поток получает блоки и умножает их на соответствующие части вектора. Если блок принадлежит “ближней” зоне, для его умножения поток использует функцию из Intel MKL. Если блок находится в “дальней” зоне, то он умножается на вектор с использованием специальной функции, учитывающей специфику хранения таких блоков. Данная функция позволяет умножать блоки “дальней” зоны на вектор за почти линейное число операций. Блоки распределяются по потокам динамически. На начальном этапе поток получает только один блок. Закончив с ним работу, он получает из стека следующий блок. Такой подход позволяет потокам заканчивать работу почти одновременно. По окончании параллельной секции происходит неявная синхронизация OpenMP потоков.

Пример 1. Рассматривается задача дифракции плоской акустической волны на единичном шаре с центром в начале координат и тремя различными наборами параметров вмещающей среды и включения. Комплексная амплитуда исходного волнового поля давлений имеет вид ${{u}_{0}}(x) = exp(i{{k}_{e}}{{x}_{3}})$, ${{f}_{0}} = u_{0}^{ + }$, ${{f}_{1}} = {{N}^{ + }}{{u}_{0}}$, параметры сред: I) ${{k}_{i}} = 8$, ${{\rho }_{i}} = 3$, ${{k}_{e}} = 5.5$, ${{\rho }_{e}} = 1$; II) ${{k}_{i}} = 15.5$, ${{\rho }_{i}} = 5$, ${{k}_{e}} = 9$, ${{\rho }_{e}} = 4$; III) ${{k}_{i}} = 21$, ${{\rho }_{i}} = 7$, ${{k}_{e}} = 30.5$, ${{\rho }_{e}} = 9.5$.

Во всех примерах задача дифракции решалась дважды: с использованием мозаично-скелетонного метода в GMRES и без него. При этом дискретизация уравнения (6) осуществлялась по формулам (11) и (12), порядок матрицы $M$ варьировался от 1000 до 64 000. Здесь и далее точность GMRES составляла ${{10}^{{ - 7}}}$, а точность малоранговой аппроксимации $\varepsilon $ равнялась ${{10}^{{ - 5}}}$. Уровень дерева кластеров менялся от 4 до 6. Далее на всех рисунках квадратами обозначается первый набор параметров сред, кругами – второй набор и треугольниками – третий набор.

В примере 1 правильность предлагаемого подхода проверялась путем сравнения приближенных решений задачи дифракции с известным аналитическим решением [23]. Последнее рассчитывалось по формулам

Здесь $r = \left| x \right|$, $cos\theta = {{x}_{3}}{\text{/}}r$, ${{J}_{{m + 1/2}}}$, $H_{{m + 1/2}}^{{(1)}}$ – функции Бесселя и функции Ханкеля I рода $(m + 1{\text{/}}2)$-го порядка соответственно, ${{P}_{m}}$ – полиномы Лежандра $m$-го порядка.

Кроме того, решения интегрального уравнения (6), найденные приближенно, сравнивались с аналитическим решением, имеющим вид

Погрешности этих решений вычислялись в норме пространства сеточных функций [12] где $q_{n}^{ * }$ – комплексно сопряженное к ${{q}_{n}}$ число,

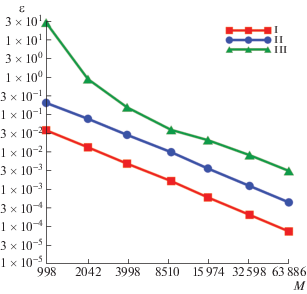
На фиг. 1 представлены относительные погрешности решений интегрального уравнения (6) в зависимости от числа узловых точек $M$ для задачи из примера 1. При удвоении $M$ погрешности уменьшаются в два раза, значит, метод имеет второй порядок точности относительно ${{h}^{2}} \sim {{M}^{{ - 1}}}$. Относительные погрешности решений задачи из примера 1 приведены на фиг. 2. Здесь и в последующих примерах они посчитаны в норме пространств сеточных функций $H_{h}^{0}({{\Omega }_{{i(e)}}})$. Сплошными линиями обозначены погрешности ${{u}_{i}}$, а штриховыми линиями – погрешности ${{u}_{e}}$. В данном случае метод также имеет второй порядок точности.

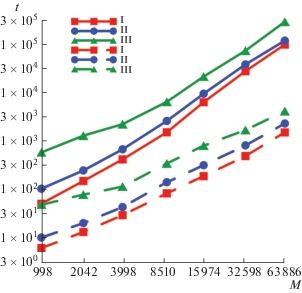
Рассмотрим теперь фиг. 3, где приведены затраты времени на решение СЛАУ, аппроксимирующих уравнение (6), в зависимости от количества точек дискретизации $M$. Штриховые линии изображают время решения СЛАУ с использованием мозаично-скелетонного метода в GMRES, а сплошные линии – время решения без применения быстрого метода. Здесь и далее время $t$ представлено в секундах. Эксперименты показали, что сложность GMRES с использованием мозаично-скелетонного метода при удвоении количества точек дискретизации возрастает в среднем в 2.4 раза, т.е. почти линейно. При этом вычислительная сложность GMRES без использования быстрого метода имеет оценку $O({{M}^{2}})$. Таким образом, использование быстрого метода приводит к существенному уменьшению времени решения задачи (до 70 раз при $M = 63\,886$ для первого набора параметров).

В табл. 1 и 2 приведены значения мозаичного ранга и фактора сжатия для СЛАУ, аппроксимирующих интегральное уравнение (6), в зависимости от количества узловых точек. Мозаичный ранг рассчитывался по формуле (13), а фактор сжатия – по формуле (14). Численные эксперименты показывают, что мозаичный ранг растет как $O(l{{n}^{3}}(M))$, а фактор сжатия, начиная с некоторого $M$, уменьшается как $O(l{{n}^{3}}(M){\text{/}}M)$.

В табл. 3 приведено число итераций для решения СЛАУ из примера 1 с указанной выше точностью. Видно, что количество итераций мало по сравнению с порядком СЛАУ и слабо изменяется с его увеличением.

На фиг. 4 представлены затраты времени на решение СЛАУ, аппроксимирующих уравнение (6), в зависимости от количества ядер вычислительного кластера. При удвоении количества ядер время уменьшается в среднем в 1.8 раза.

Пример 2. Рассматривается задача дифракции плоской акустической волны на трехосном эллипсоиде с полуосями (0.75, 1, 0.5) с центром в начале координат. Комплексная амплитуда исходного волнового поля давлений и наборы параметров такие же, как в примере 1.

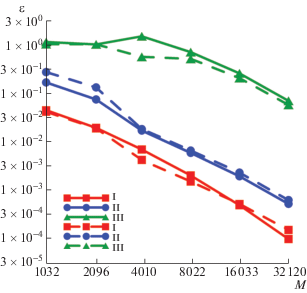
Аналитическое решение задачи из примера 2 неизвестно. Поэтому проверялась сходимость последовательности ее приближенных решений к решению, посчитанному на наиболее густой сетке. Относительные погрешности решения задачи из примера 2 приведены на фиг. 5. Сплошные линии показывают погрешности ${{u}_{i}}$, а штриховые линии – погрешности ${{u}_{e}}$. Видно, что при удвоении порядка матриц погрешности уменьшаются в два раза.

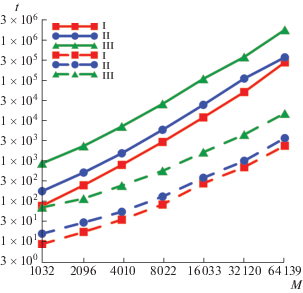
Затраты времени на решение СЛАУ в зависимости от порядка матриц $M$ с использованием мозаично-скелетонного метода и без него приведены на фиг. 6. Сплошные линии показывают время решения СЛАУ с использованием мозаично-скелетонного метода, а штриховые линии обозначают время решения систем без его использования. При использовании мозаично-скелетонного метода в GMRES время решения системы в 115 раз меньше (при $M = 64\,139$ для третьего набора параметров для уравнения (6)), чем без применения быстрого метода. При удвоении количества узловых точек время решения СЛАУ с использованием мозаично-скелетонного метода возрастает в среднем в 2.5 раза.

Результаты работы параллельной версии метода для решения задачи из примера 2 приведены на фиг. 7. При удвоении количества ядер время в среднем уменьшается в 1.7 раза.

Значения мозаичного ранга и фактора сжатия для задачи дифракции из примера 2, эквивалентной уравнению (6), приведены в табл. 4 и 5 соответственно. Как и в предыдущем примере мозаичный ранг растет как $O(l{{n}^{3}}(M))$, а фактор сжатия, начиная с некоторого $M$, уменьшается как $O(l{{n}^{3}}(M){\text{/}}M)$.

Таблица 6 показывает число итераций для решения СЛАУ из примера 2 с помощью GMRES. И в этом случае количество итераций мало по сравнению с порядком СЛАУ и слабо изменяется с его увеличением.

Пример 3. Рассматривается задача дифракции на трехосном эллипсоиде с полуосями (0.75, 1, 0.5) с центром в начале координат. Падающее поле создается точечным источником вида

где ${{x}_{0}} = (1.125,\;1,\;0.75)$. Наборы параметров вмещающей среды и включения такие же, как в примере 1.

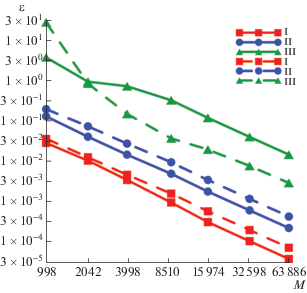
Относительные погрешности решений ${{u}_{i}}$ и ${{u}_{e}}$ для задачи из примера 3 приведены на фиг. 8 (сплошная линия – для ${{u}_{i}}$, штриховая линия – для ${{u}_{e}}$). При увеличении порядка матриц в два раза погрешности так же уменьшаются в два раза, как и в рассмотренных выше примерах.

Поскольку два последних примера отличаются только видом падающего поля, значения мозаичного ранга и фактора сжатия для соответствующих наборов параметров из примеров 2 и 3 совпадают.

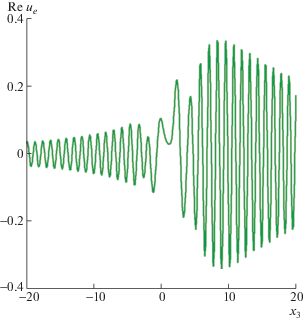
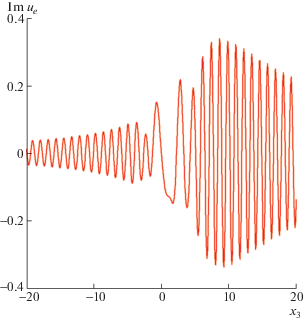
Действительная и мнимая части решения ${{u}_{e}}$ из примера 3 на отрезке ${{x}_{1}} = - 2$, ${{x}_{2}} = - 2$, $ - 20 \leqslant {{x}_{3}} \leqslant 20$ изображены на фиг. 9 и 10 соответственно. Видно, что решение ${{u}_{e}}$ быстро осциллирует и медленно убывает при удалении от включения.

ЗАКЛЮЧЕНИЕ

В работе рассмотрено применение параллельного варианта мозаично-скелетонного метода к численному решению трехмерной скалярной задачи дифракции. Она формулируется в виде граничного интегрального уравнения Фредгольма I рода с одной неизвестной функцией. Численные эксперименты показывают, что использование мозаично-скелетонного метода позволяет существенно уменьшить время решения СЛАУ, аппроксимирующих указанное интегральное уравнение, и снизить требования к ресурсам компьютера без потери точности. Поэтому данный метод можно рекомендовать к использованию при численном решении других задач математической физики, которые сводятся к граничным интегральным уравнениям.