Журнал вычислительной математики и математической физики, 2020, T. 60, № 5, стр. 900-916

1. ВВЕДЕНИЕ

Изучение различного рода явлений и процессов, наблюдаемых в таких неоднородных средах, как атмосфера и океан, представляет как научный, так и практический интерес. Неоднородность этих сред связана с эффектами плавучести – наличием силы тяжести. Плотность среды меняется по вертикали. Известно, что плотность среды зависит от температуры, давления и солености (для морской и океанических сред). Мгновенное распределение гидрофизических параметров (плотности, температуры, солености) по глубине никогда не бывает гладким, а носит ступенчатый характер: участки, где гидродинамические характеристики постоянны, сменяются участками с большими их градиентами. Это связано с тем, что в турбулентном потоке с сильно устойчивой стратификацией турбулентность распространена не повсеместно, а пятнами. Неоднородный и сильно анизотропный характер турбулентности в условиях сильной устойчивой стратификации был предсказан А.Н. Колмогоровым еще в конце 40-х годов. На существование блинообразных пятен турбулентности в океане было указано в [1].

Пятна перемешанной жидкости – это следствие взаимодействия внутренних волн, которые при определенных условиях могут опрокидываться. Другая интерпретация – это срез поперечного сечения следа за движущимся в стратифицированной среде подводным объектом. Турбулентность сосредоточена в блинообразных слоях – пятнах, простирающихся в горизонтальном направлении на расстояния, значительно превышающие их вертикальные размеры [2]–[5]. Эти блинообразные пятна оказываются резко ограниченными и долго живущими. Поэтому возникновение и развитие пятен перемешанной жидкости в стратифицированной среде представляет существенный интерес в связи с изучением тонкой структуры океана, а также исследованием динамики следа за движущимся подводным объектом.

Пятна эволюционируют, постепенно сплющиваясь и внедряясь в окружающую среду языками – интрузиями. Перемешанность жидкости в пятне создает в нем избыточное по сравнению с окружающей средой давление, которое и порождает движущую силу интрузии. Под влиянием этой силы происходит расплывание (коллапс) пятна.

Эта задача исследовалась аналитически [6], [7], изучалась в лабораторных условиях [8]–[10], а с появлением приемлемых вычислительных машин стала объектом и математического моделирования [11]–[15].

В настоящее время известен целый ряд численных методов, разработанных для исследования течений неоднородной вязкой жидкости, например [11]–[14].

Некоторые из них исторически основаны на решении уравнений Навье–Стокса в форме Гельмгольца (в переменных вихрь – функция тока) [11], что ограничивает область их применимости случаем двумерных течений. В последние годы все большее внимание уделяется разработке численных методов решения уравнений Навье–Стокса в переменных вектор скорости – давление [12]–[14]. Во всех работах, кроме [11], [13], принимается приближение Буссинеска, согласно которому изменение плотности жидкости учитывается лишь в силах плавучести. В [11] исследования проводятся для идеальной жидкости, а в [13] рассматривается только случай слабой стратификации.

За прошедшие 40 лет с момента выхода нашей работы [14] в области математического моделирования подобных течений естественно произошло много изменений. Предложены новые физические и математические модели [16], [17]. Существенно повысилось качество методов решения поставленных задач [18], [19]. Ну и, конечно же, прогресс в развитии вычислительной технике потрясающий.

В данной работе нам хотелось бы адаптировать математическую модель [16], использованную нами ранее в задачах обтекания сферы и кругового цилиндра стратифицированной жидкостью [16], [17], к задаче о коллапсе (схлопывании) пятен, которую мы решали ранее без учета диффузии стратифицирующего компонента [14], [15].

Метод также может быть обобщен на случай турбулентных течений.

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ. ПОСТАНОВКА ЗАДАЧИ

Согласно модели, предложенной в [7], возникновение и развитие турбулентности в устойчиво стратифицированной по плотности жидкости неотделимо от внутренних волн и происходит следующим образом. Под действием внешних сил в стратифицированной жидкости возникают внутренние волны большого масштаба. В результате их нелинейного взаимодействия и последующего опрокидывания или потери устойчивости возникают области перемешанной жидкости – пятна (иногда их называют зонами смешения). Эти пятна перемешанной турбулизованной жидкости эволюционируют, постепенно сплющиваясь (схлопывание, или коллапс, турбулентных пятен), что, в свою очередь, приводит к образованию новых пятен, и т. д.

В процессе эволюции пятна естественно рассматривать три ее основные стадии [7], [9].

I. Начальная стадия. Движущая сила, действующая на частицы жидкости, находящиеся внутри пятна, значительно превосходит силы сопротивления; происходит интенсивное порождение пятном внутренних волн.

II. Промежуточная стационарная стадия. Движущая сила уравновешивается в основном сопротивлением формы и волновым сопротивлением, обусловленным излучением внутренних волн; увеличение горизонтального размера пятна в зависимости от времени происходит почти по линейному закону, т.е. ускорение пренебрежимо мало.

III. Заключительная вязкая стадия. Движущая сила уравновешивается в основном вязким сопротивлением; горизонтальный размер пятна меняется слабо.

Стадии I и II непродолжительны и, по оценкам в [6], [9], [12], завершаются через промежуток времени, приблизительно равный 4T_b, где T_b = 2π/N – период, а N – частота Брента–Вяйсяля. Причем продолжительность стадии I не превосходит T_b/2. В основном же наблюдаемые пятна турбулентности находятся на заключительной III стадии эволюции.

Далее в результате диффузии пятно смешивается с окружающей жидкостью и исчезает.

Рассмотрим плоскую нестационарную задачу о течении, возникающем при коллапсе (схлопывании по вертикали) области однородной жидкости А, окруженной устойчиво и непрерывно стратифицированной по плотности (для определенности – по линейному закону) жидкостью (фиг. 1).

Течение развивается в однородном поле силы тяжести с ускорением свободного падения g. Невозмущенное линейное распределение плотности [16]:

характеризуется масштабом стратификации частотой плавучести $N = \sqrt {{g \mathord{\left/ {\vphantom {g \Lambda }} \right. \kern-0em} \Lambda }} $ и периодом плавучести T_b = 2π/N; C = Λ/R₀ – отношение масштабов, R₀ – радиус пятна, s – возмущение солености (стратифицирующего компонента), включающее коэффициент солевого сжатия.

Уравнения Навье–Стокса, описывающие течения такого типа, можно записать в виде

где v – вектор скорости с составляющими u, $v$ соответственно вдоль осей х и у декартовой системы координат, выбранной так, как указано на фиг. 1, ρ – плотность, р – давление, s – возмущение солености, k_s – коэффициент диффузии соли, μ – коэффициент динамической вязкости, g = (0, –g), g – ускорение свободного падения. В рассматриваемой задаче предполагается, что μ = const.

Будем считать, что в начальный момент времени t = 0 система на плоскости R² находится в покое, т.е.

плотность жидкости в пятне А постоянна и а вне пятна, т.е. в области R²\A, имеем Для возмущения солености имеем В качестве начального приближения, необходимого при решении уравнения для давления, выбирается распределение Поскольку давление в случае несжимаемой жидкости определяется с точностью до произвольной постоянной, не ограничивая общности, можно его выбрать равным нулю на уровне у = 0.

В силу симметрии задачи относительно плоскости х = 0, естественно искать решение только в одной полуплоскости, например при х ≥ 0. Симметрия относительно оси х не предполагается. Решение задачи будем искать в прямоугольной области {х, у: 0 ≤ х ≤ Х, –Y ≤ y ≤ Y}. На левой границе (линия 1 на фиг. 1) этой области ставятся условия симметрии течения

Верхняя (линия 2), нижняя (линия 4) и правая (линия 3) границы должны быть выбраны на достаточно большом расстоянии от источника возмущений (от пятна) так, чтобы постановка каких-либо граничных условий на этих границах, необходимых для решения задачи, не оказывала существенного влияния на картину течения.

Выбирая в качестве характерного линейного размера радиус пятна R₀ в момент времени t = 0, характерной плотности – плотность ρ₀ в пятне в начальный момент времени, характерного времени N^–1, где N = (–ag)^0.5, перейдем к безразмерным переменным

где Будем также считать, что p – давление за вычетом гидростатического. Тогда уравнения (2.1), начальные (2.2)–(2.5) и граничные (2.6) условия примут в безразмерных переменных в приближении Буссинеска следующий вид (тильда опущена): где число Рейнольдса ${\text{Rе}} = {{\rho }_{0}}R_{0}^{2}N{\text{/}}\mu $, число Фруда Fr = R₀N²/g, число Шмидта Sc = μ/ρ₀k_s, k_s – коэффициент диффузии соли, C = Λ/R₀ – отношение масштабов.

3. МЕТОД РЕШЕНИЯ

Для решения поставленной задачи будет использована одна из последних версий Метода расщепления по физическим факторам для исследования течений Несжимаемой жидкости (МЕРАНЖ). Конечно-разностная схема этого метода обладает такими свойствами, как второй порядок аппроксимации по пространственным переменным, минимальная схемная вязкость и дисперсия, работоспособная в широком диапазоне чисел Рейнольдса и Фруда и, что особенно важно при решении подобных задач, монотонность [19].

Схема расщепления. Пусть в некоторый момент времени t_n = nτ, где τ – величина шага по времени, n – число шагов, известны поля скорости v, давления p и возмущения солености s. Тогда схему нахождения неизвестных функций в момент времени t_{n + 1} = (n + 1) · τ можно представить в следующем виде:

На I этапе (3.1) предполагается, что перенос количества движения (импульса единицы массы) осуществляется только за счет конвенции, диффузии и сил плавучести. На II этапе (3.2) по найденному промежуточному полю скорости ${\mathbf{\tilde {v}}}$ с учетом условия соленоидальности вектора скорости v ^{n+ 1} из решения уравнения Пуассона находится поле давления. На III этапе (3.3) предполагается, что перенос осуществляется только за счет градиента давления (конвекция и диффузия отсутствуют). На IV этапе (3.4) по найденному полю скорости v ^{n+ 1} рассчитывается поле возмущения солености.

Конечно-разностная схема. Исследуемая область течения покрывается равномерной по х и у сеткой ячеек:

где h_x, h_у – размеры шагов сетки, a L и М – число ячеек сетки в направлении х и у соответственно (точка с координатами (i,  j) совпадает с центром ячейки). Здесь, как и в исходном методе расщепления, используется “шахматная” сетка, т.е. координаты сеточных функций разнесены в пространстве, как это показано на фиг. 2. Это дает возможность наглядно интерпретировать каждую ячейку как элемент объема среды, который характеризуется рассчитываемыми в его центре давлением p_i,j, плотностью ρ_i,j, возмущением солености s_i,j (возможно, температурой, энергией и т.п.), а также дивергенцией D_i,j (D в зависимости от знака определяет наличие источника или стока в данном объеме). Знание же нормальной составляющей вектора скорости на стороне ячейки позволяет непосредственно вычислять поток количества движения через эту сторону.

Для случая декартовой системы координат и равномерной сетки (фиг. 2) двумерная разностная схема имеет вид

где и, $v$ – составляющие вектора скорости вдоль осей ОХ и OY.

При вычислении составляющей вектора скорости $\tilde {u}_{{i + 1/2,j}}^{{}}$ записывается закон сохранения импульса для импровизированной ячейки с центром в точке (i + 1, j) (см. фиг. 2). Для первых двух членов в правой части уравнения (3.5) имеем

Рассмотрим поток DU3 через правую сторону этой ячейки где есть скорость переноса субстанции $\langle u_{{i + 1,j}}^{n}\rangle $.

Пусть

Тогда, если то используется модифицированная схема с ориентированными разностями – МОР В противном случае, если используется модифицированная схема с центральными разностями – МЦР Поток DU1 через левую сторону ячейки вычисляется аналогично потоку DU3, но в уравнениях (3.12)–(3.15) необходимо индекс i уменьшить на единицу.

Для потоков DU (3.11) в уравнении (3.5) через горизонтальные стороны ячейки имеем

где С учетом обозначений Тогда, если используется схема МОР а в противном случае, если используется схема МЦР Поток DU2 через нижнюю сторону ячейки вычисляется аналогично DU4, но в уравнениях (3.16)–(3.19) необходимо индекс j уменьшить на единицу. Оставшиеся производные, входящие в правую часть уравнения (3.5) и соответствующие вязким членам, аппроксимируются центральными разностями.

При вычислении составляющей вектора скорости ${{\tilde {v}}_{{i,j + 1/2}}}$ записывается закон сохранения импульса для вспомогательной ячейки с центрам в точке (i, j + 1/2) (см. фиг. 2). Для первых двух членов в правой части уравнения (3.6) имеем

Рассмотрим поток DV3 через правую сторону этой ячейки где есть скорость переноса субстанции $\langle v_{{i + 1/2,j + 1/2}}^{n}\rangle $. Пусть Если то используется схема МОР В противном случае, если используется схема МЦР Поток DU1 через левую сторону ячейки находится аналогично потоку DU3, но в уравнениях (3.22)–(3.25) необходимо индекс i уменьшить на единицу.

Для потоков DV (3.21) через горизонтальные стороны ячейки имеем

где есть скорость переноса субстанции $\langle v_{{i,j + 1}}^{n}\rangle $. Пусть Если то используется схема МОР В противном случае, если то используется схема МЦР

Поток DV2 через нижнюю сторону этой ячейки вычисляется аналогично потоку DV4, но в уравнениях (3.26)–(3.29) необходимо индекс j уменьшить на единицу.

Остальные производные, входящие в правую часть уравнения (3.6) и соответствующие вязким членам, аппроксимируются центральными разностями.

При вычислении возмущения солености используется такой же подход. Для первых двух членов в правой части уравнения (3.9) имеем

Рассмотрим поток DS3 через правую сторону ячейки где $u_{{i + 1/2,j}}^{{n + 1}}$ – скорость переноса субстанции $\langle s_{{i + 1/2,j}}^{n}\rangle $. Пусть Тогда, если то используется модифицированная схема с ориентированными разностями – МОР В противном случае, если используется модифицированная схема с центральными разностями – МЦР Поток $DS1 = u_{{i - 1/2,j}}^{{n + 1}} \bullet \langle s_{{i - 1/2,j}}^{n}\rangle $ через левую сторону ячейки вычисляется аналогично потоку DS3, но везде в уравнениях (3.32)–(3.35) необходимо индекс i уменьшить на единицу.

Для потоков DS (3.31) в уравнении (3.9) через горизонтальные стороны ячейки имеем

С учетом обозначений Если используется схема МОР В противном случае, если используется схема МЦР

Поток $DS2 = {v}_{{i,j - 1/2}}^{{n + 1}} \bullet \langle s_{{i,j - 1/2}}^{n}\rangle $ через нижнюю сторону ячейки вычисляется аналогично потоку DS4, но в уравнениях (3.36)–(3.39) необходимо индекс j уменьшить на единицу.

Легко видеть [19], что конечно-разностная схема аппроксимирует систему уравнений (2.7) с погрешностью порядка O(τ, Δ²), где Δ = maх(h_х, h_y).

Аппроксимация начальных условий (2.8)–(2.10) и условий симметрии (2.11) не представляет труда.

Процедура расчета. Сначала в исследуемой области течения задается начальное приближение, удовлетворяющее граничным условиям. Далее, по формулам (3.5), (3.6) находится промежуточное поле скорости ${\mathbf{\tilde {v}}}$. Затем из (3.7) рассчитывается поле давления. Для решения этого уравнения нами использовался метод верхней релаксации. Актуальное поле скорости находится из уравнений (3.8), а поле изменения солености – из уравнения (3.9). Далее вычислительный цикл повторяется до некоторого заданного момента времени либо до выполнения некоторого критерия установления (если существует стационарное решение), например,

4. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

Пусть радиус пятна R₀ = 1. Расчеты выполнены в области с размерами Х = 15, Y = 5 при следующих значениях коэффициентов и параметров: μ/ρ₀ = 0.01 cм²/c, k_s = 1.41 × 10^–5 cм²/c, N = 1 c^–1, ${{T}_{b}}$ = 2π/N s, Λ = 10 cм, C = 10, Rе = 100, Fr = 0.1, Sc = 709.2, что близко к лабораторным экспериментальным условиям. В качестве граничных условий на верхней, нижней и правой границах расчетной области, предполагая, что они достаточно удалены от пятна, выбрано состояние покоя, т.е. $u = v = s = 0$. Расчетная область была покрыта равномерной сеткой с шагами в обоих направлениях h_x = h_y = 0.1.

Тестирование программы. С целью проверки правильности работы программы были выполнены расчеты в отсутствие пятна и на различных сетках до t = 100. Характерные точки пятна (верхняя, нижняя и правая) оставались на месте, давление сохранялось постоянным, дивергенция скорости была на уровне 10^–3. Тем самым результаты этих расчетов подтвердили выполнение законов сохранения с требуемой точностью.

Методические расчеты. С целью исследования влияния размеров пространственной и временной сеток на результаты расчетов были проведены вычисления при следующих параметрах: 1 – 300 × 100, h_x = 0.05, h_y = 0.1, τ = 0.005; 2 – 150 × 200, h_x = 0.1, h_y = 0.05, τ = 0.005; 3 – 300 × 200, h_x = 0.05, h_y = 0.05, τ = 0.005; 4 – 600 × 100, h_x = 0.025, h_y = 0.1, τ = 0.0025; 5 – 150 × 400, h_x = 0.1, h_y = 0.025, τ = 0,0025; 6 – 600 × 400, h_x = 0.025, h_y = 0.025, τ = 0.0025.

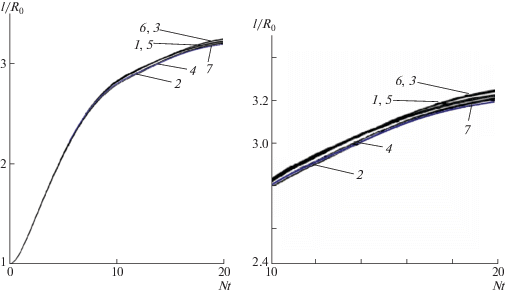
На фиг. 3 показана зависимость от времени положения правой точки пятна. Кривые отмечены цифрами, соответствующими различным сеткам, упомянутым выше. Здесь же нанесена кривая 7, соответствующая следующим параметрам: Х = 30, Y = 10 (т.е. размеры расчетной области по каждой координате увеличены в два раза с целью проверки влияния степени удаленности внешних границ на результаты расчетов), 300 × 200, h_x = 0.1, h_y = 0.1, τ = 0.01.

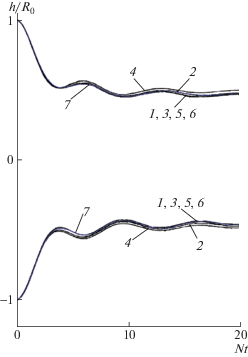
На фиг. 4 приведены зависимости от времени положения верхней и нижней точек пятна. Обозначения такие же, как и на фиг. 3. Как видно из фиг. 3 и фиг. 4, результаты практически не зависят от величины сеточных параметров и размеров области в указанном диапазоне. Это подтверждает возможность проведения дальнейших расчетов при следующих параметрах: Х = 15, Y = 5, 150 × 100, h_x = 0.1, h_y = 0.1, τ = 0.01. Здесь следует также отметить, что изменение линейных размеров пятна со временем происходит не монотонно (фиг. 4). Это связано с генерацией и динамикой внутренних волн в процессе коллапса пятна и впервые было обнаружено в нашей работе [14] и показано в фильме на конференции в сентябре 1980 г. по случаю 25-летия ВЦ АН СССР.

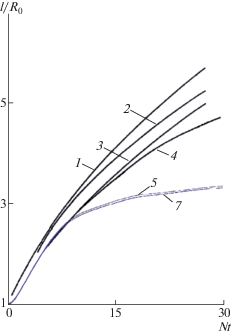
На фиг. 5 приведены результаты сравнения динамики горизонтальных размеров пятна с аналитическими оценками [6] – кривая 1, экспериментальными данными [9] – кривая 2 и расчетами других авторов [12], [14] – кривые 3 и 4 соответственно. Кривые 5 и 7 представляют результаты данной работы при следующих значениях параметров: кривая 5 – для Х = 15, Y = 5; 150 × 100, h_x = 0.1, h_y = 0.1; кривая 7 – для Х = 30, Y = 10; 300 × 200, h_x = 0.1, h_y = 0.1. Различия, наблюдаемые между кривыми на фиг. 5, можно объяснить следующим образом. Все аналитические оценки горизонтальных размеров пятна [6], [7] получены в предположении идеальности жидкости, то есть при отсутствии вязкости, а следовательно, горизонтальный размер пятна будет увеличиваться со временем быстрее, чем в экспериментах и численных расчетах. В экспериментах [8]–[10] числа Рейнольдса были существенно больше, чем в численных расчетах, а следовательно, опять горизонтальный размер пятна будет увеличиваться со временем быстрее, чем в численных расчетах. Расчеты в работах [12], [14] выполнены с использованием одинаковых моделей – уравнения Навье–Стокса в приближении Буссинеска, однако в этих моделях не учитывалась диффузия стратифицирующего компонента, что при прочих одинаковых условиях также приводит к более высоким скоростям увеличения горизонтального размера пятна. В работе [14] было также показано, что с увеличением числа Рейнольдса горизонтальный размер пятна будет увеличиваться со временем быстрее.

На фиг. 6 приведены результаты сравнения динамики вертикальных размеров пятна с расчетами [14] – кривая 4. Кривые 5 и 7 представляют результаты данной работы при следующих значениях параметров: кривая 5 – для Х = 15, Y = 5; 150 × 100, h_x = 0.1, h_y = 0.1; кривая 7 – для Х = 30, Y = 10; 300 × 200, h_x = 0.1, h_y = 0.1.

На фиг. 7–10 приведены поля изменения возмущения солености ds/dx. Белый цвет соответствует положительным значениям производной, а черный – отрицательным значениям. Границы раздела между черным и белым цветами полей при заданном уровне y соответствуют значениям ds/dx = 0, то есть минимумам и максимумам функции s или гребням и впадинам внутренних волн. Фактически это линии равной фазы. Из фиг. 7–10 также видно, что со временем линии равной фазы смещаются слева направо, а их наклон по отношению к горизонту уменьшается, что соответствует результатам работ [9], [14]. Здесь мы остановимся в основном на результатах методических расчетов.

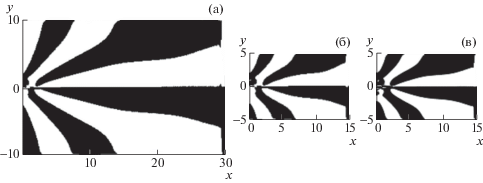
На фиг. 7 представлено поле изменения возмущения солености ds/dx при следующих значениях параметров. Область Х = 15, Y = 5, t = 10; (a) 150 × 100, h_x = 0.1, h_y = 0.1, τ = 0.01; (б) 300 × 200, h_x = 0.05, h_y = 0.05, τ = 0.005; (в) 600 × 400, h_x = 0.025, h_y = 0.025, τ = 0.0025. Как видно, результаты для различных размеров пространственной сетки достаточно хорошо согласуются между собой.

На фиг. 8 показано изменение во времени поля изменения возмущения солености ds/dx. Область Х = 15, Y = 5; 150 × 100, h_x = 0.1, h_y = 0.1, τ = 0.01; (a) t = 4; (б) t = 10; (в) t = 16; (г) t = 20. Видно, что со временем линии равной фазы смещаются слева направо, а их наклон по отношению к горизонту уменьшается, что соответствует результатам работ [9], [14].

На фиг. 9 приведено поле изменения возмущения солености ds/dx для области с размерами Х = 30, Y = 10; (a) t = 4; (б) t = 10; (в) t = 16; (г) t = 20. Из сравнения фиг. 8 и фиг. 9 можно сделать вывод, что для анализа волновой картины целесообразно либо увеличивать размеры расчетной области, либо изменять форму граничных условий на внешних границах. Хотя для небольших времен (t < 2${{T}_{b}}$) области с размерами Х = 15, Y = 5 вполне достаточно, что видно из сравнения результатов, приведенных на фиг. 10 для поля изменения возмущения солености ds/dx при t = 10; (a) oбласть Х = 30, Y = 10; 300 × 200, h_x = 0.1, h_y = 0.1, τ = 0.01; (б) oбласть Х = 15, Y = 5; 150 × 100, h_x = 0.1, h_y = 0.1, τ = 0.01; (в) oбласть Х = 15, Y = 5; 600 × 400, h_x = 0.025, h_y = 0.025, τ = 0.0025. Путем прямого наложения можно видеть, что результаты практически совпадают.

5. ЗАКЛЮЧЕНИЕ

В работе обсуждается задача о динамике (коллапсе) пятен перемешанной жидкости в стратифицированной среде. В качестве стратифицирующей компоненты выбрана соленость. Эта задача описывается уравнениями Навье–Стокса в приближении Буссинеска с соответствующими граничными и начальными условиями. Для решения поставленной задачи используется одна из последних версий разработанного авторами метода расщепления по физическим факторам. Конечно-разностная схема метода обладает такими свойствами, как высокий порядок аппроксимации, минимальная схемная вязкость и дисперсия, и что особенно важно при решении задач с большими градиентами гидрофизических параметров, задач со свободной поверхностью и внутренними волнами, свойством монотонности. Приведена конечно-разностная схема.

С целью проверки правильности работы программы были выполнены расчеты в отсутствие пятна и на различных сетках до t = 100. Характерные точки пятна (верхняя, нижняя и правая) оставались на месте, давление сохранялось постоянным, дивергенция скорости была на уровне 10^–3. Тем самым результаты этих расчетов подтвердили выполнение законов сохранения с требуемой точностью.

Проведены многочисленные тестовые и методические расчеты по изучению влияния сеточных параметров на результаты. Приведены результаты сравнения с аналитическими оценками, экспериментальными данными и расчетами других авторов. Совпадение результатов достаточно хорошее, что подтверждает возможность использования данной модели при исследовании подобных задач. Проведенные расчеты показали, что развитие пятна происходит несимметрично относительно горизонтальной оси, а изменение вертикального размера пятна немонотонно со временем и носит квазипериодический характер. Метод также может быть использован для расчета течений жидкости, стратификация которой отлична от линейной.

В качестве примера показана динамика возмущения солености, что соответствует линиям равной фазы, характеризующих поведение внутренних волн в процессе коллапса пятен.