Журнал вычислительной математики и математической физики, 2020, T. 60, № 5, стр. 815-827
Применение проективного покоординатного спуска в задаче Фекете
Б. Т. Поляк 1, *, И. Ф. Фатхуллин 2, **
1 ИПУ РАН
117342 Москва, ул. Профсоюзная, 65, Россия
2 МФТИ
141700 Долгопрудный, М. о., Институтский пер., 9, Россия
* E-mail: boris@ipu.ru
** E-mail: ilyas.fn979@gmail.com
Поступила в редакцию 21.09.2019
После доработки 21.09.2019
Принята к публикации 14.01.2020
Аннотация
Рассматривается задача минимизации энергии системы из $N$ точек, на поверхности сферы в ${{\mathbb{R}}^{3}}$, взаимодействующих с потенциалом $U = \tfrac{1}{{{{r}^{s}}}}$, $s > 0$, где $r$ – евклидово расстояние между парой точек. В работе предлагается метод проективного покоординатного спуска, использующий быстрый счет функции и градиента, а также покоординатный метод второго порядка, который достаточно быстро приближается к известным из литературы минимальным значениям. Библ. 27. Фиг. 10. Табл. 3.
1. ВВЕДЕНИЕ
Пусть задано натуральное $N \geqslant 2$. Задача Фекете порядка $N$ формулируется следующим образом [1]. Найти множество точек ${\mathbf{x}} = {\text{\{ }}{{x}_{1}},\; \ldots ,\;{{x}_{N}}{\text{\} }} \in {{\mathbb{R}}^{{3N}}}$ с ограничением для каждой точки ${{x}_{i}}$ на единичной сфере $S_{i}^{2} = {{S}^{2}} = \{ x \in {{\mathbb{R}}^{3}}:{{\left\| x \right\|}_{2}} = 1\} $ такое, что оно минимизирует потенциальную энергию системы:
т.е. формально решается задача(2)
${\mathbf{x}}{\kern 1pt} * = \mathop {{\text{argmin}}}\limits_{{\mathbf{x}} \in \prod\nolimits_{i = 1}^N S_{i}^{2}} U({\mathbf{x}}),$При $s = 1$ получается кулоновский потенциал и соответственно задача Томсона. Последняя была поставлена Дж.Дж. Томсоном еще в 1904 г. [2], однако, до сих пор остается нерешенной для произвольного $N$. Задача Фекете привлекла особое внимание математиков, потому что она появляется в списке Смейла [3] – нерешенных задач для 21-го века. Кроме того, задача имеет применения в химии и биологии [4]–[7], а также в силу своей сложности стала эталоном для тестирования численных методов оптимизации [8]. Стоит отметить, что в современных приложениях, например, в моделировании макромолекул [9] также применяются численные методы для минимизации потенциала. Конечно, часто потенциалы имеют более сложный вид и решается задача безусловной оптимизации, однако эти задачи имеют структуру, похожую на задачу Фекете в том смысле, что потенциал является суммой некоторых симметричных функций $K:\mathcal{X} \times \mathcal{X} \to \mathbb{R}$, что позволяет эффективно пересчитывать значение потенциала при смещении одной точки. В контексте вышеупомянутых приложений стоит обозначить, что целью работы является именно локальная минимзация функции (1), и в дальнейшем под ${\mathbf{x}}{\text{*}}$ понимается локальный минимум, ближайший к начальному положению ${{{\mathbf{x}}}^{0}}$.
Учитывая широкое применение, задача Фекете была хорошо изучена [10]–[12]. Известны аналитические решения при $s = 1$ для $N = 2{\kern 1pt} - {\kern 1pt} 6$ и $12$. Для различных $s$ и больших $N$ получены решения с помощью численных методов [13]. В данной статье мы остановимся на обсуждении метода проективного покоординатного градиентного спуска. Рассматриваемый метод использует быстрый счет функции и метод дробления шага. Также предлагается алгоритм второго порядка для решения данной задачи.
Определение точек Фекете есть невыпуклая задача оптимизации с нелинейными ограничениями. Следует отметить, что здесь можно легко избавиться от ограничений, параметризуя каждую точку на сфере двумя углами [14], [15], и решать задачу нелинейной оптимизации без ограничений от $2N$ переменных вместо $3N$. Однако на практике применение градиентных методов в таких координатах существенно замедляет счет оптимизируемой функции и градиента из-за относительно медленного вычисления тригонометрических функций. Поэтому остановимся подробнее на решении задачи в исходных координатах. Можно применять градиентные методы, рассматривая зависимость энергии от всех $3N$ переменных, и на каждой итерации перемещать все точки одновременно. Сравнительный анализ в разд. 5 показывает, что покоординатный метод оказывается вполне конкурентоспособным. Более того, появляется возможность использовать покоординатную версию метода второго порядка, что оказывается затруднительным для полноградиентной версии (так как это требует подсчета и обращения матрицы размера $3N \times 3N$). Поэтому интересно рассматривать проективный покоординатный спуск в исходных координатах. Еще одним аргументом в пользу изучения покоординатного спуска на примере задачи вида (1) является то, что впоследствии это дает возможность эффективно распараллелить вычисления. Если удается эффективно организовать приближенный счет функции и его градиента по ближайшим соседям, то можно на каждой итерации случайно разбивать множество точек так, чтобы в одну группу попадали близкие точки, и проводить блочно-покоординатный спуск параллельно для каждой группы [9]. В отличие от [16], в описанном ниже методе координата точки сразу после шага проектируется на поверхность сферы, а не раскладывается на нормальную и касательную составляющие.
2. МЕТОД ПЕРВОГО ПОРЯДКА
Итак, мы минимизируем функцию $3N$ переменных ${\mathbf{x}} = ({{x}_{1}},\; \ldots ,\;{{x}_{N}})$
(3)
$U({\mathbf{x}}): = {{\sum\limits_{1 \leqslant i < j \leqslant N} {\left\| {{{x}_{i}} - {{x}_{j}}} \right\|} }^{{ - s}}}$(4)
${{x}_{i}} \in {{R}^{3}},\quad {{\left\| {{{x}_{i}}} \right\|}_{2}} = 1,\quad i = 1,\; \ldots ,\;N.$Зафиксируем положения $N - 1$ точек (без $k$-й) на единичной сфере. Обозначим через
(5)
${{U}_{k}}(y,{{{\mathbf{\alpha }}}_{k}}): = {{\left. {U({\mathbf{x}})} \right|}_{{({{x}_{1}}, \ldots ,{{x}_{{k - 1}}},y,{{x}_{{k + 1}}}, \ldots ,{{x}_{N}})}}}$(6)
$y{\kern 1pt} * = \mathop {\arg \min }\limits_{y \in {{S}^{2}}} {{U}_{k}}(y,{{{\mathbf{\alpha }}}_{k}}).$Градиент и гессиан (3) можно вычислить аналитически, при $s > 0$ и $y: = {{x}_{i}}$:
(7)
$\nabla {{U}_{k}}(y,{{{\mathbf{\alpha }}}_{k}}) = - \sum\limits_{i = 1,i \ne k}^N {\frac{s}{{r_{{ik}}^{{s + 2}}}}} (y - {{x}_{i}}),$(8)
${{\nabla }^{2}}{{U}_{k}}(y,{{{\mathbf{\alpha }}}_{k}}) = s\sum\limits_{i = 1,i \ne k}^N {\frac{{ - Ir_{{ik}}^{2} + (s + 2)(y - {{x}_{i}}){{{(y - {{x}_{i}})}}^{{\text{т}}}}}}{{r_{{ik}}^{{s + 4}}}}} ,$Оценим норму гессиана (8). В силу эквивалентности норм в конечномерных пространствах ${{l}_{p}}$ и ${{l}_{q}}$ (размерность пространства $N - 1$) при $s \geqslant 1$ найдется константа $C = C(s,N)$:
(9)
$\left\| {{{\nabla }^{2}}{{U}_{k}}({{x}_{k}},{{{\mathbf{\alpha }}}_{k}})} \right\| \leqslant s(s + 1)\sum\limits_{i = 1,i \ne k}^N {\frac{1}{{r_{{ik}}^{{s + 2}}}}} \leqslant C{{\left( {\sum\limits_{i = 1,i \ne k}^N {\frac{1}{{r_{{ik}}^{s}}}} } \right)}^{{\tfrac{s}{{s + 2}}}}} = C{{(U({\mathbf{x}}))}^{{\tfrac{s}{{s + 2}}}}} = :L.$Тогда если обозначить $Q = \left\{ {{\mathbf{x}} \in \prod\nolimits_{i = 1}^N {S_{i}^{2}} :U({\mathbf{x}}) \leqslant U({{{\mathbf{x}}}^{0}})} \right\}$, то на таком множестве будет выполнено
(10)
$\left\| {\nabla {{U}_{k}}({{x}_{k}},{{{\mathbf{\alpha }}}_{k}}) - \nabla {{U}_{k}}({{y}_{k}},{{{\mathbf{\alpha }}}_{k}})} \right\| \leqslant L\left\| {{{x}_{k}} - {{y}_{k}}} \right\|\quad \forall k \in \overline {1,N} ,\quad {\mathbf{x}},{\mathbf{y}} \in Q.$Несложно показать, что минимизацией квадратичного приближения (6):
(11)
$x_{k}^{{n + 1}} = \mathop {\arg \min }\limits_{y \in {{S}^{2}}} \left\{ {{{U}_{k}}(x_{k}^{n},{\mathbf{\alpha }}_{k}^{n}) + \left\langle {\nabla {{U}_{k}}(x_{k}^{n},{\mathbf{\alpha }}_{k}^{n}),y - x_{k}^{n}} \right\rangle + \frac{L}{2}{{{\left\| {y - x_{k}^{n}} \right\|}}^{2}}} \right\}$(12)
$x_{k}^{{n + 1}} = \frac{{x_{k}^{n} - t\nabla {{U}_{k}}(x_{k}^{n},{\mathbf{\alpha }}_{k}^{n})}}{{\left\| {x_{k}^{n} - t\nabla {{U}_{k}}(x_{k}^{n},{\mathbf{\alpha }}_{k}^{n})} \right\|}},$Утверждение 1. Пусть $f({\kern 1pt} \cdot {\kern 1pt} ):{{\mathbb{R}}^{n}} \to \mathbb{R}$ дифференцируема в точке $x \in {{\mathbb{R}}^{n}}:\left\| x \right\| = 1$ и $\left\| {f{\kern 1pt} {\text{'}}(x)} \right\| \ne \left| {(f{\kern 1pt} {\text{'}}(x),x)} \right|$. Тогда существует длина шага ${{t}_{0}} > 0$, что
(13)
$f\left( {\frac{{x - {{t}_{0}}f{\kern 1pt} {\text{'}}(x)}}{{\left\| {x - {{t}_{0}}f{\kern 1pt} {\text{'}}(x)} \right\|}}} \right) < f(x).$Доказательство 1. Обозначим $y = y(x,t): = \tfrac{{x - tf{\kern 1pt} {\text{'}}(x)}}{{\left\| {x - tf{\kern 1pt} {\text{'}}(x)} \right\|}}$. В силу дифференцируемости $f({\kern 1pt} \cdot {\kern 1pt} )$:
Так как $\left\| x \right\| = 1$, то существует ${{t}_{1}} > 0:\forall t \in (0,{{t}_{1}})$Тогда $o\left( {\left\| {y - x} \right\|} \right) = o(t)$. Следовательно, найдется ${{t}_{2}} > 0$: $\forall t \in (0,{{t}_{2}})$
Определение 1. Точку ${\mathbf{x}} \in \prod\nolimits_{i = 1}^N \,S_{i}^{2}$ будем называть стационарной точкой функции $U( \cdot )$, если
В недавней работе [17] получены оценки сходимости для задачи вида (6) при некоторых предположениях. В частности, при условии липшицевости градиента на сфере метод (12) генерирует невозрастающую по функции последовательность точек. В нашем случае применим метод дробления шага, который заключается в том, чтобы уменьшать шаг ${{t}_{0}}$ вдвое, при невыполнении условия (13).
Утверждение 2. Пусть $L = C{{(U({{{\mathbf{x}}}^{0}}))}^{{\tfrac{s}{{s + 2}}}}}$ для некоторого начального положения ${{{\mathbf{x}}}^{0}}$, причем $s \geqslant 1$. Тогда последовательность точек ${\text{\{ }}{{{\mathbf{x}}}^{n}}{\text{\} }}_{{n = 1}}^{\infty }$, полученная из (12) (например, последовательным обновлением компонент ${{x}_{k}}$) методом дробления шага, монотонно $U({{{\mathbf{x}}}^{{n + 1}}}) \leqslant U({{{\mathbf{x}}}^{n}})$ $\forall n \in \mathbb{N}$ сходится к стационарной точке функции $U( \cdot )$.
Отметим, что для функции $U({\kern 1pt} \cdot {\kern 1pt} )$, условие (10) не выполнено на всем множестве $\prod\nolimits_{i = 1}^N \,S_{i}^{2}$, однако, ясно, что если (9) выполнено для некоторого ${\mathbf{x}}$, то после шага (12) данная оценка не ухудшится и (10) будет справедливо на траектории.
Итак, опишем общую структуру метода.
1. Выбрать начальное приближение ${{{\mathbf{x}}}^{0}}$.
2. Пока не достигнут критерий останова на $n$-й итерации.
2.1. Выбрать индекс $k$-й точки, которую будем изменять.
2.2. Выбрать шаг ${{t}_{0}} = 1{\text{/}}L$.
2.3. Вычислить градиент $\nabla {{U}_{k}}(x_{k}^{n},{\mathbf{\alpha }}_{k}^{n}))$ относительно $k$-й точки.
2.4. Сделать шаг (12).
2.5. Если выполнено условие (13), обновить $k$-ю компоненту ${{{\mathbf{x}}}^{n}}$.
Иначе дробить шаг ${{t}_{0}}: = {{t}_{0}}{\text{/}}2$ и перейти к п. 2.4.
3. МЕТОД ВТОРОГО ПОРЯДКА
Идея метода Ньютона и других методов второго порядка заключается в более точном приближении оптимизируемой функции квадратичной функцией вместо параболоида вращения (11), что ведет к большему выигрышу по функции на каждой итерации. Однако несмотря на быструю сходимость таких алгоритмов по количеству итераций, их главным недостатком остается сложность вычисления и обращения матрицы вторых производных. В связи с чем активно развиваются различные модификации метода Ньютона, основанные на приближенном подсчете гессиана (квазиньютоновские методы) [18], [19], а также различные покоординатные версии [20], [21]. Здесь мы остановимся на покоординатной версии метода Ньютона для оптимизации с ограничением на сфере. Разложим функцию ${{U}_{k}}(z,{{\alpha }_{k}}):{{\mathbb{R}}^{3}} \to \mathbb{R}$, зависящую только от координаты одной точки, в ряд Тейлора до второго порядка в окрестности точки ${{x}_{k}}$:
(14)
$ = \;{{U}_{k}}({{x}_{k}},{{{\mathbf{\alpha }}}_{k}}) - \nabla {{U}_{k}}({{x}_{k}},{{{\mathbf{\alpha }}}_{k}}){{x}_{k}} + \frac{1}{2}({{\nabla }^{2}}{{U}_{k}}({{x}_{k}},{{{\mathbf{\alpha }}}_{k}}){{x}_{k}},{{x}_{k}}) + \nabla {{U}_{k}}({{x}_{k}},{{{\mathbf{\alpha }}}_{k}})z - $(15)
$x_{i}^{{n + 1}} = \mathop {\arg \min }\limits_{z \in {{S}^{2}}} \left\{ {\frac{1}{2}{{z}^{{\text{т}}}}{\mathbf{A}}({{{\mathbf{x}}}^{n}})z - {{{\mathbf{b}}}^{{\text{т}}}}({{{\mathbf{x}}}^{n}})z} \right\}.$Решение данной подзадачи опирается на следующий результат.
Утверждение 3. Если ${{\lambda }_{1}} < {{\lambda }_{2}} \leqslant \; \ldots \; \leqslant {{\lambda }_{m}}$ – собственные значения матрицы ${\mathbf{A}}$, а ${{\phi }_{1}},\; \ldots ,\;{{\phi }_{m}}$ – соответствующие ортонормированные собственные векторы и ${{\beta }_{i}} = {{{\mathbf{b}}}^{{\text{т}}}}(x){{\phi }_{i}}$, $i = 1,\; \ldots ,\;m$, причем ${{\beta }_{1}} \ne 0$. Тогда $\phi = \sum\nolimits_{i = 1}^m {{{c}_{i}}} {{\phi }_{i}}$ будет решением задачи (15), если ${{c}_{i}} = \tfrac{{{{\beta }_{i}}}}{{{{\lambda }_{i}} + \mu }}$, $i = 1,\; \ldots ,\;m$, $\mu > - {{\lambda }_{1}}$, выбирается из условия
Это позволяет построить эффективный метод нахождения решения задачи (15), используя метод деления отрезка пополам. Для этого достаточно ограничить $\mu $ из утверждения (3). Поскольку $0 < {{\lambda }_{1}} + \mu < {{\lambda }_{i}} + \mu $, $1 \leqslant i \leqslant m$, то
Итак, опишем общую структуру проективного покоординатного метода Ньютона.
1. Выбрать начальное приближение ${{{\mathbf{x}}}^{0}}$.
2. Пока не достигнут критерий останова на $n$-й итерации.
2.1. Выбрать индекс $k$ точки, которую будем изменять.
2.2. Вычислить градиент $\nabla {{U}_{k}}(x_{k}^{n},{\mathbf{\alpha }}_{k}^{n}))$ и гессиан ${{\nabla }^{2}}{{U}_{k}}(x_{k}^{n},{\mathbf{\alpha }}_{k}^{n}))$.
2.3. Сделать шаг (15), обновив $k$-ю компоненту ${\mathbf{x}}$.
4. ВЫБОР НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ, БЫСТРЫЙ СЧЕТ ФУНКЦИИ И ГРАДИЕНТА
4.1. Выбор начального приближения
Функции (1), (5), как уже было отмечено, являются невыпуклыми. Более того, эти функции разрывны на своей области определения и, строго говоря, никакие проективные градиентные методы для поиска минимума здесь не применимы. Однако, если выбор шага и начальной конфигурации гарантируют, что на траектории алгоритм не попадет в область разрывов, то можно получить гарантии сходимости. Итак, при применении градиентных методов для решения (2) важную роль играет выбор начального приближения. В литературе известно множество детерминированных [22], [23] и рандомизированных [24] алгоритмов расположения точек на поверхности сферы. Один из способов – метод Монте-Карло, в котором каждый элемент ${{x}^{0}}$ выбирается из равномерного распределения на поверхности сферы. В предельном случае $N \to \infty $ метод дает равномерную плотность распределения точек на сфере. Однако данный метод имеет явный недостаток в контексте выполнения условия (10), так как положение каждой точки является независимой случайной величиной, то минимальное расстояние между любой парой точек может быть малым, что, как легко видеть из оценки (9), ведет к большой константе $L$ и медленной сходимости. В работе [25] исследован метод “generalized spiral” и поведение $U({{{\mathbf{x}}}^{0}})$ в зависимости от количества точек $N$. Данный метод стремится расположить точки в узлах правильной сферической сетки из шестиугольников (hexogonal set). Так как данный детерминированный метод ассимптотически ограничивает снизу минимальное расстояние между точками и дает разумное приближение задачи (2) по функции, ожидается, что условие (10) будет выполнено на множестве $Q$ с небольшой константой $L$.
4.2. Быстрый счет функции и градиента
В силу специфики задачи можно существенно асимптотически ускорить каждую итерацию алгоритма по сравнению с наивным подходом с помощью быстрого подсчета функции. Как видно из (1), для подсчета энергии необходимо знать лишь попарные расстояния между точками. Поэтому будем хранить в памяти матрицу расстояний. Теперь на каждой итерации (для $i$-й точки) будем обновлять энергию следующим образом: вычтем $N - 1$ слагаемое (те, которые содержат индекс $i$) до выполнения шага, а затем прибавим соответствующие слагаемые после выполнения шага. Таким образом, если положить время вычисления одного слагаемого в (1) равным $\tau $, то получим время вычисления порядка $2N\tau $ вместо ${{N}^{2}}\tau $.
Подсчет градиента на каждой итерации (т.е. для каждой точки) выполняется за линейное время по количеству точек $N$, поэтому суммарное время итерации также будет линейным. Здесь стоит отметить, что на каждой итерации мы будем хранить $N$ градиентов вида (7), упорядоченные по длине проекции на плоскость, касательную к сфере, т.е. по критерию:
(16)
$\left\| {(I - {{x}_{k}}x_{k}^{{\text{т}}})\nabla {{U}_{k}}({{x}_{k}},{{{\mathbf{\alpha }}}_{k}})} \right\|.$5. РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
Для ясности дальнейшего анализа результатов, следуя [26], введем понятие “эпоха” (epoch) – $N$ последовательных итераций покоординатного спуска, где $N$ – количество точек. Итерацией по-прежнему будем называть шаг вида (12). При сравнении с полноградиентным методом естественно сопоставить один шаг полноградиентного метода с одной эпохой покоординатного спуска.
В разд. 4 предложен способ быстрого счета функции и градиента. Время выполнения метода первого порядка при фиксированном количестве итераций определяется линейными членами по количеству точек $N$. Мы исследовали зависимость реального времени выполнения метода (от количества точек $N$), запущенного на современном ноутбуке (процессор 2.8 GHz, оперативная память 16 ГБ). Как видно из фиг. 1, гипотеза о линейности оправдана.
В предположении условия (10) было показано свойство релаксации. Интересно экспериментально выяснить скорость сходимости метода. Мы ожидаем получить сходимость по функции $U({\mathbf{x}})$ со скоростью геометрической прогрессии с параметрами $a$ и $b$:
(17)
$U({{{\mathbf{x}}}^{n}})\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \approx } aU({{{\mathbf{x}}}^{{n - 1}}}) + b$(18)
$U({{{\mathbf{x}}}^{n}})\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \approx } {{a}^{n}}U({{{\mathbf{x}}}^{0}}) + b\frac{{1 - {{a}^{{n - 1}}}}}{{1 - a}}.$Таким образом, величина $a$ приближенно равна знаменателю геометрической прогрессии, с которой убывает отклонение функции от минимального, приближенно равного $\tfrac{b}{{1 - a}}$. Для подбора параметров $a$ и $b$ используется нелинейный метод наименьших квадратов. График на фиг. 2 показывает скорость сходимости метода относительно функции (1) при $s = 1$ в режиме $epoch \leqslant N$. Это соответствует так называемому режиму “large scale” оптимизации, так как для данного покоординатного метода одна итерация оказывается в $N$ раз дешевле подсчета полного градиента. Параметры МНК и минимально найденное значение функции $U({{{\mathbf{x}}}^{n}})$ для различных $N$ указаны в табл. 1. В четвертом столбце рассчитано предельное значение аппроксимации $\tfrac{b}{{1 - a}}$, к которому ассимптотически стремится модель (17), (18). Сравнивая столбцы $U({{{\mathbf{x}}}^{n}})$ и $U({\mathbf{x}}*)$ табл. 1, можно заметить, что алгоритм достаточно близко приближается к минимально известным значениям. Различие составляет порядка 10–3%.
Таблица 1.
Параметры МНК при $s = 1$
| N | $a$ | ${{U}_{{{\text{lim}}}}}$ | $U({{{\mathbf{x}}}^{n}})$ | $U({\mathbf{x}}{\kern 1pt} *)$ | Итер. | Время, мин |
|---|---|---|---|---|---|---|
| 100 | 0.99981 | 4448.31 | 4448.49 | 4448.35 | 10 000 | 0.6 |
| 470 | 0.99997 | 104 826.19 | 104 825.40 | 104 822.89 | 220 900 | 69.5 |
| 972 | 0.99997 | 455 659.61 | 455 656.38 | 455 651.08 | 944 784 | 650.5 |
| 1300 | 0.99998 | 819 146.96 | 819 143.51 | – | 1 690 000 | 1482 |
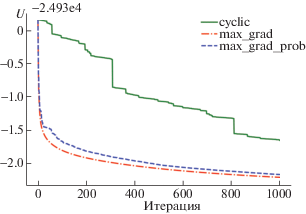
В разд. 4 также описывается возможность выбора точки для движения за время $O(N)$ на каждой итерации. На фиг. 3 изображены графики сходимости для различных стратегий при $s = 0$. Оказывается, что на начальном этапе стратегия выбора точки с максимальной проекцией градиента (max_grad) достаточно сильно обгоняет циклический перебор (cyclic). Стратегия (max_grad_prob), которая заключается в том, что точки выбираются пропорционально квадратам проекций, также оказывается достаточно хорошей. Вид графика оказывается типичным и при других $s$.
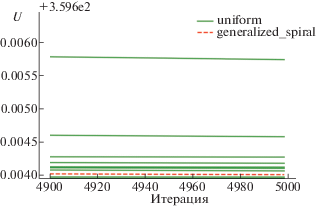
На фиг. 5 и фиг. 6 изображены графики сходимости на последних 100 из 5000 итераций для $N = 30$ для методов первого и второго порядка соответственно. Начальные положения точек генерировались методом Монте-Карло. Можно заметить, что функция (1) для $s = 1$ является многоэкстремальной уже при $N = 30$. Интересно также, что метод второго порядка намного чаще достигает глобального минимума, а метод первого порядка застревает в точках, достаточно далеких от оптимума. Прерывистыми линиями выделены графики при генерации точек методом generalized spiral.
Фиг. 4.
Сравнение полноградиентного метода с покоординатными методами с градиентным и ньютоновским шагами, N = 470, s = 1.
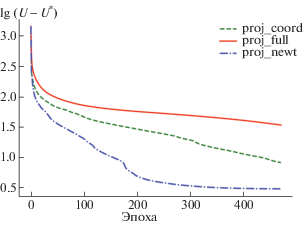
В разд. 3 предложен покоординатный аналог метода Ньютона с ограничением на сфере. Ожидается, что скорость сходимости по количеству итераций будет достаточно высокой, чтобы оправдать решение более сложной подзадачи на каждой итерации. Были проведены численные эксперименты с целью сравнить два предложенных метода в режиме $epoch \leqslant N$. На фиг. 4 изображены графики сходимости для данных двух методов и полноградиентного метода при $s = 1$. Оказывается, что время работы алгоритмов proj_newt и proj_grad в среднем отличается примерно в два раза, при этом из графиков видно, что в рассмотренном режиме proj_newt обгоняет proj_grad больше, чем в два раза по функции. То есть количество эпох, которое требуется методу proj_newt, чтобы достичь значения функции, которое достиг proj_grad за $N$ эпох меньше, чем $N{\text{/}}2$. Также можно заметить, что оба метода значительно обгоняют полноградиентный метод при рассмотрении сходимости по функции. В табл. 2 и 3 приведены результаты работы двух методов. В табл. 3 критерием останова, кроме количества итераций, задано изменение по функции на последних двух эпохах (если оно оказывается меньше ${{10}^{{ - 12}}}$, то алгоритм останавливается). Можно заметить, что метод 2 порядка (proj_newt) значительно чаще достигает меньших минимумов, при этом ему часто для этого требуется меньшее число итераций.
Таблица 2.
Результаты экспериментов при $s = 1$ для больших $N$
| N | $U({\mathbf{x}}*)$ | Минимум (метод 1) | Минимум (метод 2) | Итераций (1, 2) | Время (1), мин | Время (2), мин |
|---|---|---|---|---|---|---|
| 100 | 4448.351 | 4448.493 | 4448.450 | 10 000 | 0.7 | 2.0 |
| 200 | 18 438.843 | 18 439.644 | 18 439.156 | 40 000 | 5.3 | 9.6 |
| 312 | 45 629.314 | 45 630.736 | 45 629.926 | 97 344 | 20 | 42 |
| 400 | 75 582.449 | 75 584.100 | 75 583.854 | 160 000 | 42 | 85 |
| 470 | 104 822.886 | 1048 25.398 | 104 824.527 | 220 900 | 85 | 150 |
Таблица 3.
Результаты экспериментов при $s = 1$ для небольших $N$
| N | $U({\mathbf{x}}{\kern 1pt} *)$ | Минимум (метод 1) | Минимум (метод 2) | Итераций (1) | Итераций (2) | Время (1), сек | Время (2), сек |
|---|---|---|---|---|---|---|---|
| 2 | 0.500000000 | 0.500000000 | 0.500000000 | 56 | 9 | 0.01 | 0.01 |
| 3 | 1.732050808 | 1.732050808 | 1.732050808 | 81 | 29 | 0.02 | 0.06 |
| 4 | 3.674234614 | 3.674234614 | 3.674234614 | 94 | 36 | 0.02 | 0.08 |
| 5 | 6.474691495 | 6.474691495 | 6.474691495 | 379 | 74 | 0.10 | 0.17 |
| 6 | 9.985281374 | 9.985281374 | 9.985281374 | 287 | 90 | 0.09 | 0.17 |
| 7 | 14.452977414 | 14.452977417 | 14.452977414 | 7350 | 1911 | 2.46 | 6.02 |
| 8 | 19.675287861 | 19.675287861 | 19.675287861 | 1455 | 439 | 0.54 | 1.37 |
| 9 | 25.759986531 | 25.759986531 | 25.759986531 | 2256 | 727 | 0.94 | 2.17 |
| 10 | 32.716949460 | 32.716949460 | 32.716949460 | 2827 | 1389 | 1.30 | 4.77 |
| 11 | 40.596450508 | 40.596450508 | 40.596450508 | 3439 | 1494 | 1.73 | 5.08 |
| 12 | 49.165253058 | 49.165253058 | 49.165253058 | 630 | 353 | 0.35 | 0.99 |
| 13 | 58.853230612 | 58.853230612 | 58.853230612 | 7719 | 5354 | 4.52 | 20.54 |
| 14 | 69.306363297 | 69.306363297 | 69.306363297 | 1905 | 1266 | 1.21 | 4.39 |
| 15 | 80.670244114 | 80.670244114 | 80.670244114 | 3821 | 2066 | 2.56 | 7.76 |
| 16 | 92.911655302 | 92.920353962 | 92.920353962 | 2670 | 1981 | 1.91 | 8.92 |
| 17 | 106.050404829 | 106.050404829 | 106.050404829 | 6335 | 4067 | 4.77 | 16.18 |
| 18 | 120.084467447 | 120.084467447 | 120.084467447 | 4514 | 3711 | 3.59 | 17.08 |
| 19 | 135.089467557 | 135.089467598 | 135.089467557 | 54 150 | 54 150 | 46.95 | 282.30 |
| 20 | 150.881568334 | 150.881568334 | 150.881568334 | 9403 | 5335 | 8.46 | 24.17 |
| 21 | 167.641622399 | 167.641622399 | 167.641622399 | 32 935 | 22 896 | 31.23 | 148.31 |
| 22 | 185.287536149 | 185.287536149 | 185.287536149 | 6076 | 4306 | 5.96 | 23.12 |
| 23 | 203.930190663 | 203.930190663 | 203.930190663 | 5383 | 3439 | 5.54 | 16.05 |
| 24 | 223.347074052 | 223.347074052 | 223.347074052 | 7426 | 4837 | 7.92 | 24.45 |
| 25 | 243.812760299 | 243.812760306 | 243.812760299 | 93 750 | 76 103 | 108.55 | 442.88 |
| 26 | 265.133326317 | 265.133326317 | 265.133326317 | 45 109 | 27 332 | 52.59 | 189.53 |
| 27 | 287.302615033 | 287.302615033 | 287.302615033 | 12 481 | 7414 | 14.98 | 40.95 |
| 28 | 310.491542358 | 310.491542358 | 310.491542358 | 8950 | 5935 | 11.06 | 33.30 |
| 29 | 334.634439920 | 334.634439921 | 334.634439920 | 44 380 | 28 592 | 57.22 | 195.81 |
| 30 | 359.603945904 | 359.603945904 | 359.603945904 | 28 068 | 24 989 | 37.12 | 148.93 |
| 31 | 385.530838063 | 385.530838063 | 385.530838063 | 9762 | 4572 | 13.31 | 29.12 |
| 32 | 412.261274651 | 412.261274651 | 412.261274651 | 5476 | 3136 | 7.76 | 21.35 |
| 33 | 440.204057448 | 440.204057449 | 440.204057448 | 163 350 | 117 552 | 255.54 | 809.63 |
| 34 | 468.904853281 | 468.904853281 | 468.904853281 | 26 628 | 14 157 | 40.05 | 93.49 |
| 35 | 498.569872491 | 498.573454038 | 498.573454038 | 183 750 | 97 072 | 309.04 | 796.23 |
| 36 | 529.122408375 | 529.122408762 | 529.122408475 | 194 400 | 194 400 | 339.14 | 1710.69 |
| 37 | 560.618887731 | 560.618887731 | 560.618887731 | 39 055 | 19 634 | 63.97 | 161.08 |
| 38 | 593.038503566 | 593.038503566 | 593.038503566 | 12 768 | 6769 | 21.46 | 54.07 |
| 39 | 626.389009017 | 626.389009017 | 626.389009017 | 12 929 | 6634 | 22.17 | 48.01 |
| 40 | 660.675278835 | 660.675278835 | 660.675278835 | 15 831 | 8542 | 26.93 | 62.92 |
| 41 | 695.916744342 | 695.916744342 | 695.916744342 | 12 799 | 6691 | 22.22 | 52.37 |
| 42 | 732.078107544 | 732.078107544 | 732.078107544 | 26 700 | 14 488 | 47.95 | 98.29 |
| 43 | 769.190846459 | 769.190846460 | 769.190846460 | 213 084 | 95 671 | 436.80 | 959.87 |
| 44 | 807.174263085 | 807.174263085 | 807.174263085 | 112 652 | 40 445 | 220.13 | 400.13 |
| 45 | 846.188401061 | 846.188401062 | 846.188401062 | 303 750 | 85 123 | 711.34 | 870.44 |
| 46 | 886.167113639 | 886.170216023 | 886.171432425 | 38 313 | 26 262 | 74.65 | 210.60 |
| 47 | 927.059270680 | 927.072224565 | 927.072224565 | 164 854 | 65 438 | 357.04 | 363.51 |
| 48 | 968.713455344 | 968.713455344 | 968.713455344 | 34 190 | 16 851 | 72.21 | 152.74 |
| 49 | 1011.557182654 | 1011.557182654 | 1011.557182654 | 109 322 | 30 728 | 242.43 | 232.27 |
| 50 | 1055.182314726 | 1055.182314726 | 1055.182314726 | 32 643 | 15 879 | 72.45 | 136.42 |
$U({\mathbf{x}}{\kern 1pt} *)$ – минимально известное значение из литературы [13], [27].
Сложность задачи (2) оказывается не монотонной с точки зрения требуемого количества итераций для сходимости по функции. Так, например, при $N = 19,\;36$ обоим методам требуется значительное количество итераций, при том что задачи при $N = 20,\;37$ решаются намного быстрее.
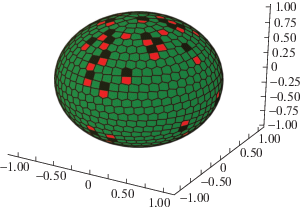
Расположение точек на сфере независимо от вида задачи (1) наглядно представляeтся с помощью сферических диаграмм Вороного. Данные диаграммы представляют собой разбиение поверхности сферы на области (многоугольники), в которых каждая точка является ближайшей к данной точке (электрону). Большинство областей – шестиугольники, многоугольники с иным числом сторон выделены цветом. Интуитивно можно ожидать, что чем меньше таких “неправильных” многоугольников, тем лучше прооптимизирована целевая функция. На фиг. 7–10 представлены диаграммы Вороного, в каждой паре слева – диаграмма при начальной генерации точек методом generalized spiral, справа – диаграмма после оптимизации с функцией (1) при $s = 1$. Отсюда можно заметить, что выбранное начальное приближение располагает точки достаточно равномерно, структура диаграмм после оптимизации согласуeтся с результатами из литературы [11], [27].
6. ЗАКЛЮЧЕНИЕ
Предложены два проективных покоординатных метода для поиска локального минимума в задаче Фекете. Алгоритмы используют быстрый счет функции, градиента и выбор наилучшей компоненты для оптимизации. Наши численные эксперименты показывают превосходство предложенных методов перед полноградиентным методом при количестве точек $N < 1000$. Можно ожидать, что предложенные методы окажутся предпочтительными для задач больших размерностей.
Список литературы
Fekete M. Über die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzagligen Koeffizienten // Mathematische Zeitschrift. 1923. V. 17. P. 228–249.
Thomson J.J. On the structure of the atom: an investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the circumference of a circle; with application of the results to the theory of atomic structure // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 1904. V. 7. P. 237–265.
Smale S. Math. problems for the next century // The Mathematical Intelligencer. 1998. V. 20. P. 7–15.
Robinson M., Suarez-Martinez I., Marks N.A. Generalized method for constructing the atomic coordinates of nanotube caps // Phys. Rev. B. 2013. V. 87. № 15. P. 155–430.
Patra M., Patriarca M., Karttunen M. Stability of charge inversion, Thomson problem, and application to electrophoresis // Physical review. E, Statistical, nonlinear, and soft matter physics. 2003. V. 67. P. 031402.
Caspar D., Klug A. Physical principles in the construction of regular viruses // Cold Spring Harbor Symposia on Quantitative Biology. 1962. V. 27. P. 1–24.
Arias E., Pérez-Torres J.F. Algorithm based on the Thomson problem for determination of equilibrium structures of metal nanoclusters // J. Chem. Phys. D. 2017.
Generalized Simulated Annealing for Global Optimization: The GenSA Package / Y. Xiang et al. // The R. J. 2013. V. 5.
Алгоритмы локальной минимизации силового поля для трехмерного представления макромолекул / П.А. Яковлев и др. // Ж. вычисл. матем. и матем. физ. 2019. Вып. 12.
Altschuler E.L., Pérez-Carrido A. New Global Mimina for Thomson’s Problem of Charges on a Sphere. 2004.
Waves D.J., McKay H., Altschuler E.L. Defect motifs for spherical topologies // Phys. Rev. B. 2009. V. 79. № 22. P. 224115.
LaFave T., Jr. Discrete Transformations in the Thomson Problem // J. Electrostatics. 2014. V. 72. P. 39–43.
Ridgway J.W., Cheviakov A.F. An iterative procedure for finding locally and globally optimal arrangements of particles on the unit sphere // Comput. Physics Commun. 2018. V. 233.
Lakhbab H., EL Bernoussi S., EL Harif A. Energy Minimization of Point Charges on a Sphere with a Spectral Projected Gradient method. 2012.
Nurmela J.K. Constructing Spherical Codes by Global Optimization Methods. 1995.
Estimation of Fekete points / E. Bendito et al. // J. Comput. Phys. 2007. V. 225. P. 2354–2376.
Polyak B.T., Balashov M.V., Tremba A.A. Gradient projection and conditional gradient methods for constrained nonconvex optimization // Numerical Functional Analysis and Optimization. 2020. P. 1–28.
Liu D.C., Nocedal J. On the limited memory BFGS method for large scale optimization // Math. Program. 1989. V. 45. P. 503–528.
A Stochastic Quasi-Newton Method for Large-Scale Optimization / H.R. Byrd et al. // SIAM Journal on Optimizat. 2014. V. 26.
Mutny M., Richtarik P. Parallel stochastic Newton method // J. Comput. Math. 2018. V. 36. P. 404.
Doikov N., Richtarik P. Randomized Block Cubic Newton Method. 2018.
Yershova A.M., LaValle S. Deterministic Sampling Methods for Spheres and SO(3) // Proc. IEEE Internat. Conference on Robotics and Automation. 2003. V. 2004.
Saff E.B., Kuijlaars A.B.J. Distributing many points on a sphere // The Math. Intelligencer. 1997. V. 19. P. 5–11.
Yershova A., LaValle S.M., Mitchell J.C. Generating Uniform Incremental Grids on SO(3) Using the Hopf Fibration // Algorithmic Foundation of Robotics VIII: Selected Contributions of the Eight International Workshop on the Algorithmic Foundations of Robotics / Ed. by G.S. Chirikjian et al. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010. P. 385–399.
Rakhmanov E., Saff B.E., Zhou M.Y. Minimal discrete energy on the sphere // Math. Research Letters. 1994. V. 1. P. 647–662.
Wright S.J. Coordinate descent algorithms // Math. Programming. 2015. V. 151. P. 3–34.
Wales D., Ulker S. Structure and dynamics of spherical crystals characterized for the Thomson problem // Phys. Rev. B. 2006. V. 74.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики