1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 5, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 5, стр. 802-814

Вычислительные алгоритмы для систем с экстрамассивным параллелизмом

В. П. Осипов 1, *, **, Б. Н. Четверушкин 1

1 ФИЦ Институт прикладной математики им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия

* E-mail: office@keldysh.ru
** E-mail: osipov@keldysh.ru

Поступила в редакцию 30.09.2019
После доработки 30.09.2019
Принята к публикации 14.01.2020

Полный текст (PDF)

Аннотация

Работа посвящена обсуждению проблем, а также некоторых возможных путей их решения, связанных с появлением в ближайшем будущем вычислительных систем сверхвысокой производительности. Приводятся примеры моделирования задач магнитной газовой динамики. Библ. 35. Фиг. 4.

Ключевые слова: высокопроизводительные вычисления, экстрамассивный параллелизм, вычислительные алгоритмы, квазигазодинамическая система уравнений, магнитная газовая динамика.

ВВЕДЕНИЕ

В настоящее время происходит бурный рост производительности вычислительной техники. Так, летом 2018 г. был достигнут рубеж в 200 PTFLOPS (PTFLOPS соответствует производительности ${{10}^{{15}}}$ операций с плавающей запятой в секунду, Summit, США). Ожидается, что в ближайшие 2–3 года будет преодолена планка производительности в 1 EXAFLOPS (1 EXAFLOPS = = 1000 PTFLOPS). Впечатляет появление в ряде стран, например, в Германии, целой группы вычислительных систем производительностью в 10 PTFLOPS и выше. Здесь речь идет о системах с уже апробированными на расчете реальных задач архитектурами. Не исключено, что через 5–7 лет придется серьезно обсуждать возможности, открываемые использованием квантовых компьютеров.

В настоящее время наша страна существенно отстает от ведущих стран в наличии вычислительных мощностей. Однако несомненно, что в силу логики научно-технического прогресса, геополитического положения России, нас ожидает быстрый рост производительности суперкомпьютерного парка.

Развитие этой в принципе дорогостоящей и энергозатратной вычислительной техники связано с теми возможностями, которые открывает ее использование. И здесь речь идет не только о научных и технологических задачах, описываемых уравнениями математической физики, но и о проблемах использования больших данных, искусственного интеллекта и связанных с ними потребностях государственного и корпоративного управления [1], [2]. (Следует отметить, что кажущаяся фантастической в настоящее время производительность в 1 EXAFLOPS вряд ли покроет потребность в детальном моделировании многих технологических задач. Так, увеличение степени детализации описания и связанное с ним увеличение аппроксимирующей разностной сетки в k-раз по каждому направлению вызовет в лучшем случае, учитывая аппроксимацию по времени, потребность в увеличении вычислительных мощностей, пропорционально ${{k}^{4}}$.)

Так, например, факторная модель [3], используемая для описания сложных процессов, опирается на поиск собственных значений матриц достаточно большой размерности [4], [5].

В данной работе не будут рассматриваться чисто технические вопросы, связанные с созданием вычислительных систем сверхвысокой производительности, например, проблемы большого энергопотребления, а также проблемы, связанные с правовыми и финансовыми аспектами использования таких вычислительных центров. Здесь остановимся на некоторых проблемах, решаемых на алгоритмической основе.

2. ЛОГИЧЕСКАЯ ПРОСТОТА – ГЛАВНОЕ ТРЕБОВАНИЕ К АЛГОРИТМАМ ДЛЯ СУПЕРВЫЧИСЛЕНИЙ

Одной из, казалось бы, парадоксальных реальностей является то, что в практике работы вычислительных центров сверхвысокой производительности количество задач, требующих для своего решения ресурса, сопоставимого с производительностью системы, невелико. Это связано с тем, что большое количество вычислительных ядер, задействованных одновременно, мешают друг другу, аналогично толпе людей, стремящихся пройти через узкую дверь.

Исключением здесь являются задачи, опирающиеся на логически простые модели, связанные, например, с переносом частиц и фотонов [6], [7]. Следовательно, для решения задач на системах с экстрамассивным параллелизмом требуются логически простые и одновременно эффективные алгоритмы. Необходимость логически простых алгоритмов важна для систем, базирующихся на процессорах CPU традиционной архитектуры, но особенно остро эта проблема встает для систем гибридной архитектуры, использующих графические платы в виде ускорителей [8].

К сожалению, одновременное выполнение требований логической простоты и вычислительной эффективности крайне редко совпадают в алгоритмах. Чтобы продемонстрировать это, рассмотрим решение систем параболических уравнений, являющихся математической моделью для многих естественно-научных и промышленных задач. Здесь достаточно вспомнить уравнения Навье–Стокса, уравнения магнитной газовой динамики с учетом магнитной вязкости, уравнение теплопроводности, диффузии и др.

Решение таких систем, например, уравнения теплопроводности

(2.1)
$\frac{{\partial T}}{{\partial t}} = \operatorname{div} K{\kern 1pt} \left( {T,{\text{\;}}\bar {x}} \right)\operatorname{grad} T + Q{\text{,}}$
где $t~$ – время, $\bar {x}$ – пространственная координата, $K{\kern 1pt} \left( {T,~\bar {x}} \right)$ – коэффициент теплопроводности, $~T$ – температура, $Q$ – заданный источник тепла, возможно двумя способами с помощью явных и неявных схем [9].

Неявные схемы обладают хорошей устойчивостью, и допустимый шаг по времени определяется только требованиями точности аппроксимации. Для их решения с помощью обращения соответствующих матриц значений функций на новом слое по времени требуется применять те или иные итерационные методы. Заметим, что аналогичные методы можно применять при обращении матриц, входящих в факторные модели [3].

Итерационные методы, обладающие хорошей скоростью сходимости, связаны с наличием достаточного количества логических переключений [9]. Они являются причиной того, что при использовании в расчете одновременно большого количества ядер эффективность параллельной обработки резко падает. (Условно в качестве такого осредненного критического количества можно назвать величину в ${{10}^{4}}$ ядер.) Исключение составляют обладающие низкой скоростью сходимости логически несложные методы, например, метод простой итерации [9].

Таким образом, детальное описание процессов, описываемых параболическими уравнениями и требующих большого количества пространственных узлов (в настоящее время до ${{10}^{{10}}}$ узлов) и соответствующего им количества ядер для проведения расчетов, сталкивается с серьезными проблемами при использовании неявных схем.

Явные схемы идеальны для адаптации к архитектуре вычислительных систем с экстрамассивным параллелизмом. Они обладают жестким условием устойчивости на допустимый шаг по времени (заметим, что для гиперболических систем первого порядка справедливо условие устойчивости Куранта $\Delta t \lesssim h~$). Это условие представляется физически оправданным, так как подробной аппроксимации по пространству должна соответствовать подробная аппроксимация по времени. Однако для параболических уравнений справедливо другое условие:

(2.2)
$\Delta t \lesssim h{{~}^{2}}{\text{\;}}{\kern 1pt} ,$

что делает их неприемлемыми при использовании аппроксимации на подробных пространственных сетках.

Таким образом, использование подробной аппроксимации, необходимой, например, при прямом моделировании турбулентности, и для которой, казалось бы, на первый взгляд, приспособлены вычислительные системы сверхвысокой производительности, при применении как явных, так и неявных схем сталкивается с серьезными трудностями.

Однако прежде чем обсудить возможность выхода из этой ситуации, обратим внимание еще на одну проблему, которая может серьезно затруднить использование вычислительных систем сверхвысокой производительности в ближайшем будущем. Эта трудность связана с проблемой отказоустойчивости при одновременном использовании большого количества процессоров [10], [11].

Суть проблемы заключается в том, что по закону больших чисел из огромного количества процессоров постоянно будут выходить из строя те или иные процессоры. И частота такой аварии будет увеличиваться с ростом числа процессоров.

Для замены выходящих из строя процессоров происходит возвращение на последнюю по времени запись данных расчета. После замены расчет продолжается, стартуя с этой записи. Однако если в ходе расчета задействовано много процессоров, то процедура возврата к фиксирующей записи будет происходить часто. Как показывают оценки [12], для вычислительных систем с производительностью в несколько экзафлопс при такой схеме замены процессоров, расчет практически не может быть осуществлен (как ожидается, эта производительность будет достигнута к середине 20-х годов нынешнего столетия). Чисто техническими средствами эта проблема в принципе не может быть решена.

В последующих разделах будет рассмотрен подход, позволяющий использовать явные схемы с более мягким условием устойчивости, чем условие (2.2). Этот подход опирается на связь между кинетическим и газодинамическим описанием сплошной среды [13], [14] и успешно применяется для моделирования задач гидро- и газодинамики [15]. Существенным здесь является замена параболической системы уравнений на гиперболическую с малым параметром при второй производной по времени [15], [16]. Помимо возможности использования явных схем при моделировании на вычислительных системах с экстрамассивным параллелизмом этот подход позволяет на алгоритмическом уровне продвинуться в решении проблемы отказоустойчивости [10].

Опишем этот подход.

3. КВАЗИГАЗОДИНАМИЧЕСКАЯ СИСТЕМА УРАВНЕНИЙ

Рассмотрим получение квазигазодинамической системы (QGS) с помощью следующей модели, описывающей поведение одночастичной функции распределения $f{\kern 1pt} \left( {t,\bar {x},\bar {\xi }} \right)$, где $\bar {\xi }$ – скорость молекулы. Рассмотрение проведем на примере пространственно-одномерного случая.

Предположим, что на момент времени ${{t}^{j}}$ существует локально-максвелловская функция распределения ${{f}_{0}}{\kern 1pt} \left( {t,x,\xi } \right)$, слабо меняющаяся на расстоянии порядка длины свободного пробега $l$

(3.1)
$f{\kern 1pt} \left( {t,x,\xi } \right) = \frac{{\rho {\kern 1pt} \left( {t,x} \right)}}{{{{{\left( {2\pi RT{\kern 1pt} \left( {t,x} \right)} \right)}}^{{3/2}}}}}e\frac{{{{{\left( {\xi - u{\kern 1pt} \left( {t,x} \right)} \right)}}^{2}}}}{{2RT}};$
здесь $\rho $ – плотность, $u$ – макроскопическая скорость, $T$ – температура, $R~$ – газовая постоянная.

Далее в течение времени $\tau $ происходит бесстолкновительный разлет частиц газа, где $\tau $ – характерное время между столкновениями молекул.

И, наконец, на момент времени ${{t}^{{j + 1}}} = {{t}^{j}} + \tau $ происходит мгновенная максвеллизация частиц газа и вся процедура повторяется вновь.

Заметим, что выбор $\tau $ в качестве шага по времени обусловлен тем, что в газовой динамике рассматривать изменение макроскопических параметров за время по порядку величины меньше, чем характерное время между столкновениями молекул, не имеет смысла. С этим и связано условие слабого изменения ${{f}_{0}}$ на расстоянии $l$.

Между значением функции распределения $f$ на новом шаге по времени ${{t}^{{j + 1}}}$ до максвеллизации и значением ${{f}_{0}}({{t}^{j}},x,\xi )$ существует соотношение

(3.2)
$f({{t}^{{j + 1}}},x,\xi ) = {{f}_{0}}({{t}^{j}},x - \tau \xi ,\xi {\text{\;}}).$
Здесь для простоты предполагается, что движение газа происходит в отсутствие поля внешних сил.

Разложим выражение (3.2) в ряд Тейлора с точностью до членов порядка $O({\text{K}}{{{\text{n}}}^{2}})$, где ${\text{Kn}}$ – число Кнудсена

(3.3)
$\frac{{{{f}^{{j + 1}}} - f_{0}^{j}}}{\tau } + \frac{{\partial \xi f_{0}^{j}}}{{\partial x}} = \frac{\partial }{{\partial x}}\frac{\tau }{2}\frac{{{{\xi }^{2}}\partial f_{0}^{j}}}{{\partial x}}.$

Умножим выражение (3.3) на сумматорные инварианты $\varphi {\kern 1pt} \left( \xi \right) = (1,\xi ,~{{\xi }^{2}}{\text{/}}2)$ и проинтегрируем по всем скоростям молекул. Учтем, что

(3.4)
$\int {f\varphi } {\kern 1pt} \left( \xi \right)d\xi = \int {{{f}_{0}}\varphi } {\kern 1pt} \left( \xi \right)d\xi {\kern 1pt} .$

Разложим временную разность значений газодинамических параметров $\phi = \left( {\rho ,u,E} \right)$, где $E$ – полная энергия с точностью до $O({\text{K}}{{{\text{n}}}^{2}})$. При этом окончательно получим квазигазодинамическую (QGS) систему уравнений, которую для простоты выпишем для пространственно-одномерного случая:

(3.5)
$\frac{{\partial \rho }}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}\rho }}{{\partial {{t}^{2}}}} + \frac{{\partial \rho u}}{{\partial x}} = \frac{\partial }{{\partial x}}\frac{\tau }{2}\frac{\partial }{{\partial x}}(\rho {{u}^{2}} + p),$
(3.6)
$\frac{{\partial \rho u}}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}\rho u}}{{\partial {{t}^{2}}}} + \frac{{\partial (\rho {{u}^{2}} + p)}}{{\partial x}} = \frac{\partial }{{\partial x}}\frac{\tau }{2}\frac{\partial }{{\partial x}}(\rho {{u}^{3}} + 3pu),$
(3.7)
$\frac{{\partial E}}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} + \frac{\partial }{{\partial x}}(u(E + p)) = \frac{\partial }{{\partial x}}{\text{\;}}\frac{\tau }{2}{\text{\;\;}}\frac{\partial }{{\partial x}}{\text{\;}}({{u}^{2}}(E + 2p)),$
где $p$ – давление. Выбор $\tau $ можно осуществить в соответствии с элементарной кинетической теорией [17]:
(3.8)
$\tau = 2\mu {\text{/}}p.$
Здесь $\mu $ – вязкость, определяемая теоретически или экспериментально. QGS отличается от традиционных уравнений Навье–Стокса прежде всего наличием вторых производных по времени и дополнительного диссипативного члена $\frac{{\partial w}}{{\partial x}}$ в правой части уравнения (3.5), являющегося следствием закона сохранения массы, где
(3.9)
$w = \frac{\tau }{2}\frac{\partial }{{\partial x}}(\rho {{u}^{2}} + p){\text{.}}$
QGS-система отличается от уравнений Навье–Стокса на члены второго порядка малости по числу Кнудсена $~O({\text{K}}{{{\text{n}}}^{2}})$. Например, дополнительные по сравнению с уравнением неразрывности
(3.10)
$\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho u}}{{\partial x}} = 0$
члены уравнения (3.5) удовлетворяют соотношению

(3.11)
$\frac{\tau }{2}\frac{{{{\partial }^{2}}\rho }}{{\partial {{t}^{2}}}} - \frac{\partial }{{\partial x}}\frac{\tau }{2}\frac{\partial }{{\partial x}}(\rho {{u}^{2}} + p) = O({\text{K}}{{{\text{n}}}^{2}}).$

Заметим, что сами уравнения Навье–Стокса получены из кинетического уравнения Больцмана с точностью до членов порядка $O({\text{K}}{{{\text{n}}}^{2}})$.

Тем самым QGS система может служить альтернативой уравнениям Навье–Стокса [15], [18], [19].

Недостатком QGS системы, наиболее отчетливо проявляющемся в ее магнитогазодинамическом варианте [20], [21], является громоздкость. Более простой по форме, сохраняющей все свойства QGS, является ее компактный вариант CQGS [22]. Расчеты и теоретические оценки для CQGS показывают фактическое отсутствие различий между ним и исходной QGS, а также уравнениями Навье–Стокса [23]. Выпишем эту систему уравнений:

(3.12)
$\frac{{\partial \rho }}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}\rho }}{{\partial {{t}^{2}}}} + {\text{div}}(\rho (\bar {u} - \bar {W})) = 0,$
(3.13)
${{W}_{i}} = \frac{1}{\rho }\frac{\tau }{2}\frac{\partial }{{\partial x}}\left( {\rho {{u}_{i}}{{u}_{k}} + {{\delta }_{{ik}}}p} \right),$
(3.14)
$\frac{{\partial \rho {{u}_{i}}}}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}\rho {{u}_{i}}}}{{\partial {{t}^{2}}}} + \frac{{\partial (\rho {{u}_{{ix}}}({{u}_{k}} - {{W}_{k}}) + p)}}{{\partial {{x}_{k}}}} = \operatorname{div} {{P}_{{NS}}}{\text{,}}$
(3.15)
$\frac{{\partial E}}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} + \operatorname{div} ((\bar {u} - \bar {W})(E + p)) = \operatorname{div} q + \operatorname{div} {{P}_{{NS}}}u,$
где ${{P}_{{NS}}}$ – тензор вязких напряжений уравнений Навье–Стокса,$~q$ – вектор теплового потока
(3.16)
${{q}_{i}} = \chi \frac{{\partial T}}{{\partial {{x}_{i}}}},$
здесь $\chi $ – коэффициент теплопроводности.

4. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ КОМПАКТНОЙ QGS

Для аппроксимации пространственных производных в CQGS системе (3.12)–(3.16) можно использовать те же самые алгоритмы, которые применялись для аппроксимации уравнений газовой динамики. Даже для аппроксимации дополнительной скорости ${{W}_{i}}$ (3.13) можно использовать алгоритмы для аппроксимации пространственных производных уравнения сохранения импульса в системе уравнений Эйлера для идеального газа. Так, в работе [23] для аппроксимации пространственных производных использовалась схема С.К. Годунова второго порядка точности.

Более интересным представляется аппроксимация по времени, учитывающая наличие вторых производных и гиперболический характер системы (3.12)–(3.16). В качестве модельного выберем уравнение гиперболической теплопроводности, достаточно широко используемое при моделировании задач физики плазмы:

(4.1)
$\frac{{\partial T}}{{\partial t}} + \tau {\text{*}}\frac{{{{\partial }^{2}}T}}{{\partial {{t}^{2}}}} = \operatorname{div} \chi \operatorname{grad} T + F.$
Здесь величина $\tau {\text{*}}$, имеющая размерность времени, выбирается из условия

(4.2)
$\left[ {\tau {\text{*}}\frac{{{{\partial }^{2}}T}}{{\partial {{t}^{2}}}}} \right] \ll \left[ {\frac{{\partial T}}{{\partial t}}} \right].$

Для аппроксимации уравнения (4.1) выберем трехслойную схему

(4.3)
$\frac{{T_{i}^{{j + 1}} - T_{i}^{{j - 1}}}}{{2\Delta t}} + \tau {\text{*}}\frac{{T_{i}^{{j + 1}} - 2T_{i}^{j} + T_{i}^{{j - 1}}}}{{\Delta {{t}^{2}}}} = \operatorname{div} \varkappa \operatorname{grad} ~{{T}^{{j{\text{\;\;}}}}} + F.$
Здесь i – совокупный индекс узлов аппроксимации по пространственным переменным, правая часть (4.3) определяется по данным на временном слое t = ${{t}^{j}}$.

Эта схема является явной. В ней значения на слое ${{t}^{{j + 1}}}$ определяются по уже известным данным на момент времени ${{t}^{j}}$ и $~{{t}^{{j - 1}}}$. Аппроксимация по времени имеет второй порядок точности. Явный характер схемы позволяет ее успешно адаптировать на архитектуры вычислительных систем с экстрамассивным параллелизмом.

Устойчивость схемы (4.3) зависит от выбора $\tau {\text{*}}$. Так, например, при выборе

(4.4)
$\tau * = h{\text{/}}с~,$
где h – характерный размер пространственной сетки, с – характерная скорость процесса, устойчивость схемы (4.3) будет определяться выражением [24]:

(4.5)
$\Delta {\tau } \lesssim {{h}^{{3/2}}}.$

Заметим, что такой выбор $\tau {\text{*}}$ гарантирует выполнение условия (4.2).

Условие устойчивости (4.5) тоже достаточно жесткое, но все же является более приемлемым, чем условие устойчивости явных схем для параболических уравнений (2.2). Особенно ярко эти преимущества в допустимом шаге по времени проявляются при использовании детальных пространственных сеток, состоящих для 3D задач из 1010 и более узлов [25]. В настоящее время использование таких сеток становится доступным при моделировании на вычислительных системах сверхвысокой производительности.

Новый гиперболический характер системы (3.11)–(3.15) открывает возможности для большого количества вариантов решения эволюционной задачи.

В частности, для ее решения можно применить характеристическо-консервативный подход [26]. Одним из возможных способов является использование представления системы (3.11)–(3.15) в виде

(4.6)
$\frac{{\partial{ \bar {Q}}}}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}\bar {Q}}}{{\partial {{t}^{2}}}} = \operatorname{div} {{\overline S }_{Q}},$
где $\bar {Q}$ – вектор газодинамических переменных, ${{\bar {S}}_{Q}}$ – поток, формируемый членами, входящими в пространственные производные, например, для плотности, когда Q эквивалентно $\rho $:

(4.7)
${{\bar {S}}_{\rho }} = \rho {{u}_{i}} - \frac{{\tau \cdot \partial (\rho {{u}_{i}}{{u}_{k}} + p)}}{{2\partial {{x}_{k}}}}.$

Систему (4.6) можно представить в виде двух уравнений:

(4.8)
$\frac{{\partial{ \bar {Q}}}}{{\partial t}} = \operatorname{div} {{\bar {\Phi }}_{Q}},$
(4.9)
$\tau {\text{*}}\frac{{\partial {{{\bar {\Phi }}}_{Q}}}}{{\partial t}} + {{\bar {\Phi }}_{Q}} = {{\bar {S}}_{Q}}.$

Систему (4.8), (4.9) можно решать с помощью явных схем следующим образом. С помощью характеристической схемы для потоковых величин $\mathop \Phi \nolimits_Q $, которые локализованы на ребрах (гранях для 3D моделирования) ячеек:

(4.10)
$\bar {\Phi }_{Q}^{{j + 1}} = \bar {\Phi }_{Q}^{j}\exp {{l}^{{{{ - \tau *} \mathord{\left/ {\vphantom {{ - \tau *} {\Delta t}}} \right. \kern-0em} {\Delta t}}}}} + \bar {S}_{Q}^{j}(1 - \exp {{l}^{{{{ - \tau *} \mathord{\left/ {\vphantom {{ - \tau *} {\Delta t}}} \right. \kern-0em} {\Delta t}}}}})$
и консервативной схемы для $\bar {Q}$:
(4.11)
$\frac{{{{{\bar {Q}}}^{{j + 1}}} - {{{\bar {Q}}}^{j}}}}{{\Delta t}} = \operatorname{div} \bar {\Phi }_{Q}^{{j + 1}},$
которая позволяет определить ${{\bar {Q}}^{{j + 1}}}$ в центре ячейки фиг. 1. После нахождения ${{Q}^{{j + 1}}}$ определяются потоки $\bar {S}_{Q}^{{j + 1}}$ на ребрах (гранях) ячеек.

Фиг. 1.

Консервативно-характеристическая схема.

Помимо представленных здесь, возможны и другие подходы к решению QGS и компактной QGS (3.12)–(3.16) систем.

Как уже отмечалось выше, данные расчетов показывают, что сколь-нибудь заметных различий, полученных на основе уравнений Навье–Стокса, QGS и компактной QGS, не существует.

Однако представляет интерес исследование средствами теоретической математики поведения решения гиперболизированной системы уравнений газовой динамики.

Как показывает анализ решения модельного параболического уравнения и гиперболического уравнения с малым параметром при второй производной по времени их разность определяется произведением квадрата этого параметра и нормой второй производной по времени исходного уравнения [27]. Эта разность может быть заметна лишь в случае высокочастотных вариаций решения по времени, которые напрямую связаны с коротковолновыми изменениями по пространству. Заметим, что в разностных схемах, как в параболическом, так и в гиперболическом вариантах эти коротковолновые вариации не описываются.

В работе [28] исследовались вопросы корректности гиперболического варианта газодинамических уравнений. Так же как и для уравнений Навье–Стокса в пространственно-двумерном случае удалось доказать единственность и существование в целом решения этой системы.

Заметим так же, что гиперболический характер QGS и компактной QGS систем позволяет продвинуться в решении проблемы отказоустойчивости актуальной для вычислительных систем сверхвысокой производительности. Здесь, используя структуру решения гиперболических уравнений, в принципе удается организовать замену вышедших из строя процессоров, не прерывая ход расчетов на базе основной массы процессоров (см. [10], [11]).

5. КВАЗИГАЗОДИНАМИЧЕСКАЯ МОДЕЛЬ ДЛЯ МАГНИТНОЙ ГАЗОВОЙ ДИНАМИКИ

Рассмотрим возможность применения кинетического подхода для описания задач магнитной гидро- и газодинамики. Учитывая, что вывод этих уравнений существенно опирается на систему уравнений Максвелла, на первый взгляд построение модели, непосредственно опирающейся на одночастичную функцию распределения, представляется затруднительным. Введем функцию [20], [21]

(5.1)
${{f}_{{OM}}} = \frac{{\rho (t,\bar {x})}}{{{{{[2\pi RT(t,\bar {x})]}}^{{3/2}}}}}\exp \left[ {\frac{{ - {{{\left\{ {{{\xi }_{k}} - {{u}_{k}}(t,\bar {x}) - i\frac{{{{B}_{k}}(t,\bar {x})}}{{\sqrt {4\pi \rho } }}} \right\}}}^{2}}}}{{2RT}}} \right],\quad k = 1,2,3.$
Здесь дополнительно использовались обозначения $\bar {B}$ – вектор напряженности магнитного поля, i – мнимая единица.

Выбор функции fOM в (5.1) для описания совокупного ансамбля заряженных и нейтральных частиц, а также магнитного поля был связан со следующими соображениями. Во-первых, величина $\frac{{\bar {B}}}{{\sqrt {4{\pi \rho }} }}$ является альфеновской скоростью, характерной для магнитной газовой динамики. Во-вторых, комплексные переменные являются удобным инструментом для описания поведения заряженных частиц в присутствии магнитного поля [29].

Во всяком случае, моменты функции fOM позволяют выразить газодинамические параметры и напряженность магнитного поля в полной аналогии с кинетической теорией газов:

(5.2)
$\rho (t,\bar {x}) = \operatorname{Re} \int {{{f}_{{OM}}}d\xi } ,$
(5.3)
$\bar {B}(t,\bar {x}) = \frac{1}{{\sqrt \rho }}\operatorname{Im} \int {\xi {\text{*}}} {{f}_{{OM}}}d\xi ,$
(5.4)
$\bar {u}(t,\bar {x}) = \frac{1}{\rho }\operatorname{Re} \int \xi {{f}_{{OM}}}d\xi ,$
(5.5)
$O = \operatorname{Im} \int {{{f}_{{OM}}}d\xi } ,$
(5.6)
$E(t,\bar {x}) = \operatorname{Re} \int {\frac{1}{2}{{\xi }^{2}}} {{f}_{{OM}}}d\xi ,$
(5.7)
$p + \frac{{{{B}^{2}}}}{{8\pi }} = \operatorname{Re} \int {{{c}^{2}}} {{f}_{{OM}}}d\xi .$
Здесь $\bar {\xi }{\text{*}}$ – комплексно-сопряженная к молекулярной скорости величина, связанная с $\bar {\xi }$ простым линейным соотношением:

(5.8)
$\bar {\xi }* = \bar {c} + \bar {u} - i\frac{{\bar {B}}}{{\sqrt {4\pi \rho } }},$
(5.9)
$\bar {c} = \bar {\xi } - \bar {u} - i\frac{{\bar {B}}}{{\sqrt {4\pi \rho } }}.$

Обратим внимание на выражение (5.5). Из него будет следовать равенство нулю дивергенции напряженности магнитного поля. Выражение (5.7) для суммы газокинетического и магнитного давления аналогично выражению

(5.10)
$p = \int {{{c}^{2}}} {{f}_{0}}d\xi $
для газодинамического давления газа, где  f0 определяется выражением (3.1).

Рассмотрим гипотетическое уравнение переноса для функции $f(t,\bar {x}~,\bar {\xi })$):

(5.11)
$\frac{{\partial f}}{{\partial t}} + {{\xi }_{k}}\frac{{\partial f}}{{\partial {{x}_{k}}}} = I\left( {f,f{\kern 1pt} {\text{'}}} \right).$

Не конкретизируя вид интеграла столкновения I, сделаем предположения, что его моменты

(5.12)
$\int {I\varphi (\xi )} d\xi = 0$
c сумматорными инвариантами $\varphi (\xi )$:
(5.13)
$\varphi (\xi ) = (1,\xi ,\xi *,{{\xi }^{2}}{\text{/}}2)$
обращаются в ноль.

Также как и при выводе уравнений Эйлера из уравнений Больцмана, умножим кинетическое уравнение (5.11) последовательно на сумматорные инварианты и проинтегрируем по пространству молекулярных скоростей ${\bar {\xi }}$:

(5.14)
$\frac{{\partial \rho }}{{\partial t}} + \operatorname{div} \rho \bar {u} = 0,$
(5.15)
$\frac{\partial }{{\partial t}}\rho {{u}_{k}} + \frac{\partial }{{\partial {{x}_{p}}}}\left[ {\left( {P + \frac{{{{B}^{2}}}}{{8\pi }}} \right){{\delta }_{{kp}}} + \rho {{u}_{k}}{{u}_{p}} - {{B}_{k}}{{B}_{p}}} \right] = 0,$
(5.16)
$\frac{{\partial E}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{k}}}}\left[ {{{u}_{k}}\left( {E + P + \frac{{{{B}^{2}}}}{{8\pi }}} \right)} \right] = 0,$
(5.17)
$\frac{{\partial {{B}_{k}}}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{k}}}}[{{u}_{k}}{{B}_{p}} - {{u}_{p}}{{B}_{k}}] = 0,$
(5.18)
$\frac{{\partial {{B}_{k}}}}{{\partial {{x}_{k}}}} = 0.$

Уравнения (5.14)–(5.18) являются уравнениями идеальной магнитной газовой динамики. Однако они получены на основе использования кинетической модели (5.11) и функции  fOM (5.1).

Аналогично описанному в разд. 3 подходу выпишем балансовое уравнение на основе функции fOM [20], [30]

(5.19)
$\frac{{{{f}^{{j + 1}}} - f_{{OM}}^{j}}}{{\widetilde \tau }} + {{\xi }_{k}}\frac{{\partial f_{{OM}}^{j}}}{{\partial {{x}_{k}}}} = \frac{\partial }{{\partial {{x}_{k}}}}\left( {\frac{{\tilde {\tau }}}{2}{{\xi }_{k}}{{\xi }_{p}}} \right)\frac{{\partial f_{{OM}}^{j}}}{{\partial {{x}_{p}}}};$
здесь в качестве $\tilde {\tau }$ при умножении (5.19) на сумматорные инварианты $\varphi (\xi ) = (1,\xi ,\xi *,{{\xi }^{2}}{\text{/}}2)$ выберем $\tau ~$ – время между столкновениями молекул, а при умножении на $\xi {\text{*}}$ в качестве $\tilde {\tau }$ выберем значение ${{\tau }_{m}}$, смысл которого поясним позднее. В результате интегрирования, а также последующего отбрасывания малых по порядку величины членов придем к магнитогазодинамическому аналогу компактной QGS (3.12)–(3.15) [22], [31]:
(5.20)
${{W}_{k}} = \frac{1}{\rho }\frac{\partial }{{\partial {{x}_{p}}}}\left[ {\left( {P + \frac{{{{B}^{2}}}}{{8\pi }}} \right){{\delta }_{{kp}}} + \rho {{u}_{k}}{{u}_{p}} - {{B}_{k}}{{B}_{p}}} \right],$
(5.21)
$\frac{{\partial \rho }}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}\rho }}{{\partial {{t}^{2}}}} + \operatorname{div} \left[ {\rho \left( {\bar {u} - \bar {w}} \right)} \right] = 0,$
(5.22)
$\frac{{\partial \rho \bar {u}}}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}\rho \bar {u}}}{{\partial {{t}^{2}}}} + {\text{div}}\left[ {\rho \bar {u} \times \left( {\bar {u} - \bar {w}} \right) + {{B}_{k}}{{B}_{p}}} \right] + \nabla \left( {P + \frac{{{{B}^{2}}}}{{8\pi }}} \right) = \operatorname{div} {{P}_{{NS}}},$
(5.23)
$\frac{{\partial E}}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} + {\text{div}}\left[ {\left( {E + P + \frac{{{{B}^{2}}}}{{8\pi }}} \right)\left( {\bar {u} - \bar {w}} \right)} \right] = \operatorname{div} q + \operatorname{div} {{P}_{{NS}}}\bar {u},$
(5.24)
$\frac{{\partial{ \bar {B}}}}{{\partial t}} + \frac{{{{\tau }_{m}}}}{2}\frac{{{{\partial }^{2}}\bar {B}}}{{\partial {{t}^{2}}}} = \operatorname{rot} \left( {\left( {\bar {u} - \bar {w}} \right) \times \bar {B} + {{\nu }_{m}}\operatorname{rot} \bar {B}} \right),$
(5.25)
$\operatorname{div} \bar {B} = 0,$
(5.26)
${{\nu }_{m}} = \frac{{{{с}^{2}}}}{{4\pi \sigma }};$
здесь с – скорость света, $\sigma $ – коэффициент электропроводности,

(5.27)
${{\tau }_{m}} = \frac{{2{{\nu }_{m}}}}{{P + \frac{{{{B}^{2}}}}{{8\pi }}}},\quad \tau = \frac{{2\mu }}{P}.$

Так же как и в компактных QGS системы (3.11)–(3.15) для аппроксимации пространственных производных можно использовать все те алгоритмы, которые ранее применялись для решения задач магнитной газовой динамики. Для аппроксимации по времени можно использовать явные схемы, например, рассмотренные в разд. 4 данной работы.

Интересной представляется связь между ${{\tau }_{m}}$ и магнитной вязкостью ${{\nu }_{m}}$. Из выражения (5.27) следует, что ${{\nu }_{m}}$ может быть определена не только следующим из элекродинамики выражением (5.26), но и как

(5.28)
${{\nu }_{m}} = \frac{{{{\tau }_{m}}\left( {P + \frac{{{{B}^{2}}}}{{8\pi }}} \right)}}{2}.$

Это выражение идентично определению молекулярной вязкости, следующему из элементарной кинетической теории [17], в котором вместо p выступает сумма газокинетического и магнитного давлений. В этом смысле ${{\tau }_{m}}$ можно трактовать по аналогии с $\tau $ как характерное время установления равновесия между магнитным полем и ансамблем, состоящим из заряженных и нейтральных частиц.

6. ПРИМЕРЫ ЧИСЛЕННОГО РАСЧЕТА

В работах [15], [22], [23] проведены многочисленные расчеты, в которых, в частности, сопоставлялись данные, полученные на основе использования уравнений Навье–Стокса и магнитной газовой динамики с данными, полученными с помощью QGS-системы в ее компактной (3.12)–(3.16) и магнитогазодинамической (5.20)–(5.27) модификации. Никаких сколь-нибудь заметных различий между этими данными расчета не обнаружено. Вместе с тем модели, построенные с помощью кинетических представлений, позволяют проводить успешное моделирование на сетках, состоящих из 1010 пространственных узлов. Так, в работах [25], [32] на таких сетках проведено моделирование поглощения массивным астрофизическим объектом вещества Галактики с образованием коллинеарной устойчивой космической струи.

В этой работе наряду с уравнениями (5.20)–(5.27) совместно решались уравнения для гравитационного потенциала $\Phi $:

(6.1)
$\Delta \Phi = 4\pi \rho .$

Уравнения (6.1), так же как и остальные уравнения системы, решались по трехслойной явной схеме:

(6.2)
$\frac{{{{\Phi }^{{j + 1}}} - {{\Phi }^{{j - 1}}}}}{{\Delta t}} + \tau {\text{*}}\frac{{{{\Phi }^{{j + 1}}} - 2{{\Phi }^{j}} + {{\Phi }^{{j - 1}}}}}{{\Delta {{t}^{2}}}} = \Delta {{\Phi }^{j}} - 4\pi {{\rho }^{j}}.$

Ниже приведен пример расчета течения несжимаемой жидкости в магнитном поле на основе использования системы (5.20)–(5.27). Краткое описание этой задачи дано в [33].

На фиг. 2 изображена двумерная расчетная область численного эксперимента.

Фиг. 2.

Расчетная область численного эксперимента. 2.5 × 2.5 см2.

Плоский прямоугольный канал сечением 2.5 × 2.5 см2 и длиной 30 см соединяется с прямоугольной каверной 2.5 × 30 × 30 см3 с последующим выходом в идентичный прямоугольный канал.

Начало входного канала длиной 10 см находится под влиянием электромагнитного поля, которое является причиной движения электропроводящей жидкости – расплавленного натрия Na.

Связь давления и плотности для замыкания системы (5.20)–(5.27) описывалась выражением:

(6.3)
$p = {{p}_{0}} + \beta (\rho - {{\rho }_{0}}).$

Большой по значению параметр $\beta ~$ отражает практическую несжимаемость среды. Как показывают ранее проведенные исследования [15], при выборе $\beta ~$ достаточно большим, его конкретное значение фактически не влияет на конечные результаты расчета. Для расчета использовалась трехслойная явная схема (см. разд. 4 данной работы).

Характеристики расплава взяты из работы [34]. Температура расплава GOOK, плотность 874 кг/м3. Показатель адиабаты $\delta = 1.2~$. Вязкость определялась в виде эмпирической зависимости:

(6.4)
$\ln \mu = - 6.44 - \ln T + {{536} \mathord{\left/ {\vphantom {{536} T}} \right. \kern-0em} T}.$

Теплопроводность и электропроводность также определены в виде эмпирических зависимостей

(6.5)
$\chi = 124 - 0.011T + 5.52 \times {{10}^{{ - 3}}}{{T}^{2}} - 1.18 \times {{10}^{{ - 8}}}{{T}^{3}},$
(6.6)
$\sigma = - 9.91 + 8.2 \times {{10}^{{ - 2}}}T - 1.32 \times {{10}^{{ - 4}}}{{T}^{2}} - 1.78 \times {{10}^{{ - 7}}}{{T}^{3}}.$

Расчетная прямоугольная сетка в 3D моделировании состояла из 200 × 2000 × 2000 узлов. Начальная скорость Na в области воздействия электромагнитного поля M = 0.15 (3.60 м/с).

На фиг. 3 изображена напряженность магнитного поля в относительных величинах.

Фиг. 3.

Начальное относительное распределение напряженности магнитного поля.

Вариации плотности, изменение которой описывается уравнением (5.21), составляло не более 0.18%, что подтверждает возможность применения данного подхода для моделирования несжимаемой жидкости. Максимальное значение скорости в области расширения канала составляло 2.70 м/с.

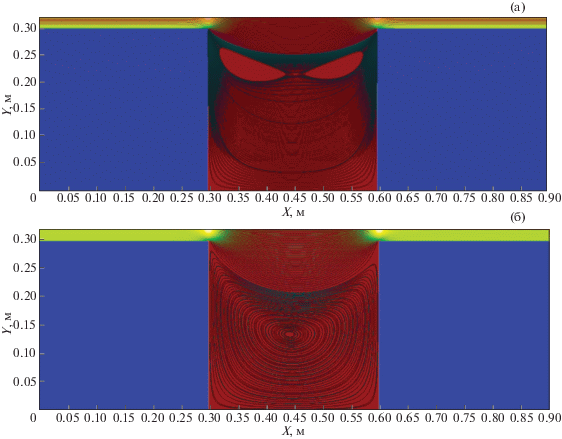
На фиг. 4а, 4б изображены линии тока натрия на различные моменты времени. Следует обратить внимание на наличие установившегося вихревого течения, характерного для течений несжимаемой жидкости в каверне [35]. Видно, что появившиеся в начальный момент вихри, впоследствии сливаются в один, что соответствует экспериментально наблюдаемой картине течения.

Фиг. 4.

Линии тока в каверне в начале процесса при t = 0.02 с (a) и линии тока в установившемся режиме при t = 0.3 c (б).

Следует отметить, что рассмотренная модель (5.20), (5.21) и алгоритм, при наличии достаточных вычислительных мощностей позволяют проводить расчеты на более подробных сетках и определять более детальную картину течения.

ЗАКЛЮЧЕНИЕ

Серьезные проблемы, возникающие при моделировании с использованием вычислительных систем сверхвысокой производительности, могут быть решены на алгоритмическом уровне, если к построению методов привлечь дополнительную информацию из смежных отраслей знания. В данном подходе активно использовалась хорошо знакомая в теоретической механике связь между кинетическим и газодинамическим описанием сплошной среды.

Использование в качестве первоосновы кинетической модели приводит к возможности описания гидро-газодинамических процессов с помощью гиперболитической системы уравнений. Ее применение в свою очередь позволяет создавать алгоритмы, адаптируемые к архитектуре вычислительных систем с экстрамассивным параллелизмом.

В заключение отметим, что данная статья, в основном, соответствует пленарному докладу, сделанному на международной конференции (июнь 2019, Москва), приуроченной к столетнему юбилею Александра Андреевича Самарского. Б.Н. Четверушкин многие годы работал в коллективе, руководимом А.А. Самарским, и влияние его научной школы во многом определило содержание данной работы.

Список литературы

  1. Четверушкин Б.Н. Суперкомпьютерные технологии: Проблемы и перспективы ближайшего будущего // Вестн. РАН. 2018. Т. 88. № 12. С. 1083–1089.

  2. Макаров В.Л., Бахтизин А.Р., Сушко Е.Д., Сушко Г.Б. Моделирование социальных процессов на суперкомпьютерах: новые технологии // Вестн. РАН. 2018. № 6. С. 508–518.

  3. Четверушкин Б.Н., Судаков В.А. Факторная модель для исследования сложных процессов. Докл. РАН. 2019. Т. 489. № 1. C. 17–21.

  4. Volkov I.I. Cesaro summation methods. Encyclopedia of Mathematics. Berlin: Springer Science + Business Media/Kluwer Acad. Publishers, 2001.

  5. Golub G.H., Van Loan C.F. Matrix Computations Baltimore Johns Hopkins University Press, 1996.

  6. Гасилов В.А., Кучугов П.А., Ольховская О.Г., Четверушкин Б.Н. Решение самосопряженного уравнения переноса излучения на гибридных вычислительных системах // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 6. С. 999–1007.

  7. Kudruashova T., Karamzin Yu., Podryga V., Polyakov S. Two-Scale commuting in multiscale problems of gas dynamics // Lobachevski J. of Mathematics. 2018. V. 39. Issue 9. P. 123–1249.

  8. Давыдов А.А., Четверушкин Б.Н., Шильников Е.В. Моделирование течений несжимаемой жидкости с слабосжимаемого газа на многоядерных гибридных вычислительных системах // Ж. вычисл. матем. и матем. физ. 2010. Т. 50. № 12. С. 2275–2284.

  9. Самарский А.А. Теория разностных схем. М.: Наука, 1977. 656 с.

  10. Четверушкин Б.Н., Якобовский М.В. Вычислительные алгоритмы и отказоустойчивость гиперэкзафлопcных вычислительных систем // Докл. АН. 2017. Т. 472. № 1. С. 1–5.

  11. Четверушкин Б.Н., Якобовский М.В. Вычислительные алгоритмы и архитектура систем высокой производительности. Препринт ИПМ им. М.В. Келдыша РАН. 2018. № 52. 12 с.

  12. Cappello F., Intern J. High Performance // Comput. Appl. 2009. V. 23. № 3. P. 212–226.

  13. Boltzmann L. Lectures on gas theory. Dover. 1964.

  14. Cercignani C. Theory and applications of the Boltzmann equations. Edinburg: Scottish Academy Press, 1988.

  15. Четверушкин Б.Н. Кинетические схемы и квазигазодинамическая система уравнений. М.: Макс Пресс, 2004.

  16. Четверушкин Б.Н., Савельев А.В., Савельев В.И. Квазигазодинамическая модель для описания магнитогазодинамических явлений // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 8. С. 1384–1394.

  17. Гиршфельдер Дж., Кертис 4, Берд Р. Молекулярная теория газов и жидкости. М.: Изд-во иностр. лит., 1961. С. 916.

  18. Злотник А.А., Четверушкин Б.Н. О балансе энтропии для одномерной гиперболической квазигазодинамической системы уравнений // Докл. АН. 2017. Т. 474. № 1. С. 22–27.

  19. Zlotnik A.A., Chetverushkin B.N. On some properties of multidimensional hyperbolic quasi-gasdynamic system of equations // Russ. J. Math. Phys. 2017. V. 24. № 3. P. 299–309.

  20. Chetverushkin B., D’Ascenzo N., Saveliev A., Saveliev V. Kinetically consistent algorithms for magneto gas dynamics // Appl. Math. Letters. 2017. V. 72. P. 75–81.

  21. Четверушкин Б.Н., Асчензо Н.Д., Савельев В.И. Математическая модель для магнитной газовой динамики // Матем. моделирование. 2017. Т. 29. № 3. С. 3–15.

  22. Четверушкин Б.Н., Савельев А.В., Савельев В.И. Компактная квазигазодинамическая система для высокопроизводительных вычислений // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 3. С. 171–178.

  23. Луцкий А.Е., Четверушкин Б.Н. Компактная квазигазодинамическая система для моделирования сжигаемого газа // Дифференц. ур-ния. 2019. Т. 55. № 4. С. 588–592.

  24. Четверушкин Б.Н., Гулин А.В. Явные схемы и моделирование на вычислительных сверхвысокой производительности // Докл. АН. 2012. Т. 446. № 5. С. 501–503.

  25. Четверушкин Б.Н., Асчензо Н.Д., Савельев В.И. Об одном алгоритме решения параболических и эллиптических уравнений // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 8. С. 1320–1328.

  26. Головизнин В.М., Четверушкин Б.Н. Новая генерация алгоритмов для вычислительной гидродинамики // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 8. С. 1217–1225.

  27. Репин С.И., Четверушкин Б.Н. Оценка разности приближенных решений задач Коши для параболического диффузного уравнения и гиперболического уравнения с малым параметром // Докл. АН. 2013. Т. 451. № 3. С. 255–258.

  28. Злотник А.А., Четверушкин Б.Н. Параболичность квазигазодинамической системы уравнений гиперболичность одной ее модификации и устойчивость малых возмущений для них // Ж. вычисл. матем. и матем. физ. 2008. Т. 49. № 3. С. 445–472.

  29. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Физматлит, 2006.

  30. Четверушкин Б.Н., Савельев В.И. Кинетические модели и высокопроизводительные вычисления. Препринт ИПМ им. М.В. Келдыша РАН, 2015. № 79.

  31. Четверушкин Б.Н., Луцкий В.Е., Осипов В.П. Законы сохранения и компактная квазигазодинамическая система // Матем. моделирование. 2019. Т. 31. № 11. С. 21–32.

  32. Четверушкин Б.Н., Асчензо Д.Н., Савельев А.В., Савельев В.И. Моделирование астрофизических явлений на основе высокопроизводительных вычислений // Докл. АН. 2017. Т. 472. № 5. С. 512–515.

  33. Четверушкин Б.Н., Савельев А.В., Савельев В.И. Компактная квазигазодинамическая система для высокопроизводительных вычислений // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 3. С. 526–533.

  34. Fink J.K., Leibowitz L. Thermodynamic and transport properties of sodium liquid and vapor. An L/Re-95/2, 1995.

  35. Chia U., Ghia K.N., Shin C.T. High –Re solutions forim-compressible flow using the Navier–Stores equations and multigrid method // J. Comput. Phys. 1982. V. 48. № 3. P. 387–411.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал