Журнал вычислительной математики и математической физики, 2020, T. 60, № 5, стр. 853-863

Исследование приближения квазипереноса в задачах с аналитическим решением

А. А. Шестаков^*

ФГУП РФЯЦ ВНИИТФ
456770 Снежинск, ул. Васильева, 13, Россия

^* E-mail: a.a.shestakov2012@yandex.ru

Поступила в редакцию 05.10.2019
После доработки 05.10.2019
Принята к публикации 14.01.2020

DOI: 10.31857/S0044466920050154

Аннотация

Квазипереносное приближение сводит численное решение кинетического уравнения к решению диффузионного уравнения через введение корректирующих коэффициентов. Переход к диффузионному уравнению упрощает численное решение кинетического уравнения и дает возможность использовать монотонные схемы второго порядка точности при решении задач переноса теплового излучения. При этом очень важно знать, как ведут себя корректирующие коэффициенты, потому что для корректности диффузионного уравнения обязательным является требование положительности коэффициента диффузии. Наиболее просто это проверить в задачах, имеющих аналитические решения. Целью данной работы является исследование приближения квазипереноса в задачах с аналитическим решением и поведения корректирующих коэффициентов в оптически плотных и прозрачных средах. Библ. 7. Фиг. 7.

Ключевые слова: перенос теплового излучения, приближения уравнения переноса.

ВВЕДЕНИЕ

При решении системы уравнений переноса теплового излучения (СУПТИ) применяют различные упрощающие приближения, сводящие задачу переноса излучения к более простой. Большая часть этих приближений не использует решение кинетического уравнения, но некоторые из них используют решение кинетического уравнения для получения вспомогательных осредненных коэффициентов, которые называются корректирующими. Приближения, которые не используют решение кинетического уравнения, дешевле по времени счета и объему занимаемой памяти ЭВМ, но имеют ограничения по областям применения. Приближения, которые используют решение кинетического уравнения, дороже и сложнее в реализации, но не имеют ограничений по областям применения. К таким приближениям относятся, в первую очередь, квазидиффузионное приближение (КД), предложенное В.Я. Гольдиным в 1964 г. [1], и квазипереносные приближения (КП), предложенные Н.Г. Карлыхановым и М.Ю. Козмановым в 2010 г. [2]. Эти приближения получили дальнейшее развитие, в частности, в работах [3]–[8 ].

При построении КД и КП приближений решение СУПТИ разбивается на два этапа. На первом этапе в этих приближениях решается кинетическое уравнение для получения корректирующих коэффициентов. На втором этапе решается квазидиффузионное или диффузионное уравнениe для получения основных величин: температуры, плотности и потока излучения. В этих приближениях при решении задач СУПТИ приходится применять итерационные процессы по нелинейности коэффициента поглощения, внутренней энергии вещества, функции Планка, расщеплению многомерных уравнений. Замечательным свойством КД и КП приближений является то, что в них не требуется согласованность схем на этапах, и вся тяжесть итерационных процессов переносится на второй, более простой этап, который считается с корректирующими коэффициентами, при этом кинетическое уравнение обычно решается один раз на временном шаге.

Приближение КП сводит численное решение кинетического уравнения к решению диффузионного уравнения через введение корректирующих коэффициентов. Переход к диффузионному уравнению упрощает численное решение кинетического уравнения и дает возможность использовать монотонные схемы второго порядка точности при решении задач переноса теплового излучения. При этом очень важно знать, как ведут себя эти коэффициенты. Потому что для корректности диффузионного уравнения обязательным является требование положительности коэффициента диффузии. При отрицательных корректирующих коэффициентах решение становится неустойчивым. Наиболее просто исследовать поведение корректирующих коэффициентов в задачах, имеющих точные решения, так как в этом случае коэффициенты вычисляются аналитически. Задачи переноса излучения можно условно разбить на три группы: перенос излучения в оптически плотных средах, в оптически прозрачных средах и задачи, включающие комбинации из оптически плотных и прозрачных сред. Для первой группы задач во втором разделе статьи через асимптотическое разложение при коэффициенте ослабления ${{\alpha }_{\nu }} \to \infty $ будет показано, что корректирующие коэффициенты не отрицательны в этих задачах. Для второй и третьей групп в общем случае это показать не удается, поэтому для них будут рассмотрены три задачи, имеющие точные решения.

Первая задача, взятая для исследований из работы [4], имеет стационарное решение в вакууме. Вторая задача имеет в вакууме нестационарное решение, полученное А.В. Вронским. Обе задачи описывают перенос излучения в сферически-симметричной геометрии.

Третья задача описывает прохождение излучения через оптически плотную и прозрачную среды [5] и имеет точное решение на стационаре в плоской геометрии [6].

Для сравнения во всех задачах приводится вид коэффициента КД.

1. ПОСТАНОВКА ЗАДАЧИ

На первом этапе в КД и КП приближениях решается кинетическое уравнение для получения корректирующих коэффициентов. В сферически-симметричном и плоском случаях без учета движения среды для изотропного рассеяния кинетическое уравнение выглядит следующим образом:

(1.1)

$\frac{1}{c}\frac{{\partial {{J}_{\nu }}}}{{\partial t}} + {\mathbf{\Omega }}\nabla {{J}_{\nu }} + {{\alpha }_{\nu }}{{J}_{\nu }} = \frac{1}{2}{{\alpha }_{{c\nu }}}{{B}_{\nu }} + \frac{1}{2}{{\alpha }_{{s\nu }}}{{U}_{\nu }}.$

Здесь ${{J}_{\nu }}(r,\mu ,\nu ,t)$ – спектральная интенсивность излучения, умноженная на 2π, c – скорость света, r – пространственная координата, t – время, ν – частота фотонов, μ – косинус угла между направлением полета фотона ${\mathbf{\Omega }}$ и осью r, ${{\alpha }_{\nu }} = {{\alpha }_{{c\nu }}} + {{\alpha }_{{s\nu }}}$ – коэффициент ослабления, ${{\alpha }_{{c\nu }}}$ – коэффициент поглощения, ${{\alpha }_{{s\nu }}}$ – коэффициент рассеяния, ${{B}_{\nu }}(\nu ,T)$ – плотность равновесного излучения, умноженная на с, $T(r,t)$ – температура среды,

${{U}_{\nu }} = \int\limits_{ - 1}^1 {{{J}_{\nu }}d\mu } $

есть спектральная плотность энергии излучения, умноженная на с,

${\mathbf{\Omega }}\nabla {{J}_{\nu }} = \frac{\mu }{{{{r}^{\eta }}}}\frac{\partial }{{\partial r}}({{r}^{\eta }}{{J}_{\nu }}) + \frac{\eta }{{2r}}\frac{\partial }{{\partial \mu }}((1 - {{\mu }^{2}}){{J}_{\nu }}),$

η – параметр геометрии (0 – плоская, 2 – сферически-симметричная).

На втором этапе в КД приближении решается система

(1.2)

$\begin{gathered} \frac{1}{c}\frac{{\partial {{U}_{\nu }}}}{{\partial t}} + \frac{1}{{{{r}^{\eta }}}}\frac{{\partial ({{r}^{\eta }}{{S}_{\nu }})}}{{\partial r}} + {{\alpha }_{{c\nu }}}{{U}_{\nu }} = {{\alpha }_{{c\nu }}}{{B}_{\nu }}, \\ \frac{1}{c}\frac{{\partial {{S}_{\nu }}}}{{\partial t}} + \frac{{\partial {{D}_{\nu }}{{U}_{\nu }}}}{{\partial r}} + \frac{\eta }{2}\frac{{2{{D}_{\nu }} - 1}}{r}{{U}_{\nu }} + {{\alpha }_{\nu }}{{S}_{\nu }} = 0, \\ \end{gathered} $

где ${{S}_{\nu }} = \int_{ - 1}^1 {\mu {{J}_{\nu }}d\mu } $ – спектральный поток излучения,

${{D}_{\nu }} = {{\left( {\int\limits_{ - 1}^1 {{{J}_{\nu }}d\mu } } \right)}^{{ - 1}}}\int\limits_{ - 1}^1 {{{\mu }^{2}}{{J}_{\nu }}d\mu } $

есть коэффициент КД.

В работе [2] для КП приближения предложено два варианта. В первом варианте решается система

$\frac{1}{c}\frac{{\partial {{U}_{\nu }}}}{{\partial t}} + \frac{1}{{{{r}^{\eta }}}}\frac{{\partial ({{r}^{\eta }}{{S}_{\nu }})}}{{\partial r}} + {{\alpha }_{{c\nu }}}{{U}_{\nu }} = {{\alpha }_{{c\nu }}}{{B}_{\nu }},$

$\frac{1}{3}\frac{{\partial {{U}_{\nu }}}}{{\partial r}} + ({{\alpha }_{{s\nu }}} + {{\alpha }_{{c\nu }}} + {{\alpha }_{{k\nu }}}){{S}_{\nu }} = 0,$

где

(1.3)

${{\alpha }_{{k\nu }}} = {{\left( {\int\limits_{ - 1}^1 {\mu {{J}_{\nu }}d\mu } } \right)}^{{ - 1}}}\left[ {\frac{1}{c}\frac{\partial }{{\partial t}}\left( {\int\limits_{ - 1}^1 {\mu {{J}_{\nu }}d\mu } } \right) + \frac{\partial }{{\partial r}}\left[ {\left( {{{D}_{\nu }} - \frac{1}{3}} \right)\int\limits_{ - 1}^1 {{{J}_{\nu }}d\mu } } \right] + \frac{\eta }{{2r}}(3{{D}_{\nu }} - 1)\int\limits_{ - 1}^1 {{{J}_{\nu }}d\mu } } \right]$

есть корректирующий коэффициент.

Во втором варианте решается система

$\frac{{{{m}_{\nu }}}}{3}\frac{{\partial {{U}_{\nu }}}}{{\partial r}} + {{\alpha }_{\nu }}{{S}_{\nu }} = 0,$

где

(1.4)

${{m}_{\nu }} = - {{\left( {\frac{1}{{3{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\int\limits_{ - 1}^1 {{{J}_{\nu }}d\mu } } \right)}^{{ - 1}}}\int\limits_{ - 1}^1 {\mu {{J}_{\nu }}d\mu } $

есть корректирующий коэффициент.

Недостатком первого варианта КП приближения является необходимость вычислять коэффициенты КД, которые в многомерной геометрии имеют сложный тензорный вид. Этого можно избежать, если доказать эквивалентность первого и второго вариантов КП приближения, так как во втором варианте для определения корректирующего коэффициента достаточно знать плотность и поток излучения.

Для доказательства эквивалентности первого и второго вариантов КП приближения запишем корректирующий коэффициент ${{\alpha }_{{k\nu }}}$ в виде

(1.5)

${{\alpha }_{{k\nu }}} = S_{\nu }^{{ - 1}}\left[ {\left( {\frac{1}{c}\frac{{\partial {{S}_{\nu }}}}{{\partial t}} + \frac{{\partial {{D}_{\nu }}{{U}_{\nu }}}}{{\partial r}} + \frac{\eta }{2}\frac{{3{{D}_{\nu }} - 1}}{r}{{U}_{\nu }} + {{\alpha }_{\nu }}{{S}_{\nu }}} \right) - \left( {\frac{1}{3}\frac{{\partial {{U}_{\nu }}}}{{\partial r}} + {{\alpha }_{\nu }}{{S}_{\nu }}} \right)} \right] = {{\alpha }_{\nu }}\left( {\frac{1}{{{{m}_{\nu }}}} - 1} \right).$

Здесь использовано равенство нулю первого слагаемого, совпадающего со вторым уравнением системы (1.2).

Подставляя выражение (1.5) во второе уравнение системы (1.3), получаем второе уравнение системы (1.4). Эквивалентность первого и второго вариантов КП приближения доказана. При этом использование выражения (1.5) для получения корректирующего коэффициента ${{\alpha }_{{k\nu }}}$ не требует вычисления коэффициентов КД. В вакууме при ${{\alpha }_{\nu }}$ = 0 получаем ${{\alpha }_{{k\nu }}} = - \frac{1}{{3{{S}_{\nu }}}}\frac{{\partial {{U}_{\nu }}}}{{\partial r}}.$

Совместно с уравнениями в КД и КП приближениях решается уравнение энергии

$\frac{{\partial E}}{{\partial t}} = \int_0^\infty {{{\alpha }_{{c\nu }}}({{U}_{\nu }} - {{B}_{\nu }})d\nu } ,$

где E – внутренняя энергия вещества.

2. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КОРРЕКТИРУЮЩИХ КОЭФФИЦИЕНТОВ В КД И КП ПРИБЛИЖЕНИЯХ

Следуя работе [7], точное значение интенсивности в плоском стационарном случае оптически плотных сред можно записать в виде бесконечного ряда

${{J}_{\nu }} = \frac{1}{2}\sum\limits_{n = 0}^\infty {{{{( - 1)}}^{n}}{{{({\mathbf{\Omega }},\alpha _{\nu }^{{ - 1}}\nabla )}}^{n}}{{B}_{\nu }}} = \frac{1}{2}\left\{ {{{B}_{\nu }} - \frac{\mu }{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}} + \frac{{{{\mu }^{2}}}}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right)} \right. - \left. {\frac{{{{\mu }^{3}}}}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left[ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right)} \right] + \ldots } \right\}.$

Для плотности, потока и давления излучения точное решение имеет вид

${{U}_{\nu }} = \int\limits_{ - 1}^1 {{{J}_{\nu }}d\mu } = {{B}_{\nu }} + \frac{1}{{3{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right) + \frac{1}{{5{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left\{ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left[ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right)} \right]} \right\} + \ldots = {{B}_{\nu }} - \frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{S}_{\nu }}}}{{\partial r}},$

${{S}_{\nu }} = \int\limits_{ - 1}^1 {\mu {{J}_{\nu }}d\mu } = - \frac{2}{{3{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}} - \frac{1}{{5{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left[ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right)} \right] - \ldots = - \frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{P}_{\nu }}}}{{\partial r}},$

${{P}_{\nu }} = \int\limits_{ - 1}^1 {{{\mu }^{2}}{{J}_{\nu }}d\mu } = \frac{1}{3}{{B}_{\nu }} + \frac{1}{{5{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right) + \frac{1}{{7{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left\{ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left[ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right)} \right]} \right\} + \ldots \;\,.$

При ${{\alpha }_{\nu }}$ = const можно получить следующие зависимости этих величин от спектрального пробега излучения ${{l}_{\nu }} = \alpha _{\nu }^{{ - 1}}$:

${{J}_{\nu }} = \frac{1}{2}{{B}_{\nu }} + O({{l}_{\nu }}),\quad {{U}_{\nu }} = {{B}_{\nu }} + {{O}_{1}}(l_{\nu }^{2}),\quad {{S}_{\nu }} = - \frac{1}{{3{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}} + {{O}_{2}}(l_{\nu }^{3}),\quad {{P}_{\nu }} = \frac{1}{3}{{B}_{\nu }} + {{O}_{3}}(l_{\nu }^{2}).$

Из этих формул видно, что при ${{\alpha }_{\nu }} \to \infty $ получаем условия локального термодинамического равновесия:

${{J}_{\nu }} \to \frac{1}{2}{{B}_{\nu }},\quad {{U}_{\nu }} \to {{B}_{\nu }},\quad {{S}_{\nu }} \to 0,\quad {{P}_{\nu }} \to \frac{1}{3}{{B}_{\nu }}.$

Для коэффициентов КД и КП получаем

(2.1)

${{D}_{\nu }} = \frac{{{{P}_{\nu }}}}{{{{U}_{\nu }}}} = \frac{1}{3}\frac{{{{B}_{\nu }} + \frac{3}{{5{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right) + \frac{3}{{7{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left\{ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left[ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right)} \right]} \right\} + \ldots }}{{{{B}_{\nu }} + \frac{1}{{3{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right) + \frac{1}{{5{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left\{ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left[ {\frac{1}{{{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right)} \right]} \right\} + \ldots }} = \frac{1}{3} + {{O}_{4}}(\alpha _{\nu }^{{ - 2}}),$

(2.2)

${{m}_{\nu }} = - \frac{{{{S}_{\nu }}}}{{\frac{1}{{3{{\alpha }_{\nu }}}}\frac{{\partial {{U}_{\nu }}}}{{\partial r}}}} = \frac{{\frac{{\partial {{P}_{\nu }}}}{{\partial r}}}}{{\frac{{\partial {{U}_{\nu }}}}{{\partial r}}}} = \frac{{\frac{{\partial {{P}_{\nu }}}}{{\partial r}}}}{{\frac{{\partial {{B}_{\nu }}}}{{\partial r}} - \frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{S}_{\nu }}}}{{\partial r}}} \right)}} = \frac{{\frac{\partial }{{\partial r}}\left\{ {{{B}_{\nu }} + \frac{3}{{5{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right) + \ldots } \right\}}}{{\frac{\partial }{{\partial r}}\left\{ {{{B}_{\nu }} + \frac{1}{{3{{\alpha }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\alpha }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right) + \ldots } \right\}}} = 1 + {{O}_{5}}(\alpha _{\nu }^{{ - 2}}),$

(2.3)

${{\alpha }_{{\nu k}}} = {{\alpha }_{\nu }}\left( {\frac{1}{{{{m}_{\nu }}}} - 1} \right) = {{O}_{6}}(\alpha _{\nu }^{{ - 1}}).$

Из этих формул видно, что при ${{\alpha }_{\nu }} \to \infty $ получаем ${{D}_{\nu }} \to 1{\text{/}}3$, ${{m}_{\nu }} \to 1$, ${{\alpha }_{{\nu k}}} \to 0$. Таким образом, коэффициенты ${{D}_{\nu }}$ и ${{m}_{\nu }}$ стремятся к постоянным положительным значениям, а порядок сходимости этих коэффициентов совпадает с порядком сходимости ${{U}_{\nu }}$ и ${{P}_{\nu }}$ к равновесным величинам. Порядок сходимости коэффициента ${{\alpha }_{{\nu k}}}$ ниже и совпадает с порядком сходимости ${{J}_{\nu }}$ и ${{S}_{\nu }}$ к равновесным значениям. То есть в оптически плотных средах решение кинетического уравнения стремится к решению диффузионного уравнения.

Полученные зависимости справедливы для всех решений уравнения переноса в случае оптически плотных сред. Рассмотрим поведение корректирующих коэффициентов в оптически прозрачных средах.

3. СРАВНЕНИЕ КОЭФФИЦИЕНТОВ В КД И КП ПРИБЛИЖЕНИЯХ НА АНАЛИТИЧЕСКИХ РЕШЕНИЯХ

В КП приближении при вычислении корректирующего коэффициента ${{m}_{\nu }}$ возникает особенность в оптически прозрачных средах при ${{\alpha }_{\nu }} \to 0$. Если в этом случае второе уравнение системы (1.4) записать в виде закона Фика ${{S}_{\nu }} = - {{\chi }_{\nu }}\frac{{\partial {{U}_{\nu }}}}{{dr}}$, где

${{\chi }_{\nu }} = \frac{{{{m}_{\nu }}}}{{3{{\alpha }_{\nu }}}} = - {{\left( {\frac{\partial }{{\partial r}}\int\limits_{ - 1}^1 {{{J}_{\nu }}d\mu } } \right)}^{{ - 1}}}\int\limits_{ - 1}^1 {\mu {{J}_{\nu }}d\mu } ,$

то можно заметить, что коэффициент ${{\chi }_{\nu }}$ не зависит от ${{\alpha }_{\nu }}$. Тогда в оптически прозрачных средах при ${{\alpha }_{\nu }}$ = 0 в системе (1.4) можно пользоваться формулой ${{S}_{\nu }} = - {{\chi }_{\nu }}\frac{{\partial {{U}_{\nu }}}}{{\partial r}}$ вместо второго уравнения системы (1.4). В отличие от диффузионного приближения, где коэффициент диффузии ${{\chi }_{{\operatorname{dif} ,\nu }}} = \frac{1}{{3{{\alpha }_{\nu }}}}$ стремится к бесконечности при ${{\alpha }_{\nu }} \to 0$, в КП приближении этого не происходит. Из условия корректности диффузионных уравнений на коэффициент ${{\chi }_{\nu }}$ накладывается требование положительности. Возникает вопрос, как часто оно может нарушаться при ${{\alpha }_{\nu }} = 0$? Для этого в данной работе рассмотрено поведение коэффициента ${{\chi }_{\nu }}$ в вакууме на двух задачах, имеющих аналитические решения. Проведено также сравнение корректирующих коэффициентов в системах (1.2), (1.3) в реальной среде, состоящей из оптически плотных и прозрачных веществ.

Задача 1. Первая задача описывает перенос излучения в вакууме от сферы радиуса r с постоянным граничным условием $J({{r}_{L}},\mu ) = {{I}_{L}}$ = const для выходящих фотонов и имеет точное решение вида

$J(r,\mu ) = \left\{ \begin{gathered} 0,\quad - {\kern 1pt} 1 \leqslant \mu < 0, \hfill \\ 0,\quad 0 \leqslant \mu \leqslant {{\mu }_{0}}(r),\quad \mu _{0}^{2} = 1 - \frac{{r_{L}^{2}}}{{{{r}^{2}}}},\quad {{\mu }_{0}}({{r}_{L}}) = 0, \hfill \\ {{I}_{L}},\quad {{\mu }_{0}}(r) \leqslant \mu \leqslant 1, \hfill \\ \end{gathered} \right.$

$U(r) = {{I}_{L}}\int\limits_{{{\mu }_{0}}}^1 {d\mu } = {{I}_{L}}(1 - {{\mu }_{0}}),$

$S(r) = {{I}_{L}}\int\limits_{{{\mu }_{0}}}^1 {\mu d\mu } = \frac{{{{I}_{L}}}}{2}(1 - \mu _{0}^{2}),\quad 0 \leqslant {{\mu }_{0}} \leqslant 1.$

Отсюда получаем корректирующие коэффициенты в КД и КП приближениях:

(3.1)

$\begin{gathered} D(r) = {{\left( {{{I}_{L}}\int\limits_{{{\mu }_{0}}}^1 {d\mu } } \right)}^{{ - 1}}}{{I}_{L}}\int\limits_{{{\mu }_{0}}}^1 {{{\mu }^{2}}d\mu } = \frac{{1 - \mu _{0}^{3}}}{{3(1 - {{\mu }_{0}})}} = \frac{1}{3}(1 + {{\mu }_{0}} + \mu _{0}^{2}) = \frac{1}{3}\left( {2 - \frac{{r_{L}^{2}}}{{{{r}^{2}}}} + \sqrt {1 - \frac{{r_{L}^{2}}}{{{{r}^{2}}}}} } \right), \\ \chi = - {{\left( {\frac{\partial }{{\partial r}}\int\limits_{ - 1}^1 {Jd\mu } } \right)}^{{ - 1}}}\int\limits_{ - 1}^1 {\mu Jd\mu } = - {{\left( {\frac{{\partial U}}{{\partial r}}} \right)}^{{ - 1}}}S = \frac{{r{{\mu }_{0}}}}{2} = \frac{1}{2}\sqrt {{{r}^{2}} - r_{L}^{2}} ,\quad {{\alpha }_{k}} = \frac{1}{{3\chi }}. \\ \end{gathered} $

Из этих формул следует, что в данной задаче выполняются условия положительности коэффициентов: $1{\text{/}}3 \leqslant D \leqslant 1$, ${{\alpha }_{k}} \geqslant 0$, $\chi \geqslant 0$.

На фиг. 1 приведены профили коэффициентов КД и КП при r = 1 см, 1 см ≤ r ≤ 2 см.

Фиг. 1.

Профили коэффициентов КД и КП.

Из рисунка видно, что коэффициенты КД и КП являются непрерывными, положительными и монотонными функциями от r. При r → r_L получаем D → 1/3, χ → 0, α_k → ∞. При r → ∞ получаем D → 1, χ → ∞, α_k → 0.

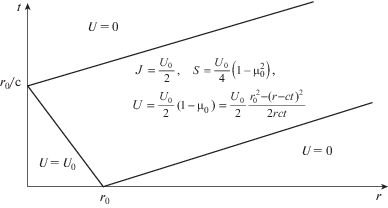
Задача 2. Вторая задача описывает поведение коэффициентов КД и КП в нестационарном случае. Задача описывает остывание в вакууме фотонного шара радиуса r₀ с постоянным начальным распределением $J = \frac{{{{U}_{0}}}}{{4\pi }}$. В результате остывания фотонного шара в центре со временем появляется вакуумный шар, который расширяется со скоростью света:

$J(r,t,\omega ) = \left\{ \begin{gathered} \frac{{{{U}_{0}}}}{{4\pi }}\quad {\text{в}}\;{\text{телесном}}\;{\text{угле}}\;\Delta \omega (r,t), \hfill \\ 0\quad {\text{вне}}\;{\text{угла}}\;\Delta \omega (r,t), \hfill \\ \end{gathered} \right.$

$\Delta \omega = 2\pi (1 - {{\mu }_{0}}) = \pi \frac{{r_{0}^{2} - {{{(r - ct)}}^{2}}}}{{rct}},$

$U(r,t) = \frac{{\Delta \omega }}{{4\pi }}{{U}_{0}}.$

В осесимметричной и сферически-симметричной геометриях можно не учитывать распределение по углу 0 ≤ φ ≤ 2π и рассматривать начальное распределение в виде

$J(t = 0,r) = {{I}_{L}} = \frac{{{{U}_{0}}}}{2}$

для системы (1.1). В сферически-симметричном случае точное решение можно записать в виде

$J(r,t,\mu ) = \left\{ \begin{gathered} {{I}_{L}}\quad {\text{при}}\quad {{\mu }_{0}} < \mu < 1, \hfill \\ 0\quad {\text{при}}\quad - {\kern 1pt} 1 < \mu < {{\mu }_{0}}, \hfill \\ \end{gathered} \right.$

${{\mu }_{0}} = - \frac{{r_{0}^{2} - {{r}^{2}} - {{c}^{2}}{{t}^{2}}}}{{2rct}},\quad - {\kern 1pt} 1 \leqslant {{\mu }_{0}} \leqslant 1,$

$U(r,t) = \frac{{{{U}_{0}}}}{2}\left\{ \begin{gathered} 2\quad {\text{при}}\quad 0 < ct < {{r}_{0}} - r, \hfill \\ 1 - {{\mu }_{0}}\quad {\text{при}}\quad {{r}_{0}} - r \leqslant ct < {{r}_{0}} + r, \hfill \\ 0\quad {\text{при}}\quad ct \geqslant {{r}_{0}} + r. \hfill \\ \end{gathered} \right.$

Для ct < r₀ получаем

$U(r,t) = \frac{{{{U}_{0}}}}{2}\left\{ \begin{gathered} 0\quad {\text{при}}\quad 0 < ct < r - {{r}_{0}}, \hfill \\ 1 - {{\mu }_{0}}\quad {\text{при}}\quad r - {{r}_{0}} \leqslant ct < {{r}_{0}} + r, \hfill \\ 0\quad {\text{при}}\quad ct \geqslant {{r}_{0}} + r, \hfill \\ \end{gathered} \right.$

для ct ≥ r₀ получаем

$S(r,t) = \frac{{{{U}_{0}}}}{4}\left\{ \begin{gathered} 0\quad {\text{при}}\quad 0 < ct < r - {{r}_{0}}, \hfill \\ 1 - \mu _{0}^{2}\quad {\text{при}}\quad r - {{r}_{0}} \leqslant ct < {{r}_{0}} + r, \hfill \\ 0\quad {\text{при}}\quad ct \geqslant {{r}_{0}} + r. \hfill \\ \end{gathered} \right.$

Решение данной задачи проиллюстрировано в фазовой плоскости (r, t) на фиг. 2, откуда видно, что вся область (r, t) разбивается на четыре подобласти.

Фиг. 2.

Решение в фазовой плоскости (r, t).

В данной задаче есть области, в которых при вычислении коэффициентов КД и КП возникают неопределенности типа 0/0. Анализ поведения коэффициентов КД и КП в пограничных точках помогает выбрать их значения так, чтобы сохранить непрерывность этих величин в таких ситуациях. К сожалению, это не удается сделать только для коэффициента ${{\alpha }_{k}}$, который неограниченно растет у границ подобластей. Поэтому во избежание бесконечно больших значений ${{\alpha }_{k}}$ при численных расчетах можно из выражения (3.1) полагать ${{\alpha }_{k}} = 1{\text{/}}3{{\chi }_{{\min }}}$, где минимальное положительное значение коэффициента ${{\chi }_{{\min }}}$ можно выбирать с точностью до “машинного нуля”.

С учетом этих предположений коэффициенты КД и КП имеют вид

$D(r,t) = \left\{ \begin{gathered} \frac{1}{3}\quad {\text{при}}\quad ct < {{r}_{0}} - r, \hfill \\ {{D}_{0}}\quad {\text{при}}\quad {{r}_{0}} - r \leqslant ct < {{r}_{0}} + r, \hfill \\ 0\quad {\text{при}}\quad ct \geqslant {{r}_{0}} + r, \hfill \\ \end{gathered} \right.$

${{D}_{0}} = \frac{1}{3}\frac{{1 - \mu _{0}^{3}}}{{1 - {{\mu }_{0}}}} = \frac{1}{3}(1 + {{\mu }_{0}} + \mu _{0}^{2}),$

${{\alpha }_{k}} = \frac{1}{{3\chi }},\quad \chi = - \frac{S}{{\frac{{\partial U}}{{\partial t}}}} = \left\{ \begin{gathered} {{\chi }_{{\min }}}\quad {\text{при}}\quad 0 < ct \leqslant r - {{r}_{0}}, \hfill \\ {{\chi }_{0}}\quad {\text{при}}\quad r - {{r}_{0}} < ct < {{r}_{0}} + r, \hfill \\ {{\chi }_{{\min }}}\quad {\text{при}}\quad ct \geqslant {{r}_{0}} + r, \hfill \\ \end{gathered} \right.$

${{\chi }_{0}} = \frac{{1 - \mu _{0}^{2}}}{2}{{\left( {\frac{{\partial {{\mu }_{0}}}}{{\partial r}}} \right)}^{{ - 1}}} = \frac{{1 - \mu _{0}^{2}}}{2}{{\left( {\frac{1}{{ct}} - \frac{{{{\mu }_{0}}}}{r}} \right)}^{{ - 1}}} = \frac{r}{4}\frac{{{{{(2rct)}}^{2}} - {{{(r_{0}^{2} - {{r}^{2}} - {{c}^{2}}{{t}^{2}})}}^{2}}}}{{r_{0}^{2} + {{r}^{2}} - {{c}^{2}}{{t}^{2}}}}.$

Из этих формул видно, что 1/3 ≤ D ≤ 1, α_k > 0, χ > 0. Коэффициент χ₀ всегда неотрицателен при $ct \leqslant \frac{r}{{\left| {{{\mu }_{0}}} \right|}}$, то есть на интервале r – r₀ ≤ ct < r₀ + r выполняется χ₀ ≥ 0.

На фиг. 3 приведены профили коэффициентов КД и КП на один из моментов времени при ct = 1 см, r₀ = 2 см.

Фиг. 3.

Профили коэффициентов КД и КП в логарифмическом масштабе.

Из рисунка видно, что при данных предположениях коэффициент α_k всегда положительный и ограниченный, так как вне интервала 1 < r < 3 (r₀ – r < ct < r₀ + r) коэффициент k полагается равным 1/3χ_min. Коэффициент D положительный, непрерывный, но немонотонный и лежит в интервале [0.29, 1]. Коэффициент χ положительный, непрерывный и лежит в интервале [0, 1].

Задача 3. Рассматривается перенос излучения в слое r₀ < r < r₁, r₀ = 100 см, r₁ = 104 см. На радиусе r₀ задан односторонний входящий поток, определяемый по единичной температуре, на радиусе r₁ – условие свободной поверхности. Коэффициенты поглощения и рассеяния берутся в виде

${{\alpha }_{{s\nu }}} = 0,\quad {{\alpha }_{{c\nu }}} = {{\kappa }_{\nu }},\quad {\text{где}}\quad {{\kappa }_{\nu }} = \frac{{{{\kappa }_{0}}{{h}^{3}}(1 - {{e}^{{ - h\nu /T}}})}}{{{{\nu }^{3}}}},\quad {{k}_{0}} = \left[ \begin{gathered} 10\,000,\quad 102 \leqslant r \leqslant 102.4, \hfill \\ 27\quad {\text{в остальной области}}{\text{.}} \hfill \\ \end{gathered} \right.$

Из работы [11 ] следует, что температура для данной задачи в плоской геометрии имеет вид

$T = \sqrt[7]{{{{T}_{1}} - {{T}_{0}}(r - {{r}_{0}})}},$

где

${{Т}_{1}} = 1,\quad {{Т}_{0}} = 0.00659\quad {\text{при}}\quad r--{{r}_{0}} < 2\;{\text{см}};$

${{Т}_{1}} = 5.8683,\quad {{Т}_{0}} = 2.44\quad {\text{при}}\quad 2\;{\text{см}} \leqslant r--{{r}_{0}} \leqslant 2.4\;{\text{см}};$

${{Т}_{1}} = 0.02636,\quad {{Т}_{0}} = 0.00659\quad {\text{при}}\quad 2.4\;{\text{см}} < r--{{r}_{0}} < 4\;{\text{см}}.$

Это решение в плоской геометрии на достаточно большом радиусе (r > 100 см) можно использовать и для сферически-симметричных задач. Для корректирующих коэффициентов из формул (2.1)–(2.3) с учетом первых двух членов при разложениях в ряды получаем

${{D}_{\nu }} = \frac{{{{P}_{\nu }}}}{{{{U}_{\nu }}}} \approx \frac{1}{3}\frac{{{{B}_{\nu }} + \frac{3}{5}{{N}_{\nu }}}}{{{{B}_{\nu }} + \frac{1}{3}{{N}_{\nu }}}} = \frac{1}{3}\frac{{1 + \frac{3}{{5\kappa _{\nu }^{4}}}{{N}_{{1\nu }}}}}{{1 + \frac{1}{{3\kappa _{\nu }^{4}}}{{N}_{{1\nu }}}}},$

${{m}_{\nu }} = - \frac{{{{S}_{\nu }}}}{{\frac{1}{{3{{\kappa }_{\nu }}}}\frac{{\partial {{U}_{\nu }}}}{{\partial r}}}} \approx \frac{{\frac{\partial }{{\partial r}}\left\{ {{{B}_{\nu }} + \frac{3}{5}{{N}_{\nu }}} \right\}}}{{\frac{\partial }{{\partial r}}\left\{ {{{B}_{\nu }} + \frac{1}{5}{{N}_{\nu }}} \right\}}} = \frac{{1 - \frac{3}{{5\kappa _{\nu }^{4}}}{{N}_{{2\nu }}}}}{{1 - \frac{1}{{3\kappa _{\nu }^{4}}}{{N}_{{2\nu }}}}},$

${{\alpha }_{{\nu k}}} = {{\kappa }_{\nu }}\left( {\frac{1}{{{{m}_{\nu }}}} - 1} \right) \approx \frac{4}{{3\kappa _{\nu }^{3}}}\frac{{{{N}_{{2\nu }}}}}{{5 - 3\kappa _{\nu }^{{ - 4}}{{N}_{{2\nu }}}}},$

${{N}_{\nu }} = \frac{1}{{{{\kappa }_{\nu }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{\kappa }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}} \right) = \frac{{{{N}_{{1\nu }}}}}{{\kappa _{\nu }^{4}}}{{B}_{\nu }},\quad \frac{{\partial {{N}_{\nu }}}}{{\partial r}} = \frac{{{{N}_{{2\nu }}}}}{{\kappa _{\nu }^{4}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}},$

где

${{N}_{{1\nu }}} = [{{p}_{0}}{{\kappa }_{0}} + 2{{\kappa }_{\nu }}({{B}_{\nu }} - 4{{p}_{0}}T{{\varepsilon }^{2}})]\frac{{{{\kappa }_{0}}}}{{{{p}_{0}}{{\varepsilon }^{4}}{{T}^{{16}}}}}{{\left( {\frac{{{{T}_{0}}}}{7}} \right)}^{2}},\quad {{B}_{\nu }} = \frac{{{{p}_{0}}{{\varepsilon }^{3}}}}{{{{e}^{{\varepsilon /T}}} - 1}},\quad {{p}_{0}} = 100,\quad \varepsilon = h\nu ,$

${{N}_{{2\nu }}} = \left\{ {{{p}_{0}}\kappa _{0}^{2} + \left[ {6\left( {\frac{{{{B}_{\nu }}}}{{{{p}_{0}}}} - 8T{{\varepsilon }^{2}}} \right){{\kappa }_{\nu }} + 8{{\kappa }_{0}}} \right]{{\kappa }_{\nu }}{{B}_{\nu }} - 24{{\kappa }_{\nu }}{{p}_{0}}T{{\varepsilon }^{2}}({{\kappa }_{0}} - 5{{\varepsilon }^{2}}{{\kappa }_{\nu }}T)} \right\}\frac{1}{{{{p}_{0}}{{\varepsilon }^{4}}{{T}^{{16}}}}}{{\left( {\frac{{{{T}_{0}}}}{7}} \right)}^{2}},$

${{U}_{\nu }} = {{B}_{\nu }} - \frac{1}{{{{\kappa }_{\nu }}}}\frac{{\partial {{S}_{\nu }}}}{{\partial r}} \approx {{B}_{\nu }} + \frac{1}{3}{{N}_{\nu }} = \left( {1 + \frac{{{{N}_{{1\nu }}}}}{{3\kappa _{\nu }^{4}}}} \right){{B}_{\nu }},\quad {{S}_{\nu }} \approx \frac{1}{{3{{\kappa }_{\nu }}}}\frac{{\partial {{B}_{\nu }}}}{{\partial r}}.$

Из этих формул видно, что коэффициент D_ν > 0 при N_1ν ≥ 0, коэффициент m_ν > 0 при $\frac{{{{N}_{{2\nu }}}}}{{\kappa _{\nu }^{4}}} < \frac{5}{3}$, коэффициент α_νk ≥ 0 при $0 \leqslant \frac{{{{N}_{{2\nu }}}}}{{\kappa _{\nu }^{4}}} < \frac{5}{3}$. В реальной среде можно ослабить требование неотрицательности коэффициента ${{\alpha }_{{\nu k}}}$ и рассматривать выполнение условия ${{\alpha }_{{c\nu }}} + {{\alpha }_{{s\nu }}} + {{\alpha }_{{\nu k}}} \geqslant 0$. Этого условия достаточно для корректности диффузионного уравнения в приближении КП. Тогда из соотношения ${{\alpha }_{{\nu k}}} + {{\kappa }_{\nu }} = \frac{{{{\kappa }_{\nu }}}}{{{{\mu }_{\nu }}}}$ получаем, что условие ${{\alpha }_{{\nu k}}} + {{\kappa }_{\nu }} \geqslant 0$ выполняется при ${{\kappa }_{\nu }} \geqslant 0$ и ${{m}_{\nu }} > 0$.

Задачи Флека рассматривают на интервале энергий фотонов 0 < ε < 15 кэВ, поэтому на фиг. 4–7 приведены профили коэффициентов КП и КД для трех значений энергии фотонов из этого интервала ε = 0.15, 2.85, 13 кэВ.

Фиг. 4.

Профили коэффициентов D, m, α_k для энергии фотонов ε = 0.15 кэВ.

Фиг. 5.

Профили коэффициентов D, m, α_k для энергии фотонов ε = 2.85 кэВ.

Фиг. 6.

Профили коэффициентов D, m, α_k для энергии фотонов ε = 13 кэВ.

Фиг. 7.

Профили коэффициентов κ и κ + α_k для энергии ε = 13 кэВ.

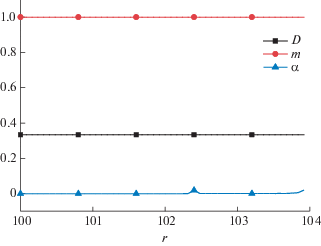
На фиг. 4 приведены профили коэффициентов D, m и α_k для энергии фотонов ε = 0.15 кэВ.

Из фигуры видно, что корректирующие коэффициенты D, m и α_k для энергии фотонов ε = = 0.15 кэВ имеют практически постоянные значения около величин D = 1/3, m = 1 и α_k = 0.

На фиг. 5 приведены профили коэффициентов D, m и α_k для энергии фотонов ε = 2.85 кэВ.

Из фигуры видно, что корректирующие коэффициенты D, m и α_k для энергии фотонов ε = = 2.85 кэВ являются ограниченными, но немонотонными функциями от r. Резкое изменение корректирующих коэффициентов на границе системы при r = 104 см и коэффициента α_k на интервале 102 см < r < 102.4 см может объясняться недостаточностью двух членов при разложениях решения в ряд. Хотя коэффициент α_k принимает отрицательные значения при r = 104 см, суммарный коэффициент κ + α_k положителен.

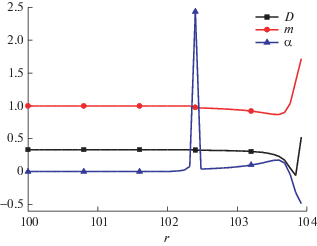
На фиг. 6 приведены профили коэффициентов D, m и α_k для энергии фотонов ε = 13 кэВ.

Из фигуры видно, что корректирующие коэффициенты D и m для энергии фотонов ε = 13 кэВ являются монотонными, положительными и ограниченными функциями от r. Коэффициент α_k является немонотонной, ограниченной и отрицательной на интервале 102 см < r < 102.4 см функцией. Несмотря на это, суммарный коэффициент κ + α_k везде положителен (см. фиг. 7).

На фиг. 7 приведены профили коэффициентов κ и κ + α_k для энергии фотонов ε = 13 кэВ.

Из фигуры видно, что, хотя коэффициент α_k является отрицательной функцией на интервале 102 см < r < 102.4 см, суммарный коэффициент κ + α_k является положительной и ограниченной функцией.

ЗАКЛЮЧЕНИЕ

В работе проведены исследование и сравнение корректирующих коэффициентов, которые используются в КД и КП приближениях. Рассмотрены свойства монотонности, положительности, непрерывности и ограниченности для этих коэффициентов на трех задачах, имеющих аналитические решения. В рассмотренных задачах получены аналитические формулы для корректирующих коэффициентов и показано, что коэффициенты D_ν, m_ν и α_c + α_k являются положительными функциями.

Доказана эквивалентность первого и второго вариантов КП приближения, позволяющая в первом варианте не использовать коэффициенты квазидиффузии.

Для оптически плотных сред получено асимптотическое представление корректирующих коэффициентов в КД и КП приближениях. Установлено, что в оптически плотных средах порядок сходимости коэффициентов D_ν и m_ν совпадает с порядком сходимости основных величин U_ν и P_ν к диффузионному пределу.

Исследования на стационарном решении в вакууме показали, что коэффициенты КД и КП являются монотонными, непрерывными и положительными функциями от r. Коэффициенты D и χ ограничены, а коэффициент α_k неограничен при r → 0.

Исследования на нестационарном решении в вакууме показали, что в областях, где коэффициенты КД и КП не определены, на них приходится вводить ограничения. Это позволяет сделать коэффициенты D и χ непрерывными и положительными функциями.

Исследования на стационарном решении в реальной среде показали, что коэффициенты D и m являются непрерывными, положительными и ограниченными функциями. Коэффициент α_k может быть отрицательным, но суммарный коэффициент α_c + α_k является положительной и ограниченной функцией.

Исследования, проведенные в данной работе на трех задачах, имеющих аналитические решения, показали, что коэффициенты КП, кроме α_k, являются положительными функциями. Отрицательность коэффициента α_k не нарушает корректность диффузионного уравнения в КП приближении. В оптически плотных средах коэффициенты КД и КП стремятся к постоянным величинам, в оптически прозрачных средах они имеют более сложный вид. Очевидно, что данные исследования не могут быть обобщены на весь класс решений СУПТИ, но они показывают, что в некоторых случаях использование корректирующих коэффициентов позволяет для численного решения кинетического уравнения использовать решение диффузионного уравнения.

Список литературы

Гольдин В.Я. Квазидиффузионный метод решения кинетического уравнения // Ж. вычисл. матем. и матем. физ. 1964. Т. 4. № 6. С. 1078–1087.
Карлыханов Н.Г., Козманов М.Ю. Учет кинетических эффектов в диффузионном приближении для расчета переноса излучения. ВАНТ. Сер. Матем. моделирование физ. процессов. 2010. № 4. С. 3–9.
Аристова Е.Н., Гольдин В.Я., Колпаков А.В. Перенос излучения через кольцевую щель в теле вращения // Матем. моделирование. 1997. Т. 9. № 4. С. 1–10.
Гаджиев А.Д., Завьялов В.В., Грабовенская С.А., Шестаков А.А. Применение TVD подхода к решению уравнения переноса теплового излучения квазидиффузионным методом. ВАНТ. Сер. Матем. моделирование физ. процессов. 2010. № 3. С. 3–14.
Fleck J.A., Cummings J.D. An implicit Monte-Carlo scheme for calculating time and frequency dependent nonlinear radiation transport // J. Comput. Phys. 1971. V. 8 (3). P. 313–342.
Завьялов В.В., Шестаков А.А. Упрощенные решения задач Флека. ВАНТ, Серия Матем. моделирование физ. процессов. 2013. № 1. С. 45–52.
Larsen E.W., Guido Thommes, Klar A., Sead M., Gotz T. Simplified PN approximations to the equations of radiative heat transfer and applications // J. Comput. Phys. 2002. V. 183. P. 652–675.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал